1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 87, № 6, 2023

Прикладная математика и механика, 2023, T. 87, № 6, стр. 970-983

Управление подавлением радиальных колебаний двухмассовой системы с одновременным ее раскручиванием

С. А. Васенин 1, *, С. А. Решмин 1, **

1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: stepan_vasenin@mail.ru
** E-mail: reshmin@ipmnet.ru

Поступила в редакцию 01.09.2023
После доработки 01.10.2023
Принята к публикации 10.10.2023

Полный текст (PDF)

Аннотация

Объектом исследования данной работы является двухмассовая управляемая механическая система, состоящая из несущего диска, вращающегося вокруг своей оси, закрепленной в пространстве, и несомого кольца, присоединенного к диску при помощи невесомых упругих элементов. Демпферов в системе нет. Процесс подавления радиальных колебаний рассматривается с позиции теории оптимального управления. На достаточно больших интервалах времени используется численный метод Ньютона для решения краевой задачи принципа максимума Понтрягина. Исследованы свойства фазовых траекторий системы в зависимости от начальных состояний диска и кольца и количества пружин в сложной модели упругого взаимодействия. Показано, как при некоторых начальных условиях и параметрах системы вследствие радиальности упругой силы и закона сохранения кинетического момента траектория центра масс кольца стремится к окружности. Указанная тенденция выхода на режим движения по окружности не является единой и зависит от количества пружин. Демонстрируется, что при малом количестве упругих элементов траектория кольца не принимает вид окружности, а происходит почти полное гашение радиальных колебаний. Установлено, что при рассматриваемых во время численного эксперимента параметрах системы управление является релейным с довольно большим количеством переключений. При этом происходит одновременное раскручивание всей системы.

Ключевые слова: релейное управление, принцип максимума, управляемое вращение, краевая задача, метод Ньютона, гашение колебаний

1. Введение. Процессы подавления колебаний и раскрутки механических систем присутствуют во многих технических устройствах. Важность исследования данных явлений обусловлена большим количеством механических объектов, которые напрямую или косвенно связаны с разными модификациями процессов раскрутки и вращения. В работе рассматривается модель колеса, состоящая из диска и кольца, соединенных между собой невесомыми упругими пружинами. Ставится задача о подавлении радиальных упругих колебаний (имеется в виду изменение расстояния между осями вращения диска и кольца) за счет изменения угла кручения между диском и кольцом. Закон управления формируется на основе соотношений принципа максимума Понтрягина [1] в соответствующей задаче оптимального управления с некоторым интегральным функционалом. Таким образом, речь идет о минимизации в некотором смысле амплитуды колебаний в течение всего процесса раскрутки (а не только в терминальный момент), связанной с энергией, закачиваемой в эту степень свободы. При численных экспериментах оказалось, что одновременно с этим удается обеспечить раскручивание системы до достаточно больших угловых скоростей. Для построения управления на большом интервале времени предлагается использовать метод Ньютона, часто применяющийся для решения соответствующей краевой задачи принципа максимума. В предыдущих работах [2, 3] предполагалось, что механическая система совершает движения при малых величинах отклонений центра масс кольца и модуля разности углов поворотов диска и кольца. В данном случае потенциальная энергия упругого взаимодействия была разложена в двумерный ряд Тейлора, что отражается на простоте полученных уравнений, описывающих движение двухмассовой системы. Отличием данной работы от предыдущих является рассмотрение более точной и сложной математической модели упругого взаимодействия при довольно больших колебаниях системы и разном количестве упругих элементов. Выбор численного метода Ньютона для решения краевой задачи принципа максимума Понтрягина обусловлен более простой реализацией на ЭВМ и быстрой сходимостью. Однако метод последовательных приближений [4, 5], использованный в предыдущих работах, также может быть успешно применен для решения задачи.

Установлено, что минимизация радиальных колебаний механической системы при выборе в качестве управления крутящего момента может быть проведена успешно. Однако в процессе раскрутки возрастает до довольно больших значений величина разности углов поворотов, что с физической точки зрения может привести к разрушению двухмассовой системы. Предполагается, что возможности прикладываемого к диску момента велики, так что в процессе управления угол крутильной деформации, т.е. разность углов вращения диска и кольца, может изменяться сколь угодно быстро в заданных пределах. Указанный угол кручения выбирается в качестве нового управления, которое гасит амплитуду радиальных колебаний. Выбором допустимого диапазона изменения управления (угла кручения) можно обеспечить дополнительно и требуемую раскрутку системы в целом.

Отметим, что существуют работы [6], численные методы расчета оптимального программного управления которых используют эволюционные алгоритмы, не основанные на решении краевой задачи принципа максимума. Решение краевой задачи принципа максимума Понтрягина проводилось в работах [7–16]. Приведена [17] задача граничного управления колебаниями двумерной пластины с целью полной остановки колебаний за конечное время. При этом на управляющие воздействия наложены ограничения на максимум абсолютной величины. Построение управления для механических систем как в данной задаче, у которых число степеней свободы превосходит размерность вектора обобщенных управляющих сил, было проведено в работе [18]. Рассматривается [19] возможный подход к осуществлению управления движением портального крана при перемещении груза. Предложено два различных метода отыскания управляющего ускорения, обеспечивающего гашение колебаний перемещаемого груза. Гашение колебаний нелинейного маятника проводилось в работе [20]. Получено [21] аналитическое оптимальное по энергии управление гармоническим осциллятором, причем задача рассматривалась на конечном интервале времени. Исследовалась [22] динамика механического изотропного стержневого упругого подвеса. Многомерные осцилляторы с нелинейным затуханием рассматривались в [23, 24].

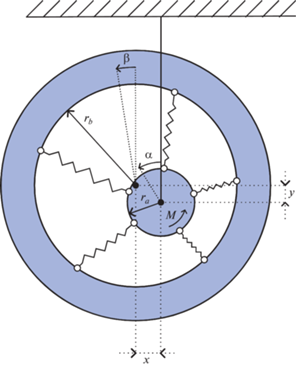
2. Описание механической системы и уравнения движения. Рассматривается управляемая механическая система, состоящая из диска и кольца, соединенных между собой при помощи невесомых предварительно растянутых пружин, концы которых не защемлены шарнирно-неподвижными опорами (рис. 1). Радиус диска равен ${{r}_{a}}$. Радиус внутренней полости кольца равен ${{r}_{b}}$. Углы поворотов диска и кольца обозначены соответственно через $\alpha $ и $\beta $. Оси вращения параллельны, причем ось вращения диска и его центр масс зафиксированы в пространстве. Положение центра масс кольца характеризуется относительными координатами $x,\;y$ в прямоугольной системе координат в плоскости, которая перпендикулярна осям вращения. Таким образом, при $x = 0$ и $y = 0$ оси вращения совпадают.

Рис. 1.

Двухмассовая система.

Упругое взаимодействие будем моделировать системой, состоящей из $N$ пружин жесткостью $k$, причем длина в свободном состоянии каждой из них равна ${{l}_{0}} < {{r}_{b}} - {{r}_{a}}$. Соответствующая внутренняя энергия каждой натянутой пружины в недеформированной системе подсчитывается по формуле:

(2.1)
${{E}_{0}} = \frac{k}{2}{{\left( {{{r}_{b}} - {{r}_{a}} - {{l}_{0}}} \right)}^{2}}$

Пусть теперь система деформировалась за счет смещения кольца $b$ на $x$ по горизонтали, на $y$ по вертикали, а диск $a$ совершил относительный поворот на угол $\varphi = \alpha - \beta $. Для $i$-й пружины запишем координаты конца, соединенного с диском:

(2.2)
${{x}_{{ai}}} = {{r}_{a}}\cos {{\gamma }_{i}},\quad {{y}_{{ai}}} = {{r}_{a}}\sin {{\gamma }_{i}};\quad {{\gamma }_{i}} = \frac{{2\pi i}}{N},\quad i = 1, \ldots ,N,$
и координаты конца, соединенного с кольцом:

(2.3)
${{x}_{{bi}}} = x + {{r}_{b}}\cos \left( {{{\gamma }_{i}} - \varphi } \right),\quad {{y}_{{bi}}} = y + {{r}_{b}}\sin \left( {{{\gamma }_{i}} - \varphi } \right);\quad i = 1, \ldots ,N$

Соответствующая энергия $i$-й пружины в деформированной системе подсчитывается по формуле:

(2.4)
${{E}_{i}} = \frac{k}{2}{{\left( {\sqrt {{{{\left( {{{x}_{{bi}}} - {{x}_{{ai}}}} \right)}}^{2}} + {{{\left( {{{y}_{{bi}}} - {{y}_{{ai}}}} \right)}}^{2}}} - {{l}_{0}}} \right)}^{2}}$

В результате запишем потенциальную энергию упругой деформации системы в виде:

(2.5)
${{\Pi }_{{{\text{tire}}}}} = \sum\limits_{i = 1}^N {{{E}_{i}}} - N{{E}_{0}}$

Учитывая выражение для кинетической энергии

(2.6)
$K = \frac{1}{2}\left[ {{{I}_{a}}{{{\dot {\alpha }}}^{2}} + {{I}_{b}}{{{\dot {\beta }}}^{2}} + {{m}_{b}}\left( {{{{\dot {x}}}^{2}} + {{{\dot {y}}}^{2}}} \right)} \right],$
составим Лагранжиан:

(2.7)
$L = \frac{1}{2}\left[ {{{I}_{a}}{{{\dot {\alpha }}}^{2}} + {{I}_{b}}{{{\dot {\beta }}}^{2}} + {{m}_{b}}\left( {{{{\dot {x}}}^{2}} + {{{\dot {y}}}^{2}}} \right)} \right] - \frac{k}{2}\sum\limits_{i = 1}^N {{{{\left( {{{l}_{i}} - {{l}_{0}}} \right)}}^{2}}} + N{{E}_{0}}$
(2.8)
${{l}_{i}} = \sqrt {{{{\left[ {{{r}_{b}}\cos \left( {{{\gamma }_{i}} - \alpha + \beta } \right) + x - {{r}_{a}}\cos {{\gamma }_{i}}} \right]}}^{2}} + {{{\left[ {{{r}_{b}}\sin \left( {{{\gamma }_{i}} - \alpha + \beta } \right) + y - {{r}_{a}}\sin {{\gamma }_{i}}} \right]}}^{2}}} $

Докажем, что суммы, указанные ниже, имеют следующую особенность:

(2.9)
$\sum\limits_{i = 1}^N {\cos {{\gamma }_{i}}} = 0,\quad \sum\limits_{i = 1}^N {\sin {{\gamma }_{i}}} = 0$

Рассмотрим сумму $\sum\nolimits_{i = 1}^N {{{e}^{{j{{\gamma }_{i}}}}}} $, где $j$ – мнимая единица, которая представляет собой геометрическую прогрессию, сумма которой равна:

(2.10)
${{S}_{N}} = \frac{{{{b}_{1}}\left( {1 - {{q}^{N}}} \right)}}{{1 - q}} = \frac{{{{e}^{{j{{\gamma }_{1}}}}}\left( {{{e}^{{j2\pi }}} - 1} \right)}}{{{{e}^{{j{{\gamma }_{1}}}}} - 1}},$
где ${{b}_{1}} = \exp \left( {j{{\gamma }_{1}}} \right)$ – первый член, $q = \exp \left( {j{{\gamma }_{1}}} \right)$ – знаменатель. Из полученной формулы (2.10) следует, что ${{S}_{N}} = 0$. Заменяя $j$ на $ - j$, аналогично доказываем равенство нулю суммы. Утверждение доказано.

Из выражений (2.9) можно получить аналогичными рассуждениями для $\forall \varphi $ следующий результат:

(2.11)
$\begin{gathered} \sum\limits_{i = 1}^N {\cos \left( {{{\gamma }_{i}} - \varphi } \right)} = 0,\quad \sum\limits_{i = 1}^N {\sin \left( {{{\gamma }_{i}} - \varphi } \right)} = 0 \\ \sum\limits_{i = 1}^N {\sin \left( {2{{\gamma }_{i}} - \varphi } \right)} = 0,\quad \sum\limits_{i = 1}^N {\sin 2\left( {{{\gamma }_{i}} - \varphi } \right)} = 0 \\ \end{gathered} $

Производные для получения уравнения для $\alpha $:

(2.12)
$\begin{gathered} \frac{{\partial L}}{{\partial{ \dot {\alpha }}}} = {{I}_{a}}\dot {\alpha },\quad \frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial{ \dot {\alpha }}}}} \right) = {{I}_{a}}\ddot {\alpha } \\ \frac{{\partial L}}{{\partial \alpha }} = - \sum\limits_{i = 1}^N {k\left( {1 - \frac{{{{l}_{0}}}}{{{{l}_{i}}}}} \right)} {{\delta }_{i}} = - k\sum\limits_{i = 1}^N {{{\delta }_{i}}} + k{{l}_{0}}\sum\limits_{i = 1}^N {\frac{{{{\delta }_{i}}}}{{{{l}_{i}}}}} \\ {{\delta }_{i}} = \left( {{{y}_{{bi}}} - y} \right)\left( {{{x}_{{bi}}} - {{x}_{{ai}}}} \right) - \left( {{{x}_{{bi}}} - x} \right)\left( {{{y}_{{bi}}} - {{y}_{{ai}}}} \right) \\ \end{gathered} $

Отметим, что в состоянии равновесия, когда $x = y = \varphi = 0$, выражение для ${{\delta }_{i}}$ представляет собой векторное произведение двух коллинеарных векторов $\left( {{{y}_{{ai}}},{{y}_{{bi}}}} \right)$ и $\left( {{{x}_{{ai}}},{{x}_{{bi}}}} \right)$. Поэтому в этом случае ${{\delta }_{i}} = 0$. Рассмотрим первую сумму в полученном выражении. Упростим данное выражение следующим образом:

(2.13)
$\begin{gathered} \sum\limits_{i = 1}^N {{{\delta }_{i}}} = \sum\limits_{i = 1}^N {\left[ {\frac{{r_{b}^{2}}}{2}\sin 2\left( {{{\gamma }_{i}} - \varphi } \right) + {{r}_{b}}\sin \left( {{{\gamma }_{i}} - \varphi } \right)x - \frac{{{{r}_{a}}{{r}_{b}}}}{2}\left( { - \sin \varphi + \sin \left( {2{{\gamma }_{i}} - \varphi } \right)} \right)} \right]} - \\ - \;\sum\limits_{i = 1}^N {\left[ {\frac{{r_{b}^{2}}}{2}\sin 2\left( {{{\gamma }_{i}} - \varphi } \right) + {{r}_{b}}\cos \left( {{{\gamma }_{i}} - \varphi } \right)y - \frac{{{{r}_{a}}{{r}_{b}}}}{2}\left( {\sin \varphi + \sin \left( {2{{\gamma }_{i}} - \varphi } \right)} \right)} \right]} = \\ = \sum\limits_{i = 1}^N {{{r}_{a}}{{r}_{b}}\sin \varphi = N{{r}_{a}}{{r}_{b}}\sin \varphi } \; \Rightarrow \;\frac{{\partial L}}{{\partial \alpha }} = - kN{{r}_{a}}{{r}_{b}}\sin \varphi + k{{l}_{0}}\sum\limits_{i = 1}^N {\frac{{{{\delta }_{i}}}}{{{{l}_{i}}}}} \\ \end{gathered} $

Аналогично полученным выражениям для $\alpha $ соотношения для $\beta $ имеют следующий вид:

(2.14)
$\frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial{ \dot {\beta }}}}} \right) = {{I}_{b}}\ddot {\beta },\quad \frac{{\partial L}}{{\partial \beta }} = \sum\limits_{i = 1}^N {k\left( {1 - \frac{{{{l}_{0}}}}{{{{l}_{i}}}}} \right)} {{\delta }_{i}} = kN{{r}_{a}}{{r}_{b}}\sin \varphi - k{{l}_{0}}\sum\limits_{i = 1}^N {\frac{{{{\delta }_{i}}}}{{{{l}_{i}}}}} $

Производные для получения уравнения для $x$:

(2.15)
$\frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial{ \dot {x}}}}} \right) = {{m}_{b}}\ddot {x},\quad \frac{{\partial L}}{{\partial x}} = - \sum\limits_{i = 1}^N {k\left( {1 - \frac{{{{l}_{0}}}}{{{{l}_{i}}}}} \right)} \left( {{{x}_{{bi}}} - {{x}_{{ai}}}} \right) = - kNx + k{{l}_{0}}\sum\limits_{i = 1}^N {\frac{{{{x}_{{bi}}} - {{x}_{{ai}}}}}{{{{l}_{i}}}}} $

Аналогично полученным выражениям для $x$ соотношения для $y$ имеют следующий вид:

(2.16)
$\frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial{ \dot {y}}}}} \right) = {{m}_{b}}\ddot {y},\quad \frac{{\partial L}}{{\partial y}} = - \sum\limits_{i = 1}^N {k\left( {1 - \frac{{{{l}_{0}}}}{{{{l}_{i}}}}} \right)} \left( {{{y}_{{bi}}} - {{y}_{{ai}}}} \right) = - kNy + k{{l}_{0}}\sum\limits_{i = 1}^N {\frac{{{{y}_{{bi}}} - {{y}_{{ai}}}}}{{{{l}_{i}}}}} $

Уравнения Лагранжа второго рода для описания движения механической системы имеют следующий вид:

(2.17)
$\begin{gathered} {{I}_{a}}\ddot {\alpha } + kN{{r}_{a}}{{r}_{b}}\sin \left( {\alpha - \beta } \right) - k{{l}_{0}}\sum\limits_{i = 1}^N {\frac{{{{\delta }_{i}}}}{{{{l}_{i}}}}} = M \\ {{I}_{b}}\ddot {\beta } - kN{{r}_{a}}{{r}_{b}}\sin \left( {\alpha - \beta } \right) + k{{l}_{0}}\sum\limits_{i = 1}^N {\frac{{{{\delta }_{i}}}}{{{{l}_{i}}}}} = 0 \\ {{m}_{b}}\ddot {x} + kNx - k{{l}_{0}}\sum\limits_{i = 1}^N {\frac{{{{x}_{{bi}}} - {{x}_{{ai}}}}}{{{{l}_{i}}}}} = 0,\quad {{m}_{b}}\ddot {y} + kNy - k{{l}_{0}}\sum\limits_{i = 1}^N {\frac{{{{y}_{{bi}}} - {{y}_{{ai}}}}}{{{{l}_{i}}}}} = 0 \\ \end{gathered} $

3. Постановка задачи управления. Предполагаем, что крутящий момент $M(t)$ может быть достаточно большим. Поэтому в качестве нового управления выбираем угол кручения и считаем, что он ограничен:

(3.1)
$u(t) = \varphi (t) = \alpha (t) - \beta (t);\quad 0 \leqslant u(t) \leqslant {{u}_{0}},$
где ${{u}_{0}}$ – заданная постоянная, которая должна быть достаточно мала. Функция $u(t)$ предполагается кусочно-непрерывной. Выберем интегральный функционал качества типа Лагранжа, соответствующий минимизации амплитуды радиальных колебаний системы в течение всего процесса:

(3.2)
$J = \int\limits_0^T {\left( {{{x}^{2}} + {{y}^{2}}} \right)} dt$

Так как функционал зависит только от $x$, $y$, а управлением является разность углов поворотов диска и кольца, то последние два уравнения системы (2.17) можно рассматривать отдельно от первых двух. Введем новые переменные: ${{{v}}_{x}}$ – скорость изменения координаты $x$, ${{{v}}_{y}}$ – скорость изменения координаты $y$. Перейдем к системе четырех уравнений первого порядка, описывающих двумерный осциллятор:

(3.3)
$\begin{gathered} \dot {x} = {{{v}}_{x}},\quad {{{{\dot {v}}}}_{x}} = - \frac{{kNx}}{{{{m}_{b}}}} + \frac{{k{{l}_{0}}}}{{{{m}_{b}}}}\sum\limits_{i = 1}^N {\frac{{{{x}_{{bi}}} - {{x}_{{ai}}}}}{{{{l}_{i}}}}} \quad \\ \dot {y} = {{{v}}_{y}},\quad {{{{\dot {v}}}}_{y}} = - \frac{{kNy}}{{{{m}_{b}}}} + \frac{{k{{l}_{0}}}}{{{{m}_{b}}}}\sum\limits_{i = 1}^N {\frac{{{{y}_{{bi}}} - {{y}_{{ai}}}}}{{{{l}_{i}}}}\,\,\,\,\,\,} \\ \end{gathered} $

Здесь в соответствии с (2.3), (2.8) зависимость правых частей от нового управления $u$ достаточно сложная и нелинейная:

${{x}_{{bi}}} = x + {{r}_{b}}\cos \left( {{{\gamma }_{i}} - u} \right),\quad {{y}_{{bi}}} = y + {{r}_{b}}\sin \left( {{{\gamma }_{i}} - u} \right)$
${{l}_{i}} = \sqrt {{{{\left( {{{x}_{{bi}}} - {{x}_{{ai}}}} \right)}}^{2}} + {{{\left( {{{y}_{{bi}}} - {{y}_{{ai}}}} \right)}}^{2}}} ;\quad i = 1, \ldots ,N,$
где величины ${{x}_{{ai}}}$, ${{y}_{{ai}}}$ не зависят от управления и заданы в (2.2). Системе (3.3) отвечают начальные условия:

(3.4)
$x\left( 0 \right) = {{x}_{0}},\quad {{{v}}_{x}}\left( 0 \right) = {{{v}}_{{x0}}},\quad y\left( 0 \right) = {{y}_{0}},\quad {{{v}}_{y}}\left( 0 \right) = {{{v}}_{{y0}}}$

Сформулируем задачу оптимального управления на конечном заданном интервале времени $t \in [0,T]$.

Задача. За счет выбора допустимого управления $u(t)$ требуется за время $T$ перевести систему (3.3) из заданного начального состояния (3.4) в произвольное терминальное состояние и минимизировать при этом функционал (3.2), т.е. уменьшить, насколько это возможно, радиальные колебания в процессе управления.

Далее будут составлены соотношения принципа максимума для поставленной задачи, на основе которых будут найдены численно соответствующие законы управления. Их оптимальность математически строго не обосновывается, так как принцип максимума является только необходимым условием оптимальности. Однако, их эффективность проверена.

Кроме того, результаты численного моделирования, приведенные далее, подтверждают, что неотрицательность управления (см. (3.1)) способствует постепенному раскручиванию исходной системы (2.17) до достаточно больших значений угловых скоростей $\dot {\beta }(T)$. Если в процессе решения задачи у построенного управления появятся точки разрыва, то в них соответствующий момент $M(t)$ окажется бесконечно большим. Данная проблема может быть успешно решена с помощью процедуры сглаживания [3].

4. Краевая задача принципа максимума. Введем вспомогательную переменную ${{x}_{0}}$ и перейдем к функционалу типа Майера:

(4.1)
$J = {{x}_{0}}\left( T \right),\quad {{\dot {x}}_{0}} = {{f}_{0}} = {{x}^{2}} + {{y}^{2}};\quad {{x}_{0}}\left( 0 \right) = 0$

Для составления соответствующей краевой задачи принципа максимума следует выполнить набор последовательных стандартных действий, а именно ввести сопряженные переменные, составить гамильтониан, выписать сопряженную систему, найти общий вид управления, максимизирующего гамильтониан в каждый момент времени, добавить начальные условия для основных переменных и граничные условия для сопряженных переменных на правом конце траектории (условия трансверсальности).

Введем соответствующие сопряженные переменные: ${{p}_{0}}\left( t \right)$, ${{p}_{1}}\left( t \right)$, ${{p}_{2}}\left( t \right)$, ${{p}_{3}}\left( t \right)$, ${{p}_{4}}\left( t \right)$, причем ${{p}_{0}}\left( t \right) = {\text{const}} = - 1$. Запишем гамильтониан:

(4.2)
$\begin{gathered} H = \left( {p,f} \right) = - {{x}^{2}} - {{y}^{2}} + {{p}_{1}}{{{v}}_{x}} + {{p}_{2}}\left( {\frac{{k{{l}_{0}}}}{{{{m}_{b}}}}\sum\limits_{i = 1}^N {\frac{{{{x}_{{bi}}} - {{x}_{{ai}}}}}{{{{l}_{i}}}} - \frac{{kNx}}{{{{m}_{b}}}}} } \right) + \\ + \;{{p}_{3}}{{{v}}_{y}} + {{p}_{4}}\left( {\frac{{k{{l}_{0}}}}{{{{m}_{b}}}}\sum\limits_{i = 1}^N {\frac{{{{y}_{{bi}}} - {{y}_{{ai}}}}}{{{{l}_{i}}}}} - \frac{{kNy}}{{{{m}_{b}}}}} \right) \\ \end{gathered} $

Здесь в скалярном произведении $p$ – вектор сопряженных переменных, $f$ – вектор-функция, у которой компоненты с ненулевым индексом задают правую часть системы. Сопряженная система имеет вид:

(4.3)
$\begin{gathered} {{{\dot {p}}}_{1}} = - \frac{{\partial H}}{{\partial x}} = 2x + {{p}_{2}}\frac{{kN}}{{{{m}_{b}}}} - {{p}_{2}}\frac{{k{{l}_{0}}}}{{{{m}_{b}}}}\sum\limits_{i = 1}^N {\frac{{{{{\left( {{{y}_{{bi}}} - {{y}_{{ai}}}} \right)}}^{2}}}}{{{{l}_{i}}^{3}}}} + {{p}_{4}}\frac{{k{{l}_{0}}}}{{{{m}_{b}}}}\sum\limits_{i = 1}^N {\frac{{\left( {{{x}_{{bi}}} - {{x}_{{ai}}}} \right)\left( {{{y}_{{bi}}} - {{y}_{{ai}}}} \right)}}{{{{l}_{i}}^{3}}}} \\ {{{\dot {p}}}_{3}} = - \frac{{\partial H}}{{\partial y}} = 2y + {{p}_{4}}\frac{{kN}}{{{{m}_{b}}}} + {{p}_{2}}\frac{{k{{l}_{0}}}}{{{{m}_{b}}}}\sum\limits_{i = 1}^N {\frac{{\left( {{{x}_{{bi}}} - {{x}_{{ai}}}} \right)\left( {{{y}_{{bi}}} - {{y}_{{ai}}}} \right)}}{{{{l}_{i}}^{3}}}} - {{p}_{4}}\frac{{k{{l}_{0}}}}{{{{m}_{b}}}}\sum\limits_{i = 1}^N {\frac{{{{{\left( {{{x}_{{bi}}} - {{x}_{{ai}}}} \right)}}^{2}}}}{{{{l}_{i}}^{3}}}} \\ {{{\dot {p}}}_{2}} = - \frac{{\partial H}}{{\partial {{{v}}_{x}}}} = - {{p}_{1}},\quad {{{\dot {p}}}_{4}} = - \frac{{\partial H}}{{\partial {{{v}}_{y}}}} = - {{p}_{3}} \\ \end{gathered} $

Граничные условия (условия трансверсальности) для системы (4.3) заданы на правом конце траектории:

(4.4)
${{p}_{1}}\left( T \right) = 0,\quad {{p}_{2}}\left( T \right) = 0,\quad {{p}_{3}}\left( T \right) = 0,\quad {{p}_{4}}\left( T \right) = 0$

Исследуемая система нелинейна по управлению $u$. Однако, при численных расчетах, представленных далее, максимальное значение гамильтониана в зависимости от управления достигалось только в граничных значениях управления. Это означает, что выражение для определения управления, доставляющего максимум гамильтониану при выбранных параметрах системы, можно записать следующим образом:

(4.5)
$u = \mathop {\arg \max }\limits_u H\left( {t,x\left( t \right),p\left( t \right),u} \right) = \left\{ \begin{gathered} 0,\quad H\left( {t,x\left( t \right),p\left( t \right),0} \right) > H\left( {t,x\left( t \right),p\left( t \right),{{u}_{0}}} \right) \\ {{u}_{0}},\quad H\left( {t,x\left( t \right),p\left( t \right),0} \right) \leqslant H\left( {t,x\left( t \right),p\left( t \right),{{u}_{0}}} \right) \\ \end{gathered} \right.$

Дополнительная численная проверка отсутствия максимума гамильтониана при промежуточных значениях управления также выполнялась.

5. Методика применения метода Ньютона. Для построения оптимального управления или экстремалей на основе составленных соотношений принципа максимума (3.3), (3.4), (4.3)–(4.5) будем численно решать их с использованием метода Ньютона в комбинации с методом “пристрелки”.

Начальные значения сопряженных переменных считаются варьируемыми параметрами. Исходная система интегрируется совместно с сопряженной системой в прямом времени при управлении, максимизирующем гамильтониан в каждый момент времени. Цель – обеспечить выполнение условий трансверсальности на правом конце траектории. Задача рассматривается формально как задача решения системы нескольких уравнений, заданных неявно. Число уравнений равно числу варьируемых параметров. Для выбора варьируемых параметров на следующей итерации и обеспечения сходимости к искомому решению используется метод Ньютона:

(5.1)
$\begin{gathered} z = \left( {{{p}_{1}}\left( 0 \right), \ldots ,{{p}_{n}}\left( 0 \right)} \right),\quad F\left( z \right) = 0,\quad F = \left( {{{F}_{1}}, \ldots ,{{F}_{n}}} \right) \\ {{z}^{{k + 1}}} = {{z}^{k}} - {{W}^{{ - 1}}}F,\quad W = \frac{{\partial {{F}_{i}}}}{{\partial {{z}_{j}}}};\quad i,j = 1, \ldots ,n, \\ \end{gathered} $
где $z$ – вектор начальных значений сопряженных переменных, $F(z)$ – вектор-функция из условий трансверсальности на правом конце, $W$ – матрица Якоби. Так как условия трансверсальности на правом конце явно не зависят от начальных значений сопряженных переменных, то для определения матрицы Якоби будем использовать выражение:

(5.2)
$W = \frac{{\partial {{F}_{i}}}}{{\partial {{z}_{j}}}} \approx \frac{{{{F}_{i}}\left( {{{z}_{1}},{{z}_{2}}, \ldots ,{{z}_{j}} + {{\Delta }_{j}}, \ldots ,{{z}_{n}}} \right) - {{F}_{i}}\left( {{{z}_{1}},{{z}_{2}}, \ldots ,{{z}_{j}}, \ldots ,{{z}_{n}}} \right)}}{{{{\Delta }_{j}}}}$

Процесс итераций заканчивается, когда будут выполнены условия трансверсальности на правом конце.

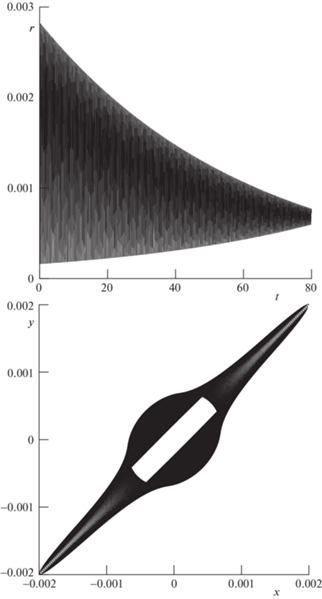
6. Численное построение экстремалей. В данном разделе представлены результаты расчетов системы при раскручивании системы управлением, полученным из соотношений принципа максимума. Была проведена серия расчетов при разных количествах упругих элементов, соединяющих диск и кольцо. Рассмотрена динамика системы как при малых, так и при больших отклонениях.

Расчет 1. При расчете были использованы следующие параметры системы с ненулевой начальной угловой скоростью и ненулевым начальным отклонением:

${{m}_{a}} = 1\;{\text{кг,}}\quad {{m}_{b}} = 1\;{\text{кг,}}\quad {{r}_{a}} = 0.621\;{\text{м}},\quad {{r}_{a}} = 0.644\;{\text{м}}$
${{I}_{a}} = 0.193\;{\text{кг}}\;{{{\text{м}}}^{2}},\quad {{I}_{b}} = 0.208\;{\text{кг}}\;{{{\text{м}}}^{2}},\quad k = 10\;\frac{{\text{Н}}}{{\text{м}}},\quad {{l}_{0}} = 0.012\;{\text{м}}$
$N = 10,\quad T = 80\;{\text{c}},\quad {{u}_{0}} = 0.01\;{\text{рад}}$
$x\left( 0 \right) = 0.002\;{\text{м}},\quad {{{v}}_{x}}\left( 0 \right) = - 0.001\;\frac{{\text{м}}}{{\text{с}}},\quad y\left( 0 \right) = 0.002\;{\text{м}},\quad {{{v}}_{y}}\left( 0 \right) = 0.001\;\frac{{\text{м}}}{{\text{с}}}$

Численным методом Ньютона было получено управление, успешно уменьшающее амплитуду радиальных колебаний механической системы. На рис. 2 представлены результаты численного моделирования. Обнаружено, что воздействие оптимального управления на механическую систему имеет приблизительно периодический характер с примерным периодом $\tau = 0.36\;{\text{c}}$. Сопряженные переменные ${{p}_{1}}$, ${{p}_{2}}$, ${{p}_{3}}$, ${{p}_{4}}$ сначала колеблются с убывающей амплитудой, а потом, когда колебания полностью пропадают, принимают нулевое терминальное значение. В конце процесса раскручивания угол и угловая скорость кольца приняли приблизительно следующие значения: $\beta = 1596\;{\text{рад}}$, $\dot {\beta } = 40\;\frac{{{\text{рад}}}}{{\text{с}}}$. Относительное изменение значения гамильтониана в течение процесса движения составляет 0.00008%, что свидетельствует о правильности и точности проделанных вычислений.

Рис. 2.

Результаты численного моделирования расчета 1 (малые колебания, большое количество пружин).

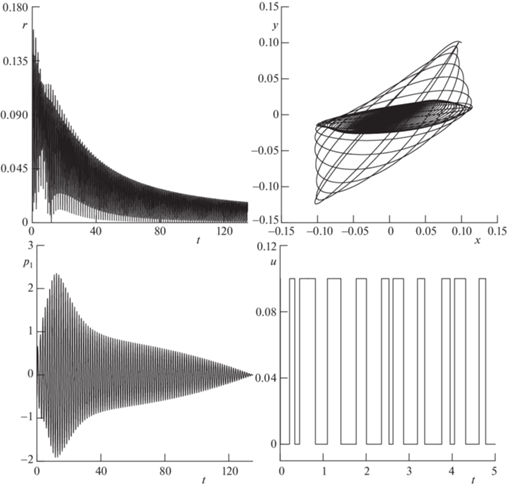
Расчет 2. При расчете были использованы следующие параметры системы с ненулевой начальной угловой скоростью и ненулевым начальным отклонением:

${{m}_{a}} = 1\;{\text{кг,}}\quad {{m}_{b}} = 1\;{\text{кг,}}\quad {{r}_{a}} = 0.055\;{\text{м}},\quad {{r}_{a}} = 0.21\;{\text{м}}$
${{I}_{a}} = 0.0015\;{\text{кг}}\;{{{\text{м}}}^{2}},\quad {{I}_{b}} = 0.0220\;{\text{кг}}\;{{{\text{м}}}^{2}},\quad k = 10\;\frac{{\text{Н}}}{{\text{м}}},\quad {{l}_{0}} = 0.1\;{\text{м}}$
$N = 3,\quad T = 135\;{\text{c}},\quad {{u}_{0}} = 0.1\;{\text{рад}}$
$x\left( 0 \right) = 0.1\;{\text{м}},\quad {{{v}}_{x}}\left( 0 \right) = - 0.1\;\frac{{\text{м}}}{{\text{с}}},\quad y\left( 0 \right) = 0.1\;{\text{м}},\quad {{{v}}_{y}}\left( 0 \right) = 0.1\;\frac{{\text{м}}}{{\text{с}}}$

Численным методом Ньютона было получено управление, успешно уменьшающее амплитуду радиальных колебаний механической системы. На рис. 3 представлены результаты численного моделирования. На графике для оптимального управления демонстрируется нетривиальный алгоритм переключения. Сложный характер поведения в течение всего процесса движения, следующий из расхождения скоростей убывания амплитуд колебаний $x$, ${{{v}}_{x}}$, $y$, ${{{v}}_{y}}$, наблюдается и для сопряженных переменных ${{p}_{1}}$, ${{p}_{2}}$, ${{p}_{3}}$, ${{p}_{4}}$. В конце процесса раскручивания угол и угловая скорость кольца приняли приблизительно следующие значения: $\beta = 2673\;{\text{рад}}$, $\dot {\beta } = 38\;\frac{{{\text{рад}}}}{{\text{с}}}$. Относительное изменение значения гамильтониана в течение процесса движения составляет 0.0001%, что свидетельствует о правильности и точности проделанных вычислений.

Рис. 3.

Результаты численного моделирования расчета 2 (конечные колебания, малое количество пружин).

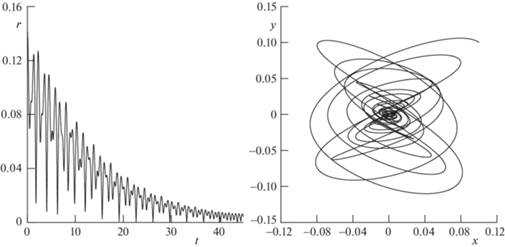
Расчет 3. При расчете были использованы следующие параметры системы с ненулевой начальной угловой скоростью и ненулевым начальным отклонением:

${{m}_{a}} = 1\;{\text{кг,}}\quad {{m}_{b}} = 1\;{\text{кг,}}\quad {{r}_{a}} = 0.055\;{\text{м}},\quad {{r}_{a}} = 0.21\;{\text{м}}$
${{I}_{a}} = 0.0015\;{\text{кг}}\;{{{\text{м}}}^{2}},\quad {{I}_{b}} = 0.0220\;{\text{кг}}\;{{{\text{м}}}^{2}},\quad k = 10\;\frac{{\text{Н}}}{{\text{м}}},\quad {{l}_{0}} = 0.1\;{\text{м}}$
$N = 2,\quad T = 45\;{\text{c}},\quad {{u}_{0}} = 0.1\;{\text{рад}}$
$x\left( 0 \right) = 0.1\;{\text{м}},\quad {{{v}}_{x}}\left( 0 \right) = - 0.1\;\frac{{\text{м}}}{{\text{с}}},\quad y\left( 0 \right) = 0.1\;{\text{м}},\quad {{{v}}_{y}}\left( 0 \right) = 0.1\;\frac{{\text{м}}}{{\text{с}}}$

Численным методом Ньютона было получено управление, успешно уменьшающее амплитуду радиальных колебаний механической системы. На рис. 4 представлены результаты численного моделирования. Установлено, что, в отличие от второго расчета, оптимальное управление стремится к периодической форме. Сопряженные переменные ${{p}_{1}}$, ${{p}_{2}}$, ${{p}_{3}}$, ${{p}_{4}}$ сначала колеблются с убывающей амплитудой, а потом, когда колебания полностью пропадают, принимают нулевое терминальное значение. В конце процесса раскручивания угол и угловая скорость кольца приняли приблизительно следующие значения: $\beta = 259\;{\text{рад}}$, $\dot {\beta } = 10\;{\text{рад/с}}$. Относительное изменение значения гамильтониана в течение процесса движения составляет 0.00005%, что свидетельствует о правильности и точности проделанных вычислений.

Рис. 4.

Результаты численного моделирования расчета 3 (конечные колебания, малое количество пружин).

Заключение. В работе рассмотрена задача об оптимальном гашении радиальных колебаний в упругой двухмассовой системе, состоящей из диска и кольца, соединенных пружинами, при ограничениях на управляющее воздействие (угол кручения). Такая задача сводится к управлению колебаниями соответствующего двумерного осциллятора. Оказалось, что закон изменения угла кручения, полученный из соотношений принципа максимума, при выбранных параметрах системы имеет релейный вид с большим количеством переключений. При этом также продемонстрировано, что одновременно может возникать режим раскрутки механической системы, причем как при малом, так и при достаточно большом количестве пружин. Показано, что с увеличением количества пружин в механической системе при неизменности остальных параметров возрастает время гашения колебаний, а в некоторых случаях траектория центра масс кольца стремится к окружности. Стремление траектории центра масс кольца к окружности при достаточно большом количестве упругих элементов следует из радиальности упругой силы. Отметим, что поведение механической системы при малых колебаниях совпало с поведением системы в упрощенной математической модели упругого взаимодействия в работах [2, 3], что показывает правильность проделанного исследования. Планируется использовать данную математическую модель для анализа раскручивания системы при контакте кольца с поверхностью, наличием трения и внутреннего демпфирования. Результаты будут применяться для исследования нежелательного эффекта потери силы тяги транспортного средства во время интенсивного старта [25].

Работа выполнена при финансовой поддержке РНФ (проект № 23-11-00128), https://rscf.ru/project/23-11-00128/.

Список литературы

  1. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1983. 392 с.

  2. Решмин С.А., Васенин С.А. Применение метода последовательных приближений при решении краевых задач принципа максимума на примере задачи управления раскручиванием двухмассовой системы // Modern Europ. Res. 2022. № 3 (Т. 1). С. 186–196.

  3. Васенин С.А., Решмин С.А. Оптимальное подавление колебаний в задаче раскручивания двухмассовой системы // Изв. РАН. ТиСУ. 2023. № 6. C. 67–80.

  4. Крылов И.А., Черноусько Ф.Л. О методе последовательных приближений для решения задач оптимального управления // ЖВММФ. 1962. Т. 2. № 6. С. 1132–1139.

  5. Черноусько Ф.Л., Баничук Н.В. Вариационные задачи механики и управления. М.: Наука, 1973. 238 с.

  6. Дивеев А.И., Шмалько Е.Ю., Рындин Д.А. Решение задачи оптимального управления группой роботов эволюционными алгоритмами // Информ. и матем. технол. в науке и управл. 2017. № 3 (7). С. 109–121.

  7. Черноусько Ф.Л. Оптимальное управление движением двухмассовой системы // Докл. РАН. 2018. Т. 480. № 5. С. 528–532.

  8. Левский М.В. Оптимальное управление кинетическим моментом во время пространственного разворота твердого тела (космического аппарата) // Изв. РАН. МТТ. 2019. № 1. С. 115–140.

  9. Шматков А.М. Периодические решения задачи оптимального управления поворотом твердого тела с помощью внутренней массы // Вестн. МГУ. Сер. 1: Математика. Механика. 2020. № 3. С. 63–67.

  10. Акуленко Л.Д., Костин Г.В. Оптимальное по быстродействию управление в системе третьего порядка с несимметричными ограничениями // Докл. РАН. 2000. Т. 372. № 2. С. 169–173.

  11. Стрелкова Н.А. Об управлении одной системой второго порядка в сопротивляющейся среде // Вестн. Пермского ун-та. Математика. Механика. Информатика. 2015. № 3 (30). С. 46–51.

  12. Григоренко Н.Л., Хайлов Е.Н., Григорьева Э.В., Клименкова А.Д. Модель конкуренции Лотки–Вольтерры с немонотонной функцией терапии для нахождения оптимальных стратегий лечения раковых заболеваний крови // Тр. Ин-та математики и механики УрО РАН. 2021. Т. 27. № 2. С. 79–98.

  13. Глазков Т.В., Решмин С.А. Оптимальное раскручивание колесного диска в составе двухмассовой модели // Инж. ж.: Наука и инновации. 2022. № 5. С. 45–51.

  14. Решмин С.А., Черноусько Ф.Л. Оптимальный по быстродействию синтез управления нелинейным маятником // Изв. РАН. ТиСУ. 2007. № 1. С. 13–22.

  15. Шматков А.М. Влияние габаритов управляемого устройства на оптимальный по быстродействию поворот с помощью подвижной внутренней массы // Докл. РАН. 2019. Т. 486. № 3. С. 292–296.

  16. Розенблат Г.М. Об оптимальном повороте твердого тела при помощи внутренних сил // Докл. РАН. 2022. Т. 505. № 1. С. 92–99.

  17. Романов И.В., Шамаев А.С. Гашение колебаний тонкой пластины ограниченным воздействием, приложенным к границе // Изв. РАН. ТиСУ. 2020. № 3. С. 64–74.

  18. Ананьевский И.М., Анохин Н.В. Управление пространственным движением многозвенного перевернутого маятника с помощью момента, приложенного к первому звену // ПММ. 2014. Т. 78. № 6. С. 755–765.

  19. Шугайло Т.С. Управление движением козлового крана с грузом заданием ускорения // Вестн. С.-Петербургского ун-та. Математика. Механика. Астрономия. 2020. Т. 7. № 1. С. 154–164.

  20. Решмин С.А. Поиск главного бифуркационного значения максимального управляющего момента в задаче синтеза оптимального управления маятником // Изв. РАН. ТиСУ. 2008. № 2. С. 5–20.

  21. Галяев А.А., Лысенко П.В. Оптимальное по энергии управление гармоническим осциллятором // АиТ. 2019. № 1. С. 21–37.

  22. Привалов Е.А., Жбанов Ю.К. Стержневая конструкция упругого подвеса инертной массы // Изв. РАН. МТТ. 2018. № 5. С. 19–28.

  23. Журавлев В.Ф. Двумерный осциллятор Ван дер Поля с внешним управлением // Нелин. динам. 2016. Т. 12. № 2. С. 211–222.

  24. Журавлев В.Ф. Пространственный осциллятор Ван дер Поля. Технические приложения // Изв. РАН. МТТ. 2020. № 1. С. 158–164.

  25. Решмин С.А. Качественный анализ нежелательного эффекта потери силы тяги транспортного средства во время интенсивного старта // Докл. РАН. 2019. Т. 484. № 3. С. 289–293.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал