Прикладная математика и механика, 2023, T. 87, № 6, стр. 954-969
К задаче об оптимальном повороте твердого тела при помощи внутренних сил
Г. М. Розенблат 1, *, С. А. Решмин 2, **
1 Московский автомобильно-дорожный государственный технический университет (МАДИ)
Москва, Россия
2 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: gr51@mail.ru
** E-mail: reshmin@ipmnet.ru
Поступила в редакцию 23.09.2023
После доработки 10.10.2023
Принята к публикации 15.10.2023
- EDN: GHQIGD
- DOI: 10.31857/S0032823523060085
Аннотация
В статье получены результаты, касающиеся численно-аналитического решения задачи о максимальном повороте твердого тела на заданном интервале времени путем перемещения подвижной внутренней массы. Движения массы реализуются при помощи приложения ограниченной силы. Ранее рассматривались аналогичные задачи, в которых перемещения внутренней массы предполагались кинематическими с ограничениями на скорость точки. Полученный аналитический результат описывается простыми и легко проверяемыми формулами. Оптимальная траектория подвижной внутренней массы является спиралью, которая накручивается на центр масс самого твердого тела с возрастающей до бесконечности частотой. Полученные численные результаты касаются построения иных оптимальных траекторий, которые не поддаются аналитическому исследованию.
1. Введение. Рассматривается задача о максимальном угле поворота за заданное время плоского твердого тела при помощи ограниченных внутренних сил, реализуемых в процессе движения внутренней точечной массы.
Более точная постановка задачи следующая. Рассматривается плоское твердое тело, которое может совершать плоское движение и на которое не действуют никакие внешние силы. Внутри этого тела имеет возможность двигаться (в плоскости тела при помощи актюаторов) материальная точка. Перемещение точки осуществляется посредством управляющей внутренней силы, которая ограничена по модулю и может быть ориентирована в произвольном направлении в плоскости движения системы. На координаты и скорости точки (относительно твердого тела) не накладываются никакие ограничения (кроме условий дифференцируемости). Требуется выбрать такой допустимый закон изменения управляющей силы, чтобы повернуть тело на максимальный угол за заданное время.
Ранее, подобного рода модели (твердое плоское тело, взаимодействующее с подвижной внутренней массой) рассматривались в качестве примеров, иллюстрирующих закон сохранения кинетического момента системы материальных точек (см., напр., ([1], разд. 333, стр. 38), ([2], задача 45, стр. 226)). Отметим, однако, что движение подвижной массы (насекомого, по терминологии Аппеля [1]) рассматривалось с кинематической точки зрения, т.е., относительная скорость подвижной массы считалась заданной функцией времени (в частности, постоянной). В учебнике [2] ситуация аналогичная. При формулировке таких задач указывалось, что система “тело + точка” в начальный момент находилась в покое, а затем, в момент $t = 0$, точка начинала двигаться с некоторой постоянной относительной скоростью ${v} = {{{v}}_{0}}$. Ясно, что переход точки из состояния ${v} = 0$ в состояние ${v} = {{{v}}_{0}}$ не может произойти мгновенно и реализуется при помощи приложения к точке некоторой ограниченной силы. Это обстоятельство приводит к необходимости определенной коррекции как формулировок, так и полученных в [1, 2] ответов к указанным задачам.
В настоящее время аналогичные модели рассматриваются для исследования управляемых робототехнических устройств, предназначенных для перемещения тел при помощи подвижных внутренних масс (см., напр. [3–5] и [6]). В частности рассматриваются кинематические перемещения внутренних масс, для которых управлением является вектор скорости, реализующий необходимое оптимальное перемещение объекта (капсюльного робота).
В настоящей работе, рассмотренные выше модели применяются для оптимального поворота объекта при помощи подвижной внутренней массы, перемещение которой осуществляется ограниченной по модулю управляющей силой (см. также [7, 8]).
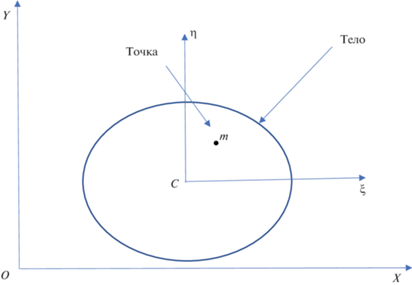
2. Описание модели, уравнения движения и постановка задачи. На рис. 1 изображено сечение твердого тела, центр масс которого находится в точке C. $Oxy$ – неподвижная система координат, $C\xi \eta $ – подвижная поступательная система координат, связанная с центром масс тела. Предполагаем, что оси этих систем координат все время параллельны друг другу. Внутри тела находится материальная точка m, которая имеет возможность двигаться посредством приложения внутренней силы $F = {{\left( {{{F}_{x}},{{F}_{y}}} \right)}^{T}}$. Для модуля силы F должно соблюдаться следующее ограничение
Пусть m – масса точки m, $M,J$ – масса тела и его момент инерции относительно центра масс C соответственно. Обозначим:
${{x}_{C}},{{y}_{C}}$ – координаты центра масс C тела в системе координат $Oxy$;
$\varphi $ – угол поворота тела относительно неподвижной системы координат $Oxy$;
$\xi ,\eta $ – координаты точки $m$ относительно подвижной системы $C\xi \eta $.
Учитывая, что при приложении к подвижной точке $m$ силы $F$, на тело в той же точке пространства действует сила $F{\kern 1pt} ' = - F$ (согласно третьему закону Ньютона), запишем уравнения движения центра масс и уравнение кинетического момента тела относительно его центра масс:
(2.2)
$M{{\ddot {x}}_{C}} = - {{F}_{x}},\quad M{{\ddot {y}}_{C}} = - {{F}_{y}},\quad J\ddot {\varphi } = \eta {{F}_{x}} - \xi {{F}_{y}}$Движение точки $m$ определяется уравнениями второго закона Ньютона
(2.3)
$m\left( {{{{\ddot {x}}}_{C}} + \ddot {\xi }} \right) = {{F}_{x}},\quad m\left( {{{{\ddot {y}}}_{C}} + \ddot {\eta }} \right) = {{F}_{y}}$Из (2.2) и (2.3) получим три уравнения
(2.4)
$\ddot {\xi } = \lambda {{F}_{x}},\quad \ddot {\eta } = \lambda {{F}_{y}},\quad \ddot {\varphi } = \mu (\ddot {\xi }\eta - \ddot {\eta }\xi );\quad \lambda = \frac{{M + m}}{{Mm}},\quad \mu = \frac{1}{{\lambda J}}$Далее, для упрощения записи, будем полагать ${{F}_{0}}$, $\lambda $, μ равными единице.
Третье уравнение в системе (2.4) можно проинтегрировать. Предполагая $\dot {\varphi }(0) = 0$, окончательно получаем следующую систему дифференциальных уравнений
(2.5)
$\begin{gathered} \ddot {\xi } = {{F}_{x}},\quad \ddot {\eta } = {{F}_{y}},\quad \dot {\varphi } = \dot {\xi }\eta - \dot {\eta }\xi + C \\ C = - \dot {\xi }(0)\eta (0) + \xi (0)\dot {\eta }(0) \\ \end{gathered} $В правой части полученного третьего уравнения в системе (2.5) добавлена константа $C = - \dot {\xi }(0)\eta (0) + \xi (0)\dot {\eta }(0)$, чтобы обеспечить выполнение условия $\dot {\varphi }(0) = 0$. Однако, нетрудно показать, что эту константу, при решении рассматриваемой оптимальной задачи, можно опустить без ограничения общности.
Систему (2.5) перепишем в стандартной форме системы Коши, вводя обозначения
(2.6)
${{x}_{1}} = \xi ,\quad {{x}_{2}} = \eta ,\quad {{x}_{3}} = \dot {\xi },\quad {{x}_{4}} = \dot {\eta },\quad {{x}_{5}} = \varphi $Получаем систему дифференциальных уравнений в стандартной форме
(2.7)
${{\dot {x}}_{1}} = {{x}_{3}},\quad {{\dot {x}}_{2}} = {{x}_{4}},\quad {{\dot {x}}_{3}} = {{F}_{x}},\quad {{\dot {x}}_{4}} = {{F}_{y}},\quad {{\dot {x}}_{5}} = {{x}_{2}}{{x}_{3}} - {{x}_{1}}{{x}_{4}}$Для системы (2.7) ставится следующая задача оптимального управления.
Пусть заданы начальные условия ${{x}_{i}}(0) = {{x}_{{i0}}}$ ${\text{(}}i = 1,5)$ и время $t = T$. Требуется определить такой закон изменения управляющих сил ${{F}_{x}},{{F}_{y}}$, которые удовлетворяют ограничениям (2.1) и обеспечивают $\max {{x}_{5}}(T)$ = $max\varphi (T)$.
В классической формулировке задачи Понтрягина последнее условие максимума можно заменить следующим
3. Основные уравнения принципа максимума и формулировка результата. Здесь приведены дифференциальные уравнения принципа максимума Понтрягина для рассматриваемой оптимальной задачи и излагается полученный результат.
В соответствии с принципом максимума Понтрягина [9], вводим сопряженные переменные ${{p}_{k}}$ $(k = 1,5)$, соответствующие фазовым переменным из (2.6), и гамильтониан $H$ для исходной системы дифференциальных уравнений (2.7) по формуле
(3.1)
$H = {{p}_{1}}{{x}_{3}} + {{p}_{2}}{{x}_{4}} + ({{p}_{3}}{{F}_{x}} + {{p}_{4}}{{F}_{y}}) + {{p}_{5}}({{x}_{2}}{{x}_{3}} - {{x}_{1}}{{x}_{4}})$Сопряженные переменные удовлетворяют следующей системе дифференциальных уравнений
В данном случае, используя (3.1), получим уравнения
(3.2)
${{\dot {p}}_{1}} = {{p}_{5}}{{x}_{4}},\quad {{\dot {p}}_{2}} = - {{p}_{5}}{{x}_{3}},\quad {{\dot {p}}_{3}} = - {{p}_{1}} - {{p}_{5}}{{x}_{2}},\quad {{\dot {p}}_{4}} = - {{p}_{2}} + {{p}_{5}}{{x}_{1}},\quad {{\dot {p}}_{5}} = 0$Из последнего уравнения системы (3.2) следует, что ${{p}_{5}} = \operatorname{const} \geqslant 0$. Тогда система (3.2) приобретает следующий вид
(3.3)
${{\dot {p}}_{1}} = {{p}_{5}}{{x}_{4}},\quad {{\dot {p}}_{2}} = - {{p}_{5}}{{x}_{3}},\quad {{\dot {p}}_{3}} = - {{p}_{1}} - {{p}_{5}}{{x}_{2}},\quad {{\dot {p}}_{4}} = - {{p}_{2}} + {{p}_{5}}{{x}_{1}}$В соответствии с принципом максимума оптимальное управление $F$ доставляет максимум функции $H$ из (3.1), и при ограничениях (2.1) имеет вид
(3.4)
${{F}_{x}} = \frac{{{{p}_{3}}}}{{\sqrt {p_{3}^{2} + p_{4}^{2}} }},\quad {{F}_{y}} = \frac{{{{p}_{4}}}}{{\sqrt {p_{3}^{2} + p_{4}^{2}} }}$Кроме того, поскольку на конечные значения ${{x}_{k}}(T)$, $(k = 1,4)$ не наложено никаких ограничений, то должны быть выполнены условия трансверсальности
Дифференцируя дважды последние два уравнения системы (3.3) и используя (2.7) и (3.4), получим следующие два уравнения для двух сопряженных переменных ${{p}_{3}}$, ${{p}_{4}}$:
(3.6)
${{\dddot p}_{3}} = - \lambda \frac{{{{p}_{4}}}}{{\sqrt {p_{3}^{2} + p_{4}^{2}} }},\quad {{\dddot p}_{4}} = \lambda \frac{{{{p}_{3}}}}{{\sqrt {p_{3}^{2} + p_{4}^{2}} }};\quad \lambda = 2{{p}_{5}} = \operatorname{const} \geqslant 0$Таким образом, задача сводится к поиску решений системы 6-го порядка (3.6) на отрезке $0 \leqslant t \leqslant T$, которые удовлетворяют краевым условиям
Мы можем понизить на две единицы порядок системы (3.6), записав следующие два ее интеграла
(3.8)
${{p}_{3}}{{\ddot {p}}_{3}} + {{p}_{4}}{{\ddot {p}}_{4}} = \frac{1}{2}\left( {\dot {p}_{3}^{2} + \dot {p}_{4}^{2}} \right) + {{C}_{1}},\quad - {\kern 1pt} {{\dot {p}}_{4}}{{\ddot {p}}_{3}} + {{\dot {p}}_{3}}{{\ddot {p}}_{4}} = \lambda \sqrt {p_{3}^{2} + p_{4}^{2}} + {{C}_{2}},$(3.9)
${{p}_{3}} = \rho \cos \alpha ,\quad {{p}_{4}} = \rho \sin \alpha ,\quad {{\dot {p}}_{3}} = {v}\cos \beta ,\quad {{\dot {p}}_{4}} = {v}\sin \beta $Из (3.8) и (3.9), обозначая $\gamma = \beta - \alpha $, получаем следующие четыре уравнения первого порядка
(3.10)
$\begin{gathered} \dot {\rho } = {v}\cos \gamma ,\quad \rho \dot {\alpha } = {v}\sin \gamma \\ \rho {\dot {v}}\cos \gamma - \rho {v}\dot {\beta }\sin \gamma = \frac{1}{2}{{{v}}^{2}} + {{C}_{1}},\quad {{{v}}^{2}}\dot {\beta } = \lambda \rho + {{C}_{2}};\quad \gamma = \beta - \alpha \\ \end{gathered} $Отсюда получаем замкнутую систему трех дифференциальных уравнений первого порядка относительно трех функций $\{ \rho ,{v},\gamma \} $ (уравнение для $\beta $ “отщепляется”):
(3.11)
$\begin{gathered} \dot {\rho } = {v}\cos \gamma ,\quad {v}\rho \dot {\gamma } = - {{{v}}^{2}}\sin \gamma + \frac{{\rho (\lambda \rho + {{C}_{2}})}}{{v}}{\text{ }} \\ {\dot {v}}\rho \cos \gamma = \frac{{\rho \left( {\lambda \rho + {{C}_{2}}} \right)}}{{v}}\sin \gamma + \frac{{{{{v}}^{2}}}}{2} + {{C}_{1}}{\text{;}}\quad \sin \gamma \ne 0 \\ \end{gathered} $Если в системе (3.11) поделить второе и третье уравнения на первое и взять за независимое переменное функцию $\rho $, то получим систему второго порядка для двух переменных $\left\{ {{v},\gamma } \right\}$.
Таким образом, нам нужно найти такие решения системы (3.11) на отрезке $0 \leqslant t \leqslant T$, которые удовлетворяют краевому условию $\rho (T) = 0$, чтобы обеспечить условие трансверсальности (3.7). Аналитически эти решения удалось найти лишь в том частном случае, когда ${{C}_{1}} = {{C}_{2}} = 0$. Справедливо следующее утверждение.
Утверждение 1. Система (3.11) в случае ${{C}_{1}} = {{C}_{2}} = 0$ имеет частное решение, которое дается соотношениями
(3.12)
$\gamma (t) = {{\gamma }_{0}} = \pm \arcsin \left( {1{\text{/}}\sqrt {10} } \right),\quad {v}(t) = {{\left( { \pm \sqrt {10} \lambda } \right)}^{{1{\text{/}}3}}}{{\left[ {\rho (t)} \right]}^{{2{\text{/}}3}}}$Справедливость утверждения 1 устанавливается непосредственной проверкой.
Далее, используя первые два уравнения системы (3.11) и соотношения (3.12), получим искомые решения системы (3.6) как функции времени на отрезке $0 \leqslant t \leqslant T$:
(3.13)
$\begin{gathered} {{p}_{3}}(t) = {{p}_{*}}{{(1 - \tau )}^{3}}cos\left[ {{{\alpha }_{0}} + \ln (1 - \tau )} \right] \\ {{p}_{4}}(t) = - {{p}_{*}}{{(1 - \tau )}^{3}}sin\left[ {{{\alpha }_{0}} + \ln (1 - \tau )} \right] \\ {{p}_{*}} = \lambda {{T}^{3}}{\text{/}}10,\quad \tau = t{\text{/}}T,\quad {{\alpha }_{0}} = \operatorname{const} ,\quad \tau \in [0,1] \\ \end{gathered} $Используя формулы (3.6) и (3.13), получаем выражения для оптимальных управлений
(3.14)
$\begin{gathered} {{F}_{x}} = cos\left[ {{{\alpha }_{0}} + \ln (1 - \tau )} \right],\quad {{F}_{y}} = - sin\left[ {{{\alpha }_{0}} + \ln (1 - \tau )} \right] \\ \tau = t{\text{/}}T,\quad {{\alpha }_{0}} = {\text{const}} \in [0,2\pi ),\quad \tau \in [0,1] \\ \end{gathered} $Подставляя функции из (3.14) в уравнения движения (2.7), находим соответствующие оптимальные траектории точки в системе координат $C\xi \eta $ и максимальный угол поворота тела. Несложно получить, что эти траектории представляют собой спирали, закручивающиеся вокруг центра масс $C$ бесконечное число раз. В конце этого процесса, при $t \to T$, направление управляющей силы $F$ меняется с увеличивающейся до бесконечности частотой.
В формулах (3.14) ${{\alpha }_{0}}$ – произвольная константа из интервала $[0,2\pi )$. Используя (3.14), мы можем решить полную систему уравнений (2.7), (3.3) на отрезке $0 \leqslant t \leqslant T$ и определить все те начальные условия ${{x}_{k}}(0) = {{x}_{{k0}}}$, $(k = 1,4)$, при которых соблюдены условия трансверсальности ${{p}_{k}}(T) = 0$, $(k = 1,4)$. Проводя элементарные выкладки, мы получаем следующий результат.
Утверждение 2. Если начальные условия в рассматриваемой задаче удовлетворяют следующим соотношениям:
(3.15)
$\begin{gathered} {{x}_{{10}}} = \xi (0) = \frac{{{{T}^{2}}}}{{10}}(\cos {{\alpha }_{0}} + 3\sin {{\alpha }_{0}}),\quad {{x}_{{20}}} = \eta (0) = \frac{{{{T}^{2}}}}{{10}}(3\cos {{\alpha }_{0}} - \sin {{\alpha }_{0}}) \\ {{x}_{{30}}} = \dot {\xi }(0) = - \frac{T}{2}(\cos {{\alpha }_{0}} + \sin {{\alpha }_{0}}),\quad {{x}_{{40}}} = \dot {\eta }(0) = \frac{T}{2}( - \cos {{\alpha }_{0}} + \sin {{\alpha }_{0}}) \\ {{\alpha }_{0}} \in [0,2\pi ], \\ \end{gathered} $Справедливость утверждения 2 следует из принципа максимума Понтрягина и непосредственного интегрирования системы уравнений (2.7), (3.3) при функциях ${{F}_{x}}$, ${{F}_{y}}$, вычисляемых по формулам (3.14).
Замечание 1. В силу однородности пространства в формулах (3.15) можно принять ${{\alpha }_{0}} = 0$. Тогда искомые начальные условия будут такими
Оптимальное управление из (3.14) примет вид
Решая систему (2.5) при указанных начальных условиях и управлениях ${{F}_{x}},{{F}_{y}}$, получим следующие формулы для координат и скоростей
(3.16)
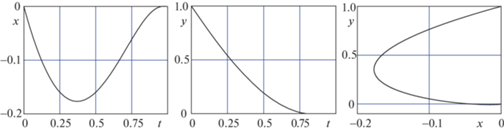
$\begin{gathered} {{x}_{3}}(t) = \dot {\xi }(t) = - \frac{T}{{\sqrt 2 }}\tau \sin \left( {\frac{\pi }{4} + \ln \tau } \right),\quad {{x}_{4}}(t) = \dot {\eta }(t) = - \frac{T}{{\sqrt 2 }}\tau \cos \left( {\frac{\pi }{4} + \ln \tau } \right) \\ {{{\dot {x}}}_{5}}(t) = \dot {\varphi }(t) = - \frac{{{{T}^{3}}}}{{10}}\left( {1 - {{\tau }^{3}}} \right),\quad {{x}_{5}}(t) = \varphi (t) = \frac{{{{T}^{4}}}}{{10}}\left( {\frac{3}{4} - \tau + \frac{{{{\tau }^{4}}}}{4}} \right) \\ \end{gathered} $Из (3.16) следует, что оптимальный угол поворота равен ${{x}_{5}}(T) = \varphi (T) = \frac{{3{{T}^{4}}}}{{40}}$, траектории точки по координатам и скоростям приближаются спиралеобразно в точку нуль. На рис. 2 представлены законы движения точки по координатам и ее траектория.
Рис. 2.
Общий вид траектории точки с законами движения $x(t)$ = ${{(1 - t)}^{2}}\sin (\ln (1 - t))$, $y(t)$ = = ${{(1 - t)}^{2}}\cos (\ln (1 - t))$ при $t \in [0.001,\;1]$.
4. Решение оптимальной задачи методом полярных координат. В предыдущем разделе решение задачи Понтрягина осуществлялось в декартовых координатах. В настоящем разделе исходная задача оптимального управления решается с использованием полярных координат. Такой метод позволяет сократить выкладки и лучше прояснить механический смысл полученных результатов.
В системе (2.7) перейдем к полярным переменным по формулам
(4.1)
${{x}_{1}} = \rho \cos \alpha ,\quad {{x}_{2}} = \rho \sin \alpha ,\quad {{x}_{3}} = {v}\cos \beta ,\quad {{x}_{4}} = {v}\sin \beta $Тогда система (2.7) примет вид
(4.2)
$\dot {\rho } = {v}\cos \gamma ,\quad \rho \dot {\alpha } = - {v}\sin \gamma ,\quad {\dot {v}} = {{F}_{{v}}},\quad {v}\dot {\beta } = {{F}_{\beta }},\quad {v}\dot {\varphi } = \rho {v}\sin \gamma $В (4.2) приняты следующие обозначения
(4.3)
${{F}_{{v}}} = {{F}_{x}}\cos \beta + {{F}_{y}}\sin \beta ,\quad {{F}_{\beta }} = - {{F}_{x}}sin\beta + {{F}_{y}}cos\beta ,\quad \gamma = \alpha - \beta $Согласно (4.3), ${{F}_{{v}}}$, ${{F}_{\beta }}$ суть проекции управляющей силы $F$ на оси скоростной системы координат (касательную и нормаль соответственно, к траектории точки в декартовой системе координат $C\xi \eta $). Ясно, что эти проекции также удовлетворяют ограничению
Путем несложных преобразований можно сократить число уравнений в системе (4.2). В результате получаем следующую систему четырех дифференциальных уравнений для четырех переменных $\{ \rho ,\gamma ,{v},\varphi \} $
(4.5)
$\dot {\rho } = {v}\cos \gamma ,\quad \dot {\gamma } = - \frac{{v}}{\rho }\sin \gamma - \frac{1}{{v}}{{F}_{\beta }},\quad {\dot {v}} = {{F}_{{v}}},\quad \dot {\varphi } = \rho {v}\sin \gamma ;\quad t \in [0,T]$Для системы (4.5) ставится аналогичная разд. 3 оптимальная задача. Найти функции ${{F}_{{v}}}$, ${{F}_{\beta }}$, которые при ограничениях (4.4) и заданных начальных условиях $\{ \rho (0)$, $\gamma (0) = \alpha (0) - \beta (0)$, ${v}(0)$, $\varphi (0) = 0\} $ обеспечивают для решения системы (4.5) $\max \varphi (T)$.
Используя принцип максимума Понтрягина, вводим сопряженные переменные $\{ {{p}_{1}},{{p}_{2}},{{p}_{3}},{{p}_{4}}\} $, которые соответствуют исходным переменным $\{ \rho ,\gamma ,{v},\varphi \} $ в написанном порядке. Далее составляем гамильтониан, который запишем в следующем виде
(4.6)
$H = {v}\left( {{{p}_{1}}\cos \gamma - \frac{{{{p}_{2}}}}{\rho }\sin \gamma + {{p}_{4}}\rho \sin \gamma } \right) + \left( { - \frac{{{{p}_{2}}}}{{v}}{{F}_{\beta }} + {{p}_{3}}{{F}_{{v}}}} \right)$В соответствии с принципом максимума оптимальные функции ${{F}_{{v}}}$, ${{F}_{\beta }}$ реализуют максимум функции $H$ из (4.6), и при ограничениях (4.4) имеют вид
где $q = {v}{{p}_{3}}$, ${{p}_{0}} = \sqrt {p_{2}^{2} + {{q}^{2}}} $.Из дифференциальных уравнений для сопряженных переменных следует, что ${{\dot {p}}_{4}} = 0$, т.е., ${{p}_{4}} = \lambda = \operatorname{const} \geqslant 0$. Записывая уравнения для других сопряженных переменных, присоединяя к ним динамические уравнения (4.5) и используя равенства (4.7), получаем следующую систему шести дифференциальных уравнений для шести функций $\{ \rho ,\gamma ,{v},{{p}_{1}},{{p}_{2}},{{p}_{3}}\} $
(4.8)
$\begin{gathered} \dot {\rho } = {v}\cos \gamma ,\quad \dot {\gamma } = - \frac{{v}}{\rho }\sin \gamma + \frac{{{{p}_{2}}}}{{{v}{{p}_{0}}}},\quad {\dot {v}} = \frac{q}{{{{p}_{0}}}} \\ {{{\dot {p}}}_{1}} = - \left( {\frac{{{{p}_{2}}}}{{{{\rho }^{2}}}} + \lambda } \right){v}\sin \gamma ,\quad {{{\dot {p}}}_{2}} = {v}\left[ {{{p}_{1}}\sin \gamma + \left( {\frac{{{{p}_{2}}}}{\rho } - \lambda \rho } \right)\cos \gamma } \right] \\ {{{\dot {p}}}_{3}} = - {{p}_{1}}\cos \gamma + \left( {\frac{{{{p}_{2}}}}{\rho } - \lambda \rho } \right)\sin \gamma + \frac{{p_{2}^{2}}}{{{{{v}}^{2}}{{p}_{0}}}};\quad t \in [0,T] \\ \end{gathered} $В системе (4.8) приняты обозначения из (4.7). Кроме того, так как на исходные переменные $\rho (t)$, $\gamma (t)$, ${v}(t)$ при $t = T$ не наложено никаких ограничений, то должны быть выполнены условия трансверсальности
Таким образом, требуется решить систему дифференциальных уравнений (4.8) на отрезке $0 \leqslant t \leqslant T$ при заданных начальных условиях для переменных $\{ \rho ,\gamma ,{v}\} $ и условиях трансверсальности (4.9) для переменных $\{ {{p}_{1}},{{p}_{2}},{{p}_{3}}\} $. Для некоторых начальных условий это удалось сделать аналитически.
Можно показать (доказательство громоздко и здесь не приводится), что система уравнений (4.8), (4.9) не имеет решений, при которых $\rho = {\text{const}}$ (т. е., оптимальные траектории не могут быть окружностями с центром в центре масс тела).
Перейдем тогда в системе (4.8) к независимой переменной $\rho $. Для этого поделим обе части всех уравнений, начиная со второго, на первое уравнение. Получим систему пяти уравнений для пяти переменных $\{ \gamma ,{v},{{p}_{1}},{{p}_{2}},{{p}_{3}}\} $ (производная по $\rho $ обозначается штрихом)
(4.10)
$\begin{gathered} \gamma {\kern 1pt} ' = - \frac{{\operatorname{tg} \gamma }}{\rho } + \frac{{{{p}_{2}}}}{{{{{v}}^{2}}{{p}_{0}}\cos \gamma }},\quad {v}{\kern 1pt} ' = \frac{q}{{{v}{{p}_{0}}\cos \gamma }} \\ p_{1}^{'} = - \left( {\frac{{{{p}_{2}}}}{{{{\rho }^{2}}}} + \lambda } \right)\operatorname{tg} \gamma ,\quad p_{2}^{'} = {{p}_{1}}\operatorname{tg} \gamma + \frac{{{{p}_{2}}}}{\rho } - \lambda \rho \\ p_{3}^{'} = - \frac{1}{{v}}\left[ {{{p}_{1}} - \left( {\frac{{{{p}_{2}}}}{\rho } - \lambda \rho } \right)\operatorname{tg} \gamma } \right] + \frac{{p_{2}^{2}}}{{{{{v}}^{3}}{{p}_{0}}\cos \gamma }} \\ \end{gathered} $Система (4.10) имеет два интеграла
(4.11)
$p_{1}^{2} + {{\left( {\frac{{{{p}_{2}}}}{\rho } + \lambda \rho } \right)}^{2}} = {{h}^{2}} = \operatorname{const} $(4.12)
$\begin{gathered} {v}\left( {{{p}_{1}}\cos \gamma - \frac{{{{p}_{2}}}}{\rho }\sin \gamma + \lambda \rho \sin \gamma } \right) + \frac{{{{p}_{0}}}}{{v}} = H = \operatorname{const} \\ {{p}_{0}} = \sqrt {p_{2}^{2} + {{q}^{2}}} ,\quad q = {v}{{p}_{3}} \\ \end{gathered} $Интеграл (4.11) получается непосредственно из третьего и четвертого уравнений системы (4.10). Интеграл (4.12) следует из сохранения значения функции Гамильтона (4.6) при значениях ${{F}_{{v}}}$, ${{F}_{\beta }}$ из (4.7) в силу уравнений (4.8). Константы $h$, $H$ в (4.11) и (4.12) определяются заданными начальными условиями для $\{ \rho ,\gamma ,{v}\} $ и условиями трансверсальности (4.9).
Благодаря интегралу (4.11), можно понизить порядок системы (4.10). Введем вместо ${{p}_{1}}$, ${{p}_{2}}$ новую переменную $\sigma $ по формулам
(4.13)
${{p}_{1}} = h\sin \sigma ,\quad {{p}_{2}} = \rho (h\cos \sigma - \lambda \rho );\quad \sigma \in [0,2\pi ]$Тогда интеграл (4.11) соблюдается автоматически, а система (4.10) будет эквивалентна следующим четырем уравнениям для четырех переменных $\{ \gamma ,\sigma ,{v},q\} $, $(q = {v}{{p}_{3}})$
(4.14)
$\begin{gathered} \gamma {\kern 1pt} ' = - \frac{{\operatorname{tg} \gamma }}{\rho } + \frac{{{{p}_{2}}}}{{{{{v}}^{2}}{{p}_{0}}\cos \gamma }},\quad {v}{\kern 1pt} ' = \frac{q}{{v{{p}_{0}}\cos \gamma }} \\ \sigma {\kern 1pt} ' = - \frac{{\operatorname{tg} \gamma }}{\rho },\quad q{\kern 1pt} ' = - {{p}_{1}} + \left( {\frac{{{{p}_{2}}}}{\rho } - \lambda \rho } \right)\operatorname{tg} \gamma + \frac{{{{p}_{0}}}}{{{{{v}}^{2}}\cos \gamma }} \\ \end{gathered} $В уравнениях (4.14) ${{p}_{1}}$, ${{p}_{2}}$ даются формулами (4.13), а ${{p}_{0}}$, $q$ определяются обозначениями из (4.7).
Введем новую переменную $p$ по формуле
Тогда имеем ${{p}_{0}} = \left| {{{p}_{2}}} \right|\sqrt {1 + {{p}^{2}}} $, и система уравнений (4.14) примет вид
(4.16)
$\begin{gathered} \gamma ' = - \frac{{\operatorname{tg} \gamma }}{\rho } + \frac{{\operatorname{sgn} {{p}_{2}}}}{{{{{v}}^{2}}\cos \gamma \sqrt {1 + {{p}^{2}}} }},\quad {v}{\kern 1pt} ' = \frac{{p\operatorname{sgn} {{p}_{2}}}}{{{v}\cos \gamma \sqrt {1 + {{p}^{2}}} }},\quad \sigma {\kern 1pt} ' = - \frac{{\operatorname{tg} \gamma }}{\rho } \\ {\text{ }}{{p}_{2}}p{\kern 1pt} ' = - h\sin \sigma - ph\sin \sigma \operatorname{tg} \gamma + \left( {h\cos \sigma - 2\lambda \rho } \right)(\operatorname{tg} \gamma - p) + \frac{{\left| {{{p}_{2}}} \right|\sqrt {1 + {{p}^{2}}} }}{{{{{v}}^{2}}\cos \gamma }} \\ \end{gathered} $Рассмотрим такие начальные условия, для которых $h = 0$. В этом случае из интеграла (4.11) следует, что
В соответствии с условиями трансверсальности (4.9) тогда имеем $\rho (T) = 0$. Уравнения (4.16) приобретают вид
(4.18)
$\begin{gathered} \gamma {\kern 1pt} ' = - \frac{{\operatorname{tg} \gamma }}{\rho } - \frac{1}{{{{{v}}^{2}}\cos \gamma \sqrt {1 + {{p}^{2}}} }},\quad {v}{\kern 1pt} ' = - \frac{p}{{{v}\cos \gamma \sqrt {1 + {{p}^{2}}} }} \\ - \lambda {{\rho }^{2}}p{\kern 1pt} ' = \left( { - 2\lambda \rho } \right)(\operatorname{tg} \gamma - p) + \frac{{\lambda {{\rho }^{2}}\sqrt {1 + {{p}^{2}}} }}{{{{{v}}^{2}}\cos \gamma }} \\ \end{gathered} $Далее полагаем $u = {{{v}}^{2}}$. Тогда система (4.18) примет вид
(4.19)
$\begin{gathered} \gamma {\kern 1pt} ' = - \frac{{\operatorname{tg} \gamma }}{\rho } - \frac{1}{{u\cos \gamma \sqrt {1 + {{p}^{2}}} }},\quad u{\kern 1pt} ' = - \frac{{2p}}{{\cos \gamma \sqrt {1 + {{p}^{2}}} }}, \\ p{\kern 1pt} ' = \frac{2}{\rho }(\operatorname{tg} \gamma - p) - \frac{{\sqrt {1 + {{p}^{2}}} }}{{u\cos \gamma }} \\ \end{gathered} $Из формулы (4.12) для рассматриваемых начальных условий получим следующий интеграл системы (4.19)
(4.20)
$2\rho \sqrt u \sin \gamma + \frac{{{{\rho }^{2}}}}{{\sqrt u }}\sqrt {1 + {{p}^{2}}} = H = \operatorname{const} $При условиях: 1) ограниченности функции $p(\rho )$, 2) стремлении $u(\rho )$ к нулю при $\rho \to 0$ медленнее, чем ${{\rho }^{4}}$, из (4.20) получим с необходимостью, что $H = 0$. Тогда из (4.20) имеем соотношение
Обозначая $p = \operatorname{tg} \psi $, из (4.21) получим соотношение
Используя (4.22), перепишем 1-е и 3-е уравнения системы (4.19) в виде следующей системы двух уравнений относительно двух переменных $\left\{ {\gamma ,\psi } \right\}$
(4.23)
$\begin{gathered} \gamma {\kern 1pt} ' = - \frac{{\operatorname{tg} \gamma }}{\rho } + 2\frac{{\operatorname{tg} \gamma }}{\rho }{{\cos }^{2}}\psi = \frac{{\operatorname{tg} \gamma }}{\rho }\frac{{1 - {{{\operatorname{tg} }}^{2}}\psi }}{{1 + {{{\operatorname{tg} }}^{2}}\psi }} \\ \left( {1 + {{{\operatorname{tg} }}^{2}}\psi } \right)\psi {\kern 1pt} ' = \frac{2}{\rho }(\operatorname{tg} \gamma - \operatorname{tg} \psi ) + 2\frac{{\operatorname{tg} \gamma }}{\rho } = \frac{2}{\rho }(2\operatorname{tg} \gamma - \operatorname{tg} \psi ) \\ \end{gathered} $Отметим, что 2-е уравнение системы (4.19) при выполнении соотношений (4.22) и (4.23) выполняется тождественно.
Введем новые переменные по формулам
(4.24)
${{z}_{1}} = p = \operatorname{tg} \psi ,\quad {{z}_{2}} = \operatorname{tg} \gamma ,\quad \rho (t) = \rho (0)\exp ( - \tau );\quad \tau \in (0, + \infty )$Заметим, что в (4.24) введено “безразмерное время” $\tau $, а условие $\rho (T) = 0$, в таком случае, реализуется при $\tau = + \infty $. Это, конечно, справедливо при монотонном убывании функции $\rho (t)$, что будет показано далее.
Уравнения (4.23) для введенных в (4.24) новых переменных приобретают вид
(4.25)
$\frac{{d{{z}_{1}}}}{{d\tau }} = 2{{z}_{1}} - 4{{z}_{2}},\quad \frac{{d{{z}_{2}}}}{{d\tau }} = {{z}_{2}}\left( {1 + z_{2}^{2}} \right)\frac{{z_{1}^{2} - 1}}{{z_{1}^{2} + 1}};\quad \tau \in [0, + \infty )$Система (4.25) есть автономная система дифференциальных уравнений 2-го порядка (“полулинейная”). Эта система имеет три особые точки с координатами $\left( {{{z}_{1}},{{z}_{2}}} \right)$:
(4.26)
$1)\;{\text{(}}1,\;1{\text{/}}2);\quad 2)\;{\text{(}}{\kern 1pt} - {\kern 1pt} 1,\; - 1{\text{/}}2);\quad 3)\;{\text{(}}0,\;0)$Эти точки являются стационарными решениями системы (4.25).
Уравнения же (4.19) тогда имеют особые решения $\gamma = {{\gamma }_{0}}$, $p = {{p}_{0}}$, $u = {{{v}}^{2}} = k\rho $, $(k > 0)$, для которых выполнены соотношения
(4.27)
$\operatorname{tg} {{\gamma }_{0}} = \pm 1{\text{/}}2,\quad {{p}_{0}} = \pm 1,\quad k = - \frac{{2{{p}_{0}}}}{{\left( {\sqrt {1 + p_{0}^{2}} } \right)\cos {{\gamma }_{0}}}},\quad {v} = \sqrt {k\rho } $Эти решения удовлетворяют также интегралу (4.20) при $H = 0$. Так как $k > 0$, то из (4.27) получим
(4.28)
$\begin{gathered} p = {{p}_{0}} = \pm 1,\quad \operatorname{tg} \gamma = \operatorname{tg} {{\gamma }_{0}} = \pm \frac{1}{2} \\ \cos {{\gamma }_{0}} = \mp \frac{2}{{\sqrt 5 }},\quad \sin {{\gamma }_{0}} = - \frac{1}{{\sqrt 5 }},\quad k = \frac{{\sqrt {10} }}{2} \\ \end{gathered} $Отметим, что в силу условий трансверсальности (4.9), формул (4.17) и обозначений (4.15), имеем $\rho (T) = 0$, ${v}(T) = \sqrt {k\rho (T)} $ = 0. В результате приходим к решениям, полученным в разд. 3.
Ясно, что, выбирая другие решения системы (4.25), которые существуют на бесконечном интервале $\tau \in [0, + \infty )$ и отличны от стационарных, могли бы быть получены новые оптимальные решения для соответствующих новых начальных условий исходной задачи. Исследование системы (4.25), однако, приводит к следующему отрицательному результату.
Утверждение 3. Решениями системы (4.25), которые продолжаются на весь бесконечный интервал $0 \leqslant \tau < + \infty $, являются только стационарные решения, представленные тремя особыми точками из (4.26).
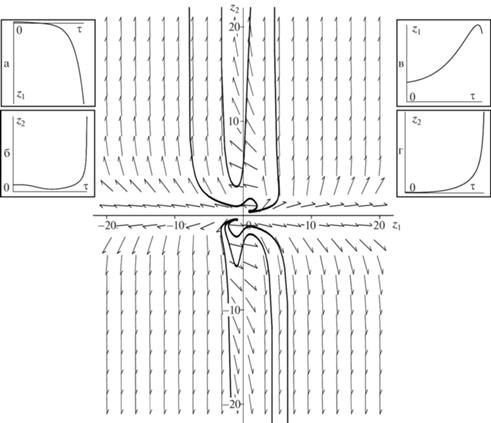
Доказательство утверждения 3 приведено в Приложении. Фазовая плоскость системы (4.25) приведена на рис. 3, где изображено соответствующее векторное поле направлений вместе с некоторыми фазовыми траекториями. Некоторые решения показаны на рис. 3,а–г, где видно, что они действительно непродолжаемые. Продемонстрировано два варианта. В первом случае ${{z}_{1}}(0) = 1.1$, ${{z}_{2}}(0) = 0.6$. При этом на конечном интервале времени первая координата становится достаточно большой по абсолютной величине, значение второй уходит на бесконечность (см. рис. 3,а,б). Во втором случае ${{z}_{1}}(0) = 0.9$, ${{z}_{2}}(0) = 0.4$. При этом на конечном интервале времени первая координата остается небольшой по величине, значение второй уходит на бесконечность (см. рис. 3,в,г). В обоих случаях есть немонотонность одной из координат, что соответствует сложному поведению фазовых траекторий на рис. 3.
Замечание 2. Нетрудно установить, используя (4.7), (4.15) и первое равенство из (4.28), что оптимальная сила $F$ удовлетворяет соотношениям $\left| {{{F}_{{v}}}} \right| = \left| {{{F}_{\beta }}} \right|$ = ${\text{1/}}\sqrt 2 $. Таким образом, сила $F$ является постоянной по модулю (равным единице) и всегда направлена под углом 45° к касательной траектории подвижной точки в системе $C\xi \eta $. Эта сила является “следящей” по скорости точки. Отметим, что в монографии [10], (см. разд. 3.5.2, стр. 115) рассматривалась задача о “следящей” силе по позиции точки (сила была также постоянна по модулю и всегда перпендикулярна радиус-вектору точки). Спиралеобразные траектории движения точки, полученные в монографии [10], вполне аналогичны траекториям в настоящей работе.
Замечание 3. В работе [11] численно исследовалась задача об оптимальной раскрутке плоской двухмассовой системы, где управлением являлся ограниченный внешний момент, приложенный к одному из тел.
Замечание 4. Аналитические выражения для оптимальных траекторий в рассматриваемой задаче удалось получить лишь для достаточно узкого класса начальных условий. При этом оказалось, что оптимальные траектории подвижной массы в конце интервала управления по спиралям приходят с нулевой предельной скоростью в центр масс тела. Весьма вероятно, что аналогичный эффект будет наблюдаться и для других начальных условий. Однако для доказательства этого факта потребуются дополнительные численно-аналитические исследования решений приведенных в статье дифференциальных уравнений.
Замечание 5. При исследовании, редукции и поиске первых интегралов дифференциальных уравнений настоящей статьи использовались идеи и методы, которые были развиты в [12, 13].
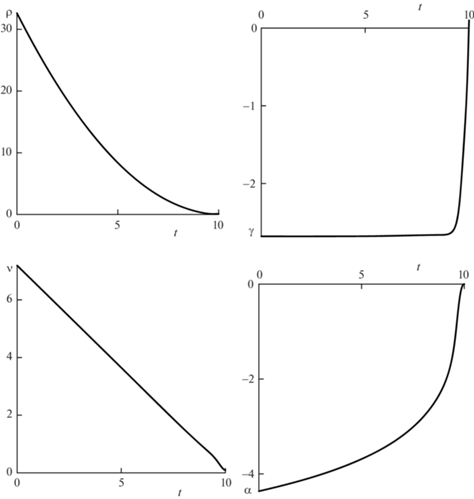
5. Результаты численного интегрирования уравнений принципа максимума. Рассчитаем теперь траекторию, начальные условия у которой такие, что не поддались аналитическому исследованию. Численно интегрировалась в обратном времени система (4.8). При этом терминальные значения фазовых координат и момент окончания были выбраны произвольно, а терминальные значения сопряженных переменных задавались достаточно малыми в соответствии с (4.9):
Отметим, что ненулевые значения сопряженных переменных здесь взяты специально, так как при нулевых значениях рассматриваемая система дифференциальных уравнений имеет особенность. На рис. 4 (на первых трех графиках) представлены зависимости фазовых координат $\rho ,\,\gamma ,\,v$ от времени. Остальные неизвестные функции, такие как $\alpha (t),\;\varphi (t)$ или зависимость от времени координат и проекций силы в исходной системе, могут быть подсчитаны с использованием уравнений (4.1)–(4.3). Для примера на рис. 4 (на четвертом графике) был подсчитан угол $\alpha (t)$ при условии, что $\alpha (T) = 0$.
Приложение. Доказательство утверждения 3. Перепишем систему (4.25) в виде следующей системы интегральных уравнений
(П1)
${{z}_{1}}(\tau ) = {{e}^{{2\tau }}}\left[ {{{z}_{1}}(0) - 4\int\limits_0^\tau {{{e}^{{ - 2s}}}{{z}_{2}}(s)ds} } \right],\quad \frac{{\left| {{{z}_{2}}(\tau )} \right|}}{{\sqrt {1 + z_{2}^{2}(\tau )} }} = \frac{{\left| {{{z}_{2}}(0)} \right|}}{{\sqrt {1 + z_{2}^{2}(0)} }}\exp \left[ {\int\limits_0^\tau {\frac{{z_{1}^{2}(s) - 1}}{{z_{1}^{2}(s) + 1}}ds} } \right]$Нас интересуют решения системы (П1), которые продолжаются на весь бесконечный интервал $0 \leqslant \tau < + \infty $. Такие решения будем называть приемлемыми. Из второго уравнения системы (П1) следует, что любое приемлемое решение ${{z}_{2}}(\tau )$ (при ${{z}_{2}}(0) \ne 0$) не обращается в нуль на любом конечном интервале времени $\tau $. Тогда из первого уравнения системы (П1) получим, что при ${{z}_{1}}(0){{z}_{2}}(0) < 0$ решение ${{z}_{1}}(\tau )$ стремится к бесконечности при $\tau \to + \infty $ не медленнее, чем ${{e}^{{2\tau }}}$. В этом случае второе уравнение системы (П1) становится противоречивым при $\tau \to + \infty $, так как левая часть этого уравнения ограничена при всех $\tau $ (меньше 1), а правая часть стремится к $ + \infty $ при $\tau \to + \infty $, как ${{e}^{\tau }}$. Таким образом, при ${{z}_{1}}(0){{z}_{2}}(0) < 0$ решения системы не продолжаются на бесконечный интервал времени, т.е., приемлемых решений нет.
Рассмотрим случай ${{z}_{1}}(0){{z}_{2}}(0) > 0$. В силу симметрии достаточно рассмотреть случай ${{z}_{1}}(0) > 0$, ${{z}_{2}}(0) > 0$. Тогда, в силу вышесказанного, имеем ${{z}_{2}}(\tau ) > 0$, $\tau \in [0, + \infty )$, а правая часть первого уравнения системы (П1) остается все время положительной (в противном случае, существует такое ${{\tau }_{1}}$, что ${{z}_{1}}({{\tau }_{1}}){{z}_{2}}({{\tau }_{1}}) < 0$, и, в силу вышесказанного, приемлемых решений нет. Таким образом, в этом случае для приемлемого решения необходимо иметь
Покажем, что для приемлемого решения должно соблюдаться точное равенство
Действительно, в противном случае, в силу монотонности по $\tau $ интеграла $\int_0^\tau {{{e}^{{ - 2s}}}} {{z}_{2}}(s)ds$ и первого уравнения системы (П1), нарушение равенства (П2) привело бы к бесконечному возрастанию при $\tau \to + \infty $ (как ${{e}^{{2\tau }}}$) функции ${{z}_{1}}(\tau )$. А это, как было уже отмечено выше, было бы противоречиво для второго уравнения системы (П1) (в случае приемлемого решения).
Используя равенство (П2), первое уравнение системы (П1) можно переписать в следующем виде
(П3)
${{z}_{1}}(\tau ) = 4{{e}^{{2\tau }}}\int\limits_\tau ^{ + \infty } {{{e}^{{ - 2s}}}} {{z}_{2}}(s)ds$Предположим, что предел функции $\left| {{{z}_{1}}(s)} \right|$ при $s \to + \infty $ существует и является конечным: $\mathop {\lim }\limits_{s \to + \infty } \left| {{{z}_{1}}(s)} \right| = {{z}_{*}} < + \infty $. Рассмотрим три случая:
1) ${{z}_{*}} > 1$. Тогда интеграл $\int_0^\tau {\frac{{z_{1}^{2}(s) - 1}}{{z_{1}^{2}(s) + 1}}ds} $ положителен и расходится при $\tau \to + \infty $, а значит второе уравнение системы (П1) противоречиво и приемлемых решений нет.
2) ${{z}_{*}} < 1$. Тогда интеграл $\int_0^\tau {\frac{{z_{1}^{2}(s) - 1}}{{z_{1}^{2}(s) + 1}}ds} $ отрицателен и расходится при $\tau \to + \infty $, а из второго уравнения системы (П1) получим $\mathop {\lim }\limits_{\tau \to + \infty } {{z}_{2}}(\tau )$ = 0. Отсюда, используя уравнение (П3), получим, что $\mathop {\lim }\limits_{s \to + \infty } \left| {{{z}_{1}}(s)} \right| = {{z}_{*}}$ = 0. Рассматривая систему линейного приближения для исходной системы (4.25) в окрестности особой точки $\{ {{z}_{1}} = 0$, ${{z}_{2}} = 0\} $, получим
Собственные числа этой системы суть ${{\lambda }_{1}} = 2$, ${{\lambda }_{2}} = 1$, следовательно, решения никак не могут входить в эту точку, что указывает на противоречивость полученных предельных значений для исходной нелинейной системы (4.25). Таким образом, в этом случае также нет приемлемых решений.
3) ${{z}_{*}} = 1$. Тогда, если интеграл $\int_0^\tau {\frac{{z_{1}^{2}(s) - 1}}{{z_{1}^{2}(s) + 1}}ds} $ расходится при $\tau \to + \infty $, то он должен быть обязательно отрицателен (иначе противоречиво второе уравнение системы (П1). Кроме того, в этом случае второе уравнение системы (П1) приводит к предельному соотношению $\mathop {\lim }\limits_{\tau \to + \infty } {{z}_{2}}(\tau )$ = 0. Согласно соотношению (П3), это предельное соотношение дает предельное соотношение $\mathop {\lim }\limits_{\tau \to + \infty } {{z}_{1}}(\tau ) = {{z}_{*}}$ = 0. Полученное противоречие указывает на отсутствие приемлемых решений в этом случае.
Если же интеграл $\int_0^\tau {\frac{{z_{1}^{2}(s) - 1}}{{z_{1}^{2}(s) + 1}}ds} $ сходится при $\tau \to + \infty $, то, согласно второму уравнению системы (П1), существует предел $\mathop {\lim }\limits_{\tau \to + \infty } {{z}_{2}}(\tau ) = {{z}_{2}}_{*}$. Переходя в равенстве (П3) к пределу при $\tau \to + \infty $, получим соотношение $1 = 2{{z}_{2}}_{*} \to {{z}_{2}}_{*} = 1{\text{/}}2$. Полученный предел является первой особой точкой из (4.26). Линеаризованные уравнения исходной системы (4.25) в окрестности этой особой точки имеют вид $z_{1}^{'} = 2{{z}_{1}} - 4{{z}_{2}}$, $z_{2}^{'} = \frac{5}{8}{{z}_{1}}$. Собственные числа полученной системы суть ${{\lambda }_{{1,2}}} = 1 \pm i\sqrt {\frac{3}{2}} $. Таким образом, и в этом случае решения никак не могут входить в рассматриваемую точку. Это указывает на отсутствие приемлемых решений в рассматриваемом случае.
Последний оставшийся случай, когда $\mathop {\lim }\limits_{s \to + \infty } \left| {{{z}_{1}}(s)} \right| = {{z}_{*}} = + \infty $, также приводит к отсутствию приемлемых решений, так как тогда, при $\tau \to + \infty $, противоречиво второе уравнение системы (П1). Утверждение 3 доказано.
Благодарности. Авторы выражают свою благодарность академику РАН В.Ф. Журавлёву за поддержку и внимание к работе, а также академику РАН Ф.Л. Черноусько и всем участникам руководимого им семинара за ценные и конструктивные замечания к настоящей работе.
Второй автор выполнял исследование с использованием средств государственного бюджета по госзаданию № 123021700055-6.
Список литературы
Аппель П. Теоретическая механика. Т. 2: Динамика системы. Аналитическая механика. М.: Ленанд, 2021. 504 с.
Татаринов Я.В. Лекции по классической динамике. М.: Изд-во МГУ, 1984. 296 с.
Chernousko F.L. Optimal control of two-dimensional motions of a body by a movable mass // Prepr. IX Vienna Int. Conf. on Math. Model. (MATHMOD). Vienna, February 21–23, 2018. Pap. WeD4.2. Vienna, 2018. P. 253–256.
Черноусько Ф.Л. Оптимальное управление движением двухмассовой системы // Докл. РАН. 2018. Т. 480. № 5. С. 528–532.
Черноусько Ф.Л. Изменение ориентации твердого тела при помощи вспомогательной массы // Докл. РАН. 2020. Т. 490. № 1. С. 79–81.
Шматков А.М. Поворот тела за кратчайшее время перемещением точечной массы // Докл. РАН. 2018. Т. 481. № 5. С. 498–502.
Розенблат Г.М. Об оптимальном повороте твердого тела при помощи внутренних сил // Докл. РАН. 2022. Т. 505. № 1. С. 92–99.
Решмин С.А., Розенблат Г.М. Численно-аналитическое исследование оптимального поворота твердого тела при помощи внутренних сил // Межд. науч. конф. “Фундаментальные и прикладные задачи механики”. Москва, 6–9 декабря 2022 г. Матер. конф. Ч. 1. М.: Изд. МГТУ им. Н.Э. Баумана, 2023. С. 182–188.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: ГИФМЛ, 1961. 391 с.
Klimov D.M., Zhuravlev V.Ph. Group-Theoretic Methods in Mechanics and Applied Mathematics. London; New York: Taylor&Francis, 2002. 230 p.
Решмин С.А. Применение метода Ньютона при решении краевых задач принципа максимума на примере задачи об оптимальном раскручивании двухмассовой системы // Modern Europ. Res. 2021. № 2 (Т. 1). С. 114–122.
Козлов В.В. Рациональные интегралы квазиоднородных динамических систем // ПММ. 2015. Т. 79. № 3. С. 307–316.
Шамолин М.В. Новые случаи интегрируемых систем нечетного порядка с диссипацией // Докл. РАН. 2020. Т. 491. № 1. С. 95–101.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика