Прикладная математика и механика, 2023, T. 87, № 6, стр. 1028-1036

Одномерное растекание нефтепродуктов по поверхности воды

А. В. Кистович^1, *, Т. О. Чаплина^1, **

¹ Институт проблем механики им. А.Ю. Ишлинского
Москва, Россия

^* E-mail: kavmendeleevo@mail.ru
^** E-mail: tanya75.06@mail.ru

Поступила в редакцию 30.03.2023
После доработки 01.10.2023
Принята к публикации 10.10.2023

EDN: GYYKUG
DOI: 10.31857/S0032823523060061

Аннотация

Экспериментально и теоретически исследован процесс квазиодномерного растекания пятен нефтепродуктов по поверхности воды. В основе теоретической модели лежит приближенное уравнение, полученное при использовании законов сохранения массы разлившегося продукта и полной энергии системы. Представлены приближенные решения этого уравнения и результаты экспериментальных исследований по растеканию в узком протяженном контейнере машинного масла и сырой нефти, и показано их хорошее соответствие теории. Проведено сравнение с процессом двумерного осесимметричного растекания пятна таких же нефтепродуктов.

Ключевые слова: моделирование, квазиодномерное растекание, машинное масло, сырая нефть, коэффициент сопротивления формы

1. Введение. Экспериментальному и теоретическому изучению растекания нефти и нефтепродуктов посвящена обширная научная литература, из которых к наиболее известным относятся работы [1–8]. Упомянутые работы содержат, ставшее почти обязательным, сравнение экспериментальных результатов с теоретическими предсказаниями, что связано с полуэмпирической природой математических моделей распространения. По этой причине необходимо проведение более глубокого изучения модели распространения, самая продвинутая версия которой, достигнутая в [6], все еще недостаточно точна для требуемого уровня понимания процессов, происходящих при распространении нефтепродуктов в различных природных условиях. Представленная в [9] простая модель осесимметричного радиального растекания, основанная на исследовании динамики полной энергии системы “вода–нефтепродукт”, показала хорошее совпадение экспериментальных и теоретических результатов. В большинстве естественных ситуаций разливы нефтепродуктов происходят на двумерной поверхности (открытые водные пространства заливов, озер, морей и т.д.), но также возможны и особые условия (каналы, реки, узкие аквариумы и т.д.), когда поверхность разлива можно считать одномерной [7, 8]. В данной работе представлена, основанная на энергетическом подходе, упрощенная математическая модель, позволяющая исследовать основные динамические параметры такого типа растекания. При этом химический состав и все термодинамические параметры сред считаются постоянными величинами, масса растекающегося пятна предполагается неизменной, все среды однородны, изотропны и несжимаемы.

2. Квазиодномерное растекание нефтепродукта. Ниже представлен приближенный расчет параметров разлива, в основу модели которого положена форма нефтяного пятна в виде полосы, ширина $D$ которой постоянна, а его длина $L(t)$ вдоль оси $x$ и толщина $h(t)$ вдоль оси $z$ являются функциями времени. Полоса и нижележащая вода ограничены непроницаемой стенкой при $x = 0$. Структура течения нефти внутри полосы такова, что в надводной части жидкие частицы нефти движутся вниз и от стенки, а в нижней части – вверх и от стенки. Этот тип течения находится в соответствии с движением поверхностей пятна при разливе: верхняя граница (граница раздела “нефть–воздух”) движется вниз, а нижняя (граница раздела “нефть–вода”) движется вверх.

Для описания энергетических соотношений системы “нефть–вода” используется модель нефтяного пятна, помещенного на поверхность воды, содержащейся в призме ширины $D$ и длины ${{L}_{w}}$. Изначально, при отсутствии нефти, глубина воды была равна $H$. Пусть в некоторый момент времени длина нефтяного пятна равна ${{L}_{o}}$, а толщина – $h$.

Координаты верхней и нижней границ нефтяного пятна в момент времени $t$ задаются величинами $z = {{h}_{ \pm }}(t)$, так что толщина пятна

(2.1)

$h(t) = {{h}_{ + }}(t) - {{h}_{ - }}(t){\text{,}}$

а его длина равна ${{L}_{o}}$. Уровень свободной поверхности воды в этот момент времени обозначен символом $H{\kern 1pt} '$. Один из параметров проблемы – объем нефтяного пятна

(2.2)

$V = D{{L}_{o}}(t)h(t) = D{{L}_{o}}(t)({{h}_{ + }}(t) - {{h}_{ - }}(t)) = {\text{const,}}$

который остается неизменным в течение всего времени разлива.

Исходя из закона сохранения объема воды

(2.3)

${{h}_{ - }}{{L}_{o}} + H{\kern 1pt} '({{L}_{w}} - {{L}_{o}}) = H{{L}_{w}}$

и закона Архимеда

(2.4)

$\left( {H{\kern 1pt} '\; - {{h}_{ - }}} \right){{\rho }_{w}} = \left( {{{h}_{ + }} - {{h}_{ - }}} \right){{\rho }_{o}} = h{{\rho }_{o}},$

получаются необходимые соотношения

(2.5)

$H{\kern 1pt} ' = \frac{{H - {{L}_{*}}{{h}_{ - }}}}{{1 - {{L}_{*}}}},\quad {{h}_{ - }} = H - \left( {1 - {{L}_{*}}} \right)\rho h,\quad {{h}_{ + }} = H + \left( {1 - \left( {1 - {{L}_{*}}} \right)\rho } \right)h,$

где $\rho = {{{{\rho }_{o}}} \mathord{\left/ {\vphantom {{{{\rho }_{o}}} {{{\rho }_{w}}}}} \right. \kern-0em} {{{\rho }_{w}}}}$, ${{L}_{*}} = {{{{L}_{o}}} \mathord{\left/ {\vphantom {{{{L}_{o}}} {{{L}_{w}}}}} \right. \kern-0em} {{{L}_{w}}}}$.

При ${{L}_{w}} \gg {{L}_{o}}\sim {{L}_{*}} \to 0$ соотношения (2.5) приобретают вид

(2.6)

$H{\kern 1pt} ' = H,\quad {{h}_{ - }} = H - \rho h,\quad {{h}_{ + }} = H + (1 - \rho )h$

Обратимся теперь к расчету энергетических характеристик системы. В постоянном поле силы тяжести потенциальная энергия системы, изображенной на рис. 1, с учетом (2.6) определяется соотношением

(2.7)

$\Pi = \frac{{{{\rho }_{w}}{{L}_{w}}D}}{2}{{H}^{2}}g + \frac{{{{\rho }_{o}}{{L}_{o}}D}}{2}{{h}^{2}}g(1 - \rho )$

Рис. 1.

Модель расчета энергетического состояния системы.

Поверхностная энергия задается выражением

(2.8)

${{E}_{S}} = {{L}_{o}}D({{\sigma }_{{ow}}} + {{\sigma }_{{oa}}}) + ({{L}_{w}} - {{L}_{o}})D{{\sigma }_{{aw}}} = {{L}_{w}}D{{\sigma }_{{aw}}} + {{L}_{o}}D({{\sigma }_{{ow}}} + {{\sigma }_{{oa}}} - {{\sigma }_{{aw}}}),$

где ${{\sigma }_{{ij}}}$ – коэффициент поверхностного натяжения на границе раздела $i$-й и $j$-й сред.

Кинетическая энергия системы складывается из кинетической энергии нефти и воды и имеет вид

(2.9)

${\rm T} = \frac{D}{2}\left[ {{{\rho }_{w}}\int\limits_{{{L}_{o}}}^{{{L}_{w}}} {\int\limits_0^H {{{{\mathbf{w}}}^{2}}dxdz} } + {{\rho }_{w}}\int\limits_0^{{{L}_{o}}} {\int\limits_0^{{{h}_{ - }}} {{{{\mathbf{w}}}^{2}}dxdz} } + {{\rho }_{o}}\int\limits_0^{{{L}_{o}}} {\int\limits_{{{h}_{ - }}}^{{{h}_{ + }}} {{{{\mathbf{v}}}^{2}}dxdz} } } \right],$

где ${\mathbf{v}}$ и ${\mathbf{w}}$ – поля скорости в нефти и воде соответственно.

Скорость вязкой диссипации энергии в системе задается выражением

(2.10)

${{\dot {E}}_{{{\nu }}}} = \frac{D}{{2{{\eta }_{w}}}}\left[ {\int\limits_{{{L}_{o}}}^{{{L}_{w}}} {\int\limits_0^H {{{\Sigma }_{w}}dxdz} } + \int\limits_0^{{{L}_{o}}} {\int\limits_0^{{{h}_{ - }}} {{{\Sigma }_{w}}dxdz} } } \right] + \frac{D}{{2{{\eta }_{o}}}}\int\limits_0^{{{L}_{o}}} {\int\limits_{{{h}_{ - }}}^{{{h}_{ + }}} {{{\Sigma }_{o}}dxdz} } ,$

где ${{\Sigma }_{i}} = \sigma _{{xx}}^{2} + 2\sigma _{{xz}}^{2} + \sigma _{{zz}}^{2}$, причем элементы тензора вязких напряжений вычисляются для $i$-той среды.

Таким образом, имеет место

(2.11)

$\begin{gathered} {{\Sigma }_{w}} = 2\eta _{w}^{2}\left[ {2{{{({{\partial {{w}_{x}}} \mathord{\left/ {\vphantom {{\partial {{w}_{x}}} {\partial x}}} \right. \kern-0em} {\partial x}})}}^{2}} + {{{({{\partial {{w}_{x}}} \mathord{\left/ {\vphantom {{\partial {{w}_{x}}} {\partial z}}} \right. \kern-0em} {\partial z}} + {{\partial {{w}_{z}}} \mathord{\left/ {\vphantom {{\partial {{w}_{z}}} {\partial x}}} \right. \kern-0em} {\partial x}})}}^{2}} + 2{{{({{\partial {{w}_{z}}} \mathord{\left/ {\vphantom {{\partial {{w}_{z}}} {\partial z}}} \right. \kern-0em} {\partial z}})}}^{2}}} \right] \\ {{\Sigma }_{o}} = 2\eta _{o}^{2}\left[ {2{{{({{\partial {{{v}}_{x}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{x}}} {\partial x}}} \right. \kern-0em} {\partial x}})}}^{2}} + {{{({{\partial {{{v}}_{x}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{x}}} {\partial z}}} \right. \kern-0em} {\partial z}} + {{\partial {{{v}}_{z}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{z}}} {\partial x}}} \right. \kern-0em} {\partial x}})}}^{2}} + 2{{{({{\partial {{{v}}_{z}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{z}}} {\partial z}}} \right. \kern-0em} {\partial z}})}}^{2}}} \right] \\ \end{gathered} $

В выражениях (2.7) и (2.8) величины ${{\rho }_{w}}{{L}_{w}}D{{H}^{2}}g{\text{/}}2$ и ${{L}_{w}}D{{\sigma }_{{aw}}}$ описывают потенциальную и поверхностную энергии воды до помещения на нее нефтяного пятна. Отбрасывание этих членов и перенос начала оси $z$ на исходную поверхность воды, и, с учетом того, что протяженность акватории существенно больше протяженности разлива, устремляя размер системы к бесконечности (${{L}_{w}} \to \infty \sim {{L}_{*}} \to 0$), а также вводя для сокращения записи обозначение ${{L}_{0}} = L(t)$, получаем окончательные выражения для энергетических характеристик одномерного нефтяного разлива

(2.12)

$\Pi = \frac{{{{M}_{o}}g}}{2}h(1 - \rho ),$

где ${{M}_{o}}$ – масса нефти, постоянная величина,

(2.13)

${{E}_{S}} = LD\left( {{{\sigma }_{{ow}}} + {{\sigma }_{{oa}}} - {{\sigma }_{{aw}}}} \right) = {{M}_{o}}g\frac{{\lambda _{S}^{2}}}{h}{\text{sgn}}\left( {{{\sigma }_{{ow}}} + {{\sigma }_{{oa}}} - {{\sigma }_{{aw}}}} \right),$

где ${{\lambda }_{S}} = \sqrt {\left| {{{\sigma }_{{ow}}} + {{\sigma }_{{oa}}} - {{\sigma }_{{aw}}}} \right|{\text{/}}{{\rho }_{o}}g} $ – капиллярная постоянная контактной линии “нефть–вода–воздух”

(2.14)

${\rm T} = \frac{D}{2}\left[ {{{\rho }_{w}}\int\limits_{{{L}_{o}}}^\infty {\int\limits_{ - H}^0 {{{{\mathbf{w}}}^{2}}dxdz} } + {{\rho }_{w}}\int\limits_0^{{{L}_{o}}} {\int\limits_{ - H}^{{{h}_{ - }}} {{{{\mathbf{w}}}^{2}}dxdz} } + {{\rho }_{o}}\int\limits_0^{{{L}_{o}}} {\int\limits_{{{h}_{ - }}}^{{{h}_{ + }}} {{{{\mathbf{v}}}^{2}}dxdz} } } \right]$

(2.15)

${{\dot {E}}_{\nu }} = \frac{D}{{2{{\eta }_{w}}}}\left[ {\int\limits_{{{L}_{o}}}^\infty {\int\limits_{ - H}^0 {{{\Sigma }_{w}}dxdz} } + \int\limits_0^{{{L}_{o}}} {\int\limits_{ - H}^{{{h}_{ - }}} {{{\Sigma }_{w}}dxdz} } } \right] + \frac{D}{{2{{\eta }_{o}}}}\int\limits_0^{{{L}_{o}}} {\int\limits_{{{h}_{ - }}}^{{{h}_{ + }}} {{{\Sigma }_{o}}dxdz} } $

Уравнение динамики энергии системы имеет вид

(2.16)

$\frac{\partial }{{\partial t}}\left( {{\rm T} + \Pi + {{E}_{S}}} \right) = - {{\dot {E}}_{\nu }}$

Для того, чтобы система уравнений (2.1), (2.2), (2.11)–(2.16) приводила к конструктивным результатам, необходимо задаться моделью поля скорости в нефти и воде.

Поле скорости в нефти должно удовлетворять граничным условиям вида

(2.17)

${{\left. {{{{v}}_{x}}} \right|}_{{x = 0}}} = 0,\quad {{\left. {{{{v}}_{x}}} \right|}_{{x = L(t)}}} = \dot {L}(t),\quad {{\left. {{{{v}}_{z}}} \right|}_{{z = {{h}_{ \pm }}(t)}}} = {{\dot {h}}_{ \pm }}(t)$

(2.18)

$\begin{gathered} {{\left. {{{w}_{x}}} \right|}_{{x = 0}}} = 0,\quad {{\left. {{{w}_{x}}} \right|}_{{x = L,\,z \in [{{h}_{ - }},0]}}} = \dot {L},\quad {{\left. {{{w}_{z}}} \right|}_{{z = 0,\,r > L}}} = 0,\quad {{\left. {{{w}_{z}}} \right|}_{{z = {{h}_{ - }},\,r \leqslant L}}} = {{{\dot {h}}}_{ - }} \\ {{\left. {\mathbf{w}} \right|}_{{x = \infty }}} = 0,\quad {{\left. {\mathbf{w}} \right|}_{{z = - H}}} = 0, \\ \end{gathered} $

где точка над символом обозначает производную по времени.

Распределение скорости в нефти с учетом вязкого увлечения воды задается выражением [9]

(2.19)

$\begin{gathered} {{{v}}_{x}} = \frac{{\dot {L}}}{L}x\left( {1 - {{\kappa }_{{ow}}}\operatorname{erfc} ({{\zeta }_{o}})} \right) \\ {{{v}}_{z}} = {{{\dot {h}}}_{ - }} - 2\frac{{\dot {L}}}{L}\sqrt {{{\nu }_{o}}t} \left[ {{{\zeta }_{o}}(1 - {{\kappa }_{{ow}}}\operatorname{erfc} ({{\zeta }_{o}})) + \frac{{{{\kappa }_{{ow}}}}}{{\sqrt \pi }}{{{\text{e}}}^{{ - \zeta _{o}^{2}}}}} \right], \\ \end{gathered} $

а в воде распределение скорости при $0\,\, \leqslant \,\,x\,\, \leqslant \,\,L(t)$ имеет вид

(2.20)

$\begin{gathered} {{w}_{x}} = \frac{{\dot {L}}}{L}x{{\kappa }_{{wo}}}\operatorname{erfc} \left( {{{\zeta }_{w}}} \right) + \frac{{\partial {{\Phi }_{w}}}}{{\partial x}} \\ {{w}_{z}} = 2{{\kappa }_{{wo}}}\frac{{\dot {L}}}{L}\sqrt {{{\nu }_{w}}t} \left[ {{{\zeta }_{w}}\operatorname{erfc} ({{\zeta }_{w}}) - \frac{1}{{\sqrt \pi }}{{{\text{e}}}^{{ - \zeta _{w}^{2}}}}} \right] + \frac{{\partial {{\Phi }_{w}}}}{{\partial z}}, \\ \end{gathered} $

где введены обозначения

(2.21)

${{\zeta }_{o}} = \frac{{z - {{h}_{ - }}}}{{2\sqrt {{{\nu }_{o}}t} }},\quad {{\zeta }_{w}} = \frac{{{{h}_{ - }} - z}}{{2\sqrt {{{\nu }_{w}}t} }},\quad {{\kappa }_{{ow}}} = \frac{{{{\rho }_{w}}\sqrt {{{\nu }_{w}}} }}{{{{\rho }_{o}}\sqrt {{{\nu }_{o}}} + {{\rho }_{w}}\sqrt {{{\nu }_{w}}} }},\quad {{\kappa }_{{wo}}} = 1 - {{\kappa }_{{ow}}}$

Расчет кинетической энергии по соотношению (2.14) дает величину главного члена (без учета той части кинетической энергии воды, которая обусловлена сопротивлением формы нефтяного пятна)

(2.22)

$T = \frac{{{{M}_{o}}{{\alpha }^{2}}}}{6}{{\dot {L}}^{2}},\quad {{\alpha }^{2}} = {{\left( {1 - {{\kappa }_{{ow}}}\operatorname{erfc} ({{\zeta }_{h}})} \right)}^{2}},\quad {{\zeta }_{h}} = \frac{h}{{2\sqrt {{{\nu }_{o}}t} }}$

Мощность производства кинетической энергии воды за счет сопротивления формы нефтяного пятна при его растекании определяется выражением

(2.23)

${{P}_{{kw}}} = {{C}_{{sh}}}{{\dot {L}}^{2}},$

где ${{C}_{{sh}}}$ – коэффициент сопротивления формы.

Анализ составляющих уравнения (2.16) и использование приближений, подобных тем, которые были проведены в случае с азимутально симметричным пятном [9], приводят к уравнению вида

(2.24)

$\ddot {L} + 2{{a}^{2}}\dot {L} - \frac{{{{b}^{2}}}}{{{{L}^{2}}}} + {{c}^{2}}\operatorname{sgn} (\sigma ) = 0,$

где введены обозначения

(2.25)

${{a}^{2}} = \frac{{3{{C}_{f}}}}{{2{{M}_{o}}{{\alpha }^{2}}}},\quad {{b}^{2}} = \frac{{3gV(1 - \rho )}}{{2D{{\alpha }^{2}}}},\quad {{c}^{2}} = \frac{{3gD\lambda _{s}^{2}}}{{V{{\alpha }^{2}}}}$

В качестве начальных условий для уравнения (2.24) выбираются значения длины разлива $L$ и скорости его края $\dot {L}$ в некоторый начальный момент времени

(2.26)

${{\left. L \right|}_{{t = 0}}} = {{L}_{0}},\quad {{\left. {\dot {L}} \right|}_{{t = 0}}} = {{L}_{1}}$

I. Сначала рассматривается случай разлива конечных размеров, когда $\operatorname{sgn} \sigma = 1$. Положение равновесия задается величиной ${{L}_{*}} = {c \mathord{\left/ {\vphantom {c b}} \right. \kern-0em} b}$.

I.1. Начальные моменты времени разлива. В этом случае толщина нефтяного пятна $h$ существенно больше капиллярной постоянной ${{\lambda }_{s}}$ и последним членом в уравнении (2.24) можно пренебречь, так что справедливо приближенное уравнение

(2.27)

$\ddot {L} + 2{{a}^{2}}\dot {L} - \frac{{{{b}^{2}}}}{{{{L}^{2}}}} = 0,$

решение которого имеет вид

(2.28)

$L = \frac{{3{{L}_{0}}}}{2} + \frac{{{{e}^{{ - {{a}^{2}}t}}}}}{\rho }\left\{ {\begin{array}{*{20}{c}} {{{L}_{1}}\sin (\rho t) - \frac{{{{L}_{0}}\rho }}{2}\left( {\cos (\rho t) + {{a}^{2}}\frac{{\sin (\rho t)}}{\rho }} \right),\quad {{a}^{4}} - \frac{{2{{b}^{2}}}}{{L_{0}^{3}}} < 0} \\ {{{L}_{1}}\operatorname{sh} (\rho t) - \frac{{{{L}_{0}}\rho }}{2}\left( {\operatorname{ch} (\rho t) + {{a}^{2}}\frac{{\operatorname{sh} (\rho t)}}{\rho }} \right),\quad {{a}^{4}} - \frac{{2{{b}^{2}}}}{{L_{0}^{3}}} > 0,} \end{array}} \right.$

где $\rho = \sqrt {\left| {{{a}^{4}} - {{2{{b}^{2}}} \mathord{\left/ {\vphantom {{2{{b}^{2}}} {L_{0}^{3}}}} \right. \kern-0em} {L_{0}^{3}}}} \right|} $.

На малых временах оба соотношения (2.28) описывают единое поведение размера нефтяного пятна во времени

$L = {{L}_{0}} + {{L}_{1}}t + \frac{{{{b}^{2}} - 2{{L}_{1}}L_{0}^{2}{{a}^{2}}}}{{2L_{0}^{2}}}{{t}^{2}} + o\left( {{{t}^{2}}} \right),$

которое определяется относительными вкладами гравитационных, инерциальных эффектов и явлением сопротивления формы нефтяного пятна.

I.2. Вблизи положения равновесия решение принимает вид

(2.29)

$L = {{L}_{*}} + {{{\text{e}}}^{{ - {{a}^{2}}t}}}\left\{ {\begin{array}{*{20}{l}} {A\cos (\rho t) + B\sin (\rho t),\quad {{a}^{4}} - \frac{{2{{b}^{2}}}}{{L_{*}^{3}}} < 0} \\ {A\operatorname{ch} (\rho t) + B\operatorname{sh} (\rho t),\quad {{a}^{4}} - \frac{{2{{b}^{2}}}}{{L_{*}^{3}}} > 0,} \end{array}} \right.$

где $\rho = \sqrt {\left| {{{a}^{4}} - {{2{{b}^{2}}} \mathord{\left/ {\vphantom {{2{{b}^{2}}} {L_{*}^{3}}}} \right. \kern-0em} {L_{*}^{3}}}} \right|} $.

II. Теперь рассматривается случай разлива неограниченных размеров, когда $\operatorname{sgn} \sigma = - 1$. Положение равновесия отсутствует.

II.1. Начальные моменты времени разлива. В этом случае так же, как и в случае I.1 толщина нефтяного пятна $h$ существенно больше капиллярной постоянной ${{\lambda }_{s}}$ и искомое решение совпадает с решением (2.28).

II.2. На больших временах, когда $L \gg {{L}_{*}}$, в уравнении (2.24) можно пренебречь членом ${{{{b}^{2}}} \mathord{\left/ {\vphantom {{{{b}^{2}}} {{{L}^{2}}}}} \right. \kern-0em} {{{L}^{2}}}}$, в результате чего это уравнение приобретает вид

(2.30)

$\ddot {L} + 2{{a}^{2}}\dot {L} - {{c}^{2}} = 0$

Пусть в некоторый “начальный” момент времени $t = {{t}_{*}}$ (отличающийся от начального момента разлива, чтобы выполнялось условие $L \gg {{L}_{*}}$) и при $t \to \infty $ выполняются условия

(2.31)

${{\left. L \right|}_{{t = {{t}_{*}}}}} = {{L}_{0}},\quad {{\left. {\dot {L}} \right|}_{{t = {{t}_{*}}}}} = {{L}_{1}},\quad \mathop {\lim }\limits_{t \to \infty } L = \infty $

Тогда решение задачи (2.30, 2.31) представимо в форме

(2.32)

$L = {{L}_{0}} + \frac{{{{c}^{2}}}}{{4{{a}^{4}}}}\left( {2{{a}^{2}}\left( {t - {{t}_{*}}} \right) - 1 + {{\operatorname{e} }^{{ - 2{{a}^{2}}\left( {t - {{t}_{*}}} \right)}}}} \right) + \frac{{{{L}_{1}}}}{{2{{a}^{2}}}}\left( {1 - {{e}^{{ - 2{{a}^{2}}\left( {t - {{t}_{*}}} \right)}}}} \right),$

причем, согласно выражению для скорости роста разлива, получаемого дифференцированием (2.32)

(2.33)

$\dot {L} = \frac{{{{c}^{2}}}}{{2{{a}^{2}}}}\left( {1 - {{\operatorname{e} }^{{ - 2{{a}^{2}}\left( {t - {{t}_{*}}} \right)}}}} \right) + {{L}_{1}}{{\operatorname{e} }^{{ - 2{{a}^{2}}\left( {t - {{t}_{*}}} \right)}}}\mathop \to \limits_{t \to \infty } \frac{{{{c}^{2}}}}{{2{{a}^{2}}}},$

на больших временах имеет место линейное приращение площади разлива, что отличается от экспоненциального приращения площади аксиально симметричного нефтяного пятна [9, 10].

3. Экспериментальные результаты и сравнение с аналитической моделью. В эксперименте использовалось машинное масло Volga M8B-SAE 20 API (${{\rho }_{{\text{o}}}} = 883.7$ кг/м³, ${{\nu }_{o}} = 3.34 \times {{10}^{{ - 4}}}$ м²/с, при температуре $T = 20^\circ {\text{C}}$) и сырая нефть Мамонтовского месторождения (${{\rho }_{{\text{o}}}} = 878.0$ кг/м³, ${{\nu }_{o}} = 2.15 \times {{10}^{{ - 5}}}$ м²/с, при температуре $T = 20^\circ {\text{C}}$). В опытах использовался пластиковый контейнер (0.29 × 0.08 × 0.08 м), который заполнялся дегазированной водой, температурой $T = 20^\circ {\text{C}}$.

Экспериментальный метод включал нанесение различных количеств (5, 10, 15 мл) моторного масла Volga M8B-S AE 20 API и сырой нефти Мамонтовского месторождения на поверхность воды площадью 37.35 см², ограниченной пластиковой перегородкой, после устранения которой, растекание происходит только в одном направлении.

На фотографии рис. 2 показана экспериментальная кювета, заполненная водой с нефтью (темная область в левой части кюветы) в первые моменты времени после устранения ограничивающей перегородки.

Рис. 2.

Фото экспериментальной кюветы с нанесенной на воду нефтью и убранной перегородкой.

Ход экспериментов записывался с помощью цифровой камеры в автоматическом режиме, съемка велась с частотой 360 кадров в минуту, а полученные последовательности кадров обрабатывались и анализировались. Положение пятна нефтепродуктов регистрировали с использованием метода фотометрии обработанных изображений, полученных из исходных кадров методами пакетной обработки.

Рис. 3,а иллюстрирует поведение размера пятна нефтепродукта в случае, когда выполняется условие ${{a}^{4}} - {{2{{b}^{2}}} \mathord{\left/ {\vphantom {{2{{b}^{2}}} {L_{*}^{3}}}} \right. \kern-0em} {L_{*}^{3}}} > 0$ (машинное масло) и возможно положение равновесия. Здесь и далее экспериментальные результаты представлены после численной обработки методом [11], устраняющим погрешности измерений при наличии различных временных масштабов, проявляющихся в исследуемом явлении. Рис. 3,а показывает хорошее качественное совпадение теоретических и экспериментальных данных изменения площади масляного пятна. Количественное сравнение результатов крайне затруднено отсутствием необходимых численных значений физических характеристик нефтепродуктов, так как производители машинных масел и нефти не могут их предоставить. По этой же причине не указаны количественные отсчеты на теоретических графиках.

Рис. 3

а: Ограниченный рост пятна машинного масла. – сплошная кривая; б: Неограниченный рост пятна сырой нефти. – сплошная кривая слева а: теория (2.28); б: теория (2.32) для больших времен; справа наборы измерительных экспериментальных точек.

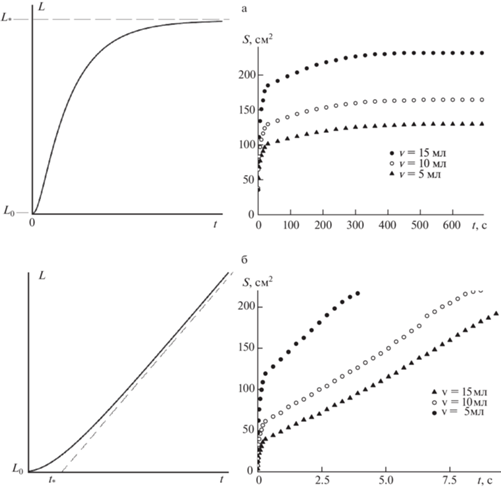
При обратном отношении ${{a}^{4}} - {{2{{b}^{2}}} \mathord{\left/ {\vphantom {{2{{b}^{2}}} {L_{*}^{3}}}} \right. \kern-0em} {L_{*}^{3}}} < 0$ изменение размеров нефтяного пятна отличается затухающим колебательным характером вблизи положения равновесия. Затухание колебаний связано с генерацией движения воды за счет сопротивления формы нефтяного пятна при его распространении по поверхности воды. Необходимо отметить, что в рассмотренных случаях характер поведения размера пятна качественно совпадает с поведением площади нефтяного пятна при аксиально симметричном разливе [9, 10].

Результаты теоретических расчетов и экспериментов с сырой нефтью приведены на рис. 3,б. В экспериментах отклонение закона роста площади пятна от линейного на конечных этапах разлива (рис. 3,б) связано с приближением края пятна к концу экспериментального контейнера, где структура течения в воде заведомо отличается от теоретической модели, в которой контейнер имеет неограниченные размеры.

Сравнение графиков рис. 3,б показывает совпадение теоретических и экспериментальных результатов – на основной и завершающей стадиях роста нефтяного пятна увеличение его площади происходит по линейному закону, в отличие от экспоненциального закона роста, наблюдаемом при двумерном осесимметричном разливе [9, 10].

Заключение. Подобно двумерному осесимметричному растеканию квазиодномерное растекание проявляет наличие тех же характерных режимов: ограниченное растекание с монотонным или колебательным характером стремления к предельному размеру пятна машинного масла и неограниченное растекание сырой нефти.

В отличие от неограниченного двумерного осесимметричного растекания сырой нефти, когда скорость роста площади пятна подчиняется экспоненциальному закону [9, 10], в одномерном случае имеет место линейная зависимость площади от времени.

Работа выполнена в рамках госзадания FFGN-2023-0006.

Список литературы

Fay J.A. The spreading of oil slicks on a calm sea from oil on the sea // in: Oil on the Sea / Ed. by Hoult D.P. New York: Plenum Press, 1969. P. 53–64.
Garrett W.D., Berger W.R. Factors affecting the use of monomolecular surface films to control oil pollution on water // Environ. Sci. & Technol. 1970. V. 4. Iss. 2. P. 123–127.
Cross R.H., Hoult D.P. Collection of oil slicks // in: Harbours and Coastal Engineering Division / Ed. by Waterways J. ASCE. 1971. V. 97. P. 313.
Hoult D.P. Oil spreading on the sea // Annu. Rev. Fluid Mech. 1972. V. 4. P. 341–368.
Buckmaster J. Viscous-gravity spreading of an oil slick // J. Fluid Mech. 1973. V. 59. Pt. 3. P. 481–491.
DiPietro N.D., Huh C., Cox R.G. The hydrodynamics of the spreading of one liquid on the surface of another // J. Fluid Mech. 1978. V. 84. Pt. 3. P. 529–549.
Hoult D.P., Suchon W. The spread of the oil in a channel // Fluid Mech. Lab. Rep. Dept. Mech. Engng. MIT. 1970. 25 p.
Huh C., Inoue M., Mason S.G. Unidirectional spreading of one liquid on the surface of another // Canad. J. Chem. Engng. 1975. V. 53. P. 367–371.
Кистович А.В., Чаплина Т.О., Пахненко В.П. Радиальное растекание нефтепродуктов по поверхности воды // ПММ. 2022. Т. 86. № 6. С. 956–974.
Кистович А.В., Чаплина Т.О., Пахненко В.П. Растекание технических масел и сырой нефти по поверхности воды // Докл. РАН. 2023. Т. 508. № 2. С. 290–296. https://doi.org/10.31857/S2686739722601211
Солодкий Д.А., Кистович А.В. Модифицированный сдвиговый алгоритм обработки измерительных данных // Измер. техн. 2014. № 11. С. 43–47.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал