Прикладная математика и механика, 2023, T. 87, № 6, стр. 1014-1027

1. Введение. Эффект релаксации поверхностного натяжения полярной жидкости, называемый также эффектом динамического поверхностного натяжения, заключается в изменении его величины между равновесным значением и некоторым максимальным, достигаемым при разрушении приповерхностного двойного электрического слоя. Этот эффект основан на том, что ориентирующее действие поверхность жидкости оказывает на диполи отдельных молекул: в приповерхностном слое молекулы выстраиваются отрицательно заряженными концами диполей молекул наружу [1, стр. 47], в результате электростатического квадрупольно-дипольного взаимодействия. При этом величина коэффициента поверхностного натяжения достигает наименьшего значения. При силовом воздействии на поверхность жидкости упорядоченность диполей разрушается, и величина коэффициента поверхностного натяжения, измеряемого плотностью свободной энергии поверхности жидкости, увеличивается. Время, необходимое для восстановления равновесной структуры приповерхностного слоя, называется временем релаксации.

Сам эффект релаксации поверхностного натяжения начал исследоваться еще в начале прошлого XX века (см., дискуссию [2, 3], и приведенные там ссылки).

Эффект динамического поверхностного натяжения изучается уже более ста лет [1–8], но вопрос об изменении закономерностей распространения капиллярных приповерхностных волн и потери ими устойчивости при его учете, остается открытым.

2. Физическая постановка задачи. Рассмотрим бесконечную струю радиусом R несжимаемой, электропроводной жидкости с плотностью ρ, коэффициентом поверхностного натяжения σ, движущуюся со скоростью $\vec {U}$ вдоль оси симметрии невозмущенной струи в вакууме. Для упрощения математических выкладок жидкость будем считать идеальной. Примем, что в области пространства вокруг струи жидкости имеется электростатическое поле, вектор напряженности которого перпендикулярен невозмущенной цилиндрической свободной поверхности струи ${{\vec {E}}_{0}} = {{E}_{0}}{{\vec {e}}_{r}}$, что приводит к появлению поверхностного заряда с поверхностной плотностью ${{\chi }_{0}}$.

Все нижеследующее рассмотрение проведем в цилиндрической системе координат $(r,\varphi ,z)$, в которой ось $z$ направлена вдоль оси симметрии невозмущенной струи, а начало системы координат движется вместе со струей со скоростью струи.

В реальных (не идеализированных) условиях поверхность струи возмущена капиллярным волновым движением, возникающим уже в силу теплового движения молекул [9]. Амплитуда капиллярных волн теплового происхождения $\xi (z,\varphi ,t)$ определяется соотношением $\left| {\xi (z,\varphi ,t)} \right|\sim \sqrt {\kappa T{\text{/}}\sigma } $, где $\kappa $ – постоянная Больцмана, $T$ – абсолютная температура [9]. Для большинства жидкостей амплитуда тепловых осцилляций $\left| {\xi (z,\varphi ,t)} \right|$ не превышает ${{10}^{{ - 8}}}$ см.

Во введенной системе координат форма поверхности струи будет описываться уравнением $r = R + \xi (z,\varphi ,t)$, движение жидкости будет определяться капиллярными волнами на поверхности струи. Зададимся целью исследовать возможные движения жидкости в описанной системе.

Примем также, что в жидкости реализуется эффект динамического поверхностного натяжения. В экспериментах [4–8] найдено, что характерное время релаксации поверхностного натяжения различных жидкостей ${{\tau }_{r}}$ (время установления упорядоченности диполей на поверхности жидкости), составляет ${{10}^{{ - 5}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 3}}}$ с, а максимальное значение динамического поверхностного натяжения ${{\sigma }_{\infty }}$ на четверть величины выше его равновесного значения ${{\sigma }_{0}}$ [8]. Поэтому для численных оценок в нижеследующем изложении примем значения: ${{\tau }_{r}} = {{10}^{{ - 4}}}$ с, ${{\sigma }_{0}} = 73$ дин/см, ${{\sigma }_{\infty }} \approx 90$ дин/см, ${{\sigma }_{*}}$ = = ${{\sigma }_{\infty }} - {{\sigma }_{0}}$ ≈ 17 дин/см, характерные для воды.

Принимая во внимание, что в результате разрушения двойного электрического слоя коэффициент поверхностного натяжения изменяется от равновесного до максимального значений, динамический коэффициент поверхностного натяжения $\sigma \left( t \right)$ можно представить в виде суммы величины коэффициента поверхностного натяжения равновесной поверхности струи и добавки, связанной с разрушением упорядоченности дипольных молекул в приповерхностном слое:

Временная зависимость (с характерным временем релаксации ${{\tau }_{r}}$) показывает, что в начальный момент времени при полном разрушении порядка в ориентации приповерхностных диполей максимальное значение коэффициента поверхностного натяжения составляет ${{\sigma }_{\infty }} = {{\sigma }_{0}} + {{\sigma }_{*}}$. Но по прошествии времени порядка ${{\tau }_{r}}$ ориентация диполей восстанавливается и поверхностное натяжение снижается до ${{\sigma }_{0}}$.

Как уже упоминалось выше эффект релаксации поверхностного натяжения жидкости объясняется отклонением строения приповерхностной структуры мгновенно деформированной поверхности от ее равновесного состояния. Известно, что лапласовское давление определяет связь между изменением давления $\Delta P$ под искривленной капиллярным волновым движением поверхностью жидкости с кривизной поверхности $u(t)$. Эффект релаксации приповерхностной структуры жидкости можно связать с тем фактом, что жидкость при весьма коротких временах воздействия обладает как вязкими, так и упругими свойствами [11]. В такой ситуации можно воспользоваться известным для вязкоупругих жидкостей принципом суперпозиции Больцмана [10, 11], согласно которому “текущее напряжение определяется суперпозицией откликов на полный спектр приращений деформации”, то есть текущее напряжение определяется всей историей деформации среды. Это позволяет записать соотношение, связывающее мгновенное изменение капиллярного давления на поверхности жидкости $\Delta {{P}_{1}}\left( t \right)$ с историей изменения ее кривизны $u\left( t \right)$ [10, 11]:

Подстановка (2.1) в (2.2) и применение прямого преобразования Фурье к результату такой подстановки позволяет перейти от временной зависимости величины поверхностного натяжения к частотной. В результате комплексный коэффициент поверхностного натяжения $\sigma $ запишем в соответствие с известной формулой Максвелла [10]:

В (2.1), (2.3) введены обозначения: $i$ – мнимая единица, ${{\tau }_{r}}$ – характерное время релаксации (время, за которое мгновенно деформированный приповерхностный слой жидкости возвращается в равновесное состояние), ${{\sigma }_{0}}$ – значение коэффициента поверхностного натяжения равновесной структуры поверхности жидкости (для нулевой частоты), ${{\sigma }_{\infty }}$ – максимальное значение коэффициента поверхностного натяжения для весьма высоких частот, соответствующих неравенству ${{\omega }_{n}}{{\tau }_{r}} \gg 1$.

3. Математическая постановка задачи. Математическая постановка задачи для идеальной несжимаемой идеально проводящей жидкости будет состоять из уравнения Эйлера

уравнения непрерывности: уравнений Максвелла:

Граничные условия к выписанным уравнениям будут иметь вид:

на свободной поверхности электропроводной струи: кинематическое: $\left( {\vec {n}(z,\varphi ,t),\vec {V}(z,\varphi ,t)} \right) = \frac{{\partial \xi (z,\varphi ,t)}}{{\partial t}}$.

динамическое: $P(z,\varphi ,t) - {{P}_{{атм}}} + {{P}_{Е}}(z,\varphi ,t) = {{P}_{\sigma }}(z,\varphi ,t)$;

условия на границе проводник–диэлектрик:

В выписанных соотношениях $\vec {V}(r,z,\varphi ,t)$ – поле скоростей в объеме жидкости, $\vec {V}(z,\varphi ,t)$ – скорость на свободной поверхности струи, $P(r,z,\varphi ,t)$ – гидродинамическое давление в объеме жидкости, $P(z,\varphi ,t)$ – давление на свободной поверхности струи, $\vec {E}(r,z,\varphi ,t)$ – напряженность приложенного электрического поля в объеме внутри и вне струи, $\vec {E}(z,\varphi ,t)$ – напряженность приложенного электрического поля на свободной поверхности струи, ${{P}_{{{\text{атм}}}}}$ – атмосферное давление, ${{P}_{\sigma }}(z,\varphi ,t)$ – давление сил поверхностного натяжения; $\chi $ – поверхностная плотность электрического заряда.

Решение задачи проведем в безразмерных переменных, в которых $R = \rho = \sigma $ = 1. За всеми физическими величинами оставим прежние обозначения, а их численные величины будут выражаться в долях своих характерных размеров.

Введем малый параметр $\varepsilon $: отношение максимальной амплитуды капиллярных волн к радиусу струи: $\varepsilon \equiv \max {{\left| \xi \right|} \mathord{\left/ {\vphantom {{\left| \xi \right|} R}} \right. \kern-0em} R}$.

4. Дисперсионное уравнение без учета эффекта динамического поверхностного натяжения. Раскладывая сформулированную задачу по малому параметру $\varepsilon $, несложно выделить задачи нулевого и первого порядков малости [12].

Решение задачи нулевого порядка определяет невозмущенную цилиндрическую струю, движущуюся вдоль оси симметрии со скоростью $\vec {U}$, с равномерно распределенным по ее поверхности электрическим зарядом, создающим электростатическое поле в окрестности струи, стремящееся к нулю при удалении от поверхности струи на бесконечность.

В первом порядке малости по $\varepsilon $ будем искать решение стандартными методами (см., напр., [12, 13]).

В указанном приближении решения задачи (3.1), удовлетворяющие граничным условиям (3.2), для возмущения границы раздела сред $\xi \left( {\varphi ,z,t} \right)$, и добавок к гидродинамическому потенциалу в струе $\psi (\vec {r},t)$, и к электрическому потенциалу $\Phi (\vec {r},t)$ будем искать в виде

где $m$ – азимутальный параметр; ${{\omega }_{{0m}}}(k)$ – частота капиллярных волн; $k$ – волновое число; ${{\xi }_{0}}$ – начальная амплитуда; $b,c$ – неизвестные коэффициенты; ${{I}_{m}}\left( {kr} \right)$ и ${{K}_{m}}\left( {kr} \right)$ – модифицированные функции Бесселя первого и второго рода, порядка $m$ [14].

Находя значения коэффициентов $b,c$ и подставляя решения в систему граничных условий задачи, можно получить дисперсионное уравнение для капиллярных волн с произвольными азимутальными числами $m$ на поверхности струи без учета эффекта релаксации поверхностного натяжения:

где штрих у функций Бесселя обозначает производную по аргументу; $w$ – безразмерный параметр, характеризующий устойчивость струи по отношению к заряду на ее поверхности.

5. Дисперсионное уравнение с учетом эффекта динамического поверхностного натяжения. Дисперсионное соотношение с учетом динамического поверхностного натяжения найдем по аналогии с [10, 15].

Перейдем к размерному квадрату частоты. Для этого необходимо квадрат безразмерной частоты $\omega _{{0m}}^{2}(k)$ умножить на квадрат масштаба обезразмеривания частоты:

где ${{\sigma }_{0}}$ – коэффициент поверхностного натяжения на нулевой частоте (статическое).

Поменяем в формуле (5.1) статическое поверхностное натяжение ${{\sigma }_{0}}$ на динамическое как это было сделано в [10, 15]:

где $\omega $ и ${{\tau }_{r}}$ – частота и характерное время релаксации, для получения которого в безразмерной форме следует разделить его на масштаб измерения времени [T] = = $\sqrt {\rho {{R}^{3}}{\text{/}}{{\sigma }_{0}}} $.

Подставив (5.2) в (5.1), получим размерную частоту с коэффициентом динамического поверхностного натяжения.

Вновь вернемся к безразмерной частоте, используя масштаб обезразмеривания частоты $[\omega ] = \sqrt {\frac{{{{\sigma }_{0}}}}{{\rho {{R}^{3}}}}} $:

при $\omega {{\tau }_{r}} \ll 1$ квадрат частоты стремится к “статическому” значению ${{\omega }^{2}} \to \omega _{0}^{2}$.

Введем новое обозначение $\Sigma \equiv {{\sigma }_{\infty }}{\text{/}}{{\sigma }_{0}}$, тогда дисперсионное уравнение с учетом эффекта динамического поверхностного натяжения примет вид:

где $\omega _{{0m}}^{2}(k)$ – определено (4.1).

Таким образом, полное дисперсионное соотношение с учетом динамического поверхностного натяжения принимает вид:

Несложно видеть, что общая степень дисперсионного уравнения по сравнению с (4.1) увеличилась на единицу, а кроме того некоторые его коэффициенты стали не вещественными, а комплексными, что может существенно изменить решения.

Интересно отметить, что дисперсионное уравнение для струи зависит от азимутального параметра $m$ [16]. Этим струя отличается от капли, для которой дисперсионное уравнение оказывается вырожденным по азимутальному параметру [17, 18]. Упомянутое различие между каплей и струей не единственное: они по разному ведут себя в смысле устойчивости по отношению к собственному электрическому заряду [17, 19] и по отношению к спонтанному разбиению на капли [19–23].

Согласно [17] сферическая капля устойчива по отношению к собственному заряду вплоть до очень больших его значений, оставаясь сферической. Критический для реализации неустойчивости заряд определяется критерием Рэлея:

При больших значениях параметра Рэлея $W$, удовлетворяющих записанному выше неравенству, капля вытягивается в фигуру типа сфероида вращения и сбрасывает около четверти заряда и примерно пять процентов массы в виде струйки мелких капелек [20], как это и наблюдается в экспериментах [20–22].

Качественно подобным образом ведут себя и незаряженные капли, помещенные в сильное внешнее однородное электростатическое поле [22].

Струя ведет себя иначе. Она изначально неустойчива, например, для нулевой азимутальной моды ($m = 0$) распадается на капли даже в отсутствии заряда [19], так как поверхностная потенциальная энергия сил поверхностного натяжения струи больше чем потенциальная энергия совокупности капель, имеющих суммарный объем, равный объему распадающегося на капли участка струи, и распад на отдельные капли энергетически выгоден. Закономерности распада струи на отдельные капли зависят от номера азимутальной моды, как это показано на рис. 1. Видно, что для азимутальной моды с $m = 0$ имеет место последовательный отрыв капель с торца струи, для моды с $m = 1$ свободный конец струи движется “хлыстообразно”, и капли отрываются с его торца, а для $m = 2$ распад на капли происходит через выброс боковых дочерних струек, который начинается при очень больших значениях заряда (приходящегося на единицу длины струи), при которых зажигается коронный разряд у поверхности струи, как это отмечается в экспериментах [23].

6. Численный анализ. Для более детального исследования влияния эффекта релаксации поверхностного натяжения на закономерности реализации капиллярных волн на струе и ее устойчивость построим по полученным дисперсионным уравнениям (4.1) и (5.3) графики для первых трех азимутальных мод.

Значения физических величин, входящих в дисперсионное уравнение (5.3), приняты следующими: радиус струи $R = 100$ мкм, плотность воды $\rho = 1$ г/см³, равновесное статическое поверхностное натяжение воды ${{\sigma }_{0}} = 73$ дин/см, неравновесное (максимальное) поверхностное натяжение воды ${{\sigma }_{\infty }} = 90$ дин/см, характерное размерное время релаксации поверхностного натяжения воды ${{\tau }_{r}} = {{10}^{{ - 4}}}$ с.

Чтобы получить безразмерное время релаксации следует разделить ${{\tau }_{r}}$ на масштаб обезразмеривания времени. При принятых значениях физических величин получим безразмерное значение ${{\tau }_{r}} \approx 0.85$. Безразмерный параметр $\Sigma $ будет иметь величину $\Sigma = 1.23$.

7. Осесимметричная мода. На рис. 2,а в безразмерном виде приведены зависимости вещественных и мнимых частей частоты от волнового числа осесимметричной ($m = 0$) капиллярной волны на поверхности струи без учета явления релаксации, то есть рассчитанные по дисперсионному уравнению (4.1). Сплошными линиями нанесены вещественные части частоты (частоты капиллярных волн), а пунктирными – мнимые: выше оси абсцисс инкремент нарастания возмущения на поверхности струи, ниже оси абсцисс – декремент его затухания.

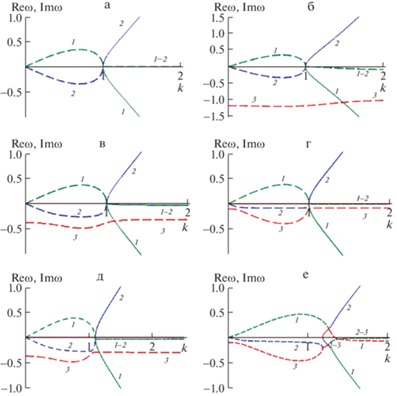
Как уже отмечалось, инкремент соответствует разбиению струи на капли [19]. Что касается декремента (напомним, что речь идет об идеальной жидкости), то на рис. 2,а при изменении $k$ в диапазоне $0 \leqslant k \leqslant 1$ он соответствует передаче энергии от нижней ветви, с убывающей амплитудой возмущения, к ветви с растущей амплитудой, так как жидкость идеальна, а внешних источников энергии для обеспечения роста амплитуды нет.

В диапазоне $k > 1$ имеются две ветви капиллярных волн: “1” и “2”, с нулевыми декрементами.

На рис. 2,б, по сравнению с рис. 2,а, учтена релаксация поверхностного натяжения, приводящая во всем диапазоне изменения $k$ к появлению ветви “3”, соответствующей непериодическому убыванию возмущений на поверхности струи, а также остаются, как и на рис. 2,а, ветви “1” и “2”. Графики на рис. 2,б рассчитаны по дисперсионному уравнению (5.3). Ветвь “3” является чисто релаксационной, как и декременты затухания ветвей “1” и “2” (в диапазоне значений волновых чисел $k > 1$) и роста инкремента – ветви “1” (в диапазоне значений волновых чисел: $0 < k < 1$). Затухание соответствует разрушению упорядоченности диполей в приповерхностном слое.

Известно [1, стр. 47], что ориентация диполей молекул воды в приповерхностном слое не антипараллельная, как было бы при учете только дипольного взаимодействия, а параллельная, что обеспечивается учетом и диполь-квадрупольного взаимодействия. Иными словами, поверхность воды оказывает ориентирующее влияние на диполи воды: они выстраиваются отрицательно заряженными концами наружу. Такая равновесная ориентация диполей обладает определенной свободной энергией, определяющей величину коэффициента поверхностного натяжения жидкости. Достаточно интенсивная капиллярная волна на поверхности струи может разрушить упорядоченность диполей, свободная энергия поверхности струи увеличится (так как поверхность станет неравновесной), а с ней и величина коэффициента поверхностного натяжения. За время порядка характерного времени релаксации ${{\tau }_{r}}$ упорядоченность диполей самопроизвольно восстановится потому, что при этом система переходит в равновесное состояние с меньшей потенциальной энергией поверхности.

На рис. 2,б ветвь “2” при изменении волнового числа $k$ в диапазоне $k \geqslant 1$, соответствует экспоненциально убывающему волновому движению, решение которого обладает вещественной частью и малой отрицательной мнимой частью. В диапазоне $0 \leqslant k \leqslant 1$ эта ветвь соответствует декременту апериодического движения. Ветвь “1” в диапазоне $0 \leqslant k \leqslant 1$ соответствует экспоненциальному росту амплитуды возмущения. Ветвь “3” соответствует чисто затухающему апериодическому движению возмущения поверхности без действительной части во всем диапазоне изменения $k$. Ветви “1” и “2” имеют место в случае отсутствия динамического поверхностного натяжения, при неменяющемся коэффициенте поверхностного натяжения. Ветвь “3” порождена именно динамическим поверхностным натяжением и соответствует апериодическому затуханию возмущений при разрушении упорядоченности диполей молекул воды.

Сама физическая картина снижения амплитуд капиллярных волн и возмущений на поверхности струи идеальной полярной жидкости представляется следующей.

Равновесному состоянию поверхности струи воды соответствует такое, при котором диполи воды параллельны друг другу [1]. При этом свободная энергия сил поверхностного натяжения минимальна [24]. Капиллярные волны на поверхности струи имеют достаточно малую амплитуду и упорядоченности диполей не нарушают. При наличии внешних силовых воздействий на поверхность струи, например, при движении струи относительно материальной среды, амплитуды капиллярных волн вследствие реализации неустойчивости Кельвина–Гельмгольца увеличиваются. В итоге капиллярные волны уже смогут разрушить упорядоченность диполей, и коэффициент поверхностного натяжения воды увеличится [24] примерно на четверть [8], то есть возрастет свободная потенциальная энергия поверхности жидкости.

Если радиус струи уменьшить вдвое, то безразмерное характерное время релаксации примет величину ${{\tau }_{r}} = 2.7$, а график будет иметь вид, приведенный на рис. 2,в. То есть в качественном отношении график на рис. 2,в полностью аналогичен рис. 2,б, изменится лишь диапазон значений по вертикальной оси. Поскольку рисунки строятся в безразмерном виде, то точно такой же вид, как рис. 2,в, будет иметь график, построенный при $R = 10$ мкм и ${{\tau }_{r}} = {{10}^{{ - 5}}}$ с.

При $R = 100$ мкм и размерном характерном времени релаксации ${{\tau }_{r}} = {{10}^{{ - 3}}}$ с график примет вид, приведенный на рис. 2,г. Видно, что декремент затухания ветвей “1” и “2” по сравнению с рис. 2,в немного уменьшится.

В случае заряженной струи, картина корней дисперсионного уравнения останется такой же, однако, область реализации затухающего капиллярного волнового движения смещается по оси абсцисс вправо, тем дальше, чем больше заряд, приходящийся на единицу длины струи, см. рис. 2,д и рис. 2,е. Видно также, что при появлении на струе заряда достаточной величины отдельные ветви начинают взаимодействовать между собой с образованием новых ветвей.

Из рис. 2,а–е видно, что ордината начала третьей ветви (релаксационной) обратно пропорциональна безразмерному характерному времени ${{\tau }_{r}}$.

8. Хлыстообразная асимметричная мода. На рис. 3,а приведен график зависимости частоты капиллярной волны от волнового числа для незаряженной струи с азимутальным числом $m = 1$ в отсутствии учета эффекта релаксации поверхностного натяжения, рассчитанный по дисперсионному уравнению (4.1). Видно, что декременты ветвей “1” и “2” равны нулю.

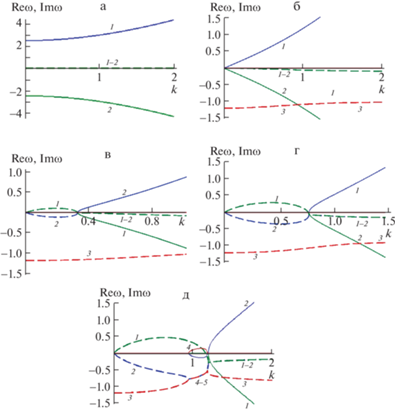
При учете эффекта релаксации поверхностного натяжения рассчитывать график будем по уравнению (5.3) и он будет иметь вид, приведенный на рис. 3,б. По сравнению с рис. 3,а на графике появилась ветвь “3”, а декременты ветвей “1” и “2”, равные друг другу, стали отличным от нуля. Иными словами, при $k > 0$ имеются две ветви капиллярных волн: “1” и “2” (сплошные линии), с отличными от нуля и равными по величине декрементами (пунктирные линии “1, 2”). Это наталкивает на мысль, что декременты капиллярных волн и чисто релаксационных движений все имеют релаксационную природу.

На рис. 3,в–д приведены рассчитанные по (5.3) графики для заряженных струй, с учетом динамического поверхностного натяжения. Из этих рисунков видно, что при появлении заряда на струе область существования капиллярного волнового движения смещается вдоль оси абсцисс в область больших значений волновых чисел (в область более коротких волн). В окрестности начала координат (для длинных капиллярных волн) вдоль оси абсцисс появляется растущая с увеличением величины заряда на единицу длины струи область апериодически растущей неустойчивости, что соответствует отрыву капель. При дальнейшем увеличении величины заряда на струе отдельные ветви начинают взаимодействовать между собой и появляются новые затухающие волновые движения.

9. Электростатическая неустойчивость моды с $m = 2$. На рис. 4,а приведен график зависимости частоты капиллярных волн от волнового числа для незаряженной струи с азимутальным числом $m = 2$ в отсутствии учета эффекта релаксации поверхностного натяжения, рассчитанный по дисперсионному уравнению (4.1). Видно, что инкремент и декремент для незаряженной не релаксирующей струи равны нулю.

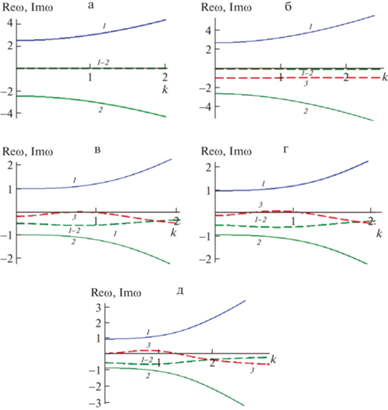
На рис. 4,б уже учтен эффект релаксации поверхностного натяжения, в итоге декременты волнового движения стали отличными от нуля, и появилась еще одна ветвь “3”, соответствующая чисто релаксационному затуханию возмущений поверхности струи.

Появление заряда на струе (см. рис. 4,в) приводит к деформации и смещению ветвей дисперсионного уравнения: ветвь затухания капиллярных волн “1, 2” (соответствующая мнимым значениям частот) уходит дальше в область отрицательных значений, т.е. декремент увеличивается, а ветвь “3”, соответствующая апериодическим движениям, поднимается вверх и при $w = 2.9$ почти доходит до оси абсцисс. При дальнейшем незначительном увеличении заряда, приходящегося на единицу длины струи, релаксационная ветвь “3” частично переходит в область положительных значений мнимых частей частот, то есть в неком диапазоне волновых чисел превращается из декремента в инкремент неустойчивости, рис. 4,г. Точка, с которой начинается такой переход, характеризуется значениями: $w \approx 2.904$, $k \approx 0.789$. При дальнейшем увеличении заряда на струе эта тенденция перехода ветви “3” в область положительных ординат усиливается (рис. 4,д). Этот факт удивительно точно (с точностью до третьего знака после запятой) совпадает с результатами работ [16, 25], в которых исследовались иными методами критические условия реализации электростатической неустойчивости азимутальной моды струи с $m = 2$.

Таким образом, электростатическая неустойчивость азимутальной моды с $m = 2$ начинается с перехода релаксационной ветви апериодических движений “3” из области отрицательных ординат в область положительных.

Следует отметить, что в [16, 25] ставилась цель: определить критические условия различных азимутальных мод струи, для более точного толкования результатов экспериментов по электродиспергированию электропроводной жидкости в [23], но не было цели связать неустойчивость с той, либо иной ветвью дисперсионного уравнения.

Заключение. Методами математического моделирования на упрощенной модели исследуется влияние эффекта релаксации поверхностного натяжения полярной жидкости на закономерности реализации капиллярного волнового движения и развития неустойчивости первых трех азимутальных мод капиллярных колебаний поверхности заряженных идеальных несжимаемых электропроводных жидких струй. Оказалось, что учет эффекта релаксации поверхностного натяжения приводит к повышению порядка дисперсионного уравнения, у которого появляется еще один затухающий непериодический корень релаксационной природы, который можно связать с разрушением упорядоченности диполей воды в приповерхностном двойном электрическом слое. При достаточно больших электрических зарядах, приходящихся на единицу длины струи, именно этот релаксационный корень становится неустойчивым.

В обнаруженном затухании интересно то, что оно имеет место в идеальной жидкости. В используемой идеализированной модели релаксационное движение, появляющееся при включении эффекта динамического поверхностного натяжения, инкременты и декременты волновых движений имеют релаксационную природу.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 19-19-00598 “Гидродинамика и энергетика капли и капельных струй: формирование, движение, распад, взаимодействие с контактной поверхностью”, https://rscf.ru/project/19-19-00598/).