Журнал общей биологии, 2022, T. 83, № 4, стр. 288-301
Нужно ли что-то знать о хищниках при моделировании динамики численности жертв?
В. Г. Суховольский 1, *, Ю. Д. Иванова 2, А. В. Ковалев 3
1 Институт леса им. В.Н. Сукачева, обособленное подразделение ФИЦ КНЦ СО РАН
660036 Красноярск, Академгородок, 50/28, Россия
2 Институт биофизики, обособленное подразделение ФИЦ КНЦ СО РАН
660036 Красноярск, Академгородок, 50/50, Россия
3 Федеральный исследовательский центр “Красноярский научный центр СО РАН”
660036 Красноярск, Академгородок, 50, Россия
* E-mail: soukhovolsky@yandex.ru
Поступила в редакцию 23.06.2022
После доработки 07.07.2022
Принята к публикации 11.07.2022
- EDN: LJNCWB
- DOI: 10.31857/S0044459622040078
Аннотация
В работе предложен новый подход к построению модели популяции жертвы в системе “хищник–жертва” без использования данных по динамике численности хищников. Для замещения этих данных рассмотрены авторегрессионные модели с набором линейных положительных и отрицательных обратных связей, которые заменяют данные по влиянию популяций хищника. В работе использовались сопряженные ряды динамики численности популяций жертв и хищников: “классические” данные по числу закупленных Компанией Гудзонова залива шкурок рыси и зайцев, а также ежегодные данные о численности лосей и волков на о. Айл-Ройал на оз. Верхнее в Северной Америке. Изученные популяции рассматривались как авторегрессионные (AR) системы с обратными связями. Для регуляции численности популяций жертв (зайцев и лосей) характерно наличие двух контуров обратной связи: положительной обратной связи между текущей плотностью популяции и плотностью популяции в предыдущий сезон и отрицательной обратной связи между текущей плотностью популяции и плотностью популяции за два года до этого. Показано, что для построения модели популяций жертв нет необходимости знать, сколько видов хищников (включая человека) воздействуют на эту популяцию. По данным о временной динамике исследуемых популяций дана оценка коэффициентов обратных связей AR-уравнений, их устойчивость и запас по устойчивости. Коэффициент детерминации R2 для рассмотренных моделей доходит до значения 0.978. Предложенный подход может быть использован для моделирования локальных популяций животных, для которых нет полных данных об их взаимодействиях с другими видами в экосистеме.
Один из основополагающих принципов в экологии – системный подход к анализу процессов динамики численности видов в экосистеме. Согласно этому подходу, для описания популяционной динамики отдельного вида необходимо учесть взаимодействия особей этой популяции с комплексом других видов – хищников, паразитов, видов, используемых как кормовой ресурс, и т.п. Для описания взаимодействий в экосистеме достаточно давно были предложены модели “хищник–жертва”, “паразит–хозяин”, модель конкуренции видов (Lotka, 1925; Volterra, 1926; Свирежев, Логофет, 1978; Базыкин, 1985, 2003; Недорезов, Утюпин, 2011). Наряду с моделью “хищник–жертва” для описания динамики временных рядов рысей и зайцев предлагаются и другие модели, в частности модель, в которую дополнительно в качестве хищника вводятся трапперы (охотники) (Deng, 2018).
Верификация моделей взаимодействующих популяций (начиная с работы Гаузе (Gause, 1934)) связана с необходимостью наличия данных по динамике численности взаимодействующих видов. Трудности моделирования численности взаимодействующих видов в экосистеме можно разделить на системные и процессные. Системные ограничения связаны с тем, что в связи с техническими трудностями учетов всех взаимодействующих популяций в изучаемой системе ведутся учеты лишь части этих видов. Процессное ограничение возникает вследствие того, что по техническим и экономическим причинам наблюдения за популяциями в экосистеме имеются лишь в короткий интервал времени. В частности, системные и процессные ограничения приводят к тому, что, несмотря на более чем 100-летние наблюдения за динамикой численности такого хозяйственно значимого вида, как сибирский шелкопряд (Dendrolimus sibiricus Tschetv.), в литературе имеется информация только о двух (!) достаточно длительных рядах динамики численности вредителя (Кондаков, 1974; Юрченко, Турова, 2007). При этом системные ограничения выражаются в том, что даже при известных данных о популяционной динамике этого вида нет информации о динамике численности популяций паразитоидов, физиологическом состоянии кормовых древесных растений.
В связи с этими трудностями для построения моделей взаимодействующих популяций используется ограниченное число длительных сопряженных рядов популяций хищников и жертв, в частности, очень популярные при построении моделей “хищник–жертва” многолетние данные по закупке шкурок зайцев (Lepus americanus) и рысей (Lynx lynx) Компанией Гудзонова залива (Hewitt, 1921; Gomatam, 1974).
В связи с этим возникает вопрос о преодолении системных и процессных ограничений при анализе и моделировании динамики численности определенного вида в экосистеме.
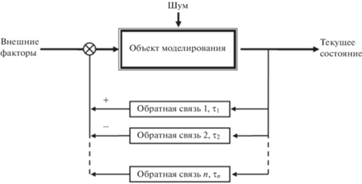
Популяцию любого вида животных можно рассматривать как авторегулируемую систему с обратными связями (в частности, для лесных насекомых такой подход успешно рассматривался в работах: Исаев, Хлебопрос, 1973; Berryman, 1981; Исаев и др., 2001; Isaev et al., 2017). Такая общая модель может быть описана через так называемую передаточную функцию с обратными связями разной силы и направленности и с разным запаздыванием во времени (Дорф, Бишоп, 2004). При этом при анализе общих свойств временной динамики популяций животных факторы, оказывающие влияние на конкретную популяцию, можно не рассматривать и достаточно оценить восприимчивость популяции к влиянию обратных связей и запаздывание отклика системы на ее состояние на входе (Royama, 1992; Turchin, 2003). На рис. 1 представлена концептуальная схема авторегулирования численности популяции животных.
Как видно из схемы на рис. 1, если задача состоит в построении модели вида-жертвы, для ее верификации не требуются данные о численности хищников (сколько бы видов хищников ни воздействовало на популяцию жертвы – рысь, трапперы, волк, росомаха, рыжая лисица, большая рогатая сова, обыкновенная сова и др. (Rohner, 1996; Stenseth et al., 1997)).
Для построения авторегуляторной модели динамики численности конкретных видов животных необходимо оценить знак и чувствительность обратных связей. Если эти характеристики найдены, то далее можно рассмотреть различия в регуляторных характеристиках для разных видов, оценить устойчивость и запас по устойчивости системы (Гайдук и др., 2011).
Настоящая работа посвящена изучению возможностей построения авторегулируемой системы с набором обратных связей для моделирования динамики популяций.
ОБЪЕКТЫ И МЕТОДЫ МОДЕЛИРОВАНИЯ
Объекты моделирования
В работе использовались сопряженные ряды динамики численности популяций жертв и хищников: “классические” данные по числу закупленных Компанией Гудзонова залива шкурок рыси и зайцев (Odum, Barrett, 1971) и данные по учетам численности волков и лосей на о. Айл-Ройал (Мичиган, США).
Данные Компании Гудзонова залива о торговле мехом (Hewitt, 1921; Elton, Nicholson, 1942; Leigh, 1968; Odum, Barrett, 1971) по канадской рыси и зайцам-белякам – это самый старый, самый длинный и самый известный набор популяционных данных. В каждом учебнике по экологии он цитируется в качестве примера в поддержку классической модели “хищник–жертва” (Lotka, 1925; Volterra, 1926), но лишь немногие (например, Britton, 2003) правильно указывают различие между полевыми данными и моделью “хищник–жертва”. В отличие от классической теории, которая предсказывает, что пиковая численность хищника будет следовать за численностью добычи, пиковый объем заячьих шкурок в среднем соответствует пиковому объему шкурок рысей в течение некоторых лет. Суммарная разница фаз рядов динамики хищника и жертвы составляет более двух лет, причем данные о шкурках рыси опережают фазу в среднем на один год по сравнению с количеством шкурок зайца (Leigh, 1968; Gilpin, 1973; Bulmer, 1974). При этом полевая популяция рысей отстает по фазе на один год от полевой популяции зайцев (Keith, 1963; O’Donoghue et al., 1998). Расхождение фаз в противоположных направлениях настолько “загадочно” (Leigh, 1968), что побудило предположить, что эти свойства рядов данных являются результатом “внутренней саморегуляции” как зайца, так и рыси (Zhang et al., 2007).
Второй набор данных по популяционной динамике хищника и жертвы был взят из ежегодных данных о численности лосей (Alces alces) и волков (Canis lupus) на о. Айл-Ройал. Айл-Ройал (Isle Royale, 48°06′00″ с.ш., 88°33′00″ з.д.) – отдаленный дикий остров площадью 544 км2 на оз. Верхнее в Северной Америке, где обитают волки и лоси. В настоящее время здесь организован Национальный парк Айл-Ройал (https://isleroyalewolf.org/). Исследователи начали ежегодные наблюдения за волками и лосями на о. Айл-Ройал в 1958 г., и животные изучаются уже более пяти десятилетий. Имеется много публикаций, посвященных анализу собранных данных (Vucetich et аl., 2011; Montgomery et аl., 2014; Hedrick et al., 2019; Hoy et al., 2019, и др.). Это исследование представляет собой одно из самых продолжительных непрерывных исследований системы “хищник–жертва” в экологии. Изучаемые популяции лосей и волков взаимодействуют, по существу, как изолированная система “один вид-хищник – один вид-жертва” (Peterson et al., 1998). Волки являются единственным хищником, охотящимся на лосей, и лоси составляют более 90% биомассы в рационе волков (Peterson, Page, 1988). Наиболее важные события в динамике популяций были непредсказуемы. В 1980 г. популяция волков резко сократилась, когда люди случайно занесли на территорию Национального парка собачье вирусное заболевание. В 1996 г. популяция лосей резко сократилась во время самой суровой зимы за всю историю наблюдений и неожиданного нашествия лосиного клеща. В конце 1990-х интенсивный уровень инбридинга среди волков был смягчен, когда волки иммигрировали из Канады. В ответ популяция волков в начале XXI в. в целом увеличилась, несмотря на сокращение численности лосей.
Методы моделирования динамики численности популяций
При моделировании возникает проблема выбора адекватной модели, которая, в частности, учитывала бы запаздывание во времени между изменением состояния моделируемой популяции жертв и запаздыванием воздействия хищников на популяцию жертвы.
Большинство исследователей полагают, что запаздывание – это наличие зависимости скорости изменения численности популяции от значений ее же численности в некоторые предыдущие моменты времени (Вольтерра, 1976; Колесов, 1981; Марри, 1983; Дьери, Перцев, 1987; Перцев, 1997; Berryman, 2003). Существуют и другие мнения, например, когда запаздывание определяется как время, необходимое для того, чтобы регуляторные механизмы вернули систему в исходное состояние (Исаев и др., 2001). И те и другие авторы считают, что именно запаздывание в действии различных популяционных регуляторных механизмов играет наиболее существенную роль в динамике численности. И если в первом случае в качестве моделей популяционной динамики рассматриваются обыкновенные дифференциальные уравнения с распределенным или сосредоточенным запаздыванием (Hutchinson, 1947; Колесов, 1981; Марри, 1983), а также рекуррентные уравнения с запаздыванием (Bjornstad et al., 1999; Gonzales-Andujar, Hughes, 2000; Benton et al., 2001; Fromentin et al., 2001), то во втором случае можно использовать эти же дифференциальные уравнения без запаздывающего аргумента. Если система находилась в состоянии равновесия и была выведена из нее, например, под воздействием модифицирующих факторов (и при этом ее динамика описывалась обыкновенными дифференциальными уравнениями), то потребуется определенное время, чтобы она вернулась в некоторую ε-окрестность стационарного состояния, из которого она была выведена. Время возвращения системы будет зависеть от величины ε отклонения и не будет постоянной.
Впрочем, эти два различных определения запаздывания вовсе не исключают друг друга: и то и другое запаздывание может присутствовать в одной и той же системе. Однако это приводит к путанице в понимании сути популяционных процессов. Эта путаница начинается с самых простых вопросов: о каком конкретно запаздывании идет речь в том или ином случае, и как именно корректно учесть это запаздывание в математической модели? В литературе встречаются также математические модели, в которых вводится непрерывное (распределенное) запаздывание (Вольтерра, 1976; Перцев и др., 2003).
В настоящей работе в качестве объектов моделирования раздельно выступали популяции хищников и жертв, для которых рассматривались авторегрессионные модели. В таких моделях обратные связи и запаздывание характеризуют влияние прошлых состояний объекта на его текущее состояние. Для анализируемых систем было предположено, что обратные связи линейны и имеют следующий вид $w(t) = ax(t - \tau )$ c запаздыванием τ и амплитудой обратной связи a > 0 для положительной обратной связи и a < 0 для отрицательной обратной связи. Количество обратных связей разного знака и с разным запаздыванием для конкретных видов неизвестно, но в общем случае, с учетом обратных связей для стационарной во времени авторегрессионной (AR) системы, можно записать следующее уравнение:
где k – порядок авторегрессии; μ – ошибка измерений; а0, …, aj, ... аk – коэффициенты, характеризующие интенсивность обратных связей с запаздыванием j.Величина ${{a}_{j}} = \frac{{\partial y(t)}}{{\partial y(t - j)}}$ в (1) характеризует восприимчивость популяции в год t к изменению ее численности в год (t – j). При этом влияние обратных связей в момент времени t пропорционально величине переменной y(t – j), а тип обратной связи (положительной или отрицательной) определяется знаком aj. Если значение aj положительно, то этот показатель характеризует линейную положительную обратную связь между годами t и (t – j). Если значение aj отрицательно, то aj характеризует линейную отрицательную обратную связь между численностями в годы t и (t – j).
Таким образом, для построения модели необходимо оценить порядок авторегрессии k, характеризующий число обратных связей в системе, величину и знаки коэффициентов (1). Для оценки порядка авторегрессии и времени запаздывания в системе обратной связи обычно рассматривается парциальная автокорреляционная функция (ПАКФ). Порядок k авторегрессии в системе оценивается по максимальному сдвигу значимой ПАКФ (Дженкинс, Ваттс, 1971). Если известен временной ряд {y(t)} и порядок k авторегрессии уравнения (1), то уравнение можно рассматривать как линейное регрессионное уравнение относительно неизвестных параметров а0, …, aj, … аk. В этом случае значения коэффициентов обратной связи в AR-уравнении можно найти, рассматривая (1) как линейное регрессионное уравнение с неизвестными переменными, для решения которого можно использовать традиционные методы наименьших квадратов (Андерсон, 1976).
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
При анализе временных рядов популяции зайцев в зоне Гудзонова залива для уменьшения дисперсии значений временных рядов {x(i)} был осуществлен переход к логарифмической шкале. Так как характеристики ПАКФ вычисляются для стационарных временных рядов, а временной ряд численности зайцев характеризуется трендом $\ln \hat {x}(t) = 28.38 - 0.0132t$ (где t – год учетов), то после логарифмирования убирался линейный тренд, и начальный логарифмированный ряд трансформировался в ряд $u(t) = \ln x(t) - \ln \hat {x}(t)$. На последнем этапе трансформации для уменьшения шума временного ряда проводилась его фильтрация с помощью фильтра Ганна, отсекающего высокочастотную (свыше 0.25 Гц) cоставляющую ряда (Хемминг, 1987):
Аналогичным образом, но без снятия линейного тренда, трансформировался ряд динамики рыси.
Для сглаженного детрендированного логарифмированного временного ряда динамики численности популяции жертв – зайцев – и аналогичным образом сглаженного логарифмированного ряда динамики численности популяции хищника – рыси (временной тренд для ряда рысей не проявлялся) – по данным Компании Гудзонова залива производилась оценка порядка авторегрессии по характеристикам ПАКФ (Дженкинс, Ваттс, 1971) (рис. 2).
Рис. 2.
ПАКФ сглаженного детрендированного логарифмированного временного ряда динамики численности зайцев и сглаженного логарифмированного ряда динамики рыси в зоне Гудзонова залива. 1 – ПАКФ ряда зайцев, 2 – ПАКФ ряда рыси; 3 – стандартная ошибка ПАКФ.
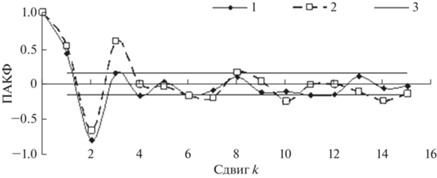
Так как порядок авторегрессии ряда зайцев, согласно рис. 2, равен двум годам, то уравнение, описывающее динамику их популяции, можно записать следующим образом:
где a0–a2 – коэффициенты AR-уравнения.Для популяции рыси порядок авторегрессии, согласно рис. 2, равен трем годам, и уравнение, описывающее трансформированную динамику z(t) популяции, можно записать следующим образом:
В табл. 1 приведены расчетные значения коэффициентов уравнений (3) и (4) для популяций зайцев и рыси и их достоверности.
Таблица 1.
Расчетные значения коэффициентов уравнений (3) и (4) и их достоверности
| Переменная | Коэффициент | Ст. ошибка | t-критерий | p-уровень |
|---|---|---|---|---|
| Зайцы | ||||
| a0 | 0.065 | 0.047 | 1.38 | 0.175457 |
| y(t – 2) | –0.836 | 0.085 | –9.80 | 0.000000 |
| y(t – 1) | 0.808 | 0.087 | 9.28 | 0.000000 |
| adjR2 | 0.75 | |||
| F-тест | 63.6 | |||
| η | 0.147 | |||
| Рыси | ||||
| b0 | 0.614 | 0.349 | 1.76 | 0.086400 |
| z(t – 3) | 0.741 | 0.107 | 6.96 | 0.000000 |
| z(t – 2) | –1.373 | 0.126 | –10.91 | 0.000000 |
| z(t – 1) | 1.439 | 0.109 | 13.25 | 0.000000 |
| adjR2 | 0.82 | |||
| F-критерий | 64.7 | |||
| η | 0.132 | |||
Как видно из табл. 1, для регуляции численности популяции зайцев характерно наличие двух контуров обратной связи: положительной обратной связи между текущей плотностью популяции и плотностью популяции в предыдущий сезон и отрицательной обратной связи между текущей плотностью популяции и плотностью популяции за два года до этого. Положительная обратная связь, по всей видимости, характеризует процесс размножения: чем больше плотность особей-родителей, тем больше и плотность особей-потомков. Что касается отрицательной обратной связи, то можно предположить, что отрицательная обратная связь, проявляющаяся через два поколения, характеризует (с запаздыванием на два года) влияние хищников и (или) изменение состояния кормовых ресурсов.
Корректность модели оценивалась, во-первых, по значению коэффициента детерминации adjR2уравнения (3): чем ближе к 1 значение adjR2, тем большую долю дисперсии переменной y(i) описывает модель. С помощью F-теста Фишера и t-критерия оценивалась значимость коэффициентов модели (Поллард, 1982).
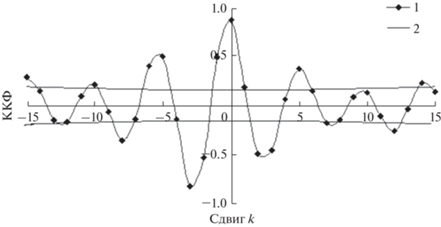
На рис. 3 приведены графики временных рядов трансформированных данных учетов зайцев (тысяч шкурок) и модельных данных. По данным табл. 1 коэффициент детерминации модели adjR2 = 0.75, т.е. предложенная модель учитывает 75% дисперсии данных, что, конечно, достаточно много. Следует отметить, что предложенная модель не только хорошо описывает динамику амплитуды временного ряда данных, но и согласуется с ним по фазе, на что указывают значения кросс-корреляционной функции (ККФ) ряда данных зайцев и модельного ряда (рис. 4).
Рис. 3.
Временные ряды трансформированных данных числа закупленных шкурок зайцев (кривая 1) и модельные данные (кривая 2).
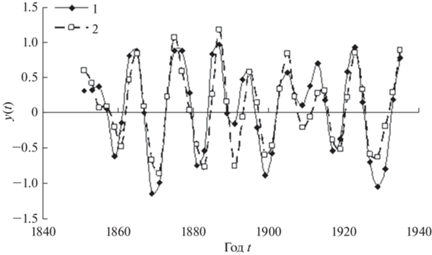
Рис. 4.
Кросскорреляционная функция (ККФ) трансформированного ряда численности зайцев и модельного ряда: 1 – ККФ, 2 – стандартная ошибка ККФ.
Таким образом, для построения модели популяции жертвы нет необходимости знать, сколько видов хищников (включая человека) воздействуют на эту популяцию.
Аналогично анализу временного ряда зайцев, можно провести анализ временного ряда рысей. В табл. 1 приведены коэффициенты уравнения (4). Как видно, все коэффициенты уравнения (4) значимы, и модель (4) описывает динамику трансформированного ряда рысей с коэффициентом детерминации adjR2 = 0.82. На рис. 5 представлены графики трансформированного ряда данных по динамике рыси и модельного ряда (4).
Рис. 5.
Трансформированный временной ряд динамики численности рыси (1) по данным Компании Гудзонова залива и модельный ряд (2).
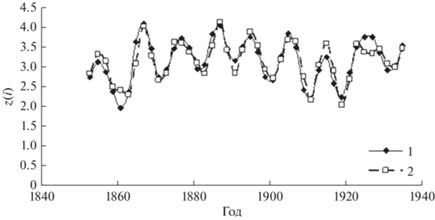
Точно так же, как для временного ряда зайцев, для оценки синхронности трансформированного временного ряда данных рыси и модельного ряда вычислялась кросскорреляционная функция для этих рядов (рис. 6).
Рис. 6.
Кросскорреляционная функция (ККФ) трансформированного и модельного рядов динамики численности рыси: 1 – ККФ, 2 – стандартная ошибка ККФ на уровне значимости р = 0.05.
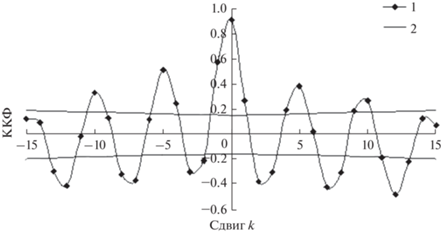
В том, что касается популяции рыси, можно полагать, что кормом для нее служат зайцы, а прочие хищники, включая трапперов, выступают в качестве конкурентов. Тем не менее всю информацию о динамике численности популяции рыси, точно так же, как и популяции зайцев, можно получить из данных только по ряду динамики этого хищника, не пользуясь данными (впрочем, неизвестными) по динамике видов-конкурентов.
Аналогично рядам “заяц–рысь” были рассмотрены результаты учетов сопряженной динамики популяции жертвы (лосей) и популяции хищников (волков) на о. Айл-Ройал. Для этой системы воздействие других видов хищников на популяцию жертв было исключено. Точно так же, как для системы “заяц–рысь”, для популяций лосей и волков были рассмотрены авторегрессионные уравнения типа (3) и (4). После трансформации данных, аналогичной трансформациям, выполненным для зайцев и рыси, были выполнены расчеты ПАКФ для этих видов и найдено, что для популяции лосей порядок авторегрессии равен 2, а для популяции волков порядок авторегрессии равен 3. Далее были вычислены коэффициенты AR(2)-уравнения для популяции лосей и коэффициенты AR(3)-уравнения для популяции волков (табл. 2).
Таблица 2.
Коэффициенты авторегрессионных уравнений для популяций лосей и волков на о. Айл-Ройал
| Переменная | Коэффициент | Ст. ошибка | t-критерий | p-уровень |
|---|---|---|---|---|
| Лоси | ||||
| a0 | 0.623 | 0.228 | 2.73 | 0.008844 |
| y(t – 2) | –0.711 | 0.104 | –6.81 | 0.000000 |
| y(t – 1) | 1.620 | 0.104 | 15.62 | 0.000000 |
| adjR2 | 0.978 | |||
| F-тест | 443.2 | |||
| η | 0.080 | |||
| Волки | ||||
| b0 | 0.244 | 0.179 | 1.36 | 0.180165 |
| z(t – 3) | 0.476 | 0.138 | 3.44 | 0.001271 |
| z(t – 2) | –1.211 | 0.222 | –5.46 | 0.000002 |
| z(t – 1) | 1.655 | 0.137 | 12.09 | 0.000000 |
| adjR2 | 0.875 | |||
| F-тест | 112.8 | |||
| η | 0.080 | |||
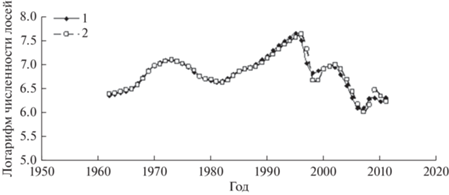
Как следует из табл. 2, модель для популяции лосей с очень высокой точностью описывает временной ряд данных наблюдений (adjR2 = 0.978) (рис. 7).
Рис. 7.
Трансформированный временной ряд динамики численности лосей (1) на о. Айл-Ройал и модельный ряд (2).
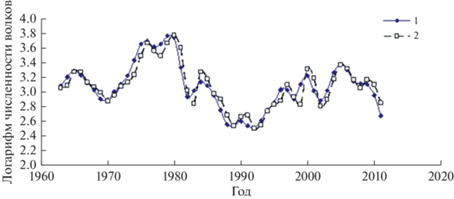
Коэффициент детерминации adjR2 = 0.875 модели для популяции волков описывает временной ряд данных наблюдений с меньшей, но все равно достаточно высокой точностью (рис. 8).
Рис. 8.
Трансформированный временной ряд динамики численности волков (1) на о. Айл-Ройал и модельный ряд (2).
Таким образом, порядок авторегрессии для популяций жертв – зайцев и лосей – составляет два года. При этом одна из обратных связей – положительная, а вторая – отрицательная. Для популяций хищников – рысей и волков – порядок модельной авторегрессии равен 3, и динамика этих популяций определяется тремя обратными связями: двумя положительными и одной отрицательной. Положительную обратную связь между численностями популяций жертв в смежные годы можно трактовать как связанную с рождаемостью, отрицательную обратную связь для популяций жертв между данным i-го и (i – 2)-го годов можно рассматривать как запаздывание воздействия хищников на жертв. Можно предположить, что для популяций хищников положительная обратная связь между данными i-го и (i – 3)-го годов связана с наличием времени взросления особей и достижения ими возраста активной охоты.
Насколько стационарны ряды динамики численности популяций жертв? Для AR(2)-моделей критерий устойчивости характеризуется выполнением следующих условий (Wei, 2006):
(5)
$\left\{ \begin{gathered} {{a}_{2}} + {{a}_{1}} < 1 \hfill \\ {{a}_{2}} - {{a}_{1}} < 1 \hfill \\ - 1 < {{a}_{2}} < 1 \hfill \\ \end{gathered} \right..$Из данных по моделям зайцев и лосей в табл. 1 и 2 следует, что для этих популяций условия (5) удовлетворяются, и динамику численности этих видов можно считать стационарной.
Методы анализа динамики численности животных и построения AR-моделей предполагают, что тип модели известен и ее параметры не изменяются во времени. Однако реальные популяции и окружающая среда, в которой эта популяция существует, не могут быть смоделированы абсолютно точно, они могут изменяться непредсказуемым образом и подвергаться воздействию различных возмущающих факторов.
В системах всегда будут возникать отклонения от идеальной модели, вызываемые различными причинами:
– изменениями параметров популяции и природной среды в силу различных обстоятельств;
– свойствами популяций и природной среды, не учтенными в модели;
– не учтенным в модели запаздыванием во времени при взаимодействии популяции со средой;
– изменением устойчивого состояния популяции;
– ошибками при учетах численности популяции;
– непредсказуемыми внешними воздействиями.
Для AR-моделей популяционной динамики важной характеристикой, позволяющей оценить изменение состояния популяции при различного рода трансформациях внешней среды и собственно характеристик популяции, является запас модели по устойчивости. Запас по устойчивости характеризует близость этой точки к границам зоны устойчивости. Для оценки запаса устойчивости дискретных систем используется критерий Михайлова и годограф Михайлова (Ким, 2007):
(6)
$D(j\nu ) = {{\left. {\bar {D}(q)} \right|}_{{q\, = \,\exp (j\nu )}}},\,\,\,\nu \in \left[ { - \pi ,\;\pi } \right],$Система с некоторым характеристическим полиномом является устойчивой, если годограф Михайлова (6) при изменении переменной ν от ‒π до π, начинаясь на вещественной оси, обходит последовательно вокруг точки q = 0 против часовой стрелки 4n квадрантов (Гайдук и др., 2011). Рассмотрим авторегрессионное уравнение для модели лосей:
Характеристический многочлен $\bar {D}(q)$ для уравнения (7) имеет следующий вид:
После перехода от переменной q к новой комплексной переменной ν: $q = \frac{{1 + \nu }}{{1 - \nu }}$ получим характеристическое уравнение относительно ν:
Для построения годографа Михайлова в выражении (9) выделяются действительная Р(ν) и мнимая Q(ν) составляющие:
(10)
$\begin{gathered} P(\nu ) = \cos 2\nu - 1.62\cos \nu + 0.711 \hfill \\ Q(\nu ) = \sin 2\nu - 1.62\sin \nu . \hfill \\ \end{gathered} $Далее в плоскости {P(ν), Q(ν)} для значений переменной ν от –π до π строится кривая годографа, каждая точка которого на плоскости есть значения P(ν0) и Q(ν0) на некотором значении ν = ν0. Запас по устойчивости η по критерию Михайлова есть радиус окружности с центром в точке q = 0, которую можно вписать в нуль годографа Михайлова.
Несмотря на внешне сложную процедуру расчета, расчет запаса по устойчивости выполняется с помощью простой программы (табл. 3) в пакете MATLAB.
Таблица 3.
Листинг программы в пакете MATLAB для расчета запаса по устойчивости авторегрессионной модели (Гайдук и др., 2011)
| Dq = [1 a[1 ] a[2 ] ; |
| Dq = Dq/Dq(1); |
| nu = (–pi: pi/(100*length(Dq)):pi; |
| j = sqrt(–1); |
| z = exp(j*nu); |
| GM = polyval (Dq, q); |
| eta = min (abs(GM)); |
| disp ([‘запас устойчивости eta =‘ num2str(eta)]) |
Для расчета запаса по устойчивости в пакете MATLAB необходимо загрузить данные из табл. 3 и выполнить лишь одну операцию: ввести в строку 1 значения коэффициентов авторегрессионной модели. По определению величина запаса по устойчивости $\eta \geqslant 0$, и чем меньше значение η, тем больше вероятность “срыва” и потери устойчивости системы при внешних воздействиях.
Показатели запаса по устойчивости для рассмотренных популяций хищников и жертв приведены в табл. 1 и 2. Как видно, запас по устойчивости для компонентов системы “рысь–заяц” практически одинаков (0.147 для зайца и 0.132 для рыси). Одинаковы (η = 0.08) и запасы по устойчивости для популяций системы “волк–лось”. Запас по устойчивости для системы “рысь–заяц” несколько больше запаса по устойчивости компонентов системы “волк–лось”. Заметим, что запасы по устойчивости для хищников значимо не отличаются от таковых для жертв, так что значение запаса по устойчивости не зависит от функциональной роли вида в экосистеме и порядка AR-модели. При меньшем запасе по устойчивости именно в системе “волк–лось” наблюдались сильные колебания численности этих видов.
В предложенных AR-моделях (кстати, точно так же, как и в классических моделях “хищник–жертва”) не учитывается влияние модифицирующих факторов (например, погодных) на динамику численности популяций. Для учета модифицирующих факторов в модель “хищник–жертва” можно было бы ввести дополнительные уравнения, связывающие коэффициенты модели и влияние погодных факторов. Однако такое преобразование модели “хищник–жертва” ведет к необходимости верификации дополнительных коэффициентов и появлению большого числа режимов динамики видов, а следовательно, к трудностям анализа таких моделей. Но влияние модифицирующих факторов достаточно просто учесть, перейдя от логарифмических AR-моделей к логарифмическим ADL-моделям (autoregressive distributed lag model), в которых влияние внешних факторов учитывается введением дополнительного аддитивного члена с коэффициентом, характеризующим восприимчивость динамики численности к погодным характеристикам (Soukhovolsky et al., 2022). В такой модели при известных данных о численности популяции и погодных условиях коэффициенты модели находятся точно так же, как и для AR-модели, расчетом регрессионной модели с неизвестными коэффициентами восприимчивости.
ЗАКЛЮЧЕНИЕ
Рассмотрена возможность построения модели популяции жертвы в системе “хищник–жертва” без использования данных по динамике численности хищников. Проведенные расчеты показали, что для моделирования популяций жертв нет необходимости иметь какую-либо информацию о популяции хищника. Авторегрессионные модели с набором линейных положительных и отрицательных обратных связей фактически заменяют данные по динамике популяции хищника. Предложенный подход может быть использован для моделирования локальных популяций животных, для которых нет полных данных об их взаимодействиях с другими видами в экосистеме.
И модель популяции зайцев в зоне Гудзонова залива, и модель популяции лосей на о. Айл-Ройал можно с достаточно высокой точностью построить без знания динамики численности хищников – рыси и волка. При этом, в частности, для популяции лосей коэффициент детерминации adjR2 = = 0.975, т.е. модель практически по точкам повторяет ряд натурных данных.
В качестве характеристики качества модели можно использовать не только невязку наборов модельных и натурных данных, но и в числе переменных в модели. Для AR(2)-модели число свободных переменных равно 3, тогда как для модели Лотки–Вольтерра оно равно 6, а для HLT-модели (hare-lynx-trapper model; Deng, 2018) число переменных равно 20. Понятно, что чем больше переменных в модели, тем длиннее должен быть ряд данных, требуемых для ее верификации и тем меньше (при одной и той же длине ряда данных) надежность расчета коэффициентов модели.
При объяснении моделируемых процессов, безусловно, нельзя говорить о том, что такой хищник, как рысь, однозначно регулирует численность своей жертвы – зайца. Видимо, в данном случае необходимо принимать во внимание характер активности еще одного “хищника” – траппера, о поведении которого, к сожалению, нет каких-либо данных. Более проста ситуация с описанием взаимодействия “волк–лось” на территории заповедника, в котором запрещена охота. Там, судя по цитированным выше работам, происходит простое взаимодействие “один вид хищников – один вид жертв”. Но во всех случаях хищничество, безусловно, влияет на динамику численности жертв, и во всех случаях запаздывание во времени в авторегрессионной модели можно трактовать как показатель влияния хищника. Хотя ряды данных по сопряженной динамике численности хищников и жертв у млекопитающих немногочисленны, в нашем распоряжении имеются многочисленные данные по динамике численности лесных насекомых – филлофагов. Хотя данные по динамике паразитов и хищников различных видов филлофагов практически всегда отсутствуют, никто не сомневается, что воздействие паразитов и хищников на популяции насекомых существует. Ранее мы описали авторегрессионные модели (чаще всего второго порядка), которые с высокой степенью точности позволили описать динамику филлофагов (Исаев и др., 2015; Isaev et al., 2017; Суховольский и др., 2020). Так что можно полагать, что использование авторегрессионных моделей (логарифмически линейных) может описать достаточно широкий “спектр” динамики разных видов. По-видимому, общность и эффективность авторегрессионных моделей для разных видов животных объясняется тем, что в их основе лежит учет влияния обратных связей (как положительных, так и отрицательных). Фактически авторегрессионная модель выступает и как инструмент описания натурных данных, и как инструмент объяснения процессов в экосистеме. Сочетание положительных и отрицательных обратных связей в системе позволяет поддерживать устойчивость динамики изучаемых популяций в течение длительного времени, ибо все изученные виды существуют в течение длительного времени – от 50 до 120 лет, как это наблюдается для серой лиственничной листовертки Zeiraphera griseana (Baltensweiler, Fischlin, 1988). Кроме того, авторегрессионые модели характеризуются спектром временных рядов, в котором присутствуют предельные циклы с разными характерными временами в зависимости от порядка авторегрессии, что позволяет учесть колебания в моделируемой системе.
Границы применения авторегресионной модели определяются техническими причинами: длиной анализируемых рядов (не менее 20–25 членов с учетом того, что при расчетах парциальной автокорреляционной функции, необходимой для оценки порядка авторегрессии, число значимых членов этой функции не превосходит четверти длины изучаемого ряда), и стационарностью процессов в экосистеме. Однако обычно можно провести фильтрацию нестационарного ряда и выделить стационарную составляющую, для которой удается построить AR-модель.
Список литературы
Андерсон Т., 1976. Статистический анализ временных рядов. М.: Мир. 755 с.
Базыкин А.Д., 1985. Математическая биофизика взаимодействующих популяций. М.: Наука. 181 с.
Базыкин А.Д., 2003. Нелинейная динамика взаимодействующих популяций. М.; Ижевск: Ин-т комп. технологий. 368 с.
Вольтерра В., 1976. Математическая теория борьбы за существование. М.: Наука. 288 с.
Гайдук А.Р., Беляев В.Е., Пьявченко Т.А., 2011. Теория автоматического управления в примерах и задачах. СПб.: Лань. 464 с.
Дженкинс Г., Ваттс Д., 1971. Спектральный анализ и его приложения. М.: Мир. Вып. 1. 316 с.; Вып. 2. 287 с.
Дорф Р.К., Бишоп P.X., 2004. Современные системы управления. М.: Лаборатория Базовых Знаний. 832 с.
Дьери И., Перцев Н.В., 1987. Об устойчивости положений равновесия функционально с дифференциальных уравнений запаздывающего типа, обладающих свойством смешанной монотонности // ДАН СССР. Т. 297. № 1. С. 23–25.
Исаев А.С., Хлебопрос Р.Г., 1973. Принцип стабильности в динамике численности лесных насекомых // ДАН СССР. Т. 208. Вып. 1. С. 225–228.
Исаев А.С., Пальникова Е.Н., Суховольский В.Г., Тарасова О.В., 2015. Динамика численности лесных насекомых-филлофагов: модели и прогнозы. М.: Т-во науч. изд. КМК. 276 с.
Исаев А.С., Хлебопрос Р.Г., Недорезов Л.В., Кондаков Ю.П., Киселев В.В., Суховольский В.Г., 2001. Популяционная динамика лесных насекомых. М.: Наука. 347 с.
Ким Д.П., 2007. Теория автоматического управления. Т. 1. М.: Физматлит. 312 с.
Колесов Ю.С., 1981. Некоторые задачи математической экологии // Дифференциальные уравнения и их применение. № 29. Вильнюс: Мокслас. С. 27–35.
Кондаков Ю.П., 1974. Закономерности массовых размножений сибирского шелкопряда // Экология популяций лесных животных Сибири. Новосибирск: Наука. С. 206–265.
Марри Дж., 1983. Нелинейные дифференциальные уравнения в биологии. Лекции о моделях. М.: Мир. 397 с.
Недорезов Л.В., Утюпин Ю.В., 2011. Непрерывно-дискретные модели динамики численности популяций: аналитический обзор. Новосибирск: ГПНТБ СО РАН. 234 с.
Перцев Н.В., 1997. Об одном обобщении логистической модели динамики популяций с ограниченным временем жизни особей // Вестн. ОмГУ. № 1. С. 14–16.
Перцев Н.В., Пичугина А.Н., Пичугин Б.Ю., 2003. Поведение решений диссипативной интегральной модели Лотки–Вольтерра // Сиб. журн. индустр. математики. Т. 6. № 2 (14). С. 95–106.
Поллард Дж., 1982. Справочник по вычислительным методам статистики. М.: Финансы и статистика. 344 с.
Свирежев Ю.М., Логофет Д.О., 1978. Устойчивость биологических систем. М.: Наука. 352 с.
Суховольский В.Г., Тарасова О.В., Ковалев А.В., 2020. Моделирование критических явлений в популяциях лесных насекомых // Журн. общ. биологии. Т. 81. № 5. С. 374–386.
Хемминг Р.В., 1987. Цифровые фильтры. М.: Недра. 221 с.
Юрченко Г.И., Турова Г.И., 2007. Сибирский и белополосый шелкопряды на Дальнем Востоке. Хабаровск: Изд-во ФГУ ДальНИИЛХ. 98 с.
Baltensweiler W., Fischlin A., 1988. The larch budmoth in the Alps // Dynamics of Forest Insect Populations. Boston: Springer. Р. 331–352.
Benton T.G., Ranta E., Kaitala V., Beckerman A.P., 2001. Maternal effects and the stability of population dynamics in noisy environments // J. Anim. Ecol. V. 70. P. 590–599.
Berryman A.A., 1981. Population Systems: A General Introduction. N.-Y.: Plenum Press. 222 p.
Berryman A.A., 2003. On principles, laws and theory in population ecology // Oikos. V. 103. № 3. P. 695–701.
Bjornstad O.N., Fromentin J.M., Stenseth N.C., Gjosaeter J., 1999. Cycles and trends in cod populations // Proc. Natl. Acad. Sci. USA. V. 96. P. 5066–5071.
Britton N.F., 2003. Essential Mathematical Biology. L.: Springer. 335 p.
Bulmer M.G., 1974. A statistical analysis of the 10-year cycle in Canada // J. Anim. Ecol. V. 43. P. 701–718.
Deng B., 2018. An inverse problem: Trappers drove hares to eat lynx // Acta Biotheor. V. 66. P. 213–242.
Elton C., Nicholson M., 1942. The ten-year cycle in numbers of the lynx in Canada // J. Anim. Ecol. V. 11. P. 215–244.
Fromentin J.M., Myers R.A., Bjornstad O.N., Stenseth N., Gjosaeter J., Christie H., 2001. Effects of density-dependence and stochastic processes on the regulation of cod populations // Ecology. V. 82. № 2. P. 567–579.
Gause G.F., 1934. The Struggle for Existence. Baltimore: Williams and Wilkins. 163 p.
Gilpin M.E., 1973. Do hares eat lynx? // Am. Nat. V. 107. № 957. P. 727–730.
Gomatam J., 1974. A new model for interacting populations two species systems // Bull. Math. Biol. V. 36. P. 347–353.
Gonzales-Andujar J.L., Hughes G., 2000. Complex dynamics in weed populations // Funct. Ecol. V. 14. P. 524–526.
Hedrick P., Robinson J., Peterson R.O., Vucetich J.A., 2019. Genetics and extinction and the example of Isle Royale wolves // Anim. Conserv. V. 22. № 3. P. 302–309.
Hewitt C.G., 1921. The Conservation of the Wild Life of Canada. N.-Y.: Charles Scribner′s Sons. 344 p.
Hoy S.R., Vucetich J.A., Liu R., DeAngelis D.L., Peterson R.O., et al., 2019. Negative frequency-dependent foraging behavior in a generalist herbivore (Alces alces) and its stabilizing influence on food-web dynamics // J. Anim. Ecol. V. 88. P. 1291–1304.
Hutchinson G.E., 1947. Theory of competition between two social species // Ecology. V. 28. P. 319–321.
Isaev A.S., Soukhovolsky V.G., Tarasova O.V., Palnikova E.N., Kovalev A.V., 2017. Forest Insect Population Dynamics, Outbreaks and Global Warming Effects. N.-Y.: Wiley. 298 p.
Keith L.B., 1963. Wildlife’s Ten-Year Cycle. Madison: Univ. Wisconsin Press. 221 p.
Leigh G., 1968. The ecological role of Volterra’s equations // Some of Mathematical Problems of Biology. Providence: American Mathematical Society. P. 1–61.
Lotka A.J., 1925. Elements of Physical Biology. Baltimore: Williams and Wilkins. 460 p.
Montgomery R.A., Vucetich J.A., Roloff G.J., Bump J.K., Peterson R.O., 2014. Where wolves kill moose: The influence of prey life history dynamics on the landscape ecology of predation // PLoS One. V. 9. № 3. https://doi.org/10.1371/journal.pone.0091414
O’Donoghue M., Boutin S., Krebs C.J., Zuleta G., Murray D.L., Hofer E.J., 1998. Functional responses of coyotes and lynx to the snowshoe hare cycle // Ecology. V. 79. P. 1193–1208.
Odum E.P., Barrett G.W., 1971. Fundamentals of Ecology. Philadelphia: Saunders. 574 p.
Peterson R.O., Page R.E., 1988. The rise and fall of Isle Royale wolves, 1975–1986 // J. Mammal. V. 69. P. 89–99.
Peterson R.O., Thomas N.J., Thurber J.M., Vucetich J.A., Waite T.A., 1998. Population limitation and the wolves of Isle Royale // J. Mammal. V. 79. № 3. P. 828–841.
Rohner C., 1996. The numerical response of great horned owls to the snowshoe hare cycle: Consequences of non-territorial ‘floaters’ on demography // J. Anim. Ecol. V. 65. P. 359–370.
Royama T., 1992. Analytical Population Dynamics. L.: Chapman and Hall. 371 p.
Soukhovolsky V., Kovalev A., Tarasova O., Modlinger R., Křenová Z. et al., 2022. Wind damage and temperature effect on tree mortality caused by Ips typographus L.: Phase transition model // Forests. V. 13. https://doi.org/10.3390/f13020180
Stenseth N.C., Falck W., Bjørnstad O.N., Krebs C.J., 1997. Population regulation in snowshoe hare and Canadian lynx: Asymmetric food web configurations between hare and lynx // Proc. Natl. Acad. Sci. V. 94. P. 5147–5152.
Turchin P., 2003. Complex Population Dynamics: A Theoretical/Empirical Synthesis. Princeton: Princeton Univ. Press. 472 p.
Volterra V., 1926. Fluctuations in the abundance of a species considered mathematically // Nature. V. 188. P. 558–560.
Vucetich J.A., Hebblewhite M., Smith D.W., Peterson R.O., 2011. Predicting prey population dynamics from kill rate, predation rate and predator-prey ratios in three wolf-ungulate systems // J. Anim. Ecol. V. 80. P. 1236–1245.
Wei W.W.S., 2006. Time Series Analysis. Boston: Addison Wesley. 614 p.
Zhang Z.B., Tao Y., Li Z.Q., 2007. Factors affecting hare-lynx dynamics in the classic time series of the Hudson Bay Company, Canada // Clim. Res. V. 34. P. 83–89.
Дополнительные материалы отсутствуют.
Инструменты
Журнал общей биологии