Микроэлектроника, 2022, T. 51, № 4, стр. 255-264

1. ВВЕДЕНИЕ

Спектроскопия, основанная на зондировании образцов легкими ионами (протонами и ионами гелия), например, ISS (Ion Scattering Spectroscopy), RBS (Rutherford Bask Scattering), ERD (Elastic Recoil Detection), находит широкое применение для исследования мишеней сложного состава [1–6]. В основе теорий, наиболее просто описывающих процессы упругого рассеяния ионов, лежит SLA приближение (Straight Line Approximation). В этом подходе рассматривается одно сильное обратное упругое рассеяние [3, 4], позволяющее с приемлемой точностью интерпретировать RBS спектры мэвных ионов. Однако, это приближение не способно с адекватной точностью описать особенности в спектрах RBS и ERD, возникающие при снижении энергии зондирующих ионов, что необходимо для определения послойных профилей с более высоким энергетическим разрешением. Для описания этих особенностей предпринимаются попытки включить в рассмотрение процессы двукратного упругого рассеяния, однако, вопрос о том, повышаем ли мы точность описания процесса, ограничиваясь двукратным приближением, не обсуждается. Еще больше трудностей возникает при использовании SLA приближения для интерпретации спектров ISS, что связано с тем, что энергия зондирующих ионов составляет единицы кэВ.

Аналитическое описание дифференциальных по углам и энергии спектров отраженных ионов традиционно строится на основе малоуглового приближения, которое базируется на “сильной вытянутости” дифференциального сечения упругого рассеяния ω_el(ψ):

Как показано в [7, 8], условие (1) позволяет на основе решения граничной задачи для уравнения переноса методом инвариантного погружения Амбарцумяна получить решение, которое принято называть OKG методом [9]. OKG метод успешно использовался исключительно для решения задач по определению угловых и энергетических характеристик отраженных электронов [7, 8, 10].

Однако, условие (1) выполняется для ионов в более широком интервале энергий, чем для электронов, что означает высокую эффективность OKG метода в спектроскопии легких ионов.

Представленная в работе методика описывает спектры однородных и многослойных мишеней на основе аналитического подхода, основанного на решении граничной задачи для уравнения переноса методом инвариантного погружения Амбарцумяна. Решение определяется параметрами сечения упругого рассеяния, на основе которого вычисляется PLDF (Pass Length Distribution Function), и энергетическими характеристиками, такими как, величина средних потерь энергии на единицу длину (stopping power), верификация которой подробно обсуждается в работе, и параметры, определяющие процесс перезарядки ионов. Энергетические спектры отраженных протонов, вычисленные на основе представленной методики, сравниваются с экспериментальными данными.

2. ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

Рассмотрим задачу упругого рассеяния электронов и легких ионов в твердых телах. Решение граничной задачи для уравнения переноса методом инвариантного погружения в азимутально симметричной ситуации приводит к формуле:

где $S\left( {\tau ,{{\mu }_{0}},\mu } \right)$ – функция отражения, определяемая геометрией рассеяния: ${{\mu }_{0}},\mu $ – косинусы углов визирования и зондирования; и безразмерной длиной пробега частицы в мишени $\tau = \frac{z}{{{{l}_{{el}}}}}$; ${{l}_{{el}}}$ – средняя длина свободного пробега между упругими соударениями. $x\left( {{{\mu }_{0}},\mu } \right)$ – нормированное на единицу дифференциальное сечение упругого рассеяния.

Функция $S\left( {\tau ,{{\mu }_{0}},\mu } \right)$ описывает распределение отраженных частиц по длинам пробега в мишени – PLDF.

В [7, 8] показано, что условие (1) позволяет упростить уравнение (2) и записать его в виде:

В [7, 8] отмечено, что переход от (2) к (3) приводит к погрешностям, величина которых определяется степенью вытянутости дифференциального сечения упругого рассеяния $x\left( \mu \right)$, а именно, малостью отношения:

В случае консервативного рассеяния (когда исключается канал неупругого рассеяния) можно получить аналитическое решение уравнения (3). Процедура этого решения и обоснование сделанных допущений на основе сравнения результатов с результатами точного численного решения уравнения (2) представлены в [8]. Полученное решение одинаково в случае электронного рассеяния и в случае рассеяния легких ионов. Однако, в случае рассеяния легких ионов, сделанные для получения аналитического решения допущения применимы в более широком интервале энергий, т.к. параметр экранирования процесса элементарного рассеяния легких ионов на порядки меньше электронного – ${{\zeta }_{{ion}}} \ll {{\zeta }_{{electron}}}$.

Получим решение уравнения (3) в SLA приближении. В подынтегральном выражении правой части уравнения (3) находится произведение функции $x\left( {\mu {\kern 1pt} ',\mu } \right)$, имеющий резкий максимум при $\mu {\kern 1pt} ' = \mu $, на функцию $S\left( {\tau ,{{\mu }_{0}},\mu {\kern 1pt} '} \right)$, плавно зависящую от $\mu {\kern 1pt} '$. Для вычисления интеграла в уравнении (3) разложим функцию отражения $S\left( {\tau ,{{\mu }_{0}},\mu {\kern 1pt} '} \right)$ в ряд Тейлора вблизи $\mu {\kern 1pt} ' = \mu $:

Подставляя разложение (5) в подынтегральное выражение уравнения (3) и ограничиваясь только первым членом разложения в ряд Тейлора, получаем:

где $\alpha \left( \mu \right) = \int_0^1 {x\left( {\mu {\kern 1pt} ',\mu } \right)d\mu {\kern 1pt} ' \ll 1} $. Например, в случае Резерфордовского рассеяния – $\alpha \left( \mu \right)\sim \eta $, где $\eta $ – параметр экранирования, равный квадрату отношения длины волны де Бройля налетающей частицы к радиусу Дебая среды, в которой движется частица. Решение уравнения (6) в SLA приближении:

Поскольку в уравнении (7) $\alpha \left( \mu \right) \ll 1$, то экспоненту в решении в SLA приближении не пишут.

Если в уравнение (3) подставить все выписанные члены ряда Тейлора (5), то перейдем к уравнению:

где ${{\vartriangle }_{\mu }} = \frac{\partial }{{\partial \mu }}\left( {1 - {{\mu }^{2}}} \right)\frac{\partial }{{\partial \mu }}$ – полярная часть оператора Лапласа в сферических координатах, ${{\sigma }_{{tr}}}$ – нормированное транспортное сечение.

Подробный вывод перехода от уравнения (3) к уравнению (8) после подстановки уравнения (5) в уравнение (3) представлен в [11].

Решение уравнения (8) находим, представив функцию $S\left( {\tau ,{{\mu }_{0}},\mu } \right)$ в виде разложения по полиномам Лежандра:

где ${{\tau }_{{tr}}}$ – измеренный в транспортных длинах пробег частицы, ${{x}^{l}}$ – коэффициенты разложения нормированного дифференциального сечения упругого рассеяния $x\left( \mu \right)$ в ряд по полиномам Лежандра.

При стремящемся к нулю пробеге частицы $\tau \to 0$ решения (7) и (9) совпадают. Допущения, в рамках которых получено решение (9), называется малоугловым диффузионным приближением [11]. На рис. 1 представлены решения (7) и (9), описывающие распределение по пробегам отраженных от титановой мишени протонов.

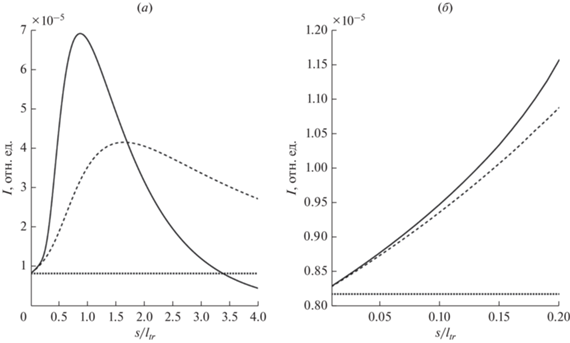
Графики на рис. 1 представляют решение чисто упругой задачи. Для электронов и легких ионов решение было получено на основе одинаковых исходных уравнений (3). Очевидно, что SLA приближение не способно адекватно описать процесс формирования потока отраженных протонов. Дело в том, что в SLA приближении не учитывается процесс изотропизации нисходящего потока частиц, который позволяет изменять нисходящее движение на восходящее при рассеянии частиц на углы, меньшие, чем угол между направлением зондирующего потока частиц и направлением на энергоанализатор. Расчет на основе диффузионного приближения на рис. 1 показывает, что многократное упругое рассеяние в нисходящем и восходящем потоках, которое исключает SLA приближение, приводит к резкому росту числа отраженных протонов. Процесс многократного упругого рассеяния в восходящем и нисходящем потоках частиц кардинально меняет число отраженных протонов с пробегом, меньшим и составляющим величину порядка транспортного пробега в мишени.

Еще раз отметим, что PLDF, представленные на рис. 1 сплошной и штрихпунктирной линией, это результат учета многократного упругого рассеяния. Подчеркнем, что модели двукратного, трехкратного и т.д. упругого рассеяния не имеют смысла. Рис. 1 указывает на то, что SLA приближение справедливо только в том случае, если транспортный пробег ${{l}_{{tr}}} = \frac{1}{{{{\sigma }_{{tr}}}n}}$, где $n$ – концентрация частиц в мишени, будет намного больше остаточного пробега (Residual Range):

где ${{E}_{0}}$ – начальная энергия зондирующего пучка частиц, $\bar {\varepsilon }$ – средние потери энергии частиц на единицы длины (stopping power).

Решение уравнения (3) методом, описанным в [7, 9], имеет вид:

Решение (3) подробно апробировано в [7, 8, 10]. В [10] показано удовлетворительное соответствие результатов, полученных на основе формулы (11), результатам моделирования методом Монте-Карло (МК). В [7] показано хорошее соответствие расчетов, выполненных на основе формулы (11), точному численному решению уравнения (2).

Для описания ионного рассеяния дифференциальные сечения упругого рассеяния $x\left( \mu \right)$ определялись в первом Борновском приближении на основе потенциала криптон-углерод (Kr-C) [1–3]. Транспортные сечения определялись в соответствии с [12]. Описание PLDF протонов, отраженных от титановой мишени, рассчитанное по OKG методу на основе формулы (11), представлено на рис. 1 сплошной линией.

Из рис. 1 видно лишь качественное соответствие PLDF, вычисленного в диффузионном приближении, результатам, полученным по OKG методу. Связано это с тем, что при расчете в диффузионном приближении учитываются лишь три первых слагаемых в разложении в ряд Тейлора (5). Диффузионное приближение позволяет объяснить такую особенность RBS спектра, как Low Energy Tail [6], которая наблюдается при снижении энергии пучка зондирующих ионов до энергии в сотни кэВ. Снижение энергии пучка зондирующих ионов в RBS методе необходимо для повышения энергетического и, как следствие, пространственного разрешения метода [6].

Энергетические спектры отраженных частиц определяются в соответствии с формулой:

где $T\left( {\tau ,\vartriangle } \right)$ – в случае ионного рассеяния определяется лишь двумя моментами сечения неупругого рассеяния: $\bar {\varepsilon }$ – средние потери энергии частицы на единице длины, $\overline {{{\varepsilon }^{2}}} $ – средний квадрат потерь энергии частицы на единице длины или страгглинг. Это следует из законов сохранения энергии и импульса, ограничивающих максимум энергии, которую ион может передать электронной подсистеме.

Функция $T\left( {\tau ,\,\vartriangle } \right)$ имеет следующий вид:

где ${{\sigma }_{\sum }} = \overline {{{\varepsilon }^{2}}s} + {{\sigma }_{{Dop}}} + {{\sigma }_{{beam}}} + {{\sigma }_{{enan}}}$ – суммарный уширяющий фактор, который есть сумма страгглинга – $\overline {{{\varepsilon }^{2}}s} $; уширения за счет эффекта Допплера – ${{\sigma }_{{Dop}}}$; уширения, возникающего за счет энергетического разброса в зондирующем пучке – ${{\sigma }_{{beam}}}$; аппаратной функции энергоанализатора – ${{\sigma }_{{enan}}}$.

Подставив PLDF (11) в формулу для расчета энергетических спектров (12), получим выражение для расчета энергетических спектров отраженных частиц в приближении непрерывного замедления или, когда $T\left( {z,\vartriangle } \right) = \delta \left( {\vartriangle - \bar {\varepsilon }z} \right)$:

В формуле (14) безразмерный параметр $\sigma {\kern 1pt} *$ является определяющим для аналитического описания процесса формирования энергетических спектров отраженных ионов:

где $\frac{{{{E}_{0}}}}{{\bar {\varepsilon }}}$ – длина пробега иона до полной его остановки или, как было отмечено выше, residual range.

Для протонов, имеющих начальную энергию в интервале – 1 кэВ $ < {{E}_{0}} < $ 30 кэВ, параметр $\sigma *\sim 1$.

Множители вида $\left( {1 - \vartriangle } \right)$ и ${{\left( {1 - \vartriangle } \right)}^{{5/2}}}$ учитывают зависимость сечения упругого рассеяния и сечения неупругого рассеяния от энергии.

Функция ${\text{exp}}\left( { - \frac{A}{{\sqrt {1 - \vartriangle } }}} \right)$ в формуле (14) введена для учета явления перезарядки отраженных ионов [1–5]. Безразмерная константа $A$, определяющая эффективность процесса нейтрализации ионов при отрыве от поверхности образца, считается подгоночным параметром.

Для того чтобы получить окончательный вид энергетического спектра отраженных ионов необходимо провести свертку формулы (14) с формулой (13).

3. АНАЛИТИЧЕСКАЯ МОДЕЛЬ ОТРАЖЕНИЯ ОТ ОДНОРОДНЫХ МИШЕНЕЙ

Энергетические спектры отраженных протонов, представленные в [1–4], в настоящей работе были проинтерпретированы на основе расчетных спектров, вычисленных по формулам (12)–(14). При расчете использовались данные по stopping power, взятые из таблиц NIST (National Institute of Standard Technology) [13]. Из полученных результатов сравнения можно заключить, что нами достигнуто полное качественное соответствие, а именно одинаковое поведение расчетных и экспериментальных спектров в зависимости от атомного номера мишени и энергии зондирующего пучка. Причины количественного различия связаны в основном с погрешностью, с которой известны данные по stopping power протонов. Наибольший разброс данных по stopping power приходится на энергии зондирующего пучка протонов, рассматриваемые в настоящей работе.

Представленное на рис. 2 сравнение расчетных (формулы (13) и (14)) и экспериментальных [14] данных по вольфраму указывает на удовлетворительное соответствие развитой в настоящей работе методики экспериментальным результатам.

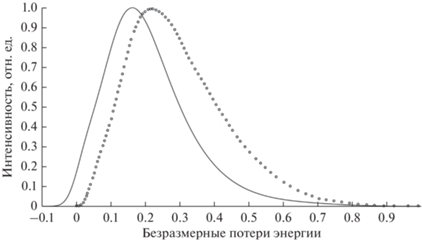
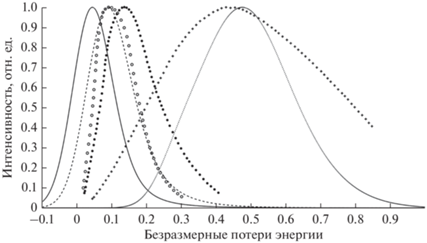
Рис. 3 отражает общие характеристики энергетических спектров отраженных протонов, наблюдаемые при изменении атомного номера мишени – Z [15]: при неизменной энергии зондирующего пучка протонов при уменьшении Z наблюдается уширение энергетического спектра и сдвиг максимума спектра в область больших потерь энергии.

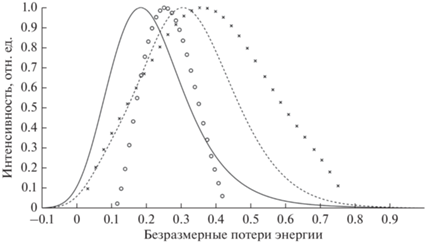
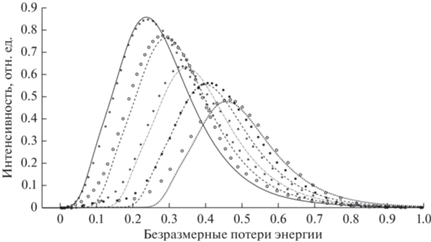
Особенности поведения энергетических спектров отраженных протонов, наблюдаемые при изменении энергии зондирующего пучка, представлены на рис. 4. С ростом энергии зондирующего пучка протонов наблюдается сдвиг максимума энергетического спектра в сторону меньших энергий и рост относительной полуширины спектра. Отмеченный сдвиг максимума спектра и уширение спектра наблюдается во всех экспериментах для энергии зондирующего пучка легких ионов в интервале от единиц до десятков кэВ [16].

Стоит отметить, что среди огромного многообразия экспериментальных данных не удалось найти спектры, подобные тем, что представлены на рис. 3, но измеренные с относительной точностью, как, например, сделано в [17]. Это важно знать при интерпретации энергетических спектров легких ионов, отраженных от слоисто неоднородных мишеней.

4. АНАЛИТИЧЕСКАЯ МОДЕЛЬ ОТРАЖЕНИЯ ОТ СЛОИСТО НЕОДНОРОДНЫХ МИШЕНЕЙ

Рассмотрим двухслойную мишень, схема которой представлена на рис. 5.

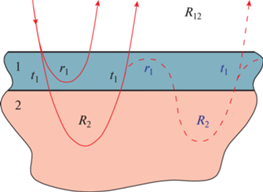
Функция пропускания представляет собой оператор, определяющий плотность потока частиц $I\left( {E,{{\theta }_{0}},\theta ,{{\varphi }_{0}} - \varphi } \right)$, прошедших сквозь слой:

Функция отражения представляет собой оператор, определяющий плотность потока частиц $I\left( {E,{{\theta }_{0}},\theta ,{{\varphi }_{0}} - \varphi } \right)$, отраженных от слоя:

В формулах (16) и (17) дана как подробная, так и матричная запись действия функции пропускания и функции отражения на плотность потока падающих частиц ${{I}_{0}}\left( {E{\kern 1pt} ',\theta {\kern 1pt} ',\varphi {\kern 1pt} '} \right)$. Плотность потока частиц, отраженных и прошедших сквозь слой, есть сумма плотностей потока частиц ${{I}_{T}}\left( {E,\theta ,\varphi } \right)$ и ${{I}_{r}}\left( {E,\theta ,\varphi } \right)$ и обозначается ${{I}_{{T,r}}}\left( {E,\theta ,\varphi } \right)$.

Воспользовавшись матричной записью, записываем плотность потока частиц, прошедших и отразившихся от слоя материала “1”, толщиной d₁, и отразившихся от материала “2”, ${{R}_{{12}}}\left( {E,{{\theta }_{0}},\theta ,{{\varphi }_{0}} - \varphi } \right)$:

В первом приближении пренебрежем последними слагаемыми:

где $t\left( {d,{{\theta }_{0}},E - E{\kern 1pt} '} \right) = t\left( {\frac{d}{{\cos {\kern 1pt} {{\theta }_{0}}}}} \right)\frac{1}{{\sqrt {{{2\pi \overline {{{\varepsilon }^{2}}} d} \mathord{\left/ {\vphantom {{2\pi \overline {{{\varepsilon }^{2}}} d} {\cos {{\theta }_{0}}}}} \right. \kern-0em} {\cos {{\theta }_{0}}}}} }} \times $ $ \times \,\,{\text{exp}}\left( { - \frac{{\left( {E - E{\kern 1pt} ' - {{\bar {\varepsilon }d} \mathord{\left/ {\vphantom {{\bar {\varepsilon }d} {\cos {\kern 1pt} {{\theta }_{0}}}}} \right. \kern-0em} {\cos {\kern 1pt} {{\theta }_{0}}}}} \right)}}{{{{2\overline {{{\varepsilon }^{2}}} d} \mathord{\left/ {\vphantom {{2\overline {{{\varepsilon }^{2}}} d} {\cos {\kern 1pt} {{\theta }_{0}}}}} \right. \kern-0em} {\cos {\kern 1pt} {{\theta }_{0}}}}}}} \right)$ – функция пропускания, описывающаяся нормальным законом распределения.

Если известны экспериментальные данные по спектрам ${{R}_{1}}\left( {E,{{\theta }_{0}},\theta ,{{\varphi }_{0}} - \varphi } \right)$ и ${{R}_{2}}\left( {E,{{\theta }_{0}},\theta ,{{\varphi }_{0}} - \varphi } \right)$, то можно получить более простую формулу для определения ${{R}_{{12}}}\left( {E,{{\theta }_{0}},\theta ,{{\varphi }_{0}} - \varphi } \right)$. Будем использовать представление (19) для записи функции отражения от однородной полубесконечной мишени из материала “1”:

Получив выражение для функции ${{r}_{1}}$ из формулы (20) и подставив ее в формулу (19), получаем:

Формулу (21) можно легко обобщить на трехслойную мишень. Покроем мишень, представленную на рис. 5, сверху слоем, толщиной d₀ из материала “0”, тогда получим:

Аналогично формуле (20), получаем:

Для трехслойной модели получаем итоговую формулу:

На рис. 6 представлены результаты расчета энергетических спектров протонов, отраженных от мишени из вольфрама, покрытого слоями лития различной толщины.

5. ОСНОВНЫЕ РЕЗУЛЬТАТЫ

В настоящей работе определены границы применимости метода описания энергетических спектров отраженных частиц, основанного на приближении одного сильного упругого рассеяния или приближении прямолинейных траекторий – SLA. В данном приближении полагается, что движение частиц до и после сильного упругого рассеяния происходит по прямолинейным траекториям (исключается изменение направления движения частицы за счет многократного упругого рассеяния), однако неупругое рассеяние, приводящее к торможению частицы, имеет место. На рис. 1 представлено решение задачи об упругом рассеянии протонов в различных приближениях. Из их сравнения следует, что SLA приближение применимо только тогда, когда остаточный пробег иона много меньше транспортного пробега:

Решение консервативной, чистой упругой задачи отражения легких ионов от поверхности твердого тела получено по OKG методу. Этот метод с большим успехом применяется для решения задач отражения электронов от поверхности твердого тела [7, 8, 10]. В настоящей работе показано, что для перехода от электронного рассеяния к протонному рассеянию, в OKG методе необходимо лишь заменить дифференциальные сечения упругого рассеяния. Применение OKG метода в задачах протонного рассеяния возможно в более широком интервале энергий, что является следствием малоуглового приближения (т.к. длина волны де Бройля протонов меньше, чем у электронов, а, следовательно, и параметр экранирования меньше). Полученное на основе OKG метода распределение отраженных ионов по длинам пробега в мишени описывается формулой (11). Положение максимума распределения отраженных ионов по длинам пробега в мишени, измеренного в длинах транспортного пробега ${{\tau }_{{tr}}}$, не зависит от атомного номера мишени и энергии зондирующего пучка протонов. Определяется оно видом выбранного сечения дифференциального упругого рассеяния.

Расчет энергетических спектров отраженных ионов выполнялся на основе формулы (12). Вид этой формулы объясняется независимостью процессов упругого и неупругого рассеяния. Функция, описывающая спектр энергетических потерь ионов с пробегом, равным $s$, представлена формулой (13). Аналитическое выражение для энергетического спектра отраженных ионов, записанное в приближении непрерывного замедления, представлено формулой (14). Удовлетворительное количественное совпадение расчетных энергетических спектров наблюдается для экспериментальных данных, полученных на большом масс-монохроматоре МИФИ [14] (рис. 2 и рис. 6). На рис. 3, 4 наблюдается качественное соответствие расчетных и экспериментальных данных. Причиной количественного различия результатов является большая погрешность данных по средним потерям энергии протонов на единице длины $\bar {\varepsilon }$.

Расчетные и экспериментальные данные, представленные на рис. 6, демонстрируют хорошее качество представленной в работе методики расчета спектров протонов, отраженных от слоисто неоднородных мишеней. Результаты, представленные на рис. 6, наиболее ярко демонстрируют возможности для реализации процедуры измерения величины $\bar {\varepsilon }$, если нам известна толщина покрытия, которую можно определить, например, методами рентгеновской фотоэлектронной спектроскопии.

На основе метода, ранее успешно использованного для задач электронного и ионного рассеяния [17–19], построены расчетные схемы для определения энергетических спектров ионов, отраженных от слоисто неоднородных мишеней. Показано удовлетворительное качественное описание энергетических спектров ионов, отраженных от неоднородных поверхностей, на основе описанных в настоящей работе методов. Причиной количественного различия является не неприменимость OKG метода и не подходы, представленные в [7, 8, 10], а недостаточная апробация данных по упругому рассеянию легких ионов и отсутствие данных по сечениям неупругого рассеяния легких ионов в поверхности твердого тела.

ЗАКЛЮЧЕНИЕ

Спектроскопия, основанная на зондировании поверхности легкими ионами средних энергий, обладает широкими и, в ряде ситуаций, уникальными возможностями [1–5]. Как по интенсивности отраженных от поверхности твердого тела ионов, так и по интенсивности выбитых из твердого тела ионами атомам (атомам отдачи), можно осуществлять поэлементным анализ поверхности. Метод, основанный на ионном зондировании поверхностного слоя твердого тела, обладает высочайшей чувствительностью. С помощью данного метода возможно исследование процессов адсорбции и десорбции ионов [5], исследование многослойных структур на основе измерения полных коэффициентов отражения ионов, исследование структуры и релаксации поверхности кристаллов [5].

Внимательное исследование результатов анализа твердых тел на основе ионного зондирования указывает на одно важное обстоятельство: в существующих в настоящее время методиках, основанных на расшифровке спектров рассеянных ионов, можно говорить лишь о качественном анализе образца. Исследование в качестве примера работ [20, 21] одной научной группы, посвященных экспериментальному анализу покрытий на основе энергетических спектров отраженных протонов, и работ [20, 22] той же научной группы, посвященных МК моделированию энергетических спектров протонов, отраженных от двухслойных мишеней, приводит к важному заключению – авторы не производят сравнения, сопоставления полученных экспериментальных данных и расчетов по МК моделированию. С подобными ситуациями мы столкнулись, анализируя данные на рис. 3 и рис. 4. В настоящей работе мы наблюдаем удовлетворительное качественное соответствие экспериментальных данных и результатов расчета по предложенной методике, однако отсутствует количественное совпадение, причиной которого, как мы считаем, является огромная погрешность существующих данных по средним потерям энергии ионов на единице длины – $\bar {\varepsilon }$. Однако, причиной также могут быть данные по дифференциальным сечениям упругого рассеяния ионов – $x\left( \mu \right)$.

Авторы настоящей работы, имеющие большой опыт в расшифровке спектров электронного рассеяния, спектров рентгеновского фотоэлектронной спектроскопии, видели путь становления количественной электронной спектроскопии. Надежные данные по дифференциальным сечениям упругого рассеяния электронов – это результат экспериментальной верификации данных по сечениям и угловым распределениям упруго отраженных электронов, выполненной Бронштейном и Прониным [23, 24]. Анализ спектров характеристических потерь энергии электронов позволил сформулировать основные механизмы потерь энергии электронов в веществе, позволил построить дифференциальные сечения неупругого рассеяния электронов ${{x}_{{in}}}\left( \vartriangle \right)$ и определить моменты этого сечения. С особой аккуратностью выверен нулевой момент сечения неупругого рассеяния электронов – полное сечение неупругого рассеяния – ${{\sigma }_{{in}}}$ или inelastic mean free pass – ${{l}_{{in}}} = \frac{1}{{n{{\sigma }_{{in}}}}}$, где $n$ – концентрация атомов твердого тела [25, 26]. Базой для определения дифференциальных сечений неупругого рассеяния электронов стали надежные данные по дифференциальным сечениям упругого рассеяния электронов [27], апробированные на основе методик, развитых в [23, 24].

Данные, необходимые для теоретического описания спектроскопии легких ионов средних энергий, можно найти, например, в таблицах NIST. Однако данные по первому моменту дифференциального сечения неупругого рассеяния – $\bar {\varepsilon }$ в них даны с огромной погрешностью. Данных по виду дифференциального сечения неупругого рассеяния ионов не существует, т.к. не были проведены эксперименты, подобные измерению спектров характеристических потерь энергии электронов, или эксперименты по измерению с высоким энергетическим разрешением области спектра, соответствующей потерям энергии ионов от нуля до сотни эВ. Если рассмотреть задачу упругого рассеяния ионов, то существует целый ряд потенциалов взаимодействия быстрых ионов с атомами твердого тела, однако строгих правил, в соответствии с которыми можно выбрать наиболее надежный вариант, не существует. Эксперименты, необходимые для апробации дифференциальных сечений упругого рассеяния ионов, подобных экспериментам Бронштейна и Пронина [23, 24], не проводились.

В настоящей работе установлено, что наибольшее качественное совпадение экспериментальных и расчетных спектров отраженных протонов наблюдается при использовании транспортного сечения упругого рассеяния протонов, предложенного в работе Фирсова [12]. Коэффициенты разложения сечения в ряд по полиномам Лежандра – ${{x}^{l}}$ определялись в соответствии с потенциалом криптон-углерод (Kr-C).

Энергетические спектры отраженных протонов очень чувствительны к величине средних потерь энергии протонов на единице длины – $\bar {\varepsilon }$. Развитая в настоящей работе методика представляет удобный и эффективный инструмент верификации данных по $\bar {\varepsilon }$.

Работа была выполнена в рамках Госзадания № FSFW-2020-0023.