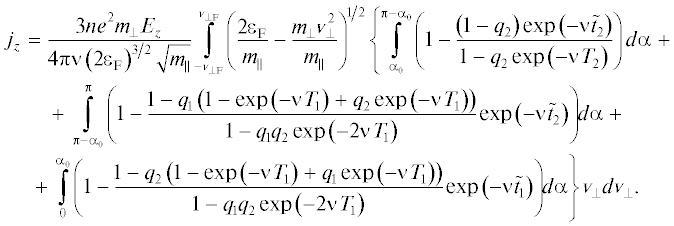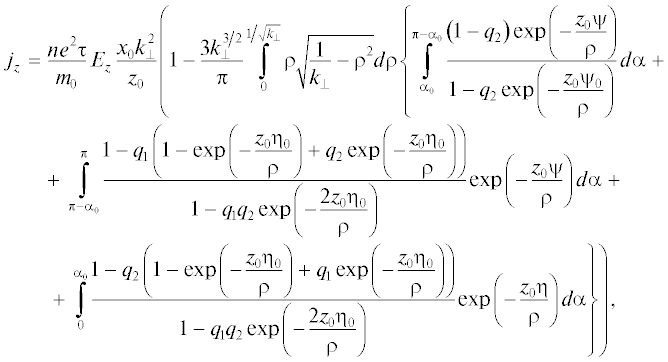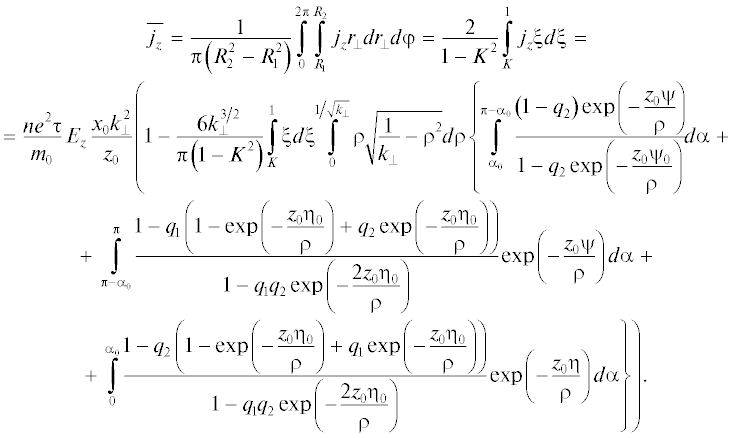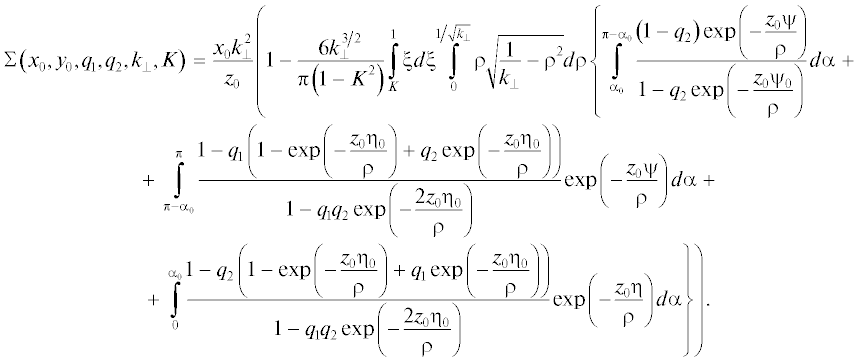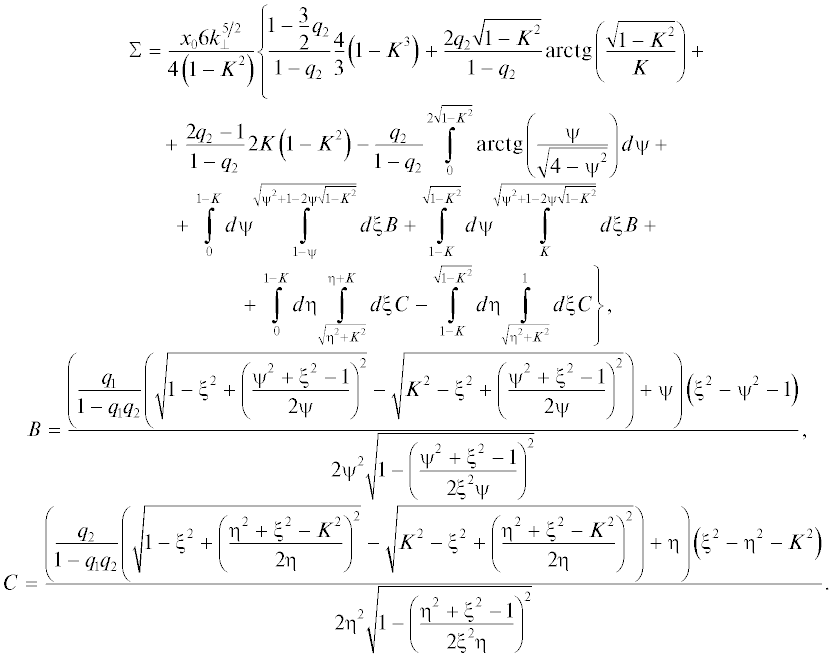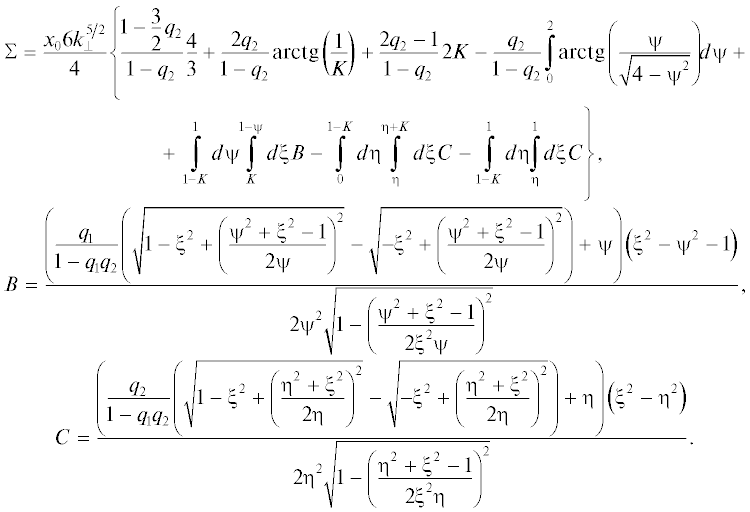Микроэлектроника, 2019, T. 48, № 2, стр. 111-124
Влияние анизотропии поверхности ферми на электропроводность тонкой неоднородной металлической проволоки
И. А. Кузнецова 1, *, Д. Н. Романов 1, А. А. Юшканов 2
1 Ярославский государственный университет им. П.Г. Демидова
150003 Ярославль, ул. Советская, 14, Россия
2 Московский государственный областной университет
105005 Москва, ул. Радио, д. 10, Россия
* E-mail: kuz@uniyar.ac.ru
Поступила в редакцию 24.08.2018
Аннотация
В рамках кинетического подхода проведен расчет высокочастотной электропроводности тонкой неоднородной металлической проволоки с диэлектрическим ядром. Предполагается, что поверхности Ферми металла имеет вид эллипсоида вращения, ось вращения которого совпадает с осью проволоки. Рассматривается случай изотропного рассеяния электронов, при котором объемное время релаксации не зависит ни от энергии, ни от направления рассеяния электронов. На соотношение между длиной свободного пробега электронов проводимости и радиусом проволоки ограничений не накладывается. Проанализированы зависимости модуля и аргумента безразмерной проводимости от безразмерной поперечной эффективной массы, безразмерного радиуса проволоки, безразмерной частоты электрического поля и от соотношения радиусов проволоки и диэлектрического ядра.
ВВЕДЕНИЕ
Уменьшение характерных размеров транзисторов в полупроводниковых интегральных схемах приводит к повышению их быстродействия, однако накладывает ограничения на металлические соединительные линии. В случае, когда линейный размер образца становится сравнимым с длиной свободного пробега носителей заряда, возникают классические размерные эффекты, обуславливающие рост сопротивления проводящего элемента, при этом увеличиваются время задержки сигнала и расход энергии. Нагрев образцов усиливает интенсивность электромиграции атомов металла, что снижает надежность схемы. Международный план по развитию полупроводниковых технологий, одобренный группой экспертов, представляющих Ассоциацию полупроводниковой промышленности, нацеливает на поиск новых материалов, заменяющих классические медные соединительные провода, которые из-за высокого сопротивления становятся непригодными для использования в качестве соединительных элементов схем. В последние годы проведено исследование на вольфрамовых тонких пленках [1]. Анализ показал, что удельное сопротивление малых металлических пленок зависит от направления, если даже объемное сопротивление изотропно и электронное сечение рассеяние не зависит от импульса, поверхностной ориентации и направления переноса. В работе [2] сообщается, что основной причиной анизотропии является несферическая поверхность Ферми. Таким образом, уменьшить сопротивление тонкопленочного образца можно с помощью изменения его кристаллической ориентации.
В ряде случаев изоэнергетическую поверхность металла можно рассматривать как трехосный эллипсоид [3], что является естественным обобщением более простой и часто используемой при описании явлений переноса модели сферической поверхности Ферми [4]. Систематического изучения процессов переноса в случае эллипсоидальной поверхности Ферми для таких систем как тонкие пленки и проволоки до сих пор не проводилось.
Расчет статической проводимости тонкой металлической проволоки круглого сечения выполнен в работе [5], проволоки прямоугольного сечения – в работе [6]. Теоретическое исследование металлической пленки в квазиклассическом приближении при наличии постоянных магнитного и электрического полей проводились Зондгеймером [7] c учетом диффузного механизма отражения электронов от верхней и нижней границы пленки. Расчет высокочастотной электропроводимости тонкой цилиндрической полупроводниковой проволоки проведен в работе [8]. В упомянутых работах применяется подход, основанный на решение кинетического уравнения Больцмана для свободных носителей заряда с применением граничных условий Фукса [9]. Высокочастотная электропроводность тонкой цилиндрической проволоки с применением граничных условий Соффера [10] получена в работе [11]. Выражение для электропроводности тонкого поликристаллического металлического провода круглого сечения c учетом граничных условий Соффера и возможных колебаний диаметра провода по его длине рассчитано в [12]. Во всех отмеченных работах расчет выполнялся для квазичастиц со сферической поверхностью Ферми.
В данной работе исследуется влияние эллиптичного характера поверхности Ферми на удельную высокочастотную электропроводность тонкой неоднородной металлической проволоки круглого сечения с применением диффузно-зеркальных граничных условий Фукса.
ПОСТАНОВКА ЗАДАЧИ
Рассматривается длинная цилиндрическая проволока длиной $L,$ состоящая из диэлектрического ядра радиусом ${{R}_{1}},$ окруженного металлической оболочкой радиусом ${{R}_{2}}$ (считаем, что $L \gg {{R}_{2}}$), к концам которой приложено переменное электрическое напряжение частотой $\omega .$ Направление электрического поля ${\mathbf{E}}$ совпадает с осью цилиндра. Скин-эффект не учитывается (предполагается, что ${{R}_{2}} < \delta ,$ $\delta $ – глубина скин-слоя). На соотношение между радиусом проволоки ${{R}_{2}}$ и длиной свободного пробега носителей заряда λ ограничений не накладывается.
Однородное периодическое по времени электрического поле
воздействует на носители заряда и вызывает появление внутри проволоки высокочастотного тока ${\mathbf{j}}.$Равновесная функция Ферми–Дирака ${{f}_{0}}$ для электронов проводимости в металлах имеет ступенчатый вид
(2)
${{f}_{0}} = \left\{ {\begin{array}{*{20}{c}} {1,\,\,\,\,\quad\varepsilon < {{{\varepsilon }}_{F}}} \\ {0,\,\,\,\,\quad\varepsilon > {{{\varepsilon }}_{F}}} \end{array}} \right.,$В случае слабого внешнего электрического поля ${\mathbf{E}}$ (1) линейное отклонение функции распределения f от равновесной функции Ферми–Дирака ${{f}_{0}}$ (2) можно представить следующим образом
Для достаточно слабых внешних полей это уравнение можно линеаризовать по внешнему полю ${\mathbf{E}}$ и по малым отклонениям ${{f}_{1}}\left( {{\mathbf{r}},{\mathbf{v}}} \right)$ от равновесной фермиевской функции распределения ${{f}_{0}}{\text{:}}$
(3)
$ - i{\omega }{{f}_{1}} + {\mathbf{v}}\frac{{\partial {{f}_{1}}}}{{\partial {\mathbf{r}}}} + e\left( {{\mathbf{vE}}} \right)\frac{{\partial {{f}_{1}}}}{{\partial {\varepsilon }}} = - \frac{{{{f}_{1}}}}{{\tau }}.$Ось тонкой проволоки совпадает с осью Z, соответственно, две другие оси 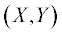 направлены перпендикулярно боковой поверхности. В данной работе поверхность Ферми
– эллипсоид вращения, ось вращения которого совпадает с осью $Z,$ поэтому энергия электронов проводимости определяется следующим образом [3]:
направлены перпендикулярно боковой поверхности. В данной работе поверхность Ферми
– эллипсоид вращения, ось вращения которого совпадает с осью $Z,$ поэтому энергия электронов проводимости определяется следующим образом [3]:
(4)
${\varepsilon } = \frac{{{{m}_{ \bot }}\text{v}_{ \bot }^{2}}}{2} + \frac{{{{m}_{\parallel }}\text{v}_{\parallel }^{2}}}{2},$Энергия, соответствующая поверхности Ферми, равна:
Внешнее электрическое поле (1) действует на носители заряда, что приводит к появлению внутри проволоки высокочастотного тока плотностью j :
(5)
${\mathbf{j}} = en\left\langle {\mathbf{v}} \right\rangle = e\int {{\mathbf{v}}f\frac{{2{{d}^{3}}\left( {m\text{v}} \right)}}{{{{h}^{3}}}}} = 2e\frac{{m_{ \bot }^{2}{{m}_{\parallel }}}}{{{{h}^{3}}}}\int {{\mathbf{v}}{{f}_{1}}{{d}^{3}}v} ,$(6)
$n = 2\frac{{m_{ \bot }^{2}{{m}_{\parallel }}}}{{{{h}^{3}}}}\int {{{f}_{0}}{{d}^{3}}\text{v}} = \frac{{8{\pi }}}{3}\frac{{{{m}_{ \bot }}\sqrt {{{m}_{\parallel }}} }}{{{{h}^{3}}}}{{\left( {2{{\varepsilon }_{{\text{F}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}.$Для однозначного решения уравнения (3) и нахождения вида функции ${{f}_{1}}$ необходимо задать для нее граничные условия на цилиндрической поверхности металлической оболочки и диэлектрического ядра проволоки. В качестве таковых используем условие зеркально-диффузного отражения электронов от этих поверхностей [11]. Поскольку электроны могут отражаться от внутренней (R1) и внешней (R2) границ металлического слоя, то необходимо записать два граничных условия:
(7)
${{f}_{{11}}}\left( {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }},{{{\mathbf{v}}}_{\parallel }}} \right) = {{q}_{1}}{{f}_{{11}}}\left( {{{{\mathbf{r}}}_{ \bot }},{\mathbf{v}}_{ \bot }^{'},{{{\mathbf{v}}}_{\parallel }}} \right)\,\,\,\,{\text{п р и }}\,\,\,\,\quad\left\{ {\begin{array}{*{20}{c}} {\left| {{{{\mathbf{r}}}_{ \bot }}} \right| = {{R}_{1}},} \\ {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }} > 0,} \end{array}} \right.$(8)
${{f}_{{12}}}\left( {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }}} \right) = {{q}_{2}}{{f}_{{12}}}\left( {{{{\mathbf{r}}}_{ \bot }},{\mathbf{v}}_{ \bot }^{'},{{{\mathbf{v}}}_{\parallel }}} \right)\,\,\,\,{\text{п р и }}\,\,\,\,\left\{ {\begin{array}{*{20}{c}} {\left| {{{{\mathbf{r}}}_{ \bot }}} \right| = {{R}_{2}},} \\ {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }} < 0,} \end{array}} \right.$ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
Для решения кинетического уравнения (3) используется подход, описанный в работах [9, 13, 14]. Изменение ${{f}_{1}}$ вдоль траектории (характеристики) $d{\mathbf{r}} = {\mathbf{v}}d\tilde {t}$ определяется уравнением
(9)
$\frac{{d{{f}_{1}}}}{{d\tilde {t}}} = - \nu {{f}_{1}} - e\left( {{\mathbf{vE}}} \right)\frac{{\partial {{f}_{0}}}}{{\partial {\varepsilon }}},$Граничное условие (7), (8) позволяет проследить за изменением функции ${{f}_{1}}\left( {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }},{{{\mathbf{v}}}_{\parallel }}} \right)$ вдоль зеркально отражающейся траектории. В точке отражения $\tilde {t} = {{\tilde {t}}_{N}}$ функция ${{f}_{1}}\left( t \right)$ испытывает скачок
(10)
${{f}_{1}}\left( {{{{\tilde {t}}}_{N}} + 0} \right) = q{{f}_{1}}\left( {{{{\tilde {t}}}_{N}} - 0} \right).$Знак ${ + \mathord{\left/ {\vphantom { + - }} \right. \kern-0em} - }$ обозначает предел функции ${{f}_{1}}\left( {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }},{{{\mathbf{v}}}_{\parallel }}} \right)$ в точке отражения ${{\tilde {t}}_{N}}$ справа или слева по времени пролета, q – коэффициент зеркальности внутренней поверхности $\left( {q = {{q}_{1}}} \right)$ или внешней поверхности $\left( {q = {{q}_{2}}} \right).$
При зеркальном отражении сохраняется угловой момент $\left[ {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }}} \right]$ = $\left[ {{{{\mathbf{r}}}_{ \bot }},{\mathbf{v}}_{ \bot }^{'}} \right],$ поэтому на рассматриваемой траектории $\left[ {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }}} \right] = {\text{const}}{\text{.}}$ Величина $\left( {{\mathbf{vE}}} \right)$ также постоянна на траектории. Разность ${{\tilde {t}}_{N}} - {{\tilde {t}}_{{N - 1}}}$ не зависит от номера N точки отражения
где T – время пролета электрона со скоростью ${{{\mathbf{v}}}_{ \bot }}$ от точки ${{{\mathbf{r}}}_{{N - 1 \bot }}}$ до точки ${{{\mathbf{r}}}_{{N \bot }}}{\text{:}}$Решением уравнения (9) является функция
(11)
${{f}_{1}} = C\exp \left( { - \nu \tilde {t}} \right) + A,\quad\,\,\,\,A = - \frac{{e\left( {{\mathbf{vE}}} \right)}}{\nu }\frac{{\partial {{f}_{0}}}}{{\partial \varepsilon }}.$Параметр $\tilde {t}$ в выражении (11) имеет смысл времени движения электрона вдоль траектории от границы проволоки, на которой происходит отражение, до точки ${{{\mathbf{r}}}_{ \bot }}$ со скоростью ${{{\mathbf{v}}}_{ \bot }}.$
Проведем решение уравнения (11) на интервале $\left( {{{{\tilde {t}}}_{{N - 1}}},\,\,{{{\tilde {t}}}_{N}}} \right)$ для случая движения электрона по траектории, которая при его зеркальном отражении не пересекается с цилиндрическим диэлектрическим ядром проволоки.
В момент начала отсчета времени $\left( {\tilde {t} = 0} \right)$
Откуда ищется значение постоянной C:
Теперь получим связь между начальными значениями функции ${{f}_{1}}$ на двух соседних звеньях траектории. Поскольку ${{\tilde {t}}_{N}} - 0 = {{\tilde {t}}_{{N - 1}}} + {{T}_{2}},$ то с учетом (11)
Применяя условие (10), получаем
Выражая затем с помощью этого рекуррентного соотношения ${{f}_{1}}\left( {{{{\tilde {t}}}_{{N - 1}}} + 0} \right)$ через ${{f}_{1}}\left( {{{{\tilde {t}}}_{{N - 2}}} + 0} \right)$ и т.д., приходим к выражению для ${{f}_{1}}\left( {{{{\tilde {t}}}_{N}} + 0} \right)$ через сумму бесконечной геометрической прогрессии со знаменателем ${{q}_{2}}\exp \left( { - \nu {{T}_{2}}} \right).$ Суммируя ее, имеем
С другой стороны согласно (11)
Откуда
Поэтому
(12)
${{f}_{{10}}}\left( {{{{\tilde {t}}}_{2}}} \right) = A\left\{ {\frac{{{{q}_{2}} - 1}}{{1 - {{q}_{2}}\exp \left( { - \nu {{T}_{2}}} \right)}}} \right\}\exp \left( { - \nu {{{\tilde {t}}}_{2}}} \right) + A = A\left\{ {1 - \frac{{\left( {1 - {{q}_{2}}} \right)\exp \left( { - \nu {{{\tilde {t}}}_{2}}} \right)}}{{1 - {{q}_{2}}\exp \left( { - \nu {{T}_{2}}} \right)}}} \right\}.$Параметры ${{\tilde {t}}_{2}}$ и ${{T}_{2}}$ можно связать с координатами точки $\left( {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }}} \right)$ в фазовом пространстве (при $N = 0,\quad$ ${{{\mathbf{v}}}_{{0 \bot }}} = {{{\mathbf{v}}}_{ \bot }}$) условиями
Исключая отсюда ${{{\mathbf{r}}}_{{0 \bot }}},$ получаем
(13)
${{T}_{2}} = \frac{{2\sqrt {{{{\left( {{{{\mathbf{v}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }}} \right)}}^{2}} + \left( {R_{2}^{2} - r_{ \bot }^{2}} \right)\text{v}_{ \bot }^{2}} }}{{\text{v}_{ \bot }^{2}}},$(14)
${{\tilde {t}}_{2}} = \frac{{{{{\mathbf{v}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }} + \sqrt {{{{\left( {{{{\mathbf{v}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }}} \right)}}^{2}} + \left( {R_{2}^{2} - r_{ \bot }^{2}} \right)\text{v}_{ \bot }^{2}} }}{{\text{v}_{ \bot }^{2}}}.$Соотношения (12)–(14) полностью определяют функцию ${{f}_{1}}\left( {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }},{{{\mathbf{v}}}_{z}}} \right)$ в случае движение электронов по траектории, не пересекающейся с ядром проволоки.
Теперь перейдем к случаю двойного зеркального отражения электрона (от цилиндрического ядра и от внешней цилиндрической границы металла).
Решение кинетического уравнения (11) на интервале $\left( {{{{\tilde {t}}}_{{N - 1}}},{{{\tilde {t}}}_{N}}} \right)$ проведем, допустив, что в некоторый момент времени электрон отражается от границы металлического слоя (до этого он отражался от ядра). Тогда
Используя рекуррентные соотношения ${{f}_{1}}\left( {{{{\tilde {t}}}_{{N - 2}}} + 0} \right)$ через ${{f}_{1}}\left( {{{{\tilde {t}}}_{{N - 4}}} + 0} \right)$ и т.д. и ${{f}_{1}}\left( {{{{\tilde {t}}}_{{N - 3}}} + 0} \right)$ через ${{f}_{1}}\left( {{{{\tilde {t}}}_{{N - 5}}} + 0} \right)$ и т.д., получим суммы бесконечных геометрических прогрессий с общим знаменателем ${{q}_{1}}{{q}_{2}}\exp \left( { - 2\nu {{T}_{1}}} \right)$
Отсюда
Поэтому
(15)
${{f}_{{12}}}\left( {{{{\tilde {t}}}_{2}}} \right) = A\left\{ {1 - \frac{{1 - {{q}_{1}}\left( {1 - \exp \left( { - \nu {{T}_{1}}} \right) + {{q}_{2}}\exp \left( { - \nu {{T}_{1}}} \right)} \right)}}{{1 - {{q}_{1}}{{q}_{2}}\exp \left( { - 2\nu {{T}_{1}}} \right)}}\exp \left( { - \nu {{{\tilde {t}}}_{2}}} \right)} \right\}.$Аналогичным образом ищется отклонение ${{f}_{{11}}}\left( {{{{\tilde {t}}}_{1}}} \right)$ функции распределения электронов, отражающихся от цилиндрического ядра проволоки
(16)
${{f}_{{11}}}\left( {{{{\tilde {t}}}_{1}}} \right) = A\left\{ {1 - \frac{{1 - {{q}_{2}}\left( {1 - \exp \left( { - \nu {{T}_{1}}} \right) + {{q}_{1}}\exp \left( { - \nu {{T}_{1}}} \right)} \right)}}{{1 - {{q}_{1}}{{q}_{2}}\exp \left( { - 2\nu {{T}_{1}}} \right)}}\exp \left( { - \nu {{{\tilde {t}}}_{1}}} \right)} \right\},$(17)
${{T}_{1}} = \frac{{\sqrt {{{{\left( {{{{\mathbf{v}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }}} \right)}}^{2}} + \left( {R_{2}^{2} - r_{ \bot }^{2}} \right)\text{v}_{ \bot }^{2}} - \sqrt {{{{\left( {{{{\mathbf{v}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }}} \right)}}^{2}} + \left( {R_{1}^{2} - r_{ \bot }^{2}} \right)\text{v}_{ \bot }^{2}} }}{{\text{v}_{ \bot }^{2}}},$(18)
${{\tilde {t}}_{1}} = \frac{{{{{\mathbf{v}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }} - \sqrt {{{{\left( {{{{\mathbf{v}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }}} \right)}}^{2}} + \left( {R_{2}^{2} - r_{ \bot }^{2}} \right)\text{v}_{ \bot }^{2}} }}{{\text{v}_{ \bot }^{2}}}.$Соотношения (15–18) полностью определяют функцию ${{f}_{1}}\left( {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }},{{{\mathbf{v}}}_{z}}} \right)$ в случае движения электронов по траектории, когда они испытывают двойное отражение от цилиндрического ядра и от внешней цилиндрической границы частицы.
РАСЧЕТ ПРОВОДИМОСТИ
Найденные функции распределения позволяют рассчитать плотность тока (5) внутри проволоки.
При вычислении интеграла (5) удобно перейти к цилиндрическим координатам как в пространстве
координат (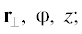 полярная ось – ось $Z;$ вектор ${{{\mathbf{E}}}_{0}}$ параллелен оси Z), так и в пространстве скоростей (${{\text{v}}_{ \bot }},\quad\alpha ,{{\text{v}}_{\parallel }},{{\text{v}}_{\parallel }}$ – полярная ось).
полярная ось – ось $Z;$ вектор ${{{\mathbf{E}}}_{0}}$ параллелен оси Z), так и в пространстве скоростей (${{\text{v}}_{ \bot }},\quad\alpha ,{{\text{v}}_{\parallel }},{{\text{v}}_{\parallel }}$ – полярная ось).
Поле (1) в цилиндрических координатах имеет лишь z-компоненту:
(19)
${\mathbf{E}} = {{E}_{z}}{{{\mathbf{e}}}_{z}};\,\,\,\,{{E}_{z}} = {{E}_{0}}{\text{exp}}\left( { - i\omega t} \right).$Воспользовавшись свойствами δ-функции, имеем
(20)
$\begin{gathered} \delta \left( {\varepsilon - {{\varepsilon }_{{\text{F}}}}} \right) = \delta \left( {\frac{{{{m}_{ \bot }}v_{ \bot }^{2}}}{2} + \frac{{{{m}_{\parallel }}v_{\parallel }^{2}}}{2} - {{\varepsilon }_{{\text{F}}}}} \right) = \frac{2}{{{{m}_{\parallel }}}}\delta \left( {v_{\parallel }^{2} - \left( {\frac{{2{{\varepsilon }_{{\text{F}}}}}}{{{{m}_{\parallel }}}} - \frac{{{{m}_{ \bot }}v_{ \bot }^{2}}}{{{{m}_{\parallel }}}}} \right)} \right) = \\ = \frac{1}{{{{m}_{\parallel }}\sqrt {\frac{{2{{\varepsilon }_{{\text{E}}}}}}{{{{m}_{\parallel }}}} - \frac{{{{m}_{ \bot }}v_{ \bot }^{2}}}{{{{m}_{\parallel }}}}} }}\left[ {\delta \left( {{{v}_{\parallel }} - \sqrt {\frac{{2{{\varepsilon }_{{\text{F}}}}}}{{{{m}_{\parallel }}}} - \frac{{{{m}_{ \bot }}v_{ \bot }^{2}}}{{{{m}_{\parallel }}}}} } \right) + \delta \left( {{{v}_{\parallel }} + \sqrt {\frac{{2{{\varepsilon }_{{\text{F}}}}}}{{{{m}_{\parallel }}}} - \frac{{{{m}_{ \bot }}v_{ \bot }^{2}}}{{{{m}_{\parallel }}}}} } \right)} \right]. \\ \end{gathered} $Будем предполагать, что объемное время релаксации τ не зависит от направления рассеяния (то есть будем рассматривать случай изотропного рассеяния).
При интегрировании соотношения (5) следует иметь в виду, что место отражения электронов внутри проволоки в пространстве скоростей определяется углом $\alpha \left( {0 < \alpha \leqslant 2\pi } \right):$
1. Если выполняется неравенство ${{\alpha }_{0}} \leqslant \alpha \leqslant \pi - {{\alpha }_{0}},$ где угол ${{\alpha }_{0}}$ задается выражением
(21)
${{\alpha }_{0}} = \arccos \left[ {\frac{{{{{\left( {r_{ \bot }^{2} - R_{1}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{r}_{ \bot }}}}} \right],$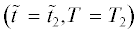 (12)–(14).
(12)–(14).
2. Если $\pi - {{\alpha }_{0}} < \alpha \leqslant \pi ,$ то электроны летят к ядру частицы и под функцией ${{f}_{1}}$ снова понимается ${{f}_{{12}}}\left( {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }},{{{\mathbf{v}}}_{{\text{z}}}}} \right)$ $\left( {\tilde {t} = {{{\tilde {t}}}_{2}},\quad\,\,T = {{T}_{1}}} \right)$ ((15), (14), (17)).
3. Наконец, если $0 < \alpha \leqslant {{\alpha }_{0}},$ то электроны летят от ядра частицы и под функцией ${{f}_{1}}$ понимается ${{f}_{{11}}}\left( {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }},{{{\mathbf{v}}}_{{\text{z}}}}} \right)$ $\left( {\tilde {t} = {{{\tilde {t}}}_{1}},\quad\,\,T = {{T}_{1}}} \right)$ (16)–(18).
Движение электронов симметрично относительно любой диаметральной плоскости, в которой лежит точка их положения на траектории, поэтому можно считать, что угол α в пространстве скоростей изменяется от 0 до π и удваивать результат интегрирования по этой переменной.
В силу симметрии задачи интегрирование по всему диапазону скоростей ${{\text{v}}_{\parallel }}$ заменяется интегрированием по положительному диапазону, и результат удваивается.
Соответственно, ток (5) обладает z-компонентой (линии тока являются прямыми, параллельными оси Z) и согласно ((6), (12), (15), (16), (19), (20)) получаем
Вводя новые безразмерные переменные, для плотности тока (22) с учетом ((13), (14), (17), (18), (21)) получим
Отдельно стоит отметить взаимосвязь параметров эллиптичности, т.к. ${{m}_{0}} = \sqrt[3]{{m_{ \bot }^{2}{{m}_{\parallel }}}},$ то ${{k}_{\parallel }}k_{ \bot }^{2} = 1,$ поэтому ${{k}_{\parallel }} = {1 \mathord{\left/ {\vphantom {1 {k_{ \bot }^{2}.}}} \right. \kern-0em} {k_{ \bot }^{2}.}}$ Кроме того, при изменении параметров эллиптичности предполагается постоянство концентрации свободных носителей заряда (6), следовательно, $m_{ \bot }^{2}{{m}_{\parallel }} = {\text{const}},\quad$ ${{m}_{0}} = {\text{const,}}$ а ${{k}_{ \bot }} \propto {{m}_{ \bot }},$ ${{k}_{\parallel }} \propto {{m}_{\parallel }}.$
В экспериментальных условиях обычно находят усредненный по радиусу ток (24)
Ток $\overline {{{j}_{z}}} $ связан с напряженность ${{E}_{z}}$ через удельную проводимость ${\sigma }$ из локального закона Ома:
Отсюда получаем выражение для удельной электропроводности
(24)
$\sigma = {{\sigma }_{0}}\Sigma \left( {{{x}_{0}},{{y}_{0}},{{q}_{1}},{{q}_{2}},{{k}_{ \bot }},K} \right),\quad\,\,\,\,{{\sigma }_{0}} = \frac{{n{{e}^{2}}\tau }}{{{{m}_{0}}}},$Независимо от характера отражения носителей заряда на границе в предельном случае ${{x}_{0}} \gg 1$ (толстая пленка) в выражении (25) можно пренебречь экспонентами, содержащими параметр ${{z}_{0}}.$ В этом случае безразмерная электрическая проводимость Σ переходит в классический результат (формула Друде) для цилиндрической проволоки:
(26)
${\Sigma } = \frac{{{{x}_{0}}k_{ \bot }^{2}}}{{{{z}_{0}}}} = \frac{{{{x}_{0}}}}{{{{z}_{0}}{{k}_{\parallel }}}},$(27)
$\sigma = {{\sigma }_{0}}\Sigma = \frac{{n{{e}^{2}}\tau }}{{{{m}_{0}}}}\frac{{{{x}_{0}}}}{{{{z}_{0}}{{k}_{\parallel }}}} = \frac{{n{{e}^{2}}\tau }}{{{{m}_{\parallel }}\left( {1 - i\omega \tau } \right)}}.$При ${{y}_{0}} \gg 1$ (высокие частоты) экспоненты в выражении (25) сильно осциллируют. Непосредственно пренебречь этими экспонентами нельзя, но интегралы от них будут малы из-за быстрой осцилляции подынтегральных выражений. Поэтому в случае высоких частот электропроводность определяется выражениями (26) и (27).
В классическом случае (26), (27) электропроводность не зависит ни от коэффициента зеркальности поверхности проволоки, ни от соотношения радиусов между диэлектрическим ядром и металлической проволоки.
Для зеркального отражения $\left( {{{q}_{1}} = {{q}_{2}} = 1} \right)$ поверхность не оказывает влияние на функцию распределения носителей заряда, что соответствует классическому случаю (26), (27). Высокочастотный ток внутри слоя с зеркально отражающими границами удовлетворяет локальному закону Ома при любом соотношении между радиусом проволоки ${{R}_{2}}$ и длиной свободного пробега $\lambda .$ Таким образом, при зеркальном отражении нелокальные (поверхностные) эффекты отсутствуют.
Если продольная масса много больше поперечной массы $\left( {{{k}_{\parallel }} \gg {{k}_{ \bot }}} \right),$ то второе слагаемое в скобках у безразмерной электропроводности (26) стремится к единице, и проводимость стремится к нулю. В обратном случае $\left( {{{k}_{\parallel }} \ll {{k}_{ \bot }}} \right)$ второе слагаемое много меньше первого слагаемого, поэтому электропроводность описывается формулами (26), (27).
Для однородной проволоки $\left( {K = 0,\quad\quad{{\alpha }_{0}} = 0} \right)$
(28)
$\Sigma \left( {{{x}_{0}},{{y}_{0}},{{q}_{2}},{{k}_{ \bot }}} \right) = \frac{{{{x}_{0}}k_{ \bot }^{2}}}{{{{z}_{0}}}}\left( {1 - \frac{{6k_{ \bot }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}{\pi }\int\limits_0^1 {\xi d\xi } \int\limits_0^{{1 \mathord{\left/ {\vphantom {1 {\sqrt {{{k}_{ \bot }}} }}} \right. \kern-0em} {\sqrt {{{k}_{ \bot }}} }}} {\rho \sqrt {\frac{1}{{{{k}_{ \bot }}}} - {{\rho }^{2}}} } d\rho \int\limits_0^\pi {\frac{{\left( {1 - {{q}_{2}}} \right)\exp \left( { - \frac{{{{z}_{0}}\psi }}{\rho }} \right)}}{{1 - {{q}_{2}}\exp \left( { - \frac{{{{z}_{0}}{{\psi }_{0}}}}{\rho }} \right)}}d\alpha } } \right).$В предельном случае сферической поверхности Ферми $\left( {{{k}_{ \bot }} = 1} \right)$ полученные выражения переходят в результаты работы [14].
ЭЛЕКТРОПРОВОДНОСТЬ В НИЗКОЧАСТОТНОМ РЕЖИМЕ
Подробно остановимся на случае, когда частота внешнего поля ω и частота столкновений электронов в объеме металла $\left( {{1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau }} \right)$ малы по сравнению с частотой столкновения электронов с поверхностями цилиндрического металлического слоя проволоки. Другими словами, рассмотрим случай $\left| {{{z}_{0}}} \right| \ll 1.$ Тогда экспоненты, входящие в выражение (25), можно разложить по известной формуле Тейлора, ограничиваясь первыми двумя членами разложения. Выполнив преобразования, аналогичные работе [15], получим
В случае диффузного рассеяния носителей заряда $\left( {{{q}_{1}} = {{q}_{2}} = 0} \right)$ и сферической поверхности Ферми $\left( {{{k}_{ \bot }} = 1} \right)$ получаем
Рассмотрим возможные предельные случаи.
Если радиус диэлектрического ядра ${{R}_{1}}$ много меньше внешнего радиуса проволоки ${{R}_{2}},$ т.е. $K \ll 1,$ то из формулы (29) можно отбросить слагаемые, пропорциональные K в степени два и выше, вклад которых в интеграл пренебрежительно мал:
Для однородной проволоки $\left( {K = 0} \right)$ из (30) следует, что
АНАЛИЗ РЕЗУЛЬТАТОВ
На рис. 1 изображены зависимости модуля и аргумента безразмерной проводимости Σ (25) от параметра $K = {{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} {{{R}_{2}}}}} \right. \kern-0em} {{{R}_{2}}}}$ соответственно. Сплошные кривые построены для случая зеркального отражения электронов $\left( {{{q}_{1}} = {{q}_{2}} = 1} \right)$ и описываются формулой (26). Кривые под номером 2 соответствуют случаю сферической поверхности Ферми $\left( {{{k}_{ \bot }} = 1} \right).$ При увеличении параметра K (т.е. при увеличении радиуса диэлектрического ядра ${{R}_{1}}$) модуль и аргумент проводимости убывают. Это связано с тем, что при росте ${{R}_{1}}$ толщина металлической оболочки уменьшается, что сопровождается увеличением вклада поверхностного рассеяния по сравнению с объемным рассеянием и его возрастающим влиянием на проводимость.
Рис. 1.
Зависимость модуля (а) безразмерной проводимости Σ от параметра K = R1/R2 при x0 = 0.1, y0 = 0.1. Сплошные, пунктирные и точечные кривые: q1 = q2 = 1; q1 = 0.4; q2 = 0.6; q1 = q2 = 0 соответственно. Кривые 1 – k⊥ = 10; 2 – k⊥ = 1; 3 – k⊥ = 0.1. Зависимость аргумента (б) безразмерной проводимости Σ от параметра K = R1/R2 при x0 = 0.1, y0 = 0.1. Сплошные, пунктирные и точечные кривые: q1 = q2 = 1; q1 = 0.4; q2 = 0.6; q1 = q2 = 0 соответственно. Кривые 1 – k⊥ = 10; 2 – k⊥ = 1; 3 – k⊥ = 0.1.
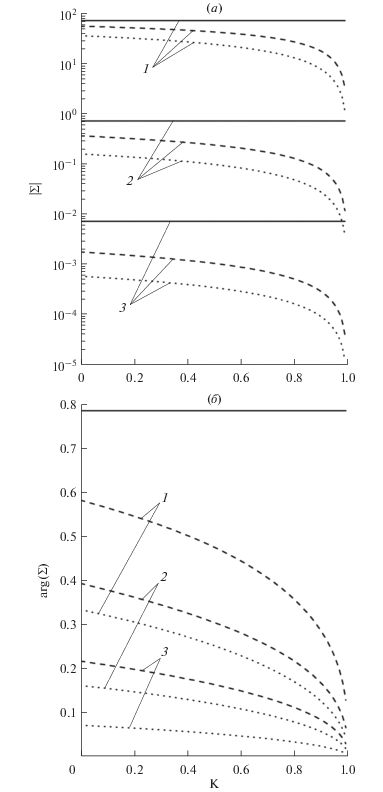
На рис. 2 показаны зависимости соответственно модуля и аргумента безразмерной проводимости Σ (25) от безразмерной поперечной эффективной массы ${{k}_{ \bot }}.$ Кривые под номером 1 построены для случая однородной проволоки $\left( {K = 0,\quad\quad{{\alpha }_{0}} = 0} \right),$ который соответствует формуле (28). При постоянной концентрации (6) рост поперечной эффективной массы ${{m}_{ \bot }}$ сопровождается снижением продольной эффективной массы ${{m}_{\parallel }}.$ Уменьшение продольной эффективной массы приводит к возрастанию скорости электронов проводимости и модуля и аргумента проводимости проволоки, а увеличение поперечной эффективной массы – к снижению интенсивности поверхностного рассеяния, что также увеличивает удельную электрическую проводимость как по модулю, так и по аргументу.
Рис. 2.
Зависимость модуля (а) безразмерной проводимости Σ отбезразмерной поперечной эффективной массы k⊥ при x0 = 0.1, y0 = 0.1. Сплошные, пунктирные и точечные кривые: q1 = q2 = 1; q1 = 0.4; q2 = 0.6; q1 = q2 = 0 соответственно. Кривые 1 – K = 0; 2 – K = 0.5; 3 – K = 0.95. Зависимость аргумента (б) безразмерной проводимости Σ от безразмерной поперечной эффективной массы k⊥ при x0 = 0.1, y0 = 0.1. Сплошные, пунктирные и точечные кривые: q1 = q2 = 1; q1 = 0.4; q2 = 0.6; q1 = q2 = 0 соответственно. Кривые 1 – k⊥ = 0; 2 – K = 0.5; 3 – K = 0.95.
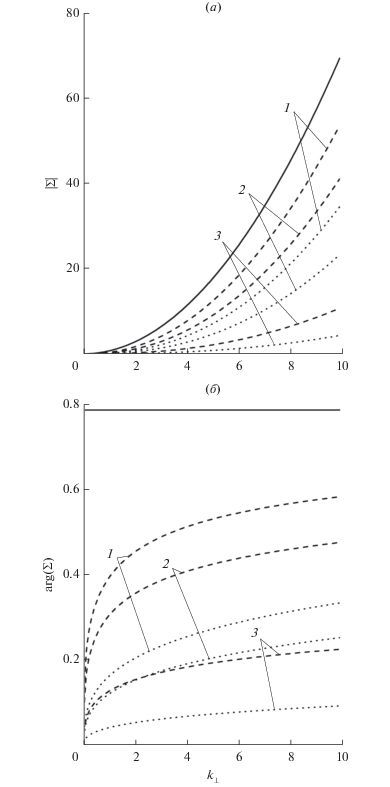
На рис. 3 изображены зависимости соответственно модуля и аргумента безразмерной проводимости Σ от безразмерной частоты электрического поля ${{y}_{0}}.$ С возрастанием частоты носители заряда перестают быть свободными и ведут себя как совокупностью связанных зарядов, энергия квазичастиц идет не на разогрев проводника, а на излучение. При высокой частоте аргумент проводимости стремится к ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},$ а модуль проводимости стремится к нулю.
Рис. 3.
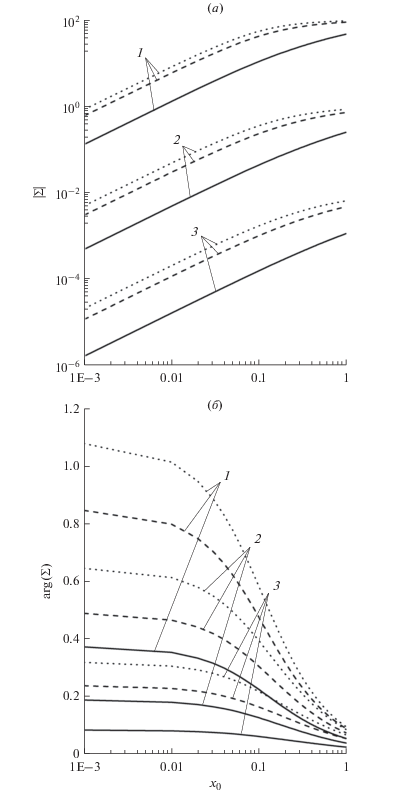
Зависимость модуля (а) безразмерной проводимости ${\Sigma }$ от безразмерного радиуса проволоки ${{x}_{0}}$ при ${{y}_{0}} = 0.1$ и ${{q}_{1}} = 0.4,\quad$ ${{q}_{2}} = 0.6.$ Точечные, пунктирные и сплошные кривые: $K = 0;$ $K = 0.5;$ $K = 0.95$ соответственно. Кривые 1 – ${{k}_{ \bot }} = 10;$ 2 – ${{k}_{ \bot }} = 1;$ 3 – ${{k}_{ \bot }} = 0.1.$ Зависимость аргумента (б) безразмерной проводимости ${\Sigma }$ от безразмерного радиуса проволоки ${{x}_{0}}$ при ${{y}_{0}} = 0.1$ и ${{q}_{1}} = 0.4,\quad$ ${{q}_{2}} = 0.6.$ Точечные, пунктирные и сплошные кривые: $K = 0;$ $K = 0.5;$ $K = 0.95$ соответственно. Кривые 1 – ${{k}_{ \bot }} = 10;$ 2 – ${{k}_{ \bot }} = 1;$ 3 – ${{k}_{ \bot }} = 0.1.$
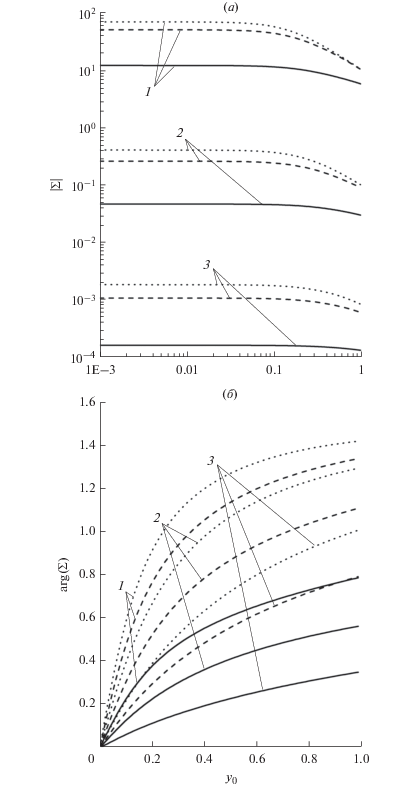
На рис. 4 построены зависимости соответственно модуля и аргумента безразмерной проводимости Σ от безразмерного радиуса проволоки ${{x}_{0}}.$ С ростом радиуса проволоки снижается вероятность поверхностного рассеяния по сравнению с объемным рассеянием, что приводит к росту модуля проводимости. При увеличении радиуса проволоки ${{R}_{2}}$ (или с уменьшением ${{x}_{0}}$) частота поля ${\omega }$ растет, так как ${{y}_{0}} = {\omega }{{{{R}_{2}}} \mathord{\left/ {\vphantom {{{{R}_{2}}} {{{\text{v}}_{0}}}}} \right. \kern-0em} {{{\text{v}}_{0}}}} = {\text{const}}{\text{.}}$ Из графика 3б видно, что при повышении частоты аргумент проводимости возрастает, поэтому при снижении безразмерного радиуса проволоки аргумент также увеличивается. Для толстой проволоки $\left( {{{x}_{0}} \gg 1} \right)$ наблюдается макроскопическая асимптотика (26).
Рис. 4.
Зависимость модуля (а) безразмерной проводимости Σ от безразмерной частоты электрического поля ${{y}_{0}}$ при ${{x}_{0}} = 0.1$ и ${{q}_{1}} = 0.4,\quad$ ${{q}_{2}} = 0.6.$ Точечные, пунктирные и сплошные кривые: $K = 0;$ $K = 0.5;$ $K = 0.95$ соответственно. Кривые 1 – ${{k}_{ \bot }} = 10;$ 2 – ${{k}_{ \bot }} = 1;$ 3 – ${{k}_{ \bot }} = 0.1.$ Зависимость аргумента (б) безразмерной проводимости ${\Sigma }$ от безразмерной частоты электрического поля ${{y}_{0}}$ при ${{x}_{0}} = 0.1$ и ${{q}_{1}} = 0.4,\quad$ ${{q}_{2}} = 0.6.$ Точечные, пунктирные и сплошные кривые: $K = 0;$ $K = 0.5;$ $K = 0.95$ соответственно. Кривые 1 – ${{k}_{ \bot }} = 10;$ 2 – ${{k}_{ \bot }} = 1;$ 3 – ${{k}_{ \bot }} = 0.1.$
ЗАКЛЮЧЕНИЕ
В данной работе показано, что анизотропия поверхности Ферми оказывает существенное влияние на электропроводность тонкой металлической неоднородной проволоки. Внешняя и внутренняя поверхности проволоки оказывают влияние на анизотропное движение носителей заряда. При увеличении радиуса диэлектрического ядра ${{R}_{1}}$ модуль и аргумент проводимости убывают. Классический размерный эффект наиболее существенен при меньшей поперечной эффективной массы ${{m}_{ \bot }}.$ С увеличением ${{m}_{ \bot }}$ модуль и аргумент безразмерной электропроводности возрастают. В случае, когда безразмерная продольная эффективная масса ${{m}_{\parallel }}$ много больше поперечной эффективной массы ${{m}_{ \bot }},$ диэлектрическое ядро и поверхности проволоки не оказывают влияние на характер движения носителей заряда, поэтому наблюдается переход к макроскопической асимптотике (26), (27).
Список литературы
Choi D., Katayun B. On the potential of tungsten as next-generation semiconductor interconnects // Electron. Mater. Lett. 2017. V. 13. № 5. P. 449–456.
Pengyuan Zheng, Daniel Gall. The anisotropic size effect of the electrical resistivity of metal thin films: Tungsten // J. App. Phys. 2017. V. 122. P. 135301.
Абрикосов А.А. Основы теории металлов. М.: Наука, 1987. 520 с.
Mackey H.J., Sybert J.R. Boundary-Scattering Effects in the Conductivity of Thick Wires in Zero Magnetic Field and in Large Transverse Magnetic Field // Phys. Rev. 1968. V. 172. № 3. P. 603–607.
Dingle R.B. The electrical conductivity of thin wires // Proc. Roy. Soc. A. 1950. V. 201. Issue 1067. P. 545.
Pierre F., Gougam A.B., Anthore A., Pothier H., Esteve D., Birge N.O. Dephasing of electrons in mesoscopic metal wires // Phys. Rev. B. 2003. V. 68. № 8. P. 085413.
Sondheimer E.H. The mean free path of electrons in metals // Advances in Physics. 2001. V. 50. № 6. P. 499–537.
Кузнецова И.А., Хадчукаева Р.Р., Юшканов А.А. Влияние поверхностного рассеяния носителей заряда на высокочастотную проводимость тонкой цилиндрической полупроводниковой проволоки // ФТТ. 2009. Т. 51. Вып. 10. С. 2022–2027.
Fuchs K. The conductivity of thin metallic films according to the electron theory of metals // Proc. Camb. Phil. Soc. 1938. V. 34. P. 100–108.
Soffer S.B. Statistical model for the size effect in electrical conduction // J. Appl. Phys. 1967. V. 38. P. 1710.
Кузнецова И.А., Савенко О.В., Юшканов А.А. Влияние граничных условий на электропроводность тонкой цилиндрической проволоки // Микроэлектроника. 2016. Т. 45. № 2. С. 126–134.
Dimmich R., Warkusz F. Electrical conductivity of thin wires // Active and Passive Elec. Comp. 1986. V. 12. P. 103–109.
Завитаев Э.В., Юшканов А.А. Влияние характера отражения электронов от поверхности на электрические свойства цилиндрической частицы // Физика низких температур. 2005. Т. 31. № 12. С. 1–7.
Завитаев Э.В., Юшканов А.А. Поглощение электромагнитной волны неоднородной цилиндрической частицей // Квантовая электроника. 2005. Т. 35. № 6. С. 547–553.
Завитаев Э.В., Юшканов А.А. Электрическое поглощение мелкой металлической частицы цилиндрической формы // ЖТФ. 2005. Т. 75. Вып. 9. С. 1–7.
Дополнительные материалы отсутствуют.
Инструменты
Микроэлектроника