Известия РАН. Механика жидкости и газа, 2023, № 2, стр. 113-122

ДВИЖЕНИЕ НАГРУЗКИ ПО ЛЕДЯНОМУ ПОКРОВУ ПРИ НАЛИЧИИ ТЕЧЕНИЯ СО СДВИГОМ СКОРОСТИ

Л. А. Ткачева^*

Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

Поступила в редакцию 22.06.2022
После доработки 20.12.2022
Принята к публикации 20.12.2022

EDN: NTTSET
DOI: 10.31857/S0568528123700044

Аннотация

Исследовано поведение ледяного покрова на поверхности идеальной несжимаемой жидкости конечной глубины под действием движущейся прямолинейно с постоянной скоростью области давления при наличии потока со сдвигом скорости. Течение жидкости не потенциально. Ледяной покров моделируется тонкой упругой пластиной с учетом равномерного сжатия. Движение нагрузки может происходить под произвольным углом к направлению течения. Предполагается, что в системе координат, движущейся вместе с нагрузкой, прогиб льда является установившимся. Использован метод преобразования Фурье в рамках линейной теории волн. Исследованы критические скорости и прогиб ледяного покрова в зависимости от градиента скорости течения, направления движения и коэффициента сжатия.

Ключевые слова: тонкая упругая плавающая пластина, изгибно-гравитационные волны, сдвиг скорости, движущаяся нагрузка, критическая скорость

Ледяной покров на поверхности рек, озер, морей и океана часто используется для создания дорог, взлетных полос, причалов и плавающих платформ для разведочного бурения. Для безопасности работ на льду необходимо изучать закономерности его поведения при механическом воздействии.

В настоящее время задача о поведении ледяного покрова под действием прямолинейно движущейся нагрузки изучена достаточно хорошо при ее стационарном и нестационарном движении. Имеется значительное число работ о действии различных физических факторов на характер распространения изгибно-гравитационных волн в плавающем ледяном покрове [1–9]. Однако влияние течения со сдвигом скорости изучено недостаточно. Имеется несколько работ на эту тему [10–15], в которых рассмотрена двумерная задача для линейного профиля скорости течения. В этом случае возмущения в жидкости носят потенциальный характер. Достаточно хорошо изучено воздействие сдвига скорости течения на поверхностные волны (см. [16–23] и имеющуюся в них библиографию). В трехмерном случае возмущения не потенциальны, носят вихревой характер [23].

Задача о влиянии сдвигового течения на изгибно-гравитационные волны в ледяном покрове в трехмерной постановке находится на начальной стадии изучения. В [24] исследована трехмерная начально-краевая задача о поведении ледяного покрова под действием импульсной и периодической нагрузки осесимметричного вида при наличии сдвигового потока. В работе [25] решена задача Коши–Пуассона для случая, когда имеются линейный сдвиг скорости по двум направлениям и неравномерное сжатие ледяного покрова.

В настоящей работе приведено решение задачи о поведении плавающего ледяного покрова под действием прямолинейно с постоянной скоростью движущейся нагрузки при наличии течения с линейным сдвигом скорости.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается бесконечный ледяной покров, плывущий на поверхности потока идеальной несжимаемой жидкости конечной глубины H с вертикальным сдвигом скорости. Ледяной покров моделируется упругой бесконечной пластиной постоянной толщины. В подвижной декартовой системе координат $Oxyz$, связанной с пластиной, с центром $O$ на верхней границе жидкости, осью $Ox$, направленной противоположно основному течению и осью $Oz$, направленной вертикально вверх, вектор скорости жидкости можно представить в виде

${\mathbf{v}}(x,y,z,t) = (U(z) + u,{v},w),\quad U(z) = \gamma z$

где $\gamma $ – константа, основное течение жидкости $U(z)$ не потенциально, имеет постоянную завихренность, $u$, ${v}$, $w$ – возмущенные компоненты скорости, малые по сравнению с основным течением. Предполагается, что заданное внешнее давление ${{p}_{0}}$ равномерно распределено по прямоугольной области шириной $2b$ и длиной $2a$. Область давления движется с постоянной скоростью $V$ под углом $\psi $ к оси $Ox$. Давление внешней нагрузки равно ${{p}_{0}} = gM{\text{/}}(4ab)$, где $M$ – масса движущегося тела, $g$ – ускорение свободного падения. Данная нагрузка моделирует судно на воздушной подушке.

Рассмотрим движение жидкости. Скорость течения жидкости удовлетворяет уравнениям Эйлера и неразрывности

(1.1)

$\begin{gathered} \frac{{d{\mathbf{v}}}}{{dt}} = - \nabla P{\text{/}}\rho - g{{{\mathbf{i}}}_{z}},\quad \nabla \cdot {\mathbf{v}} = 0 \\ P = - \rho gz + p \\ \end{gathered} $

Здесь $d{\text{/}}dt$ – полная производная по времени, P – гидродинамическое давление, которое складывается из гидростатической части и возмущенного гидродинамического давления $p$, $\rho $ – плотность жидкости, ${{{\mathbf{i}}}_{z}}$ – единичный орт оси $Oz$. Прогиб ледяного покрова $\eta (x,y,t)$ описывается уравнением изгиба тонких упругих пластин Кирхгофа-Лява

(1.2)

$\begin{gathered} D{{\Delta }^{2}}\eta + Q\Delta \eta + {{\rho }_{0}}h{{d}^{2}}\eta {\text{/}}d{{t}^{2}} = - \rho g\eta + p(x,y,0,t) - {{p}_{0}}(x,y,t), \\ \Delta = {{\partial }^{2}}{\text{/}}\partial {{x}^{2}} + {{\partial }^{2}}{\text{/}}\partial {{y}^{2}},\quad D = \frac{{E{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}} \\ \end{gathered} $

где $D$ – цилиндрическая жесткость пластины, $E$ – модуль Юнга, ${{\rho }_{0}}$, $h$ – плотность и толщина льда, $\nu $ – коэффициент Пуассона, $Q$ – сжимающие усилия в пластине.

Ставятся граничные условия: условие непротекания на дне

(1.3)

$w(x,y, - H,t) = 0$

а на верхней границе жидкости кинематическое условие

(1.4)

$w(x,y,0,t) = d\eta {\text{/}}dt$

и динамическое условие (1.2). Условие излучения ставится в следующем виде: перед нагрузкой распространяются только те волны, групповая скорость которых больше скорости нагрузки.

2. РЕШЕНИЕ ЗАДАЧИ

Решение строится аналогично работе [21]. Введем безразмерные переменные, параметры и функции по формулам

$(x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} ',H{\kern 1pt} ',b{\kern 1pt} ') = (x,y,z,H,b){\text{/}}a,\quad t{\kern 1pt} ' = t\sqrt {g{\text{/}}a} $

$F = \frac{V}{{\sqrt {ag} }},\quad S = \gamma \sqrt {a{\text{/}}g} ,\quad \beta = \frac{D}{{\rho g{{a}^{4}}}},\quad q = \frac{Q}{{\rho g{{a}^{2}}}},\quad \chi = \frac{{{{\rho }_{0}}h}}{{\rho a}}$

$(U{\kern 1pt} ',u{\kern 1pt} ',{v}{\kern 1pt} ',w{\kern 1pt} ') = (U,u,{v},w){\text{/}}\sqrt {ag} ,\quad \eta {\kern 1pt} ' = \eta {\text{/}}a,\quad (p{\kern 1pt} ',p_{0}^{'}) = (p,{{p}_{0}}){\text{/}}(\rho ga)$

Штрихи далее опускаем. Поскольку мы ищем стационарное решение в системе координат, движущейся вместе с нагрузкой, то в исходной системе координат, связанной с ледяной пластиной, возмущенные скорости движения жидкости имеют вид

$(u,{v},w) = (u({{{\mathbf{r}}}_{1}},z),{v}({{{\mathbf{r}}}_{1}},z),w({{{\mathbf{r}}}_{1}},z)),\quad {{{\mathbf{r}}}_{1}} = {\mathbf{r}} - {\mathbf{F}}t$

${\mathbf{r}} = (x,y),\quad {\mathbf{F}} = (F\cos \psi ,F\sin \psi )$

В предположении малости возмущенных скоростей по сравнению с основным течением уравнения (1.1) линеаризуются. Применяем преобразование Фурье по переменным x, y. Неизвестные функции $u$, ${v}$, $w$, $\eta $, p ищем в виде

$(u,{v},w)({{{\mathbf{r}}}_{1}},z) = \frac{1}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty \int\limits_{ - \infty }^\infty (\bar {u},{\bar {v}},\bar {w})({\mathbf{k}},z){\kern 1pt} e{{{\kern 1pt} }^{{i{\mathbf{k}} \cdot {{{\mathbf{r}}}_{1}}}}}d{{k}_{x}}d{{k}_{y}},\quad {\mathbf{k}} = ({{k}_{x}},{{k}_{y}}),$

$\eta ({{{\mathbf{r}}}_{1}}) = \frac{1}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty \int\limits_{ - \infty }^\infty \bar {\eta }({\mathbf{k}}){\kern 1pt} e{{{\kern 1pt} }^{{i{\mathbf{k}} \cdot {{{\mathbf{r}}}_{1}}}}}d{{k}_{x}}d{{k}_{y}}$

$p({{{\mathbf{r}}}_{1}},z) = \frac{1}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty \int\limits_{ - \infty }^\infty \bar {p}({\mathbf{k}},z){\kern 1pt} e{{{\kern 1pt} }^{{i{\mathbf{k}} \cdot {{{\mathbf{r}}}_{1}}}}}d{{k}_{x}}d{{k}_{y}}$

Функцию ${{p}_{0}}({{{\mathbf{r}}}_{1}})$ также представим в виде

${{p}_{0}}({{{\mathbf{r}}}_{1}}) = \frac{1}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty \int\limits_{ - \infty }^\infty {{\bar {p}}_{0}}({\mathbf{k}}){\kern 1pt} e{{{\kern 1pt} }^{{i{\mathbf{k}} \cdot {{{\mathbf{r}}}_{1}}}}}d{{k}_{x}}d{{k}_{y}}$

Тогда из системы уравнений (1.1) получаем

$i({{k}_{x}}U - {\mathbf{k}} \cdot {\mathbf{F}})\bar {u} + S\bar {w} = - i{{k}_{x}}\bar {p}$

(2.1)

$\begin{gathered} i({{k}_{x}}U - {\mathbf{k}} \cdot {\mathbf{F}}){\bar {v}} = - i{{k}_{y}}\bar {p} \\ i({{k}_{x}}U - {\mathbf{k}} \cdot {\mathbf{F}})\bar {w} = - {{{\bar {p}}}_{z}} \\ \end{gathered} $

$i{{k}_{x}}\bar {u} + i{{k}_{y}}{\bar {v}} + {{\bar {w}}_{z}} = 0$

Умножим первое уравнение на $i{{k}_{x}}$, второе уравнение на $i{{k}_{y}}$ и сложим. С помощью четвертого уравнения находим

(2.2)

$ - i({{k}_{x}}U - {\mathbf{k}} \cdot {\mathbf{F}})\frac{{\partial{ \bar {w}}}}{{\partial z}} + i{{k}_{x}}S\bar {w} = {{k}^{2}}\bar {p},\quad k = \sqrt {k_{x}^{2} + k_{y}^{2}} $

Дифференцируем по $z$ и получаем с учетом третьего уравнения

$i({{k}_{x}}U - {\mathbf{k}} \cdot {\mathbf{F}})\left( {\frac{{{{\partial }^{2}}\bar {w}}}{{\partial {{z}^{2}}}} - {{k}^{2}}\bar {w}} \right) = 0$

Отсюда следует

(2.3)

$\frac{{{{\partial }^{2}}\bar {w}}}{{\partial {{z}^{2}}}} - {{k}^{2}}\bar {w} = 0$

Решение уравнения (2.3) с условием (1.3) на дне записывается в виде

$\bar {w}({\mathbf{k}},z) = kA({\mathbf{k}}){\kern 1pt} {\text{sh}}{\kern 1pt} k(z + H)$

Подставляем это выражение в уравнения (2.1), (2.2) и находим остальные компоненты скорости и давление

$\bar {u}({\mathbf{k}},z) = iA({\mathbf{k}})\left( {{{k}_{x}}{\kern 1pt} {\text{ch}}{\kern 1pt} k(H + z) + \frac{{Sk_{y}^{2}{\kern 1pt} {\text{sh}}{\kern 1pt} k(z + H)}}{{k({{k}_{x}}U - {\mathbf{k}} \cdot {\mathbf{F}})}}} \right)$

${\bar {v}}({\mathbf{k}},z) = iA({\mathbf{k}})\left( {{{k}_{y}}{\kern 1pt} {\text{ch}}{\kern 1pt} k(H + z) - \frac{{S{{k}_{x}}{{k}_{y}}{\kern 1pt} {\text{sh}}{\kern 1pt} k(z + H)}}{{k({{k}_{x}}U - {\mathbf{k}} \cdot {\mathbf{F}})}}} \right)$

$\bar {p}({\mathbf{k}},z) = - i({{k}_{x}}U - {\mathbf{k}} \cdot {\mathbf{F}})A({\mathbf{k}}){\kern 1pt} {\text{ch}}{\kern 1pt} k(H + z) + i{{k}_{x}}SA({\mathbf{k}}){\kern 1pt} {\text{sh}}{\kern 1pt} k(H + z){\text{/}}k$

Из условия (1.4) следует

$ - i{\mathbf{k}} \cdot {\mathbf{F}}\bar {\eta } = kA({\mathbf{k}}){\kern 1pt} {\text{sh}}{\kern 1pt} kH$

Тогда уравнение движения пластины (1.2) записывается в виде

$[\beta {{k}^{4}} - q{{k}^{2}} + 1 - \chi {{({\mathbf{k}} \cdot {\mathbf{F}})}^{2}} - {{k}_{x}}S({\mathbf{k}} \cdot {\mathbf{F}}){\text{/}}{{k}^{2}} - {{({\mathbf{k}} \cdot {\mathbf{F}})}^{2}}{\kern 1pt} {\text{cth}}{\kern 1pt} kH{\text{/}}k]\bar {\eta } = - {{\bar {p}}_{0}}$

С помощью обратного преобразования Фурье находим

(2.4)

$\begin{gathered} \eta ({{{\mathbf{r}}}_{1}}) = \frac{{ - 1}}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty \int\limits_{ - \infty }^\infty \frac{{{{{\bar {p}}}_{0}}({\mathbf{k}}){\kern 1pt} e{{{\kern 1pt} }^{{i{\mathbf{k}} \cdot {{{\mathbf{r}}}_{1}}}}}k{\kern 1pt} {\text{th}}{\kern 1pt} kHd{{k}_{x}}d{{k}_{y}}}}{{[(\beta {{k}^{4}} - q{{k}^{2}} + 1 - \chi {{{({\mathbf{k}} \cdot {\mathbf{F}})}}^{2}})k - S{{k}_{x}}({\mathbf{k}} \cdot {\mathbf{F}}{\text{/}}k)]{\kern 1pt} {\text{th}}{\kern 1pt} kH - {{{({\mathbf{k}} \cdot {\mathbf{F}})}}^{2}}}} = \\ \, = - \frac{1}{{4{{\pi }^{2}}}}\int\limits_{ - \pi }^\pi \int\limits_0^\infty \frac{{{{{\bar {p}}}_{0}}({\mathbf{k}}){\kern 1pt} e{{{\kern 1pt} }^{{i{\mathbf{k}} \cdot {{{\mathbf{r}}}_{1}}}}}{{k}^{2}}{\kern 1pt} {\text{th}}{\kern 1pt} kHdkd\alpha }}{{[(\beta {{k}^{4}} - q{{k}^{2}} + 1 - \chi {{{({\mathbf{k}} \cdot {\mathbf{F}})}}^{2}})k - S\cos \alpha ({\mathbf{k}} \cdot {\mathbf{F}})]{\kern 1pt} {\text{th}}{\kern 1pt} kH - {{{({\mathbf{k}} \cdot {\mathbf{F}})}}^{2}}}} \\ \end{gathered} $

где $(k,\alpha )$ – полярные координаты в $k$-плоскости.

Для того, чтобы картина волн была стационарна, компонента скорости источника, нормальная к гребню волны, должна быть равна фазовой скорости гребня [1]. В размерных переменных получаем $({\mathbf{k}} \cdot {\mathbf{V}}){\text{/}}k = \omega {\text{/}}k$. Поэтому функция в знаменателе формулы (2.4) представляет собой дисперсионное соотношение изгибно-гравитационных волн в ледяной пластине, вызванных движением нагрузки, при наличии течения со сдвигом скорости, где $\omega $ заменено на $({\mathbf{k}} \cdot {\mathbf{F}})$.

Теперь удобно перейти в систему координат $O{{x}_{1}}{{y}_{1}}z$, движущуюся вместе с нагрузкой, повернутую относительно исходной системы координат на угол $\psi $, с осью $O{{x}_{1}}$, направленной вдоль линии движения, осью $O{{y}_{1}}$ – перпендикулярной к ней. В этой системе координат получаем

$\sigma = \alpha - \psi ,\quad {{\bar {p}}_{0}}({\mathbf{k}}) = 4{{p}_{0}}\frac{{\sin (k\cos \sigma )\sin (kb\sin \sigma )}}{{{{k}^{2}}\cos \sigma \sin \sigma }}$

(2.5)

$\begin{gathered} \eta ({{x}_{1}},{{y}_{1}}) = - \frac{{{{p}_{0}}}}{{{{\pi }^{2}}}}\int\limits_{ - \pi }^\pi \int\limits_0^\infty \frac{{{{f}_{1}}(k,\sigma )}}{{f(k,\sigma )}}{\kern 1pt} e{{{\kern 1pt} }^{{ik({{x}_{1}}\cos \sigma + {{y}_{1}}\sin \sigma )}}}dkd\sigma \\ f(k,\sigma ) = [\beta {{k}^{4}} - q{{k}^{2}} + 1 - \chi {{k}^{2}}{{F}^{2}}{{\cos }^{2}}\sigma - SF\cos (\sigma + \psi )\cos \sigma ]{\kern 1pt} {\text{th}}{\kern 1pt} kH - k{{F}^{2}}{{\cos }^{2}}\sigma \\ \end{gathered} $

${{f}_{1}}(k,\sigma ) = \frac{{\sin (k\cos \sigma )\sin (kb\sin \sigma ){\kern 1pt} {\text{th}}{\kern 1pt} kH}}{{k\sin \sigma \cos \sigma }}$

Из полученных ранее результатов в отсутствие течения известно, что существует критическое значение скорости, равное минимальной фазовой скорости изгибно-гравитационных волн. При скорости движения нагрузки, меньшей критической, волны в ледяном покрове не образуются, деформации льда носят локальный характер вблизи области нагрузки. При наличии течения со сдвигом скорости также существует критическая скорость и находится аналогично работе [4]. Преобразуем уравнение $f(k,\sigma ) = 0$ к виду

(2.6)

$\begin{gathered} \text{[}2(\beta {{k}^{4}} - q{{k}^{2}} + 1) - \chi {{F}^{2}}{{k}^{2}}(1 + \cos 2\sigma ) - SF\cos \psi (1 + \cos 2\sigma ) + SF\sin \psi \sin 2\sigma ]{\kern 1pt} {\text{th}}{\kern 1pt} kH - \\ \, - k{{F}^{2}}(1 + {\text{cos}}2\sigma )\, = \,G(k,\psi ) - {\text{cos}}2\sigma [{{F}^{2}}k(1 + \chi k{\kern 1pt} {\text{th}}{\kern 1pt} kH) + SF{\kern 1pt} {\text{th}}{\kern 1pt} kH{\text{cos}}\psi ] + SF{\kern 1pt} {\text{th}}{\kern 1pt} kH{\text{sin}}\psi {\text{sin}}2\sigma = 0 \\ G(k,\psi ) = [2(\beta {{k}^{4}} - q{{k}^{2}} + 1) - \chi {{F}^{2}}{{k}^{2}} - SF\cos \psi ]{\kern 1pt} {\text{th}}{\kern 1pt} kH - {{F}^{2}}k \\ \end{gathered} $

Обозначим

$\varphi = \arcsin \left( {\frac{{SF{\kern 1pt} {\text{th}}{\kern 1pt} kH\sin \psi }}{{B(k,\psi )}}} \right)$

$B(k,\psi ) = \sqrt {{{S}^{2}}{{F}^{2}}{\kern 1pt} {\text{th}}{{{\kern 1pt} }^{2}}kH{{{\sin }}^{2}}\psi + {{{({{F}^{2}}k(1 + \chi k{\kern 1pt} {\text{th}}{\kern 1pt} kH) + SF{\kern 1pt} {\text{th}}{\kern 1pt} kH\cos \psi )}}^{2}}} $

Тогда (2.6) можно записать в виде

$G(k,\psi ) - B(k,\psi )\cos (2\sigma + \varphi ) = 0$

Отсюда находим

(2.7)

$\cos (2\sigma + \varphi ) = \frac{{G(k,\psi )}}{{B(k,\psi )}}$

Чтобы решение существовало, необходимо, чтобы

$\left| {\frac{{G(k,\psi )}}{{B(k,\psi )}}} \right| \leqslant 1$

Возводим в квадрат, преобразуем и в результате получаем: критическое значение числа Фруда $F_{*}^{{}}$ определяется как минимум функции $\Phi (k)$

$\Phi (k) = 2d(k)\frac{{\sqrt {{{S}^{2}}{\kern 1pt} {\text{th}}{{{\kern 1pt} }^{2}}kH + 4d(k){{d}_{1}}(k){\kern 1pt} {\text{th}}{\kern 1pt} kH} - S{\kern 1pt} {\text{th}}{\kern 1pt} kH\cos \psi }}{{{{S}^{2}}{\kern 1pt} {\text{th}}{{{\kern 1pt} }^{2}}kH{{{\sin }}^{2}}\psi + 4d(k){{d}_{1}}(k)}}$

$d(k) = \beta {{k}^{4}} - q{{k}^{2}} + 1,\quad {{d}_{1}}(k) = k(1 + \chi k{\kern 1pt} {\text{th}}{\kern 1pt} kH)$

$F_{*}^{{}} = \Phi (k_{*}^{{}}),\quad \Phi {\kern 1pt} '(k_{*}^{{}}) = 0$

При $F > F_{*}^{{}}$ функция $f(k,\sigma )$ имеет нули ${{k}_{1}} = {{k}_{1}}(\sigma )$ и ${{k}_{2}} = {{k}_{2}}(\sigma )$, ${{k}_{1}} < {{k}_{2}}$ в некоторых областях значений угла $\sigma $. Поэтому при этих значениях угла $\sigma $ интеграл по $k$ в выражении (2.5) является интегралом в смысле главного значения. Контур интегрирования деформируется таким образом, чтобы выполнить условие излучения. Известно, что групповая скорость изгибно-гравитационных волн больше их фазовой скорости для коротких волн и меньше для длинных волн. Короткие волны соответствуют упругой ветви дисперсионной кривой, а длинные волны – гравитационной ветви. Поэтому при $\cos \sigma > 0$ корень ${{k}_{1}}$ обходится сверху, а корень ${{k}_{2}}$ – снизу, при $\cos \sigma < 0$ – наоборот.

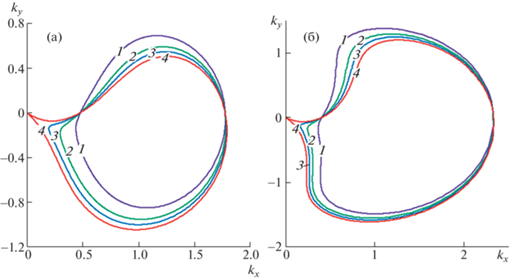
Картины гребней изгибно-гравитационных волн в дальнем поле строятся с помощью асиптотических методов аналогично тому, как в случае отсутствия течения [1, 26]. Положения гребней волн в дальнем поле определяются с помощью кривой волновых чисел ${{C}_{k}}$ в k-плоскости, удовлетворяющей уравнению $f(k,\sigma ) = 0$. Кривые ${{C}_{k}}$ удобно строить с помощью формулы (2.7). Примеры вида кривых ${{C}_{k}}$ изображены на рис. 1 при $\psi = \pi {\text{/}}2$, $S = 0.3$, 0.7, 0.9, 1.1, в случаях отсутствия сжатия $Q = 0$ (а) и $Q{\text{/}}\sqrt {\rho gD} = 1.5$ (б).

Рис. 1.

Кривые волновых чисел ${{C}_{k}}$ при $\psi = \pi {\text{/}}2$ в случаях отсутствия сжатия $\bar {Q} = 0$ (а) и $\bar {Q} = 1.5$ (б): 1–4 – $S = 0.3$, 0.7, 0.9, 1.1.

Стационарная картина волн содержит только те волны, волновые числа которых лежат на кривой C_k. Из любой точки ${{P}_{0}} = ({{k}_{0}},{{\sigma }_{0}})$ на C_k волны излучаются в направлении, нормальном к C_k и соответствующем возрастанию $\omega $. Вертикальное смещение ледяного покрова $\eta $ в дальнем поле от этой точки выражается формулой

(2.8)

$\eta ({{{\mathbf{r}}}_{1}}) \approx - \frac{{{{f}_{1}}({{k}_{0}},{{\sigma }_{0}})}}{{2\pi }}{{\left[ {{{{\left( {\frac{{\partial f}}{{\partial n}}} \right)}}_{{{{P}_{0}}}}}} \right]}^{{ - 1}}}{{\left( {\frac{{2\pi }}{{{{\kappa }_{0}}{{r}_{1}}}}} \right)}^{{1/2}}}{\kern 1pt} e{{{\kern 1pt} }^{{i({{k}_{0}}{{r}_{1}}\cos ({{\sigma }_{0}} - \theta ) + \mu )}}}$

Здесь ${{{\mathbf{r}}}_{1}} = ({{r}_{1}}\cos \theta ,{{r}_{1}}\sin \theta )$; ${{\kappa }_{0}}$ – величина кривизны кривой C_k в точке ${{P}_{0}}$; $\partial {\text{/}}\partial n$ – дифференцирование по нормали к C_k, соответствующей возрастанию $\omega $; $\mu = \pi {\text{/}}4$, если кривая C_k выпукла в этой точке и $3\pi {\text{/}}4$ в противном случае. Гребни волн являются линиями постоянной фазы ${{k}_{0}}{{r}_{1}}{\text{cos}}({{\sigma }_{0}}\, - \,\theta )$ = K, $K$ – константа. Таким образом, каждой точке ${{P}_{0}}$ на C_k соответствует точка на волновом гребне с полярными координатами в $({{x}_{1}},{{y}_{1}})$-плоскости

$\left( {\frac{K}{{{{k}_{0}}\cos ({{\sigma }_{0}} - \theta )}},\theta } \right)$

Если кривая волновых чисел C_k имеет точку перегиба, то соответствующая линия распространения волны $L$ является каустикой, и линии гребней имеют заострения в точке их пересечения с линией $L$ [1, 26]. В точке перегиба константа K меняется скачком, так как меняется сдвиг фазы μ в формуле (2.8).

С ростом параметра $S$ кривая C_k приближается к началу координат в $k$-плоскости. При $S > S_{*}^{{}}$ кривая C_k проходит через начало координат, где критическое значение параметра $S_{*}^{{}}$ находится из условия

$\mathop {\lim }\limits_{k \to 0} \left| {\frac{{G(k,\psi )}}{{B(k,\psi )}}} \right| - 1 = 0$

При $S = S_{*}^{{}}$ касательные к верхней и нижней ветвям кривой C_k при $k = 0$ совпадают. При $S > S_{*}^{{}}$ касательные к кривой C_k в начале координат составляют некоторый угол с ${{k}_{x}}$-осью. Существует область за нагрузкой, в которой волны не распространяются, так как нет нормалей к кривой C_k в этих направлениях.

Из формулы (2.8) следует, что амплитуда волн в дальнем поле в общем случае порядка $O({{r}^{{ - 1/2}}})$ и пропорциональна $\kappa _{0}^{{ - 1/2}}$. Таким образом, относительно плоские участки кривой C_k с малой кривизной дают большие амплитуды волн в соответствующих направлениях, поскольку все точки этого участка кривой C_k излучают волны примерно в одном направлении [1]. Из рис. 1 видно, что в случае $Q = 0$ такие направления находятся за нагрузкой под некоторым углом к оси $Ox$. В случае $Q{\text{/}}\sqrt {\rho gD} = 1.5$ такие участки дают большие амплитуды в отрицательной части оси $Ox$, если $S < S_{*}^{{}}$. Асимптотика амплитуд изгибно-гравитационных волн в дальнем поле в каустических направлениях дана в работе [1].

3. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Численные расчеты проводились для ледяного покрова при следующих входных параметрах задачи: $E = 5$ ГПа, $\rho = 1025$ кг/м³, ${{\rho }_{0}} = 922.5$ кг/м³, $\nu = 0.3$, a = 20 м, b = 10 м, толщина льда $h = 1$ м, глубина жидкости $H = 100$ м, скорость движения нагрузки $V = 20$ м/с. Сжимающие усилия в пластине заданы в виде $Q = \bar {Q}\sqrt {\rho gD} $, $\bar {Q} = 0$ и 1.5.

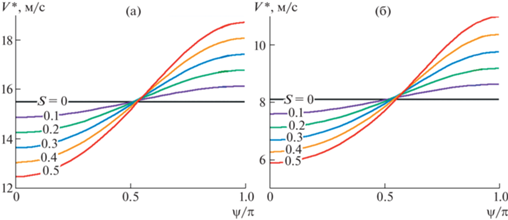
На рис. 2 приведены зависимости критических скоростей изгибно-гравитационных волн в ледяном покрове от направления движения нагрузки при различных значениях параметра сдвига $S$ и $\bar {Q} = 0$, 1.5. Из графиков видно, что минимальные критические скорости достигаются при $\psi = 0$, когда нагрузка движется противоположно течению жидкости. Максимальные критические скорости наблюдаются при $\psi = \pi $, когда нагрузка движется по течению. При $\psi = \pi {\text{/}}2$ критическая скорость при любых значениях параметра $S$ близка к ее значению в отсутствие течения. При увеличении коэффициента сжатия льда критические скорости значительно уменьшаются. Видно, что сдвиг скорости, направление движения и коэффициент сжатия льда оказывают существенное влияние на критические скорости изгибно-гравитационных волн.

Рис. 2.

Критические скорости изгибно-гравитационных волн в ледяном покрове при $h = 1$ м и различных значениях параметра сдвига $S$: а, б – $\bar {Q} = 0$, 1.5.

На рис. 3а показаны зависимости прогиба ледяного покрова вдоль линии движения нагрузки $\eta ({{x}_{1}},0)$ от координаты ${{x}_{1}}$ в отсутствие сжатия $\bar {Q} = 0$ при $S = 0$, а также $S = 0.4$ и $\psi = 0,\pi $. При наличии сдвига скорости и $\psi = 0$ нагрузка движется против течения, при этом волны перед нагрузкой укорачиваются, встречая сопротивление, а волны за нагрузкой удлиняются, что объясняется двумя причинами. С одной стороны, они сносятся потоком. С другой стороны, выполаживание волн за нагрузкой для изгибно-гравитационных волн при увеличении разности между скоростью нагрузки и критической скоростью наблюдается и в отсутствие течения [1]. При $\psi = \pi $ нагрузка движется по течению, в этом случае волны перед нагрузкой удлиняются, а после нагрузки укорачиваются, амплитуды волн значительно выше, чем в предыдущих случаях, т.к. скорость движения нагрузки ближе к критической скорости.

Рис. 3.

Зависимость прогиба ледяного покрова от координаты ${{x}_{1}}$: (а) – $\bar {Q} = 0$, 1 – $S = 0$, 2, 3 – $(S,\psi ) = (0.4,0)$, $(0.4,\pi )$; (б) – $S = 0$, 4, 5 – $\bar {Q} = 0$, 1.5.

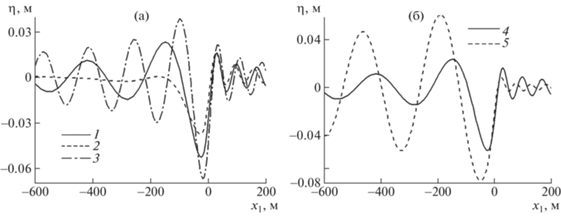
На рис. 3б приведены зависимости прогиба ледяного покрова на линии движения от координаты ${{x}_{1}}$ в отсутствие течения $S = 0$, при $\bar {Q} = 0$ и $\bar {Q} = 1.5$. Видно, что при увеличении коэффициента сжатия льда прогиб за нагрузкой значительно увеличивается, а перед нагрузкой уменьшается.

На рис. 4 изображены картины гребней изгибно-гравитационных волн при $\bar {Q} = 0$, $\psi = 0$, π/3, π/2, $2\pi {\text{/}}3$ и различных значений параметра сдвига S. При $\psi = 0$ изменение картин волновых гребней аналогично тому, как меняются картины гребней при увеличении скорости нагрузки в отсутствие течения [1]. При увеличении параметра S волны за нагрузкой становятся длиннее, амплитуда их меньше, появляются каустики и заострения. При $S > {{S}_{*}}$ кривая C_k проходит через начало координат, и волн за нагрузкой нет. Этому случаю соответствуют картины волновых гребней в крайнем правом столбце рис. 4 при $\psi < 2\pi {\text{/}}3$.

Рис. 4.

Картины гребней изгибно-гравитационных волн в дальнем поле при $\bar {Q} = 0$, $\psi = 0$, π/3, π/2, $2\pi {\text{/}}3$ и различных значениях параметра S.

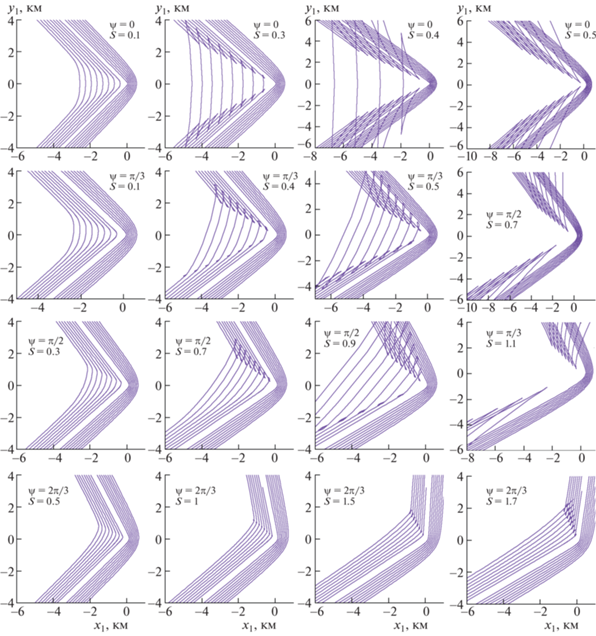
При $\psi = \pi {\text{/}}6$ картины волновых гребней аналогичны картинам при $\psi = 0$ при тех же значениях параметра S, но симметрия слегка нарушена. При дальнейшем увеличении угла $\psi $ симметрия нарушается еще сильнее. Например при $\psi = \pi {\text{/}}3$, $S = 0.4$ и $\psi = \pi {\text{/}}2$, $S = 0.7$ заострения наблюдаются только при ${{y}_{1}} > 0$.

При фиксированном значении угла $\psi \ne 0,\pi $ симметрия сильнее нарушается с ростом параметра S. С увеличением угла $\psi $ критическая скорость изгибно-гравитационных волн растет, разница между скоростью нагрузки и критической уменьшается. Поэтому при $\psi = 2\pi {\text{/}}3$ каустики и заострения линий гребней наблюдаются только при больших значениях параметра $S$.

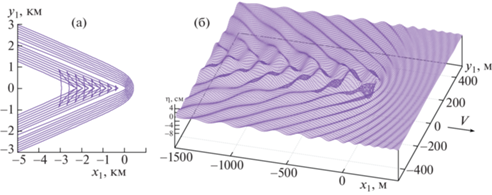
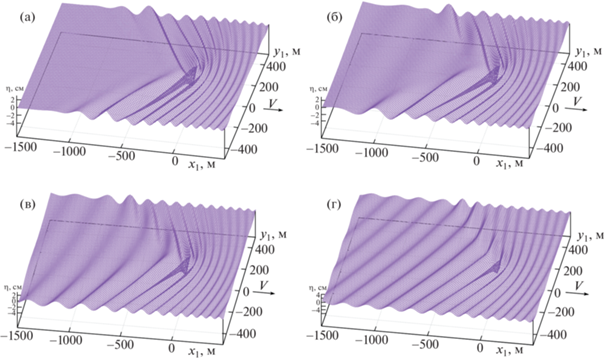
На рис. 5 представлены трехмерные графики прогиба ледяного покрова в ближнем поле при $\bar {Q} = 0$ и различных значениях угла $\psi $ и параметра сдвига S. При $\psi = 0$ и $S = 0.4$ (рис. 5а) волны за нагрузкой очень длинные и малой амплитуды, близкой к нулю. При $\psi = \pi {\text{/}}3$ и $S = 0.4$ (рис. 5б) волны за нагрузкой длинные, симметрия нарушена. На рис. 5в ($\psi = \pi {\text{/}}3$, $S = 0.4$) и 5 г ($\psi = 2\pi {\text{/}}3$, $S = 1$) волновое движение ярко выражено во всех областях.

Рис. 5.

Вертикальные смещения ледяного покрова при $\bar {Q} = 0$: (а–г) – $(S,\psi ) = (0.4,0)$, $(0.4,\pi {\text{/}}3)$, $(0.4,\pi {\text{/}}2)$, $(1,2\pi {\text{/}}3)$.

Как указано выше, сжатие льда оказывает сильное влияние на критические скорости изгибно-гравитационных волн, при $\bar {Q} = 1.5$ они почти в два раза меньше, чем при $\bar {Q} = 0$. Скорость нагрузки $V = 20$ м/с значительно выше критических скоростей при $\bar {Q} = 1.5$, и гребни изгибно-гравитационных волн имеют заострения и каустики даже для $S = 0$. Если скорость нагрузки уменьшить, например, до $V = 12$ м/с, то картины гребней волн в дальнем поле будут похожи на те, что при $\bar {Q} = 0$.

Картина волновых гребней в дальнем поле (а) и прогиб ледяного покрова в ближнем поле (б) при $\bar {Q} = 1.5$, $V = 20$ м/с, $\psi = 0$, $S = 0.1$ изображены на рис. 6. Трехмерные графики ледяного покрова при $\bar {Q} = 1.5$, $V = 20$ м/с и различных значениях параметров $\psi $ и $S < S_{*}^{{}}$ визуально типичны и похожи на тот, который изображен на рис. 6б. Амплитуды прогиба ледяного покрова значительно выше, чем при отсутствии сжатия.

Рис. 6.

Картина гребней изгибно-гравитационных волн в дальнем поле (а) и вертикальные смещения ледяного покрова в ближнем поле (б) при $\bar {Q} = 1.5$, $\psi = 0$, $S = 0.1$.

ЗАКЛЮЧЕНИЕ

Исследовано влияние сдвига скорости жидкости на стационарные изгибно-гравитационные волны в ледяном покрове при равномерном прямолинейном движении нагрузки под произвольным углом к направлению течения с учетом однородного сжатия льда. Поле скоростей жидкости не потенциально. Показано, что сдвиг скорости, направление движения нагрузки и коэффициент сжатия льда оказывают существенное влияние на критические скорости изгибно-гравитационных волн и прогиб ледяного покрова. Максимальные критические скорости наблюдаются в тех случаях, когда нагрузка движется по течению. При увеличении коэффициента сжатия льда критические скорости значительно уменьшаются.

Если нагрузка движется против течения, то волны перед нагрузкой укорачиваются, встречая сопротивление, а волны за нагрузкой удлиняются. Если нагрузка движется по течению, то волны перед нагрузкой удлиняются, а за нагрузкой укорачиваются, и амплитуды волн значительно выше, чем в предыдущем случае. При увеличении коэффициента сжатия амплитуды прогиба льда значительно увеличиваются за нагрузкой и уменьшаются перед нагрузкой. Увеличение параметра сдвига S оказывает качественно такое же влияние, как увеличение скорости движения нагрузки. Картины гребней изгибно-гравитационных волн имеют такой же характер, что и в отсутствие течения, но симметрия нарушена при боковом натекании.

Список литературы

Davys J.W., Hosking R.I., Sneyd A.D. Waves due to a steadily moving source on a floating ice plate// J. Fluid Mech. 1985. V. 158. P. 269–287.
Schulkes R.M.S.M., Hosking R.J., Sneyd A.D. Waves due to a steadily moving source on a floating ice plate. Pt 2 // J. Fluid Mech. 1987. V. 180. P. 297–318.
Milinazzo F., Shinbrot M., Evans N.W. A mathematical analysis of the steady response of floating ice to the uniform motion of a rectangle load // J. Fluid Mech. 1995. V. 287. P. 173–197.
Букатов А.Е., Жарков В.В., Завьялов Д.Д. Трехмерные изгибно-гравитационные волны при неравномерном сжатии // ПМТФ. 1991. № 6. С. 51–57.
Жесткая В.Д., Козин В.М. Исследования напряженно-деформированного состояния полубесконечного ледяного покрова под действием движущейся нагрузки // ПМТФ. 1994. Т. 35, № 5. С. 112–117.
Squire V.A. Moving Loads on Ice Plates / V.A. Squire, R.J. Hosking, A.D. Kerr, et al. Dordrecht: Kluwer, 1996.
Yeung R.W., Kim J.W. Effects of a translating load on a floating plate-structural drag and plate deformation // J. Fluids Structures. 2000. V. 14. № 7. P. 993–1011.
Nugroho W.S., Wang K., Hosking R.J., Milinazzo F. Time-dependent response of a floating flexible plate to an impulsively started steadily moving load // J. Fluid Mech. 1999. V. 381. P. 337–355.
Погорелова А.В., Козин В.М., Матюшина А.А. Исследование напряженно-деформируемого состояния ледяного покрова при взлете и посадке на него самолета // ПМТФ. 2015. Т. 56. № 5. С. 214–221.
Букатов А.Е., Мордашев В.И. Влияние продольно сжатой упругой пластинки на развитие волнового возмущения потока однородной жидкости с вертикальным сдвигом скорости // ПМТФ. 1981. № 1. С. 122–129.
Суворов А.М. Развитие колебаний ледяного покрова в море при наличии горизонтального течения со сдвигом скорости // Поверхностные и внутренние волны. Севастополь: МГИ АН УССР. 1979. С. 63–69.
Суворов А.М., Черкесов Л.В. Нестационарные вынужденные колебания упругой пластинки, плавающей на поверхности потока жидкости со сдвигом скорости // Прикладная механика. 1980. № 5. С. 102–106.
Букатов А.Е. Волны в море с плавающим ледяным покровом. Морской гидрофизический институт РАН. Севастополь. 2017. 357 с.
Das S., Kar P., Sahoo T., Meylan M.H. Flexural-gravity wave motion in the presence of shear current: Wave blocking and negative energy waves // Phys. Fluids. 2018. V. 30. 106606. https://doi.org/10.1063/1.5052228
Стурова И.В. Задача Коши–Пуассона для жидкости под ледяным покровом при наличии сдвигового течения (двумерный случай)// Изв. РАН. Механика жидкости и газа. 2022. № 1. С. 47–56.
Суворов А.М., Тананаев А.Н., Черкесов Л.В. Нестационарные пространственные волны в потоке однородной жидкости со сдвигом скорости. Севастополь: МГИ АН УССР. 1979. С. 14–21.
Санников В.Ф. Корабельные волны в однородном море с линейным профилем скорости по глубине // Поверхностные и внутренние волны. Севастополь: МГИ АН УССР. 1979. С. 22–31.
Суворов А.М., Черкесов Л.В. Волны от поверхностных возмущений в потоке стратифицированной жидкости со сдвигом скорости // Поверхностные и внутренние волны. Севастополь: МГИ АН УССР. 1979. С. 128–138.
Ellingsen S.A. Initial surface disturbance on shear current: The Cauchy-Poisson problem with a twist // Phys. Fluids. 2014. V. 26. 082104.
Li Y., Ellingsen S.A. Initial Value Problems for Water Waves in the Presence of a Shear Current // Proc. 25-th Intern. Ocean and Polar Engng Conf. 2015. Kona. Big Island. Hawaii. USA. June 21-26 2015. P. 543–549.
Ellingsen S.A. Ship waves in the presence of uniform vorticity // J. Fluid Mech. 2014. V. 742. R2. https://doi.org/10.1017/jfm.2014.28
Li Y., Ellingsen S.A. Ship waves on uniform shear current at finite depth: wave resistance and critical velocity // J. Fluid Mech. 2016. V. 791. P. 539–567.
Ellingsen S.A. Oblique waves on a vertical sheared current are rotational // Eur. J. Mech. B/Fluids. 2016. V. 56. P. 156–160.
Ткачева Л.А. Начально-краевая задача о поведении ледяного покрова под действием нагрузки при наличии сдвигового потока// Изв. РАН. Механика жидкости и газа. 2022. № 2. С. 66–76.
Стурова И.В. Задача Коши–Пуассона для жидкости со сдвиговым течением и неравномерно сжатым ледяным покровом // Известия РАН. Механика жидкости и газа. 2022. № 4. С. 69–76.
Лайтхилл Дж. Волны в жидкостях. М.: Изд-во Мир. 1981.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал