Известия РАН. Механика жидкости и газа, 2023, № 2, стр. 123-137

НЕРАВНОВЕСНОЕ СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ЗАТУПЛЕННОЙ ПЛАСТИНЫ ПОД БОЛЬШИМ УГЛОМ АТАКИ

С. Т. Суржиков^a, *

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

Поступила в редакцию 05.10.2022
После доработки 11.10.2022
Принята к публикации 11.10.2022

EDN: EPLRMF
DOI: 10.31857/S0568528122600722

Аннотация

Сформулирована компьютерная модель, предназначенная для изучения процессов неравновесной физико-химической газовой динамики при обтекании затупленной пластины конечных размеров сверхзвуковым потоком разреженного воздуха для условий лабораторных экспериментов. Компьютерная модель основана на двухмерных уравнениях Навье–Стокса, сохранения энергии поступательных степеней свободы атомов и молекул, колебательных степеней свободы двухатомных молекул, уравнений химической кинетики и диффузии отдельных компонент частично ионизованного газового потока. Дан анализ основных газодинамических и кинетических процессов при обтекании затупленной пластины при числах Маха М = 10 и 20. Показано образование областей термической неравновесности.

Ключевые слова: обтекание затупленной пластины, уравнения Навье–Стокса, неравновесные процессы колебательной релаксации, физико-химическая кинетика разреженных газовых потоков

Задача обтекания сверхзвуковым потоком острых и затупленных пластин является одной из классических задач газовой динамики, изучаемой экспериментально, теоретически и с использованием численного моделирования уже более 70 лет. Несмотря на кажущуюся простоту постановки такой задачи, оказалось, что структура течения у пластины является весьма сложной. Особенно это проявляется при больших сверхзвуковых скоростях обтекания, когда все поперечные размеры существенно уменьшаются, а нелинейные взаимодействия структурных элементов течения усиливаются.

Во-первых, стало ясно, что постановка задачи обтекания острой пластины является идеализированной настолько, что описать структуру течения в рамках теории механики сплошной среды не представляется возможным. Небольшой участок течения вблизи передней кромки может быть описан с привлечением уравнения Больцмана или, что реализуется гораздо чаще – в рамках компьютерных методов типа имитационного моделирования, основанного на алгоритмах Монте-Карло. Фактически эти задач решаются в рамках самостоятельного научного направления, исследующего течения сильно разреженных газов [1].

В монографии [2] при обсуждении вопроса, какую пластину можно считать заостренной, вводится приближенный критерий, основанной на теории механики сплошной среды: кромку можно считать острой, если ее затупление не оказывает заметного влияния на распределение давления вдоль пластины при течении невязкого газа. Дается приближенная количественная оценка условий обтекания острой кромки: число Рейнольдса ${{\operatorname{Re} }_{{b,\infty }}} = {{{{\rho }_{\infty }}{{V}_{\infty }}{{R}_{b}}} \mathord{\left/ {\vphantom {{{{\rho }_{\infty }}{{V}_{\infty }}{{R}_{b}}} {{{\mu }_{\infty }}}}} \right. \kern-0em} {{{\mu }_{\infty }}}}$ < 100, где ${{R}_{b}}$ – радиус скругления кромки, ${{\rho }_{\infty }},\,\,{{\mu }_{\infty }}$ – плотность и коэффициент динамической вязкости в набегающем со скоростью ${{V}_{\infty }}$ потоке.

Очевидно, что сложность постановки аэродинамических экспериментов состоит в том, что, во-первых, не существует реально абсолютно заостренных кромок, а во-вторых – организация измерений на очень малых расстояниях от кромки практически невозможна. В экспериментальных исследованиях кромки пластин всегда затуплены. При очень малых радиусах скругления, например при ${{R}_{b}}$ ~ 0.005 см [3], можно с запасом считать, что течение формируется у заостренной кромки. При этом заметим, что, по крайней мере, одна сторона пластины представляет собой клин, поэтому структуры течения у двух поверхностей хотя и независимы, но различны. В работе [2] были выделены элементы структуры сжатого слоя у поверхности заостренной пластины: пограничный слой, ударная волна, область смыкания пограничного слоя с ударной волной и область течения, где пограничный слой отделен от ударной волны зоной невязкого течения. Вблизи кромки выделяется область свободно-молекулярного движения и область использования моделей течения со скольжением. В этой же работе изложена теория сильного и слабого вязко-невязкого взаимодействия пограничного слоя и ударной волны, которая получила признание и широкое распространение до настоящего времени. Заметим, что указанные выше структурные элементы течения наблюдаются не только в эксперименте, но хорошо идентифицируются в результатах компьютерного моделирования в рамках уравнений Навье–Стокса, где никаких искусственных разделений поля течения не производится.

При обтекании затупленной пластины необходимо учитывать еще один структурный элемент поля течения – энтропийный слой, появление которого обусловлено образованием отошедшей ударной волны вблизи затупления. За фронтом ударной волны формируется не только пограничный слой у поверхности, но и область нагретого газа между пограничным слоем и фронтом ударной волны. Иногда пограничный слой сливается с ударной волной, но в достаточно плотном газе и вниз по течению между ними образуется область невязкого течения. При больших числах Маха газ может нагреваться до очень высоких температур, при которых наблюдается диссоциация и даже ионизация газа. В первых работах [4–7] и в большом числе последующих публикаций было установлено сильное влияние энтропийного слоя на всю газодинамическую структуру сжатого слоя над затупленной пластиной, на распределение давления, поверхностного трения, плотности тепловых потоков к поверхности.

Важным развитием работ по обтеканию затупленных пластин гиперзвуковым потоком явилось установление роли нагрева пластины, взаимодействия с внешними акустическими возмущениями, нелинейного взаимодействия между акустическими модами возмущений в пограничных слоях на развитие неустойчивости течения, ламинарно-турбулентного перехода и развития структурных особенностей турбулентного пограничного слоя [8–10].

Отдельный раздел гиперзвуковой аэродинамики острых и затупленных пластин включает класс задач химически неравновесных течений у поверхности и, как отдельный подкласс – изучение процессов физико-химической кинетики, включая процессы релаксации внутренних степеней свободы молекулярных компонент течения [11–16].

В данной работе рассматривается задача о сверхзвуковом обтекании затупленной пластины под углами атаки α = 10–45° разреженным потоком воздуха, в котором протекают неравновесные процессы физико-химической кинетики, включая химические реакции, диссоциацию и ионизацию. Особое внимание уделяется изучению закономерностей релаксационных процессов термализации колебательных степеней свободы молекул N₂ и O₂, которые оказывают заметное влияние на скорость химических превращений в газе и на структуру течения газа у наветренной и подветренной поверхностей.

С использованием методов компьютерного моделирования представлены результаты решения двух задач. Исходные данные для первой задачи отвечают условиям эксперимента [3], где набегающий на пластину сильно разреженный поток газа формировался в сопле гиперзвуковой аэродинамической трубы при числе Маха М = 20. Продольный размер испытуемой пластины составил L = 10 см.

Во второй задаче рассмотрено обтекание такой же пластины существенно более плотным потоком воздуха М = 10. Главной целью данного исследования, выполненного в рамках полной системы уравнений Навье–Стокса, является изучение конфигурации поля течения с учетом химических реакций вплоть до диссоциации и ионизации, а также термализации внутренних степеней свободы при увеличении угла атаки затупленной пластины и плотности набегающего потока вплоть до появления отрывного течения над подветренной поверхностью.

1. РАСЧЕТНАЯ МОДЕЛЬ

Двумерная задача ламинарного обтекания затупленной пластины конечного размера потоком вязкого, теплопроводного, сжимаемого химически и термически неравновесного воздуха без выделения фронта ударной волны формулируется на основе уравнений неразрывности, Навье–Стокса, сохранения энергии поступательного движения частиц в форме уравнения теплопроводности Фурье–Кирхгоффа, сохранения массы химических компонент (уравнений диффузии), сохранения колебательной энергии в отдельных колебательных модах двухатомных молекул модах и химической кинетики в каждом элементарном объеме эйлеровой расчетной сетки

(1.1)

$\frac{{\partial \rho }}{{\partial t}} + {\text{div}}\left( {\rho {\mathbf{V}}} \right) = 0,$

(1.2)

$\frac{{\partial \rho u}}{{\partial t}} + {\text{div}}\,\left( {\rho u{\mathbf{V}}} \right) = - \frac{{\partial p}}{{\partial x}} + {{S}_{{\mu ,x}}},$

(1.3)

$\frac{{\partial \rho {v}}}{{\partial t}} + {\text{div}}\,\left( {\rho {v}{\mathbf{V}}} \right) = - \frac{{\partial p}}{{\partial x}} + {{S}_{{\mu ,y}}},$

(1.4)

$\rho {{c}_{p}}\frac{{\partial T}}{{\partial t}} + \rho {{c}_{p}}{\mathbf{V}}\operatorname{grad} T = \operatorname{div} \left( {\lambda \operatorname{grad} T} \right) + {\mathbf{V}}\operatorname{grad} p + {{\Phi }_{\mu }} + {{Q}_{V}} - {{Q}_{h}} + {{Q}_{d}},$

(1.5)

$\frac{{\partial {{\rho }_{i}}}}{{\partial t}} + \operatorname{div} {{\rho }_{i}}{\mathbf{V}} = - \operatorname{div} {{{\mathbf{J}}}_{i}} + {{\dot {w}}_{i}},\quad i = 1,2, \ldots ,{{N}_{s}},$

(1.6)

$\frac{{\partial {{\rho }_{{i(m)}}}{{e}_{{{\text{V,}}i{\text{(}}m)}}}}}{{\partial t}} + \operatorname{div} \left( {{{\rho }_{{i(m)}}}{{e}_{{{\text{V,}}i{\text{(}}m)}}}{\mathbf{V}}} \right) = - \operatorname{div} \left( {{{e}_{{{\text{V,}}i{\text{(}}m)}}}{{{\mathbf{J}}}_{{i(m)}}}} \right) + {{\dot {e}}_{{{\text{V,}}i{\text{(}}m)}}},\quad m = 1,2, \ldots ,{{N}_{{\text{V}}}},$

(1.7)

${{\left( {\frac{{{\text{d}}{{X}_{i}}}}{{{\text{d}}t}}} \right)}_{n}} = \left( {{{b}_{{i,n}}} - {{a}_{{i,n}}}} \right)\left[ {{{k}_{{f,n}}}\prod\limits_j^{{{N}_{s}}} {X_{j}^{{{{a}_{{j,n}}}}}} - {{k}_{{r,n}}}\prod\limits_j^{{{N}_{s}}} {X_{j}^{{{{b}_{{j,n}}}}}} } \right],$

где t – время; x, y – ортогональные декартовы координаты; u, ${v}$ – проекции вектора скорости V на оси координат x и y; $p,\rho ,\,T$ – давление, плотность и температура поступательного движения частиц; $\lambda $ – коэффициент теплопроводности; ${{Y}_{i}}$ – массовая доля i-го компонента смеси газов общим числом ${{N}_{s}}$; ${{c}_{p}},\,\,{{c}_{{p,i}}}$ – удельная теплоемкость при постоянном давлении смеси газов и отдельных компонент; ${{c}_{p}} = \sum\limits_i^{{{N}_{s}}} {{{Y}_{i}}{{c}_{{p,i}}}} $; ${{{\mathbf{J}}}_{i}}$ – плотность диффузионного потока и эффективный коэффициент диффузии i-го компонента; ${{{\mathbf{J}}}_{i}} = - \rho {{D}_{i}}\operatorname{grad} {{Y}_{i}}$.

В правой части уравнения (1.4) присутствуют слагаемые ${{Q}_{V}},\,\,{{Q}_{h}},\,\,{{Q}_{d}}$ – объемные мощности тепловыделения, обусловленные процессами колебательной релаксации в газовой смеси, химическими реакциями и диффузионными процессами переноса тепла ${{Q}_{{\text{V}}}} = - \sum\limits_{m = 1}^{{{N}_{{\text{V}}}}} {{{{\dot {e}}}_{{{\text{V,}}i{\text{(}}m)}}}} $, ${{Q}_{h}} = \sum\limits_{i = 1}^{{{N}_{s}}} {{{h}_{i}}{{{\dot {w}}}_{i}}} $, ${{Q}_{d}} = \sum\limits_{i = 1}^{{{N}_{s}}} {\rho {{c}_{{p,i}}}{{D}_{i}}} \left( {\operatorname{grad} {{Y}_{i}} \cdot \operatorname{grad} T} \right)$. Здесь: N_V – число колебательных мод (в рассматриваемом случае ${{N}_{{\text{V}}}} = 2$: m = 1 для колебательной энергии N₂, m = 2 для колебательной энергии O₂); ${{h}_{i}},\,\,{{\dot {w}}_{i}}$ – энтальпия и массовая скорость химических превращений для i-го компонента смеси; ${{\dot {e}}_{{{\text{V,}}m}}}$ – источник колебательной энергии в m-й моде; ${{R}_{{i(m)}}} = {{{{R}_{0}}} \mathord{\left/ {\vphantom {{{{R}_{0}}} {{{M}_{{i(m)}}}}}} \right. \kern-0em} {{{M}_{{i(m)}}}}}$, ${{R}_{0}} = 8.314 \times {{10}^{7}}$ эрг/(K ⋅ моль) – универсальная газовая постоянная; ${{\rho }_{{i(m)}}}$, ${{M}_{{i(m)}}},\,\,{{D}_{{i(m)}}},\,\,\,{{{\mathbf{J}}}_{{i(m)}}} = - {{\rho }_{{i(m)}}}{{D}_{{i(m)}}}\operatorname{grad} {{Y}_{i}}$ – плотность, молекулярный вес, эффективный коэффициент диффузии в многокомпонентной газовой смеси, вектор плотности диффузионного потока i-го компонента газовой смеси, обладающего m-й модой колебательного движения; ${{{{\theta }}}_{m}}$ – характеристическая колебательная температура (${{{{\theta }}}_{{m = 1}}}({{{\text{N}}}_{{\text{2}}}})$ = 3396 К, ${{{{\theta }}}_{{m = 2}}}({{{\text{O}}}_{{\text{2}}}})$ = 2275 К).

Компоненты тензора вязких напряжений ${{S}_{{\mu ,x}}},\,\,{{S}_{{\mu ,y}}}$ и диссипативная функция ${{\Phi }_{\mu }}$ содержат переменные в пространстве динамические коэффициенты вязкости $\mu $, определяемые температурой поступательных степеней свободы и химическим составом газовой смеси, которые находятся в процессе решения задачи

${{S}_{{\mu ,x}}} = - \frac{2}{3}\frac{\partial }{{\partial x}}\left( {\mu \,{\text{div}}{\mathbf{V}}} \right) + \frac{\partial }{{\partial y}}\left[ {\mu \left( {\frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)} \right] + 2\frac{\partial }{{\partial x}}\left( {\mu \frac{{\partial u}}{{\partial x}}} \right),$

${{S}_{{\mu ,y}}} = - \frac{2}{3}\frac{\partial }{{\partial y}}\left( {\mu \,{\text{div}}{\mathbf{V}}} \right) + \frac{\partial }{{\partial x}}\left[ {\mu \,\left( {\frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)} \right] + \,2\frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial {v}}}{{\partial y}}} \right),$

${{\Phi }_{\mu }} = \mu \left[ {2{{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}}^{2}}} \right.\left. { + 2{{{\left( {\frac{{\partial {v}}}{{\partial y}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)}}^{2}} - \frac{2}{3}{{{\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}}} \right)}}^{2}}} \right].$

Система уравнений (1.1)–(1.7) замыкается калорическим уравнением состояния – термодинамическим соотношением для определения внутренней энергии смеси газов и каждой ее компоненты, а также термическим уравнением состояния идеального газа

(1.8)

$\frac{p}{\rho } = \frac{{{{R}_{0}}T}}{{{{M}_{\Sigma }}}},$

где ${{M}_{\Sigma }} = {{\left( {\sum\limits_i^{{{N}_{s}}} {{{{{Y}_{i}}} \mathord{\left/ {\vphantom {{{{Y}_{i}}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}} } \right)}^{{ - 1}}}$ – суммарный молекулярный вес смеси газов.

Принципиальной особенностью рассматриваемой задачи является учет неравновесного возбуждения внутренних степеней свободы двухатомных молекул. Уравнение (1.6) в общем виде описывает процессы колебательного возбуждения молекулярных компонент газовой смеси N₂ и O₂, поэтому далее будем считать, что каждая из упомянутых молекул кроме 3 поступательных и 2 вращательных степеней свободы обладают по одной колебательной моде движения (одной формой колебательного движения). Считается, что вращательное возбуждение молекул находится в равновесии с поступательными степенями свободы, что обосновано в [17–20]. Мерой колебательного возбуждения молекул является так называемая температура колебательного возбуждения молекулы i-й молекулы в m-й моде ${{T}_{{V,m(i)}}}$. Тогда удельная внутренняя энергия i-й компоненты газовой смеси записывается в виде

(1.9)

${{e}_{i}} = \frac{3}{2}{{R}_{i}}T + {{\delta }_{i}}{{R}_{i}}T + {{\delta }_{i}}{{R}_{i}}\frac{{{{\theta }_{{i(m)}}}}}{{\exp \left( { - \frac{{{{\theta }_{{i(m)}}}}}{{{{T}_{{V,i(m)}}}}}} \right) - 1}},\quad {{R}_{i}} = \frac{{{{R}_{0}}}}{{{{M}_{i}}}},$

где ${{\delta }_{i}}$ = 1 для двухатомных молекул, ${{\delta }_{i}}$ = 0 для атомов. Уравнение (1.6) позволяет определить удельную внутреннюю энергию m-й колебательной моды i-й молекулы

${{e}_{{{\text{V}},i(m)}}} = \frac{{{{R}_{{i(m)}}}{{\theta }_{{i(m)}}}}}{{\exp \left( {{{{{\theta }_{{i(m)}}}} \mathord{\left/ {\vphantom {{{{\theta }_{{i(m)}}}} {{{T}_{{{\text{V}},i(m)}}}}}} \right. \kern-0em} {{{T}_{{{\text{V}},i(m)}}}}}} \right) - 1}},$

откуда и находится температура колебательного возбуждения. Предполагается использование межъядерного потенциала вида гармонического осциллятора, а остальные молекулы, кроме N₂ и O₂, возбуждены равновесно с температурой поступательного движения.

В итоге калорическое уравнение состояния смеси газов формулируется в виде

(1.10)

$e = \int\limits_{{{T}_{0}}}^T {{{c}_{V}}dT,} \quad {{c}_{V}} = \sum\limits_i^{{{N}_{s}}} {{{Y}_{i}}{{c}_{{V,i}}}} ,$

а энтальпия вычисляется по формуле

(1.11)

$h = e + {p \mathord{\left/ {\vphantom {p \rho }} \right. \kern-0em} \rho }.$

При определении ${{\dot {e}}_{{{\text{V,}}i{\text{(}}m)}}}$ учитывались процессы колебательно-поступательной (VT) релаксации и изменения удельной колебательной энергии за счет химических реакций (VC- процессы)

${{\dot {e}}_{{{\text{V,}}m}}} = {{\dot {e}}_{{{\text{V,}}m}}}({\text{VT}}) + {{\dot {e}}_{{{\text{V,}}m}}}({\text{VC}}).$

Релаксационное изменение энергии в каждой колебательной моде рассчитывалось по приближенной теории Ландау–Теллера

${{\dot {e}}_{{{\text{V,}}i{\text{(}}m)}}}({\text{VT}}) = {{\rho }_{{i(m)}}}\frac{{e_{{{\text{V,}}i{\text{(}}m)}}^{0} - {{e}_{{{\text{V,}}i{\text{(}}m)}}}}}{{{{\tau }_{{i{\text{(}}m)}}}}},$

$e_{{{\text{V,}}m}}^{0} = {{e}_{{{\text{V,}}m}}}\left( {{{T}_{{\text{V}}}} = T} \right)$ – равновесная удельная энергия колебательного движения в m-й колебательной моде i-го компонента; ${{\tau }_{{i(m)}}}$ – характерное время релаксации m-й колебательной моды, которое определялось по приближенным соотношениям Милликена и Вайта [20] с поправкой Парка [19], ограничивающей величину ${{\tau }_{{i(m)}}}$ снизу

${{\tau }_{m}} = {{\tau }_{{{\text{VT,}}i{\text{(}}m)}}} + \frac{1}{{{{N}_{t}}{{\sigma }_{{V,i(m)}}}\sqrt {{{8kT} \mathord{\left/ {\vphantom {{8kT} {\left( {\pi {{m}_{{i(m)}}}} \right)}}} \right. \kern-0em} {\left( {\pi {{m}_{{i(m)}}}} \right)}}} }},\quad {{\sigma }_{{V,i(m)}}} = \sigma _{{V,i(m)}}^{'}{{\left( {{{50000} \mathord{\left/ {\vphantom {{50000} T}} \right. \kern-0em} T}} \right)}^{2}},$

$p{{\tau }_{{{\text{VT,}}i(m)}}} = \exp [{{A}_{{VT,i(m)}}}({{T}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}} - {{B}_{{VT,i(m)}}}) - 18.42],$

${{A}_{{{\text{VT,}}i(m)}}} = 0.00116\eta _{{i(m)}}^{{0.5}}\theta _{m}^{{1.333}},\quad {{B}_{{{\text{VT,}}i(m)}}} = 0.015\eta _{m}^{{0.25}},$

${{\eta }_{m}}$ – приведенная масса двухатомной молекулы, ${{m}_{{i(m)}}}$ – масса молекулы i-го компонента; ${{N}_{t}}$ – полная концентрация всех молекул при заданных темпратуре T и давлении р; ${{\sigma }_{{V,i(m)}}}$ – сечение столкновения колебательно-возбужденной частицы, характерное значение которого равно 3 × 10^–17 см².

Изменение колебательной энергии за счет протекания химических реакций учитывалось по модели

${{e}_{{V,m}}}({\text{VC}}) = {{e}_{{V,m}}}\frac{1}{2}\left( {{{{\dot {w}}}_{{i(m)}}} - \left| {{{{\dot {w}}}_{{i(m)}}}} \right|} \right),$

где предполагалось, что уменьшение колебательной энергии в m-й моде в 1 см³ за 1 с пропорционально объемной скорости исчезновения молекул, имеющих эту колебательную моду.

Диффузионный перенос энергии колебательного возбуждения молекул учитывался за счет их диффузии, т.е. плотность потока колебательной энергии за счет диффузии определялась по формуле

${{e}_{{{\text{V,}}m}}}{{{\mathbf{J}}}_{{{\text{V,}}i(m)}}} = - {{e}_{{{\text{V,}}m}}}{{\rho }_{{i(m)}}}{{D}_{{{\text{V,}}i(m)}}}{\text{grad}}{{Y}_{i}},$

где ${{D}_{{{\text{V, }}i(m)}}}$ – эффективный коэффициент диффузии энергии колебательного возбуждения, который принимался равным определенному выше эффективному коэффициенту диффузии.

Кроме термического и калорического уравнений состояния важными для решаемой задачи является способ расчета переносных свойств многокомпонентного газа: вязкости, теплопроводности и коэффициентов диффузии.

Для этих целей используются комбинаторные соотношения [21]

$\mu = \frac{1}{{\sum\limits_{i = 1}^{{{N}_{c}}} {\left( {{{{{Y}_{i}}} \mathord{\left/ {\vphantom {{{{Y}_{i}}} {{{\mu }_{i}}}}} \right. \kern-0em} {{{\mu }_{i}}}}} \right)} }},\quad \lambda = 0.5\left[ {\sum\limits_{i = 1}^{{{N}_{c}}} {{{x}_{i}}{{\lambda }_{i}}} + \frac{1}{{\sum\limits_{i = 1}^{{{N}_{c}}} {\left( {{{{{x}_{i}}} \mathord{\left/ {\vphantom {{{{x}_{i}}} {{{\lambda }_{i}}}}} \right. \kern-0em} {{{\lambda }_{i}}}}} \right)} }}} \right],\quad {{D}_{i}} = \frac{{1 - {{x}_{i}}}}{{\sum\limits_{j \ne i}^{{{N}_{c}}} {\left( {{{{{x}_{j}}} \mathord{\left/ {\vphantom {{{{x}_{j}}} {{{D}_{{ij}}}}}} \right. \kern-0em} {{{D}_{{ij}}}}}} \right)} }},$

а также соотношения, получаемые в первом приближении теории Чепмена–Энскога для динамических коэффициентов вязкости, коэффициентов теплопроводности и бинарной диффузии [22]

${{\mu }_{i}} = 2.67 \times {{10}^{{ - 5}}}\frac{{\sqrt {{{M}_{i}}T} }}{{\sigma _{i}^{2}\Omega _{i}^{{(2,2){\kern 1pt} }}{\kern 1pt} *}},\;~{\text{г/см}} \cdot {\text{с}}$

${{\lambda }_{i}} = 8330\sqrt {\frac{T}{{{{M}_{i}}}}} \frac{1}{{\sigma _{i}^{2}\Omega _{i}^{{(2,2)}}{\kern 1pt} *}},\;{\text{эрг/см}} \cdot {\text{K}}$

${{D}_{{i,j}}} = 1.858 \times {{10}^{{ - 3}}}\sqrt {{{T}^{3}}\frac{{{{M}_{i}} + {{M}_{j}}}}{{{{M}_{i}}{{M}_{j}}}}} \frac{1}{{p\sigma _{{i,j}}^{2}\Omega _{{i,j}}^{{(1,1)}}{\kern 1pt} *}},\;~{\text{с}}{{{\text{м}}}^{{\text{2}}}}{\text{/с}}$

где x_i – относительная мольная концентрация, ${{x}_{i}} = {{{{p}_{i}}} \mathord{\left/ {\vphantom {{{{p}_{i}}} {p = {{Y}_{i}}{{{{M}_{\Sigma }}} \mathord{\left/ {\vphantom {{{{M}_{\Sigma }}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}}}} \right. \kern-0em} {p = {{Y}_{i}}{{{{M}_{\Sigma }}} \mathord{\left/ {\vphantom {{{{M}_{\Sigma }}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}}}$, σ_i – радиус частицы i-го типа, A; $\Omega _{i}^{{(2,2)}}{\kern 1pt} * = f\left( {{{T}_{i}}} \right)$– интеграл столкновений для вязкости и теплопроводности; ${{T}_{i}} = {{kT} \mathord{\left/ {\vphantom {{kT} {{{\varepsilon }_{i}}}}} \right. \kern-0em} {{{\varepsilon }_{i}}}}$, ε_i – параметр потенциала Ленарда–Джонса, характеризующий глубину потенциальной ямы. Интегралы столкновений для вязкости и диффузии рассчитывались по аппроксимациям Анфимова

$\Omega _{i}^{{(2,2)}}{\kern 1pt} * = 1.157T_{i}^{{ - 0.1472}},\quad \Omega _{{i,j}}^{{(1,1)}}{\kern 1pt} * = 1.074T_{{i,j}}^{{ - 0.1604}},$

где ${{T}_{{i,j}}} = \frac{{kT}}{{{{\varepsilon }_{{i,j}}}}},$ ${{\varepsilon }_{{i,j}}} = \sqrt {{{\varepsilon }_{i}}{{\varepsilon }_{j}}} ,$ ${{\sigma }_{{i,j}}} = \frac{1}{2}\left( {{{\sigma }_{i}} + {{\sigma }_{j}}} \right)$.

Массовая скорость химических превращений в каждом элементарном расчетном объеме определялась при решении системы кинетических уравнений (1.7). Здесь ${{X}_{i}}$ – объемно-мольная концентрация i-й компоненты; ${{N}_{r}}$ – число химических реакций; ${{S}_{{f,n}}}$, $S{{}_{{r,n}}}$ – скорости прямой и обратной реакции; ${{k}_{{f,n}}},\,\,{{k}_{{r,n}}}$ – константы скоростей прямых и обратных реакций; ${{a}_{{i,n}}},{{b}_{{i,n}}}$ – стехиометрические коэффициенты n-й химической реакции, определяемые с использованием канонической формы уравнений химической кинетики:

$\sum\limits_{j = 1}^{{{N}_{s}}} {{{a}_{{j,n}}}\left[ {{{X}_{j}}} \right]} = \sum\limits_{j = 1}^{{{N}_{s}}} {{{b}_{{j,n}}}\left[ {{{X}_{j}}} \right]} ,\quad n = 1,2, \ldots ,{{N}_{r}},$

где [X_j] – химические символы реагентов и продуктов химических реакций. Массовая скорость образования i-й компоненты в единице объема определяется по формуле

${{\dot {w}}_{i}} = {{M}_{i}}\sum\limits_{n = 1}^{{{N}_{r}}} {\left( {{{b}_{{i,n}}} - {{a}_{{i,n}}}} \right)\left( {{{S}_{{f,n}}} - {{S}_{{r,n}}}} \right)} ,\;{\text{г/(с}}{{{\text{м}}}^{3}} \cdot {\text{с}})$

Константы скоростей прямой (f) и обратной (r) реакций определяются обобщенной аррениусовской зависимостью

(1.12)

${{k}_{{f(r),n}}} = {{A}_{{f(r),n}}}{{T}^{{{{n}_{{f(r),n}}}}}}\exp \left( { - \frac{{{{E}_{{f(r),n}}}}}{{kT}}} \right),$

где ${{A}_{{f(r),n}}},\;{{n}_{{f(r),n}}},\;{{E}_{{f(r),n}}}$ – аппроксимирующие коэффициенты; k – постоянная Больцмана; n – номер химической реакции в кинетической модели. Константы аппроксимации скоростей прямых реакций заимствовались из [19]. Константы скоростей обратных реакций рассчитывались с использованием констант равновесия [23], аппроксимированных в форме обобщенного закона Аррениуса

(1.13)

${{K}_{n}} = {{A}_{n}}{{T}^{{{{n}_{n}}}}}\exp \left( { - \frac{{{{E}_{n}}}}{{kT}}} \right).$

Аппроксимация констант равновесия в форме (1.13) тестировалась в [24] сравнением с данными Парка [19], основанными на данных JANAF [25].

Малость концентраций заряженных частиц позволила использовать условие квазинейтральности для нахождения мольных концентраций электронов.

Используемые в расчетах константы скоростей диссоциации ${{k}_{f}} = {{k}_{D}}$ подвергались модификации с целью учесть термическую неравновесность молекул. Исследование разных моделей неравновесной диссоциации показало на заметное их влияние на результаты расчетов интенсивности ионизационных процессов. Однако в данной работе применялась лишь эвристическая модель Парка [19]. В этой модели температура ${{T}_{a}}$, используемая в (1.12), рассчитывалась для каждой из колебательных мод по формуле

(1.14)

${{T}_{{a,i(m)}}} = \sqrt {T{{T}_{{V,i(m)}}}} ,$

где $T$ – поступательная температура, ${{T}_{{V,i(m)}}}$ – колебательная температура в m-й колебательной моде.

Сформулированная расчетная модель, основанная на системе уравнений в частных производных (1.1)–(1.6), системе кинетических дифференциальных уравнений первого порядка (1.7) для каждой компоненты газовой смеси, включающая термическое и калорические уравнения состояния (1.8), (1.9)–(1.11), а также систему замыкающих соотношений для определения теплофизических свойств индивидуальных компонент газового течения позволяют решить задачу обтекания затупленной пластины конечного размера вязким, теплопроводным и химически реагирующим газом с учетом ионизации и неравновесной диссоциации. Подчеркнем, что эта задача решалась без выделения ударных волн и каких-либо разрывов газодинамических параметров. На внешних границах расчетной области, кроме выходного сечения, задавались параметры невозмущенного потока. В выходном сечении, где течение также всегда было сверхзвуковым, задавались нулевые производные компонент скорости, плотности, давления, концентраций химических компонент и энергии колебательных мод вдоль соответствующих линий тока. Считалось, что на поверхности происходит рекомбинация заряженных частиц, и массовые доли всех компонент восстанавливаются до условий в набегающем потоке. Задавались условия прилипания и постоянная температура поверхности T_w = 297 К.

В расчетах использовался авторский компьютерный код, в котором реализована многосеточная многоблочная расчетная технология. Схема решаемой задачи с четырьмя расчетными блоками показана на рис. 1. Здесь представлена промежуточная расчетная сетка. Окончательное решение получалось после двукратного удвоения числа узлов. Использовался конечно-разностный метод с численным методом определения компонентов якобиана в пределах каждого блока, применявшихся для трансформации реальной криволинейной сетки в прямоугольную область. Первый блок расчетной сетки предназначался для описания течения в окрестности затупления пластины с радиусом ${{R}_{b}}$ = 0.1 см. Вдоль пластины длиной $L = $ 10 см и 130 см с наветренной стороны располагался блок 3, а с подветренной – блок 2. Четвертый блок предназначался для описания течения в следе. Замыкающая граница пластины толщиной h = 0.2 см была плоской. Течение в этой области описывалось достаточно подробно, так что различались элементы возвратно-вихревого течения за срезом пластины, которые взаимодействовали с пограничными слоями, развивающимися вдоль нижней и верхней поверхностей.

Рис. 1.

Схема решаемой задачи и расчетная четырехблочная сетка. Показаны номера блоков и характерных точек аналитически созданной расчетной сетки.

Для получения численного решения использовался гибридный явно-неявный алгоритм интегрирования. Уравнения Навье–Стокса и неразрывности интегрировались с использованием AUSM-алгоритма [26] в варианте аппроксимации функций на контактном разрыве второго порядка. Система уравнений сохранения энергии поступательных и колебательных степеней свободы (1.4), (1.6), а также уравнений диффузии (1.5) интегрировалась неявным методом второго порядка аппроксимации. Система кинетических уравнений (1.7) интегрировалась с использованием обобщенного метода Ньютона [27]. Такая комбинация методов позволила выполнять интегрирование уравнений движения с предельно допустимым уровнем критерия Куранта–Фридрихса–Леви (Courant–Friedrichs–Lewy, CFL). На каждом шаге по времени уточнялись теплофизические, переносные и кинетические функции и коэффициенты, входящие в систему интегрируемых уравнений.

В подавляющем большинстве случаев получалось установившееся решение с величиной невязки менее 10^–6. В расчетных вариантах, где наблюдалось появление отрывного течения над подветренной поверхностью, наблюдалось периодическое нестационарное решение с величиной численной невязки компонент скорости и температуры порядка 10^–3. Попытки увеличения точности нестационарного расчета за счет уменьшения параметра CFL не приводили к видимому изменению решения, а задача изучения особенностей нестационарной структуры течения в данной работе не ставилась. Подробности разработанной методики компьютерного моделирования приведены в [24].

2. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Выполнены две серии численных экспериментов для исходных данных, представленных в табл. 1. Первая серия расчетов проводилась для условий экспериментов [3].

Таблица 1.

Исходные данные обтекания пластины длинной L = 10 см под разными углами атаки

№ вар.	${{p}_{\infty }}$, эрг/см³	${{\rho }_{\infty }}$, г/см³	${{T}_{\infty }}$, K	${{M}_{\infty }}$	${{T}_{w}}$, K
1	12	3.25 × 10^–7	12.4	20	12.4
2	12000	1.84 × 10^–5	227	10	227

На рис. 2 показаны числа Маха и температура поступательных степеней свободы при угле атаки α = 10°, для которого проводились измерения в экспериментах [3]. Хорошо видны основные структурные элементы поля, о которых говорилось выше, – ударные волны, отходящие от затупления пластины, области пограничного слоя с дозвуковыми скоростями движения и повышенной температурой внутри пограничного слоя. Например, на расстоянии х = 20 см от кромки пластины температура внутри пограничного слоя достигает ~380 К в то время, когда на внешней границе динамического пограничного слоя она составляет ~120 K, а для поверхности – 297 К. Самая высокая температура поступательных степеней свободы достигается в окрестности затупления пластины ~1000 K, что близко к теоретическому значению температуры торможения T₀ = = 1004 К.

Рис. 2.

Распределение чисел Маха и температуры поступательных степеней свободы для исходных данных первого варианта при угле атаки $\alpha = 10^\circ $. Дискретные точки – экспериментальные данные [3] для $\alpha = 10^\circ $ (квадраты) и $\alpha = - 10^\circ $ (кружки).

Еще одна зона повышенной температуры наблюдается в ближнем следе, где встречаются потоки, сходящие с верхней и нижней поверхностей (рис. 2б). Здесь газ нагревается до температуры Т ~ 350 К. В среднем, температура в сжатом слое над подветренной поверхностью снижается при увеличении угла атаки. Над наветренной поверхностью и в ближнем следе, наоборот, при увеличении угла атаки температура возрастает.

На рис. 3 приведено распределение температур колебательного возбуждения молекул N₂ (далее, для краткости, колебательных температур), а также разницы между температурами колебательного возбуждения и температурой поступательных степеней свободы (далее, для краткости, поступательная температура) $\Delta {{T}_{V}} = {{T}_{V}} - T$. Подчеркнем, что положительные значения величины $\Delta {{T}_{V}}$ означают превышение колебательной температуры над поступательной температурой.

Рис. 3.

Колебательная температура ${{T}_{{{\text{V}}1}}} = {{T}_{{\text{V}}}}\left( {{{{\text{N}}}_{2}}} \right)$ (а) и разность $\Delta {{T}_{{{\text{V}}1}}} = {{T}_{{\text{V}}}}\left( {{{{\text{N}}}_{2}}} \right) - T$ (б) для условий эксперимента [3] при $\alpha = 10^\circ $.

Хорошо видно (рис. 3a), что в области ближнего следа формируются две области повышенной температуры колебательного возбуждения (на рис. 3а они обозначены римскими цифрами I и II), а в пограничном слое у наветренной стороны пластины, наоборот – поступательная температура систематически превышает колебательную температуру (зона III на рис. 3а). Поэтому отметим существование трех областей термической неравновесности в потоке, причем первые две области с повышенной колебательной температурой разделены почти равновесной областью с незначительным превышением колебательной температуры над поступательной. Однако следует учитывать тот факт, что образование указанных областей колебательной неравновесности во многом зависит от характерных релаксационных времен колебательных мод. В частности, распределения колебательных температур для кислорода свидетельствуют о большей скорости процессов термализации колебаний молекул О₂. Это не удивительно, поскольку хорошо известно соотношение между характерными временами колебательной релаксации ${{\tau }_{{{{{\text{O}}}_{2}}}}} < {{\tau }_{{{{{\text{N}}}_{2}}}}}$ [19].

Появление зон неравновесного колебательного возбуждения двухатомных молекул является следствием общих закономерностей неравновесного обтекания пластины под углом атаки. За фронтом ударной волны, образующейся вблизи затупления пластины, наблюдается быстрый рост поступательной температуры и существенно более медленное возрастание колебательных температур, что непосредственно связано с фундаментальными физическими закономерностями – для возбуждения колебаний двухатомных молекул требуется в десятки тысяч раз большее число столкновений между ними, чем для возбуждения поступательных степеней свободы. Таким образом, течение за фронтом ударной волны у затупления начинается с явного запаздывания колебательной температуры от поступательной. Вблизи наветренной поверхности поступательная температура резко возрастает при увеличении давления и плотности, а колебательные степени свободы не успевают термализоваться.

Поступательная температура за фронтом косой ударной волны значительно ниже, чем за прямой, поэтому температура колебательного возбуждения может даже ее превосходить. Вблизи подветренной поверхности и в следе наблюдается хорошо изученная закономерность превосходства колебательных температур над поступательной. Картина процесса становится обратной той, которая наблюдается за ударной волной. В течение разрежения поступательная температура резко падает, а для падения температуры колебательного возбуждения не хватает интенсивности столкновений молекул. И только в области столкновения потоков, истекающих с наветренной и подветренной сторон пластины (зоны I и II на рис. 3а), снова наблюдается резкое увеличение поступательной температуры.

На рис. 4 показаны результаты расчетов обтекания затупленной пластины при тех же самых условиях, но при угле атаки α = 45°. Все отмеченные выше закономерности в изменении структуры течения при увеличении угла атаки остаются прежними, но проявляются в большей степени. Давление от значений в пограничном слое у наветренной поверхности падает до давления у подветренной поверхности более, чем в 1000 раз (рис. 4г). Наблюдаются две области течения с повышенной поступательной температурой (рис. 4в): одна – вблизи наветренной стороны, где набегающий поток создает зону сжатия у поверхности. Вторая – в верхней части следа над подветренной стороной. Здесь поступательная температура достигает величины примерно 0.5Т₀.

Рис. 4.

Распределение чисел Маха (а), y-компоненты скорости ${{V}_{y}} = {{v} \mathord{\left/ {\vphantom {{v} {{{V}_{\infty }}}}} \right. \kern-0em} {{{V}_{\infty }}}}$ (б), температуры поступательных степеней свободы (в) и давления (Pres, в эрг/см³; г) условий эксперимента [3] под углом атаки $\alpha = 45^\circ $.

На рис. 5а,б приведены распределения колебательных температур, а на рис. 5в,г разницы между температурами колебательных и поступательных степеней свободы. Эти данные хорошо иллюстрируют влияние характерных времен релаксации колебаний молекул на температуру колебательного возбуждения. В областях наибольшего разрежения над поверхностью колебательные температуры превосходят поступательную температуру более, чем на 300 К.

Рис. 5.

Температурное распределение колебательных степеней свободы молекул N₂ (а) и O₂ (б) и разности $\Delta {{T}_{{{\text{V}}1}}} = {{T}_{{\text{V}}}}\left( {{{{\text{N}}}_{2}}} \right) - T$ (в), $\Delta {{T}_{{{\text{V2}}}}} = {{T}_{{\text{V}}}}\left( {{{{\text{O}}}_{2}}} \right) - T$ (г) для условий эксперимента [3] при угле атаки $\alpha = 45^\circ $.

Изменения, происходящие в потоке при увеличении плотности набегающего потока, отражены на рис. 6 и 7 , где показаны условия течения при статическом давлении в набегающем потоке в 10³ раз больше, чем в предыдущем варианте. При этих условиях у подветренной поверхности вблизи заднего среза пластины уже возникает небольшая зона возвратно-вихревого течения. Она отвечает числам Маха М = 0.1 (рис. 6а). На рис. 6б вблизи верхней задней кромки видна область отрицательных значений у-компоненты скорости, что подтверждает наличие небольшой вихревой зоны. Отметим, что в этой области наблюдается повышенная осцилляция численного решения, которая, однако, не приводит к катастрофическим последствиям в численном решении.

Рис. 6.

Распределение чисел Маха (а) и y-компоненты скорости потока ${{V}_{y}} = {{v} \mathord{\left/ {\vphantom {{v} {{{V}_{\infty }}}}} \right. \kern-0em} {{{V}_{\infty }}}}$(б) для условий второго расчетного варианта при угле атаки $\alpha = 45^\circ $.

Рис. 7.

Температурное распределение поступательных степеней свободы (а), плотности электронов (б) и разность между температурой колебательного возбуждения молекул $\Delta {{T}_{{{\text{V}}1}}} = {{T}_{{\text{V}}}}\left( {{{{\text{N}}}_{2}}} \right) - T$ (в) и $\Delta {{T}_{{{\text{V2}}}}} = {{T}_{{\text{V}}}}\left( {{{{\text{O}}}_{2}}} \right) - T$ (г) для второго расчетного варианта при угле атаки $\alpha = 45^\circ $.

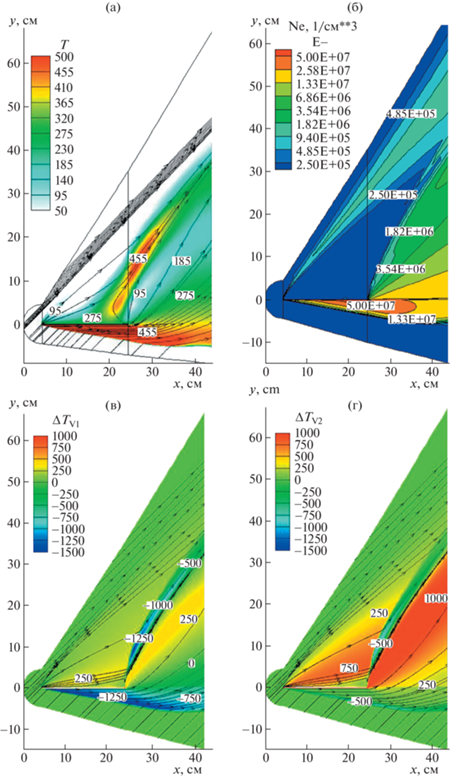
Поступательная температура достигает у нижней (наветренной) поверхности значений T ~ ~ 2300 К, а над верхней поверхностью, в зоне разрежения, падает до значений ~200 К (рис. 7a). Примечательно, что в следе, где сходятся потоки, обтекающие пластину сверху и снизу, температура опять возрастает до ~2000 К. Напомним, что в предыдущем расчетном варианте (при меньшей плотности набегающего потока) масштаб температур в наиболее горячих областях был порядка 500 К. Еще до больших температур нагреваются колебательные степени свободы молекул N₂ и O₂ (рис. 7в,г). В данном случае, как и прежде, наблюдается наличие двух зон повышенных колебательных температур, отходящих от передней и задней кромок пластины, разделенных областью относительно больших поступательных температур.

Еще одним важным итогом увеличения давления в набегающем потоке является заметная ионизация воздуха в сжатом слое у наветренной поверхности и в ближнем следе (рис. 7б). В области пониженного давления над подветренной поверхностью ионизация не наблюдается.

ЗАКЛЮЧЕНИЕ

Для решения задачи неравновесной аэрофизики обтекания затупленнной пластины конечных размеров разработана и реализована сопряженная модель физико-химической газовой динамики, в которой наряду с уравнениями Навье–Стокса численно интегрируются уравнения химической кинетики, сохранения энергии поступательных и колебательных степеней свободы, кинетики диссоциации и ионизации. Для повышения вычислительной эффективности разработанного численного метода использована многосеточная многоблочная технология гибридного явно-неявного алгоритма.

Выполненное расчетное исследование показало, что обтекание затупленной пластины конечных размеров сверхзвуковым потоком разреженного воздуха под большими углами атаки сопровождается образованием нескольких областей течения, в которых не достигается термализация внутренних степеней свободы. Это оказывает сильное влияние как на структуру течения в окрестности обтекаемой пластины, так и на протекание химических реакций в потоке, которые в конечном счете определяют степень ионизации газа при больших сверхзвуковых скоростях.

Разработанный метод использовался для интерпретации экспериментальных данных по сверхзвуковому обтеканию пластины под углом атаки.

Работа выполнена при поддержке Российского научного фонда (грант № 22-11-00062).

Список литературы

Bird G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Clarendon Press. Oxford. 1994. 458 p.
Hayes W.D., Probstein R.F. Hypersonic Flow Theory. New York.: Acad.Press, 1959. 464 p.
Маслов А.А., Миронов С.Г., Поплавская Т.В., Ветлуцкий В.Н. О влиянии угла атаки на гиперзвуковое обтекание пластины // ТВТ. 1998. Т. 36. № 5. С. 754–760.
Черный Г.Г. Течение газа с большой сверхзвуковой скоростью. М.: Физматлит, 1959. 220 с.
Лунев В.В. Течение реальных газов с большими скоростями. М.: Физматлит. 2007. 760 с.
Cheng H.K., Hall J.G., Golian T.C., Hertzberg A. Boundary-Layer Displacement and Leading-Edge Bluntness Effects in High-Temperature Hypersonic Flow // JARS. 1961. V. 28. № 5. P. 353–381. https://doi.org/10.2514/8.9002
Yakura J.K. Theory of Entropy Layers and Nose Bluntness in Hypersonic Flow // P. 421–470. https://doi.org/10.2514/5.9781600864810.0421.0470 in book Hypersonic Flow Research / Ed. by Riddel F.R. New York.: Academic Press, 1962. 758 p.
Маслов А.А., Поплавская Т.В., Миронов С.Г., Цирюльников И.С. Волновые процессы в ударном слое на пластине, расположенной под углом атаки // ПМТФ. 2010. Т. 51. № 4. С. 39–47.
Маслов А.А., Миронов С.Г., Кудрявцев А.Н., Поплавская Т.В., Цирюльников И.С. Управление возмущениями в гиперзвуковом ударном слое на пластине нестационарным воздействием с поверхности // Изв. РАН. МЖГ. 2008. № 3. С. 52–161.
Лысенко В.И. Влияние энтропийного слоя на устойчивость сверхзвукового ударного слоя и переход ламинарного пограничного слоя в турбулентный // ПМТФ. 1990. № 6. С. 74–80.
Hall J.G., Eschenroeder A.Q., Marrone P V. Blunt–nose inviscid airflows with coupled nonequilibrium processes // J. Aerosp. Sci. 1962. V. 29. P. 1038–1051.
Mallinson S.G., Mudford N.R., Gai S.L. Leading-edge bluntness effects in hypervelocity flat plate flow // Phys. Fluids. 2020. 32. 046106. https://doi.org/10.1063/1.5138205
Rose P., Stark W. Stagnation Point Heat Transfer Measurements in Dissociated Air // JAS. 1958. № 2. P. 86–97.
Lees L. Laminar Heat Transfer over Blunt-Nosed Bodies at Hypersonic Flight Speeds // Jet Propulsion. 1956. № 4. P. 259–274.
Fay J.A. and Riddel F. Theory of Stagnation Point Heat Transfer in Dissociated Air // JAS. 1958. № 2.
Shang J.S., Surzhikov S.T. Nonequilibrium radiative hypersonic flow simulation // Progress in Aerospace Sciences. 2012. V. 53. P. 46–65.
Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Наука. Гл. редакция физ.-мат. лит. 1966. 687 с.
Clarke J.F., McChesney M. The Dynamics of Real Gases. London.: ButterWorths, 1964. 419 p.
Park C. Nonequilibrium Hypersonic Aerothermodynamics. N.Y.: Wiley-Intern. Publ.1990. 358 p.
Millikan R.C. and White D.R. Systematic of Vibrational Relaxation // J. Chemical Physics.1963. V. 39. № 12. P. 3209–3212.
Bird R.B., Stewart W.E., Lightfoot E.W. Transport Phenomena / 2nd Ed. N.Y.: Wiley. 2002912 p.
Hirschfelder J.O., Curtiss C.F., Bird R.B. The Molecular Theory of Gases and Liquids Revised Edition. Wiley-Interscience, 1964. 1280 p.
Гурвич Л.В., Вейц И.В., Медведев В.А. и др. Термодинамические свойства индивидуальных веществ. М.: Наука. 1978. 495 с.
Суржиков С.Т. Компьютерная аэрофизика спускаемых космических аппаратов. Двухмерные модели. М.: Физматлит, 2018. 543 с.
Chase M.W., Davies C.A., Downey J.R. Jr., Frutrip D.J., McDonald R., Syverud A.N. JANAF Thermochemical Tables / Third ed. Parts 1 and 2 // J. Physical and Chemical Reference Data. 1985.V. 14. № 1 Supl. P. 1–1856.
Liou M.-S. A Sequel to AUSM: AUSM+ // J. Comput. Phys. 1996.V. 129. P. 364–382.
Seleznev R.K., Surzhikov S.T. A Generalized Newton Method for Differential Equation of Chemical Kinetics // AIAA 2013-3009. 2013. 17 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал