Известия РАН. Механика жидкости и газа, 2023, № 2, стр. 90-101

ФИЛЬТРАЦИЯ ФЛЮИДА К СКВАЖИНЕ ЧЕРЕЗ РАДИАЛЬНУЮ ТРЕЩИНУ ГРП ПРИ ПОСТОЯННОМ РАСХОДЕ

Е. П. Аносова^a, *, З. М. Нагаева^a, b, **, В. Ш. Шагапов^b, ***

^a Уфимский государственный нефтяной технический университет
Уфа, Россия

^b Институт механики им. Р.Р. Мавлютова Уфимского федерального исследовательского центра РАН
Уфа, Россия

^* E-mail: ae0809@mail.ru
^** E-mail: Nagaeva_Zilya@mail.ru
^*** E-mail: Shagapov@rambler.ru

Поступила в редакцию 28.09.2022
После доработки 31.10.2022
Принята к публикации 10.11.2022

EDN: NTEWPR
DOI: 10.31857/S0568528122600692

Полный текст (PDF)

Аннотация

Рассматривается задача об отборе жидкости из пласта в скважину или закачке жидкости из скважины в пласт при наличии трещины ГРП, перпендикулярной стволу скважины, в режиме постоянного расхода. Получены аналитические решения, описывающие эволюцию давления в трещине при постоянном расходе флюида из пласта в скважину. Построены приближенные решения с использованием метода последовательной смены стационарных состояний (ПССС). Сравнение численных результатов точного и приближенного решений показывает, что они практически совпадают. Проанализировано влияние коллекторских характеристик пласта и трещины на эволюцию давления в трещине и в скважине.

Ключевые слова: трещина гидроразрыва пласта (ГРП), постоянный расход, распределение давления, интегродифференциальное уравнение, аналитическое решение

В настоящее время в связи с тем, что значительная часть запасов нефти является трудноизвлекаемой в силу низкой проницаемости пластов или высокой вязкости самой нефти, представляют большой интерес задачи, описывающие фильтрацию флюида в призабойной зоне, подверженной различным физико-химическим и механическим воздействиям. Существенная часть работ [1–5] посвящена задачам фильтрации вокруг скважины при наличии трещин, полученных путем гидроразрыва пласта (ГРП).

В работах [6–9] приведена модель, описывающая фильтрацию флюида в трещине ГРП и в окружающем трещину пласте. В [6] приводится решение, описывающее изменение давления жидкости на скважине при поддержании постоянного дебита. В статьях [7–9] описывается распределение давления в трещине ГРП при режиме поддержания постоянного давления на скважине и при поддержании постоянного расхода жидкости. Во всех упомянутых выше работах рассматривались наиболее распространенные в настоящее время вертикальные скважины с вертикальной трещиной ГРП, симметричной относительно оси скважины.

В данной работе рассматривается процесс нестационарной фильтрации флюида в трещине ГРП, перпендикулярной оси скважины, при поддержании постоянного расхода жидкости на скважине. Для решения поставленной задачи предложена математическая модель в виде интегро-дифференциального уравнения. Найдены точное аналитическое решение через функции Бесселя и приближенное решение, полученное с помощью метода последовательной смены стационарных состояний (ПССС), удобное для практического применения и хорошо согласующееся с точным решением.

1. ОСНОВНЫЕ УРАВНЕНИЯ

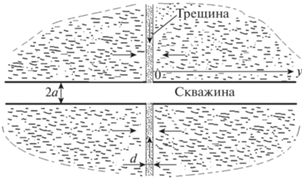
Рассматривается трещина ширины d_f, образованная гидроразрывом пласта и представляющая собой область пористой и проницаемой среды между двумя параллельными вертикальными плоскостями, расположенная перпендикулярно к горизонтальной цилиндрической скважине (рис. 1). Течение жидкости в трещине – радиально симметричное. Запишем уравнение неразрывности для флюида в трещине

(1.1)

${{\left. {\frac{{\partial \left( {{{m}_{f}}{{\rho }_{f}}} \right)}}{{\partial t}} + \frac{1}{r}\frac{{\partial \left( {r{{\rho }_{f}}{{{v}}_{f}}} \right)}}{{\partial r}} = - 2\frac{{\left( {{{\rho }_{p}}{{{v}}_{p}}} \right)}}{{{{d}_{f}}}}} \right|}_{{y = 0}}}\quad \left( {a < r} \right)$

где ${{m}_{i}}$ и ${{\rho }_{i}}$ – пористость и плотность флюида (здесь и в дальнейшем нижние индексы f и p соответствуют значениям параметров в трещине и окружающей ее пористой среде), ${{{v}}_{i}}$ – скорость фильтрации жидкости, $a$ – радиус скважины. Величина в правой части уравнения (1.1) выражает приток флюида из пласта в трещину. Для ее определения решим сопряженную фильтрационную задачу в пласте вне трещины. Для этого запишем уравнение неразрывности в пористой среде

(1.2)

$\frac{{\partial \left( {{{m}_{p}}{{\rho }_{p}}} \right)}}{{\partial t}} + \frac{{\partial \left( {{{\rho }_{p}}{{{v}}_{p}}} \right)}}{{\partial y}} = 0\quad \left( {0 < y < \infty } \right)$

Рис. 1.

Схема системы “скважина–трещина ГРП”.

Ось $Oy$ отсчитывается от стенки трещины.

Для описания процесса фильтрации в трещине и в пласте примем закон Дарси

(1.3)

${{{v}}_{f}} = - \frac{{{{k}_{f}}}}{\mu }\frac{{\partial {{P}_{f}}}}{{\partial r}}\quad \left( {a < r < \infty } \right),\quad {{{v}}_{p}} = - \frac{{{{k}_{p}}}}{\mu }\frac{{\partial {{P}_{p}}}}{{\partial y}}\quad \left( {a < r < \infty ,\;\;0 < y < \infty } \right)$

где k_i $\left( {i = f,p} \right)$ – коэффициент проницаемости, $\mu $ – динамическая вязкость флюида. Сжимаемость жидкости учитывается в акустическом приближении

(1.4)

${{P}_{i}} - {{P}_{0}} = {{C}^{2}}\left( {{{\rho }_{i}} - {{\rho }_{0}}} \right)\quad \left( {i = f,p} \right)$

где C – скорость звука для жидкости, индекс (0) внизу для давления и плотности соответствует их невозмущенным значениям. Флюид считаем слабо сжимаемым $\left( {\left| {{{\rho }_{i}} - {{\rho }_{0}}} \right| \ll {{\rho }_{i}} \approx {{\rho }_{0}}} \right)$. Тогда уравнения (1.1) и (1.2) с учетом (1.3) и (1.4) можно привести к виду

(1.5)

${{\left. {\frac{{\partial {{P}_{f}}}}{{\partial t}} = \frac{{{{\unicode{230} }_{f}}}}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{P}_{f}}}}{{\partial r}}} \right) + 2\frac{{{{m}_{p}}}}{{{{m}_{f}}}}\frac{{{{\unicode{230} }_{p}}}}{{{{d}_{f}}}}\left( {\frac{{\partial {{P}_{p}}}}{{\partial y}}} \right)} \right|}_{{y = 0}}}\quad \left( {a < r < \infty } \right)$

(1.6)

$\frac{{\partial {{P}_{p}}}}{{\partial t}} = {{\unicode{230} }_{p}}\frac{{{{\partial }^{2}}{{P}_{p}}}}{{\partial {{y}^{2}}}}\quad \left( {a < r < \infty ,\;\;0 < y < \infty } \right)$

где ${{\unicode{230} }_{i}} = \frac{{{{k}_{i}}{{\rho }_{0}}{{C}^{2}}}}{{{{m}_{i}}\mu }}$ $\left( {i = f,p} \right)$.

Отметим, что ${{P}_{f}}$ – функция переменных $t$ и $r$, а ${{P}_{p}}$ – функция переменных, $t,\;r$ и y. В результате система (1.5) и (1.6) может быть сведена к одному интегро-дифференциальному уравнению для P_f. Действительно, величина давления ${{P}_{p}}$ на поверхности стенки трещины $\left( {y = 0} \right)$ должна быть равна ${{P}_{f}}.$ Это условие запишется как

${{P}_{p}} = {{P}_{f}}\quad \left( {a < r < \infty ,\;\;y = 0} \right)$

Будем считать, что в пористой среде вдали от трещины давление однородное и равно P₀, т.е.

${{P}_{p}} = {{P}_{0}}\quad \left( {a < r < \infty ,\;\;y = \infty } \right)$

Согласно уравнению (1.6) линии тока для фильтрационного течения в пласте полагаются прямыми, направленными перпендикулярно к границе трещин ГРП. Это допущение основано на том, что, во-первых, забойный участок скважины обсажен (поступление флюида в скважину происходит только из трещины). Во-вторых, проницаемость пласта k_p на несколько порядков ниже, чем проницаемость в трещине ГРП k_f $\left( {{{k}_{p}} \ll {{k}_{f}}} \right)$. Вследствие этого составляющая скорости фильтрации ${{{v}}_{{p\left( r \right)}}}$ в пласте вблизи трещины вдоль нее значительно меньше, чем скорость фильтрации ${{{v}}_{f}}$ в трещине $\left( {\left| {{{{v}}_{{p\left( r \right)}}}} \right| < \left| {{{{v}}_{f}}} \right|} \right)$. Ниже, в п. 3 будет представлен более детальный анализ для диапазона расстояния $r$ и времени t, когда линии тока в пласте вблизи трещины ГРП почти прямые. Отметим также, что это допущение о прямолинейности линий тока сильно упрощает решение задачи.

Согласно принципу Дюамеля [10] решение уравнения (1.6), удовлетворяющее начальному и граничному условиям

(1.7)

${{P}_{p}} = {{P}_{0}}\quad \left( {t \leqslant {{t}_{0}},\;\;0 < y < \infty } \right),\quad {{P}_{p}} = {{P}_{f}}\quad \left( {t > {{t}_{0}},\;\;y = 0} \right)$

может быть записано как

(1.8)

${{P}_{p}} - {{P}_{0}} = \int\limits_{{{t}_{0}}}^t {\frac{{\partial u\left( {y,t - \tau } \right)}}{{\partial t}}\left( {{{P}_{f}}\left( {\tau ,r} \right) - {{P}_{0}}} \right)d\tau } $

где

$u\left( {y,t - \tau } \right) = 1 - \Phi ({y \mathord{\left/ {\vphantom {y {(2\sqrt {{{\unicode{230} }_{p}}\left( {t - \tau } \right)} )}}} \right. \kern-0em} {(2\sqrt {{{\unicode{230} }_{p}}\left( {t - \tau } \right)} )}}) = \frac{2}{{\sqrt \pi }}\int\limits_{{y \mathord{\left/ {\vphantom {y {(2\sqrt {{{\unicode{230} }_{p}}\left( {t - \tau } \right)} )}}} \right. \kern-0em} {(2\sqrt {{{\unicode{230} }_{p}}\left( {t - \tau } \right)} )}}}^{ + \infty } {{{e}^{{ - {{\alpha }^{2}}}}}d\alpha } $

После несложных преобразований с учетом условий (1.7) решение (1.8) можно привести к виду

(1.9)

${{P}_{p}} - {{P}_{0}} = \int\limits_{{{t}_{0}}}^t {\frac{{\partial \left( {{{P}_{f}}\left( {\tau ,r} \right) - {{P}_{0}}} \right)}}{{\partial \tau }}u\left( {y,t - \tau } \right)d\tau } $

Подставляя (1.9) в уравнение (1.5) и полагая ${{t}_{0}} = - \infty $, получим следующее линейное интегродифференциальное уравнение для P_f, как

(1.10)

$\frac{{\partial {{P}_{f}}}}{{\partial t}} = \frac{{{{\unicode{230} }_{f}}}}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{P}_{f}}}}{{\partial r}}} \right) - 2\frac{{{{m}_{p}}}}{{{{m}_{f}}}}\frac{{{{\unicode{230} }_{p}}}}{{{{d}_{f}}}}\int\limits_{ - \infty }^t {\frac{{\partial \left( {{{P}_{f}}\left( {\tau ,r} \right) - {{P}_{0}}} \right)}}{{\partial \tau }}\frac{{d\tau }}{{\sqrt {\pi {{\unicode{230} }_{p}}\left( {t - \tau } \right)} }}} $

Левая часть этого уравнения связана с упругоемкостью трещины. Как показано в [7], для рассматриваемых задач это слагаемое не существенное, и в дальнейшем им пренебрегаем.

2. ФИЛЬТРАЦИЯ ФЛЮИДА В СКВАЖИНУ ЧЕРЕЗ ТРЕЩИНУ В РЕЖИМЕ ПОСТОЯННОГО РАСХОДА

На основе уравнения (1.10), пренебрегая эффектом упругоемкости флюида в трещине (полагая равной нулю левую часть этого уравнения), рассмотрим радиальный режим фильтрации в трещине.

Пусть в исходном состоянии $(t \leqslant 0)$ жидкость в трещине и в пласте находится в покое, и, следовательно, давление однородно. В момент времени $t = 0$ начинается с постоянным расходом отбор $(q > 0)$ или нагнетание $(q < 0)$ жидкости из скважины в трещину. Требуется определить поле давления P_f в трещине и закон изменения давления ${{P}_{{f(w)}}}$ в скважине. Рассмотрим случай, когда $q > 0$. В рамках отмеченных допущений уравнение (1.10) и его система начальных и граничных условий запишутся как

(2.1)

$\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial \Delta {{P}_{f}}}}{{\partial r}}} \right) = {{\chi }_{f}}\int\limits_0^t {\frac{{\partial \Delta {{P}_{f}}}}{{\partial \tau }}\frac{{d\tau }}{{\sqrt {\pi \left( {t - \tau } \right)} }}} \quad \left( {a < r < \infty } \right)\quad \left( {{{\chi }_{f}} = \frac{2}{{{{d}_{f}}}}\frac{{{{m}_{p}}}}{{{{m}_{f}}}}\frac{{\sqrt {{{\unicode{230} }_{p}}} }}{{{{\unicode{230} }_{f}}}}} \right)$

(2.2)

$\Delta {{P}_{f}} = 0\quad (\Delta {{P}_{f}} = {{P}_{f}} - {{P}_{0}})\quad \left( {t \leqslant 0,\;\;r > a} \right)$

(2.3)

${{\left. {q = - \frac{{2\pi a{{d}_{f}}{{k}_{f}}}}{\mu }\left( {\frac{{\partial \Delta {{P}_{f}}}}{{\partial r}}} \right)} \right|}_{{r = a}}} = {\text{const}}$

Из условия (2.3) следует

(2.4)

${{\left. {\frac{{\partial \Delta {{P}_{f}}}}{{\partial r}}} \right|}_{{r = a}}} = - \frac{{q\mu }}{{2\pi a{{d}_{f}}{{k}_{f}}}}$

Далее будем использовать преобразование Лапласа [11]

$\Delta \overline {{{P}_{f}}} = \int\limits_0^\infty {{{e}^{{ - \lambda t}}}\Delta {{P}_{f}}dt} $

Из уравнения (2.1) с учетом (2.2) получаем для $\Delta \overline {{{P}_{f}}} $ следующее обыкновенное дифференциальное уравнение

(2.5)

$\frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{d\Delta \overline {{{P}_{f}}} }}{{dr}}} \right) = {{\chi }_{f}}\sqrt \lambda \Delta \overline {{{P}_{f}}} $

Решение уравнения (2.5) имеет вид

(2.6)

$\Delta \overline {{{P}_{f}}} \left( {\lambda ;r} \right) = {{C}_{1}}\,{{I}_{0}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } r) + {{C}_{2}}\,{{K}_{0}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } r)$

где ${{I}_{0}}\left( z \right)$ и ${{K}_{0}}\left( z \right)$ – модифицированные функции Бесселя 1-го и 2-го рода нулевого порядка соответственно [12]. Учитывая ограниченность $\Delta {{P}_{f}}$ на бесконечности, имеем ${{C}_{1}} = 0.$ Следовательно,

(2.7)

$\Delta \overline {{{P}_{f}}} \left( {\lambda ;r} \right) = {{C}_{2}}\,{{K}_{0}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } r)$

Продифференцируем обе части уравнения (2.7) по переменной $r$, тогда

(2.8)

$\frac{\partial }{{\partial r}}(\Delta \overline {{{P}_{f}}} \left( {\lambda ;r} \right)) = {{C}_{2}}K_{0}^{'}(\sqrt {{{\chi }_{f}}\sqrt \lambda } r)\sqrt {{{\chi }_{f}}\sqrt \lambda } $

Учитывая, что производная $K_{0}^{'}\left( z \right) = - {{K}_{1}}\left( z \right)$, (${{K}_{1}}\left( z \right)$ – модифицированная функция Бесселя второго рода первого порядка [10, 12]) из (2.8) при r = a получим

(2.9)

${{С}_{2}} = \frac{{q\mu }}{{2\pi a{{d}_{f}}{{k}_{f}}{{\lambda }^{{\frac{5}{4}}}}\sqrt {{{\chi }_{f}}} {{K}_{1}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } a)}}$

Тогда решение (2.6) с учетом выражения для C₂ из (2.9) будет иметь вид

$\Delta \overline {{{P}_{f}}} \left( {\lambda ;r} \right) = \frac{{q\mu \,{{K}_{0}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } r)}}{{2\pi a{{d}_{f}}{{k}_{f}}{{\lambda }^{{\frac{5}{4}}}}\sqrt {{{\chi }_{f}}} {{K}_{1}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } a)}}\quad \left( {a < r < \infty } \right)$

Найдем производную $\frac{\partial }{{\partial t}}\left( {\Delta {{P}_{f}}\left( {t;r} \right)} \right)$ функции $\Delta {{P}_{f}}\left( {t;r} \right)$, используя формулу Меллина (формулу обратного преобразования Лапласа)

$\frac{\partial }{{\partial t}}\left( {\Delta {{P}_{f}}\left( {t;r} \right)} \right) = \frac{1}{{2\pi i}}\int\limits_{\gamma - \infty }^{\gamma + \infty } {\lambda \,\overline {{{P}_{f}}} (\lambda ;r){{e}^{{\lambda t}}}d\lambda } $

Тогда

(2.10)

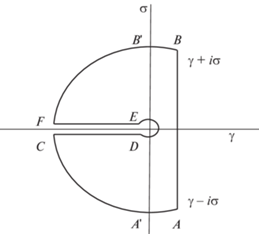
$\frac{\partial }{{\partial t}}\left( {\Delta {{P}_{f}}\left( {t;r} \right)} \right) = \frac{{q\mu }}{{4{{\pi }^{2}}ia{{d}_{f}}{{k}_{f}}\sqrt {{{\chi }_{f}}} }}\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\frac{{{{K}_{0}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } r)}}{{{{\lambda }^{{\frac{1}{4}}}}{{K}_{1}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } a)}}{{e}^{{\lambda t}}}d\lambda } $

где $\gamma $ – положительное вещественное число.

Подынтегральная функция в (2.10) аналитична при всех комплексных значениях переменной $\lambda $ за исключением нуля. Для вычисления этого интеграла воспользуемся контуром, изображенным на рис. 2. Согласно теореме Коши имеем

$\int\limits_{\gamma - i\sigma }^{\gamma + i\sigma } {\kern 1pt} = \int\limits_{AC} {\kern 1pt} + \int\limits_{CD} {\kern 1pt} + \int\limits_{DE} {\kern 1pt} + \int\limits_{EF} {\kern 1pt} + \int\limits_{FB} {\kern 1pt} $

Рис. 2.

Контур интегрирования.

Интегралы вдоль дуг $AC,\;FB$ при $R \to \infty $ стремятся к нулю. Интеграл по дуге $DE$ при $\xi \to 0$ тоже стремится к нулю. Интеграл по отрезку $CD$ равен

$\int\limits_{CD} {\frac{{{{K}_{0}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } r)}}{{{{\lambda }^{{\frac{1}{4}}}}{{K}_{1}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } a)}}{{e}^{{\lambda t}}}d\lambda = } \int\limits_\varepsilon ^{ + \infty } {\frac{{{{K}_{0}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{ - i\frac{\pi }{4}}}}r} \right){{e}^{{ - {{u}^{4}}t}}}4{{u}^{2}}du}}{{{{K}_{1}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{ - i\frac{\pi }{4}}}}a} \right){{e}^{{ - i\frac{\pi }{4}}}}}}} $

Интеграл по отрезку $EF$ равен

$\int\limits_{EF} {\frac{{{{K}_{0}}(\sqrt {{{\chi }_{f}}\sqrt \lambda } r)}}{{{{\lambda }^{{\frac{1}{4}}}}{{K}_{1}}({{\chi }_{f}}\sqrt {\sqrt \lambda } a)}}{{e}^{{\lambda t}}}d\lambda = - } \int\limits_\varepsilon ^{ + \infty } {\frac{{{{K}_{0}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{i\frac{\pi }{4}}}}r} \right){{e}^{{ - {{u}^{4}}t}}}4{{u}^{2}}du}}{{{{K}_{1}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{i\frac{\pi }{4}}}}a} \right){{e}^{{i\frac{\pi }{4}}}}}}} $

Следовательно, выражение для производной $\frac{\partial }{{\partial t}}\left( {\Delta {{P}_{f}}\left( {t;r} \right)} \right)$ можем записать в виде

(2.11)

$\frac{\partial }{{\partial t}}\left( {\Delta {{P}_{f}}\left( {t;r} \right)} \right) = \frac{{q\mu }}{{{{\pi }^{2}}ia{{d}_{f}}{{k}_{f}}\sqrt {{{\chi }_{f}}} }}\int\limits_0^{ + \infty } {\left( {\frac{{{{K}_{0}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{ - i\frac{\pi }{4}}}}r} \right)}}{{{{K}_{1}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{ - i\frac{\pi }{4}}}}a} \right){{e}^{{ - i\frac{\pi }{4}}}}}} - \frac{{{{K}_{0}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{i\frac{\pi }{4}}}}r} \right)}}{{{{K}_{1}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{i\frac{\pi }{4}}}}a} \right){{e}^{{i\frac{\pi }{4}}}}}}} \right){{e}^{{ - {{u}^{4}}t}}}{{u}^{2}}du} $

Интегрируя выражение для производной (2.11) по переменной $t$, находим искомую функцию $\Delta {{P}_{f}}\left( {r;t} \right)$

(2.12)

$\Delta {{P}_{f}}(t;r) = \frac{{q\mu }}{{{{\pi }^{2}}ia{{d}_{f}}{{k}_{f}}\sqrt {{{\chi }_{f}}} }}\int\limits_0^{ + \infty } {\frac{1}{{{{u}^{2}}}}\left( {\frac{{{{K}_{0}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{ - i\frac{\pi }{4}}}}r} \right)}}{{{{K}_{1}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{ - i\frac{\pi }{4}}}}a} \right){{e}^{{ - i\frac{\pi }{4}}}}}} - \frac{{{{K}_{0}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{i\frac{\pi }{4}}}}r} \right)}}{{{{K}_{1}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{i\frac{\pi }{4}}}}a} \right){{e}^{{i\frac{\pi }{4}}}}}}} \right)\left( {1 - {{e}^{{ - {{u}^{4}}t}}}} \right)du} $

Из решения (2.12), полагая $r = a$, получим закон изменения давления в скважине как

(2.13)

$\begin{gathered} {{P}_{{f(w)}}} = {{P}_{0}} + \Delta {{P}_{{f(w)}}} \\ \Delta {{P}_{{f(w)}}}(t) = \frac{{q\mu }}{{{{\pi }^{2}}ia{{d}_{f}}{{k}_{f}}\sqrt {{{\chi }_{f}}} }}\int\limits_0^{ + \infty } {\frac{1}{{{{u}^{2}}}}\left( {\frac{{{{K}_{0}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{ - i\frac{\pi }{4}}}}a} \right)}}{{{{K}_{1}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{ - i\frac{\pi }{4}}}}a} \right){{e}^{{ - i\frac{\pi }{4}}}}}} - \frac{{{{K}_{0}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{i\frac{\pi }{4}}}}a} \right)}}{{{{K}_{1}}\left( {\sqrt {{{\chi }_{f}}} u{{e}^{{i\frac{\pi }{4}}}}a} \right){{e}^{{i\frac{\pi }{4}}}}}}} \right)\left( {1 - {{e}^{{ - {{u}^{4}}t}}}} \right)du} \\ \end{gathered} $

Отметим, что полученные решения при граничных условиях ${{P}_{p}} = {{P}_{0}}$ при $y \to \infty $ и ${{P}_{f}} = {{P}_{0}}$ при $r \to \infty $ соответствуют начальному этапу функционирования скважины, когда влияние границы пласта, влияние фильтрационных полей соседних трещин (в случае системы радиальных трещин), а также радиальной границы трещины слабые.

3. ПРИБЛИЖЕННОЕ РЕШЕНИЕ МЕТОДОМ ПССС ЗАДАЧИ О ФИЛЬТРАЦИИ К СКВАЖИНЕ ЧЕРЕЗ ТРЕЩИНУ В РЕЖИМЕ ПОСТОЯННОГО РАСХОДА

Одним из наиболее широко использующихся приближенных методов решения задач теории упругого режима фильтрации является метод последовательной смены стационарных состояний (ПССС). Он основан на предположении, что давление в пласте меняется во времени значительно медленнее, чем по координатам [13].

Рассмотрим функционирование скважины в режиме постоянного расхода ($q = {\text{const}},$ $t > 0$), исходные состояния в пласте и в трещине примем, как в п. 2. Требуется определить эволюцию распределения давления в трещине $\Delta {{P}_{f}}$ и закон изменения давления в скважине $\Delta {{P}_{{f(w)}}}$ при граничном условии, аналогичном (2.3).

Согласно гипотезе, принятой в методе ПССС, для распределения давления в пластах вблизи трещины ГРП имеем

(3.1)

${{P}_{p}} = - \Delta {{P}_{f}}\frac{y}{{{{l}_{p}}}} + {{P}_{f}},\quad {{l}_{p}} = \sqrt {2{{\unicode{230} }_{p}}t} \quad \left( {0 < y < {{l}_{p}}} \right)$

Из этого выражения следует

(3.2)

$\frac{{\partial {{P}_{p}}}}{{\partial y}} = - \Delta {{P}_{f}}\frac{1}{{\sqrt {2{{\unicode{230} }_{p}}t} }}.$

Подставляя (3.2) в (1.5) и учитывая вышеизложенное допущение относительно левой части этого уравнения, получим

(3.3)

$\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial \Delta {{P}_{f}}}}{{\partial r}}} \right) - \frac{{{{\chi }_{f}}}}{{\sqrt {2t} }}\Delta {{P}_{f}} = 0$

Общее решение уравнения (3.3) имеет вид

(3.4)

$\Delta {{P}_{f}}\left( {t;r} \right) = {{C}_{1}}{{I}_{0}}(r\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } ) + {{C}_{2}}{{K}_{0}}(r\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )$

Учитывая ограниченность $\Delta {{P}_{f}}$ на бесконечности, из (3.4) получим

(3.5)

$\Delta {{P}_{f}}\left( {t;r} \right) = {{C}_{2}}{{K}_{0}}(r\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )$

Продифференцируем выражение (3.5) по переменной $r$

$\frac{{\partial \Delta {{P}_{f}}(t;r)}}{{\partial r}} = {{C}_{2}}K_{0}^{'}(r\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } $

Учитывая условие (2.4), при $r = a$ получим

${{C}_{2}} = - \frac{{q\mu }}{{{{d}_{f}}{{k}_{f}}}}\sqrt {\frac{{\sqrt {2t} }}{{{{\chi }_{f}}}}} \frac{1}{{{{K}_{1}}(a\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )}}$

Тогда общее решение запишется как

(3.6)

$\Delta {{P}_{f}}\left( {t;r} \right) = - \frac{{q\mu }}{{2\pi a{{d}_{f}}{{k}_{f}}}}\sqrt {\frac{{\sqrt {2t} }}{{{{\chi }_{f}}}}} \frac{{{{K}_{0}}(r\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )}}{{{{K}_{1}}(a\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )}}$

Отсюда, для закона изменения давления в скважине $\left( {r = a} \right)$ имеем

(3.7)

$\Delta {{P}_{{f(w)}}}\left( t \right) = - \frac{{q\mu }}{{2\pi a{{d}_{f}}{{k}_{f}}}}\sqrt {\frac{{\sqrt {2t} }}{{{{\chi }_{f}}}}} \frac{{{{K}_{0}}(a\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )}}{{{{K}_{1}}(a\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )}}$

Проведем анализ решения (3.7) для больших времен, когда $\xi _{*}^{{}} = 1$ $(\xi _{*}^{{}} = a\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )$. Из этого условия получим следующее неравенство для времени

${{t}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}} \gg t_{*}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}},\quad t_{*}^{{}} = \chi _{f}^{2}{{a}^{4}}$

Примем некоторые типичные характерные величины для системы “скважина, пласт и радиальная трещина ГРП”: ${{m}_{p}} = {{m}_{f}} = {{10}^{{ - 1}}},$ ${{k}_{p}} = {{10}^{{ - 15}}}$ м², ${{k}_{f}} = {{10}^{{ - 10}}}$ м², ${{\rho }_{0}} = 860$ кг/м³, $\mu = {{10}^{{ - 2}}}$ Па ⋅ с, $а = {{10}^{{ - 1}}}$ м, ${{d}_{f}} = 3 \times {{10}^{{ - 3}}}$ м. Тогда, согласно выражению для ${{\chi }_{f}}$ из (2.5), имеем следующую оценку ${{\chi }_{f}} \approx 0.15\;\sqrt {\text{c}} {\text{/}}{{{\text{м}}}^{2}}$ и для вышеприведенных характерных величин рассматриваемой системы получим $t_{*}^{{}} = 2.25 \times {{10}^{{ - 6}}}$ c. Следовательно, в рассматриваемой задаче всегда $t \gg t_{*}^{{}}$, и поэтому можно считать $\xi \ll 1$. Для функций ${{K}_{0}}\left( \xi \right)$ и ${{K}_{1}}\left( \xi \right)$ справедливы при малых значениях параметра $\xi $ асимптотики [10]

(3.8)

${{K}_{0}}\left( \xi \right) = - \left( {\gamma + \ln \left( {\frac{\xi }{2}} \right)} \right)\quad {\text{и}}\quad {{K}_{1}}\left( \xi \right) = {{\xi }^{{ - 1}}}$

Здесь $\gamma = 0.5772$ – постоянная Эйлера. Подставляя (3.8) в (3.7), находим

(3.9)

$\Delta {{P}_{{f\left( w \right)}}}\left( t \right) = \frac{{q\mu }}{{2\pi {{k}_{f}}{{d}_{f}}}}\left( {\gamma + \ln \left( {\frac{1}{2}a\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } } \right)} \right) \approx \frac{{q\mu }}{{2\pi {{k}_{f}}{{d}_{f}}}}\ln (0.75a\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )$

Полученное выражение может быть использовано при гидродинамическом исследовании скважины, подверженной ГРП. Действительно, из (3.9) следует

(3.10)

$\Delta {{P}_{{f\left( w \right)}}} = \frac{{q\mu }}{{2\pi {{k}_{f}}{{d}_{f}}}}\left( {\ln \left( {0,75\sqrt {{{\chi }_{f}}} \,a} \right) - \frac{1}{4}\ln t} \right)$

Это асимптотическое решение можно, в свою очередь, записать как

(3.11)

$\Delta {{P}_{{f\left( w \right)}}} = B - A\ln t,\quad A = \frac{{q\mu }}{{8\pi {{k}_{f}}{{d}_{f}}}},\quad B = 4A\ln \left( {0.75\sqrt {{{\chi }_{f}}} a} \right)$

Выражение (3.11) в координатной плоскости ($\ln t,\Delta {{P}_{{f(w)}}}$) является уравнением прямой. Причем, как показывают вышеприведенные численные оценки для $t_{*}^{{}}$, при отборе жидкости с постоянным расходом q, функционирование скважины почти мгновенно должно выйти на этот асимптотический режим. Поэтому, обрабатывая промысловые данные в координатах (lnt, $\Delta {{P}_{{f(w)}}}$), можем определить $A$ и $B$, и тем самым найти проводимость трещины ${{k}_{f}}{{d}_{t}}$ и величину ${{\chi }_{f}}$. Этот метод аналогичен способу, изложенному в [13], по определению проводимости пласта по кривым восстановления давления при больших временах.

Отметим, что формулы (3.10) и (3.11) можно записать для системы из $n$ радиальных трещин. Если считать, что параметры всех трещин близки, то для этого в этих формулах надо q заменить на nq.

Используя выражение для ${{K}_{1}}\left( \xi \right)$, решение (3.6) можно записать как

(3.12)

$\Delta {{P}_{f}} = \frac{{q\mu }}{{2\pi {{k}_{f}}{{d}_{f}}}}{{K}_{0}}(r\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } )$

Следовательно, для распределения давления в трещине ГРП имеет место автомодельное решение. Отсюда, если перепад давления $\Delta {{P}_{f}}$ принять за постоянное фиксированное значение, то величины $r$ и $t$ связаны следующим законом

$r = \xi \sqrt {{{\sqrt {2t} } \mathord{\left/ {\vphantom {{\sqrt {2t} } {{{\chi }_{f}}}}} \right. \kern-0em} {{{\chi }_{f}}}}} \quad \left( {\xi = {\text{const}}} \right)$

Таким образом, фиксированное значение давления в трещине для рассматриваемого режима фильтрации распространяется по закону $r \sim {{t}^{{1/4}}}$.

Как отмечено в п. 1, приведенные выше точные и приближенные решения получены при допущении, что линии тока в пласте прямые, перпендикулярные к границам (“берегам”) трещины ГРП. Определим зоны в плоскости (r, t) (радиальная координата – время), где выполняется принятое допущение с некоторой точностью. Для радиальной ${{{v}}_{{p\left( r \right)}}}$ и нормальной ${{{v}}_{{p\left( n \right)}}}$ составляющих скоростей фильтрации в пласте вблизи стенок трещины можем записать

${{{v}}_{{p\left( r \right)}}} = - \frac{{{{k}_{p}}}}{\mu }\frac{{\partial {{P}_{p}}}}{{\partial y}}\quad {\text{и}}\quad {{{v}}_{{p\left( n \right)}}} = - \frac{{{{k}_{p}}}}{\mu }\frac{{\partial {{P}_{f}}}}{{\partial r}}$

поскольку вблизи стенки трещины имеет место

$\frac{{\partial {{P}_{p}}}}{{\partial r}} = \frac{{\partial {{P}_{f}}}}{{\partial r}}$

Тогда, используя решения (3.1) для P_p и (3.12) для P_f, для отношения величин радиальной и нормальной составляющих скоростей фильтрации будем иметь

(3.13)

$\frac{{\left| {{{{v}}_{{p\left( r \right)}}}} \right|}}{{\left| {{{{v}}_{{p\left( n \right)}}}} \right|}} = \sqrt {{{\chi }_{f}}{{\unicode{230} }_{p}}\sqrt {2t} } \left| {\frac{{{{K}_{1}}\left( {r\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } } \right)}}{{{{K}_{0}}\left( {r\sqrt {{{\chi }_{f}}{\text{/}}\sqrt {2t} } } \right)}}} \right| = \varepsilon $

Отсюда следует, для того чтобы линии тока для скоростей фильтрации приближались к трещинам ГРП под углом, близким к прямому углу, должно выполняться условие $\varepsilon \ll 1$.

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Для параметров, определяющих свойства и состояния пористого пласта, флюида и трещины, приняты величины ${{m}_{p}} = {{m}_{f}} = {{10}^{{ - 1}}},$ ${{k}_{f}} = {{10}^{{ - 10}}}$ м², ${{\rho }_{0}} = 860$ кг/м³, $C = 1.5 \times {{10}^{3}}$ м/с, $\mu = {{10}^{{ - 2}}}$ Па ⋅ с, $а = {{10}^{{ - 1}}}$ м, ${{d}_{f}} = 3 \times {{10}^{{ - 3}}}$ м, ${{P}_{0}} = 10$ МПа. Для величины расхода принято значение $q = 5 \times {{10}^{{ - 5}}}$ м³/с.

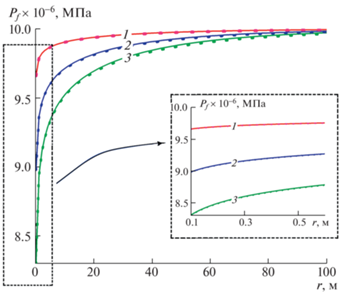
На рис. 3 показано распределение давления в трещине при различных значениях коэффициента проницаемости пласта для фиксированного момента времени. На этом и в следующих рисунках сплошными и точечными линиями изображены графики, построенные по точным и приближенным решениям соответственно. Кроме того, на рисунках представлены фрагменты графиков вблизи призабойного участка в увеличенных масштабах.

Рис. 3.

Распределение давления в трещине в момент времени $t = {{10}^{5}}$ c для различных значений коэффициента проницаемости пласта: 1–3 – $k_{p}^{{}} = {{10}^{{ - 16}}},$ ${{10}^{{ - 15}}},$ ${{10}^{{ - 14}}}$ м². Сплошные линии соответствуют точным аналитическим решениям, точечные – приближенным.

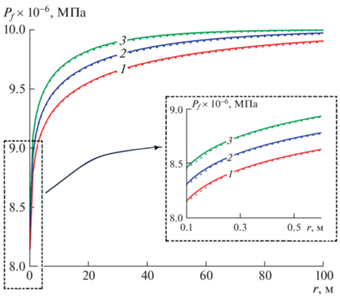
Из характера кривых распределения давления следует, что уменьшение коэффициента проницаемости пласта на один порядок (в десять раз) приводит примерно к двукратному росту перепада давления $\Delta {{P}_{f}}$ между пластовым значением ${{P}_{0}}$ (${{P}_{p}} = {{P}_{0}}$, $y \to \infty $) и значением в трещине. Следует также отметить, что в случае более низкопроницаемых пластов давление трещине ГРП приближается к пластовому значению медленнее с ростом радиальной координаты $r$. Так, если в случае более низкопроницаемого пласта (${{k}_{p}} = {{10}^{{ - 16}}}$ м²) расстояние от скважины, на котором перепад давления $\Delta {{P}_{f}} = {{P}_{f}} - {{P}_{0}} \approx 0.25$ МПа, составляет около 60 м, то при проницаемости ${{k}_{p}} = {{10}^{{ - 14}}}$ м² такое значение перепада наблюдается при гораздо более близком к скважине расстоянии (примерно на 20 м).

На рис. 4 изображены графики, иллюстрирующие эволюцию давления в трещине для различных моментов времени. Здесь также видно, что точные и приближенные решения практически совпадают.

Рис. 4.

Эволюция давления в трещине для различных моментов времени: 1–3 – $t = {{10}^{4}}{\text{,}}$ 10⁵, 10⁶ c при ${{k}_{p}} = {{10}^{{ - 15}}}$ м².

На рис. 5 представлены графики для распределения давления в трещине для различных значений дебита.

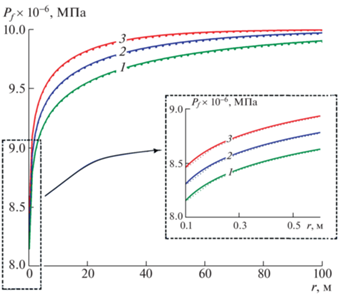
Рис. 5.

Распределение давления в трещине для различных значений дебита: 1–3 – $q = {{10}^{{ - 5}}},$ $3 \times {{10}^{{ - 5}}},$ $5 \times {{10}^{{ - 5}}}$ м³/c при ${{k}_{p}} = {{10}^{{ - 15}}}$ м² в момент времени $t = {{10}^{5}}$ c.

На рис. 6 показаны законы снижения давления в скважине для различных значений коэффициента проницаемости пласта (a) и проводимости трещины ${{C}_{f}} = {{k}_{f}}{{d}_{f}}$ (б). Для времени принята логарифмическая шкала. Сплошные линии получены на основе общего решения (2.13), точечные линии построены согласно решению (3.9).

Рис. 6.

Динамика снижения давления в скважине при дебите $q = 5 \times {{10}^{{ - 5}}}$ м³/c для (а) различных значений коэффициента проницаемости пласта и (б) для различных значений проводимости трещины при проницаемости пласта ${{k}_{p}} = {{10}^{{ - 15}}}$ м²: 1–3 – $k_{p}^{{}} = {{10}^{{ - 16}}},$ ${{10}^{{ - 15}}},$ ${{10}^{{ - 14}}}$ м²; 4–6 – ${{C}_{f}} = {{10}^{{ - 13}}},$ 10^–12, 10^–11 м³.

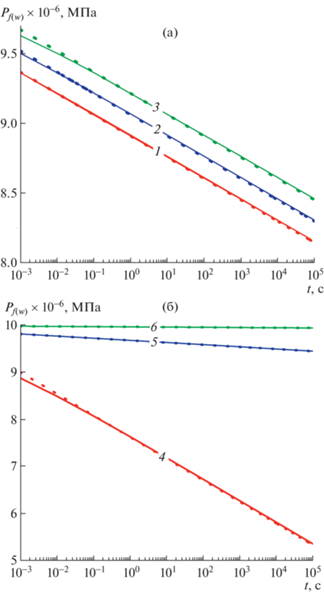
Таким образом, из представленных результатов расчетов также видно, что решения, полученные с использованием метода ПССС, практически совпадают с точными аналитическими решениями.

На рис. 7 зона, расположенная ниже линии 1, определяемой уравнением (3.13) при $\varepsilon = 1$, соответствует множеству значений (r, t), для которых в пласте величина нормальной скорости фильтрации ${{{v}}_{{p\left( n \right)}}}$ больше величины радиальной скорости ${{{v}}_{{p\left( r \right)}}}$. Зона, расположенная ниже линии 2, определяемой тем же уравнением при $\varepsilon = 0.1$, соответствует области переменных (r, t), где величина нормальной скорости фильтрации ${{{v}}_{{p\left( n \right)}}}$ в 10 раз больше величины радиальной скорости ${{{v}}_{{p\left( r \right)}}}$. Для параметров скважины, пласта и трещины ГРП приняты вышеприведенные значения.

Рис. 7.

Зоны фильтрации на плоскости : 1–2 – значения = 1, 0.1 в (3.13). В зоне, расположенной ниже линии 1, нормальная скорость больше радиальной скорости фильтрации, а в зоне, ниже линии 2, нормальная скорость превышает радиальную скорость фильтрации в пласте вблизи стенки трещины ГРП более чем в 10 раз.

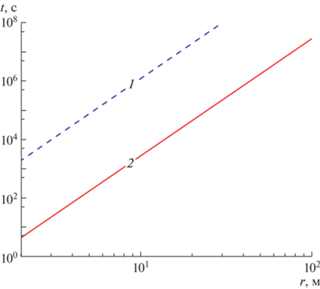
Отметим, что в представленных картинах зона (r, t), где радиальная скорость фильтрации меньше, чем нормальная скорость, несколько занижена, поскольку в приведенных оценках не учтено торможение радиальной скорости фильтрации вблизи обсаженной скважины. Кроме того, как нам представляется, в плане определения расхода флюида из пласта в трещину, некоторое отклонение линий тока от прямых, перпендикулярных по отношению к трещине ГРП, несущественно.

ЗАКЛЮЧЕНИЕ

Полученные точные и приближенные решения, описывающие эволюцию давления в трещине ГРП и, в том числе, на забое скважины при задании постоянного значения расхода флюида, позволяют определять параметры трещины ГРП по кривым изменения давления в призабойной зоне, сопоставляя их с промысловыми данными, получаемыми на скважине при прочих известных значениях параметров пласта и флюида. Показано хорошее согласование результатов, полученных с помощью метода последовательной смены стационарных состояний (ПССС) с точными, но значительно более сложными решениями. Это обстоятельство может быть полезным при разработке численных алгоритмов, учитывающих в наиболее полном объеме особенности реальных систем “скважина–пласт, подверженный ГРП”, такие как многомерные эффекты, реальные условия на границах пласта и трещины ГРП, а также переходные режимы функционирования скважин.

Предложен метод оценки неизвестных значений коллекторских характеристик призабойной зоны (например, величины проводимости трещины) на основе сравнения дебита скважины и давления в забое с точными теоретическими решениями.

Исследование выполнено за счет гранта Российского научного фонда № 21-11-00207, https://rscf.ru/project/21-11-00207/.

Список литературы

Prats M. Effect of vertical fractures on reservoir behavior – incompressible fluid case // Soc. Petrol. Eng. Journal. 1961. V. 1. № 2. P. 105–118.
Prats M., Hazebroek P., Strickler W.R. Effect of vertical fractures on reservoir behavior – compressible fluid case // Soc. Petrol. Eng. Journal. 1962. V. 2. № 2. P. 87–94.
Каневская Р.Д., Дияшев И.Р., Некипелов Ю.В. Применение гидравлического разрыва пласта для интенсификации добычи и повышения нефтеотдачи // Нефтяное хозяйство. 2002. № 5. С. 96–101.
Астафьев В.И., Федорченко Г.Д. Моделирование фильтрации жидкости при наличии трещины гидравлического разрыва пласта // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2007. № 2 (15). С. 128–132.
Экономидес М., Олини Р., Валько П. Унифицированный дизайн гидроразрыва пласта: от теории к практике. Москва-Ижевск: Институт компьютерных технологий, 2007. 237 с.
Cinco-Ley H., Samaniego V.F., Dominguez A.N. Transient pressure behavior for a well with a finite-conductivity vertical fracture // Soc. Pet. Eng. J. 1978. V. 18. № 4. P. 253–264.
Шагапов В.Ш., Нагаева З.М. К теории фильтрационных волн давления в трещине, находящейся в пористой проницаемой среде // ПМТФ. 2017. Т. 58. № 5 (345). С. 121–130.
Нагаева З.М., Шагапов В.Ш. Об упругом режиме фильтрации в трещине, расположенной в нефтяном или газовом пласте // ПММ. 2017. Т. 81. № 3. С. 319–329.
Хабибуллин И.Л., Хисамов А.А. Нестационарная фильтрация в пласте с трещиной гидроразрыва // Изв. РАН. МЖГ. 2019. № 5. С. 6–14.
Тихонов А.Н., Самарский А.Н. Уравнения математической физики. М.: Наука, 1972. 736 с.
Диткин В.А., Прудников А.П. Операционное исчисление. 2-е изд., доп. М.: Высшая школа, 1975. 408 с.
Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001. 576 с.
Баренблатт Г.И., Ентов В.М., Рыжик В.М. Теория нестационарной фильтрации жидкости и газа. М.: Недра, 1972. 288 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал