Известия РАН. Механика жидкости и газа, 2023, № 2, стр. 85-89

ОБ ОБТЕКАНИИ ПОЛУТЕЛА ВРАЩЕНИЯ РЭНКИНА

Г. Л. Королев^a, *, Вик. В. Сычёв^a

^a Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Жуковский, Россия

Поступила в редакцию 20.08.2022
После доработки 10.10.2022
Принята к публикации 11.10.2022

EDN: NSYFUF
DOI: 10.31857/S0568528122600576

Аннотация

Исследовано осесимметричное течение несжимаемой жидкости при больших числах Рейнольдса около полутела вращения Рэнкина. Установлено, что в решении задачи для системы уравнений пограничного слоя линии нулевого поверхностного трения не возникает. Рассмотренное течение является безотрывным, что находится в полном соответствии с имеющимся экспериментальным результатом.

Ключевые слова: решение Рэнкина, пограничный слой, отрыв

При рассмотрении обтекания тонкого тела вращения при больших числах Рейнольдса $\operatorname{Re} \to \infty $ течение в масштабах последнего описывается решением краевой задачи теории малых возмущений (см. [1, 2]). Оно становится несправедливым вблизи передней точки торможения [3, 4]. В настоящей работе изучено осесимметричное течение в пограничном слое, который развивается в малой окрестности этой точки для сильно затупленного тела.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим осесимметричное установившееся течение несжимаемой жидкости около тонкого тела вращения, установленного под нулевым углом атаки к однородному набегающему потоку.

Введем следующие обозначения: $\ell x\,,\,$ $\ell r\,,\,$ − оси цилиндрической системы координат; ${{u}_{\infty }}u$, ${{u}_{\infty }}\upsilon $ − соответствующие проекции вектора скорости; ${{p}_{\infty }} + \rho {\kern 1pt} *u_{\infty }^{2}p$ − давление; ${{\ell }^{2}}{{u}_{\infty }}\psi $ − функция тока; $\operatorname{Re} = {{u}_{\infty }}\ell {\text{/}}\nu {\kern 1pt} *$ − число Рейнольдса. Здесь $\ell $ − продольный размер тела; ${{u}_{\infty }}$ и ${{p}_{\infty }}$ − абсолютная величина вектора скорости и значение давления в набегающем потоке, направленном вдоль оси Ox; $\rho {\kern 1pt} *$ − плотность, $\nu {\kern 1pt} *$ − кинематический коэффициент вязкости. Поместим начало системы координат на оси симметрии в малой окрестности передней критической точки.

Пусть $r = \tau f(x)$, $0 < x < 1$ и $f(x)$ – гладкая функция, определяющая форму поверхности тела в меридиональной плоскости. При этом $\tau $ − малый параметр: $\tau = \tau (\operatorname{Re} ) \to 0$ при $\operatorname{Re} \to \infty $. Предположим, что носовая часть тела имеет степенную форму

(1.1)

$f(x) = {{a}_{0}}{{x}^{\alpha }} + o({{x}^{\alpha }})$

при $x \to + 0$, ${{a}_{0}} > 0$, $0 \leqslant \alpha < 1$. Согласно результатам теории малых возмущений, как для плоских [3–5], так и осесимметричных течений [1], асимптотические разложения решений теряют свою равномерную пригодность при $x = O({{\tau }^{\lambda }})$, $r = O({{\tau }^{\lambda }})$, $\lambda = {{(1 - \alpha )}^{{ - 1}}}$. Изменения скорости и давления здесь суть величины порядка единицы. Тогда асимптотическое представление решения в этой области имеет вид

(1.2)

$\begin{gathered} X = {{\tau }^{{ - \lambda }}}x = O(1),\quad R = {{\tau }^{{ - \lambda }}}r = O(1) \\ (u,\upsilon ,p) = (U,V,P) + o(1) \\ \end{gathered} $

Рассмотрим течение для предельного случая, когда в (1.1) значение α = 0.

Подстановка (1.2) в систему уравнений Навье–Стокса при условии, что локальное число Рейнольдса ${\text{Re*}} = {{\tau }^{\lambda }}\,\operatorname{Re} \, \to \infty $ при $\operatorname{Re} \, \to \,\,\infty $ $(\lambda \,\, = \,\,1)$, приводит к уравнению для потенциального течения идеальной жидкости

(1.3)

$\frac{{{{\partial }^{2}}\Phi }}{{\partial {{X}^{2}}}} + \frac{{{{\partial }^{2}}\Phi }}{{\partial {{R}^{2}}}} + \frac{1}{R}\frac{{\partial \Phi }}{{\partial R}} = 0,\quad U = \frac{{\partial \Phi }}{{\partial X}} = \frac{1}{R}\frac{{\partial \Psi }}{{\partial R}},\quad V = \frac{{\partial \Phi }}{{\partial R}} = - \frac{1}{R}\frac{{\partial \Psi }}{{\partial X}}$

где $\Psi (X,R)$ и $\Phi (X,R)$ – функция тока и потенциал течения в рассматриваемой области. Пусть последнее описывается здесь решением Рэнкина [6], которое есть сумма потенциалов однородного потока и источника, помещенного (для простоты) в точку $X = R = 0$

(1.4)

$\begin{gathered} \Phi = X - \frac{{{{Q}_{0}}}}{{4\pi \rho }},\quad U = 1 + \frac{{{{Q}_{0}}X}}{{4\pi {{\rho }^{3}}}} \\ \Psi = \frac{{{{R}^{2}}}}{2} - \frac{{{{Q}_{0}}X}}{{4\pi \rho }},\quad \rho = {{({{X}^{2}} + {{R}^{2}})}^{{1/2}}} \\ \end{gathered} $

где ${{Q}_{0}}$ − обильность источника. Нетрудно видеть, что на оси симметрии находится точка торможения

(1.5)

$U(X,0) = 1 + \frac{{{{Q}_{0}}X}}{{4\pi {{{\left| X \right|}}^{3}}}} = 0,\quad X = {{X}_{0}} = - {{\left( {\frac{{{{Q}_{0}}}}{{4\pi }}} \right)}^{{1/2}}}$

Тогда поверхность тока, проходящая через эту точку, согласно (1.4), (1.5), есть

(1.6)

$\Psi = \frac{{{{R}^{2}}}}{2} - \frac{{{{Q}_{0}}X}}{{4\pi \rho }} = \frac{{{{Q}_{0}}}}{{4\pi }}$

Введем сферические координаты $\rho ,\;\theta $

(1.7)

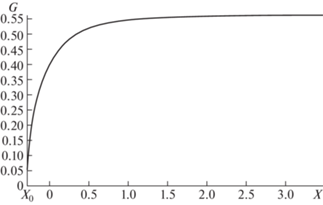
$\rho = {{({{X}^{2}} + {{R}^{2}})}^{{1/2}}},\quad \theta = {\text{arctg}}\left( {\frac{R}{X}} \right)$

Приняв (1.6) за поверхность обтекаемого тела и введя для нее обозначение $R = G(X)$, имеем

(1.8)

${{G}^{2}} = \frac{{{{Q}_{0}}}}{{2\pi }}\left( {\frac{X}{{{{{({{X}^{2}} + {{G}^{2}})}}^{{1/2}}}}} + 1} \right)$

или, используя (1.6), (1.7), запишем соответствующие уравнения в параметрической форме

(1.9)

$\begin{gathered} X = {{x}_{0}}(t) = - {{r}_{0}}(t){\text{ctg}}t,\quad t = \pi - \theta ,\quad 0 \leqslant t < \pi \\ R = {{r}_{0}}(t) = {{\left( {\frac{{{{Q}_{0}}}}{{2\pi }}} \right)}^{{1/2}}}{{(1 - \cos t)}^{{1/2}}} \\ \end{gathered} $

Наконец, из (1.3), (1.4), (1.6)−(1.9) следует (см. [7]), что скорость ${{U}_{s}}(t)$ вдоль поверхности тока $\Psi = {{Q}_{0}}{\text{/}}4\pi $ есть

(1.10)

${{U}_{s}} = {{\left( {\frac{1}{2}(1 - \cos t) + \frac{3}{4}{{{\sin }}^{2}}t} \right)}^{{1/2}}}$

При $X \to \infty $, согласно (1.8), (1.9), $G \to {{({{Q}_{0}}{\text{/}}\pi )}^{{1/2}}}$, т.е. ${{a}_{0}} = {{({{Q}_{0}}{\text{/}}\pi )}^{{1/2}}}$ (см. (1.1)

Замена $X = {{Q}_{0}}^{{1/2}}{{X}^{0}}$, $R = {{Q}_{0}}^{{1/2}}{{R}^{0}}$, $\Phi = {{Q}_{0}}^{{1/2}}{{\Phi }^{0}}$, $\Psi = {{Q}_{0}}{{\Psi }^{0}}$ в (1.4) исключает постоянную Q₀. Вариация этого параметра приводит лишь к изменению масштаба течения в целом. Поэтому, не ограничивая общности, будем полагать ${{Q}_{0}} = 1$.

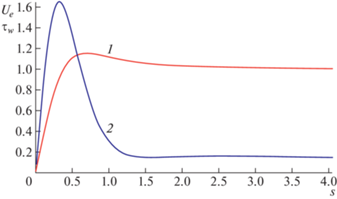
График функции $G(X)$ (см. [6]) дан на рис. 1. На рис. 2 представлена функция ${{U}_{e}}(s) = {{U}_{s}}(t)$ из (1.10), где s − длина дуги, отсчитываемая от точки торможения вдоль поверхности тела в меридиональной плоскости

(1.11)

$s(t) = \int\limits_0^t {(x_{0}^{{'2}}} + r_{0}^{{'2}}{{)}^{{1/2}}}d{{t}^{0}}$

Рис. 1.

Контур полутела Рэнкина в меридиональной плоскости.

Рис. 2.

Касательная составляющая вектора скорости ${{U}_{e}}\,(s)$ (1) и распределение трения ${{\tau }_{w}}\,(s)$ (2) вдоль поверхности тела.

2. РЕШЕНИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ПОГРАНИЧНОГО СЛОЯ

Для удовлетворения условию прилипания на поверхности тела в области, где $x = O(\tau )$, $r = O(\tau )$, введем пограничный слой. Пусть s, n ортогональная криволинейная система координат, связанная здесь с поверхностью тока $\Psi = {{Q}_{0}}{\text{/}}4\pi $, $\Psi = {{\tau }^{{ - 2}}}\psi $. Для пограничного слоя, как обычно [8]

(2.1)

$\begin{gathered} s = O(1),\quad n = {\text{Re}}{\kern 1pt} {{*}^{{ - 1/2}}}N,\quad \Psi = \frac{{{{Q}_{0}}}}{{4\pi }} + {\text{Re}}{\kern 1pt} {{*}^{{ - 1/2}}}{{\Psi }_{0}}(s,N) + o({\text{Re}}{\kern 1pt} {{*}^{{ - 1/2}}}) \\ {{U}_{0}}\frac{{\partial {{U}_{0}}}}{{\partial s}} + {{V}_{0}}\frac{{\partial {{U}_{0}}}}{{\partial N}} - {{U}_{e}}\frac{{d{{U}_{e}}}}{{ds}} = \frac{{{{\partial }^{2}}{{U}_{0}}}}{{\partial {{N}^{2}}}} \\ {{R}_{0}}{{U}_{0}} = \frac{{\partial {{\Psi }_{0}}}}{{\partial N}},\quad {{R}_{0}}{{V}_{0}} = - \frac{{\partial {{\Psi }_{0}}}}{{\partial s}} \\ \end{gathered} $

где ${{R}_{0}}\,(s)\,\, = \,\,G\,(X)$ − расстояние точки на поверхности тела от оси симметрии.

Преобразование Степанова–Манглера

(2.2)

$\xi = \int\limits_0^s {R_{0}^{2}} d{{s}^{0}},\quad \eta = {{R}_{0}}N,\quad {{\Psi }_{0}} = {{\psi }_{0}}(\xi ,\eta ),\quad {{U}_{e}} = {{u}_{e}}(\xi )$

приводит (2.1) к виду, соответствующему плоскому течению

(2.3)

$\begin{gathered} \frac{{\partial {{\psi }_{0}}}}{{\partial \eta }}\frac{{{{\partial }^{2}}{{\psi }_{0}}}}{{\partial \xi \partial \eta }} - \frac{{\partial {{\psi }_{0}}}}{{\partial \xi }}\frac{{{{\partial }^{2}}{{\psi }_{0}}}}{{\partial {{\eta }^{2}}}} - {{u}_{e}}\frac{{d{{u}_{e}}}}{{d\xi }} = \frac{{{{\partial }^{3}}{{\psi }_{0}}}}{{\partial {{\eta }^{3}}}} \\ \eta = 0{\text{:}}\;\;{{\psi }_{0}} = \frac{{\partial {{\psi }_{0}}}}{{\partial \eta }} = 0,\quad \eta \to \infty {\text{:}}\;\;\frac{{\partial {{\psi }_{0}}}}{{\partial \eta }} \to {{u}_{e}}(\xi ) \\ \end{gathered} $

Здесь также приведены краевые условия прилипания на поверхности и сращивания с решением в области, где $X = O(1)$, $R = O(1)$.

Рассмотрим решение вблизи точки торможения $s = n = 0$. Согласно (1.9)–(1.11), при $s \to 0{\text{:}}$ ${{R}_{0}} = s + O({{s}^{3}})$, ${{U}_{e}} = {{q}_{0}}s + O({{s}^{3}})$, ${{q}_{0}} = 2{{(\pi {\text{/}}{{Q}_{0}})}^{{1/2}}}$. Тогда течение в пограничном слое при s → 0 описывается известным решением Хомана [9]. Это решение в переменных ξ, η имеет вид

(2.4)

$\begin{gathered} {{u}_{e}} = {{q}_{0}}{{(3\xi )}^{{1/3}}} + O(\xi ),\quad {{\psi }_{0}} = {{({{3}^{{4/3}}}{{q}_{0}}{\text{/}}2)}^{{1/2}}}{{\xi }^{{2/3}}}h(\zeta ) + O({{\xi }^{{5/3}}}) \\ \zeta = {{(2 \cdot {{3}^{{ - 2/3}}}{{q}_{0}})}^{{1/2}}}\eta {\text{/}}{{\xi }^{{1/3}}},\quad \xi \to 0 \\ h{\kern 1pt} '{\kern 1pt} '{\kern 1pt} '\; + hh{\kern 1pt} '{\kern 1pt} '\; + \frac{1}{2}(1 - {{h}^{{'2}}}) = 0,\quad h(0) = h{\kern 1pt} '(0) = 0,\quad h{\kern 1pt} '(\infty ) = 1 \\ \end{gathered} $

Решение задачи для уравнения в (2.4), относящегося к типу Фолкнера-Скан, дано в [9] (см. также [8]).

Заметим, что при $s = O({\text{Re}}{\kern 1pt} {{*}^{{ - 1/2}}})$, $n = O({\text{Re}}{\kern 1pt} {{*}^{{ - 1/2}}})$ течение описывается точным решением [9] системы уравнений Навье–Стокса.

Численное решение задачи (2.3), (2.4) было получено после следующего представления

(2.5)

$\begin{gathered} \mu = {{\xi }^{{1/3}}},\quad \nu = {{(2{{q}_{0}})}^{{1/2}}}{{(3\xi )}^{{ - 1/3}}}{{Q}_{e}}^{{1/2}}(\mu )\eta \\ {{u}_{e}} = {{q}_{0}}{{(3\xi )}^{{1/3}}}{{Q}_{e}}(\mu ),\quad {{\psi }_{0}} = {{\left( {\frac{{{{q}_{0}}}}{2}} \right)}^{{1/2}}}{{(3\xi )}^{{2/3}}}{{Q}_{e}}^{{1/2}}(\mu )F(\mu ,\nu ) \\ \end{gathered} $

которое учитывает особое поведение в (2.4) и, в силу регулярности $F(\mu ,\nu )$ при $\mu \to 0$, позволяет проводить расчет от сечения $\mu = 0$. В результате внесения (2.5) в (2.3), (2.4) приходим к задаче

$\begin{gathered} \frac{\mu }{2}\left( {\frac{{\partial F}}{{\partial \nu }}\frac{{{{\partial }^{2}}F}}{{\partial \mu \partial \nu }} - \frac{{\partial F}}{{\partial \mu }}\frac{{{{\partial }^{2}}F}}{{\partial {{\nu }^{2}}}}} \right) - \frac{\mu }{4}\frac{{Q_{e}^{'}}}{{{{Q}_{e}}}}\left( {F\frac{{{{\partial }^{2}}F}}{{\partial {{\nu }^{2}}}} - 2{{{\left( {\frac{{\partial F}}{{\partial \nu }}} \right)}}^{2}} + 2} \right) + \frac{1}{2}\left( {{{{\left( {\frac{{\partial F}}{{\partial \nu }}} \right)}}^{2}} - 1} \right) - F\frac{{{{\partial }^{2}}F}}{{\partial {{\nu }^{2}}}} = \frac{{{{\partial }^{3}}F}}{{\partial {{\nu }^{3}}}} \\ \nu = 0{\text{:}}\;\;F = \frac{{\partial F}}{{\partial \nu }} = 0,\quad \nu \to \infty {\text{:}}\;\;\frac{{\partial F}}{{\partial \nu }} \to 1,\quad F(0,\nu ) = h(\nu ) \\ \end{gathered} $

На рис. 2 представлен график функции

${{\tau }_{w}}(s) = {{\left. {\frac{{\partial {{U}_{0}}}}{{\partial N}}} \right|}_{{N = 0}}} = {{(2{{q}_{0}}^{3})}^{{1/2}}}{{R}_{0}}(s){{Q}_{e}}^{{3/2}}{{\left. {\frac{{{{\partial }^{2}}F}}{{\partial {{\nu }^{2}}}}} \right|}_{{\nu = 0}}}$

которая определяет поверхностное трение согласно (2.1), (2.2), (2.5). Оказалось, что, как и в случае плоского течения около полутела Рэнкина [10], ${{\tau }_{w}}(s)$ всюду положительна, несмотря на существование интервала s, где градиент давления неблагоприятен. Точки $s$ = 1.526 и $s$ = 2.467 являются для нее точками слабо выраженных минимума и максимума. При $s \to \infty $ решение задачи имеет асимптотику Прандтля-Блазиуса: ${{\tau }_{w}} = O({{s}^{{ - 1/2}}})$.

Таким образом обтекание полутела вращения Рэнкина является безотрывным, что находится в соответствии с экспериментальным результатом Верле [11] (см. [12]), полученным путем визуализации.

ЗАКЛЮЧЕНИЕ

Проведенный анализ показал, что обтекание при больших числах Рейнольдса полутела вращения в форме Рэнкина является безотрывным.

Список литературы

Van Dyke M.D. Second-order slender-body theory − axisymmetric flow // NASA Tech. Rep. 1959. R-47. 26 p.
Cole J.D. Perturbation methods in applied mathematics. Waltham: Blaisdell, 1968. 260 p.
Jones R.T. Leading-edge singularities in thin-airfoil theory // J. Aeronaut. Sci. 1950. V. 17. № 5. P. 307−310.
Van Dyke M.D. Second-order subsonic airfoil theory including edge effects // NACA Rep. 1956. № 1274. 23 p.
Van Dyke M. Perturbation methods in fluid mechanics. Stanford: Parabolic Press, 1975. 271 p.
Rankine W.J.M. On the mathematical theory of stream-lines, especially those with four foci and upwards // Phil. Trans. Roy. Soc. London. 1871. V. 161. Pt. II. P. 267–306.
Сычев В.В., Башкин В.А. Лекции по теоретической гидродинамике. Ч. I. Учебное пособие. М.: МФТИ, 2003. 188 с.
Rosenhead L. (Ed.) Laminar boundary layers. Oxford: Clarendon Press, 1963, 688 p.
Homann F. Der Einfluβ groβer Zähigkeit bei der Strömung um den Zylinder und um die Kugel // ZAMM. 1936. Bd. 16. H. 3. S. 153−164.
Королев Г.Л., Сычев Вик. В. О пограничном слое при обтекании полутела Рэнкина // Изв. РАН. МЖГ. 2021. № 6. С. 62–65.
Werlé H. Le décollement sur les corps de révolution à basse vitesse // La Rech. Aéron. 1962. № 90. P. 3−14.
Van Dyke M. An album of fluid motion. Stanford: Parabolic Press, 1982. 176 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал