1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 1, 2023

Известия РАН. Механика жидкости и газа, 2023, № 1, стр. 127-134

НЕСУЩИЕ ПРОФИЛИ, БЛИЗКИЕ К ОБТЕКАЕМЫМ С НАИБОЛЬШИМИ КРИТИЧЕСКИМИ ЧИСЛАМИ МАХА

А. Н. Крайко a, *, В. А. Шаповалов a

a Центральный институт авиационного моторостроения им. П.И. Баранова
Москва, Россия

* E-mail: akraiko@ciam.ru

Поступила в редакцию 29.08.2022
После доработки 11.10.2022
Принята к публикации 11.10.2022

Полный текст (PDF)

Аннотация

Прямым методом построения двумерных оптимальных по критическим числам Маха М* тел построены близкие к оптимальным по М* несущие профили. Их практически нулевые коэффициенты волнового сопротивления сх остаются таковыми не только при числах Маха набегающего потока М0 меньших М*, но и при М0 заметно превышающих М*. Этим новые несущие профили отличаются от суперкритических несущих профилей, сх которых стремительно растут при превышении расчетных значений М0. При равных толщинах и М0 = М* суперкритические профили реализуют большие коэффициенты подъемной силы су. Однако из-за отмеченного выше отличия в поведении сх при М0, больших расчетных, качество суперкритических профилей может стать ниже даже как отношение су не к сх, а к коэффициенту полного сопротивления.

Ключевые слова: несущие профили, близкие к оптимальным по наибольшим критическим числам Маха, отрезки звуковых линий тока, аппроксимируемые кривыми Бернштейна–Безье, генетический алгоритм

Анализ [1] для симметричных профилей и тел вращения в равномерных набегающих потоках с числами Маха М0 < 1 и его обобщения [2] на тела в цилиндрических каналах и в решетках, на контуры с отрезками горизонталей и областями поступательного звукового течения определили важную роль отрезков звуковых линий тока в контурах конфигураций, обтекаемых идеальным (невязким и нетеплопроводным) газом с наибольшими критическими числами Маха М0 = М* < 1. Анализ обтекания таких тел включал доказательство и применение “свойства прямолинейности” звуковых линий (“линий перехода”), отличных от звуковых линий тока, отрезки которых формируют оптимальные контуры. Второе утверждение – принцип максимума, согласно которому в таких течениях число Маха может достигать своего максимального значения М = 1 только на обтекаемых контурах. Свойство прямолинейности линий перехода и принцип максимума справедливы и при “дозвуковом” (как и в [1, 2], с М ≤ 1) обтекании несимметричных профилей. Однако для них доказать ключевые при выяснении структуры оптимальных тел утверждения, названные в [1] “теоремой сравнения” и “леммой граничной точки”, не удалось.

Построенные в [3–10] примеры оптимальных тел в безграничном равномерном дозвуковом набегающем потоке включают симметричные профили и замкнутые тела вращения, обтекаемые под нулевым углом атаки, а также головные или кормовые части полубесконечных пластины и кругового цилиндра. Для их построения созданы численно-аналитические инструменты с весьма сложными аналитическими составляющими. Подход, развитый в [11], оказался намного проще. В его основе – прямой метод оптимального профилирования с численным решением “установлением” уравнений Эйлера, описывающих дозвуковое обтекание идеальным газом искомых тел, представление выпуклых звуковых участков их контуров кривыми Бернштейна–Безье (КББ) и нахождение оптимальных КББ с помощью генетического алгоритма (ГА). При этом минимизируются интегралы по выпуклым участкам контура от квадрата разности давления р и его известной отвечающей М = 1 “критической” величины ${{p}_{*}}$. У оптимальных по М* тел выпуклые участки – отрезки звуковых линий тока и эти интегралы равны нулю.

1. БЛИЗКИЕ К ОПТИМАЛЬНЫМ ПО М* НЕСУЩИЕ ПРОФИЛИ

Все построенные в [11] плоские и осесимметричные оптимальные по М* тела, как и в [3–10], обтекаются равномерным набегающим потоком под нулевым углом атаки. Далее, как и в [11], ось х декартовых координат ху направлена по скорости V0 набегающего потока. При построении близких к оптимальным по М* несущих профилей зададим и примем за линейный масштаб проекцию их хорды на ось х. При передней точке профиля i, помещенной на ось у, и концевой точке  f, помещенной на ось х, профилю отвечают 0 ≤ х ≤ 1. Как и в [1–11], возможны и иные ограничения, например

(1.1)
$\frac{{dy}}{{dx}} \equiv {\text{tg}}\theta \geqslant {\text{tg}}{{\theta }_{m}},\quad S \equiv \int\limits_i^f {({{y}^{ + }} - {{y}^{ - }})dx} \geqslant {{S}_{m}}$
с заданными константами θm < 0 и Sm > 0 и уравнениями у = у+(х) и у = у–(х) верхней и нижней образующими профиля.

Первое ограничение (1.1) приводило к появлению у построенных ранее оптимальных по М* симметричных обтекаемых под нулевым углом атаки профилей прямолинейных участков dy/dx = tgθm, заканчивающихся в их концевой точке x = 1, y = 0. Ограничение же на площадь “продольного” сечения S, введенное еще в [1], приводило к появлению у этих профилей переднего торца ia, на котором x = 0, и выпуклого отрезка звуковой линии тока, на котором М = 1 и р = ${{p}_{*}}$. При гладкой стыковке всех участков оптимальных образующих (непрерывности угла наклона касательной к ним θ) кривизна звуковых участков в их концевых точках обращается в бесконечность [7–12]. При приближении к этим точкам по отрезкам θ = const бесконечны производные p и V, а при приближении по нормали к контуру – производные всех параметров [12].

Согласно “Заключению” [11]: “… ставшие легко доступными оптимальные по М* конфигурации по-прежнему ограничены симметричными профилями, телами вращения и головными и кормовыми частями, обтекаемыми под нулевым углом атаки. Тем не менее хочется верить, что легкость проб поможет найти структуру принципиально иных оптимальных по М* двумерных конфигураций”. Ниже построены примеры именно таких, близких к оптимальным по М* несущих профилей.

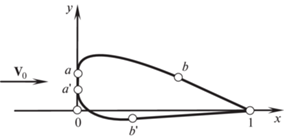
Изображенный на рис. 1 несущий профиль отличается от профилей, построенных ранее, несимметрией его верхней и нижней образующих. Во-первых, отрезок a'b' звуковой при M0 = M* линии тока меньше подобного верхнего отрезка ab. По этой причине при построении искомых профилей прямым методом [11] минимизируются интегралы

(1.2)
$I = \int\limits_a^b {{{{(p - p_{*}^{{}})}}^{2}}d\xi } ,\quad I' = \int\limits_{a{\kern 1pt} '}^{b{\kern 1pt} '} {{{{(p - p_{*}^{{}})}}^{2}}d\xi } $
Рис. 1.

Близкий к оптимальному по М* несущий профиль с отрезками звуковых (при М0 = М*) линий тока ab и a'b'.

Здесь и далее, как в [11], ξ – расстояние, отсчитываемое вдоль контура, ${{p}_{*}}$ – отвечающее М = 1 критическое давление, за масштабы плотности ρ и скоростей взяты их размерные (с индексом “градус”) критические величины $\rho _{*}^{^\circ }$ и $a_{*}^{^\circ }$, а за масштаб р – $\rho _{*}^{^\circ }a_{*}^{{^\circ 2}}$. Для совершенного газа с постоянными теплоемкостями и их отношением (показателем адиабаты) γ безразмерное ${{p}_{*}}$ = 1/γ. Во-вторых, для увеличения подъемной силы дозвуковой при М0 = М* концевой участок нижнего контура, плавно примыкающий к отрезку a'b', может быть вогнутым.

Наряду с функционалом (1.2) вычисляются коэффициенты волнового сопротивления сх и подъемной силы су и площадь S продольного сечения профиля

(1.3)
${{c}_{x}} = \frac{2}{{{{\rho }_{0}}V_{0}^{2}}}\oint\limits_{fif} {(p - {{p}_{0}})dy} ,\quad {{c}_{y}} = \frac{2}{{{{\rho }_{0}}V_{0}^{2}}}\oint\limits_{fif} {(p - {{p}_{0}})dx} ,\quad S = \int\limits_i^f {({{y}^{ + }} - {{y}^{ - }})dx} $
со средней точкой i торца a'a. Для совершенного газа давление р0 и ${{\rho }_{0}}V_{0}^{2}$ – функции числа Маха М0 набегающего потока
$V_{0}^{2} = \frac{{(\gamma + 1)M_{0}^{2}}}{{2 + (\gamma - 1)M_{0}^{2}}},\quad {{p}_{0}} = \frac{1}{\gamma }{{\left( {\frac{{\gamma + 1}}{2} - \frac{{\gamma - 1}}{2}V_{0}^{2}} \right)}^{{\gamma /(\gamma - 1)}}},\quad {{\rho }_{0}}V_{0}^{2} = \gamma {{p}_{0}}M_{0}^{2}.$
КББ, которыми аппроксимировались криволинейные участки контуров искомых несущих профилей, задаются формулами [13]
$P(t) = \sum\limits_{k = 0}^K {B_{k}^{K}(t){{P}_{k}}} ,\quad B_{k}^{K}(t) = \frac{{K!}}{{k!(K - k)!}}{{t}^{k}}{{(1 - t)}^{{K - k}}},\quad t \in [0,1]$
в которых P – координаты (x, y), t – параметр, $B_{k}^{K}(t)$ – полиномы Бернштейна, а Pk – координаты концов (контрольных точек) отрезков ломаной (“полигона”). В общем случае КББ проходит лишь через крайние контрольные точки, касаясь в них соответствующего отрезка полигона. Существенна линейная зависимость координат КББ от координат Pk ее контрольных точек.

Верхние звуковые при М0 = М* отрезки образующих искомых профилей КББ определяют так же, как при построении симметричных профилей в [11]. При построении выпуклого и вогнутого участков нижних образующих две КББ обеспечивают гладкую стыковку выпуклого участка a'b' с торцом a'a в точке a' и с вогнутым концевым участком в точке b'. Гладкую стыковку в точке b' реализует помещение этой точки и двух соседних с ней контрольных точек КББ на отрезок заранее неизвестной прямой линии.

Близкие к оптимальным по М* несущие профили строились прямым методом [11], который ранее развивался и применялся при построении оптимальных аэродинамических форм в [14–18]. Оптимальные параметры КББ – оставшиеся не заданными (“свободными”) координаты контрольных точек, включая координаты точек стыковки уа, xb, ${{x}_{{b'}}}$ и ${{y}_{{b{\text{'}}}}}$ (индексы a, b, … метят величины в точках a, b, …), обеспечивающие близкие к нулю значения введенных в (1.2) и (1.3) функционалов I, I' и сх, находил ГА, описанный в [11].

Распределения параметров и значения I, I', сх и су при стационарном обтекании каждого сгенерированного ГА профиля находились установлением по времени при численном решении уравнений течения идеального газа (уравнений Эйлера). Записанные в дивергентной форме нестационарные уравнения Эйлера интегрировались разностной схемой Годунова [19] повышенного согласно [20, 21] порядка аппроксимации (на гладких решениях). Как и в [11], в плоскости ху уравнения Эйлера численно интегрировались в области, ограниченной окружностью r ≡ (x2 + + y2)1/2 = 15 с параметрами невозмущенного потока в примыкающем к окружности слое “вспомогательных” ячеек [22]. Ячейки разностной сетки, адаптированной к обтекаемым телам, увеличивались линейно по r. Чтобы избежать связанного с этим роста времени установления, интегрирование уравнений велось по неявной разностной схеме [23] с числом Куранта cu = 10–20. Не вдаваясь в дальнейшие подробности, перейдем к примерам построенных близких к оптимальным по М* несущим профилям.

2. ПРИМЕРЫ БЛИЗКИХ К ОПТИМАЛЬНЫМ ПО М* НЕСУЩИХ ПРОФИЛЕЙ

Все расчеты выполнены для γ = 7/5 = 1.4 с заданием выпуклых звуковых участков симметричных профилей кривыми Бернштейна–Безье 10-го порядка (K = 10). Вогнутые концевые участки их нижних образующих задавались КББ 3-го порядка, а при представлении полей чисел Маха координаты х и у отнесены к проекции хорды профиля на ось х.

В табл. 1 приведены числа Маха М0, углы атаки α и относительные толщины h – максимальные разности у при фиксированном х верхней и нижней образующих трех построенных прямым методом оптимизации близких к оптимальным по М* = М0 несущих профилей. Четвертый несущий профиль – суперкритический для М0 = 0.785 несущий профиль SC(2)_NASA_0410 из [24]. С этим профилем будет сравниваться один из построенных близкий к оптимальному по М* = 0.785 несущий профиль. Существенно, что все четыре профиля обтекаются под небольшими отрицательными углами атаки. Методы построения двумерных суперкритических конфигураций, обтекаемых на расчетном режиме с местными безударными сверхзвуковыми зонами, развивались в [25–29].

Таблица 1
M0 –α h
0.7 0.0211 0.1774
0.785 0.009 0.101
0.785 (NASA) 0.0076 0.1
0.85 0.0044 0.0546

В табл. 2 собраны величины I, I', cx, cy и отличие от единицы максимальных чисел Маха Mm при числах Маха набегающего потока М0 и углах атаки, указанных в табл. 1. Все перечисленные величины были получены на двух разностных сетках с числом ячеек N и 4N. Сравнение значений, полученных на исходных и более “тонких” сетках (в скобках), демонстрирует достоверность результатов расчета. Из приведенных величин практически неизменен коэффициент подъемной силы, слегка изменяются интегралы I и I′ и умеренно – максимальные числа Маха Mm. Уменьшение же почти на порядок крайне малых значений сх, близких к оптимальным по М* несущих профилей, как и в [11], – свидетельство высокой точности результатов, ибо здесь отличие сх от нуля – следствие погрешностей счета. С учетом сказанного далее приводятся результаты, полученные на исходных сетках.

Таблица 2
M0 N I × 104 I' × 104 cx × 105 cy × 103 (Mm– 1) × 103
0.7 13744 (×4) 18 (17) 18 (19) 42 (8) 488 (489) 11 (37)
0.785 14688 (×4) 64 (63) 14 (16) 17 (2) 246 (246) 29 (31)
0.785 (NASA) 16960 (×4)     58 (20) 395 (398) 139 (121)
0.85 15664 (×4) 31 (31) 44 (47) 8 (1) 150(150) 25 (32)

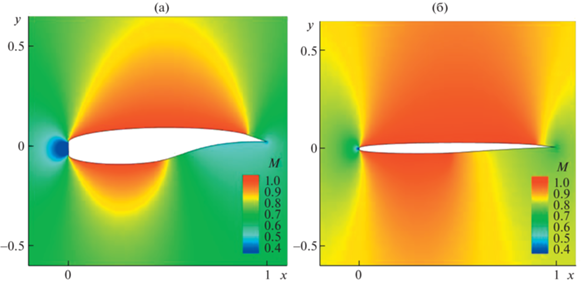
На рис. 2 показаны поля чисел Маха при обтекании с М0 = 0.785 несущего профиля, близкого к оптимальному по М* = 0.785 (а), и суперкритического профиля SC(2)_NASA_0410, спрофилированного на М0 = 0.785 (б). Хотя согласно табл. 2 отличие Mm от единицы у второго профиля вчетверо больше, чем у первого, на расчетном режиме (при М0 = 0.785), он обтекается почти безударно с сх ≈ 0.2 × 10–3.

Рис. 2.

Поля чисел Маха при обтекании с М0 = 0.785 несущего профиля, близкого к оптимальному по М* = = 0.785 (а), и суперкритического профиля SC(2)_NASA_0410, спрофилированного на М0 = 0.785 (б).

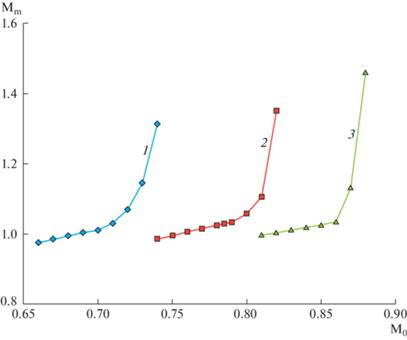
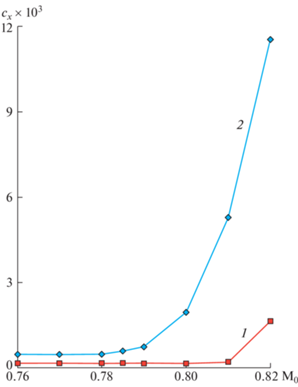
Согласно рис. 3 ситуация резко меняется при М0, больших расчетного значения М0 = 0.785. У близкого к оптимальному по М* несущего профиля сх не изменяется до М0 = 0.81, возрастая затем до сх = 1.64 × 10–3 при М0 = 0.82 на исходной сетке и до сх = 1.48 × 10–3 на вчетверо более густой. В отличие от этого сх суперкритического профиля NASA начинает при М0 > 0.785 расти сразу, достигая при М0 = 0.82 много большей величины сх ≈ 1.2 × 10–2. На рис. 3 и далее ломанные кривые образуют прямолинейные отрезки, которые соединяют представленные значками результаты расчета.

Рис. 3.

Зависимость сх от М0 профилей: близкого к оптимальному по М* = 0.785 (1) и профиля SC(2)_NASA_0410 (2).

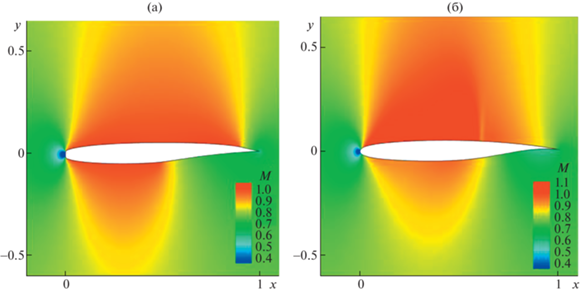
На рис. 4 даны поля чисел Маха при обтекании с М0 = М* несущих профилей, близких к оптимальным по М* = 0.7 (а) и М* = 0.85 (б). Зависимости от М0 коэффициентов волнового сопротивления этих несущих профилей показывает рис. 5. Как и у несущего профиля с М* = 0.785, увеличение сх этих несущих профилей начинается не сразу при превышении расчетных значений чисел Маха набегающего потока М0 = М* и идет не столь стремительно, как рост сх суперкритических профилей [24] с такими же относительными толщинами h и расчетными числами Маха М0.

Рис. 4.

Поля чисел Маха около близких к оптимальным по М* несущих профилей: (а, б) –М* = 0.7, 0.85.

Рис. 5.

Зависимость сх близких к оптимальным по М* несущих профилей, отвечающих М* = 0.7 (а) и М* = = 0.85 (б), от М0.

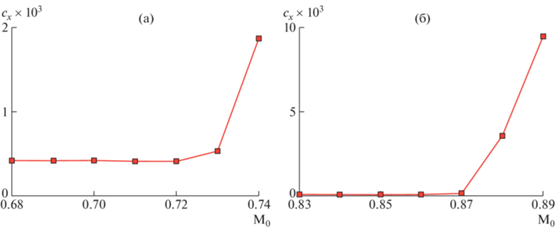
Рисунок 6 для близких к оптимальным по М* несущих профилей дает зависимости от числа Маха набегающего потока М0 максимальных чисел Маха Mm, которые реализуются на выпуклых участках их контуров. Для всех трех построенных профилей величина Mm слегка превышает единицу на расчетных М0 = М*, линейно по М0 уменьшается при М0 < М* и, ускоряясь, возрастает при М0 > М*. Сравнение кривых рис. 6 с кривыми рис. 3 и 5 показывает, что для близких к оптимальным по М* несущих профилей ускоренный рост Mm начинается заметно раньше ускоренного роста волнового сопротивления.

Рис. 6.

Зависимость от М0 максимальных чисел Маха Mm на близких к оптимальным по М* несущих профилях, отвечающих М* = 0.7 (1), 0.785 (2) и 0.85 (3).

ЗАКЛЮЧЕНИЕ

Как и ожидалось, построение близких к оптимальным по М* несущих профилей удалось благодаря простоте примененного для их построения прямого метода. Второй существенный, но понятый не сразу момент – отрицательные углы атаки. При положительных углах атаки искомые несущие профили не получались.

Авторы благодарны К.С. Пьянкову за предоставленные программы, консультации и обсуждения.

Работа выполнена при поддержке РФФИ (код проекта 20-01-00100).

Список литературы

  1. Gilbarg D., Shiffman M.On Bodies Achieving Extreme Values of the Critical Mach Number. I // J. Ration. Mech. and Analysis. 1954. V. 3. № 2. P. 209–230.

  2. Крайко А.Н. Плоские и осесимметричные конфигурации, обтекаемые с максимальным критическим числом Маха // ПММ. 1987. Т. 51. Вып. 6. С. 941–950.

  3. Fisher D.D. Calculation of Subsonic Cavities with Sonic Free Streamlines // J. Math. Phys. 1963. V. 42. № 1. P. 14–26.

  4. Брутян М.А., Ляпунов С.В. Оптимизация формы симметричных плоских тел с целью увеличения критического числа Маха // Учен. зап. ЦАГИ. 1981. Т. 12. № 5. С. 10–22.

  5. Щербаков С.А. Расчет головной или кормовой части плокого тела, обтекаемого дозвуковым потоком с максимально возможным критическим числом Маха // Учен. зап. ЦАГИ. 1988. Т. 19. № 4. С. 10–18.

  6. Schwendeman D.W., Kropinski M.C.A., Cole J.D. On the Construction and Calculation of Optimal Nonlifting Critical Airfoils // ZAMP. 1993. Bd 44. P. 556–571.

  7. Зигангареева Л.М., Киселев О.М. О расчете кавитационного обтекания кругового конуса дозвуковым потоком сжимаемой жидкости // ПММ. 1994. Т. 58. Вып. 4. С. 93–107.

  8. Зигангареева Л.М., Киселев О.М. Отрывное обтекание диска идеальным газом и тела с наибольшими критическими числами Маха // Изв. РАН. МЖГ. 1996. № 3. С. 166–172.

  9. Зигангареева Л.М., Киселев О.М. О полубесконечных телах вращения, обтекаемых с максимальным критическим числом Маха // ПММ. 1997. Т. 61. Вып. 1. С. 97–107.

  10. Зигангареева Л.М., Киселев О.М. О плоских конфигурациях, обтекаемых потоком идеального газа с максимальным критическим числом Маха // ПМТФ. 1998. № 5. С. 106–115.

  11. Крайко А.Н., Шаповалов В.А. Плоские и осесимметричные тела, обтекаемые с наибольшими “критическими” числами Маха // Изв. РАН. МЖГ. 2022. № 4. С. 86–95.

  12. Крайко А.Н., Тилляева Н.И. О кривизне граничных линий тока течений идеального газа в точках схода и присоединения // ПММ. 2022. Т. 96. Вып. 3. С. 349–364.

  13. Крайко А.Н. Теоретическая газовая динамика: классика и современность. М.: Торус пресс, 2010. 440 с.

  14. Пьянков К.С., Тилляева Н.И. Многокритериальная многодисциплинарная оптимизация лопатки рабочего колеса вентилятора на основе генетического алгоритма // ТВФ. 2010. № 3. С. 58–67.

  15. Крайко А.А., Пьянков К.С., Тилляева Н.И. и др. Оптимизация биротативного вентилятора с учетом напряженно-деформированного состояния на основе генетического алгоритма // ТВФ. 2014. № 1. С. 22–34.

  16. Крайко А.А., Пьянков К.С., Тилляева Н.И. Профилирование двусторонних несимметричных плоских сопел максимальной тяги // Изв. РАН МЖГ. 2016. № 1. С. 115–120.

  17. Тилляева Н.И. Сравнение эффективности штыревых и комбинированных кольцевых сопел // Изв. РАН. МЖГ. 2017. № 4. С. 140–152.

  18. Крайко А.Н., Пьянков К.С., Тилляева Н.И. и др. Внутренние скачки уплотнения при сверхзвуковом обтекании контуров оптимальных тел и сопел // Изв. РАН. МЖГ. 2020. № 6. С. 121–138.

  19. Годунов С.К., Забродин А.В., Иванов М.Я. и др. Численное решение многомерных задач газовой динамики // М.: Наука, 1976. 400 с.

  20. Колган В.П. Применение принципа минимальных значений производной к построению конечноразностных схем для расчета разрывных решений газовой динамики // Учен. зап. ЦАГИ. 1972. Т. 3. № 6. С. 68–77.

  21. Тилляева Н.И. Обобщение модифицированной схемы С.К. Годунова на произвольные нерегулярные сетки // Учен. зап. ЦАГИ. 1986. Т. 17. № 2. С. 18–26.

  22. Гринь В.Т., Крайко А.Н., Славянов Н.Н. Решение задачи о запуске сопла, вмонтированного в торец ударной трубы // Изв. АН СССР. МЖГ. 1981. № 6. С. 117–123.

  23. Браилко И.А., Попов Е.Н. Расчеты стационарных двух- и трехмерных вязких течений в межлопаточных каналах турбин // Труды НПО Энергомаш им. акад. В.П. Глушко. 2002. № 20. 448 с. С. 4–22.

  24. Harris C.D. NASA Supercritical Airfoils. A Matrix of Family-Related Airfoils. 1990. NASA TR-2969.

  25. Sobieczky H., Yu N.J., Fung K.-Y., Seebass A.R. A New Method for Designing Shock-Free Transonic Configurations // AIAA J. 1979. V. 17. № 7. P. 722–729.

  26. Nakamura M. A Method for Obtaining Shockless Transonic Flows past Two-Dimensional Airfoils whose Profiles are Partially Modified from a Given Arbitrary Profile // Trans. Japan Soc. Aeronaut. and Space Sci. 1981. V. 23. № 62. P. 195–213.

  27. Dulikravich D.S., Sobieczky H. Shockless Design and Analysis of Transonic Cascade Shapes // AIAA J. 1982. V. 20. № 11. P. 1572–1578.

  28. Beauchamp P., Seebass A.R. Shock-Free Turbomachinery Blade Design // AIAA J. 1985. V. 23. № 2. P. 249–253.

  29. Крайко А.Н., Пьянков К.С. Построение профилей и мотогондол, суперкритических в околозвуковом потоке идеального газа // ЖВМиМФ. 2000. Т. 40. № 12. С. 1890–1904.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал