1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 1, 2023

Известия РАН. Механика жидкости и газа, 2023, № 1, стр. 135-143

ПОСТРОЕНИЕ ТОЧНЫХ РЕШЕНИЙ СИСТЕМЫ УРАВНЕНИЙ ОДНОМЕРНОЙ ГАЗОВОЙ ДИНАМИКИ БЕЗ ГРАДИЕНТНОЙ КАТАСТРОФЫ

А. В. Аксенов a, b, *, К. П. Дружков a, c, **

a Московский государственный университет им. М.В. Ломоносова
Москва, Россия

b Национальный исследовательский ядерный университет “МИФИ”
Москва, Россия

c Московский физико-технический институт (государственный университет)
Долгопрудный, Россия

* E-mail: aksenov@mech.math.msu.su
** E-mail: konstantin.druzhkov@gmail.com

Поступила в редакцию 10.10.2022
После доработки 12.10.2022
Принята к публикации 12.10.2022

Полный текст (PDF)

Аннотация

Рассмотрена система уравнений, описывающая одномерные политропные движения газа. Получена классификация инвариантов характеристик вплоть до второго порядка рассматриваемой системы уравнений. Предложен метод сведения задач Коши к системам обыкновенных дифференциальных уравнений. С помощью инвариантов характеристик, дополнительных к инвариантам Римана, построены примеры решений без градиентной катастрофы.

Ключевые слова: газовая динамика, инварианты Римана, инварианты характеристик, градиентная катастрофа, точные решения

Хорошо известные в газовой динамике инварианты Римана [1] представляют собой функции, постоянные на характеристиках одномерной системы уравнений, описывающей движения газа при баротропных процессах. При этом инварианты Римана зависят только от скорости и плотности газа. Понятие инварианта характеристик было естественным образом обобщено Дарбу [2] при исследовании промежуточных интегралов скалярных гиперболических уравнений. Инварианты характеристик представляют собой функции, постоянные на характеристиках систем дифференциальных уравнений. Вообще говоря, они могут зависеть от производных сколь угодно высоких порядков и тесно связаны с понятием интегрируемости уравнений в частных производных по Дарбу [2–5].

С помощью дополнительных инвариантов характеристик можно строить общее решение системы уравнений одномерной газовой динамики. Примеры построения общих решений без использования инвариантов характеристик приведены в работе [6].

Основной целью этой работы является построение решений, в которых невозможно наступление градиентной катастрофы. Известно, что в случае одномерных политропных движений газа по начальным условиям можно однозначно сказать, наступит ли градиентная катастрофа в соответствующем решении [7]. В нашей работе проводится исследование решений задач Коши на всей пространственной оси, в которых наступление градиентной катастрофы невозможно. С помощью инвариантов характеристик, дополнительных к инвариантам Римана, построение таких решений сводится к исследованию систем обыкновенных дифференциальных уравнений. Рассматриваемые решения обладают конечными массой, импульсом и энергией. Другие примеры решений без градиентной катастрофы, в том числе записанные в неявной аналитической форме, приведены в работе [8].

1. ПОСТАНОВКА ЗАДАЧИ

В безразмерных переменных система уравнений одномерной газовой динамики для политропных движений газа (давление задается соотношением $p = {{\gamma }^{{ - 1}}}{{\rho }^{\gamma }}$, $\gamma = {\text{const}}$) может быть записана в виде

(1.1)
$\begin{gathered} {{u}_{t}} + u{{u}_{x}} + {{\rho }^{{\gamma - 2}}}{{\rho }_{x}} = 0 \\ {{\rho }_{t}} + u{{\rho }_{x}} + {{u}_{x}}\rho = 0 \\ \end{gathered} $

Здесь безразмерные величины $t$, $x$, $u$, $\rho $, $c$, p связаны с размерными временем t*, пространственной координатой x*, компонентой скорости u*, плотностью $\rho {\kern 1pt} * > 0$, скоростью звука $c{\kern 1pt} {\text{*}}\left( {\rho {\kern 1pt} {\text{*}}} \right) > 0$ и давлением p* с помощью соотношений

$t = \frac{{{{c}_{c}}t{\kern 1pt} *}}{{{{l}_{c}}}},\quad x = \frac{{x{\kern 1pt} *}}{{{{l}_{c}}}},\quad u = \frac{{u{\kern 1pt} *}}{{{{c}_{c}}}},\quad \rho = \frac{{\rho {\kern 1pt} *}}{{{{\rho }_{c}}}},\quad c = \frac{{c{\kern 1pt} *}}{{{{c}_{c}}}},\quad p = \frac{{p{\kern 1pt} *}}{{{{\rho }_{c}}c_{c}^{2}}}$

Характерные длина ${{l}_{c}}$ и плотность ${{\rho }_{c}}$ могут быть определены для конкретных задач. Характерная скорость звука ${{c}_{c}}$ соответствует характерной плотности.

Законы сохранения массы, импульса и энергии для системы уравнений (1.1) при $\gamma \ne 1$ могут быть записаны в виде

(1.2)
$\begin{gathered} \frac{{d{\kern 1pt} }}{{dt}}\int\limits_\mathbb{R} {\rho {\kern 1pt} dx} = \left. { - (u\rho )} \right|_{{ - \infty }}^{{ + \infty }} \\ \frac{{d{\kern 1pt} }}{{dt}}\int\limits_\mathbb{R} {u\rho {\kern 1pt} dx} = - \left. {({{u}^{2}}\rho + {{\gamma }^{{ - 1}}}{{\rho }^{\gamma }})} \right|_{{ - \infty }}^{{ + \infty }} \\ \frac{{d{\kern 1pt} }}{{dt}}\int\limits_\mathbb{R} {\left( {\frac{{{{u}^{2}}\rho }}{2} + \frac{{{{\rho }^{\gamma }}}}{{\gamma (\gamma - 1)}}} \right)dx} = - \left. {\left( {\frac{{{{u}^{3}}\rho }}{2} + \frac{{u{{\rho }^{\gamma }}}}{{\gamma - 1}}} \right)} \right|_{{ - \infty }}^{{ + \infty }} \\ \end{gathered} $

Система уравнений (1.1) обладает на характеристиках ${{C}_{ + }}$ и ${{C}_{ - }}$ инвариантами Римана:

$r = u + \frac{2}{{\gamma - 1}}{\kern 1pt} {{\rho }^{{\frac{{\gamma - 1}}{2}}}},\quad {{C}_{ + }}:\;dx = \left( {u + {{\rho }^{{\frac{{\gamma - 1}}{2}}}}} \right)dt$
$l = u - \frac{2}{{\gamma - 1}}{\kern 1pt} {{\rho }^{{\frac{{\gamma - 1}}{2}}}},\quad {{C}_{ - }}:\;dx = \left( {u - {{\rho }^{{\frac{{\gamma - 1}}{2}}}}} \right)dt$
которые представляют собой примеры инвариантов характеристик, т.е. функций, постоянных вдоль характеристик.

Далее инварианты характеристик системы уравнений (1.1) будут использованы при построении ее точных решений.

2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Для определения инвариантов характеристик системы уравнений (1.1) удобно использовать операторы полных производных

${{D}_{x}} = {{\partial }_{x}} + {{u}_{x}}{{\partial }_{u}} + {{\rho }_{x}}{{\partial }_{\rho }} + \ldots $
${{D}_{t}} = {{\partial }_{t}} + {{u}_{t}}{{\partial }_{u}} + {{\rho }_{t}}{{\partial }_{\rho }} + \ldots $

Здесь мы предполагаем, что эти операторы продолжены на производные всех порядков. Введем в рассмотрение операторы полных производных в силу системы уравнений (1.1)

${\kern 1pt} {{\overline {D} }_{x}} = {{\partial }_{x}} + {{u}_{x}}{{\partial }_{u}} + {{\rho }_{x}}{{\partial }_{\rho }} + \ldots $
${\kern 1pt} {{\overline D }_{t}} = {{\partial }_{t}} - (u{{u}_{x}} + {{\rho }^{{\gamma - 2}}}{{\rho }_{x}}){{\partial }_{u}} - (u{{\rho }_{x}} + {{u}_{x}}\rho ){{\partial }_{\rho }} + \ldots $

Теперь характеристики ${{C}_{ \pm }}$ могут быть описаны в терминах полных производных вдоль характеристических направлений

${{X}_{ \pm }} = {\kern 1pt} {{\overline {D} }_{t}} + \left( {u \pm {{\rho }^{{\frac{{\gamma - 1}}{2}}}}} \right){{\overline {D} }_{x}}$

Назовем функцию f инвариантом характеристики ${{C}_{ + }}$, если она удовлетворяет условию ${{X}_{ + }}(f) = 0$. Здесь f может зависеть от переменных $t,x,u,\rho $ и производных по $x$ вплоть до некоторого конечного порядка. Аналогично определяются инварианты характеристики ${{C}_{ - }}$.

3. КЛАССИФИКАЦИЯ ИНВАРИАНТОВ ХАРАКТЕРИСТИК

Будем искать инварианты второго порядка характеристики ${{C}_{ + }}$, т.е. функции вида $f = f(t,x,u,\rho ,{{u}_{x}},{{\rho }_{x}},{{u}_{{xx}}},{{\rho }_{{xx}}})$, удовлетворяющие условию

${{X}_{ + }}(f) = 0$

Прямыми вычислениями получаем следующее соотношение:

$\begin{gathered} {{u}_{{xxx}}}\left( {{{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{f}_{{{{u}_{{xx}}}}}} - \rho {{f}_{{{{\rho }_{{xx}}}}}}} \right) - {{\rho }_{{xxx}}}\left( {{{\rho }^{{\gamma - 2}}}{{f}_{{{{u}_{{xx}}}}}} - {{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{f}_{{{{\rho }_{{xx}}}}}}} \right) + {{f}_{t}} + \left( {u + {{\rho }^{{\frac{{\gamma - 1}}{2}}}}} \right){{f}_{x}} + \left( {{{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{u}_{x}} - {{\rho }^{{\gamma - 2}}}{{\rho }_{x}}} \right){{f}_{u}} - \\ \, - \left( {\rho {{u}_{x}} - {{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{\rho }_{x}}} \right){{f}_{\rho }} + \left( {{{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{u}_{{xx}}} - {{\rho }^{{\gamma - 2}}}{{\rho }_{{xx}}} - u_{x}^{2} - (\gamma - 2){{\rho }^{{\gamma - 3}}}\rho _{x}^{2}} \right){{f}_{{{{u}_{x}}}}} - \left( {\rho {{u}_{{xx}}} - {{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{\rho }_{{xx}}} + 2{{u}_{x}}{{\rho }_{x}}} \right){{f}_{{{{\rho }_{x}}}}} - \\ \, - (3{{u}_{x}}{{u}_{{xx}}} + 3(\gamma - 2){{\rho }^{{\gamma - 3}}}{{\rho }_{x}}{{\rho }_{{xx}}} + ({{\gamma }^{2}} - 5\gamma + 6){{\rho }^{{\gamma - 4}}}\rho _{x}^{3}){{f}_{{{{u}_{{xx}}}}}} - 3\left( {{{\rho }_{x}}{{u}_{{xx}}} + {{u}_{x}}{{\rho }_{{xx}}}} \right){{f}_{{{{\rho }_{{xx}}}}}} = 0 \\ \end{gathered} $

Поскольку искомая функция f не зависит от производных третьего порядка, коэффициенты при ${{u}_{{xxx}}}$ и ${{\rho }_{{xxx}}}$ должны быть нулевыми и рассматриваемое уравнение расщепляется на систему из трех уравнений, из которых только два уравнения независимы. Независимые уравнения имеют следующий вид:

(3.1)
${{\rho }^{{\frac{{\gamma - 3}}{2}}}}{{f}_{{{{u}_{{xx}}}}}} - {{f}_{{{{\rho }_{{xx}}}}}} = 0$
(3.2)
$\begin{gathered} \\ {{f}_{t}} + \left( {u + {{\rho }^{{\frac{{\gamma - 1}}{2}}}}} \right){{f}_{x}} + \left( {{{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{u}_{x}} - {{\rho }^{{\gamma - 2}}}{{\rho }_{x}}} \right){{f}_{u}} - \left( {\rho {{u}_{x}} - {{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{\rho }_{x}}} \right){{f}_{\rho }} + \\ \, + \left( {{{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{u}_{{xx}}} - {{\rho }^{{\gamma - 2}}}{{\rho }_{{xx}}} - u_{x}^{2} - (\gamma - 2){{\rho }^{{\gamma - 3}}}\rho _{x}^{2}} \right){{f}_{{{{u}_{x}}}}} - \left( {\rho {{u}_{{xx}}} - {{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{\rho }_{{xx}}} + 2{{u}_{x}}{{\rho }_{x}}} \right){{f}_{{{{\rho }_{x}}}}} - \\ \, - (3{{u}_{x}}{{u}_{{xx}}} + 3(\gamma - 2){{\rho }^{{\gamma - 3}}}{{\rho }_{x}}{{\rho }_{{xx}}} + ({{\gamma }^{2}} - 5\gamma + 6){{\rho }^{{\gamma - 4}}}\rho _{x}^{3}){{f}_{{{{u}_{{xx}}}}}} - 3({{\rho }_{x}}{{u}_{{xx}}} + {{u}_{x}}{{\rho }_{{xx}}}){{f}_{{{{\rho }_{{xx}}}}}} = 0 \\ \end{gathered} $

В дальнейшем вместо аргумента $u$ искомой функции  f удобно использовать инвариант Римана r.

Из уравнения (3.1) следует, что искомая функция имеет вид $f = f(t,x,r,\rho ,{{u}_{x}},{{\rho }_{x}},q)$, где $q = {{\rho }^{{\frac{{\gamma - 3}}{2}}}}\left( {{{u}_{{xx}}} + {{\rho }^{{\frac{{\gamma - 3}}{2}}}}{{\rho }_{{xx}}}} \right)$. Подставляя искомую функцию f в уравнение (3.2) и исключая переменную ${{u}_{{xx}}}$ с помощью написанного выше выражения для q, получаем линейное по переменной ${{\rho }_{{xx}}}$ соотношение. Тогда, расщепляя найденное соотношение по ${{\rho }_{{xx}}}$, получаем два уравнения на искомую функцию f :

(3.3)
$4{{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{f}_{{{{u}_{x}}}}} - 4\rho {{f}_{{{{\rho }_{x}}}}} + (\gamma - 3)\left( {{{u}_{x}} + 5{{\rho }^{{\frac{{\gamma - 3}}{2}}}}{{\rho }_{x}}} \right){{\rho }^{{\frac{{\gamma - 3}}{2}}}}{{f}_{q}} = 0$
(3.4)
$\begin{gathered} {{f}_{t}} + \left( {r + \frac{{\gamma - 3}}{{\gamma - 1}}{{\rho }^{{\frac{{\gamma - 1}}{2}}}}} \right){{f}_{x}} - \left( {\rho {{u}_{x}} - {{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{\rho }_{x}}} \right){{f}_{\rho }} - (u_{x}^{2} + (\gamma - 2){{\rho }^{{\gamma - 3}}}\rho _{x}^{2} - \rho q){{f}_{{{{u}_{x}}}}} - \\ \, - \left( {2{{u}_{x}}{{\rho }_{x}} + {{\rho }^{{\frac{{5 - \gamma }}{2}}}}q} \right){{f}_{{{{\rho }_{x}}}}} - \left( {\frac{{\gamma + 3}}{2}q{{u}_{x}} + ({{\gamma }^{2}} - 5\gamma + 6){{\rho }^{{\frac{{3\gamma - 11}}{2}}}}\rho _{x}^{3} - \frac{{\gamma - 9}}{2}{{\rho }^{{\frac{{\gamma - 3}}{2}}}}q{{\rho }_{x}}} \right){{f}_{q}} = 0 \\ \end{gathered} $

Из уравнения (3.3) следует, что искомая функция имеет вид $f = f(t,x,r,\rho ,a,b)$, где

(3.5)
$\begin{gathered} a = {{\rho }^{{\frac{{\gamma - 3}}{4}}}}\left( {{{u}_{x}} + {{\rho }^{{\frac{{\gamma - 3}}{2}}}}{{\rho }_{x}}} \right) \\ b = \frac{{{{\gamma }^{2}} - 2\gamma - 3}}{{16(\gamma - 1)\rho }}u_{x}^{2} + \frac{{3{{\gamma }^{2}} - 10\gamma + 3}}{{8(\gamma - 1)}}{{\rho }^{{\frac{{\gamma - 5}}{2}}}}{{u}_{x}}{{\rho }_{x}} + \frac{{13{{\gamma }^{2}} - 50\gamma + 33}}{{16(\gamma - 1)}}{{\rho }^{{\gamma - 4}}}\rho _{x}^{2} + q \\ \end{gathered} $

Подставляя искомую функцию f в уравнение (3.4) и исключая переменные ${{\rho }_{x}}$ и $q$ с помощью соотношений (3.5), получаем соотношение, линейное по переменной ${{u}_{x}}$ и тождественно равное нулю по этой переменной. Расщепляя его по переменной ${{u}_{x}}$, получаем два уравнения на искомую функцию f. Первое уравнение имеет простой вид ${{f}_{\rho }} = 0$. Второе уравнение является классифицирующим уравнением и имеет следующий вид:

(3.6)
${{f}_{t}} + r{{f}_{x}} + \frac{{\gamma - 3}}{{\gamma - 1}}{{\rho }^{{\frac{{\gamma - 1}}{2}}}}{{f}_{x}} - \frac{{\gamma + 1}}{4}{{\rho }^{{\frac{{3 - \gamma }}{4}}}}a\left( {a{{f}_{a}} + 3b{{f}_{b}}} \right) + \frac{{3{{\gamma }^{3}} - 7{{\gamma }^{2}} - 7\gamma + 3}}{{64(\gamma - 1)}}{{\rho }^{{\frac{{5 - 3\gamma }}{4}}}}{{a}^{3}}{{f}_{b}} = 0$

Здесь $\gamma \ne 1$ и $f = f(t,x,r,a,b)$.

Замечание 1. Случай $\gamma = 1$ выделяется отдельно. Прямыми вычислениями можно показать, что в этом случае нет дополнительных инвариантов второго порядка.

Используя отсутствие явной зависимости функции f от переменной $\rho $, из классифицирующего уравнения (3.6) находим только пять случаев существования дополнительных инвариантов.

Случай 1. $\gamma = - 1$. В этом случае дополнительным инвариантом является

$I = \frac{{{{\rho }^{3}}}}{{{{\rho }_{x}} + {{\rho }^{2}}{{u}_{x}}}}$

Случай 2. $\gamma = 1{\text{/}}3$. В этом случае дополнительным инвариантом является

$I = \frac{b}{{{{a}^{3}}}}$

Случай 3. $\gamma = 5{\text{/}}3$. В этом случае дополнительным инвариантом является

$I = x - \left( {u + 3{{\rho }^{{\frac{1}{3}}}}} \right)t + \frac{{3\rho }}{{{{\rho }_{x}} + {{\rho }^{{\frac{2}{3}}}}{\kern 1pt} {{u}_{x}}}}$

Случай 4. $\gamma = 7{\text{/}}5$. В этом случае дополнительным инвариантом является

$I = x - \left( {u + 5{{\rho }^{{\frac{1}{5}}}}} \right)t - \frac{{25b}}{{3{{a}^{3}}}}$

Случай 5. $\gamma = 3$. В этом случае дополнительным инвариантом является

$I = x - (u + \rho )t$

Кроме того, в случаях 1, 3, 5 имеются дополнительные инварианты порядка не выше второго. Они могут быть получены из найденных инвариантов с помощью действия оператора инвариантного дифференцирования

$\frac{1}{{{{r}_{x}}}}{\kern 1pt} {{\overline {D} }_{x}}$

4. СВЕДЕНИЕ ИСХОДНОЙ СИСТЕМЫ УРАВНЕНИЙ К ОДУ

Запишем исходную систему уравнений (1.1) в терминах инвариантов Римана (при $\gamma \ne 1$)

(4.1)
$\begin{gathered} {{r}_{t}} + \frac{{(1 + \gamma )r + (3 - \gamma )l}}{4}{\kern 1pt} {{r}_{x}} = 0 \hfill \\ {{l}_{t}} + \frac{{(1 + \gamma )l + (3 - \gamma )r}}{4}{\kern 1pt} {{l}_{x}} = 0 \hfill \\ \end{gathered} $

Дополнительные инварианты характеристик позволяют свести большинство задач Коши для соответствующих систем уравнений к системам обыкновенных дифференциальных уравнений (ОДУ). Для этого к системе (4.1) добавим соотношение:

(4.2)
${{I}_{ - }} = h(l)$
между инвариантом Римана l на характеристике ${{C}_{ - }}$ и ее дополнительным инвариантом ${{I}_{ - }}$. Возникающие при этом условия совместности оказываются выполненными автоматически. Если используемый инвариант ${{I}_{ - }}$ корректно определен на начальных данных рассматриваемой задачи Коши, то соотношение (4.2) позволяет определить соответствующую функцию $h(l)$. Интегрирование характеристического поля ${{X}_{ + }}$, рассматриваемого в силу переопределенной системы уравнений (4.1), (4.2), сводится к замкнутой конечной системе ОДУ.

Замечание 2. Порядок инварианта ${{I}_{ - }}$ накладывает ограничения на порядок гладкости подходящих начальных условий.

Ниже при разных значениях параметра $\gamma $ приведены соотношения между инвариантами характеристики ${{C}_{ - }}$ и соответствующие им системы ОДУ.

Случай 1. $\gamma = - 1$. В этом случае, используя соотношение между инвариантами

$(r - l){{l}_{x}} = h(l)$
получаем следующую систему ОДУ:

$\dot {x} = l,\quad \dot {l} = - h(l)$

Случай 2. $\gamma = 1{\text{/}}3$. В этом случае, используя соотношение между инвариантами

$\frac{{{{l}_{{xx}}}(r - l) + 2{{r}_{x}}{{l}_{x}}}}{{{{{(r - l)}}^{3}}l_{x}^{3}}} = h(l)$
получаем следующую систему ОДУ:

$\dot {x} = \frac{{r + 2l}}{3},\quad \dot {r} = 0,\quad \dot {l} = \frac{{l - r}}{3}{{l}_{x}},\quad {{\dot {l}}_{x}} = - \frac{{l_{x}^{2} + {{{(r - l)}}^{3}}h(l)}}{3}$

Случай 3. $\gamma = 5{\text{/}}3$. В этом случае, используя соотношение между инвариантами

$x - tl + \frac{{l - r}}{{2{{l}_{x}}}} = h(l)$
получаем следующую систему ОДУ:

(4.3)
$\dot {x} = \frac{{2r + l}}{3},\quad \dot {r} = 0,\quad \dot {l} = \frac{{{{{(r - l)}}^{2}}}}{{6(x - tl - h(l))}}$

Случай 4. $\gamma = 7{\text{/}}5$. В этом случае, используя соотношение между инвариантами

$x - tl + (l - r)\frac{{2{{l}_{x}}(4{{l}_{x}} - {{r}_{x}}) - (l - r){{l}_{{xx}}}}}{{12l_{x}^{3}}} = h(l)$
получаем следующую систему ОДУ:

(4.4)
$\begin{gathered} \dot {x} = \frac{{3r + 2l}}{5},\quad \dot {r} = 0,\quad \dot {l} = - \frac{{l - r}}{5}{{l}_{x}} \hfill \\ {{{\dot {l}}}_{x}} = - \left( {\frac{{12\left( {x - tl - h(l)} \right)l_{x}^{3}}}{{5(l - r)}} + \frac{{11}}{5}l_{x}^{2}} \right) \hfill \\ \end{gathered} $

Случай 5. $\gamma = 3$. В этом случае, используя соотношение между инвариантами

$x - tl = h(l)$
получаем следующую систему ОДУ:

$\dot {x} = r,\quad \dot {r} = 0$

5. ПРИМЕРЫ РЕШЕНИЙ БЕЗ ГРАДИЕНТНОЙ КАТАСТРОФЫ

В монографии [7] приводится следующий критерий невозможности наступления градиентной катастрофы в решении гладкой задачи Коши для системы уравнений (4.1) при $ - 1 < \gamma \leqslant 3$:

$r{\kern 1pt} _{0}^{'}(x) \geqslant 0,\quad l{\kern 1pt} _{0}^{'}(x) \geqslant 0$

Далее рассмотрим две задачи Коши на всей пространственной оси для различных $\gamma $:

(5.1)
$\begin{gathered} (a):\;{{r}_{0}}(x) = \exp (x) + \exp ( - {{x}^{2}}),\quad {{l}_{0}}(x) = \exp (x) \\ (b):\;{{r}_{0}}(x) = 2{\text{arctg}}(x) + \exp ( - {{x}^{2}}),\quad {{l}_{0}}(x) = 2{\text{arctg}}(x) \\ \end{gathered} $

В соответствующих решениях невозможно наступление градиентной катастрофы.

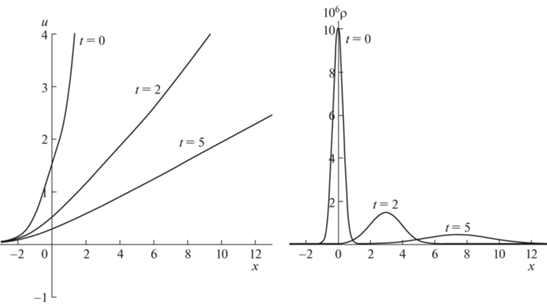
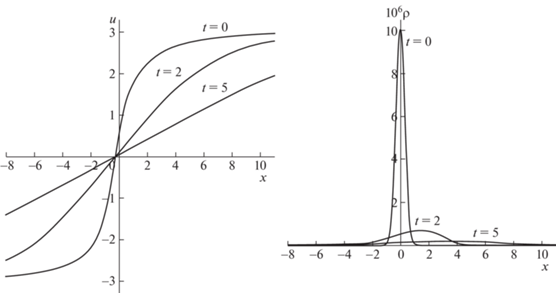
5.1. Случай $\gamma = 5{\text{/}}3$

В этом случае начальным условиям (5.1) соответствуют начальные скорость и плотность

$(a):\;{{u}_{0}} = \exp (x) + \frac{1}{2}\exp ( - {{x}^{2}}),\quad {{\rho }_{0}} = \frac{1}{{216}}\exp ( - 3{{x}^{2}})$
$(b):\;{{u}_{0}} = 2{\text{arctg}}(x) + \frac{1}{2}\exp ( - {{x}^{2}}),\quad {{\rho }_{0}} = \frac{1}{{216}}\exp ( - 3{{x}^{2}})$

При этом начальные масса, импульс и энергия в законах сохранения (1.2) конечны, а начальная скорость в задаче (b) ограничена. Соотношение между инвариантами при $t = 0$

$x + \frac{{{{l}_{0}} - {{r}_{0}}}}{{2l_{0}^{'}}} = h({{l}_{0}})$
позволяет определить соответствующие функции $h(l)$:

$(a):\;h(l) = \ln l - \frac{1}{{2{{l}^{{\ln l + 1}}}}}$
$(b):\;h(l) = {\text{tg}}\left( {\frac{l}{2}} \right) - \frac{1}{4}\exp \left( { - {\text{t}}{{{\text{g}}}^{2}}\left( {\frac{l}{2}} \right)} \right)\left( {{\text{t}}{{{\text{g}}}^{2}}\left( {\frac{l}{2}} \right) + 1} \right)$

Результаты численного исследования решений рассматриваемых задач Коши с помощью системы уравнений (4.3) представлены на рис. 1, 2.

Рис. 1.

Задача Коши (a) для $\gamma = 5{\text{/}}3$ в моменты t = 0, 2, 5.

Рис. 2.

Задача Коши (b) для $\gamma = 5{\text{/}}3$ в моменты t = 0, 2, 5.

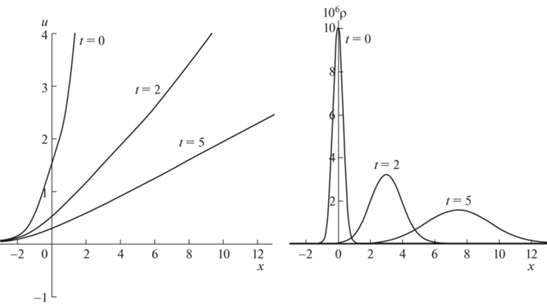
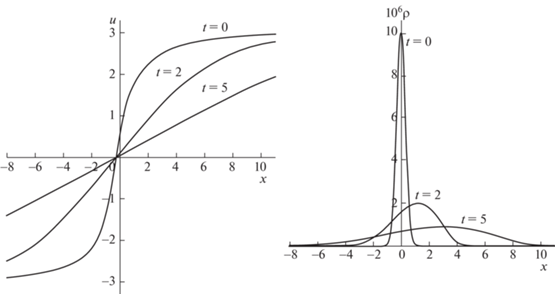
5.2. Случай $\gamma = 7{\text{/}}5$

В этом случае начальным условиям (5.1) соответствуют начальные скорость и плотность

$(a):\;{{u}_{0}} = \exp (x) + \frac{1}{2}\exp ( - {{x}^{2}}),\quad {{\rho }_{0}}{{ = 10}^{{ - 5}}}\exp ( - 5{{x}^{2}})$
$(b):\;{{u}_{0}} = 2{\text{arctg}}(x) + \frac{1}{2}\exp ( - {{x}^{2}}),\quad {{\rho }_{0}}{{ = 10}^{{ - 5}}}\exp ( - 5{{x}^{2}})$

При этом начальные масса, импульс и энергия в законах сохранения (1.2) также конечны, а начальная скорость в задаче (b) ограничена. Соотношение между инвариантами при t = 0

$x + ({{l}_{0}} - {{r}_{0}})\frac{{2l_{0}^{'}(4l_{0}^{'} - r_{0}^{'}) - ({{l}_{0}} - {{r}_{0}})l_{0}^{{''}}}}{{12l_{0}^{'}}} = h({{l}_{0}})$
позволяет определить соответствующие функции $h(l)$:

$(a):\;h(l) = \ln l - \frac{1}{3}{{l}^{{ - 2(\ln l + 1)}}}\ln l - \frac{1}{2}{{l}^{{ - (\ln l + 1)}}} - \frac{1}{{12}}{{l}^{{ - 2(\ln l + 1)}}}$
$\begin{gathered} (b):\;h(l) = {\text{tg}}\left( {\frac{l}{2}} \right) - \exp \left( { - 2{\text{t}}{{{\text{g}}}^{2}}\left( {\frac{l}{2}} \right)} \right)\left( {\frac{1}{2}{\text{t}}{{{\text{g}}}^{5}}\left( {\frac{l}{2}} \right) + \frac{1}{8}{\text{t}}{{{\text{g}}}^{3}}\left( {\frac{l}{2}} \right) + \frac{1}{{24}}{\text{tg}}\left( {\frac{l}{2}} \right)} \right) - \\ \; - \frac{1}{4}\exp \left( { - {\text{t}}{{{\text{g}}}^{2}}\left( {\frac{l}{2}} \right)} \right)\left( {{\text{t}}{{{\text{g}}}^{2}}\left( {\frac{l}{2}} \right) + 1} \right) \\ \end{gathered} $

Результаты численного исследования решений рассматриваемых задач Коши с помощью системы уравнений (4.4) представлены на рис. 3, 4.

Рис. 3.

Задача Коши (a) для $\gamma = 7{\text{/}}5$ в моменты t = 0, 2, 5.

Рис. 4.

Задача Коши (b) для $\gamma = 7{\text{/}}5$ в моменты t = 0, 2, 5.

ЗАКЛЮЧЕНИЕ

Для некоторых уравнений состояния найдены инварианты характеристик порядка два, дополнительные к инвариантам Римана. Дополнительные инварианты характеристик позволяют свести решения задач Коши к решению систем ОДУ и построить решения без градиентной катастрофы. Результаты исследования могут быть использованы при апробации численных методов решения уравнений газовой динамики.

Список литературы

  1. Riemann B. Über die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite // Aus dem achten Bande der Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, Mathematischphysikalische Klasse. 1860. Band 8. Nr. 43. S. 43–66. [Retrieved from https://eudml.org/doc/135717]

  2. Darboux M.G. Sur la théorie des équations aux dérivées partielles du second ordre // Comptes rendus hebdomadaires des sкnces de l’Académie des sciences Paris. 1870. V. 70. P. 675–678.

  3. Darboux M.G. Sur la théorie des équations aux dérivées partielles // Comptes rendus hebdomadaires des séances de l’Académie des sciences Paris. 1870. V. 70. P. 746–749.

  4. Goursat M.E. Leçons sur l’intégration des équations aux deréeves partielles du second order a deux variables indépendantes. Tome II. Paris. 1898. 174 p. (Librairie scientifique A. Hermann)

  5. Капцов О.В. Методы интегрирования уравнений с частными производными. М.: ФИЗМАТЛИТ, 2009. 184 с.

  6. Аксенов А.В. Нелинейные периодические волны в газе // Изв. РАН. МЖГ. 2012. № 5. С. 88–98.

  7. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения к газовой динамике, М.: Наука. Главная редакция физико-математической литературы, 1978. 687 с.

  8. Aksenov A.V., Druzhkov K.P., Kaptsov O.V. Application of invariants of characteristics to construction of solutions without gradient catastrophe // International Journal of Non-Linear Mechanics. 2022. V. 147. № 104249. P. 1–8.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал