Известия РАН. Механика жидкости и газа, 2023, № 1, стр. 115-126

ДВИЖЕНИЕ ПОРШНЯ, РАЗДЕЛЯЮЩЕГО МАГНИТНУЮ И НЕМАГНИТНУЮ ЖИДКОСТИ, В МАГНИТНОМ ПОЛЕ

У. В. Волкова^a, *, Д. И. Меркулов^a, С. А. Калмыков^a, Д. А. Пелевина^a, В. А. Налетова^a

^a МГУ им. М.В. Ломоносова
Москва, Россия

Поступила в редакцию 10.07.2022
После доработки 11.10.2022
Принята к публикации 11.10.2022

EDN: AJJFHX
DOI: 10.31857/S0568528122600485

Аннотация

Теоретически и экспериментально исследовано перекачивание немагнитной жидкости с помощью насоса-дозатора на основе магнитной жидкости, содержащей тело из намагничивающегося материала. Изучен процесс перекачивания жидкости в приложенном вертикальном однородном магнитном поле. Вычислены и измерены зависимости высоты поднятия поршня, разделяющего магнитную и немагнитную жидкости, от времени в постоянном и ступенчатом магнитном поле. Получено хорошее совпадение теории и эксперимента. Вычислена зависимость времени подъема поршня от величины постоянного магнитного поля. Теоретически исследовано движение поршня при выключении магнитного поля.

Ключевые слова: магнитная жидкость, насос-дозатор, однородное магнитное поле

Магнитная жидкость – это коллоидный раствор ферромагнитных частиц микро и наноразмеров в несущей жидкости. Основы физики и гидродинамики магнитной жидкости и двухфазных магнитных систем изложены в [1–3]. В [4] изложены различные модели магнитной жидкости и приведены решения классических задач феррогидродинамики. Изменение формы поверхности магнитной жидкости в неоднородных магнитных полях может применяться в технике, в частности, при создании насосов, дозаторов и клапанов.

Методы определения статической формы свободной поверхности магнитной жидкости предложены в [5, 6]. В работе [5] представлены результаты численного расчета формы свободной поверхности капли магнитной жидкости, удерживаемой магнитным полем намагничивающего клина на наклонной плоскости, а также формы свободной поверхности бесконечного объема магнитной жидкости, расположенной около острия клина, при увеличении внешнего поля. В работе [6] проведены экспериментальные и теоретические исследования деформации поверхности магнитной жидкости, содержащей намагничивающийся цилиндр, в однородном приложенном магнитном поле разного направления. В работах [7, 8] рассмотрена динамика формы поверхности тонкого слоя магнитной жидкости в поле проводника с током [7] и формы поверхности капли вязкой магнитной жидкости, во вращающемся однородном магнитном поле [8].

В [9–11] экспериментально и теоретически исследован линейный перистальтический насос на основе магнитной жидкости. Перекачивание происходит за счет волнообразной деформации поверхности магнитной жидкости в переменных периодических магнитных полях системы электромагнитов. В [12, 13] разработан перистальтический насос на основе магнитной жидкости в бегущем магнитном поле вращающегося постоянного магнита. Из-за вращения магнита происходит течение магнитной жидкости и перекачивание немагнитной жидкости. В [14] предложен перистальтический насос на основе волнообразной деформации поверхности магнитной жидкости и упругой мембраны в пульсирующем периодическом магнитном поле. В [15] аналитически получено существование ненулевого среднего расхода при двухслойном течении вязких несжимаемых жидкостей, с разными магнитными свойствами, в неоднородном бегущем магнитном поле, которое может быть создано при помощи движущихся намагничивающихся тел в однородном постоянном приложенном магнитном поле.

В работе [16] представлен прототип пипетки, в котором объем магнитной жидкости использован в качестве поршня, положением которого управляет электромагнит. В прототипе, описанном в [17], поршень из магнитной жидкости перемещается при помощи постоянного магнита. В [18] теоретически рассмотрено движение поршня из магнитной жидкости в цилиндрическом канале в поле магнитного диполя. В работах [19, 20] представлен прототип насоса, в котором деформация капель магнитной жидкости в поле нескольких электромагнитов использована как для создания поршня, так и клапанов, предотвращающих обратный ток перекачиваемой жидкости. В прототипе [21] клапаны и поршень реализованы при помощи перемещения капель магнитной жидкости постоянными магнитами. В [22–24] экспериментально исследована работа схожих прототипов насоса с сосудом особой формы, в котором объем магнитной жидкости вращается постоянным магнитом и перекачивает немагнитную жидкость.

В работах, приведенных выше, описаны насосы, управляемые неоднородным магнитным полем, создаваемым при помощи постоянных магнитов или электромагнитов. При таком способе создания поля трудно уменьшить размер устройства и необходим подвод энергии к магнитам. В отличие от этих работ в данной статье использовано внешнее однородное управляющее магнитное поле, а неоднородность магнитного поля создается хорошо намагничивающимся телом внутри магнитной жидкости. Это позволяет создать насосы-дозаторы малых размеров для перекачивания небольших объемов жидкости.

В статье теоретически и экспериментально исследовано движение поршня, разделяющего магнитную и немагнитную жидкости в однородном вертикальном приложенном магнитном поле. Магнитная жидкость содержит сферическое тело из хорошо намагничивающегося материала. Объем жидкостей в кювете в приложенном магнитном поле может меняться за счет притока или оттока жидкостей через тонкие каналы круглого сечения. При включении поля магнитная жидкость поднимает поршень и вытесняет немагнитную жидкость, а при выключении магнитного поля поршень опускается. Теоретически и экспериментально показана возможность использования магнитной жидкости, содержащей тело из намагничивающегося материала, для перекачивания и дозирования немагнитной жидкости в однородном магнитном поле.

1. ЭКСПЕРИМЕНТ

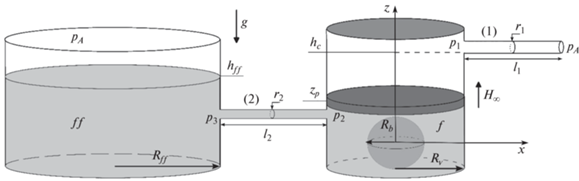
Пусть магнитная жидкость находится в закрытом сверху цилиндрическом сосуде f радиуса R_v, полностью покрывает сферическое тело с магнитной проницаемостью μ_b из намагничивающегося материала радиуса R_b, закрепленное в центре дна сосуда, а также полностью смачивает поршень (массой M_p, площадью S_p, толщиной d_p), разделяющий магнитную и немагнитную жидкости (см. рис. 1). Введем вертикальную ось z, которая проходит через ось цилиндрического сосуда. В центре сферического тела z = 0. Далее индексы p, b, s, f обозначают параметры поршня, сферического тела, перекачиваемой жидкости, магнитной жидкости. Магнитная жидкость в сосуде f сообщается с открытой кюветой ff по каналу 2 (радиуса r₂, длиной l₂ и площадью S₂= π$r_{2}^{2}$). Ось канала 2 расположена на высоте z = R_b. Кювета ff имеет радиус R_ff, площадь S_ff и наполнена магнитной жидкостью до уровня z = h_ff(t). Поверх поршня в сосуде f налита немагнитная жидкость. Немагнитная жидкость может вытекать по каналу 1 (радиуса r₂, длиной l₁ и площадью S₁= π$r_{2}^{2}$). Координата z оси канала 1 обозначена h_c. Канал 1 отделяется от сосуда f клапаном. В начальный момент времени масло налито до сливного отверстия и полностью заполняет сливной канал 1. Эксперимент проводился при параметрах, указанных в табл. 1.

Рис. 1.

Схема экспериментальной установки.

Таблица 1.

Параметры экспериментальной установки и жидкостей, использованных в эксперименте

Магнитная жидкость	Немагнитная жидкость	Намагничивающееся тело
ρ_f = 1.1 г/см³	ρ_s = 0.87 г/см³	R_b = 0.6 см
μ_f = 1.3	μ_s = 1	μ_b = 100
η_f = 0.01 П	η_s = 0.02 П
Поршень	Размеры установки
M_p = 0.25 г	h_c = 2 см	${{R}_{{v}}}$ = 0.615 см
S_p = 1.16 см³	z₀ = 0.68 см	S_ff = 11.946 см²
d_p = 0.3 см	l₁ = 2.8 см, l₂ = 28.5 см	r_1,2 = 0.155 см²

В эксперименте была использована магнитная жидкость на основе воды с магнетитовыми микрочастицами и вазелиновое масло в качестве перекачиваемой немагнитной жидкости. Цилиндрический сосуд f помещается в центр системы катушек в область однородного поля. Однородное вертикальное магнитное поле H_∞ создается электромагнитными катушками Гельмгольца радиуса R_H ≫ ${{R}_{{v}}}$. Кювета ff находится вне действия магнитного поля катушек. При включении магнитного поля уровень магнитной жидкости в сосуде f над сферическим телом увеличивается из-за притока магнитной жидкости из кюветы ff по каналу 2, поршень поднимается, и немагнитная жидкость вытекает из канала 1 (см. рис. 2). На рис. 2 представлены фотографии равновесного положения поршня (поршень покрашен в белый цвет) при разных полях H_∞.

Рис. 2.

Фотографии кюветы f экспериментального прототипа: H_∞ = 0,100, 200 Э (а, б, в). В экспериментальной кювете на фотографиях: серая область – немагнитная жидкость, белая область – поршень, черная область – магнитная жидкость.

Постоянное магнитное поле. При включении постоянного магнитного поля H_∞ = 100 Э поршень начинает подниматься и через некоторое время t_p занимает равновесное положение. Процесс подъема поршня фиксируется на камеру. Раскадровка видео позволяет построить график зависимости z_p от времени t, который изображен на рис. 3a точками.

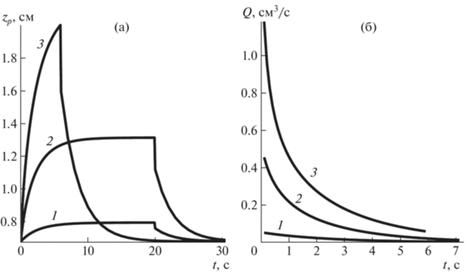
Рис. 3.

Зависимость координаты z_p от времени t (точки – эксперимент, линия – теория): при постоянном магнитном поле H_∞ = 100 Э (а), при ступенчатом магнитном поле (ΔH_∞= 6.2 Э, Δt = 75 c) (б).

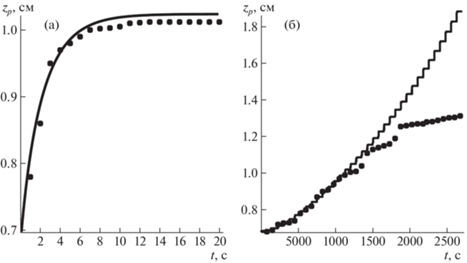
Ступенчатое магнитное поле. В этой серии экспериментов использовалось переменное ступенчатое магнитное поле: постоянное магнитное поле удерживается в течение Δt = 75 c, затем увеличивается на ΔH_∞ = 6.2 Э. Магнитное поле увеличивалось до максимального значения H_max = 223 Э, при котором поршень находится на уровне сливного отверстия. В эксперименте на каждом шаге по полю, когда устанавливается равновесное положение поршня, делается фотография. После обработки фотографий эксперимента построена экспериментальная зависимость вертикальной координаты поршня z_p от времени t, эта зависимость обозначена точками на рис. 3б.

Таким образом, экспериментально показана возможность использования магнитной жидкости, содержащей тело из намагничивающегося материала, для перекачивания и дозирования немагнитной жидкости, а также возможность управления работой прототипа с помощью однородного магнитного поля.

2. МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ПОРШНЯ, РАЗДЕЛЯЮЩЕГО МАГНИТНУЮ И НЕМАГНИТНУЮ ЖИДКОСТИ

Постановка задачи. Рассмотрим задачу о движении поршня, разделяющего магнитную и немагнитную жидкости, в приложенном однородном вертикальном магнитном поле H_∞. В начальный момент времени включается однородное вертикальное магнитной поле напряженностью H_∞ и открывается клапан в канале 1. При включенном поле поршень из-за магнитных сил начинает двигаться вверх, тем самым выталкивая немагнитную жидкость в сливной канал 1. Далее в некоторый момент времени t_p магнитное поле выключается H_∞ = 0, а клапан в канале 1 закрывается. При выключенном поле поршень опускается и сверху осуществляется залив перекачиваемой жидкости. Положение поршня в любой момент времени определяет координата его контакта с магнитной жидкостью – z_p. Сделаем следующие предположения: намагниченность магнитной жидкости линейно зависит от напряженности магнитного поля M_f = χ_fH, χ_f = const (μ_f = 1 + 4πχ_f); намагниченность окружающей среды равна нулю M_s = 0, χ_s = 0; намагниченность тела линейно зависит от напряженности магнитного поля M_b = χ_bH, χ_b = const (μ_b = 1 + 4πχ_b). Задача решается c учетом силы тяжести, в безындукционном приближении χ_f ≪ 1.

Закон движения поршня имеет вид:

(1)

${{M}_{p}}{{\ddot {z}}_{p}} = - {{M}_{p}}g + {{S}_{p}}\left( {{{p}_{f}}\left( {z = {{z}_{p}}} \right) - {{p}_{s}}\left( {z = {{z}_{p}} + {{d}_{p}}} \right)} \right) + \mathop \smallint \limits_{{{S}_{p}}}^{} \left[ {{{\tau }_{{zz}}}} \right]_{f}^{s}{{\left. \right|}_{{z = {{z}_{p}}}}}dS$

Тензор напряжений в невязких жидкостях имеет вид:

(2)

${{p}_{{ij}}} = - p{{g}_{{ij}}} + {{\tau }_{{ij}}},\quad {{\tau }_{{ij}}} = \frac{{{{H}_{i}}{{B}_{j}}}}{{4\pi }} - \frac{{HB}}{{8\pi }}{{g}_{{ij}}}$

где g_ij = e_i × e_j – компоненты метрического тензора.

До момента включения магнитного поля жидкости находятся в покое и в равновесии. Координату поршня z_p, координату поверхности жидкости в кювете ff и скорость поршня в начальный момент t = 0 обозначим следующим образом:

(3)

$t = 0{\text{\;}}:{{z}_{p}} = {{z}_{0}},\quad {{h}_{{ff}}} = {{h}_{{ff0}}},\quad {{\dot {z}}_{p}} = 0$

Отметим, что h_ff0 зависит от начального положения поршня z₀ ≥ R_b, высоты сливного отверстия h_c, до которого налита немагнитная жидкость, и других параметров задачи следующим образом:

(4)

${{h}_{{ff0}}} = {{z}_{0}}\left( {1 - \frac{{{{\rho }_{s}}}}{{{{\rho }_{f}}}}} \right) + ({{h}_{c}} - {{d}_{p}})\frac{{{{\rho }_{s}}}}{{{{\rho }_{f}}}} + \frac{{{{M}_{p}}}}{{{{\rho }_{f}}{{S}_{p}}}}~$

На поверхности раздела магнитной жидкости и поршня при z = z_p за счет скачка магнитных свойств среды существует скачок тензора Максвелловских напряжений τ_ij. Скачок τ_zz при z = = z_p с учетом непрерывности вектора H_τ и компоненты B_n в безындукционном приближении имеет вид [4]:

(5)

$\left[ {{{\tau }_{{zz}}}} \right]_{f}^{s}\left( {z = {{z}_{p}}} \right) \approx \frac{{{{\mu }_{f}} - 1~}}{{8\pi }}{{H}^{2}}\left( {z = {{z}_{p}}} \right)$

При расчетах в сосудах ff и f пренебрегаем течением жидкостей, так как скорость в данных сосудах мала (${{R}_{{v}}}$ ≫ max (r₂, r₂)). Уравнения гидростатики жидкостей в сосуде f при χ_i = const имеют вид:

(6)

$ - \nabla {{p}_{i}} + {{\rho }_{i}}g = 0~{\text{,}}\quad i = f,s~$

Проинтегрировав уравнения (6), получим формулу для давлений в жидкостях в сосуде f:

(7)

${{p}_{i}} = {{C}_{i}} - {{\rho }_{i}}~gz,\quad i = f,s$

С учетом (2), (5), (7) уравнение движения поршня (1) может быть записано в виде

(8)

${{M}_{p}}{{\ddot {z}}_{p}} = - {{M}_{p}}g - g{{S}_{p}}\left( {{{\rho }_{f}}{{z}_{p}} - {{\rho }_{s}}\left( {{{z}_{p}} - {{d}_{p}}} \right)} \right) + ({{C}_{f}} - {{C}_{s}}){{S}_{p}} + \mathop \smallint \limits_{{{S}_{p}}}^{} \frac{{\left( {{{\mu }_{f}} - 1} \right){{H}^{2}}\left( {z = {{z}_{p}}} \right)}}{{8\pi }}dS{\text{\;}}$

Константы C_f и C_s в формуле (8) определяются из граничных условий, которые в случае наличия и отсутствия магнитного поля на поверхности кюветы ff отличаются друг от друга. Кроме того, важно, поднимается ли поршень или опускается. Одно из граничных условий сохраняется в любом случае: над поверхностью магнитной жидкости в сосуде ff в окружающей среде давление равно атмосферному p = p_A.

Уравнение движения поршня вверх в однородном магнитном поле. Когда магнитное поле H_∞ включено, поршень поднимается и жидкости текут в каналах 1 и 2. Жидкости считаются несжимаемыми, поэтому расход в сосудах f, ff и тонких каналах 1, 2 одинаковый:

(9)

${{S}_{p}}~{\text{|}}{{\dot {z}}_{p}}{\text{|}} = {{S}_{1}}{{u}_{{m1}}} = {{S}_{{ff}}}{\text{|}}{{\dot {h}}_{{ff}}}{\text{|}} = {{S}_{2}}{{u}_{{m2}}},\quad {{h}_{{ff}}} = {{h}_{{ff0}}} - \frac{{{{S}_{p}}}}{{{{S}_{{ff}}}}}\left( {{{z}_{p}} - {{z}_{0}}} \right)$

Здесь h_ff(t) – вертикальная координата поверхности магнитной жидкости в сосуде ff; u_m1 – средняя скорость, с которой течет перекачиваемая жидкость из сливного отверстия в канале 1; u_m2 – средняя скорость, с которой течет магнитная жидкость из кюветы в сосуд f с поршнем в канале 2. Предполагается, что в тонких длинных трубках устанавливается течение Пуазейля, и имеет место следующая связь средней скорости и перепада давления в каналах:

(10)

${{u}_{{m1}}} = \frac{{\left| {{{p}_{1}} - {{p}_{A}}} \right|}}{{{{k}_{1}}}}~,\quad {{k}_{1}} = \frac{{8\pi {{\eta }_{s}}{{l}_{1}}}}{{{{S}_{1}}}},\quad {{u}_{{m2}}} = \frac{{\left| {{{p}_{3}} - {{p}_{2}}} \right|}}{{{{k}_{2}}}}~,\quad {{k}_{2}} = \frac{{8\pi {{\eta }_{f}}{{l}_{2}}}}{{{{S}_{2}}}}$

Здесь p₁ – давление жидкости в сосуде f на уровне канала 1, p_A – атмосферное давление на выходе канала 1, p₃ и p₂ – давление магнитной жидкости на концах канала 2, η_s, η_f – коэффициенты динамической вязкости немагнитной и магнитной жидкостей. Считается, что на выходе из канала 1 (как и на поверхности магнитной жидкости в сосуде ff) давление равно атмосферному. На свободной поверхности магнитной жидкости в кювете ff при z = h_ff поле равно нулю и выполнено условие:

(11)

${{p}_{f}}\left( {z = {{h}_{{ff}}}} \right) = {{p}_{A}}$

С учетом граничного условия на поверхности раздела жидкостей в кювете ff выражение (11) для давления в магнитной жидкости в кювете ff при z = R_b (на входе в канал 2) имеет вид:

(12)

${{p}_{3}} = {{p}_{A}} + {{\rho }_{f}}g\left( {{{h}_{{ff}}} - {{R}_{b}}} \right)$

С учетом (9), (10) и (12) выпишем выражение для константы C_f в выражении для давления в магнитной жидкости:

(13)

${{C}_{f}} = {{p}_{A}} + {{\rho }_{f}}g{{h}_{{ff}}} - {{\dot {z}}_{p}}\frac{{{{S}_{p}}{{k}_{2}}}}{{{{S}_{2}}}}$

Теперь определим константу C_s в выражении для давления в немагнитной жидкости в сосуде ff. С учетом (9) и (10), считая, что на выходе из канала 1 при z = h_c давление атмосферное, выражение для C_sимеет вид:

(14)

${{C}_{s}} = {{\dot {z}}_{p}}\frac{{{{S}_{p}}{{k}_{1}}}}{{{{S}_{1}}}} + {{p}_{A}} + {{\rho }_{s}}g{{h}_{c}}$

Подставляя в закон движения (8) выражения (13), (14) с учетом (4), (9) получим следующее дифференциальное уравнение относительно z_p ($\rho _{f}^{*}$ = ρ_f + ρ_fS_p/S_ff):

(15)

$\begin{gathered} {{M}_{p}}{{{\ddot {z}}}_{p}} = ~ - S_{p}^{2}\left( {\frac{{{{k}_{2}}}}{{{{S}_{2}}}} + \frac{{{{k}_{1}}}}{{{{S}_{1}}}}} \right){{{\dot {z}}}_{p}} + {{S}_{p}}g({{\rho }_{s}} - \rho _{f}^{*}){{z}_{p}} - {{M}_{p}}g + {{\rho }_{f}}g{{S}_{p}}\left( {{{h}_{{ff0}}} + \frac{{{{S}_{p}}}}{{{{S}_{{ff}}}}}{{z}_{0}}} \right) - \\ \, - {{\rho }_{s}}g{{S}_{p}}~({{h}_{c}} - {{d}_{p}})~ + \mathop \smallint \limits_{{{S}_{p}}}^{} \frac{{\left( {{{\mu }_{f}} - 1} \right){{H}^{2}}~}}{{8\pi }}dS{\text{\;}}~ \\ \end{gathered} $

Выражение для квадрата модуля магнитного поля в безындукционном приближении равно квадрату магнитного поля вне сферического тела и имеет вид [25]:

(16)

${{H}^{2}} = H_{\infty }^{2}\left( {\frac{{9{{z}^{2}}({{x}^{2}} + {{y}^{2}}){{D}^{2}}}}{{{{{({{z}^{2}} + {{x}^{2}} + {{y}^{2}})}}^{5}}}} + {{{\left( {1 + \frac{D}{{{{{({{z}^{2}} + {{x}^{2}} + {{y}^{2}})}}^{{\frac{3}{2}}}}}} - \frac{{3{{z}^{2}}D}}{{{{{({{z}^{2}} + {{x}^{2}} + {{y}^{2}})}}^{{\frac{5}{2}}}}}}} \right)}}^{2}}} \right),\quad D = {{R}^{3}}\frac{{{{\mu }_{s}} - {{\mu }_{b}}}}{{2{{\mu }_{s}} + {{\mu }_{b}}}}$

Интеграл F_M = (μ_f – 1)$\int_{Sp} {{{H}^{2}}} $dS/8π назовем магнитной силой, эта сила линейно зависит от магнитной проницаемости μ_f и от квадрата приложенного магнитного поля H_∞, и нелинейно зависит от координаты поршня z_p. Из-за наличия этой магнитной силы уравнение движения поршня вверх в магнитном поле (15) является нелинейным и решается численно.

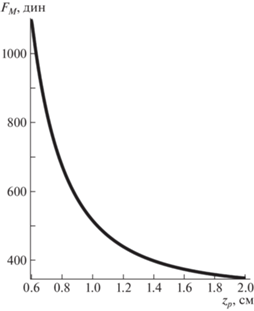
Численные расчеты в случае постоянного магнитного поля. Рассмотрим случай постоянного магнитного поля H_∞ = const. График зависимости магнитной силы F_M, действующей на поршень, от координаты поршня z_p при H_∞ = 150 Э приведен на рис. 4. По данному графику видно, что чем ближе поршень к сферическому телу z_p ≈ R_b, которое искажает приложенное поле, тем действующая на поршень сила больше. Когда поршень удаляется от сферического намагничивающегося тела, то сила убывает.

Рис. 4.

Зависимость магнитной силы F_M, действующей на поршень, от координаты поршня z_p при H_∞ = 150 Э.

Уравнение движения (15) решается с учетом выражения для магнитного поля (16) с начальными условиями (3). Написана программа в пакете Maple, в которой методом Рунге-Кутты 4 порядка рассчитывается движение поршня. Все расчеты здесь и далее проведены при экспериментальных параметрах, указанных в таблице.

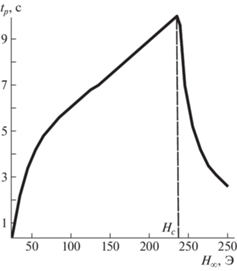
Графики зависимости координаты поршня z_p и расхода немагнитной жидкости Q от времени при различных H_∞ приведены на рис. 5а и 5б. На рис. 5а монотонно возрастающие части графиков соответствуют подъему поршня. На графиках линия 1 – H_∞ = 50 Э, 2 – H_∞ = 150 Э, 3 – H_∞ = = 300 Э. Чем большее приложенное магнитное поле H_∞, тем больше скорость и, соответственно, расход жидкости. Скорость поршня и расход жидкости максимальны в начальный момент времени, сразу после включения магнитного поля, и уменьшаются до нуля с течением времени, когда поршень останавливается. Максимум графиков на рис. 5а в приложенном магнитном поле H_∞ < H_c (H_c – поле, при котором равновесное положение поршня совпадает с координатой сливного отверстия) достигается в тот момент времени, когда скорость движения поршня становится мала (рис. 5а линии 1 и 2), и поршень занимает свое равновесное положение. При H_∞ = H_c = 239 Э равновесное положение поршня совпадает с вертикальной координатой сливного отверстия z_p = h_c. При H_∞ > H_c расчет подъема поршня прекращается, когда координата поршня достигает сливного отверстия (рис. 5а линия 3). Время движения поршня t_p – это время, за которое при соответствующем приложенном магнитном поле H_∞ < H_c устанавливается равновесие поршня, или в случае H_∞ > H_c – это время, за которое поршень достигает координаты сливного отверстия z_p = h_c. Эта зависимость имеет максимум при H_∞ = H_c, и для полей, больших этого значения, резко убывает. График зависимости времени движения поршня t_p от приложенного магнитного поля H_∞ построен на рис. 6. На рис. 3а приведены теоретическая и экспериментальная зависимости координаты поршня z_p от времени t при H_∞ = 100 Э. Видно хорошее совпадение теории и эксперимента.

Рис. 5.

Теоретические зависимости при разных H_∞ : 50, 150, 300 Э (1–3) (a) – z_p(t), (б) – Q(t).

Рис. 6.

Теоретическая зависимость времени подъема поршня t_p от H_∞ (H_c = 239 Э).

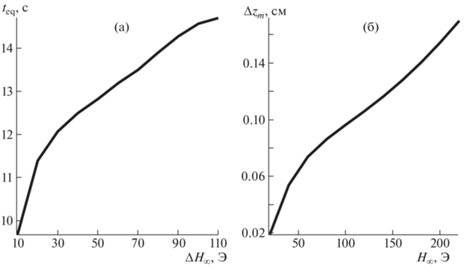
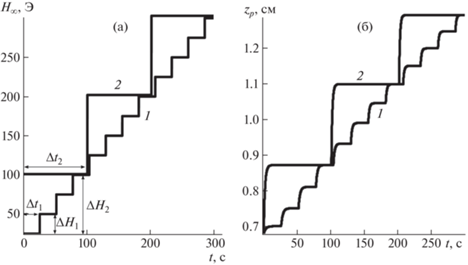
Численные расчеты в случае ступенчатого магнитного поля H_∞(t). Магнитное поле H_∞ может меняться со временем. Например, рассмотрим ступенчатые функции H_∞(t) = ΔH[t/Δt], где [t/Δt] – целая часть числа. Ступенчатое магнитное поле позволяет дозировать поток перекачиваемой жидкости, а также обеспечить более равномерный расход жидкости. Для наглядности рассмотрим два случая. На рис. 7a изображены зависимости поля, меняющегося скачками при ΔH₁ = 25 Э, Δt₁ = 25 с (линия 1) и при ΔH₂ = 100 Э, Δt₂ = 100 с (линия 2). На рис. 7б изображена зависимость вертикальной координаты поршня от времени для таких ступенчатых полей (линии 1 и 2 соответственно). При увеличении поля скачком на ΔH_∞ поршень начинает подниматься, и за время t_eq устанавливается новое положение равновесия выше на Δz. Теоретическая зависимость времени t_eq от величины скачка магнитного поля ΔH_∞ показана на рис. 8а. При увеличении скачка поля ΔH_∞, время t_eq возрастает. При достаточно больших полях ~100 Э время t_eq выходит на постоянное значение t_eq ≈ 15 с, при указанных в таблице параметрах. Отметим, что в эксперименте, рассмотренном выше, Δt > 15 с, поэтому на каждом шаге поршень выходит на равновесное положение. Можно отметить, что максимальное изменение вертикальной координаты поршня Δz_m возрастает с ростом значения ступенчатого поля H_∞(t), а значит со временем t (см. рис. 8б). Это означает, что ступенчатое магнитное поле с одинаковыми ступеньками не гарантирует одинаковый подъем поршня при каждом изменении ступенчатого поля.

Рис. 7.

Примеры ступенчатого изменения поля H_∞(t) от времени (а). Теоретическая зависимость z_p от t для этих примеров (б).

Рис. 8.

Теоретические зависимости: (a) – t_eq (H_∞), (б) – Δz_m (H_∞).

На рис. 3б приведены теоретические и экспериментальные зависимости z_p от t в ступенчатом поле, использованном в эксперименте. Видно хорошее совпадение теории и эксперимента, при малых временах, соответствующих малым магнитным полям H_∞ < 100 Э. При больших временах, соответствующих большим полям H_∞ > 120 Э, наблюдается расхождение теории и эксперимента, связанное с тем, что при этих полях надо учитывать зависимость магнитной проницаемости от H (μ_f= μ_f(H)) и магнитная сила при этом становится меньше силы, рассчитанной теоретически при μ_f= const.

Уравнение движения поршня при выключении магнитного поля. Пусть после включения поля H_∞ поршень поднялся до уровня h_cc > z₀, величина h_cc ограничена h_cc ≤ h_c. И в этот момент t = t_cc поле выключается. Поршень начинает опускаться. Вид уравнения движения поршня при выключении магнитного поля существенно зависит от способа залива перекачиваемой жидкости. Будем считать, что пространство между z = z_p и z = h_c мгновенно заполняется перекачиваемой жидкостью, и при z = h_c поддерживается давление p_s = p_A. При этом уравнение движения поршня имеет вид, отличающийся от уравнения (15). Выражение для константы C_s при указанных выше граничных условиях имеет вид:

(17)

${{C}_{s}} = {{p}_{A}} + {{\rho }_{s}}g{{h}_{c}}$

Для определения C_f учтем, что p_f = p_A при z = h_ff в сосуде ff. Давление магнитной жидкости в сосуде ff при z = R_b этом имеет вид:

(18)

${{p}_{3}} = {{p}_{A}} + {{\rho }_{f}}\left( {{{h}_{{ff}}} - {{R}_{b}}} \right)$

Давление магнитной жидкости в сосуде f при z = R_b равно:

(19)

${{p}_{2}} = {{C}_{f}} - {{\rho }_{f}}g{{R}_{b}}$

Так как p₂ – p₃ = k₂u_m2 и p₂ > p₃, то выражение для C_f имеет вид:

(20)

${{C}_{f}} = {{p}_{A}} - {{\rho }_{f}}g{{h}_{{ff}}} + {{k}_{2}}{{u}_{{m2}}}$

Величина h_ff(t) связана с z_p законом сохранения массы магнитной жидкости:

(21)

$\left( {{{h}_{{ff}}}\left( t \right) - {{h}_{{ff}}}\left( {t = {{t}_{{cс}}}} \right)} \right){{S}_{{ff}}} = ({{h}_{{cc}}} - {{z}_{p}}){{S}_{p}}$

Здесь h_cc = z_p(t = t_cc) – положение поршня в момент выключения магнитного поля. Величины h_cc(t = t_cc) и h_ff(t = t_cc) определяются из решения задачи при 0 ≤ t ≤ t_cc, когда магнитное поле включено (H_∞ ≠ 0). Из закона сохранения массы следует выражение для h_ff (K = V_f/S_ff, здесь V_f – объем магнитной жидкости, при z > 0, V_f = const):

(22)

${{h}_{{ff}}} = {{h}_{{ff}}}\left( {t = {{t}_{{сс}}}} \right) + \frac{{\left( {{{h}_{{cc}}} - {{z}_{p}}} \right)~{{S}_{p}}}}{{{{S}_{{ff}}}}} = \frac{{({{h}_{{ff}}}\left( {t = {{t}_{{сс}}}} \right){{S}_{{ff}}} + {{h}_{{cc}}}{{S}_{p}})~}}{{{{S}_{{ff}}}}} - \frac{{{{z}_{p}}{{S}_{p}}}}{{{{S}_{{ff}}}}} = K - \frac{{{{z}_{p}}{{S}_{p}}}}{{{{S}_{{ff}}}}}$

С учетом (9), (17), (20), (22) уравнение для z_p (8) в отсутствие магнитного поля можно записать в виде ($\rho _{f}^{*}$ = ρ_f + ρ_fS_p/S_ff):

(23)

${{M}_{p}}{{\ddot {z}}_{p}} = - {{M}_{p}}g + \frac{{{{k}_{2}}\left| {{{{\dot {z}}}_{p}}} \right|S_{p}^{2}}}{{{{S}_{2}}}} - {{z}_{p}}g{{S}_{p}}(\rho _{f}^{*} - {{\rho }_{s}}) + {{\rho }_{f}}gK{{S}_{p}} - {{\rho }_{s}}g({{h}_{c}} - {{d}_{p}}){{S}_{p}}$

Это уравнение верно при ${{\dot {z}}_{p}} < 0,~{\text{|}}{{\dot {z}}_{p}}{\text{|}} = - {{\dot {z}}_{p}}$. Данное уравнение решается с начальными условиями:

(24)

$t = {{t}_{c}}:{{z}_{p}} = {{h}_{{cc}}},\quad {{\dot {z}}_{p}} = 0$

Уравнение (23) является линейным дифференциальным уравнением второго порядка с постоянными коэффициентами и решается аналитически. Введем обозначения: A = k₂$S_{p}^{2}$/S₂; B = = gS_p($\rho _{f}^{*}$ – ρ_s); C = ρ_fgKS_p – ρ_sg(h_c – d_p)S_p – M_pg. При этом уравнение (23) имеет вид:

(25)

${{M}_{p}}{{\ddot {z}}_{p}} + A~{{\dot {z}}_{p}} + B~{{z}_{p}} - C = 0$

Для дифференциального уравнения (25) можно написать характеристическое уравнение: M_pλ²+ Aλ + B = 0. Из решения характеристического уравнения получаем: λ_1,2 = (–A ± √(A²– ‒ 4BM_p))/2M_p). При параметрах, указанных в таблице A = 1775 [г · с^–1], B = 652 [дин · см^–1], C = 443 [дин], λ₁= –7100 [c^–1], λ₂= –0.37 [c^–1].

Решение дифференциального уравнения второго порядка (25) имеет вид:

(26)

${{z}_{p}} = {{C}_{1}}{{e}^{{{{\lambda }_{1}}t}}} + {{C}_{2}}{{e}^{{{{\lambda }_{2}}t}}} + \frac{С}{В}$

Константы C₁, C₂ находятся из начальных условий (24).

На основании решения (26) можно продолжить графики зависимости координаты поршня от времени. Для параметров, указанных в таблице, данные зависимости показаны на рис. 5а (монотонно убывающие части графиков) при разных значениях постоянного магнитного поля до его выключения.

ЗАКЛЮЧЕНИЕ

Создан прототип насоса-дозатора на основе взаимодействия тела из намагничивающего материала и магнитной жидкости в однородном магнитном поле. Основное достоинство такого прототипа в том, что управление процессом перекачивания происходит бесконтактно с помощью однородного магнитного поля. Это позволяет уменьшать размеры устройства, которые не ограничиваются характерными размерами изменения магнитного поля.

Экспериментальное исследование движения вверх поршня насоса-дозатора при включении постоянного или ступенчатого поля показало возможность управления насосом-дозатором с помощью однородного магнитного поля. Различные способы изменения во времени однородного магнитного поля могут быть использованы для регулирования расхода перекачиваемой жидкости. В частности, ступенчатое изменение магнитного поля позволяет дозировать поток перекачиваемой жидкости, если это необходимо.

Выведены уравнения, описывающие движение поршня, разделяющего магнитную и перекачиваемую жидкости в предложенном прототипе, как при включении магнитного поля, так и при его выключении.

Теоретически рассмотрено движение поршня вниз при выключении магнитного поля для одного из возможных способов залива перекачиваемой жидкости. Выписано аналитическое решение и построены зависимости положения поршня от времени при движении поршня вниз. Эти зависимости позволяют оценить время опускания поршня после выключения магнитного поля.

Численные расчеты движения поршня при включении постоянного магнитного поля позволили получить зависимость времени подъема поршня от величины поля. Эта зависимость имеет максимум при некотором значении магнитного поля, и для полей, больших этого значения, резко убывает. Получено выражение для магнитной силы, действующей на поршень в магнитном поле. Показано, что магнитная сила убывает при удалении поршня от тела, окруженного магнитной жидкостью. Рассчитаны зависимости положения поршня и текущего расхода перекачиваемой жидкости от времени при разных значениях магнитного поля. Показано, что скорость движения поршня и расход растут с ростом величины поля и уменьшаются до нуля со временем.

В случае ступенчатого магнитного поля рассчитана зависимость оптимального времени ожидания равновесия поршня от величины ступеньки переключаемого поля. Обнаружено, что время ожидания ограничено сверху некоторым значением. Это означает, если время выдержки ступеньки поля больше этого значения, то поршень успевает остановиться перед очередным увеличением поля. Вычислена зависимость изменения вертикальной координаты поршня при увеличении поля на очередной ступеньке от величины магнитного поля. Показано, что эта зависимость является возрастающей. Это означает, что ступенчатое магнитное поле с одинаковыми ступеньками не гарантирует одинаковый подъем поршня при каждом изменении поля.

Траектории подъема поршня, рассчитанные численно, как для постоянного, так и для ступенчатого достаточно малых магнитных полей, хорошо совпадают с измеренными в эксперименте.

Работа поддержана Российским научным фондом (№ 20-71-10002).

Список литературы

Neuringer J.L., Rosensweig R.E. Ferrohydrodynamics // The Physics of Fluids. 1964. V. 7. № 12. P. 1927–1937.
Розенцвейг Р. Феррогидродинамика. Пер. с англ. М.: Мир, 1989. С. 357.
Гогосов В.В., Налетова В.А., Шапошникова Г.А. Гидродинамика намагничивающихся жидкостей // Итоги науки и техники. Механика жидкости и газа. 1981. Т. 16. С. 76–208.
Налетова В.А. Лекции по феррогидродинамике. М.: Изд-во ЦПИ при механико-математическом факультете МГУ, 2005. С. 152.
Кирюшин В.В., Параскевопуло О.Р. Форма поверхности капли магнитной жидкости вблизи острия магнитного клина // Изв. РАН. МЖГ. 1992. № 4. С. 113–117.
Пелевина Д.А. Форма свободной поверхности магнитной жидкости с цилиндрическим концентратором магнитного поля // Изв. РАН. МЖГ. 2016. № 6. С. 15–24.
Тятюшкин А.Н. Течение тонкого слоя намагничивающейся жидкости в магнитном поле. // Известия РАН. МЖГ. 2019. № 4. С. 27–32.
Тятюшкин А.Н. Деформация капли невязкой намагничивающейся жидкости в нестационарном магнитном поле // Изв. РАН. МЖГ. 2021. № 5. С. 138–150.
Park G.S., Park S.H. Design of magnetic fluid linear pump // IEEE Trans. Magn. 1999. V. 35. № 5. P. 4058–4060.
Park G.S., Park S.H. New structure of the magnetic fluid linear pump // IEEE Trans. Magn. 2000. V. 36. № 5. P. 370–3711.
Park G.S., Kang S. New Design of the magnetic fluid linear pump to reduce the discontinuities of the pumping forces // IEEE Trans. Magn. 2004. V. 40. № 2. P. 916–919.
Zhao M., Zou J.B., Xu Y.X., Zhao B., Li Y. Investigation of spin travelling wave pump on magnetic fluid // Materials Research Innovations. 2015. V. 19. № 5. P. 429–432.
Zhao Meng, Zou Jibin, Hu Jianhui, Xu Yongxiang. Analysis of driving capacity on traveling wave pump of magnetic fluid // Abstract Book of 12th International Conference on Magnetic Fluids (ICMF12), Sendai. 2010. P. 138–139.
Ido Y., Tanaka K., Sigiura Y. Fluid transportation mechanisms by a coupled system of elastic membranes and magnetic fluid // Journal of Magnetism and Magnetic Materials. 2002. V. 252. P. 344–346.
Калмыков С.А., Налетова В.А., Пелевина Д.А., Турков В.А. Двухслойное течение намагничивающихся жидкостей // Изв. РАН. МЖГ. 2013. № 5. С. 3–13.
Greivell N.E., Hannaford B. The Design of a Ferrofluid Magnetic Pipette // Transactions on Biomedical Engineering. 1997. V. 44. № 3. P. 129–135.
Yamahata C., Chastellain M., Parashar V.K., Petri A., Hofmann H., Gijs M.A.M. Plastic micropump with ferrofluidic actuation // Journal of Microelectromechanical Systems. 2005. V. 14. № 1. P. 96–102.
Das K., Sarkar M., Mukhopadhyay A., Ganguly R. Transient response of a ferrofluid plug-driven micropump // Magnetohydrodynamics. 2013. V. 49. № 3/4. P. 499–504.
Ando B., Ascia A., Baglio S., Pitrone N. Ferrofluidic pumps: A valuable implementation without moving parts // IEEE Transactions on Instrumentation and Measurement. 2009. V. 58. № 9. P. 3232–3237.
Andò B., Ascia A., Baglio S., Pitrone N. Magnetic Fluids and Their Use in Transducers // IEEE Instrumentation & Measurement Magazine. 2006. V. 9. № 6. P. 44–47.
Hartshorne H., Backhouse C.J., Lee W.E. Ferrofluid-based microchip pump and valve // Sensors and Actuators. 2004. V. 99. № 2–3. P. 592–600.
Hatch A., Kamholz A.E., Holman G., Yager P., Böhringer K.F. A Ferrofluidic Magnetic Micropump // Journal of microelectromechanical systems. 2001. V. 10. № 2. P. 215–221.
Ashouri M., Shafii M.B., Moosavi A., Hezave H.A. A novel revolving piston minipump // Sensors and Actuators. 2015. V. 218. P. 237–244.
Liu B., Zhang Z., Yang J.,Yang J., Li D. A rotary ferrofluidic vane micropump with C shape baffle // Sensors and Actuators. 2018. V. 263. P. 452–458.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1992. С. 632.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал