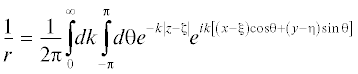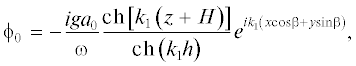Известия РАН. Механика жидкости и газа, 2022, № 2, стр. 123-140

ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ ВОЛН ПОГРУЖЕННЫМ ТЕЛОМ В СЛОЕ ВОДЫ КОНЕЧНОЙ ГЛУБИНЫ ПРИ НАЛИЧИИ ЛЕДЯНОГО ПОКРОВА

L. Z. Hao^a, *, Z. Y. Pan^a, **

^a State Key Laboratory of Hydrodynamics, China Ship Scientific Research Center
Wuxi, China

^* E-mail: haolizhu@hrbeu.edu.cn
^** E-mail: panziyingship@126.com

Поступила в редакцию 25.05.2021
После доработки 28.09.2021
Принята к публикации 29.09.2021

EDN: TFNJRR
DOI: 10.31857/S0568528122020049

Аннотация

Для описания процессов излучения и дифракции волн, инициируемых погруженным телом в слое воды постоянной конечной глубины с ледяным покровом, предлагается использовать метод, основывающийся на трехмерной функции Грина. Предполагается, что жидкость идеальная и течение безвихревое, ледяной покров моделируется упругой пластиной. Функция Грина, удовлетворяющая линеаризованному условию на покрытой льдом поверхности, выводится в трехмерном случае для тела без продольного движения в слое воды конечной глубины и приводятся численные результаты для функции Грина и ее производных. С помощью распределения объемного расхода источников на поверхности тела выводятся интегральные уравнения и решаются задачи излучения и дифракции волн. В качестве примера рассматривается погруженная сфера и анализируется влияние глубины слоя воды и изгибной жесткости ледяного покрова на гидродинамику рассматриваемой задачи. Хорошее согласие полученных результатов с аналитическими решениями подтверждает корректность и достоверность предлагаемого метода.

Ключевые слова: метод функции Грина, погруженное тело, ледяной покров, упругая пластина, конечная глубина

Многочисленные исследования, основывающиеся на теории потенциальных течений, были проведены при рассмотрении тела, погруженного в воду со свободной поверхностью. Гидродинамическая задача решалась численно посредством реализации метода функции Грина для случая свободной поверхности [1–4], в котором требовалось интегрирование по каждой из дискретизированных частей поверхности тела. Кроме того, для обоснования результатов, полученных численным методом, для специальной геометрии были получены аналитические решения, например, процесс излучения и дифракции волн погруженной сферой в воде был исследован в различных случаях, а именно, в случае бесконечной [5] и конечной [6] глубины воды, при поступательном движении среди волн [7], а также в некоторых других случаях. Таким образом, гидродинамическая задача была успешно решена для тела, погруженного в воду со свободной поверхностью.

С недавнего времени все большее и большее внимание стало уделяться полярным областям в силу экономической эффективности, обусловленной огромными запасами природных ископаемых и открытию новых проходов. Это сделало гидродинамическую задачу о теле, погруженном в воду с ледяным покровом, горячей темой исследований более сложных по сравнению с исследованиями для тела, погруженного в воду со свободной поверхностью. Ледяной покров имеет существенное влияние на гидродинамическое нагрузки в случае погруженного тела, когда при движении тела формируется изгибно-гравитационная волна, которая вынуждает ледяной покров изгибаться и даже ломаться [8]. Таким образом, как гидродинамическое нагрузки, действующие на погруженное тело, так и прогиб ледяного покрова стали притягательными точками внимания исследователей.

Для исследования нагрузок, действующих на погруженное тело, с помощью надлежащего использования интегральной теоремы Грина в двумерном случае было исследовано рассеяние наклонно падающих волн на длинном круговом цилиндре, погруженном в жидкость, находящуюся под тонким слоем льда, в случае как однородной, так и двуслойной жидкостей [9, 10]. В дальнейшем, в случае горизонтального цилиндра произвольного поперечного сечения, погруженного в воду с ледяным покровом [11], двумерная задача о малых колебаниях была решена в приближении Буссинеска, при этом для колебаний цилиндра была получена двумерная функция Грина. При рассмотрении задачи об однородном течении, взаимодействующем с круговым цилиндром, находящимся под бесконечным ледяным покровом, была выведена функция Грина [12], обусловленная наличием источника массы, и при дифференцировании функции Грина по отношению к расположению источника возбуждения колебаний, была получена картина мультиполей, а также произведена оценка коэффициентов сопротивления и подъемной силы и найден прогиб ледяного покрова. В трехмерном случае, используя метод мультипольного разложения для погруженной сферы, колеблющейся в воде бесконечной [13] и конечной [14] глубины с ледяным покровом, были найдены коэффициенты присоединенных массы и затухания. Было рассчитано рассеяние волн погруженной сферой в однородном слое воды конечной глубины [15] и в двуслойной жидкости бесконечной [16] и конечной [17] глубины с ледяным покровом. Далее [18], используя метод мультипольного разложения, были решены задачи об излучении изгибных гравитационных волн (всплеск, боковой снос, вертикальное перемещение) погруженной сферой, перемещающейся поступательно на постоянной скорости. Результаты были получены для коэффициентов сопротивления, подъемной силы, присоединенных массы и затухания, обусловленных волновым воздействием. Было обсуждено влияние сплошного ледяного покрова и битого льда на гидродинамические нагрузки.

Чтобы рассчитать прогиб льдины, исследователи обычно выбирают источник массы или диполь в качестве объекта исследования. В [19] было рассмотрено тело, движущееся близко к поверхности льда, и гидродинамическая задача была идеализирована и приведена к стационарному движению точечного источника в воде под плавающей льдиной. Прогиб льдины был найден с использованием аналитической теории функций комплексного переменного и рассчитан численно. В [20] было исследовано прямолинейного нестационарное движение точечного источника, погруженного в жидкость конечной глубины под плавающей льдиной, и, используя интегральные и асимптотические методы, была выведена формула, описывающая прогиб льдины в этом случае. В [21] было проведено дальнейшее исследование гидроупругого поведения плавающей бесконечной пластины, вызванное нестационарным прямолинейным движением точечного источника в жидкости бесконечной глубины. В [22] было проанализировано влияние глубины воды на прогиб ледяного покрова, когда тело движется под ним, была выбрана некоторая система, состоящая из источника и стока для моделирования тела в теоретическом исследовании. В [23] было изучено фундаментальное решение задачи для изгибных и капиллярно-гравитационных волн, вызванных линейными, точечными и кольцевыми источниками возбуждения колебаний, погруженными в невязкую жидкость конечной глубины, накрытой тонкой упругой пластиной или имеющей инерционную поверхность с капиллярным эффектом. Кроме того, в [24] были исследованы поверхностные волны, возбуждаемые нестационарными концентрированными возмущениями в первоначально покоящейся жидкости конечной глубины в двух- и трехмерных случаях, решения для поверхностного возвышения были получены в интегральном виде с помощью совместного преобразования Лапласа–Фурье. В [25, 26] было исследовано возмущение ледяного покрова при прямолинейном горизонтальном движении диполя в воде с постоянной скоростью в двумерном и трехмерном случаях соответственно.

Вышеупомянутые исследования очень важны для изучения рассматриваемого явления и они заложили основу для дальнейшего развития гидродинамики погруженного тела при наличии ледяного покрова. Многие полученные результаты обеспечили отправные точки для проверки численных методов. Однако до сих пор никаких достаточно надежных трехмерных численных методов для одновременного предсказания гидродинамических нагрузок и прогиба льдин не было предложено; это побудило нас провести ряд самостоятельных исследований.

Рассматривая успешное применение метода, использующего функцию Грина при наличии свободной поверхности, для решения гидродинамических задач о теле, погруженном в жидкость со свободной поверхностью, в [27] был предложен метод, использующий функцию Грина в случае поверхности с ледовым покровом, в котором была использована функция Грина, которая удовлетворяет граничным условиям на поверхности с покровом (функция Грина для поверхности с покровом), для решения гидродинамической задачи при наличии ледяного покрова. Была выведена функция Грина для поверхности с покровом в случае отсутствия поступательного движения тела в жидкости бесконечной глубины и получено решение задачи об излучении погруженным телом произвольной формы волн в воде с ледяным покровом в случае бесконечной глубины. Настоящая работа является продолжением и расширением исследования, проведенного в [27], при этом случай конечной глубины получает дальнейшее применение. Хотя и имелись немногочисленные исследования функции Грина для поверхности с покровом в случае конечной глубины жидкости, в [28] была выведена функция Грина в случае конечной глубины для гармонического усилия, направленного вниз со стороны бесконечной тонкой плавающей пластины. Для того, чтобы обеспечить единственное решение в рассматриваемой модели, было введено некоторое малое положительное число. В итоге функция Грина была выражена в виде ряда. Хотя исследование [28] заложило основу для развития функций Грина для поверхности с покровом, основной интерес в этом исследовании состоял в нахождении смещения ледяного покрова и сама по себе функция Грина и ее свойства не получили достаточного внимания. В то же время введение малого положительного числа затемнило физическую значимость. В этой связи в настоящем исследовании основное внимание концентрируется на функции Грина для поверхности с покровом в случае конечной глубины жидкости и выполняется оригинальная работа по получению интегральной формы функции Грина для поверхности с покровом с ясным физическим значением, что может иметь далеко идущие последствия для приложений.

Основная часть статьи организована следующим образом. Первое и самое главное, ледяной покров моделируется упругой пластиной, так что функция Грина для поверхности с покровом определяется как функция Грина в случае покрова в виде упругой пластины. Впервые, в предположении, что жидкость идеальная, функция Грина для покрова в виде упругой пластины при отсутствии поступательного движения при конечной глубине выводится в интегральной форме в трехмерном случае. Приводятся численные результаты для функции Грина и ее производных. Далее, поверхность погруженного тела разделяется на секции, интегральные уравнения задаются посредством распределения интенсивности источников на поверхности тела и, далее, рассчитываются излучение и дифракция волн, генерируемых в воде погруженным телом, и прогибы ледяного покрова. Наконец, в качестве примера рассматривается погруженная сфера, анализируется влияние глубины воды и изгибной жесткости ледяного покрова на гидродинамику. Проверка правильности предлагаемой модели проводится посредством сравнения с аналитическим решением для гидродинамических параметров при наличии ледяного покрова и конечной глубины жидкости; получено хорошее согласие.

1. ПОСТАНОВКА ЗАДАЧИ

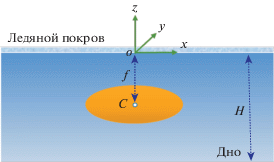
Чтобы исследовать излучение и дифракцию волн, генерируемых погруженным телом в воде конечной глубины при наличии ледяного покрова, вводится декартова система координат $o{\text{ - }}xyz~$, заданная в пространстве, как это изображено на рис. 1, так что ось oz направлена вертикально вверх, а плоскость o–xy совпадает с невозмущенным положением покрывающей поверхности. Центр погруженного тела расположен в точке $\left( {0,0, - f} \right)$. Дно водоема расположено на постоянной конечной глубине $z = - H$, где H – некоторая положительная постоянная.

Рис. 1.

Декартова система координат.

Предполагается, что жидкость невязкая и несжимаемая, а ее движение считается безвихревым. Для исследования жидкости в области Ω вокруг погруженного тела применяется теория потенциальных течений. Прогиб льдины и общий потенциал скорости обозначим ${{\bar {\eta }}}\left( {x,y,t} \right)$ и ${{\Phi }}\left( {x,y,z,t} \right)$ соответственно. На поверхности воды, которая, будучи подвижной, всегда состоит из жидких частиц, справедливо кинематическое условие [29], которое определяется соотношением

(1.1)

$\frac{\partial }{{\partial z}}{{\Phi }} = \frac{\partial }{{\partial t}}{{\bar {\eta }}} + \frac{{\partial {{\Phi }}}}{{\partial x}}\frac{{\partial {{\bar {\eta }}}}}{{\partial x}} + \frac{{\partial {{\Phi }}}}{{\partial y}}\frac{{\partial {{\bar {\eta }}}}}{{\partial y}}\quad {\text{при}}\quad z = 0.$

Предполагается, что амплитуда возмущений поверхности воды достаточно мала по сравнению с длиной волны, поэтому нелинейными слагаемыми можно пренебречь и кинематическое условие (1.1) может быть линеаризовано

(1.2)

$\frac{\partial }{{\partial z}}{{\Phi }} = \frac{\partial }{{\partial t}}{{\bar {\eta }}}\quad {\text{при}}\quad z = 0.$

Поскольку течение предполагается безвихревым, можно применить динамическое условие, задаваемое уравнением Бернулли [30]

(1.3)

$\frac{\partial }{{\partial t}}{{\Phi }} + \frac{P}{{{{\rho }_{w}}}} + g{{\bar {\eta }}} = 0\quad {\text{при}}\quad z = 0.$

Здесь, g – ускорение свободного падения, ${{\rho }_{w}}$ – плотность воды и $P$ – давление на поверхности воды. Поскольку поверхность воды покрыта льдом, который моделируется упругой пластиной и имеет толщину $T$ и плотность ${{\rho }}$, то уравнение движения задается уравнением упругой пластины

(1.4)

$P = L\nabla _{{xy}}^{4}{{\bar {\eta }}} + \rho T\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\bar {\eta }}}~\quad {\text{при}}\quad z = 0,$

где

(1.5)

$\nabla _{{xy}}^{4} = \frac{{{{\partial }^{4}}}}{{\partial {{x}^{4}}}} + 2\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{4}}}}{{\partial {{y}^{4}}}},$

где $L$ – постоянная жесткости ледяной пластины, которая задается выражением L = $Y{{T}^{3}}{\text{/}}(12(1 - {{{{\upsilon }}}^{2}}))~$, где $Y$ – эффективный модуль Юнга и ${{\upsilon }}$ – коэффициент Пуассона. Приравнивая (1.3) и (1.4), получаем

(1.6)

$\frac{\partial }{{\partial t}}{{\Phi }} + \frac{1}{{{{\rho }_{w}}}}\left( {L\nabla _{{xy}}^{4}{{\bar {\eta }}} + \rho T\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\bar {\eta }}}} \right) + g{{\bar {\eta }}} = 0\quad {\text{при}}\quad z = 0.$

Дифференцируя уравнение (1.6) по времени и используя уравнение (1.2), можно получить

(1.7)

$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Phi }} + \frac{1}{{{{\rho }_{w}}}}L\nabla _{{xy}}^{4}\frac{\partial }{{\partial z}}{{\Phi }} + \frac{1}{{{{\rho }_{w}}}}\rho T\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{\partial }{{\partial z}}{{\Phi }} + g\frac{\partial }{{\partial z}}{{\Phi }} = 0\quad {\text{при}}\quad z = 0.$

В дальнейшем все движения предполагаются гармоническими функциями времени с угловой частотой ${{\omega }}$, так что потенциал скорости можно записать в виде ${{\Phi }}(x,y,z,t)$ = $\operatorname{Re} \left\{ {\mathop \sum \limits_{{\text{j}} = 0}^7 {{a}_{{\text{j}}}}{{\phi }_{{\text{j}}}}\left( {x,y,z} \right){{e}^{{ - i{{\omega }}t}}}} \right\}$, где ϕ_j (j = 1, …, 6) – потенциалы излучения, индуцированные шестью степенями свободы колебаний погруженного тела и ${{a}_{j}}$(j = 1, …, 6) – соответствующие амплитуды движения, включая фазы, ${{\phi }_{0}}$ и ${{\phi }_{7}}$ – потенциалы падающей и преломленной волн соответственно, и ${{a}_{0}} = {{a}_{7}}$ – амплитуда падающей волны. Для удобства определим k₀ = ω²/g, $D = L{\text{/}}\left( {g{{\rho }_{w}}} \right)~$ и ${{\varepsilon }} = T\rho {\text{/}}{{\rho }_{w}}$. Тогда линеаризованное условие на поверхности с покровом может быть получено из уравнения (1.7) и выражено следующим образом:

(1.8)

$(D\nabla _{{xy}}^{4} + 1 - {{\varepsilon }}{{k}_{0}})\frac{\partial }{{\partial z}}{{\phi }_{j}} - {{k}_{0}}{{\phi }_{j}} = 0\quad {\text{при}}\quad z = 0,$

откуда можно обнаружить влияние ледяного покрова на гидродинамику.

Помимо линеаризованного условия на поверхности с покровом, потенциалы скорости ϕ_j (j = 0, 1, …, 7) должны удовлетворять следующим уравнениям:

(1.9)

${{\nabla }^{2}}{{\phi }_{j}} = 0$

во всей жидкой области.

Поскольку поверхность тела непроницаемая, нормальная скорость на поверхности тела должна равняться нормальной скорости прилегающей жидкости. Тогда потенциал скорости должен удовлетворять следующим линейным условиям на границе тела [31]:

(1.10)

$\left\{ \begin{gathered} \frac{\partial }{{\partial n}}{{\phi }_{j}} = - i\omega {{n}_{j}}\quad (j = 1,2, \cdots ,6) \hfill \\ \frac{\partial }{{\partial n}}{{\phi }_{j}} = - \frac{\partial }{{\partial n}}{{\phi }_{0}}~\quad \left( {j = 7} \right) \hfill \\ \end{gathered} \right.$

где $\vec {n} = \left( {{{n}_{1}},{{n}_{2}},{{n}_{3}}} \right)$ – вектор нормали к поверхности тела S₀ и $\vec {r} \times \vec {n} = \left( {{{n}_{4}},{{n}_{5}},{{n}_{6}}} \right)$, $\vec {r}$ – радиус-вектор точки на S₀, проведенный из центра тяжести тела.

Считая, что поверхность твердого горизонтального дна также непроницаемая, имеем

(1.11)

$\frac{{\partial {{\phi }_{j}}}}{{\partial z}} = 0\quad {\text{при}}\quad z = - H$

на дне водоема постоянной конечной глубины $z = - H$.

Кроме того, потенциалы скорости должны удовлетворять условию излучения: излучаемые волны распространяются вовне тела.

В дальнейшем будет предполагаться, что потенциалы скорости найдены и известны. Тогда давление может быть определено из линеаризованной формы уравнения Бернулли [30] и может быть разделено на гидростатическую и гидродинамическую составляющие. Гидростатическая составляющая может быть уравновешена силой тяжести и моментом, обусловленным массой погруженного тела. В настоящем исследовании большее внимание уделяется гидродинамической составляющей давления, которое является гармонической функцией времени: P_d(x, y, z, t) = = $\operatorname{Re} \left\{ {\mathop \sum \limits_{j = 0}^7 {{a}_{j}}{{p}_{j}}\left( {x,y,z} \right){{e}^{{ - i{{\omega }}t}}}} \right\}$, где ${{p}_{j}}$ (j = 1, …, 6) представляют собой давления излучения, индуцированные шестью степенями свободы колебаний погруженного тела с единичной амплитудой движения, ${{p}_{0}}$ и ${{p}_{7}}$ – падающее и преломленное давления, соответствующие единичной амплитуде приходящей волны; тогда имеем

(1.12)

${{p}_{j}} = {{\rho }_{w}}i\omega {{\phi }_{j}}\quad \left( {j = 0,1,...,7} \right).$

Сила излучения, определенная присоединенной массой μ_ij и коэффициентами затухания λ_ij (i, j = 1, 2, …, 6), может быть вычислена посредством интегрирования давлений излучения по поверхности тела

(1.13)

${{{{\omega }}}^{2}}{{{{\mu }}}_{{ij}}} + i{{\omega }}{{{{\lambda }}}_{{ij}}} = \int\limits_{{{S}_{0}}} {\int {{{p}_{j}}{{n}_{i}}ds} } $.

Нагрузки возбуждающих волн ${{\hat {F}}_{i}}$, вызванные задачей дифракции, можно выразить в виде ${{\hat {F}}_{i}}$ = = ${{a}_{0}}{{F}_{i}}{{e}^{{ - i\omega t}}}$ (i = 1, 2, …, 6), где F_i – комплексный коэффициент давления

(1.14)

${{F}_{{\text{i}}}} = \int {\int\limits_{{{S}_{0}}} {({{p}_{0}} + {{p}_{7}}){{n}_{i}}ds.} } $

Прогиб льдины ${{\bar {\eta }}}\left( {x,y,t} \right)$ можно записать в виде гармонической функции времени ${{\bar {\eta }}}(x,y,t)$ = = $\operatorname{Re} \{ {{\bar {\eta }}_{0}}(x,y){{e}^{{i\theta }}}{{e}^{{ - i{{\omega }}t}}}\} $ с амплитудой ${{\bar {\eta }}_{0}}(x,y)$ и фазой θ. С помощью линейного кинематического условия (1.2) можно исключить зависимость от времени; тогда получим

(1.15)

${{\bar {\eta }}_{0}}\left( {x,y} \right){{e}^{{i{{\theta }}}}} = - \frac{1}{{i{{\omega }}}}\frac{\partial }{{\partial z}}\phi \left( {x,y,z} \right)\quad {\text{при}}\quad z = 0.$

2. ФУНКЦИЯ ГРИНА В СЛУЧАЕ ПОКРОВА В ВИДЕ УПРУГОЙ ПЛАСТИНЫ

Когда ледяной покров моделируется как тонкая упругая пластина (линеаризованное условие на поверхности с покровом записано в виде уравнения (1.8)), функция Грина, которая удовлетворяет всем граничным условиям, за исключением условия на теле, называется функцией Грина в случае покрова в виде упругой пластины. В настоящем разделе будет выведена функция Грина в случае упругой пластины для конечной глубины жидкости, которая послужит основанием для расчетов излучения и дифракции волн в воде, возбужденных погруженным телом произвольной формы при наличии ледяного покрова в жидкости конечной глубины.

Функция Грина в случае упругой пластины может быть записана в виде

(2.1)

$G\left( {P,Q} \right) = \frac{1}{r} + \frac{1}{{{{r}_{2}}}} + G{\text{*}}\left( {P,Q} \right),$

где r и ${{r}_{2}}$ обозначают расстояния между точкой поля $P\left( {x,y,z} \right)$ и точкой источника возбуждения колебаний $Q\left( {{{\xi }},{{\eta }},{{\zeta }}} \right)$ и между $P\left( {x,y,z} \right)$ и точкой источника возбуждения колебаний, зеркально отраженной относительно поверхности дна ${{Q}_{2}}\left( {{{\xi }},{{\eta }}, - 2H - {{\zeta }}} \right)$ соответственно; в (2.1) G* обозначает волновой член, обусловленный наличием ледяного покрова.

Здесь $\frac{1}{r}$ и $\frac{1}{{{{r}_{2}}}}$ можно представить в виде двойных интегралов Фурье

(2.2)

(2.3)

$\frac{1}{{{{r}_{2}}}} = \frac{1}{{2\pi }}\mathop \smallint \limits_0^\infty dk\mathop \smallint \limits_{ - \pi }^\pi d{{\theta }}{{e}^{{ - k\left( {z + {{\zeta }} + 2H} \right)}}}{{e}^{{ik\left[ {\left( {x - {{\xi }}} \right)\cos {{\theta }} + \left( {y - {{\eta }}} \right)\sin {{\theta }}} \right]}}}$

на плоскости Фурье с полярными координатами $\left( {k,{{\theta }}} \right)$.

Подставляя выражения (2.2) и (2.3) в (2.1), можно получить

$(D\nabla _{{xy}}^{4} + 1 - {{\varepsilon }}{{k}_{0}})\frac{\partial }{{\partial z}}G{\text{*}} - {{k}_{0}}G{\text{*}}\;{\text{ = }}$

(2.4)

$ = \frac{1}{\pi }\mathop \smallint \limits_0^\infty dk\mathop \smallint \limits_{ - \pi }^\pi d{{\theta }}[D{{k}^{5}} + \left( {1 - {{\varepsilon }}{{k}_{0}}} \right)k + {{k}_{0}}]{{e}^{{ - kH}}}\operatorname{ch} \left[ {k\left( {{{\zeta }} + H} \right)} \right]{{e}^{{ik\left[ {\left( {x - {{\xi }}} \right)\cos {{\theta }} + \left( {y - {{\eta }}} \right)\sin {{\theta }}} \right]}}}\quad \left( {z = 0} \right).$

На основе уравнения (2.4) можно выразить G* в виде

(2.5)

$G{\text{*}} = \frac{1}{\pi }\mathop \smallint \limits_0^\infty dk\mathop \smallint \limits_{ - \pi }^\pi d{{\theta }}A\left( k \right)\operatorname{ch} \left[ {k\left( {z + H} \right)} \right]{{e}^{{ik\left[ {\left( {x - {{\xi }}} \right)\cos {{\theta }} + \left( {y - {{\eta }}} \right)\sin {{\theta }}} \right]}}}.$

Без потери общности G* должно удовлетворять уравнению Лапласа и граничным условиям на дне. Подставляя выражение (2.5) в уравнение (2.4), можно получить

(2.6)

$A\left( k \right) = \frac{{{{S}_{1}}\left( k \right)}}{{{{S}_{2}}\left( k \right)}}\frac{{{\text{ch}}\left[ {k\left( {{{\zeta }} + H} \right)} \right]}}{{{{e}^{{kH}}}\operatorname{ch} \left( {kH} \right)}},$

где ${{S}_{1}}\left( k \right) = D{{k}^{5}} + \left( {1 - {{\varepsilon }}{{k}_{0}}} \right)k + {{k}_{0}}$ и ${\text{\;}}{{S}_{2}}\left( k \right) = (D{{k}^{4}} + 1 - \varepsilon {{k}_{0}})k\operatorname{th} \left( {kH} \right) - {{k}_{0}}$.

Определим $x - {{\xi }} = R\cos {{\alpha }}$ и $y - {{\eta }} = R\sin {{\alpha }}$, где $R$ обозначает расстояние по горизонтали между точкой поля и точкой источника возбуждения колебаний, а именно $R = \sqrt {{{{\left( {x - {{\xi }}} \right)}}^{2}} + {{{\left( {y - {{\eta }}} \right)}}^{2}}} $, тогда функция Грина в случае покрова в виде упругой пластины может быть записана в виде

(2.7)

$G\left( {P,Q} \right) = \frac{1}{r} + \frac{1}{{{{r}_{2}}}} + \frac{1}{\pi }\mathop \smallint \limits_0^\infty dk\mathop \smallint \limits_{ - {{\pi }}}^\pi d{{\theta }}\frac{{{{S}_{1}}\left( k \right)}}{{{{S}_{2}}\left( k \right)}}\mathcal{F}\left( k \right){{e}^{{ikR\cos \left( {{{\theta }} - {{\alpha }}} \right)}}},$

где $\mathcal{F}\left( k \right) = \frac{1}{{{{e}^{{kH}}}\operatorname{ch} \left( {kH} \right)}}\operatorname{ch} \left[ {k\left( {{{\zeta }} + H} \right)} \right]\operatorname{ch} \left[ {k\left( {z + H} \right)} \right]$. Использование функции ${{J}_{0}}\left( {kR} \right)$, определенной следующим образом

(2.8)

${{J}_{0}}\left( {kR} \right) = \frac{1}{{2\pi }}\mathop \smallint \limits_{ - \pi }^\pi {{e}^{{ikR\cos {{\theta }}}}}d{{\theta }}{\text{.}}$

Непосредственно дает

(2.9)

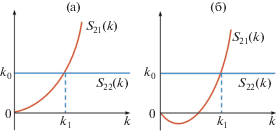
$G\left( {P,Q} \right) = \frac{1}{r} + \frac{1}{{{{r}_{2}}}} + \mathop \smallint \limits_0^\infty dkg\left( k \right),$

где $g\left( k \right) = 2\frac{{{{S}_{1}}\left( k \right)}}{{{{S}_{2}}\left( k \right)}}\mathcal{F}\left( k \right){{J}_{0}}\left( {kR} \right)$.

Чтобы изучить свойства подынтегрального выражения в третьем члене соотношения (2.9), дадим следующие определения ${{S}_{{21}}}\left( k \right) = (D{{k}^{4}} + 1 - {{\varepsilon }}{{k}_{0}})k\tanh \left( {kH} \right)$ и $~{{S}_{{22}}}\left( k \right) = {{k}_{0}}$. Поскольку $D > 0$ при $k \to + \infty $, то ${{S}_{{21}}}\left( k \right) > {{S}_{{22}}}\left( k \right)$. Поскольку $\left( {1 - {{\varepsilon }}{{k}_{0}}} \right)$ в ${{S}_{{21}}}\left( k \right)~$задано, то, какое бы значение это выражение не принимало, должно быть одно и только одно пересечение кривых, представляющих ${{S}_{{21}}}\left( k \right)$ и ${{S}_{{22}}}\left( k \right)$ при $k \in \left( {0, + \infty } \right)$, считая, что ${{k}_{0}} > 0$, как это проиллюстрировано на рис. 2. Это указывает на то, что должен существовать один и только один действительный положительный корень k₁ соответствующего многочлена ${{S}_{2}}\left( k \right) = 0$ (одна и только одна особая точка k₁ в подынтегральном выражении в третьем члене соотношения (2.9)), при этом k₁ можно определить, используя стандартные процедуры нахождения корней многочлена.

Рис. 2.

Схематическое изображение пересечения кривых, представляющих ${{S}_{{21}}}\left( k \right)$ и ${{S}_{{22}}}:$ $\left( {1 - {{\varepsilon }}{{k}_{0}}} \right) \geqslant 0$ (а) и $~\left( {1 - {{\varepsilon }}{{k}_{0}}} \right) < 0$ (б).

В этой связи можно заметить, что помимо действительного корня k₁, который соответствует бегущим волнам, многочлен ${{S}_{2}}\left( k \right) = 0$ имеет четыре комплексных корня, соответствующих затухающим бегущим волнам (эти бегущие волны затухают экспоненциально вдали от точки источника возбуждения колебаний), и бесконечные мнимые корни, которые дают волновые моды, не имеющие распространяющейся компоненты и затухающие быстро вдали от точки источника возбуждения колебаний [28]. Поскольку интервал интегрирования третьего члена в соотношении (2.9) простирается от нуля до плюс бесконечности вдоль действительной оси переменной k, в данной работе рассматривается только влияние особой точки k₁ на значение интеграла и какое-либо объяснение должно быть дано только по поводу интегрирования вблизи особой точки k₁. Как показано на рис. 3, есть три возможных пути ${{L}_{1}}$, ${{L}_{2}}$ и ${{L}_{3}}$ интегрирования третьего члена в соотношении (2.9). Стрелки указывают направления пути интегрирования, под $\ell $ понимается малый положительный параметр, а именно, $\ell = + 0$, тогда пути ${{L}_{{s1}}}$ и ${{L}_{{s2}}}$ представляют собой интервалы интегрирования $\left( {0,{{k}_{1}} - \ell } \right)$ и $\left( {{{k}_{1}} + \ell ,~ + \infty } \right)$ соответственно. Траектории ${{C}_{{cw}}}$ и ${{C}_{{acw}}}$ представляют собой полуокружности с направлениями интегрирования по и против часовой стрелки, соответственно, на комплексной плоскости, переменная k обозначена как $k = {{k}_{1}} + \ell {{e}^{{i{{{{\theta }}}_{{cw}}}}}}$ на траектории ${{C}_{{cw}}}$ с аргументом ${{{{\theta }}}_{{cw}}}$, изменяющимся от π до 0. Аналогично, $k = {{k}_{1}} + \ell {{e}^{{i{{{{\theta }}}_{{acw}}}}}}$ на траектории ${{C}_{{acw}}}$ с аргументом ${{{{\theta }}}_{{acw}}}$, изменяющимся от $ - \pi $ до 0.

Рис. 3.

Определение путей интегрирования: (а) ${{L}_{1}} = {{L}_{{s1}}} + {{L}_{{s2}}} + {{C}_{{cw}}}$, (б) ${{L}_{2}} = {{L}_{{s1}}} + {{L}_{{s2}}}$, (в) ${{L}_{3}} = {{L}_{{s1}}} + {{L}_{{s2}}} + {{C}_{{acw}}}$.

На основании теоремы о вычетах

(2.10)

$\int\limits_{{{C}_{{cw}}}}^{} g \left( k \right)dk = - 2\pi i\frac{{{{S}_{1}}\left( {{{k}_{1}}} \right)}}{{S_{2}^{'}\left( {{{k}_{1}}} \right)}}\mathcal{F}\left( {{{k}_{1}}} \right){{J}_{0}}\left( {{{k}_{1}}R} \right),$

(2.11)

$\int\limits_{{{C}_{{acw}}}}^{} g \left( k \right)dk = 2\pi i\frac{{{{S}_{1}}\left( {{{k}_{1}}} \right)}}{{S_{2}^{'}\left( {{{k}_{1}}} \right)}}\mathcal{F}\left( {{{k}_{1}}} \right){{J}_{0}}\left( {{{k}_{1}}R} \right),$

где $S_{2}^{'}\left( k \right)$ представляет собой производную функции ${{S}_{2}}\left( k \right)$, и $S_{2}^{'}\left( k \right) = (5D{{k}^{4}} + 1 - {{\varepsilon }}{{k}_{0}})\tanh \left( {kH} \right)$ + + $(D{{k}^{4}} + 1 - \varepsilon {{k}_{0}})kH[1 - {{\tanh }^{2}}(kH)]$. Здесь ${{S}_{1}}\left( {{{k}_{1}}} \right),$ $S_{2}^{'}\left( {{{k}_{1}}} \right)$, и $\mathcal{F}\left( {{{k}_{1}}} \right)$ – значения функций ${{S}_{1}}\left( k \right),$ $S_{2}^{'}\left( k \right)$, и $\mathcal{F}\left( k \right)$ при $k = {{k}_{1}}~$ соответственно.

Между тем,

(2.12)

$\int\limits_{\left( {{{L}_{{s1}}} + {{L}_{{s2}}}} \right)}^{} g \left( k \right)dk = {\text{P}}.{\text{V}}.\mathop \smallint \limits_0^\infty 2\frac{{{{S}_{1}}\left( k \right)}}{{{{S}_{2}}\left( k \right)}}\mathcal{F}\left( k \right){{J}_{0}}\left( {kR} \right)dk,$

и тогда выражение (2.9) может быть записано в следующем виде

(2.13)

$G\left( {P,Q} \right) = \frac{1}{r} + \frac{1}{{{{r}_{2}}}} + {\text{P}}.{\text{V}}.\mathop \smallint \limits_0^\infty 2\frac{{{{S}_{1}}\left( k \right)}}{{{{S}_{2}}\left( k \right)}}\mathcal{F}\left( k \right){{J}_{0}}\left( {kR} \right)dk + \delta 2\pi i\frac{{{{S}_{1}}\left( {{{k}_{1}}} \right)}}{{S_{2}^{'}\left( {{{k}_{1}}} \right)}}\mathcal{F}\left( {{{k}_{1}}} \right){{J}_{0}}\left( {{{k}_{1}}R} \right),$

в котором P.V. обозначает главное значение интеграла в смысле Коши и $\delta = - {\text{1}},~0,~$ и 1 соответствует путям интегрирования ${{L}_{1}},{{L}_{2}},$ и ${{L}_{3}}$, соответственно.

Чтобы однозначно определить функцию Грина, рассматривается условие излучения, которое указывает, что волны распространяются наружу вовне тела. Единственный и значимый путь интегрирования будет определен в следующей части при анализе свойств функции Грина на бесконечном расстоянии от точки источника возбуждения колебаний.

Когда точка поля P расположена далеко от точки источника возбуждения колебаний Q, тогда, при $R \to \infty $, имеем $\frac{1}{r} \sim O\left( {\frac{1}{R}} \right)$, $\frac{1}{{{{r}_{2}}}} \sim O\left( {\frac{1}{R}} \right)$, и

(2.14)

${{J}_{0}}\left( {kR} \right) \sim \sqrt {\frac{2}{{\pi Rk}}} \cos \left( {kR - \frac{\pi }{4}} \right) + O\left( {\frac{1}{R}} \right).$

Отметим, что

(2.15)

$\cos \left( {kR - \frac{\pi }{4}} \right) = \cos \left( {{{k}_{1}}R - \frac{\pi }{4}} \right)\cos R\left( {k - {{k}_{1}}} \right) - \sin \left( {{{k}_{1}}R - \frac{\pi }{4}} \right)\sin R\left( {k - {{k}_{1}}} \right),$

в то же время, обращаясь к теореме об интеграле Фурье

(2.16)

$\mathop \smallint \limits_b^\infty g\left( x \right)\frac{{\sin R\left( {x - {{x}_{0}}} \right)}}{{x - {{x}_{0}}}}dx = \pi g\left( {{{x}_{0}}} \right) + O\left( {\frac{1}{R}} \right),$

${\text{P}}{\text{.V}}{\text{.}}\mathop \smallint \limits_b^\infty g\left( x \right)\frac{{\cos R\left( {x - {{x}_{0}}} \right)}}{{x - {{x}_{0}}}}dx = O\left( {\frac{1}{R}} \right)$

можно получить

(2.17)

$\mathop {{\text{lim}}}\limits_{R \to \infty } G = \left\{ \begin{gathered} - \frac{{2\pi i{{S}_{1}}\left( {{{k}_{1}}} \right)}}{{S_{2}^{'}\left( {{{k}_{1}}} \right)}}\mathcal{F}\left( {{{k}_{1}}} \right)\sqrt {\frac{2}{{\pi R{{k}_{1}}}}} {{e}^{{ - i\left( {{{k}_{1}}R - \frac{\pi }{4}} \right)}}} + O\left( {\frac{1}{R}} \right)~~\left( {L = {{L}_{1}}} \right) \hfill \\ - \frac{{2\pi {{S}_{1}}\left( {{{k}_{1}}} \right)}}{{S_{2}^{'}\left( {{{k}_{1}}} \right)}}\mathcal{F}\left( {{{k}_{1}}} \right)\sqrt {\frac{2}{{\pi R{{k}_{1}}}}} \sin \left( {{{k}_{1}}R - \frac{\pi }{4}} \right) + O\left( {\frac{1}{R}} \right)\left( {L = {{L}_{2}}} \right) \hfill \\ \frac{{2\pi i{{S}_{1}}\left( {{{k}_{1}}} \right)}}{{S_{2}^{'}\left( {{{k}_{1}}} \right)}}\mathcal{F}\left( {{{k}_{1}}} \right)\sqrt {\frac{2}{{\pi R{{k}_{1}}}}} {{e}^{{i\left( {{{k}_{1}}R - \frac{\pi }{4}} \right)}}} + O\left( {\frac{1}{R}} \right)~~~\left( {L = {{L}_{3}}} \right) \hfill \\ \end{gathered} \right.$

Учитывая множитель ${{e}^{{ - i{{\omega }}t}}}$, зависящий от времени, в (2.17), множитель ${{e}^{{ - i\left( {{{k}_{1}}R - \frac{\pi }{4} + {{\omega }}t} \right)}}}$ включен в выражение для G при $R \to \infty $, и $L = {{L}_{1}}$, это указывает, что путь интегрирования L₁ соответствует волне, распространяющейся вовнутрь. Аналогично, ${{L}_{2}}$ соответствует стационарной волне и L₃ соответствует волне, распространяющейся вовне от тела. Таким образом, L₃ представляет собой требуемый путь интегрирования, который обеспечивает выполнение условий излучения для G, так что функция Грина в случае упругой пластины окончательно выражается в виде

$G\left( {P,Q} \right) = \frac{1}{r} + \frac{1}{{{{r}_{2}}}} + {\text{P}}{\text{.V}}.\mathop \smallint \limits_0^\infty \frac{{2{{S}_{1}}\left( k \right)}}{{{{S}_{2}}\left( k \right)}}\mathcal{F}\left( k \right){{J}_{0}}\left( {kR} \right) + 2\pi i\frac{{{{S}_{1}}\left( {{{k}_{1}}} \right)}}{{S_{2}^{'}\left( {{{k}_{1}}} \right)}}\mathcal{F}\left( {{{k}_{1}}} \right){{J}_{0}}\left( {{{k}_{1}}R} \right).$

Кстати, производные функции Грина в случае покрова в виде упругой пластины имеют вид

(2.19)

$\begin{gathered} \frac{\partial }{{\partial x}}G(P,Q)\, = \, - {\kern 1pt} (x\, - \,{{\xi }})\left[ {{{{\left( {\frac{1}{r}} \right)}}^{3}}\, + \,{{{\left( {\frac{1}{{{{r}_{2}}}}} \right)}}^{3}}} \right] + \\ + \frac{{(x\, - \,{{\xi }})}}{R}\left[ {{\text{P}}{\text{.V}}{\text{.}}\mathop \smallint \limits_0^\infty \frac{{2{{S}_{1}}(k)}}{{{{S}_{2}}(k)}}\mathcal{F}(k)kJ_{0}^{'}(kR)dk\, + \,2\pi i\frac{{{{S}_{1}}({{k}_{1}})}}{{S_{2}^{'}({{k}_{1}})}}\mathcal{F}({{k}_{1}}){{k}_{1}}J_{0}^{'}({{k}_{1}}R)} \right], \\ \end{gathered} $

(2.20)

$\begin{gathered} \frac{\partial }{{\partial y}}G\left( {P,Q} \right) = - \left( {y - {{\eta }}} \right)\left[ {{{{\left( {\frac{1}{r}} \right)}}^{3}} + {{{\left( {\frac{1}{{{{r}_{2}}}}} \right)}}^{3}}} \right] + \\ + \frac{{\left( {y - {{\eta }}} \right)}}{R}\left[ {{\text{P}}{\text{.V}}{\text{.}}\mathop \smallint \limits_0^\infty \frac{{2{{S}_{1}}\left( k \right)}}{{{{S}_{2}}\left( k \right)}}\mathcal{F}\left( k \right)kJ_{0}^{'}\left( {kR} \right)dk + 2\pi i\frac{{{{S}_{1}}\left( {{{k}_{1}}} \right)}}{{S_{2}^{'}\left( {{{k}_{1}}} \right)}}\mathcal{F}\left( {{{k}_{1}}} \right){{k}_{1}}J_{0}^{'}\left( {{{k}_{1}}R} \right)} \right], \\ \end{gathered} $

(2.21)

$\begin{gathered} \frac{\partial }{{\partial z}}G\left( {P,Q} \right) = - \left( {z - {{\zeta }}} \right){{\left( {\frac{1}{r}} \right)}^{3}} - \left( {z + {{\zeta }} + 2H} \right){{\left( {\frac{1}{{{{r}_{2}}}}} \right)}^{3}} + \\ + \left[ {{\text{P}}{\text{.V}}{\text{.}}\mathop \smallint \limits_0^\infty \frac{{2{{S}_{1}}\left( k \right)}}{{{{S}_{2}}\left( k \right)}}{{\mathcal{F}}_{z}}\left( k \right){{J}_{0}}\left( {kR} \right)dk + 2\pi i\frac{{{{S}_{1}}\left( {{{k}_{1}}} \right)}}{{S_{2}^{'}\left( {{{k}_{1}}} \right)}}{{\mathcal{F}}_{z}}\left( {{{k}_{1}}} \right){{J}_{0}}\left( {{{k}_{1}}R} \right)} \right], \\ \end{gathered} $

где ${{\mathcal{F}}_{z}}\left( k \right)$ обозначает производную функции $\mathcal{F}\left( k \right)$ по z и

(2.22)

${{\mathcal{F}}_{z}}\left( k \right) = \frac{k}{{{{e}^{{kH}}}\cosh \left( {kH} \right)}}\operatorname{ch} \left[ {k\left( {\zeta + H} \right)} \right]\operatorname{sh} \left[ {k\left( {z + H} \right)} \right].$

Методы вычислений функции Грина и ее производных в случае покрова в виде упругой пластины приведены в Приложении A , а численные результаты приведены в разделе 4 данной статьи.

3. ПОЛУЧЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ

В области жидкости неизвестные потенциалы скорости и их нормальные производные в окрестности точки поля могут быть представлены распределением источников на поверхности тела S₀ с применением функции Грина:

(3.1)

${{\phi }_{{\text{j}}}}\left( P \right) = \iint\limits_{{{S}_{0}}} {G\left( {P,Q} \right){{{{\sigma }}}_{{\text{j}}}}\left( Q \right)ds\left( Q \right),}$

(3.2)

$\frac{\partial }{{\partial {{n}_{P}}}}{{\phi }_{j}}\left( P \right) = \iint\limits_{{{S}_{0}}} {\frac{\partial }{{\partial {{n}_{P}}}}G\left( {P,Q} \right) \cdot {{{{\sigma }}}_{j}}\left( Q \right)ds\left( Q \right),}$

где σ_j (j = 1, 2, …, 7) – интенсивности источников, которые соответствуют шести степеням свободы для колебаний и дифракционного движения тела, когда векторы нормали направлены внутрь тела.

Поверхность тела разделяется на M секций, на каждой секции интенсивность источников колебаний считается постоянной. Потенциал скорости ϕ_j, интенсивность источников колебаний σ_j и компонента нормали n_j на секции с номером α обозначены $\phi _{j}^{{{\alpha }}}$, ${{\sigma }}_{j}^{{{\alpha }}},$ и $n_{j}^{{{\alpha }}}$, соответственно. ${{G}^{{{{\alpha \beta }}}}}$ представляет собой функцию Грина $G\left( {P,Q} \right)$, когда точка поля P и точка источника колебаний Q находятся на α-й и β-й секциях. Площадь β-й секции обозначим ${{s}_{{{\beta }}}}\left( Q \right)$. Тогда выражения (3.1) и (3.2) можно аппроксимировать следующим образом:

(3.3)

$\phi _{j}^{\alpha }\left( P \right) = \mathop \sum \limits_{{{\beta }} = 1}^M {{c}_{{{{\alpha \beta }}}}}{{\sigma }}_{j}^{{{\beta }}}\left( Q \right),$

(3.4)

$\frac{\partial }{{\partial {{n}_{P}}}}\phi _{j}^{{{\alpha }}}\left( P \right) = 2\pi {{\sigma }}_{j}^{{{\alpha }}}\left( P \right) + \mathop \sum \limits_{{{\beta }} = 1}^M {{d}_{{{{\alpha \beta }}}}} \cdot {{\sigma }}_{j}^{{{\beta }}}\left( Q \right),$

где ${{c}_{{{{\alpha \beta }}}}} = \iint\limits_{{{S}_{{{\beta }}}}} {{{G}^{{{{\alpha \beta }}}}}d{{s}_{{{\beta }}}}\left( Q \right)}$ и ${{d}_{{{{\alpha \beta }}}}} = \iint\limits_{{{S}_{{{\beta }}}}} {\frac{\partial }{{\partial {{n}_{P}}}}{{G}^{{{{\alpha \beta }}}}}d{{s}_{{{\beta }}}}\left( Q \right)}$.

Поскольку верхний индекс α изменяется от 1 до M, уравнения (3.3) and (3.4) могут быть записаны в матричной форме:

(3.5)

$\left\{ {{{\phi }_{j}}} \right\} = \left[ C \right]\left\{ {{{{{\sigma }}}_{j}}} \right\},$

(3.6)

$\left\{ {\frac{\partial }{{\partial {{n}_{p}}}}{{\phi }_{j}}} \right\} = \left[ {2\pi \left[ E \right] + \left[ D \right]} \right]\left\{ {{{{{\sigma }}}_{j}}} \right\}.$

Здесь $\left[ C \right]$ и $\left[ D \right]$ – матрицы, составленные из ${{c}_{{\alpha \beta }}}$ и ${{d}_{{\alpha \beta }}}$, $\left[ E \right]$ – единичная матрица размера $M \times M$, а {ϕ_j}, $~\left\{ {\frac{\partial }{{\partial {{n}_{P}}}}{{\phi }_{j}}} \right\}$, и {σ_j} – векторы-столбцы, каждый из которых состоит из $\phi _{j}^{{{\alpha }}}$, $\frac{\partial }{{\partial {{n}_{P}}}}\phi _{j}^{{{\alpha }}}$, и ${{\sigma }}_{j}^{{{\alpha }}}$ соответственно.

Рассматривая условия на поверхности тела (1.10), можно найти интенсивности источников σ_j с помощью соотношения (3.6). Далее, подставляя σ_j в уравнение (3.5), получим потенциалы скорости ϕ_j. Коэффициенты присоединенной массы и затухания, так же как нагрузки возбуждающих волн, могут быть вычислены с использованием уравнений (1.13) и (1.14) с помощью интегрирования потенциала скорости ϕ_j по поверхности тела ${{S}_{0}}$.

Когда точка поля P расположена на поверхности воды, производные потенциалов скорости по переменной z могут быть найдены следующим образом:

(3.7)

$\frac{\partial }{{\partial z}}{{\phi }_{j}}\left( P \right) = \iint\limits_{{{S}_{0}}} {\frac{\partial }{{\partial z}}G\left( {P,Q} \right){{{{\sigma }}}_{j}}\left( Q \right)ds\left( Q \right)}$

Далее, объединяя уравнения (1.15) и (3.7), можно рассчитать прогиб льдины.

4. РЕЗУЛЬТАТЫ И АНАЛИЗ

4.1. Численные результаты для функции Грина в случае покрова в виде упругой пластины

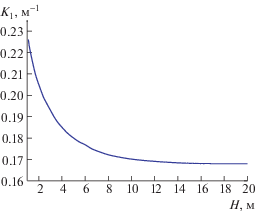
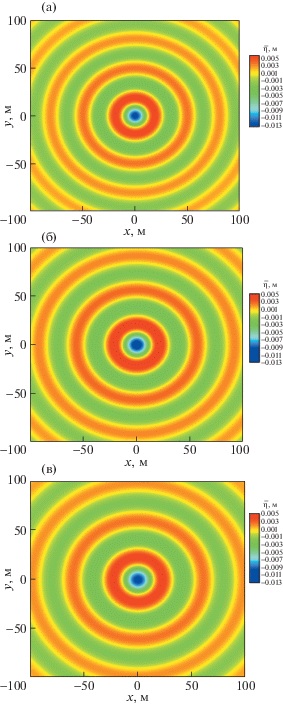
В данном разделе представлены некоторые численные результаты для функции Грина и ее производных в случае покрова в виде упругой пластины в воде конечной глубины, как изображено на рис. 4. Точка источника колебаний имеет координаты (0, 0, –1.0 м), точки поля описываются различными значениями $x$, соответствующими y = 1.0 м и z = 0 м. Все расчеты выполнены для следующих значений основных параметров: ${{\rho }_{w}} = 1025$ кг/м³, $\rho = 922.5$ кг/м³, ${{\upsilon }} = 0.3$, $Y = 6 \times {{10}^{9}}$ Н/м², T = 0.5 м и${{k}_{0}} = 1.0$ м^–1. Взяты три значения глубины воды: H = 2.0, 5.0 и 20.0 м, соответствующие особые точки функции Грина для покрова в виде упругой пластины есть ${{k}_{1}} = 0.205$, 0.180 и 0.168 м^–1 соответственно.

Рис. 4.

Численные результаты для функции Грина и ее производных в случае покрова в виде упругой пластины для различных глубин воды при $T = 0.5~$ м, ${{k}_{0}} = 1.0~$ м^–1. (a) Действительная часть функции Грина в случае покрова в виде упругой пластины, (б) мнимая часть функции Грина в случае покрова в виде упругой пластины, (в) действительная часть производной по $x$, (г) мнимая часть производной по x, (д) действительная часть производной по $y$, (е) мнимая часть производной по y, (ж) действительная часть производной по $z$, (з) мнимая часть производной по $z$.

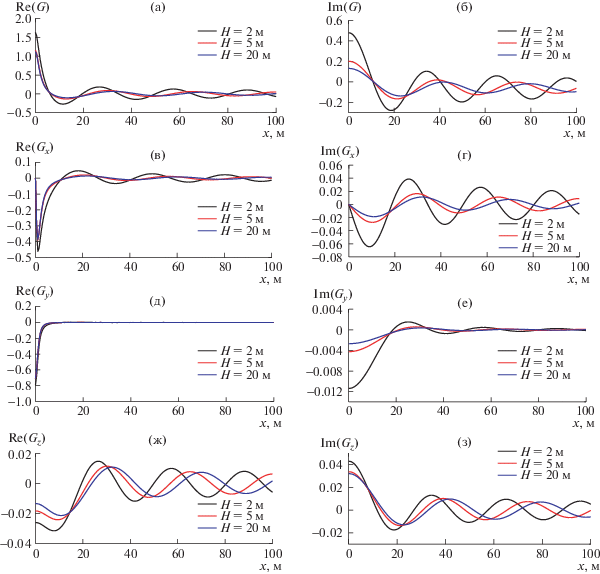
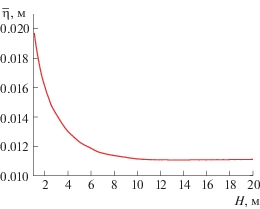
В настоящей работе физической интерпретацией функции Грина для покрова в виде упругой пластины является потенциал скорости, генерируемой пульсирующим источником единичной интенсивности в некоторой точке поля, тогда прогиб льдины, обусловленный точкой источника пульсаций, может быть вычислен из уравнения (1.15). Максимальное значение прогиба ледяного покрова получается, когда эта точка поля расположена в начале координат (0, 0, 0). Максимальное значение $\bar {\eta }$ и особая точка ${{k}_{1}}$ уменьшаются при увеличении глубины воды и держатся примерно на постоянном уровне, когда вода достаточно глубокая ($H \geqslant 12$ м) и влиянием глубины можно пренебречь, как показано на рис. 5 и 6 . Поскольку особая точка ${{k}_{1}}~$соответствует бегущей волне, длина волны растет с глубиной воды. На рис. 7 воспроизведены прогибы ледяного покрова для различных значений глубины при t = 0 с. Можно отчетливо видеть, что волны кольцевые и центрированные в точке источника пульсаций, с ростом глубины воды волны становятся более разреженными. Это совпадает с выводами, которые можно сделать из рис. 5 и 6 .

Рис. 5.

Максимальный прогиб льдины.

Рис. 6.

Изменение особой точки ${{k}_{1}}$ в зависимости от глубины воды.

Рис. 7.

Контуры прогибов льдины для различных глубин воды при $T = 0.5~$ м и м^–1${{k}_{0}} = 1.0~$ м^–1 при t = 0 c. (а) H = 2.0 м, (б) H = 5.0 м, (c) H = 20.0 м.

4.2. Погруженная сфера под ледяным покровом

Чтобы проверить правильность применения трехмерной функции Грина в настоящей работе, были рассмотрены излучение и дифракция волн погруженной сферой в однородном слое воды конечной глубины с ледяным покровом. Поверхность сферы была разбита на 400 биквадратных элементарных участков, как это показано на рис. 8. Радиус сферы и глубина погружения обозначены ${{r}_{0}}$ и f соответственно.

Рис. 8.

Сетка, использованная для представления погруженного тела.

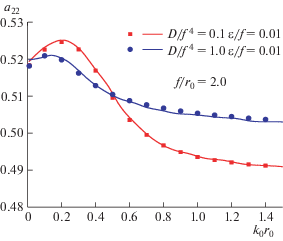
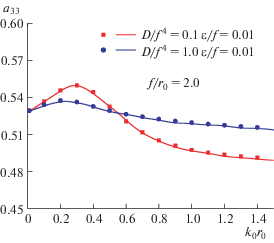
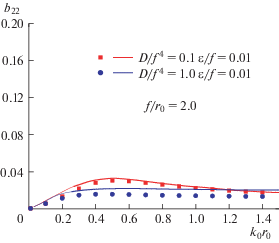
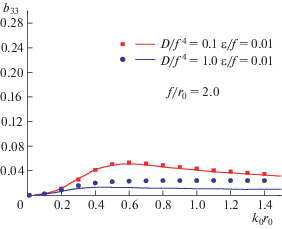
4.2.1. Излучение волн в воде. Задача об излучении волн в воде решается впервые. Рассчитываются коэффициенты присоединенной массы и затухания, обезразмеренные в виде ${{a}_{{ij}}} = {{{{\mu }}}_{{ij}}}{\text{/}}\left( {\rho V} \right)$ и ${{b}_{{ij}}} = {{{{\lambda }}}_{{ij}}}{\text{/}}\left( {{{\omega }}\rho V} \right)$, где V – объем погруженного тела. Численные результаты сравниваются с аналитическими результатами [13]. Они изображены на рис. 9–12 как функции ${{k}_{0}}{{r}_{0}}$ для глубины погружения $f{\text{/}}{{r}_{0}} = 2.0$ и постоянной конечной глубины воды $H{\text{/}}{{r}_{0}} = 5.0$. Кроме того, оценивается влияние изгибной жесткости ледяного покрова.

Рис. 9.

Коэффициенты присоединенной массы при боковом раскачивании a₂₂.

Рис. 10.

Коэффициенты присоединенной массы при вертикальных колебаниях a₃₃.

Рис. 11.

Damping coefficients при боковом раскачивании b₂₂.

Рис. 12.

Damping coefficients при вертикальных колебаниях b₃₃.

Гидродинамические коэффициенты представлены закрашенными кружками и квадратами, полученными с помощью предлагаемого численного метода, и сплошными кривыми для аналитического решения. Вообще говоря, численные результаты хорошо согласуются с аналитическими решениями, за исключением расхождения на рис. 11 и 12 при $D{\text{/}}{{f}^{4}}{\text{\;}} = 1.0$. При большей изгибной жесткости ледяной покров стремится стать более жестким, коэффициенты затухания приближаются очень близко к нулю, ошибки в численных результатах для коэффициентов затухания возрастают по причине того, что близкое к нулю решение труднее рассчитывать с надлежащей точностью. Ошибки можно уменьшить, разбивая сферу на большее число элементарных участков, что сказывается на эффективности расчетов. Таким образом, результаты показывают, что в данной работе метод функции Грина достаточно эффективен для вычисления излучения волн в воде погруженным телом при наличии ледяного покрова.

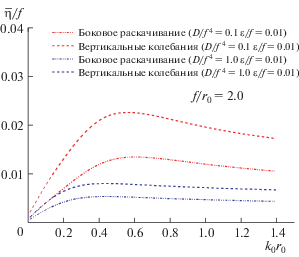
Кроме того, прогиб ледяного покрова может быть найден из уравнений (1.15) и (3.7) и на рис. 13 изображены наибольшие прогибы льдины, возникающие при боковом раскачивании и вертикальных колебаниях сферы при разных волновых числах и различной изгибной жесткости. Отметим, что наибольший прогиб льдины возрастает по мере того, как изгибная жесткость упругого ледяного покрова снижается. При постоянной изгибной жесткости прогибы льдины наиболее значительны при вертикальных движениях сферы.

Рис. 13.

Максимальные прогибы льдины в зависимости от волнового числа ${{k}_{0}}{{r}_{0}}$.

4.2.2. Дифракция волн в воде. В этом параграфе будет рассчитана дифракция волн в воде. Падающая плоская волна с амплитудой a₀ может быть описана выражением

(4.1)

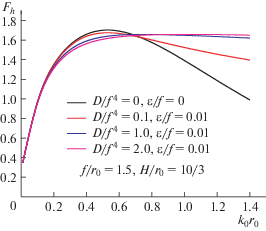
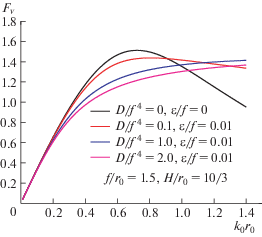
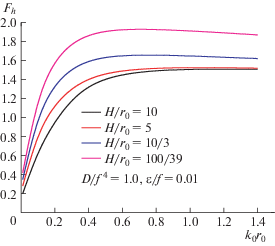
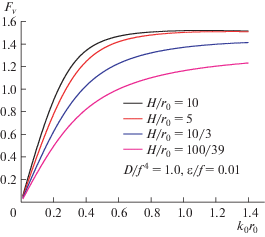
где β обозначает угол подхода (курсовой угол) и ${{\beta }} = 0$ обозначает попутное волнение. Подставляя условия (1.10) на поверхности тела в уравнение (3.2) и используя выражения (1.12) и (1.14), можно получить нагрузки возбуждающих волн. Горизонтальные и вертикальные силы обезразмерены в виде ${{F}_{h}} = \left| {{{{\hat {F}}}_{1}}{\text{/}}({{\rho }_{w}}gr_{0}^{2}{{a}_{0}})} \right|$ и ${{F}_{{v}}} = \left| {{{{\hat {F}}}_{3}}{\text{/}}({{\rho }_{w}}gr_{0}^{2}{{a}_{0}})} \right|$.

Для удобства верификации было взято значение 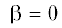, глубина погружения поддерживается постоянной при $f{\text{/}}{{r}_{0}} = 1.5$. На рис. 14 и 15 изображены графики ${{F}_{h}}$ и ${{F}_{{v}}}$ соответственно как функции волнового числа ${{k}_{0}}{{r}_{0}}$ для различных значений изгибной жесткости $D{\text{/}}{{f}^{4}}$, а именно, $D{\text{/}}{{f}^{4}} = 0~$, 0.1, 1.0 и 2.0 и $\varepsilon {\text{/}}f = 0~$ и 0.01 при $H{\text{/}}{{r}_{0}} = 1{\text{0/}}3$. На рис. 16 и 17 изображены графики ${{F}_{h}}$ и ${{F}_{{v}}}$ при переменной глубине воды $H{\text{/}}{{r}_{0}}$, а именно, $H{\text{/}}{{r}_{0}} = 10,~5,~10{\text{/}}3,$ и 100/39 при $D{\text{/}}{{f}^{4}} = 1.0$ и $\varepsilon {\text{/}}f = 0.01$.

Рис. 14.

Горизонтальная сила при различных значениях изгибной жесткости.

Рис. 15.

Вертикальная сила при различных значениях изгибной жесткости.

Рис. 16.

Горизонтальная сила при различных значениях глубины воды.

Рис. 17.

Вертикальная сила при различных значениях глубины воды.

На рис. 14 и 15 случай $D{\text{/}}{{f}^{4}} = 0$ и $\varepsilon {\text{/}}f = 0$ соответствует погруженной сфере при наличии свободной поверхности (без ледяного покрытия), результаты совпадают с теми, что приведены в [6]. При росте изгибной жесткости ледяного покрова горизонтальные и вертикальные силы постепенно достигают промежуточных значений.

Рисунки 16 и 17 иллюстрируют влияние уменьшения глубины воды на вертикальные и горизонтальные силы при фиксированных значениях $D{\text{/}}{{f}^{4}} = 1.0$ и $\varepsilon {\text{/}}f = 0.01$. Можно отметить, что горизонтальные силы убывают, а вертикальные силы возрастают при увеличении глубины воды. Кроме того, влияние глубины воды постепенно снижается при росте глубины воды.

ВЫВОДЫ

Предложен метод расчета излучения и дифракции погруженным телом волн в воде с ледяным покровом на основе трехмерной функции Грина. Можно сделать следующие выводы:

1. Согласие между численными результатами и аналитическими решениями для гидродинамических коэффициентов погруженной сферы указывает на то, что функция Грина для ледяного покрова в виде упругой пластины, предложенная в настоящей работе, является адекватной и метод, использующий трехмерные функции Грина, может быть в дальнейшем применен к решению гидродинамических задач о погруженном теле произвольной формы в воде с ледовым покрытием.

2. Вычислен прогиб льдины; это весьма перспективно для получения оценки разрушений в ледяном покрове, вызванных изгибно-гравитационными волнами в дальнейших исследованиях.

3. Проанализировано влияние глубины воды и изгибной жесткости ледяного покрова на дифракцию волн в воде. Найдено, что горизонтальные силы убывают, а вертикальные силы возрастают при увеличении глубины воды. Кроме того, изгибная жесткость упругого ледяного покрова оказывает большое влияние на численные результаты, свойства льда играют чрезвычайно важную роль в расчетах и должны быть определены настолько точно, насколько это только возможно.

Для численного решения гидродинамических задач о теле, погруженном в жидкость конечной глубины с ледяным покровом, в будущем необходимо предпринять еще большие усилия. Прежде всего должно быть учтено влияние скорости движения погруженного тела и построена функция Грина для покрова в виде упругой пластины при поступательном движении тела в воде конечной глубины, после чего необходимо будет исследовать механическую модель, для того чтобы предсказать повреждения льда, обусловленные движением погруженного тела.

Работа выполнена при поддержке Фонда Базовой лаборатории гидродинамики (грант № 350324100K3012AA00).

Список литературы

Lamb H. Hydrodynamics. Cambridge: Cambridge Univ. Press, 1932.
Peters A.S. A new treatment of the ship wave problem // Comm. Pure Appl. Math. 1949. V. 2. № 2–3. P. 123–148.
Ursell F. On Kelvin’s ship-wave pattern // J. Fluid Mech. 1960. V. 8. № 3. P. 418.
Lighthill M.J. Waves in Fluids. Cambridge: Cambridge Univ. Press, 1978.
Wang S. Motions of spherical submarine in waves // Ocean Engineering. 1986. V. 13. № 3. P. 249–271.
Linton C.M. Radiation and diffraction of water waves by a submerged sphere in finite depth // Ocean Eng. 1991. V. 18. № 1/2. P. 61–74.
Wu G.X., Taylor R.E. Radiation and diffraction of water waves by a submerged sphere at forward speed // Proc. R. Soc. Lond. 1988. V. 417. № 1853. P. 433–461.
Козин В.М., Онищук А.В. Модельные исследования волнообразования в сплошном ледяном покрове от движения подводного судна // Прикл. Мех. Техн. Физ. 1994. Т. 35. № 2. С. 78–81.
Das D., Mandal B.N. Oblique wave scattering by a circular cylinder submerged beneath an ice-cover // Int. J. Eng. Sci. 2006. V. 44. № 3–4, P. 166–179.
Das D., Mandal B.N. Wave scattering by a horizontal circular cylinder in a two-layer fluid with an ice-cover // Int. J. Eng. Sci. 2007. V. 45. № 10. P. 842–872.
Стурова И.В. Гидродинамические нагрузки, действующие на колеблющийся цилиндр, погруженный в стратифицированную жидкость, при наличии ледяного покрова // Прикл. Мех. Техн. Физ. 2011. Т. 52. № 3. С. 102–115.
Li Z.F., Wu G.X., Shi, Y.Y. Interaction of uniform current with a circular cylinder submerged below an ice sheet // Applied Ocean Research. 2019. V. 86. P. 310–319.
Das D., Mandal B.N. Water wave radiation by a sphere submerged in water with an ice-cover // Archive of Applied Mechanics. 2008. V. 78. № 8. P. 649–661.
Mohapatra S., Bora S.N. Radiation of water waves by a sphere in an ice-covered two-layer fluid of finite depth // Journal of Advanced Research in Applied Mathematics. 2010. V. 2. № 1. P. 46–63.
Das D., Thakur N. Water wave scattering by a sphere submerged in uniform finite depth water with an ice-cover // J. Mar. Struct. 2013. V. 30. P. 63–73.
Das D., Thakur N. Wave scattering by a sphere submerged in a two-layer fluid with an ice cover // Int. J. Appl. Math. Eng. Sci. 2014. V. 8. № 1. P. 45–63.
Mohapatra S., Bora S.N. Exciting forces due to interaction of water waves with a submerged sphere in an ice-covered two-layer fluid of finite depth // Appl. Ocean Res. 2012. V. 34. P. 187–197.
Sturova I.V. Unsteady three-dimensional sources in deep water with an elastic cover and their applications // J. Fluid Mec. 2013. V. 730. P. 392–418.
Kozin V.M., Pogorelova A.V. Submarine moving close to ice surface conditions // International Journal of Offshore and Polar Engineering. 2008. V. 18. № 4. P. 271–276.
Pogorelova A.V., Kozin V.M. Flexural-gravity waves due to unsteady motion of point source under a floating plate in fluid of finite depth // Journal of Hydrodynamics. Series B. 2010. V. 22. № 5. P. 71–76.
Погорелова А.В. Нестационарное движение источника в жидкости под плавающей пластиной // Прикл. Мех. Техн. Физ. 2011. Т. 52. № 5. С. 49–59.
Pogorelova A.V., Zemlyak V.L., Kozin V.M. Moving of a submarine under an ice cover in fluid of finite depth // J. Hydrodyn., Ser. B. 2019. V. 31. № 3. P. 562–569.
Lu D.Q., Dai S.Q. Flexural- and capillary-gravity waves due to fundamental singularities in an inviscid fluid of finite depth // International Journal of Engineering Science. 2008. V. 46. № 11. P. 1183–1193.
Lu D.Q., Dai S.Q. Generation of unsteady waves by concentrated disturbances in an inviscid fluid with an inertial surface // Acta Mech Sin. 2008. V. 24. № 3. P. 267–275.
Савин A.А., Савин А.С. Возмущение ледяного покрова движущимся в жидкости диполем // Изв. РАН, МЖГ. 2012. Т. 47. № 2. С. 3–10.
Савин A.А., Савин А.С. Пространственная задача о возмущении ледяного покрова движущимся в жидкости диполем // Изв. РАН. МЖГ. 2015. Т. 50. № 5. С. 16–23.
Hao L.Z., Pan Z.Y., Wu B.S. Three-dimensional Green-function method to predict the water wave radiation of a submerged body with ice cover // Applied Ocean Research. 2020. V. 101-C. P. 1–11.
Fox C., Chung H.J. Green’s function for forcing of a thin floating plate // Department of Mathematics-Research Report. Series number 408. The University of Auckland. 1998. P. 1–34.
Johnson R.S. A Modern Introduction to the Mathematical Theory of Water Waves. Cambridge: Cambridge Univ. Press, 1997.
Stoker J.J. Water Waves: The Mathematical Theory with Applications. John Wiley & Sons, 2011.
Newman J.N. The theory of ship motions // Adv. App. Mec. 1978. V. 18. P. 221–283.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал