1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 2, 2022

Известия РАН. Механика жидкости и газа, 2022, № 2, стр. 141-150

ЛОКАЛИЗОВАННЫЕ ТУРБУЛЕНТНЫЕ СТРУКТУРЫ В ТЕЧЕНИИ В ДЛИННОЙ ТРУБЕ ПРИ МИНИМАЛЬНОМ КОЛИЧЕСТВЕ ОГРАНИЧЕНИЙ НА СИММЕТРИЮ

S. Altmeyer a, *

a Castelldefels School of Telecom and Aerospace Engineering (EETAC), Universitat Politècnica de Catalanya
08860 Barcelona, Spain

* E-mail: sebastian.andreas.altmeyer@upc.edu

Поступила в редакцию 06.09.2021
После доработки 04.10.2021
Принята к публикации 21.10.2021

Полный текст (PDF)

Аннотация

Граница ламинарно-турбулентного перехода, называемая также гранью (edge), отделяет – по крайней мере, на конечном промежутке времени – траектории, стремящиеся к турбулентному аттрактору, от траекторий, притягиваемых ламинарным аттрактором. Для изучения динамики течения на этой границе (сепаратрисе) в работе выполнено прямое численное моделирование переходного течения в трубе в длинной расчетной области при числах Рейнольдса Re ∈ [2200, 2800]. Полученное решение имеет форму структуры, локализованной в пространстве и движущейся вниз по течению. По своим качественным характеристикам эти течения близки к турбулентным порывам, наблюдаемым в экспериментах в режиме переходных чисел Рейнольдса. Динамика состояний в области седла в фазовом пространстве на сепаратрисе, представляющей собой гиперповерхность течения в трубе, является хаотичной. Описаны локализованные решения на сепаратрисе для течений в трубах и изучена их взаимосвязь с турбулентными порывами при минимальном числе искусственных ограничений на структуру течения. Именно, рассмотрена только зеркальная симметрия и исследовано поведение решения в данном подпространстве. В отличие от решений, на которые наложены симметрии более высокого порядка, найденные в работе решения на сепаратрисе, обладают той же сложностью, что и решения в полном пространстве и, следовательно, представляют собой реальные физические (симметричные) течения.

Ключевые слова: уравнения Навье–Стокса, турбулентные порывы, пограничные состояния, вычислительная гидромеханика

Турбулентность в природе представляет собой скорее правило, чем исключение, однако наше ее понимание ограничено ее статистическими характеристиками. Поэтому общая цель состоит в выявлении динамики в области зарождающейся турбулентности. В частности, переход к турбулентности при течении в трубе все еще остается открытой проблемой теории устойчивости. Течение в трубе, а именно течение жидкости в бесконечно длинной трубе кругового сечения, или течение Гагена—Пуазейля, остается всегда устойчивым по отношению к бесконечно малым возмущениям [1], но на практике известно, что оно становится турбулентным [2, 3].

Характерным параметром, определяющим течение, является число Рейнольдса, определяемое как Re = UD/ν, где U – средняя скорость потока, D – диаметр трубы и ν – кинематическая вязкость. Как правило, неустойчивости при течениях в трубах наблюдаются при Re бóльших, чем 1750 [3, 4]. В диапазоне Re ∈ [1750, 2700] возмущения могут инициировать переход к перемежающимся турбулентным пятнам, обычно называемым порывами; они сосуществуют с ламинарным течением Гагена–Пуазейля [2, 5]. При значениях Re вплоть до 2250 турбулентность локализована в виде порывов, в результате чего скорости передних и задних фронтов этих структур одинаковы. Увеличение Re приводит к уменьшению скорости фронтов. В работе [6] введено понятие “равновесного порыва” (при 2100 < Re < 2300), в котором параметры (размеры и фиксированное число Рейнольдса) не изменяются при движении в трубе. В то же время при Re < 2100 подобные турбулентные порывы могут спонтанно исчезать, а при Re ≥ 2300 они становятся неустойчивыми, либо разделяясь на несколько таких структур, что приводит к увеличению числа порывов в трубе, либо расширяясь в осевом направлении с образованием длинных перемежающихся структур, так называемых пробок [5]. Эти расширяющиеся турбулентные пробки являются следствием увеличения скорости нижнего по потоку фронта и, следовательно, отклонения его скорости от скорости верхнего по потоку фронта. При уменьшении скорости порыва скорость нижнего по потоку фронта в диапазоне, когда существуют пробки, может возрастать [7]. Общее понимание явления перехода от порывов к пробкам состоит в переходе от возбудимости к бистабильности. На более глубоком уровне проблема фронтов в порывах и пробках исследована в работе [7], а статистика реламинаризации в упрощенной модели приведена в работе [8]. Природа ламинарно-турбулентного перехода изучалась более, чем столетие. В недавней работе [9] дан подробный обзор на эту тему, основанный на теоретическом, экспериментальном и численном исследовании течений и турбулентных структур в круглой трубе при переходных числах Рейнольдса.

Подход, использующий динамические системы, предполагает, что инвариантные решения уравнений Навье–Стокса, такие как бегущие волны (БВ) [10–12] и неустойчивые периодические орбиты для течений в трубах, действуют как структурные элементы в беспорядочной и хаотической динамике [13, 14]. Таким образом, турбулентность можно понимать как “сквозной контроль” (рис. 1а) поля инвариантных решений [14, 15]. Преобладающая точка зрения состоит в том, что хаотический аттрактор может характеризовать турбулентность, вследствие чего полагается, что ее скелет может быть собран из подобных инвариантных решений уравнений Навье–Стокса [16].

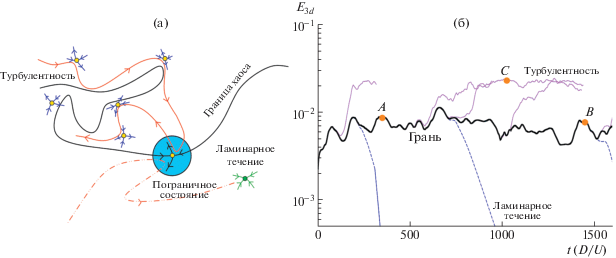
Рис. 1.

(а) Схематическое представление пространства состояний нестационарной турбулентности для течения в трубе. Ламинарное состояние течения представляет собой аттрактор, пространство притяжения которого сокращается с увеличением Re. Граница хаоса разделяет траектории, приводящие к реламинаризации и турбулентности, но в то же время она заворачивается в турбулентное седло [23, 35], что позволяет разворот к ламинарному состоянию. (b) Динамика течения в трубе вблизи пограничного состояния при Re = 2250. Представлена зависимость от времени кинетической энергии E3d (трехмерных Фурье-мод). Тонкие сплошные (красно-лиловые) линии соответствуют траекториям, приводящим к турбулентности, а пунктирные (голубые) линии представляют траектории, приводящие к реламинаризации. Сплошная толстая линия отмечает граничные траектории, группирующиеся вокруг пограничного состояния: они не приводят ни к турбулентности, ни к реламинаризации. A, B и C отмечают значения параметров, при которых построены изображения изоповерхностей на рис. 3.

Рассматривая турбулентные порывы как структурные единицы турбулентности, мы понимаем их как предвестники полностью турбулентной динамики, что делает из них весьма интересный гидродинамический объект. К сожалению, их действительная динамика крайне сложна и неопределенна, поскольку связанные с ними процессы являются стохастическими, а индивидуальные траектории следуют друг за другом случайным образом. Поэтому основная идея заключается в том, чтобы получить некоторую информацию из анализа более простых структур. При использовании метода слежения за границей [13, 17–19] такие решения возникают на сепаратрисе в фазовом пространстве между обеими различимыми областями притяжения, соответствующими ламинарному и турбулентному режимам течения. Какой именно вид (относительной) периодической орбиты определяет пограничное состояние, может зависеть от наличия некоторых пространственных симметрий, как, например, БВ, возникающие при наличии вращательной симметрии или зеркальной симметрии, дополненной сдвигом [10, 11, 20]. Эти пограничные состояния, обладающие качественными характеристиками турбулентного порыва, являются периодическими во времени в системе координат, движущейся в трубе с постоянной скоростью. Их простая общая структура позволяет выполнить детальное исследование их свойств. Показано, что такие пограничные состояния не только возникают между ламинарной и турбулентной динамикой течения в трубе [20, 21], но и представляют собой промежуточную стадию между ними [22]. В работе [23] отмечается, что пограничное состояние не является независимой динамической структурой, но представляет собой часть хаотического седла, облекающего структуры, порождающие турбулентность. В [24] существование пограничного состояния подтверждено в лабораторных экспериментах и обнаружено, что эти состояния определяют динамику течения во время затухания турбулентности, тем самым указывая на возможное средство управления турбулентностью. В [25] концепция пограничного состояния применена к пространственно развивающемуся пограничному слою и на этой основе дана новая интерпретация пограничного состояния как многообразия, разделяющего пространство состояний на классический переход и переход, сопровождаемый сменой прилипания на стенках на скольжение, – это два основных типа перехода в пограничном слое. Кроме того, пограничное состояние играет критическую роль в определении оптимальных возмущений и в методах управления [26, 27].

Однако в связи с большими вычислительными расходами исследований динамики турбулентных течений применялись различные ограничения. Первым и наиболее часто используемым ограничением такого рода являются ограничение на длину расчетной области (короткие трубы) и наблюдение над различными инвариантными решениями. Простейшими такими решениями являются точные бегущие волны (БВ) [10–12, 20]. Общая проблема с исследованиями БВ состоит в том, что численные исследования захватывают пространственную область, простирающуюся лишь на несколько диаметров трубы. В результате эти решения не способны дать объяснение ни крупномасштабной перемежаемости, ни локализации. Помимо того, следующими по уровню сложности в иерархии инвариантных решений являются модулированные БВ и относительные периодические орбиты (ОПО) [28]. Ограниченные короткими областями, эти исследования не обнаруживают наиболее важного явления локализации, наблюдаемого в экспериментах.

Протяженные области, достаточные для обнаружения локализации в БВ и ОПО, также рассматривались в расчетах, но за счет большего числа ограничений на симметрию. В основном для ограничения вычислительных расходов, а иногда и для того, чтобы сделать моделирование возможным в принципе, прибегали к диаметральной симметрии и π-периодичности. В работе [13] получено, что при таких ограничениях решения на сепаратрисе представляют собой ОПО, имеющие вид структур, локализованных в пространстве и периодических во времени в совместно движущейся системе координат. Это указывает на тот факт, что они содержат в себе механизмы, управляющие динамикой турбулентных решений. В работах [29, 30] представлен подробный анализ решений на сепаратрисе относительно механизмов, ответственных за их самоподдержание. Обнаружен нелинейный механизм зарождения продольных вихрей, отвечающий за поддержание пристенных полос. Следует заметить, что относительная простота этих решений имеет место лишь в рассмотренном подпространстве симметрий, где решениями являются ОПО. Хотя все эти работы углубляют понимание динамики течений, они пренебрегают тем фактом, что реальное, полное пограничное состояние является хаотическим [21, 22, 31, 32].

На этом обстоятельстве сосредоточена настоящая работа. Избегая сложности, присущей полному пространству [31, 32], мы находим множество решений, определяющих хаотическую динамику, используя лишь малое (или минимальное) количество ограничений симметрии (только лишь отражательную симметрию) для того, чтобы возможно ближе отразить реальный сценарий. Пограничные состояния, представленные в работе, являются асимптотическими состояниями, расположенными на границе ламинарно-турбулентного перехода.

1. ЧИСЛЕННЫЙ МЕТОД

Течение несжимаемой ньютоновской жидкости описывается уравнениями Навье–Стокса, которые могут быть приведены к безразмерному виду. Выбирая в качестве масштабов длины и скорости величины D/2 и 2U, соответственно, получим

(1.1)
${{\partial }_{t}}{\mathbf{u}} + {\mathbf{u}} \cdot \nabla {\mathbf{u}} = - \nabla p + 1{\text{/Re}}{{\nabla }^{2}}{\mathbf{u}},\quad \nabla u = 0.$

Единственным определяющим параметром является число Рейнольдса Re. На стенках ставится граничное условие прилипания u = 0, а в продольном направлении ставится условие периодичности, так что локализованные структуры в достаточно длинных трубах вполне соответствуют случаю бесконечной области.

Численное моделирование выполняется посредством гибридного спектрально-разностного метода [28, 33, 34], реализованного в цилиндрических координатах (r, θ, z). Метод обеспечивает выполнение постоянства массового расхода через трубу; при этом условие периодичности в осевом направлении ставится на расстоянии Λ = 40D.

Если не оговорено противное, динамика течения намеренно – для упрощения задачи – ограничена случаем зеркальной симметрии относительно диаметральной плоскости

(1.2)
${\mathbf{S}}{\text{:}}\,{\text{ }}(u,{v},w){\text{ }}(r,\theta ,z,t) = (u, - {v},w)(r, - \theta ,z,t)~~~$
где u, ${v}$ и w – радиальная, азимутальная и осевая скорости  соответственно. Это условие запрещает вращения относительно оси трубы. Никакие другие условия симметрии не задаются в явном виде, но они могут спонтанно выявиться в ходе моделирования.

Сходимость решения обеспечивалась выбором высокого пространственного разрешения, при котором использовались до M = ±16 Фурье-мод в азимутальном направлении (при θ ∈ [0, π]), N = 64 точек конечно-разностной сетки в радиальном направлении и K = ±17 × Λ/D Фурье-мод в продольном направлении. Использованная методика позволила ранее добиться отличного количественного совпадения с экспериментальными данными по таким тонким свойствам турбулентных порывов, как статистика времен жизни [19]. Динамика течения на границе ламинарно-турбулентного перехода рассчитывалась при помощи интегрирования по времени (схема “предиктор–корректор” второго порядка точности с шагом по времени ∆t = 0.0025) с применением методики уточнения границы перехода [17, 21]. Эта процедура заключается в следующем. В ламинарном потоке задается достаточно сильное локализованное возмущение, превращающееся затем в турбулентный порыв. Таким образом, задается первое начальное условие ${v}$puf, f. Это предварительно определенное турбулентное решение ${v}$puf,f используется далее в итерационной процедуре расчета предельного решения на сепаратрисе. Отсюда новые начальные условия получаются перенормирокой амплитуды этого порыва (за вычетом ламинарного параболического течения): vα = vlam + α(vpuf,f – vlam), α ∈ (0, 1), где vpuf,f и vlam – поля скоростей порыва и ламинарного течения соответственно.

2. РЕЗУЛЬТАТЫ

2.1. Пограничные состояния – решения на сепаратрисе

Траектория границы перехода ограничена двумя соседствующими, но качественно существенно различными траекториями, из которых одна ведет к реламинаризации, а другая к турбулентности. На рис. 1б показаны некоторые траектории, включая граничную траекторию (сплошная толстая линия) и траектории, соответствующие либо турбулентному течению (тонкие красно-лиловые линии), либо реламинаризации (пунктирные голубые линии), при Re = 2250 на протяжении примерно 1600 единиц времени. Траектория границы получена при помощи алгоритма отслеживания границы [13, 17, 31]. Следует заметить, что отслеживание этой траектории при помощи метода пристрелки и деления отрезка пополам [19, 21] становится возможным благодаря существенному различию между энергиями пограничного и турбулентного состояний.

В противоположность подпространствам, включающим более высокие симметрии (включая дополнительную π-вращательную симметрию), граничная траектория не демонстрирует никаких признаков эволюции к упорядоченным, периодическим или квазипериодическим колебаниям, например, БВ [10, 11] или ОПО [13, 29, 36] (по крайней мере, при временах t(D/U) до 2000). Она не сводится ни к какому простому инвариантному решению, т.е. остается хаотической, как и при моделировании в полном пространстве [31]. Это поддерживает гипотезу о лежащей в основе структуры странного седла в фазовом пространстве. Это означает, что полученные в подпространстве с зеркальной симметрией упрощенные решения приводят к тому же результату, что и решения, полученные в полном пространстве при переходе к турбулентности в течениях в трубах [37]. Все это говорит в пользу вывода о том, что динамика пограничного состояния не завершается достижением периодического или квазипериодического состояния. В любом случае энергия граничных траекторий остается существенно ниже уровней турбулентности (рис. 1б) и, таким образом, различима на их фоне.

2.1.1. Свойства и характеристики пограничного состояния. На рис. 2 представлены скорости Uc на центральной линии для пограничного состояния (ПС) и турбулентного порыва (ТП), полученные численным моделированием при Re = 2250 (поток слева направо). Рассмотрим профиль скорости для ТП (рис. 2б); он обнаруживает резкое падение на заднем фронте порыва. Это типичный признак порывов, указывающий на резкий переход от ламинарного к турбулентному течению. Это четко определяемое падение часто используется для определения положения порыва. С другой стороны, на переднем фронте отмечается постепенное увеличение скорости, соответствующее медленному восстановлению ламинарного течения.

Рис. 2.

Распределение продольной скорости Uc вдоль центральной линии трубы при наличии лишь одной структуры. Вверху: пограничное состояние (ПС). Внизу: турбулентный порыв (ТП) при Re = 2250. Поток направлен слева направо (в направлении x). Вертикальные линии (a−e) указывают положения поперечных сечений, представленных на рис. 4.

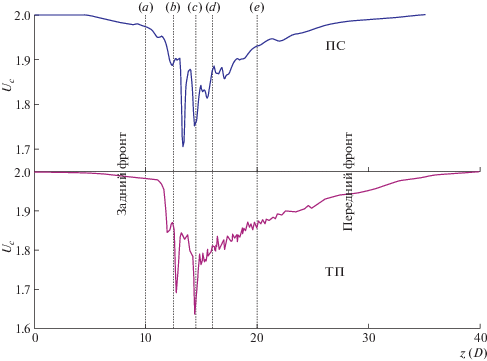
Вдали от локализованного порыва, вверх и далеко вниз по течению от него, скорость на центральной линии Uc приближается к удвоенной массовой скорости UB, представляющей собой теоретическое значение скорости ламинарного течения. Постепенный рост скорости на центральной линии у переднего фронта делает затруднительным точное определение длины порыва. Немедленно после резкого падения величины Uc наблюдаются сильные пульсации скорости. Соответствующая область проявляет свойства полностью развитой турбулентности [38].

Основные черты ТП (рис. 2, внизу) сохраняются и в случае ПС (рис. 2, вверху); это говорит о том, что свойства локализованной турбулентности могут быть выявлены при численном решении уравнений Навье–Стокса на сепаратрисе. Однако существуют два отличия. Прежде всего рост скорости Uc (более крутой наклон) с возвратом к ламинарному состоянию (Uc = 2) происходит гораздо быстрее в случае ПС, что приводит к меньшему осевому расширению или укорочению ПС (рис. 5). Во-вторых, пульсации скорости за ее падением менее выражены, чем в соответствующем порыве. Однако эти пульсации четко различимы при использованном минимальном числе симметрий по сравнению с ранними работами, в которых рассматривались симметрии высшего порядка (π-вращение + отражение) (рис. 2 в [13]). В последнем случае пульсации в ПС практически исчезают и, таким образом, динамика, определенная в настоящей работе, оказывается ближе к сценарию в полном пространстве.

2.1.2. Сравнение пограничного состояния и порыва. На рис. 3 проводится качественное сравнение ПС в два различные момента времени на сепаратрисе (см. рис. 1) с турбулентным порывом. Трехмерные поля течений, представленные изоповерхностями мгновенной осевой скорости, демонстрируют качественное соответствие, хотя структура ПС остается проще, чем структура ТП во все моменты времени. Общей характеристикой всех структур являются длинные области ускоренного и замедляющегося движения вблизи стенок трубы. Оба поля течения ПC значительно менее сложны и обнаруживают более высокую пространственную когерентность, чем в случае ТП. Помимо того что изоповерхности в случае ПС более гладкие, осевые длины пограничных состояний, в частности, переднего фронта, значительно короче, чем в случае турбулентного порыва. Это следует из упомянутого выше медленного убывания осевой скорости на переднем фронте и более резкого восстановления на заднем фронте в случае ТП. В то же время пограничному состоянию свойственны умеренные изменения при осевом расширении с сохранением его суммарных характеристик и формы в результате хаотического поведения (см. рис. 1б) на границе (сильное изменение продольной скорости uz и энергии E во времени). Задний фронт порыва проявляет более сложное динамическое поведение с вихревыми структурами, наклоненными внутрь объема и разрывающими полосы на части. Последнее есть одна из причин существенного увеличения энергии внутри турбулентного порыва по сравнению с обоими случаями ПС (см. рис. 5а).

Рис. 3.

Изоповерхности (uz = ±0.07) в два момента времени для локализованных пограничных состояний ПС (а, б) и локализованных турбулентных состояний (порывов, ПС) (в) (см. точки A, B и C на рис. 1) при Re = 2250. Зеленый и желтый цвета соответствуют положительным и отрицательным значениям продольной скорости. Направление потока слева направо. Представлена только центральная область трубы протяженностью 20D.

Мгновенные изображения полей скорости в поперечных сечениях в координатах (r, θ) для ПС и ТП приведены на рис. 4. Качественное подобие между обоими состояниями (осевые положения сечений указаны прямыми линиями на рис. 2) означает подобие характеристик течения. ПС (рис. 4а) содержит бóльшую часть динамики ТП (рис. 4б) внутри в целом более гладкой структуры. Заметные мелкомасштабные модуляции в ТП сохраняются и отражают внутреннюю хаотическую динамику вихревой структуры (линии 2б и 2в). Меньший рост и более сложная динамика этих структур на переднем фронте ТП видны на рис. 4 (линия 2д).

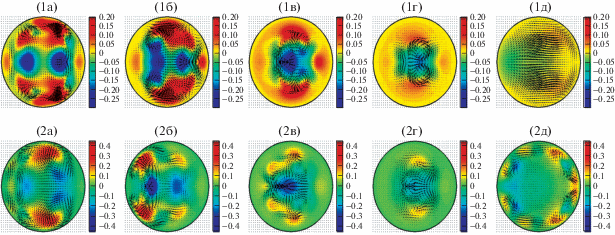
Рис. 4.

Мгновенные изображения полей скорости в поперечных сечениях в координатах (r, θ) при различных осевых положениях сечений, указанных на рис. 2 для (1) пограничного состояния и (2) турбулентного порыва при Re = 2250. Компоненты скорости, лежащие в плоскостях, указаны стрелками, а значения осевой скорости представлены цветами (синий для отрицательных и красный для положительных значений). Всюду вычтен ламинарный профиль скорости. Палитра представляет диапазон скоростей от −0.3U to 0.2U. Максимальное значение для компонент скорости, лежащих в плоскости, составляет −0.302U. Красные, желтые и синие цвета отмечают области, где продольная скорость течения больше чем, сравнима с и меньше чем в соответствующем параболическом профиле.

Рис. 5.

Статистические характеристики ПС и ТП в зависимости от Re. (а) Энергия E3d в зависимости от осевого расстояния z в единицах радиуса трубы. (б) Осредненная по времени энергия E3d. (в) Длина по оси lz ПС и ТП в рассмотренном диапазоне Re.

2.2. Зависимость от числа Рейнольдса

Далее мы рассмотрим течения при больших числах Рейнольдса Re, при которых характер турбулентности в трубе меняется и она может проявиться в виде растущих пробок [5], а не равновесных порывов. Для того чтобы справиться с тем обстоятельством, что все анализируемые структуры хаотичны, будут использованы статистические характеристики. Следовательно, вместо характеристик течения в заданные моменты времени будут использованы значения, осредненные по длинным интервалам времени t(D/U) (порядка 1500 единиц времени).

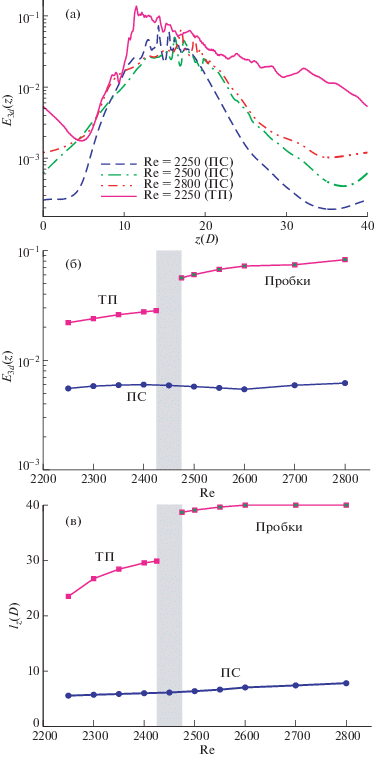
На рис. 5а представлено осевое распределение полной модальной кинетической энергии E3d для различных пограничных состояний и турбулентного состояния, соответствующего указанному значению Re. При Re = 2250 порыв имеет обычное распределение энергии: с одной стороны это широко растянутый передний фронт, с медленным и нерезким экспоненциальным затуханием энергии в области вниз по потоку. С другой стороны, это острый задний фронт, характеризуемый быстрым экспоненциальным убыванием энергии в области выше по потоку. По сравнению с ТП, соответствующее пограничное состояние при том же значении Re = 2250 очевидно короче. ПС в целом характеризуется растянутыми передним и задним фронтами. Более того, максимальная энергия и, особенно, осредненная энергия для ПС значительно ниже. С ростом Re основная форма ПС остается неизменной, лишь с легким осевым расширением области пика энергии. В то же время энергия в переднем фронте убывает медленнее, стремясь к типичной форме турбулентного порыва. При увеличении Re максимальные значения E(z) для ПС остаются в основном на одном уровне, тогда как минимальные значения немного растут.

На рис. 5б представлена зависимость от Re осредненных по времени энергий пограничного и турбулентного состояний, к которым асимптотически приближаются пограничные и турбулентные траектории (см. рис. 1). В рассмотренном диапазоне Re энергия пограничного состояния не претерпевает существенных изменений. Уровень энергии турбулентности для всех Re не только выше, чем для пограничного состояния, но и постоянно растет с ростом Re. Особенно сильно энергия турбулентного режима растет в интервале между Re = 2400 и 2500. Это есть результат неограниченного роста турбулентных структур в этом режиме: они превращаются в пробку, которая в конце концов заполняет всю область. Это показывает и рис. 5в, где представлена зависимость осевой длины lz данных структур. Здесь за lz принята минимальная осевая длина, содержащая 98% энергии (рис. 5а). При Re ≥ 2500 турбулентные структуры заполняют всю область (40D).

ЗАКЛЮЧЕНИЕ

Показано, что численные решения уравнений Навье–Стокса с минимальным количеством (искусственных) ограничений на симметрию (в работе используется только зеркальная симметрия) позволяют получить основные характеристики течений в трубах в переходном режиме к турбулентности. Для определения порога перехода по отношению к амплитуде возмущений исследовано состояние на сепаратрисе (границе с хаосом), отделяющей затухающие возмущения, возвращающие систему к ламинарному режиму, от возмущений, которые в конечном счете инициируют турбулентность. Обнаруженные пограничные состояния обладают теми же структурными свойствами и той же пространственной сложностью, что и турбулентные порывы. Сама сепаратриса оказывается хаотической, как это было обнаружено и при моделировании в полном пространстве. Это важный вывод, так как, пользуясь им, можно преодолеть основную проблему, присущую подпространствам с наложенными симметриями высшего порядка, а именно, диаметральной симметрией и π-периодичностью [13, 29, 30], когда сепаратриса оказывается периодической (квазипериодической) во времени. Насколько нам известно, решения, обладающие лишь зеркальной симметрией, для течений в трубах получены впервые.

Полученные решения так же сложны, как и решения, полученные без дополнительных ограничений. Хотя этот вывод не предоставляет особенно больших новых возможностей по сравнению с решениями, полученными в полном пространстве, он очевидным образом подчеркивает важность того, чтобы иметь представление, в каком подпространстве проводится решение, так как этот факт может сильно изменить и (или) упростить динамику течения. Представленные в работе решения с наложенной зеркальной симметрией хорошо согласуются с ранее опубликованными результатами по локализованным пограничным состояниям в течениях в трубах при отсутствии симметрии [31]. Таким образом, они представляют собой первый важный шаг в быстром и простом получении информации о динамике течения перед использованием более сложных и затратных моделирований. В изученном диапазоне переходных режимов Re ∈ [2200, 2800] пограничные состояния могут дать более глубокое представление о переходе к турбулентности, чем исследование уже полностью сформировавшихся турбулентных состояний при течениях в трубах. Помимо того, с ростом Re расширение турбулентных порывов и их превращение в пробки с потерей локализации приобретают критическую роль. Для воспроизведения этого процесса необходимы бóльшие расчетные области и, следовательно, бóльшие вычислительные расходы. Необходимость дальнейших исследований очевидна, но знание о подобии динамики и структуры течения, полученных в подпространстве с наложенной отражательной симметрией и в полном пространстве, безусловно может оказать помощь в решении одной из главных проблем, связанных с турбулентным движением.

Настоящая работа поддержана грантом PID2019-105162RB-I00 Правительства Испании.

Список литературы

  1. Meseguer A., Trefeten L.N. Linearized pipe flow to Reynolds number 107 // J. Comput. Phys. 2003. V. 186. P. 178.

  2. Reynolds O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels // Phil. Trans. Roy. Soc. London. A. 1883. V. 174. P. 935.

  3. Hof B., Juel A., Mullin T. Scaling of the threshold of pipe flow turbulence // Phys. Rev. Lett. 2003. V. 91. P. 244502.

  4. Peixinho J., Mullin T. Decay of turbulence in pipe flow // Phys. Rev. Lett. 2006. V. 96. P. 094501.

  5. Wygnanski I.J., Champagne F.H. On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug // J. Fluid Mech. 1973. V. 59. P. 281.

  6. Wygnanski I., Sokolov J.M., Friedman D. On transition in a pipe. Part 2. The equilibrium puff // J. Fluid Mech. 1975. V. 69. P. 283.

  7. Barkley D., Song B., Mukund V., Lemoult G., Avila M., Hof B. The rise of fully turbulent flow // Nature. 2015. V. 526. P. 550–553.

  8. Willis A.P., Kerswell R.R. Turbulent dynamics of pipe flow captured in a reduced model: puff relaminarization and localized ’edge’ states // J. Fluid Mech. 2009. V. 619. P. 213–233.

  9. Никитин Н.В. Проблема перехода и локализованные турбулентные структуры в трубах // Изв. РАН. МЖГ. 2021. № 1. С. 32–46.

  10. Faisst H., Eckhardt B. Traveling waves in pipe flow // Phys. Rev. Lett. 2003. V. 91. P. 224502.

  11. Pringle C.C.T., Kerswell R.R. Asymmetric, helical, and mirror-symmetric traveling waves in pipe flow // Phys. Rev. Lett. 2007. V. 99. P. 074502.

  12. Mellibovsky F., Meseguer A. Critical threshold in pipe flow transition // Phil. Trans. Roy. Soc. Londjn. A. 2009. V. 367. P. 545.

  13. Avila M., Mellibovsky F., Roland N., Hof B. Streamwise-localized solutions at the onset of turbulence in pipe flow // Phys. Rev. Lett. 2013. V. 110. P. 224502.

  14. Hof B., van Doorne C.W.H., Westerweel J., Nieuwstadt F.T.M., Faisst H., Eckhardt B., Wedin H., Kerswell R.R., Waleffe F. Experimental observation of nonlinear traveling waves in turbulent pipe flow // Science. 2004. V. 305. P. 1594.

  15. Hof B., de Lozar A., Kuik D.J., Westerweel J. Repeller or attractor? Selecting the dynamical model for the onset of turbulence in pipe flow // Phys. Rev. Lett. 2008. V. 101. P. 214501.

  16. Gibson J.F., Halcrow J., Cvitanovi’c P. Visualizing the geometry of state space in plane Couette flow // J. Fluid Mech. 2008. V. 611. P. 107–130.

  17. Itano T., Toh S. The dynamics of bursting process in wall turbulence // J. Phys. Soc. Japan. 2001. V. 70. P. 703–716.

  18. Skufca J.D., Yorke J.A., Eckhardt B. Edge of chaos in a parallel shear flow // Phys. Rev. Lett. 2013. V. 96. P. 174101.

  19. Avila M., Willis A.P., Hof B. On the transient nature of localized pipe flow turbulence // J. Fluid Mech. 2010. V. 646. P. 127.

  20. Duguet Y., Willis A.P., Kerswell R.R. Transition in pipe flow: the saddle structure on the boundary of turbulence // J. Fluid Mech. 2008. V. 613. P. 255–274.

  21. Schneider T.M., Eckhardt B., Yorke J.A. Turbulence transition and the edge of chaos in pipe flow // Phys. Rev. Lett. 2007. V. 99. P. 034502.

  22. Schneider T.M., Eckhardt B. Edge states intermediate between laminar and turbulent dynamics in pipe flow // Phil. Trans. Roy. Soc. London. A. 2008. V. 367. P. 577–587.

  23. Chantry M., Schneider T.M. Studying edge geometry in transiently turbulent shear flows // J. Fluid Mech. 2014. V. 747. P. 506–517.

  24. De Lozar A., Mellibovsky F., Avila M., Hof B. Edge state in pipe flow experiments // Phys. Rev. Lett. 2012. V. 108. P. 214502.

  25. Beneitez M., Duguet Y., Schlatter P., Henningson D.S. Edge tracking in spatially developing boundary layer flows // J. Fluid Mech. 2019. V. 881. P. 164–181.

  26. Kerswell R.R. Nonlinear nonmodal stability theory // Annu. Rev. Fluid Mech. 2018. V. 50. P. 319–345.

  27. Rabin S.M.E., Caulfield C.P., Kerswell R.R. “Triggering turbulence efficiently in plane Couette flow // J. Fluid Mech. 2012. V. 712. P. 244–272.

  28. Willis A.P., Cvitanovi’c P., Avila M. Revealing the state space of turbulent pipe flow by symmetry reduction // J. Fluid Mech. 2013. V. 721. P. 514.

  29. Никитин Н.В., Пиманов О.В. Численное исследование локализованных структур в трубах // Изв. РАН. МЖГ. 2015. № 5. С. 64–75.

  30. Никитин Н.В., Пиманов О.В. О поддержании колебаний в локализованных турбулентных структурах в трубах // Изв. РАН. МЖГ. 2018. № 1. С. 68–76.

  31. Mellibovsky F., Meseguer A., Schneider T., Eckhardt B. Transition in localized pipe flow turbulence // Phys. Rev. Lett. 2009. V. 103. P. 054502.

  32. Avila K., Moxey D., de Lozar A., Avila M., Barkley D., Hof B. The onset of turbulence in pipe flow // Science. 2011. V. 333. P. 192.

  33. Willis A.P., Kerswell R.R. Turbulent dynamics of pipe flow captured in a reduced model: puff relaminarization and localized ‘edge’ states // J. Fluid Mech. 2009. V. 619. P. 213.

  34. Willis A.P. The Openpipeflow Navier–Stokes solver // SoftwareX. 2017. V. 6. P. 124–127.

  35. Lebovitz N.R. Boundary collapse in models of shear-flow transition // Commun. Nonlinear Sci. Numer. Simul. 2012. V. 17. № 5. P. 2095–2100.

  36. Chantry M., Willis A.P., Kerswell R.R. Genesis of streamwise-localized solutions from globally periodic traveling waves in pipe flow // Phys. Rev. Lett. 2014. V. 112. P. 164501.

  37. Eckhard B. Turbulence transition in pipe flow: some open questions // Nonlinearity. 2007. V. 21. № 1. P. 1–11.

  38. Bandyopadhyay P.R. Aspects of the equilibrium puff in transitional pipe-flow // J. Fluid Mech. 1986. V. 163. P. 439.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал