Известия РАН. Механика жидкости и газа, 2022, № 2, стр. 105-122

СЛАБОНЕЛИНЕЙНЫЕ ТРЕХМЕРНЫЕ ГРАВИТАЦИОННЫЕ НЕСВЯЗАННЫЕ ВОЛНЫ НА ГРАНИЦЕ РАЗДЕЛА: МЕТОД ВОЗМУЩЕНИЙ И ВАРИАЦИОННАЯ ПОСТАНОВКА

S. Salmi^a, b, *, N. Allalou^c, **, M. Debiane^c, ***

^a Departement de physique, Faculte des sciences, Universitee M’Hamed Bougara de Boumerdes
Boumerdes, Algeria

^b Laboratoire revêtements, Matériaux et Environnement, Université M’Hamed Bougara de Boumerdes
Boumerdes, Algeria

^c Faculté de physique, Laboratoire mécanique des fluides théoriques et appliqués, Université des Sciences et de la Technologie Houari Boumediene
Algiers, Algeria

^* E-mail: s.salmi@univ-boumerdes.dz
^** E-mail: nallalou1@usthb.dz
^*** E-mail: debianemd@yahoo.fr

Поступила в редакцию 23.01.2021
После доработки 01.04.2021
Принята к публикации 19.05.2021

EDN: FYEEHD
DOI: 10.31857/S0568528122010091

Полный текст (PDF)

Аннотация

Рассматривается слабо нелинейное поведение коротко-гребневых волн на границе раздела двух сред при наличии течения в одной из сред. При нахождении аналитических решений используются два подхода. В первом из них при нахождении решений с пятым порядком аппроксимации применяется метод возмущений. Преимущество этого метода состоит в том, что он позволяет определить условие гармонического резонанса, который является одним из главных характеристик волн с короткими гребнями. Вторым методом является вариационный подход, предложенный Уиземом. На базе этого метода находится квадратное дисперсионное уравнение. В линейном случае показано, что есть критическая скорость течения, при превышении которой решения со стационарными волнами не могут существовать. Это критическое течение связано с появлением неустойчивости. В нелинейном случае критическая скорость течения растет вместе с амплитудой волн, как и в двумерном случае.

Ключевые слова: гармонический резонанс, волна с короткими гребнями на границе раздела, метод возмущений, вариационная формулировка, течение

В течение нескольких лет большие усилия были приложены к изучению волн на границе раздела двух сред в связи с их причастностью к многим практическим приложениям. Один из примеров относится к моделированию задач двухфазных течений, схожих с газожидкостным течением в трубопроводах. В течение долгого времени задача, имеющая дело с волнами на границе раздела между средами при наличии течения, была ориентирована на изучение двумерных волновых полей. В [1] была рассмотрена задача о бегущих межфазных волнах с постоянным профилем, распространяющихся на границе раздела двух бесконечных жидких слоев. Адекватные решения были получены для значений амплитуд волн от малых до умеренных. Было показано, что имеется критическая скорость течения U_c, при превышении которой стационарные решения перестают существовать и, кроме того, критическая скорость течения возрастает с ростом амплитуды волн. В [2] анализ, проведенный в [1], был расширен, чтобы учесть эффект конечной глубины жидкости. В частности было показано, что при некоторых глубинах критическая скорость течения является убывающей функцией амплитуды волн.

В трехмерном случае в большинстве опубликованных работ рассматриваются поверхностные волны. Из-за сложности задачи зачастую исследуются волны с короткими гребнями, которые являются самым простым видом рассматриваемых волн. В [3] были получены решения третьего порядка, которые остаются справедливыми для слабо нелинейных волн. В [4], используя метод возмущений, был изучен случай бесконечной глубины. Численные решения были рассчитаны до 27-го порядка. Особое внимание было обращено на явление гармонического резонанса. В [5] метод, использованный в [4], был развит для вычисления решений 35-го порядка в случае волн, распространяющихся в жидкости конечной глубины. В [6] был представлен метод Фурье для вычисления высших гармоник волн с короткими гребнями. Не так давно было проведено исследование распада волн с короткими гребнями с использованием численных моделей. В [7] коротко-гребневые волны в зоне прибоя были исследованы, используя приближение гидродинамики сглаженных частиц. В [8] были проведены расчеты с использованием FUNWAVE-TVD подхода, который является TVD-версией полной нелинейной модели волн в приближении Буссинеска. При проведении исследования авторы обнаружили образование отбойных волн и формирование вертикальной завихренности. В [9] коротко-гребневые гравитационно-капиллярные волны были исследованы, используя метод Лагранжа, в случае бесконечной глубины жидкости. Эта методика может быть использована для расчета резонансных волн. В [10] была сформулирована проблема, состоящая в том, что набор глубин жидкости, на которых условие резонанса делает несправедливым разложение возмущения в виде стоячих волн, представляет собой плотное множество, что подвергает сомнению весь рассматриваемый подход. Этот вопрос был окончательно разрешен в [11] с использованием теории Нэша–Мозера, чтобы преодолеть проблему малого делителя. Для трехмерных бегущих волн, аналогично коротко-гребневым волнам, задача малого делителя была разрешена в [12], используя теорию Нэша–Мозера для нерезонансных углов. Там же было разработано формальное асимптотическое разложение. В [13] были получены аналитические решения для гравитационно-капиллярных волн на конечной глубине в присутствии однородного течения. Внимание было сконцентрировано на влиянии течения на характеристики волны (профиль, частота, давление и т.д.). В частности, полученные результаты показали, что волна становится круче при увеличении скорости потока.

В небольшом числе исследований было уделено внимание трехмерным волнам на границе раздела, а именно тем, которые существуют только для уединенных волн [14–17]. В противном случае, в [18] были детально изучены коротко-гребневые волны на границе раздела, которые являются простейшими трехмерными прогрессивными волнами. Были получены аналитические решения третьего порядка и численные решения 27-го порядка. В этом исследовании было определено условие резонанса в случае трехмерных волн на границе раздела и в этом сысле оно является обобщением работ [4, 5]. Более недавним примером, включающим изучение волн на границе раздела, является теоретическое исследование [19]. В нем было проведено детальное исследование стационарных резонансных волн на границе раздела в двуслойной жидкости внутри канала без трения.

Цель настоящей работы состоит в расширении исследования [18] на случай наличия течения в одной из сред. Настоящее исследование также представляет собой обобщение работы [1] на трехмерный случай. В разд. 1 дано физическое и математическое описание проблемы коротко-гребневых волн при наличии течения в одной из сред. В разд. 2 метод возмущений используется для получения аналитических решений до пятого порядка включительно с уделением наибольшего внимания явлению гармонического резонанса. После этого в разд. 3 вариационный подход применяется для решения той же задачи и выписывается соответствующий лагранжиан. Наконец, в разд. 4 обсуждаются полученные результаты.

1. ПОСТАНОВКА ЗАДАЧИ

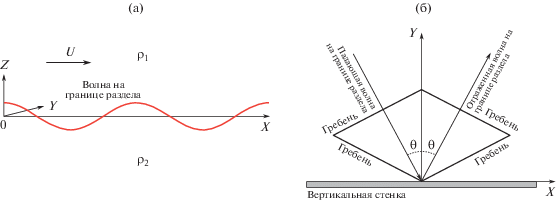
Рассмотрим двуслойную систему неограниченных жидкостей с однородным течением в одной из них со скоростью $U$, параллельной границе раздела (рис. 1а). Верхний и нижний слои жидкостей имеют плотности ${{\rho }_{1}}$ и ${{\rho }_{2}}$ соответственно. Предполагается, что эти два слоя горизонтальные и имеют бесконечную глубину. Используемая декартова система координат состоит из горизонтальной плоскости $(xOy)$ и оси z, направленной вертикально вверх. Начало координат находится на невозмущенной границе раздела двух слоев жидкости (рис. 1а). В нашем случае поле течения коротко-гребневых волн генерируется при нелинейном взаимодействии двух волновых пакетов, распространяющихся навстречу друг другу и имеющих одинаковые характеристики. Длина падающей волны равна $L$ и угол между направлением падения и нормалью к стенке равен $\theta $ (рис. 1б). Обе жидкости предполагаются невязкими, несжимаемыми и однородными, а движение считается безвихревым. Рассматривается ситуация, в которой расположение жидкостей является устойчиво стратифицированным по отношению к силе тяжести, т.е. ${{\rho }_{1}} < {{\rho }_{2}}$.

Рис. 1.

Схематическое представление волны на границе раздела двух сред в присутствии течения, параллельного оси Ox (a); отражение плоской волны от вертикальной стенки (б).

В рамках сформулированных предположений поле скорости в верхнем слое является суммой двух компонент

(1.1)

${{\vec {V}}_{1}} = U\vec {i} + \vec {\nabla }{{\phi }_{1}}.$

Первая компонента обусловлена присутствием однородного течения, а вторая компонента является безвихревой и находится из потенциала скорости. В нижнем слое вектор скорости задается в следующем виде:

(1.2)

${{\vec {V}}_{2}} = \vec {\nabla }{{\phi }_{2}}.$

Движение жидкости может быть описано потенциалами скоростей ${{\phi }_{1}}(x,y,z,t)$ и ${{\phi }_{2}}(x,y,z,t)$, которые удовлетворяют уравнению Лапласа в области в виде двух слоев жидкости, что записывается в следующем виде:

(1.3)

$\Delta {{\phi }_{1}} = 0\quad {\text{для}}\quad \eta (x,y,t) < z < + \infty ,$

(1.4)

$\Delta {{\phi }_{2}} = 0\quad {\text{для}}\quad - \infty < z < \eta (x,y,t).$

Для этих двух жидкостей кинематические граничные условия на границе раздела имеют вид:

(1.5)

${{\eta }_{t}} + {{\eta }_{x}}{{\phi }_{{1x}}} + U{{\eta }_{x}} + {{\eta }_{y}}{{\phi }_{{1y}}} - {{\phi }_{{1z}}} = 0\quad {\text{при}}\quad z = \eta (x,y,t),$

(1.6)

${{\eta }_{t}} + {{\eta }_{x}}{{\phi }_{{2x}}} + {{\eta }_{y}}{{\phi }_{{2y}}} - {{\phi }_{{2z}}} = 0\quad {\text{при}}\quad z = \eta (x,y,t).$

Динамическое граничное условие на границе раздела имеет вид:

$\left( {{{\rho }_{2}}\left( {{{\phi }_{{2t}}} + g\eta + \frac{1}{2}(\phi _{{2x}}^{2} + \phi _{{2y}}^{2} + \phi _{{2z}}^{2})} \right)} \right) - \left( {{{\rho }_{1}}\left( {{{\phi }_{{1t}}} + g\eta + \frac{1}{2}(\phi _{{1x}}^{2} + \phi _{{1y}}^{2} + \phi _{{1z}}^{2})} \right)} \right) + C = 0$

(1.7)

${\text{при}}\quad z = \eta (x,y,t).$

Оно может быть выведено из уравнения Бернулли и описывает баланс сил давления по обе стороны от границы раздела. Здесь C есть постоянная Бернулли. Условия, что нормальные скорости должны равняться нулю далеко внизу и далеко вверху от границы раздела, дают граничные условия

(1.8)

${{\phi }_{{1z}}} = 0\quad {\text{при}}\quad z \to + \infty ,$

(1.9)

${{\phi }_{{2z}}} = 0\quad {\text{при}}\quad z \to - \infty .$

Безразмерные уравнения могут быть получены введением характерного времени ${1 \mathord{\left/ {\vphantom {1 {\sqrt {gk} }}} \right. \kern-0em} {\sqrt {gk} }}$ и характерной длины $1{\text{/}}k$, где $k$ есть волновое число $2\pi {\text{/}}L$, $L$ представляет собой длину падающей волны и g есть ускорение силы тяжести. Можно ввести следующие безразмерные величины:

$\tilde {x} = kx,\quad \tilde {y} = ky,\quad \tilde {z} = kz,\quad \tilde {\eta } = k\eta ,\quad \tilde {t} = t\sqrt {gk} ,\quad \tilde {U} = U\sqrt {k{\text{/}}g} .$

В дальнейшем знаки тильда ~, обозначающие безразмерность соответствующих величин, будут опущены для упрощения записи. Благодаря периодичности решений с периодом $2\pi $ по обеим направлениям $(ox)$ и $(oy)$ и тому факту, что рассматриваемые волны распространяются без изменения формы, можно ввести переменные

$X = px - \omega t,\quad Y = qy,\quad Z = z,$

где $p$ и $q$ представляют собой два волновых числа по направлениям $(ox)$ и $(oy)$ соответственно, которые задаются следующим образом:

$p = \sin \theta ,\quad q = \cos \theta .$

Определяющие уравнения теперь могут быть записаны с помощью введенных безразмерных величин:

(1.10)

${{p}^{2}}{{\phi }_{{iXX}}} + {{q}^{2}}{{\phi }_{{iYY}}} + {{\phi }_{{iZZ}}} = 0\quad i = (1,\;2),$

(1.11)

$(pU - \omega ){{\eta }_{X}} + {{p}^{2}}{{\eta }_{X}}{{\phi }_{{1X}}} + {{q}^{2}}{{\eta }_{Y}}{{\phi }_{{1Y}}} - {{\phi }_{{1Z}}} = 0\quad {\text{при}}\quad Z = \eta ,$

(1.12)

$ - \omega {{\eta }_{X}} + {{p}^{2}}{{\eta }_{X}}{{\phi }_{{2X}}} + {{q}^{2}}{{\eta }_{Y}}{{\phi }_{{2Y}}} - {{\phi }_{{2Z}}} = 0\quad {\text{при}}\quad Z = \eta ,$

(1.13)

${{\phi }_{{1Z}}} = 0\quad {\text{при}}\quad Z \to + \infty ,$

(1.14)

${{\phi }_{{2Z}}} = 0\quad {\text{при}}\quad Z \to - \infty ,$

$\mu \left\{ {(pU - \omega ){{\phi }_{{1X}}} + \eta + \frac{1}{2}({{p}^{2}}\phi _{{1X}}^{2} + {{q}^{2}}\phi _{{1Y}}^{2} + \phi _{{1Z}}^{2})} \right\} + \omega {{\phi }_{{2X}}} - \eta $

(1.15)

$ - \frac{1}{2}({{p}^{2}}\phi _{{2X}}^{2} + {{q}^{2}}\phi _{{2Y}}^{2} + \phi _{{2Z}}^{2}) + C = 0\quad {\text{при}}\quad Z = \eta ,$

где $\mu = {{\rho }_{1}}{\text{/}}{{\rho }_{2}}$ – отношение плотностей на границе раздела.

2. МЕТОД ВОЗМУЩЕНИЙ

2.1. Решение пятого порядка

В этом разделе задача будет решаться методом возмущений. Переменные задачи раскладываются в степенные ряды по степеням малого параметра возмущений $h$ следующим образом:

(2.1)

$\left\{ \begin{gathered} {{\phi }_{i}} = \sum\limits_{r = 1}^\infty {{{h}^{r}}} \phi _{i}^{{(r)}}(X,Y,Z)\quad i = (1,2), \hfill \\ \eta = \sum\limits_{r = 1}^\infty {{{h}^{r}}} {{\eta }^{{(r)}}}(X,Y), \hfill \\ \omega = \sum\limits_{r = 1}^\infty {{{h}^{r}}} {{\omega }_{r}}, \hfill \\ C = \sum\limits_{r = 1}^\infty {{{h}^{r}}} {{C}^{{(r)}}}, \hfill \\ \end{gathered} \right.$

где $h$ – крутизна волны, определенная соотношением $h = 1{\text{/}}2(\eta (0,0) - \eta (\pi ,0))$. Граничные условия задаются на границе раздела $Z = \eta (X,Y)$, которая неизвестна заранее. Чтобы преодолеть это затруднение, граничные условия на границе раздела сносятся на плоскость $Z = 0$. Это достигается за счет разложения потенциалов скоростей ${{\phi }_{1}}$ и ${{\phi }_{2}}$ в ряды Тейлора около плоскости $Z = 0$

(2.2)

${{\phi }_{i}}\left( {X,Y,\eta } \right) = {{\phi }_{i}}\left( {X,Y,0} \right) + {{\left. {{{\phi }_{{iZ}}}} \right|}_{{Z = 0}}}\eta + \frac{1}{2}{{\left. {{{\phi }_{{iZZ}}}} \right|}_{{Z = 0}}}{{\eta }^{2}} + \; \ldots $

Подставляя выражения (2.1) и (2.2) в основные уравнения (1.10)–(1.14), получим уравнения первого порядка аппроксимации

(2.3)

$\left\{ \begin{gathered} {{p}^{2}}\phi _{{iXX}}^{{(1)}} + {{q}^{2}}\phi _{{iYY}}^{{(1)}} + \phi _{{iZZ}}^{{(1)}} = 0,\quad i = (1,\;2), \hfill \\ {{\omega }_{0}}\eta _{X}^{{(1)}} + \phi _{{2Z}}^{{(1)}} = 0, \hfill \\ ({{\omega }_{0}} - pU)\eta _{X}^{{(1)}} + \phi _{{1Z}}^{{(1)}} = 0, \hfill \\ {{\omega }_{0}}(\phi _{{2X}}^{{(1)}} - \mu \phi _{{1X}}^{{(1)}}) + (\mu - 1){{\eta }^{{(1)}}} + \mu pU\phi _{{1X}}^{{(1)}} = 0, \hfill \\ \phi _{{1Z}}^{{(1)}} = 0,Z \to + \infty , \hfill \\ \phi _{{2Z}}^{{(1)}} = 0,Z \to - \infty . \hfill \\ \end{gathered} \right.$

После решения системы уравнений (2.3) получаются следующие линейные решения:

(2.4)

$\left\{ \begin{gathered} {{\eta }^{{(1)}}} = \cos X\cos Y, \hfill \\ \phi _{1}^{{(1)}} = ( - {{\omega }_{0}} + pU)\sin X\cos Y{{e}^{{ - Z}}}, \hfill \\ \phi _{2}^{{(1)}} = {{\omega }_{0}}\sin X\cos Y{{e}^{Z}}, \hfill \\ \omega _{0}^{2} + \mu {{\left( {{{\omega }_{0}} - pU} \right)}^{2}} = 1 - \mu , \hfill \\ {{C}^{{(1)}}} = 0. \hfill \\ \end{gathered} \right.$

Когда $U = 0$, это решение сводится к решению, полученному в [18]. Исследование линейного дисперсионного уравнения показывает, что присутствуют две волновые моды: $\omega _{0}^{ + }$ и $\omega _{0}^{ - }$, такие что $\omega _{0}^{ + } > \omega _{0}^{ - }$. Эти две моды задаются выражениями

(2.5)

$\omega _{0}^{ + } = \frac{{\mu pU + \sqrt {1 - {{\mu }^{2}} - \mu {{p}^{2}}{{U}^{2}}} }}{{\mu + 1}},$

(2.6)

$\omega _{0}^{ - } = \frac{{\mu pU - \sqrt {1 - {{\mu }^{2}} - \mu {{p}^{2}}{{U}^{2}}} }}{{\mu + 1}}.$

Аппроксимации второго порядка имеют вид

(2.7)

${{p}^{2}}\phi _{{iXX}}^{{(2)}} + {{q}^{2}}\phi _{{iYY}}^{{(2)}} + \phi _{{iZZ}}^{{(2)}} = 0\quad i = (1,\;2),$

(2.8)

$\left( {{{\omega }_{0}} - Up} \right)\eta _{X}^{{(2)}} + \phi _{{1Z}}^{{(2)}} = {{q}^{2}}\phi _{{1Y}}^{{(1)}}\eta _{Y}^{{(1)}} + {{p}^{2}}\phi _{X}^{{(1)}}\eta _{X}^{{(1)}} - \phi _{{1ZZ}}^{{(1)}}{{\eta }^{{(1)}}} - {{\omega }_{1}}\eta _{X}^{{(1)}}\quad {\text{при}}\quad Z = 0,$

(2.9)

${{\omega }_{0}}\eta _{X}^{{(2)}} + \phi _{{2Z}}^{{(2)}} = {{q}^{2}}\phi _{{2Y}}^{{(1)}}\eta _{Y}^{{(1)}} + {{p}^{2}}\phi _{{2X}}^{{(1)}}\eta _{X}^{{(1)}} - \phi _{{2ZZ}}^{{(1)}}{{\eta }^{{(1)}}} - {{\omega }_{1}}\eta _{X}^{{(1)}}\quad {\text{при}}\quad Z = 0,$

(2.10)

$\begin{gathered} {{\omega }_{0}}(\mu \phi _{{1X}}^{{(2)}} - \phi _{{2X}}^{{(2)}}) + {{\eta }^{{(2)}}}\left( {1 - \mu } \right) - \mu pU\phi _{{1X}}^{{(2)}} = \frac{1}{2}\mu [{{p}^{2}}{{(\phi _{{1X}}^{{(1)}})}^{2}} + {{q}^{2}}{{(\phi _{{1Y}}^{{(1)}})}^{2}} + {{(\phi _{{1Z}}^{{(1)}})}^{2}}] - \\ - \;\frac{1}{2}[{{p}^{2}}{{(\phi _{{2X}}^{{(1)}})}^{2}} + {{q}^{2}}{{(\phi _{{2Y}}^{{(1)}})}^{2}} + {{(\phi _{{2Z}}^{{(1)}})}^{2}}] + {{\omega }_{0}}{{\eta }^{{(1)}}}(\phi _{{2XZ}}^{{(1)}} - \mu \phi _{{1XZ}}^{{(1)}} + \mu pU\phi _{{1XZ}}^{{(1)}}) + \\ + \;{{\omega }_{1}}(\phi _{{2X}}^{{(1)}} - \mu \phi _{{1X}}^{{(1)}}),\quad {\text{при}}\quad Z = 0 \\ \end{gathered} $

(2.11)

$\phi _{{1Z}}^{{(2)}} = 0\quad Z \to + \infty ,$

(2.12)

$\phi _{{2Z}}^{{(2)}} = 0\quad Z \to - \infty .$

Будет искать решения в следующем виде:

(2.13)

$\left\{ \begin{gathered} {{\eta }^{{(2)}}} = a_{{20}}^{{(2)}}\cos \left( {2X} \right) + a_{{02}}^{{(2)}}\cos \left( {2Y} \right) + a_{{22}}^{{(2)}}\cos \left( {2X} \right)\cos \left( {2Y} \right), \hfill \\ \phi _{1}^{{(2)}} = b_{{02}}^{{(2)}}\cos \left( {2Y} \right)\exp \left( { - 2{{\alpha }_{{02}}}Z} \right) + b_{{22}}^{{(2)}}\sin \left( {2X} \right)\cos \left( {2Y} \right)\exp \left( { - 2{{\alpha }_{{22}}}Z} \right), \hfill \\ \phi _{2}^{{(2)}} = c_{{02}}^{{(2)}}\cos \left( {2Y} \right)\exp \left( {2{{\alpha }_{{02}}}Z} \right) + c_{{22}}^{{(2)}}\sin \left( {2X} \right)\cos \left( {2Y} \right)\exp \left( {2{{\alpha }_{{22}}}Z} \right), \hfill \\ \end{gathered} \right.$

где $\alpha _{{mn}}^{2} = (mp{{)}^{2}} + {{(nq)}^{2}}$, а $m$ и $n$ – целые числа одинаковой четности.

Очевидно, $\phi _{1}^{{(2)}}$ и $\phi _{2}^{{(2)}}$ удовлетворяют уравнению Лапласа и граничным условиям. После подстановки решений первого порядка в уравнения (2.8), (2.9) и (2.10) и алгебраических преобразований можно получить коэффициенты второго порядка. Эти коэффициенты даны в табл. 1. Как можно проверить, в особом случае $U = 0$ решения второго порядка совпадают с решениями, полученными в [18].

Таблица 1.

Решение второго порядка, полученное с помощью метода возмущений

$a_{{2,2}}^{{(2)}} = - \frac{1}{4}\frac{{ - \omega _{0}^{2} - 2\mu pU{{\omega }_{0}} + \mu {{\omega }^{2}} + \mu {{p}^{2}}{{U}^{2}}}}{{\mu - 1 + 2\omega _{0}^{2} + 2\mu {{{( - {{\omega }_{0}} + pU)}}^{2}}}},$

$a_{{02}}^{{(2)}} = - \frac{1}{4}\frac{{(p - 1)(p + 1)(\mu {{{\left( {pU - {{\omega }_{0}}} \right)}}^{2}} - \omega _{0}^{2})}}{{\mu - 1}},$

$a_{{20}}^{{(2)}} = - \frac{1}{4}\frac{{p({{p}^{2}} - 2 - 2p)(\mu {{{(pU - {{\omega }_{0}})}}^{2}} - \omega _{0}^{2})}}{{p(\mu - 1) + 2\omega _{0}^{2} + 2\mu {{{( - {{\omega }_{0}} + pU)}}^{2}}}},$

$b_{{22}}^{{(2)}} = \frac{1}{4}\frac{{( - {{\omega }_{0}} + pU)(\mu {{{( - {{\omega }_{0}} + pU)}}^{2}}) - 1 + \mu + 3\omega _{0}^{2}}}{{\mu - 1 + 2\omega _{0}^{2} + 2\mu {{{( - {{\omega }_{0}} + pU)}}^{2}}}},$

$b_{{20}}^{{(2)}} = - \frac{1}{4}\frac{{( - {{\omega }_{0}} + pU)(\mu ({{p}^{2}} - 2){{{(pU - {{\omega }_{0}})}}^{2}}) - p{{{(p{{\omega }_{0}})}}^{2}} - p + \mu p + 4{{\omega }_{0}}{{)}^{2}}) + 2{{\omega }_{0}}{{)}^{2}}}}{{p(\mu - 1) + 2\omega _{0}^{2} + 2\mu {{{( - {{\omega }_{0}} + pU)}}^{2}}}},$

$c_{{22}}^{{(2)}} = - \frac{1}{4}\frac{{{{\omega }_{0}}{{{({{\omega }_{0}})}}^{2}} + 3\mu {{{( - {{\omega }_{0}} + pU)}}^{2}} + \mu - 1)}}{{\mu - 1 + 2\omega _{0}^{2} + 2\mu {{{( - {{\omega }_{0}} + pU)}}^{2}}}},$

$c_{{20}}^{{(2)}} = - \frac{1}{4}\frac{{\mu ({{p}^{2}} + 4p - 2){{{( - {{\omega }_{0}} + pU)}}^{2}} + 2\omega _{0}^{2} + {{p}^{2}}( - \omega _{0}^{2} - 1 + \mu )}}{{p(\mu - 1) + 2\omega _{0}^{2} + 2\mu {{{( - {{\omega }_{0}} + pU)}}^{2}}}},$

${{\omega }_{1}} = 0$

Аналогично, система уравнений третьего порядка имеет вид:

(2.14)

${{p}^{2}}\phi _{{iXX}}^{{(3)}} + {{q}^{2}}\phi _{{iYY}}^{{(3)}} + \phi _{{iZZ}}^{{(3)}} = 0\quad i = (1,\;2),$

$\left( {{{\omega }_{0}} - Up} \right)\eta _{X}^{{(3)}} + \phi _{{1Z}}^{{(3)}} = {{\eta }^{{(1)}}}({{p}^{2}}\phi _{{1XZ}}^{{(1)}}\eta _{X}^{{(1)}} + {{q}^{2}}\phi _{{1YZ}}^{{(1)}}\eta _{Y}^{{(1)}} - \phi _{{1ZZ}}^{{(2)}}) + {{p}^{2}}\phi _{{1X}}^{{(2)}}\eta _{X}^{{(1)}} + {{q}^{2}}\phi _{{1Y}}^{{(2)}}\eta _{Y}^{{(1)}} - $

(2.15)

$ - \frac{1}{2}\phi _{{1ZZZ}}^{{(1)}}{{({{\eta }^{{(1)}}})}^{2}} + {{p}^{2}}\phi _{{1X}}^{{(1)}}\eta _{X}^{{(2)}} + {{q}^{2}}\phi _{{1Y}}^{{(1)}}\eta _{Y}^{{(2)}} - \phi _{{1ZZ}}^{{(1)}}{{\eta }^{{(2)}}} - {{\omega }_{2}}\eta _{X}^{{(1)}}\quad {\text{при}}\quad Z = 0,$

$\begin{gathered} {{\omega }_{0}}\eta _{X}^{{(3)}} + \phi _{{2Z}}^{{(3)}} = {{\eta }^{{(1)}}}({{p}^{2}}\phi _{{2XZ}}^{{(1)}}\eta _{X}^{{(1)}} + {{q}^{2}}\phi _{{2YZ}}^{{(1)}}\eta _{Y}^{{(1)}} - \phi _{{2ZZ}}^{{(2)}}) + \\ + \;{{p}^{2}}\phi _{{2X}}^{{(2)}}\eta _{X}^{{(1)}} + {{q}^{2}}\phi _{{2Y}}^{{(2)}}\eta _{Y}^{{(1)}} - \frac{1}{2}\phi _{{2ZZZ}}^{{(1)}}{{({{\eta }^{{(1)}}})}^{2}} + \\ \end{gathered} $

(2.16)

$ + \;{{p}^{2}}\phi _{{2X}}^{{(1)}}\eta _{X}^{{(2)}} + {{q}^{2}}\phi _{{2Y}}^{{(1)}}\eta _{Y}^{{(2)}} - \phi _{{2ZZ}}^{{(1)}}{{\eta }^{{(2)}}} - {{\omega }_{2}}\eta _{X}^{{(1)}}\quad {\text{при}}\quad Z = 0,$

${{\omega }_{0}}(\mu {\kern 1pt} \phi _{{1X}}^{{(3)}} - \phi _{{2X}}^{{(3)}}) + {{\eta }^{{(3)}}}\left( {1 - \mu } \right) - \mu {\kern 1pt} p{\kern 1pt} U\phi _{{1X}}^{{(3)}} = - ({{p}^{2}}\phi _{{2X}}^{{(1)}}\phi _{{2X}}^{{(2)}} + {{q}^{2}}\phi _{{2Y}}^{{(1)}}\phi _{{2Y}}^{{(2)}} + \phi _{{2Z}}^{{(1)}}\phi _{{2Z}}^{{(2)}}) + $

$ + \;{{\eta }^{{(1)}}}\mu ({{p}^{2}}\phi _{{1X}}^{{(1)}}\phi _{{1XZ}}^{{(1)}} + {{q}^{2}}\phi _{{1Y}}^{{(1)}}\phi _{{1YZ}}^{{(1)}} + \phi _{{1ZZ}}^{{(1)}}\phi _{{1Z}}^{{(1)}}) - {{\eta }^{{(1)}}}({{p}^{2}}\phi _{{2X}}^{{(1)}}\phi _{{2XZ}}^{{(1)}} + {{q}^{2}}\phi _{{2Y}}^{{(1)}}\phi _{{2YZ}}^{{(1)}} + \phi _{{2ZZ}}^{{(1)}}\phi _{{2Z}}^{{(1)}}) + $

$ + {{\eta }^{{(1)}}}{{\omega }_{0}}(\phi _{{2XZ}}^{{(2)}} - \mu \phi _{{1XZ}}^{{(2)}}) + \mu ({{p}^{2}}\phi _{{1X}}^{{(1)}}\phi _{{1X}}^{{(2)}} + {{q}^{2}}\phi _{{1Y}}^{{(1)}}\phi _{{1Y}}^{{(2)}} + \phi _{{1Z}}^{{(1)}}\phi _{{1Z}}^{{(2)}}) + {{\omega }_{2}}(\phi _{{2X}}^{{(1)}} - \mu \phi _{{1X}}^{{(1)}}) + $

$ + \frac{1}{2}{{\omega }_{0}}{{({{\eta }^{{(1)}}})}^{2}}(\phi _{{2XZZ}}^{{(1)}} - \mu \phi _{{1XZZ}}^{{(1)}}) + {{\omega }_{0}}{{\eta }^{{(2)}}}(\phi _{{2XZ}}^{{(1)}} - \mu \phi _{{1XZ}}^{{(1)}}) + $

(2.17)

$ + \;\mu pU\left( {\phi _{{1XZ}}^{{(2)}}{{\eta }^{{(1)}}} + \phi _{{1XZ}}^{{(1)}}{{\eta }^{{(2)}}} + \frac{1}{2}\phi _{{1XZZ}}^{{(2)}}{{{({{\eta }^{{(1)}}})}}^{2}}} \right)\quad {\text{при}}\quad Z = 0,$

(2.18)

$\phi _{{1Z}}^{{(3)}} = 0\quad Z \to + \infty ,$

(2.19)

$\phi _{{2Z}}^{{(3)}} = 0\quad Z \to - \infty .$

Коэффициенты для этого порядка аппроксимации даны в Приложении.

Приближения четвертого и пятого порядков находятся подобным образом. Однако по причине большой громоздкости выражений и их большой длины привести их в данной статье невозможно.

2.2. Гармонический резонанс

В [4] было показано, что задача о поверхностных волнах не имеет единственного решения при некоторых значениях угла ${{\theta }}$. Это является следствием явления гармонического резонанса между основными модами и модами высших порядков. В [18] было получено условие резонанса в случае коротко-гребневых волн на границе раздела двух сред. Определим условие резонанса в случае коротко-гребневых волн на границе раздела двух сред в присутствии однородного течения в одной из них. Вначале заметим, что кинематические и динамические уравнения порядка r могут быть записаны в следующем виде:

(2.20)

$\left\{ \begin{gathered} \left( {{{\omega }_{0}} - Up} \right)\eta _{X}^{{(r)}} + \phi _{{1Z}}^{{(r)}} = I_{1}^{{(r)}}\quad {\text{при}}\quad Z = 0, \hfill \\ {{\omega }_{0}}\eta _{X}^{{(r)}} + \phi _{{2Z}}^{{(r)}} = I_{2}^{{(r)}}\quad {\text{при}}\quad Z = 0, \hfill \\ {{\omega }_{0}}(\mu \phi _{{1X}}^{{(r)}} - \phi _{{2X}}^{{(r)}}) + {{\eta }^{{(r)}}}\left( {1 - \mu } \right) - \mu pU\phi _{{1X}}^{{(r)}} = I{{I}^{{(r)}}}\quad {\text{при}}\quad Z = 0, \hfill \\ \end{gathered} \right.$

где члены $I_{1}^{{(r)}}$, $I_{2}^{{(r)}}$ и $I{{I}^{{(r)}}}$ зависят от решений порядка $(r - 1)$. Будем искать решения в следующем виде:

(2.21)

$\left\{ \begin{gathered} {{\eta }^{{(r)}}} = \sum\limits_{mn}^r {a_{{mn}}^{{(r)}}} \cos \left( {mX} \right)\cos \left( {nY} \right), \hfill \\ \phi _{1}^{{(r)}} = \sum\limits_{mn}^r {b_{{mn}}^{{(r)}}} \sin \left( {mX} \right)\cos \left( {nY} \right)\exp \left( { - {{\alpha }_{{mn}}}Z} \right), \hfill \\ \phi _{2}^{{(r)}} = \sum\limits_{mn}^r {c_{{mn}}^{{(r)}}} \sin \left( {mX} \right)\cos \left( {nY} \right)\exp \left( {{{\alpha }_{{mn}}}Z} \right). \hfill \\ \end{gathered} \right.$

Более того, можно показать, что члены $I_{1}^{{(r)}}$, $I_{2}^{{(r)}}$ и $I{{I}^{{(r)}}}$ могут быть записаны в следующем виде:

(2.22)

$\left\{ \begin{gathered} I_{1}^{{(r)}} = \sum\limits_{mn}^r {F_{{1mn}}^{{(r)}}} \sin \left( {mX} \right)\cos \left( {nY} \right), \hfill \\ I_{2}^{{(r)}} = \sum\limits_{mn}^r {F_{{2mn}}^{{(r)}}} \sin \left( {mX} \right)\cos \left( {nY} \right), \hfill \\ I{{I}^{{(r)}}} = \sum\limits_{mn}^r {G_{{mn}}^{{(r)}}} \cos \left( {mX} \right)\cos \left( {nY} \right). \hfill \\ \end{gathered} \right.$

После подстановки выражений (2.21) и (2.22) в систему уравнений (2.20), получим систему

(2.23)

$\left\{ \begin{gathered} - m\left( {{{\omega }_{0}} - Up} \right)a_{{mn}}^{{(r)}} - {{\alpha }_{{mn}}}b_{{mn}}^{{(r)}} = F_{{1mn}}^{{(r)}}, \hfill \\ - m{{\omega }_{0}}a_{{mn}}^{{(r)}} + {{\alpha }_{{mn}}}c_{{mn}}^{{(r)}} = F_{{2mn}}^{{(r)}}, \hfill \\ {{\omega }_{0}}m(\mu b_{{mn}}^{{(r)}} - c_{{mn}}^{{(r)}}) + \left( {1 - \mu } \right)a_{{mn}}^{{(r)}} - \mu pUmb_{{mn}}^{{(r)}} = G_{{mn}}^{{(r)}}, \hfill \\ \end{gathered} \right.$

которая имеет решение вида

(2.24)

$\left\{ \begin{gathered} a_{{mn}}^{{(r)}} = - \frac{{m\mu \left( {{{\omega }_{0}} - pU} \right)F_{{1mn}}^{{(r)}} + m{{\omega }_{0}}F_{{2mn}}^{{(r)}} + {{\alpha }_{{mn}}}G_{{mn}}^{{(r)}}}}{{{{\alpha }_{{mn}}}\left( {\mu - 1} \right) + {{m}^{2}}(\omega _{0}^{2} + \mu {{{\left( {{{\omega }_{0}} - pU} \right)}}^{2}})}}, \hfill \\ b_{{mn}}^{{(r)}} = - \frac{{({{m}^{2}}\omega _{0}^{2} + {{\alpha }_{{mn}}}\left( {\mu - 1} \right))F_{{1mn}}^{{(r)}} + {{m}^{2}}{{\omega }_{0}}\left( {pU - {{\omega }_{0}}} \right)F_{{2mn}}^{{(r)}} + m{{\alpha }_{{mn}}}\left( { - {{\omega }_{0}} + pU} \right)G_{{mn}}^{{(r)}}}}{{{{\alpha }_{{mn}}}({{\alpha }_{{mn}}}\left( {\mu - 1} \right) + {{m}^{2}}(\omega _{0}^{2} + \mu {{{\left( {{{\omega }_{0}} - pU} \right)}}^{2}}))}}, \hfill \\ c_{{mn}}^{{(r)}} = - \frac{{ - {{m}^{2}}{{\omega }_{0}}\mu \left( { - {{\omega }_{0}} + pU} \right)F_{{1mn}}^{{(r)}} - ({{\alpha }_{{mn}}}\left( { - 1 + \mu } \right) + \mu {\kern 1pt} {{m}^{2}}{{{\left( { - {{\omega }_{0}} + pU} \right)}}^{2}})F_{{2mn}}^{{(r)}} + m{{\omega }_{0}}{{\alpha }_{{mn}}}G_{{mn}}^{{(r)}}}}{{{{\alpha }_{{mn}}}({{\alpha }_{{mn}}}\left( {\mu - 1} \right) + {{m}^{2}}(\omega _{0}^{2} + \mu {{{\left( {{{\omega }_{0}} - pU} \right)}}^{2}}))}}. \hfill \\ \end{gathered} \right.$

Коэффициенты в выражениях (2.24) содержат деления на ноль при определенных значениях параметров. Эти делители на ноль соответствуют появлению гармонических резонансов и это происходит при

(2.25)

${{\alpha }_{{mn}}}\left( {\mu - 1} \right) + {{m}^{2}}(\omega _{0}^{2} + \mu {{\left( {{{\omega }_{0}} - pU} \right)}^{2}}) = 0.$

Используя линейное дисперсионное уравнение, выражение (2.25) можно упростить, приведя его к виду

(2.26)

${{m}^{2}} = {{\alpha }_{{mn}}}.$

Из этого выражения можно получить критический угол резонанса ${{\theta }_{c}}$:

(2.27)

${{\cos }^{2}}{{\theta }_{c}} = \frac{{{{m}^{4}} - {{m}^{2}}}}{{{{n}^{2}} - {{m}^{2}}}},$

который совпадает с найденным в [4]. Угол, при котором происходит гармонический резонанс, не зависит от скорости течения U и отношения плотностей $\mu $.

3. ВАРИАЦИОННЫЙ ПРИНЦИП

Для гравитационных коротко-гребневых волн на границе раздела при течении со скоростью U в одной из сред в случае двух неограниченных жидкостей усредненный лагранжиан задается выражением

(3.1)

$\begin{gathered} L = - \overline {\left[ {\int\limits_{ - \infty }^\eta {\frac{1}{2}({{p}^{2}}\phi _{{2X}}^{2} + {{q}^{2}}\phi _{{2Y}}^{2} + \phi _{{2Z}}^{2}) - \omega {{\phi }_{{2X}}} + \eta } } \right]dZ} - \\ - \;\mu \overline {\left[ {\int\limits_\eta ^{ + \infty } {\frac{1}{2}({{{\left( {p{{\phi }_{{1X}}} + U} \right)}}^{2}} + {{q}^{2}}\phi _{{1Y}}^{2} + \phi _{{1Z}}^{2}) - \omega {{\phi }_{{1X}}} + \eta } } \right]dZ} - {{L}_{0}}, \\ \end{gathered} $

где черта сверху обозначает усреднение по пространству, а ${{L}_{0}}$ есть плотность лагранжиана невозмущенного течения (см. [1]). Эта величина введена для того, чтобы обеспечить сходящееся значение $L$, и задается выражением

(3.2)

${{L}_{0}} = - \int\limits_{ - \infty }^0 \eta dZ - \int\limits_0^\infty {\left( {\mu \eta dZ + \frac{1}{2}\mu {{U}^{2}}} \right)} dZ.$

Отметим, что выражение (3.1) есть обобщение исследования [1] на трехмерный случай.

Следуя Уизему [20], профиль волны на границе раздела $\eta $ и потенциалы скорости ${{\phi }_{1}}$ и ${{\phi }_{2}}$ могут быть записаны в следующем усеченном виде:

(3.3)

$\left\{ \begin{gathered} \eta (X,Y) = {{A}_{{11}}}\cos X\cos Y + {{A}_{{22}}}\cos 2X\cos 2Y + {{A}_{{20}}}\cos 2X + {{A}_{{02}}}\cos 2Y, \hfill \\ {{\phi }_{1}}(X,Y,Z) = {{B}_{{11}}}\sin X\cos Y{{e}^{{ - {{\alpha }_{{11}}}Z}}} + {{B}_{{22}}}\sin 2X\cos 2Y{{e}^{{ - {{\alpha }_{{22}}}Z}}} + {{B}_{{20}}}\sin 2X{{e}^{{ - {{\alpha }_{{20}}}Z}}}, \hfill \\ {{\phi }_{2}}(X,Y,Z) = {{C}_{{11}}}\sin X\cos Y{{e}^{{{{\alpha }_{{11}}}Z}}} + {{C}_{{22}}}\sin 2X\cos 2Y{{e}^{{{{\alpha }_{{22}}}Z}}} + {{C}_{{20}}}\sin 2X{{e}^{{{{\alpha }_{{20}}}Z}}}. \hfill \\ \end{gathered} \right.$

Отметим, что ${{A}_{{11}}}$, ${{B}_{{11}}}$ и ${{C}_{{11}}}$ имеют первый порядок по амплитуде волны, тогда как другие коэффициенты имеют второй порядок. Подставим эти выражения в соотношение (3.1), вычислим $L$, разрешим полученные выражения и исключим ${{B}_{{11}}}$, ${{B}_{{20}}}$, ${{B}_{{22}}}$, ${{C}_{{11}}}$, ${{C}_{{20}}}$ и ${{C}_{{22}}}$ с помошью уравнений

(3.4)

$\frac{{\partial L}}{{\partial {{B}_{{11}}}}} = \frac{{\partial L}}{{\partial {{B}_{{20}}}}} = \frac{{\partial L}}{{\partial {{B}_{{22}}}}} = \frac{{\partial L}}{{\partial {{C}_{{11}}}}} = \frac{{\partial L}}{{\partial {{C}_{{20}}}}} = \frac{{\partial L}}{{\partial {{C}_{{22}}}}} = 0,$

и после некоторых алгебраических преобразований получим:

$L = \frac{1}{{4p}}( - p + p\mu + 2{\kern 1pt} {{\omega }^{2}} + 2{\kern 1pt} \mu {\kern 1pt} {{(\omega - pU)}^{2}})A_{{20}}^{2} + \frac{1}{8}((2{\kern 1pt} {{(\omega - pU)}^{2}} + 1)\mu + 2{\kern 1pt} {{\omega }^{2}} + \mu - 1)A_{{22}}^{2} + $

(3.5)

$ + \frac{1}{8}(({{\left( {\omega - pU} \right)}^{2}})\mu + {{\omega }^{2}} + \mu - 1)A_{{11}}^{2} + \frac{1}{8}\left( {p - 1} \right)\left( {p + 1} \right)(\mu {\kern 1pt} {{\left( {\omega - pU} \right)}^{2}} - {{\omega }^{2}})A_{{11}}^{2}{{A}_{{02}}} + $

$ + \;\frac{1}{{64}}( - 1 + 2{\kern 1pt} {{p}^{3}} - 4{\kern 1pt} {{p}^{2}})(\mu {\kern 1pt} {{\left( {\omega - pU} \right)}^{2}} + {{\omega }^{2}})A_{{11}}^{4} + \frac{1}{{16}}(\mu {\kern 1pt} {{\left( {\omega - pU} \right)}^{2}} - {{\omega }^{2}})A_{{11}}^{2}{{A}_{{22}}} + $

$ + \;\frac{1}{8}( - 2 + {{p}^{2}} + 2p)(\mu {{\left( {\omega - pU} \right)}^{2}} - {{\omega }^{2}})A_{{11}}^{2}{{A}_{{20}}} + \frac{1}{4}{\kern 1pt} \left( { - 1 + \mu } \right)A_{{02}}^{2} + O(A_{{11}}^{6}).$

Слагаемые низшего порядка дают линейное дисперсионное уравнение для вариации $L$ по отношению к ${{A}_{{11}}}$

(3.6)

$\omega = {{\omega }_{0}} + O(A_{{11}}^{2}),\quad {\text{где}}\quad \mu {{\left( {{{\omega }_{0}} - pU} \right)}^{2}} + \omega _{0}^{2} + \mu - 1 = 0,$

что идентично соотношению, найденному с помощью метода возмущений.

При введении последнего соотношения в выражение для лагранжиана значения величин ${{A}_{{22}}}$, ${{A}_{{20}}}$ и ${{A}_{{02}}}$ находятся из уравнений

(3.7)

$\frac{{\partial L}}{{\partial {{A}_{{22}}}}} = \frac{{\partial L}}{{\partial {{A}_{{20}}}}} = \frac{{\partial L}}{{\partial {{A}_{{02}}}}} = 0,$

что дает

(3.8)

${{A}_{{22}}} = - \frac{1}{4}{\kern 1pt} \frac{{A_{{11}}^{2}(\mu + 2{\kern 1pt} \omega _{0}^{2} - 1)}}{{ - 1 + \mu }},$

(3.9)

${{A}_{{20}}} = \frac{1}{4}{\kern 1pt} \frac{{A_{{11}}^{2}p( - 2 + {{p}^{2}} + 2{\kern 1pt} p)(\mu + 2{\kern 1pt} \omega _{0}^{2} - 1)}}{{\left( {p - 2} \right)\left( { - 1 + \mu } \right)}},$

(3.10)

${{A}_{{02}}} = \frac{1}{4}{\kern 1pt} \frac{{A_{{11}}^{2}\left( {p - 1} \right)\left( {p + 1} \right)(\mu + 2{\kern 1pt} \omega _{0}^{2} - 1)}}{{ - 1 + \mu }}.$

Легко проверить, что эти коэффициенты аналогичны тем, что были найдены с помощью метода возмущений.

После подстановки выражений для ${{A}_{{22}}}$, ${{A}_{{02}}}$ и ${{A}_{{20}}}$ лагранжиан можно окончательно упростить, приведя его к виду

(3.11)

$\begin{gathered} L = \frac{1}{{64}}\frac{{A_{{11}}^{4}p{{{({{p}^{2}} - 2 + 2p)}}^{2}}{{{(\mu {\kern 1pt} {{{\left( {{{\omega }_{0}} - pU} \right)}}^{2}} - \omega _{0}^{2})}}^{2}}}}{{ - p + p\mu + 2\omega _{0}^{2} + 2\mu {{{\left( {{{\omega }_{0}} - pU} \right)}}^{2}}}} + \\ + \;\frac{1}{{128}}\frac{{A_{{11}}^{4}{{{(\mu {\kern 1pt} {{{\left( {{{\omega }_{0}} - pU} \right)}}^{2}} - \omega _{0}^{2})}}^{2}}}}{{2\omega _{0}^{2} + 2\mu {{{\left( {{{\omega }_{0}} - pU} \right)}}^{2}} + \mu - 1}} + \\ + \;\frac{1}{{64}}\frac{{A_{{11}}^{4}{{{\left( {p - 1} \right)}}^{2}}{{{\left( {p + 1} \right)}}^{2}}{{{(\mu {{{\left( {{{\omega }_{0}} - pU} \right)}}^{2}} - \omega _{0}^{2})}}^{2}}}}{{ - 1 + \mu }} - \\ - \;\frac{1}{8}A_{{11}}^{2}( - 1 + \mu + {{\omega }^{2}} + \mu {{\left( {\omega - pU} \right)}^{2}}) - \\ - \;\frac{1}{{64}}A_{{11}}^{4}( - 1 - 4{{p}^{2}} + 2{{p}^{3}})(\omega _{0}^{2} + \mu {{\left( {{{\omega }_{0}} - pU} \right)}^{2}}) + O(A_{{11}}^{6}). \\ \end{gathered} $

Тогда нелинейное дисперсионное уравнение получается из соотношения $\partial L{\text{/}}\partial {{A}_{{11}}} = 0$, что дает

(3.12)

$\begin{gathered} {{\omega }^{2}} + \mu {{\left( {\omega - pU} \right)}^{2}} = \\ = \;(1 - \mu )\left[ {1 + A_{{11}}^{2}\left( {\frac{{{{\lambda }^{2}}}}{8}\frac{{4{{p}^{5}} + 4{{p}^{4}} - 4{{p}^{3}} - 8{{p}^{2}} + 9p - 2}}{{(2 - p)(1 - \mu {{)}^{2}}}} - \frac{1}{4}(2{{p}^{3}} - 4{{p}^{2}} - 1)} \right)} \right], \\ \end{gathered} $

где $\lambda = \omega _{0}^{2} - \mu {{({{\omega }_{0}} - pU)}^{2}}$.

4. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

4.1. Динамический предел

Динамический предел связан с существованием некоторой критической скорости течения, при превышении которой задача не допускает решений в виде стационарных волн. В [1] было определено значение критической скорости в случае двумерных волн на границе раздела при бесконечной глубине. Это значение было вычислено с помощью дисперсионного уравнения как в линейном, так и в слабо нелинейном случае. В общем случае критическая скорость течения ${{U}_{c}}$ является функцией отношения плотностей $\mu $, угла $\theta $ и значения ${{A}_{{11}}}$, которое представляет собой амплитуду волны. Расширим это исследование на случай трехмерных волн на границе раздела. При ${{A}_{{11}}} \to 0$ уравнение (3.12) становится линейным. Его исследование для заданных значений отношения плотностей $\mu $, скорости течения $U$ и угла $\theta $ показывает, что имеются два решения этого квадратного уравнения относительно $\omega $. Эти два различных решения равняются $\omega _{0}^{ + }$ и $\omega _{0}^{ - }$, причем $\omega _{0}^{ + } > \omega _{0}^{ - }$.

Линейное критическое течение определено, когда $\omega _{0}^{ + } = \omega _{0}^{ - }$. Значение критической скорости задается выражением

(4.1)

${{U}_{{lc}}} = \frac{{\sqrt {\mu (1 - {{\mu }^{2}})} }}{{\mu p}},$

где второй индекс $l$ соответствует линейному случаю. В этом случае имеем

(4.2)

$\omega _{0}^{ + } = \omega _{0}^{ - } = \frac{{\mu p{{U}_{{lc}}}}}{{\mu + 1}}.$

В нелинейном случае (${{A}_{{11}}} \ne 0$) есть два семейства решений, обозначенных как ${{\omega }_{ + }}({{A}_{{11}}},\mu ,U,\theta )$ и ${{\omega }_{ - }}({{A}_{{11}}},\mu ,U,\theta )$, которые удовлетворяют нелинейному дисперсионному уравнению (3.12). При заданных ${{A}_{{11}}}$, $\mu $ и $\theta $ опять имеется критическая скорость ${{U}_{c}}$, которая определяется равенством ${{\omega }_{ + }}({{A}_{{11}}},\mu ,{{U}_{c}},\theta ) = {{\omega }_{ - }}({{A}_{{11}}},\mu ,{{U}_{c}},\theta )$. При большей скорости задача не допускает стационарных решений. С точностью до второго порядка значение ${{U}_{c}}$ определяется приравниванием нулю дискриминантной функции в уравнении (3.12)

(4.3)

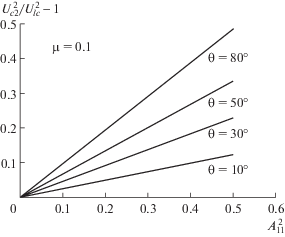
${{U}_{{c2}}} = {{U}_{{lc}}}{{\left[ {1 + A_{{11}}^{2}\left( {\frac{{{{{(1 - \mu )}}^{2}}}}{{8(1 + \mu {{)}^{2}}}}\frac{{\left( {9p - 8{{p}^{2}} + 4{{p}^{4}} + 4{{p}^{5}} - 2 - 4{{p}^{3}}} \right)}}{{2 - p}} + \frac{1}{4} - \frac{1}{2}{{p}^{3}} + {{p}^{2}}} \right)} \right]}^{{1/2}}},$

где

(4.4)

${{\omega }_{{ + ,2}}} = {{\omega }_{{ - ,2}}} = \frac{{\mu p{{U}_{{c2}}}}}{{1 + \mu }},$

а индекс $2$ обозначает приближение второго порядка.

При заданных значениях $\mu $ и $\theta $ соотношение (4.3) показывает, что критическая скорость ${{U}_{{c2}}}$ растет при увеличении амплитуды волны ${{A}_{{11}}}$. Это означает, что амплитуда волны имеет стабилизирующий эффект на распространение волн на поверхности раздела. На рис. 2 графики этого соотношения изображены для четырех значений $\theta $.

Рис. 2.

Величина $U_{{c2}}^{2}{\text{/}}U_{{lc}}^{2} - 1$ как функции $A_{{11}}^{2}$ для заданного значения $\mu $ и различных значений $\theta $.

4.2. Вариация частоты

Частота является одним из важных характеристиеских параметров коротко-гребневых волн. Метод возмущений был использован для вычисления решений вплоть до пятого порядка, когда частота задается следующим разложением:

(4.5)

$\omega = {{\omega }_{0}} + {{h}^{2}}{{\omega }_{2}} + {{h}^{4}}{{\omega }_{4}} + O({{h}^{6}}).$

При небольших значениях крутизны волны $h$ можно ограничить разложение третьим порядком. Такая процедура позволяет упростить исследование изменения $\omega $ как функции $h$, просто исследуя знак $\omega $. Действительно, в третьем порядке выражение для $\omega $ задается следующим образом:

(4.6)

$\omega = {{\omega }_{0}} + {{h}^{2}}{{\omega }_{2}} + O({{h}^{4}}).$

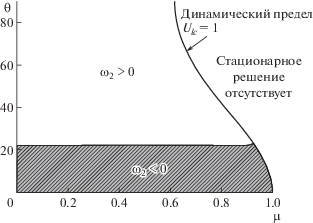
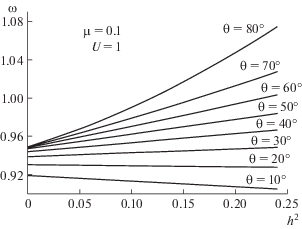
Это выражение показывает, что монотонность $\omega (h)$ определяется знаком ${{\omega }_{2}}$. Знаки ${{\omega }_{2}}$ в плоскости $(\mu ,\theta )$ для скорости $U = 1$ даны на рис. 3. Также изображено динамическое условие, выше которого стационарных решений нет. Имеются две области, в которых ${{\omega }_{2}}$ может быть положительным или отрицательным. Эти две области разделяются линией, соответствующей ${{\omega }_{2}} = 0$. Вдоль этой линии $\omega = {{\omega }_{0}}$, поэтому $\omega $ не зависит от крутизны волны $h$. С другой стороны, при ${{\omega }_{2}} < 0$ частота $\omega $ является убывающей функцией крутизны волны $h$, тогда как при ${{\omega }_{2}} > 0$ частота $\omega $ возрастает с ростом $h$. В качастве примера на рис. 4 иллюстрировано изменение $\omega $ в зависимости от $h$ при $\mu = 0.1$ и $U = 1$. Изменение монотонности имеет место между $20^\circ < \theta < 30{\kern 1pt} ^\circ $. Этот угол обращения частоты может быть найден на рис. 3, его значение при $\mu = 0.1$ равно ${{\theta }_{c}} = 22.1^\circ $.

Рис. 3.

Знак ${{\omega }_{2}}$ в плоскости $(\mu ,\theta )$ при ${{U}_{{lc}}} = 1$. Динамический предел также показан.

Рис. 4.

Частота $\omega $ как функция квадрата крутизны волны ${{h}^{2}}$ при $U = 1$, $\mu = 0.1$ для разных значений угла $\theta $.

4.3. Неустойчивость Кельвина–Гельмгольца

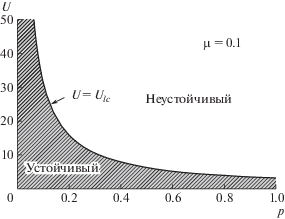
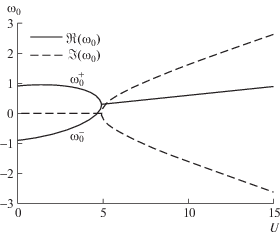
Как будет показано ниже, наличие критического значения $U$ связано с появлением неустойчивости. Используемая постановка задачи следует [1] для трехмерного случая. В работе [1] было показано, что для очень маленьких значений амплитуды волны и при достаточно больших значениях скорости потока возникает неустойчивость Кельвина–Гельмгольца. Этот результат был также интерпретирован как отсутствие стационарных линейных волн. Заметим, что корни уравнения (3.6) могут быть либо действительными, либо комплексными сопряженными. В первом случае течение устойчивое. Во втором случае течение неустойчивое и мнимые части решений этого уравнения относительно $\omega $ соответствуют коэффициенту в экспоненциальной функции, которая определяет рост в виде множителя ${{e}^{{{{\omega }_{i}}t}}}$, где ω_i = Im(ω). В качестве примера на рис. 5 показано изменение корней линейного дисперсионного уравнения как функций скорости при отношении плотностей $\mu = 0.1$ и угле $\theta = 40^\circ $. Слияние двух действительных корней приводит к появлению неустойчивости, которая соответствует комплексным сотряженным корням. Эти комплексные корни существуют при $U \geqslant {{U}_{{lc}}}$.

Рис. 5.

Два корня линейного дисперсионного уравнения при $\mu = 0.1$ и $\theta = 40^\circ $. Сплошная кривая обозначает действительную часть и пунктирная кривая обозначает мнимую часть.

Имеется область значений ($p$, $U$), при которых ${{\omega }_{0}}$ является мнимым. Эта область определяется знаком дискриминантной функции в квадратном уравнении (3.6), которая задается выражением

(4.7)

$\Delta = 4(1 - {{\mu }^{2}}) - 4\mu {{p}^{2}}{{U}^{2}}.$

На рис. 6 изображены устойчивые и неустойчивые области, которые соответствуют знакам дискриминантной функции. Если $\Delta > 0$, волна устойчива; в противном случае, если $\Delta < 0$, волна рассматривается как неустойчивая. Сплошная линия, разделяющая две зоны, определяет значение ${{U}_{{lc}}}$. В данном случае имеются два предельных случая, представляющих интерес. Первый случай имеет место при $\theta = 0{\kern 1pt} ^\circ $ и это соответствует стоячим волнам на границе раздела. В этом случае линейная критическая скорость течения ${{U}_{{lc}}} \to \infty $. Физически это означает, что стоячие волны на границе раздела всегда устойчивы в присутствии течения. Второй предельный случай соответствует $\theta = 90^\circ $ и возникают двумерные прогрессивные волны. В этом случае существует некоторое предельное значение скорости потока, при котором состояние становится неустойчивым и, следовательно, прогрессивные волны неизменного вида не могут наблюдаться. Эта область определяется условием

(4.8)

$U \geqslant {{U}_{{lc}}},\quad {\text{где}}\quad {{U}_{{lc}}} = \frac{{\sqrt {\mu (1 - {{\mu }^{2}})} }}{{\mu p}}.$

Рис. 6.

Области устойчивости и неустойчивости в плоскости $(U,p)$. Граничная кривая между областями устойчивости и неустойчивости соответствует линейному критическому течению.

4.4. Влияние течения на профиль границы раздела

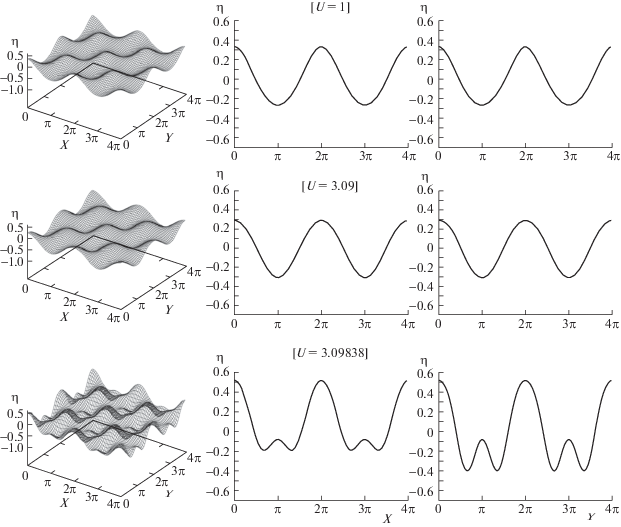
На рис. 7 представлены репрезентативные трехмерные профили и их поперечные сечения в плоскостях $Y = 0$ и $X = 0$ для коротко-гребневых волн на границе раздела двух сред при наличии течения. Эти профили соответствуют полностью трехмерному случаю $(\theta {{ = 45}^{ \circ }})$ при $\mu = 0.2$ и $h = 0.30$ в случае различных значений скорости течения U. Как показано на рис. 7, форма волны находится под сильным влиянием скорости U. Действительно, при небольших значениях скорости ($U = 1$) профиль типичен для коротко-гребневых волн с резкими гребнями и закругленными впадинами. По мере того, как скорость U возрастает, гребни становятся более плоскими, как это можно видеть при $U = 3.09$. Как только критическая скорость достигает $U \approx {{U}_{{lc}}}$, появляются вторичные пики вдоль обоих направлений (Ox) и (Oy), они расположены при $(X,Y) = (\pi ,\pi )$. Появление этих вторичных пиков объясняется тем, что волны регулярной формы не могут существовать в окрестности критического течения.

Рис. 7.

Трехмерные волновые профили и из сечения плоскостями $Y = 0$ и $X = 0$ на двух длинах волн для выбранных значений скорости $U$ и при заданных значениях $h = 0.30$, $\mu = 0.2$ и $\theta = 45^\circ $.

ВЫВОДЫ

Представлено аналитическое исследование коротко-гребневых волн на границе раздела двух сред при наличии течения в одной из сред. Предложены два разных метода решения и выяснены преимущества каждого из них. Вначале для определения решения по пятого порядка включительно использован метод возмущений. Достоинством этого метода является возможность определения условия гармонического резонанса, который является одним из наиболее важных характеристик коротко-гребневых волн. Важно отметить, что метод возмущений не может быть использован в окрестности особенностей из-за наличия гармонического резонанса. Кроме того, найдена частота обращения, при которой ${{\omega }_{2}}$ меняет знак. Во втором методе для нахождения решений второго порядка использован вариационный подход. Эта методика дала возможность определить критическое течение, связанное с динамическим условием. В линейном случае показано, что критическое течение связано с появлением неустойчивости. Более того, критическое течение зависит от трехмерности задачи через угол падения $\theta $. В нелинейном случае критическая скорость течения возрастает при увеличении кривизны, что может интерпретироваться как стабилизирующий эффект.

Список литературы

Saffman P.G., Yuen H. Finite-amplitude interfacial waves in the presence of a current // J. Fluid Mech. 1982. V. 123. P. 459–476.
Bontozoglou V., Hanratty T.J. Effects of finite depth and current velocity on large amplitude Kelvin-Helmholtz waves // J. Fluid Mech. 1988. V. 196. P. 187–204.
Hsu J.R.C., Tsushiya Y., Silvester R. Third-order approximation to short-crested waves // J. Fluid Mech. 1979. V. 90. № 1. P. 179–196.
Roberts A.J. Highly nonlinear short-crested water waves // J. Fluid Mech. 1983. V. 135. P. 301–321.
Marchant T.R., Roberts A.J. Properties of short-crested waves in water of finite depth // J. Aust. Math Soc. 1987. V. 29. № 1. P. 103–125.
Tsai C.P., Jeng D.S. A Fourier approximation for finite amplitude short-crested waves // J. Chinese Inst. Engineers. 1992. V. 15. № 6. P. 713–721.
Wei Z., Dalrymple R.A., Xu M., Garnier R., Derakhti M. Short-crested waves in the surf zone // J. Geophys. Res. Oceans. 2017. V. 122. № 5. P. 4143–4162 .
Kirby J.T., Derakhti M. Short-crested wave breaking // European Journal of Mechanics – B/Fluids. 2019. V. 73, P. 100–111.
Debiane M., Kharif C. Calculation of resonant short-crested waves in deep water // Phys. Fluids. 2009. V. 21. № 6. P. (062106) 1–12.
Concus P. Standing capillary-gravity waves of finite amplitude: Corrigendum // J. Fluid Mech. 1964. V. 19. № 2. P. 264–266.
Plotnikov P.I., Toland J.F. Nash-Moser theory for standing water waves // Arch. Rational Mech. Anal. 2001. V. 159. № 1. P. 1–83.
Iooss G., Plotnikov P. Asymmetrical three-dimensional travelling gravity waves // Arch Rational Mech. Anal. 2011. V. 200. № 3. P. 789–880.
Jian Y.J., Zhu Q.Y., Zhang J., Wang Y.F. Third order approximation to capillary gravity short crested waves with uniform currents // Appl. Math. Modelling. 2009. V. 33. № 4. P. 2035–2053.
Grimshaw R., Zhu Y. Oblique interactions between internal solitary waves // Stud. Appl. Math. 1994. V. 92. № 3. P. 249–270.
Pennell S., Mirie R.M. Weak oblique collisions of interfacial solitary waves // Wave Motion. 1995. V. 21. № 4. P. 385–404.
Tsuji H., Oikawa M. Oblique interaction of internal solitary waves in a two-layer fluid of infinite depth // Fluid Dynam. Res. 2001. V. 29. № 4. P. 251–267.
Părău E.I., Vanden-Broeck J.M., Cooker M.J. Three-dimensional gravity and gravity-capillary interfacial flows // Math. Comput. Simulation. 2007. V. 74. № 3. P. 105–112.
Allalou N., Debiane M., Kharif C. Three-dimensional periodic interfacial gravity waves: Analytical and numerical results // Eur. J. Mech. B Fluids. 2011. V. 30. № 4. P. 371–386.
Li J., Liu Z., Liao S., Borthwick A.G.L. Steady-state multiple near resonances of periodic interfacial waves with rigid boundary // Phys. Fluids. 2020. V. 32. № 8. P. 087104.
Whitham G.B. Linear and non-linear waves. New York: Wiley, 1974.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал