1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 5, 2021

Известия РАН. Механика жидкости и газа, 2021, № 5, стр. 76-81

АСИМПТОТИКИ ДАЛЬНИХ ПОЛЕЙ ВНУТРЕННИХ ГРАВИТАЦИОННЫХ ВОЛН, ВОЗБУЖДЕННЫХ ИСТОЧНИКОМ РАДИАЛЬНОЙ СИММЕТРИИ

В. В. Булатов a, *, Ю. В. Владимиров a, **

a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: internalwave@mail.ru
** E-mail: vladimyura@yandex.ru

Поступила в редакцию 11.02.2021
После доработки 23.03.2021
Принята к публикации 23.03.2021

Полный текст (PDF)

Аннотация

Решена задача о дальнем поле внутренних гравитационных волн от возникшего в начальный момент времени источника возмущений радиальной симметрии. Рассмотрено постоянное модельное распределение частоты плавучести, и с помощью преобразования Фурье–Ханкеля получено аналитическое решение задачи в виде суммы волновых мод. Получены асимптотики решений, описывающие пространственно-временные характеристики возвышения изопикн, вертикальной и горизонтальной компонент скорости вдали от источника возмущений. Вблизи волновых фронтов отдельной волновой моды асимптотики компонент волнового поля выражаются через квадрат функции Эйри и ее производные. Проведено сравнение точных и асимптотических результатов, и показано, что на временах порядка десяти и более периодов Брента–Вяйсяля асимптотический метод позволяет эффективно рассчитывать дальние волновые поля.

Ключевые слова: стратифицированная среда, внутренние гравитационные волны, частота плавучести, дальние поля, вспыхнувший источник

Аналитические и численные исследования эволюции диспергирующих внутренних гравитационных волн (ВГВ) от нелокальных источников возмущений в природных стратифицированных средах показывают, что структура волновых картин на больших расстояниях от этих источников (много больших их характерных размеров) практически не зависит от их формы и определяется только законами дисперсии этих сред [1–3]. Поэтому, используя модельные представления для описания различных источников, волновое поле в дальней зоне можно описать сравнительно простыми аналитическими формулами [4–6]. При этом начальные или граничные условия должны определяться из результатов прямого численного моделирования ближнего поля с учетом нелинейных уравнений гидродинамики, или из сугубо оценочных (полуэмпирических) соображений [6–8]. Возможной моделью волновой генерации можно считать предположение о возбуждении пакетов ВГВ импульсным воздействием [4, 5, 9–11]. Для проведения оценочных расчетов ВГВ необходимо подбирать параметры использованной модели источника так, чтобы приблизить смоделированные волновые системы к реально наблюдаемым, в том числе по фотоснимкам из космоса, волновым картинам [12–14]. Таким образом, математические модели волновой генерации могут быть не только верифицированы, но и использованы для проведения прогнозных оценок, так как в этих заданных a priori модельных условиях заложено много реальной информации, на основе которой линейная теория вдали от различных источников возмущений может давать удовлетворительные результаты [3, 4, 15–18].

Целью настоящей работы является построение асимптотик, описывающих дальние поля линейных внутренних гравитационных волн, возбуждаемых возникшим в начальный момент времени источником возмущения радиальной симметрии в слое стратифицированной среды конечной толщины.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается слой стратифицированной среды конечной толщины H. Уравнение линейных ВГВ в цилиндрических координатах $(r,z)$ (предполагается, что зависимости от угла нет, ось z направлена вверх) для малых возмущений возвышения изопикн $\eta (r,z,t)$ в приближении Буссинеска имеет вид [1, 6]

$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)\eta (r,z,t) + {{N}^{2}}(z)\Delta \eta (r,z,t) = 0$
$\Delta = \frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{\partial }{{\partial r}}$
где далее частота Брента–Вяйсяля (частота плавучести) предполагается постоянной: ${{N}^{2}}(z)\, = \,{{N}^{2}}$ = = const. Начальные и граничные условия берутся в виде
$\eta (r,z,0) = {{\eta }_{0}}(r,z) = \Phi (r)\Pi (z)$
$\frac{{\partial \eta (r,z,t)}}{{\partial t}} = W(r,z,t) = 0\quad {\text{при}}\quad t = 0$
$\eta (r,z,t) = 0\quad {\text{при}}\quad z = 0, - H$
где $W(r,z,t)$т – вертикальная компонента скорости, и предполагается, что начальное возмущение изопикн $\mathop \eta \nolimits_0 (r,z)$ обладает радиальной симметрией. Все искомые функции зависят от радиальной координаты r, времени t и вертикальной координаты z, зависимость от угла отсутствует. Решение полученной начально-краевой задачи строится с помощью преобразования Фурье–Ханкеля [19, 20], в результате можно получить
(1.1)
$\eta (r,z,t) = \sum\limits_{n = 1}^\infty {{{\eta }_{n}}} = \sum\limits_{n = 1}^\infty {{{a}_{n}}} {{\varphi }_{n}}(z){{g}_{n}}(r,t),\quad {{\varphi }_{n}}{{(z)}_{n}} = \sin (\pi nz{\text{/}}H)\quad {{a}_{n}} = \frac{2}{H}\int\limits_{ - H}^0 {\Pi (z){{\varphi }_{n}}(z)dz} $
$\mathop g\nolimits_n (r,t) = \int\limits_0^\infty {A(k)k{{J}_{0}}} (kr)\cos ({{\omega }_{n}}(k)t)dk,{{\omega }_{n}}(k) = kN{\text{/}}\sqrt {\mathop k\nolimits^2 + \mathop {(\pi n{\text{/}}H)}\nolimits^2 } ,\quad A(k) = \int\limits_0^\infty {r{{J}_{0}}(kr)\Phi (r)dr} $
где J0 – функция Бесселя нулевого порядка. Отметим, что в силу постоянства частоты плавучести функция $A(k)$ не зависит от номера моды n и ${{g}_{n}}(r,0) = \Phi (r)$ для всех номеров $n$. Выражение для вертикальной компоненты скорости имеет вид

(1.2)
$W(r,z,t) = \sum\limits_n {\mathop W\nolimits_n } = \sum\limits_n {{{a}_{n}}{{\varphi }_{n}}(z){{p}_{n}}(r,t),\quad {{p}_{n}}(r,t) = - \int\limits_0^\infty {A(k){{J}_{0}}} } (kr){{\omega }_{n}}(k)\sin ({{\omega }_{n}}(k)t)dk$

Горизонтальная (радиальная) компонента скорости $U(r,z,t)$ определяется из уравнения несжимаемости в цилиндрических координатах [6]

$\frac{{\partial U}}{{\partial r}} + \frac{U}{r} + \frac{{\partial W}}{{\partial z}} = 0$

Учитывая, что решением уравнения [19, 20]

$\frac{{\partial Y(kr)}}{{\partial r}} + \frac{{Y(kr)}}{r} = {{J}_{o}}(kr)$
является функция $Y(kr) = {{J}_{1}}(kr){\text{/}}k$ (J1 – функция Бесселя первого порядка), можно получить

(1.3)
$U(r,z,t) = \sum\limits_{n = 1}^\infty {{{U}_{n}}} = \sum\limits_{n = 1}^\infty {{{d}_{n}}{{\psi }_{n}}} (z){{q}_{n}}(r,t)$
${{\psi }_{n}}(z) = \cos ({{b}_{n}}z),\quad {{d}_{n}} = \pi n{{a}_{n}}{\text{/}}H,\quad {{q}_{n}}(r,t) = \int\limits_0^\infty A (k){{J}_{1}}(kr){{\omega }_{n}}(k)\sin ({{\omega }_{n}}(k)t)dk$

Полученные решения (1.3) показывают, что горизонтальная (радиальная) компонента скорости $U(r,z,t)$ равна нулю при r = 0 и всех значениях z, t, т.е. $U(0,z,t) \equiv 0$. В безразмерных переменных $r* = r\pi {\text{/}}H$, $z* = z\pi {\text{/}}H$, $k* = k\pi {\text{/}}H$, $\tau = Nt$ (знак “*” далее опускается) выражения (1.1)–(1.3) можно представить в виде

${{g}_{n}}(r,\tau ) = \int\limits_0^\infty {A(k)k{{J}_{0}}} (kr)\cos ({{\omega }_{n}}(k)\tau )dk$
(1.4)
${{p}_{n}}(r,\tau ) = - \int\limits_0^\infty {A(k)k{{J}_{0}}} (kr){{\omega }_{n}}(k)\sin ({{\omega }_{n}}(k)\tau )dk$
${{q}_{n}}(r,\tau ) = \int\limits_0^\infty {A(k){{J}_{1}}} (kr){{\omega }_{n}}(k)\sin ({{\omega }_{n}}(k)\tau )dk$
${{\varphi }_{n}}(z) = \sin (nz),\quad {{\psi }_{n}}(z) = \cos (nz),\quad {{a}_{n}} = \frac{2}{\pi }\int\limits_{ - \pi }^0 {\Pi (z)\sin (nz)dz} ,\quad {{d}_{n}} = n{{a}_{n}},\quad {{\omega }_{n}}(k) = k{\text{/}}\sqrt {{{k}^{2}} + {{n}^{2}}} $

2. АСИМПТОТИКИ РЕШЕНИЙ ВБЛИЗИ ВОЛНОВЫХ ФРОНТОВ

В заданном начальном распределении возвышения изопикн ${{\eta }_{0}}(r,z)$ будем считать, что функции $\Phi (r)$, $\Pi (z)$ нормированы на свои максимальные (по модулю)значения. Далее, в качестве модельного, рассмотрим следующее радиальное распределение начального возмущения: Φ(r) = = $\exp ( - {{r}^{2}}{\text{/}}4){\text{/}}2$ (множитель 1/2 используется для простоты выкладок). Тогда из (1.1) имеем: A(k) = = $\exp ( - {{k}^{2}})$. Интегралы (1.4) при больших значениях $r \gg 1$, $\tau \gg 1$ можно вычислить с помощью метода стационарной фазы. С этой целью необходимо заменить функцию Бесселя на ее асимптотику: ${{J}_{0}}(kr) \approx \sqrt {2{\text{/}}\pi kr} \cos (kr - \pi {\text{/}}4)$ [19, 20]. Подставляя это выражение в (1.4), можно получить

${{g}_{n}}(r,\tau ) = \sqrt {2{\text{/}}\pi r} \int\limits_0^\infty {\exp ( - {{k}^{2}})\sqrt k \cos (kr - \pi {\text{/}}4)} \cos ({{\omega }_{n}}(k)\tau )dk = I_{n}^{ + } + I_{n}^{ - }$
$I_{n}^{ + } = \sqrt {1{\text{/}}2\pi r} )\int\limits_0^\infty {\exp ( - {{k}^{2}})\sqrt k \cos (kr \pm {{\omega }_{n}}(k)\tau - \pi {\text{/}}4)dk} $

При больших значениях r, τ интеграл $I_{n}^{ + }$ экспоненциально мал, так как стационарных точек на интервале интегрирования нет. С помощью метода стационарной фазы можно получить уравнение для нахождения стационарных точек: $\omega _{n}^{'}(k) = \rho $, $\rho = r{\text{/}}\tau $. Решение этого уравнения имеет вид: ${{k}_{n}}(\rho ) = n\sqrt {\mathop {(\rho n)}\nolimits^{ - 2/3} - 1} $. Окончательно можно получить: ${{g}_{n}}(r,\tau ) \approx {{G}_{n}}(r,\tau )\cos ({{\Phi }_{n}}(r,\tau ))$, Φn(r, τ) = = $\tau {{(1 - \mathop {(n\rho )}\nolimits^{2/3} )}^{{3/2}}}$. Аналогично, с помощью метода стационарной фазы имеем: pn(r, τ) ≈ Pn(r, τ)${\text{sin}}({{\Phi }_{n}}$(r, τ)), ${{P}_{n}}(r,\tau ) = - {{(1 - \mathop {(n\rho )}\nolimits^{2/3} )}^{{1/2}}}{{G}_{n}}(r,\tau )$, ${{q}_{n}}(r,\tau )$ ≈ ${{Q}_{n}}(r,\tau )\cos ({{\Phi }_{n}}(r,\tau ))$. Полученные асимптотические формулы для функций ${{g}_{n}}(r,\tau )$, ${{p}_{n}}(r,\tau )$, ${{q}_{n}}(r,\tau )$ позволяют рассчитывать на фиксированной глубине пространственно-временные характеристики возвышения изопикн, вертикальной и горизонтальной (радиальной) компонент скорости ВГВ вдали от вспыхнувшего в начальный момент времени нелокального источника возмущений радиальной симметрии в приближении стационарной фазы. Однако эти асимптотики неприменимы вблизи волновых фронтов [6, 20]. Для построения локальных асимптотик, т.е. асимптотик, описывающих поле ВГВ вблизи волновых фронтов, заменим далее в интеграле $I_{n}^{ - }$ функцию ${{\omega }_{n}}(k)$ при малых волновых числах разложением: ${{\omega }_{n}}(k) \approx k{\text{/}}n - {{k}^{3}}{{n}^{{ - 3}}}{\text{/}}2$. Тогда можно получить

${{g}_{n}}(r,\tau ) \approx \sqrt {/2\pi r} \int\limits_0^\infty {\exp ( - {{k}^{2}})\sqrt k \cos ({{k}^{3}}r{{n}^{{ - 3}}}{\text{/}}2 - \xi k - \pi {\text{/}}4)} \cos ({{\omega }_{n}}(k)\tau )dk,\quad \xi = \tau {\text{/}}n - r$

При малых значениях ξ (вблизи волновых фронтов) стационарные точки стремятся к нулю, т.е. к краю области интегрирования и одновременно к особенности подынтегрального выражения $\sqrt k $. В этом случае метод стационарной фазы неприменим, и для построения локальных асимптотик с помощью подходящей замены следует свести исходный интеграл к более сложному эталонному интегралу. Выбор эталонного интеграла определяется распределением стационарных точек фазовой функции и особых точек подынтегральной функции в зависимости от параметров задачи. В основе метода построения локальных асимптотик лежит сведение исходного интеграла к эталонному интегралу, т.е. такому простейшему интегралу, у которого имеется требуемый набор критических точек, расположенных аналогично их взаимному расположению в рассматриваемом интеграле. Таким образом, построение асимптотики сводится к выбору соответствующей специальной функции, ее нескольких первых производных и к определению зависимости аргументов этой специальной функции, а также амплитудных и фазовых множителей от параметров задачи. Модельным интегралом, который выражается через квадрат функции Эйри, в этом случае будет следующий [20, 21]

$G(x) = \int\limits_0^\infty {\frac{1}{{\sqrt u }}\cos ({{u}^{3}}{\text{/}}12 - xu - \pi {\text{/}}4)} du = 2{{\pi }^{{3/2}}}A{{i}^{2}}(x)$
$Ai(x) = \frac{1}{{2\pi }}\int\limits_0^\infty {\cos ({{u}^{3}}{\text{/}}3 - xu)} du$

Функция G(x) удовлетворяет уравнению: $G{\text{'''}}(x) = 4xG{\text{'}}(x) + 2G(x)$, которое решается методом Лапласа [20, 21]. Тогда, с помощью замены $k = tn{{(6\tau )}^{{ - 1.3}}}$ можно получить выражения для локальной асимптотики вблизи волнового фронта, имеющей вид

(2.1)
${{g}_{n}}(r,\tau ) \approx \frac{{{{n}^{{3/2}}}J(\Theta )}}{{2\sqrt {3\pi r\tau } }},\quad \Theta = (\tau - nr){{(6\tau )}^{{ - 1.3}}}$
$J(x) = G{\text{'}}(x) = 4{{\pi }^{{3/2}}}Ai(x)Ai{\text{'}}(x) = \int\limits_0^\infty {\sqrt u \cos ({{u}^{3}}{\text{/12}} - xu - \pi {\text{/}}4)} du$

Локальные асимптотики вблизи волновых фронтов для функций ${{p}_{n}}(r,\tau )$ получаются из (2.1) дифференцированием по переменной τ (при этом дифференцируется только функция J)

${{p}_{n}}(r,\tau ) \approx \frac{{{{n}^{{3/2}}}F(\Theta )}}{{{{{(6\tau )}}^{{5/6}}}\sqrt {2\pi r} }},\quad F(\Theta ) = 4{{\pi }^{{3/2}}}(Ai{\text{'}}{{(\Theta )}^{2}} - \Theta Ai{{(\Theta )}^{2}})$

Выражения для локальных асимптотик горизонтальной (радиальной) компоненты скорости имеют вид

${{q}_{n}}(r,\tau ) \approx \frac{{{{n}^{{1/2}}}J(\Theta )}}{{2\sqrt {3\pi r\tau } }}$

Можно отметить, что выражения для асимптотик возвышения изопикн ${{g}_{n}}(r,\tau )$ и горизонтальной (радиальной) компоненты скорости ${{q}_{n}}(r,\tau )$ совпадают с точностью до множителя n (номера моды).

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

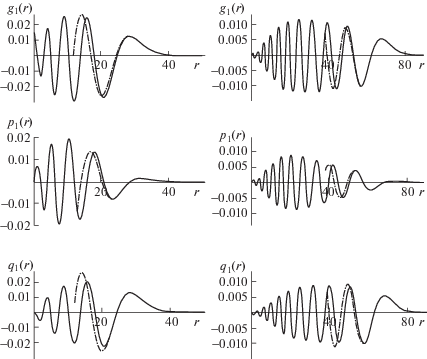
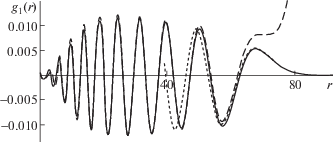
Для численных расчетов было использовано следующее представление функции Π(z), имеющее один максимум: $\Pi (z) = {{z}^{\alpha }}(1 - {{z}^{\beta }})$, значения параметров были следующие: α = 33, β = 57. Использованные пространственные масштабы и характер изменчивости начального возмущения изопикн соответствуют типичным горизонтальным и вертикальным масштабам реальных источников возбуждения ВГВ в океане [3–5, 12–14]. На рис. 1 представлены результаты расчетов функции ${{g}_{1}}(r,\tau )$, (первая мода возвышения) при значении τ = 30 (левый рисунок) и τ = 70 (правый рисунок). Сплошная линия – точное решение, пунктир – приближение локальной асимптотики по формуле (2.1). Из представленных результатов видно хорошее совпадение точных и асимптотических результатов в окрестности волновых фронтов при больших значениях r, τ. На рис. 2 представлены результаты расчетов функций ${{g}_{1}}(r,\tau )$ (первая мода возвышения) при τ = 70. Сплошная линия – точное решение, штриховая линия – расчеты по методу стационарной фазы, пунктир – приближение локальной асимптотики по формуле (2.1). Как показывают численные расчеты, на временах порядка десяти и более периодов Брента–Вяйсяля полученные асимптотики позволяют достаточно точно рассчитывать дальние волновые поля. Вблизи волновых фронтов отдельной моды асимптотики компонент волнового поля ВГВ (возвышение изопикн, вертикальная и горизонтальная компоненты скорости) выражаются через квадрат функции Эйри и ее производные, вдали от волновых фронтов можно использовать метод стационарной фазы.

Рис. 1.

Возвышение первой моды: точное решение и локальная асимптотика вблизи фронта.

Рис. 2.

Возвышение первой моды: точное решение, локальная асимптотика и асимптотика стационарной фазы.

Общую схему моделирования дальних полей ВГВ от возникшего нелокального источника возмущений можно представить следующим образом. Используя численное решение полной системы уравнений гидродинамики, определяются основные характеристики параметров волнового поля (возвышение изопикн, компонент скорости, плотность, давление), можно задать некоторое начальное пространственное распределение этих компонент [6–8]. Вдали от источников возмущений, предполагая адекватность использования линейной модели волновой динамики, дальние поля ВГВ рассчитываются по асимптотическим формулам, причем, как показывают результаты расчетов, для большинства реальных гидрологических условий Мирового океана основой вклад в дальние поля вносят только несколько первых волновых мод [3, 4, 16–18].

ЗАКЛЮЧЕНИЕ

Полученные в работе асимптотики решений позволяют эффективно рассчитывать волновые поля ВГВ вдали от нелокальных источников возмущений и проводить качественную оценку получаемых решений. В результате проведения модельных многовариантных расчетов по асимптотическим формулам смоделированная волновая система может быть приближена к наблюдаемым в натурных условиях волновым системам, что позволяет оценить физические параметры реальных источников возбуждения внутренних гравитационных волн в океане. Поэтому полученные асимптотические результаты дают возможность определить основные характеристики начальных возмущений, варьируя модельные значения исходных параметров.

Работа выполнена при финансовой поддержке РФФИ проект № 20-01-00111А.

Список литературы

  1. Лайтхилл Дж. Волны в жидкостях. М.: Мир, 1981. 598 с.

  2. Коняев К.В., Сабинин К.Д. Волны внутри океана. СПб.: Гидрометеоиздат, 1992. 272 с.

  3. Morozov E.G. Oceanic internal tides. Observations, analysis and modeling. Berlin: Springer, 2018. 317 p.

  4. Velarde M.G., Tarakanov R.Yu., Marchenko A.V. (Eds.). The ocean in motion. Springer Oceanography. Springer International Publishing AG, 2018. 625 p.

  5. Mei C.C., Stiassnie M., Yue D.K.-P. Theory and applications of ocean surface waves. London: World Scientific Publishing, 2017. 1500 p.

  6. Булатов В.В., Владимиров Ю.В. Волны в стратифицированных средах. М.: Наука, 2015. 735 с.

  7. Гущин В.А., Матюшин П.В. Моделирование и исследование течений стратифицированной жидкости около тел конечных размеров // ЖВМ и МФ. 2016. Т. 56. № 6. С. 1049–1063.

  8. Матюшин П.В. Процесс формирования внутренних волн, инициированных начальным движением тела в стратифицированной вязкой жидкости // Изв. РАН. МЖГ. 2019. № 3. С. 83–97.

  9. Voelker G.S., Myers P.G., Walter M., Sutherland B.R. Generation of oceanic internal gravity waves by a cyclonic surface stress disturbance // Dynamics Atm. Oceans. 2019. V. 86. P. 116–133.

  10. Haney S., Young W.R. Radiation of internal waves from groups of surface gravity waves // J. Fluid Mech. 2017. V. 829. P. 280–303.

  11. Wang J., Wang S., Chen X., Wang W., Xu Y. Three-dimensional evolution of internal waves rejected from a submarine seamount // Physics Fluids. 2017. V. 29. P. 106601.

  12. Беляев М.Ю., Десинов Л.В., Крикалев С.К., Кумакшев С.А., Секерж-Зенькович С.Я. Идентификация системы океанских волн по фотоснимкам из космоса // Изв. РАН. Теория и системы управления. 2009. № 1. С. 117–127.

  13. Morozov E.G., Tarakanov R.Yu., Frey D.I., Demidova T.A., Makarenko N.I. Bottom water flows in the tropical fractures of the Northern Mid-Atlantic Ridge // J. of Oceanography. 2018. V. 74. № 2. P. 147–167.

  14. Khimchenko E.E., Frey D.I., Morozov E.G. Tidal internal waves in the Bransfield Strait, Antarctica // Russ. J. Earth. Science. 2020. V. 20. ES2006.

  15. Свиркунов П.Н., Калашник М.В. Фазовые картины диспергирующих волн от движущихся локализованных источников // Успехи физических наук. 2014. Т. 184. № 1. С. 89–100.

  16. Bulatov V.V., Vladimirov Yu.V., Vladimirov I.Yu. Far fields of internal gravity waves from a source moving in the ocean with an arbitrary buoyancy frequency distribution // Russ. J. Earth Sciences. 2019. V. 19 (5). ES5003

  17. Bulatov V., Vladimirov Yu. Generation of internal gravity waves far from moving non-local source // Symmetry. 2020. V. 12 (11). P. 1899.

  18. Булатов В.В., Владимиров Ю.В. Дальние поля внутренних гравитационных волн от нелокальных источников возмущений // Процессы в геосредах. 2020. № 3 (25). С. 772–779.

  19. Watson G.N. A treatise on the theory of Bessel functions (Reprint of the 2nd ed.). Cambridge: Cambridge University Press, 1995. 804 p.

  20. Froman N., Froman P. Physical problems solved by the phase-integral method. Cambridge. Cambridge University Press, 2002. 214 p.

  21. Грикуров В.Э. Явление перекрытия при акустических зонах в приповерхностном волноводе и связанное с ним обобщение лучевого метода // Изв. ВУЗов. Радиофизика. 1980. Т. 23. № 9. С. 1038–1045.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал