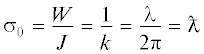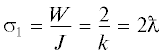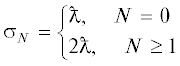Известия РАН. Механика жидкости и газа, 2021, № 5, стр. 82-88

РЕЗОНАНСНОЕ ПОГЛОЩЕНИЕ ГРАВИТАЦИОННЫХ ВОЛН

Н. Г. Канев^a, b, *, М. А. Миронов^a, b, **

^a Акустический институт им. акад. Н.Н. Андреева
Москва, Россия

^b Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

^* E-mail: nikolay.kanev@mail.ru
^** E-mail: mironov_ma@mail.ru

Поступила в редакцию 27.11.2020
После доработки 26.03.2021
Принята к публикации 06.04.2021

DOI: 10.31857/S0568528121050066

Полный текст (PDF)

Аннотация

Решена задача о поглощении гравитационной волны, распространяющейся по поверхности несжимаемой жидкости, малым по сравнению с длиной волны резонатором. Найдены резонансные, т.е. максимально возможные, сечения поглощения резонаторов разных типов для свободной поверхности жидкости. Показано, что резонансное сечение поглощения зависит только от длины волны. Также рассмотрена задача о поглощении гравитационной волны, распространяющейся в канале. Показано, что совместное использование монопольного и дипольного резонаторов обеспечивает полное поглощение энергии волны в канале, ширина которого не превышает длину волны.

Ключевые слова: гравитационные волны, резонатор, сечение поглощения

Морские и океанические волны рассматриваются как источник возобновляемой энергии [1, 2], поэтому вопрос о возможностях преобразования энергии поверхностного волнения представляет практический интерес. Исследованы различные физические механизмы поглощения волн на поверхности жидкости локальными [3, 4] и распределенными структурами [4–6]. Из теории волн известно, что наибольшее поглощение энергии происходит на резонансном режиме. Эффективность поплавковых резонаторов впервые получена в работах [7, 8].

Резонансное поглощение энергии волн препятствием малого по сравнению с длиной волны размера происходит при двух условиях: действительная часть импеданса препятствия должна быть равна действительной части импеданса излучения, и сумма мнимых частей импедансов препятствия и излучения должна быть равна нулю. В этом случае сечение поглощения зависит только от длины волны и может значительно превышать размеры препятствия. Поэтому использование малых препятствий особенно эффективно на низких частотах.

Механические резонаторы, как правило, обеспечивают выполнение обоих условий на одной – резонансной – частоте. Сечения поглощения монопольных и дипольных резонаторов найдены для звуковых волн в свободном пространстве [9–11], волноводе [12], для изгибных волн в пластинах [13], для поверхностных волн в твердом теле [14]. В настоящей работе рассматривается задача о максимальном поглощении энергии гравитационных волн малым по сравнению с длиной волны препятствием, погруженным в жидкость.

1. ПОСТАНОВКА ЗАДАЧИ

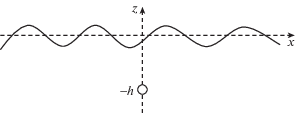
Постановка задачи приведена на рис. 1. Гармоническая плоская волна распространяется вдоль оси x, совпадающей с поверхностью невозмущенной жидкости, направление оси z противоположно направлению силы тяжести, ось y направлена по нормали к плоскости рисунка. Точечный резонатор находится на глубине h. Под резонатором понимаем препятствие, импеданс которого удовлетворяет условиям максимального поглощения хотя бы на одной частоте. Необходимо найти сечение поглощения на этой частоте.

Рис. 1.

Постановка задачи.

Поле давления падающей волны зададим следующим образом

(1.1)

${{p}_{{in}}} = {{p}_{0}}{{e}^{{ikx + kz}}}$

где $k = {{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} g}} \right. \kern-0em} g}$, ω – круговая частота, g – ускорение свободного падения. Множитель ${{e}^{{ - i\omega t}}}$, будем опускать, где t – время.

Вертикальное смещение поверхности, советующее полю (1.1), имеет вид

(1.2)

$\eta (x) = a{{e}^{{ikx - i\omega t}}}$

где ρ – плотность жидкости, $a = {{{{p}_{0}}} \mathord{\left/ {\vphantom {{{{p}_{0}}} {\rho g}}} \right. \kern-0em} {\rho g}}$ – амплитуда волны.

Далее рассмотрим поглощение гравитационной волны резонаторам разных типов в свободном пространстве и в прямоугольном канале.

2. МОНОПОЛЬНЫЙ РЕЗОНАТОР

Решим задачу о поле монопольного источника [15]

(2.1)

$\Delta \varphi = q\delta (x,y,z + h)$

с граничным условием

(2.2)

${{\left( {\frac{{\partial \varphi }}{{\partial z}} + \frac{1}{g}\frac{{{{\partial }^{2}}\varphi }}{{\partial {{t}^{2}}}}} \right)}_{{z = 0}}} = 0$

где $\varphi $ – потенциал скорости, q – объемная скорость монополя.

Давление в среде задается отношением $p = - \rho {{\partial \varphi } \mathord{\left/ {\vphantom {{\partial \varphi } {\partial t}}} \right. \kern-0em} {\partial t}}$. Решение уравнения (2.1) в свободном пространстве ${{\varphi }_{0}} = - {q \mathord{\left/ {\vphantom {q {4\pi r}}} \right. \kern-0em} {4\pi r}}$, где $r = \sqrt {{{x}^{2}} + {{y}^{2}} + {{{(z - h)}}^{2}}} $.

Решение (2.1) и (2.2) найдем методом Фурье

(2.3)

$\varphi = - \frac{q}{{4\pi }}\int\limits_0^{ + \infty } {\left( {{{e}^{{ - \kappa \left| {z + h} \right|}}} + {{e}^{{\kappa (z - h)}}}\frac{{\kappa g + {{\omega }^{2}}}}{{\kappa g - {{\omega }^{2}}}}} \right){{J}_{0}}(\kappa R)d\kappa } $

где $R = \sqrt {{{x}^{2}} + {{y}^{2}}} $. Интегрирование в (2.3) производится по действительной оси, полюс ${{\kappa }_{0}} = {{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} g}} \right. \kern-0em} g}$ = k обходится снизу.

Для вычисления сопротивления излучения монополя (действительная часть импеданса) необходимо найти мнимую часть потенциала φ. Для этого (2.3) запишем в виде

(2.4)

$\varphi = {{\varphi }_{0}} - \frac{q}{{4\pi }}\int\limits_0^{ + \infty } {{{e}^{{\kappa (z - h)}}}\frac{{\kappa g + {{\omega }^{2}}}}{{\kappa g - {{\omega }^{2}}}}{{J}_{0}}(\kappa R)d\kappa } - i\frac{{q{{\omega }^{2}}}}{{2g}}{{e}^{{\frac{{{{\omega }^{2}}}}{g}\left( {z - h} \right)}}}{{J}_{0}}\left( {\frac{{{{\omega }^{2}}}}{g}R} \right)$

Интеграл во втором слагаемом в (2.4) берется в смысле главного значения, и поэтому имеет действительное значение, третье слагаемое – полувычет в полюсе κ₀. Поле в окрестности излучателя находим при $z = - h$ и $R \to 0$. Принимая во внимание, что ${{J}_{0}}(x) \approx 1$ при $x \to 0$, находим из (2.4) мнимую часть потенциала

$\operatorname{Im} \varphi = - \frac{{q{{\omega }^{2}}}}{{2g}}{{e}^{{ - 2h\frac{{{{\omega }^{2}}}}{g}}}}$

Сопротивление излучения монополя равно

(2.5)

$\operatorname{Re} Z = \frac{{\operatorname{Re} p}}{q} = - \frac{{\omega \rho }}{q}\operatorname{Im} \varphi = \frac{1}{2}\rho \omega k{{e}^{{ - 2kh}}}$

Максимальная мощность, поглощаемая монополем во внешнем поле, т.е. мощность, поглощаемая на резонансе, равна [4]

(2.6)

$W = \frac{{p_{0}^{2}}}{{8\operatorname{Re} Z}}$

где ${{p}_{0}}$ – давление в падающей волне.

Пусть монополь находится в поле волны (1.1), тогда мощность, поглощаемая монопольным резонатором, согласно (2.5) и (2.6) равна $W = \frac{g}{{4\rho {{\omega }^{3}}}}p_{0}^{2}$.

Плотность потока мощности в падающей волне составляет

(2.7)

$J = uE = \frac{{p_{0}^{2}}}{{4\rho \omega }}$

где $u = \frac{g}{{2\omega }}$ – групповая скорость распространения гравитационных волн [15], $E = \frac{{p_{0}^{2}}}{{2\rho g}}$ – энергия на единицу площади горизонтальной поверхности [4].

Находим сечение поглощения резонатора

(2.8)

где λ – длина волны. Таким образом, резонансное сечение поглощения монополя зависит только от длины волны и не зависит от глубины погружения резонатора. Для монополя на поверхности жидкости этот результат был получен в работах [7, 8].

3. ДИПОЛЬНЫЙ РЕЗОНАТОР

Рассмотрим поглощение поверхностной гравитационной волны диполем, ориентированным вдоль направления распространения волны. Поле диполя может быть получено дифференцированием поля монополя (2.3) или может быть представлено в виде суммы полей двух противофазных близкорасположенных монополей. Если момент диполя $\mu $ направлен вдоль оси $x$, тогда поле диполя имеет вид

(3.1)

$\varphi = \frac{\mu }{{4\pi }}\cos \theta \int\limits_0^{ + \infty } {\left( {{{e}^{{ - \kappa \left| {z + h} \right|}}} + {{e}^{{\kappa (z - h)}}}\frac{{\kappa g + {{\omega }^{2}}}}{{\kappa g - {{\omega }^{2}}}}} \right){{J}_{1}}(\kappa R)\kappa d\kappa } $

где $\theta $ – угол между осью x и направлением на точку наблюдения.

Определим импеданс диполя следующим образом $Z = {{\rho {{{{\dot {v}}}}_{x}}} \mathord{\left/ {\vphantom {{\rho {{{{\dot {v}}}}_{x}}} \mu }} \right. \kern-0em} \mu }$, где ${{{v}}_{x}}$ – скорость среды в направлении x. Скорость среды ${{{v}}_{x}} = {{\partial \varphi } \mathord{\left/ {\vphantom {{\partial \varphi } {\partial x}}} \right. \kern-0em} {\partial x}}$ находим из (3.1). Действительная часть импеданса диполя определяется полувычетом в полюсе $\kappa = {{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} g}} \right. \kern-0em} g}$:

(3.2)

$\operatorname{Re} Z = \frac{{\rho \operatorname{Re} {{{{\dot {v}}}}_{x}}}}{\mu }\varphi = \frac{1}{4}\rho \omega {{k}^{3}}{{e}^{{ - 2kh}}}$

Отметим, что введенный выше импеданс монополя (2.5) имеет размерность, отличную от импеданса диполя (3.2).

Мощность, поглощаемая диполем на резонансе, равна

(3.3)

$W = \frac{{{{{\left| {\rho {{{{\dot {v}}}}_{{0x}}}} \right|}}^{2}}}}{{8\operatorname{Re} Z}}$

где ${{{v}}_{{0x}}}$ – скорость в падающей волне.

Если монополь находится в поле волны (1.1), тогда скорость в точке расположения диполя равна ${{{v}}_{{0x}}} = {{p}_{0}}\frac{k}{{\omega \rho }}{{e}^{{ - kh}}}$. Согласно (3.3) поглощенная мощность равна $W = \frac{{p_{0}^{2}}}{{2\rho \omega k}}$. С учетом (2.7) находим сечение поглощения диполя

(3.4)

Отметим, что сечение поглощения монополя (2.8) не зависит от направления распространения волны, а сечение поглощения диполя (3.4) достигается только при распространении волны вдоль момента диполя.

Максимальное поглощение плавающим на поверхности жидкости несжимаемым препятствием определяется суммой поглощенной мощности монополем (колебания препятствия в направлении, перпендикулярном поверхности жидкости) и диполем (колебания вдоль поверхности). Максимальное сечение поглощения такого препятствия составляет 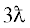[4].

4. МУЛЬТИПОЛЬНЫЙ РЕЗОНАТОР

Рассмотрим поглощение резонатором, являющимся мультипольным рассеивателем, ограничившись поиском максимального сечения поглощения по всем направлениям распространения падающей волны без анализа индикатрисы поглощения. Полем мультиполя является гравитационная цилиндрическая волна соответствующего порядка, распространяющаяся по поверхности жидкости. Падающая плоская волна, задаваемая вертикальным смещением жидкости (1.2), может быть представлена в виде суммы расходящихся и сходящихся цилиндрических волн

(4.1)

$\eta (x) = a\left[ {\frac{1}{2}H_{0}^{{(1)}}\left( {kR} \right) + \sum\limits_{n = 1}^\infty {{{i}^{n}}H_{n}^{{(1)}}\left( {kR} \right)\cos n\theta } } \right] + a\left[ {\frac{1}{2}H_{0}^{{(2)}}\left( {kR} \right) + \sum\limits_{n = 1}^\infty {{{i}^{n}}H_{n}^{{(2)}}\left( {kR} \right)\cos n\theta } } \right]$

где $H_{n}^{{(1)}}$ и $H_{n}^{{(2)}}$ – функции Ханкеля первого и второго родов.

Если поле мультиполя порядка N инвертировано по отношению к N-й расходящейся волне в разложении (4.1), то сумма этой компоненты падающего поля и поля мультиполя дают нуль, что означает поглощение N-й расходящейся компоненты падающего поля. Найдем мощность ${{W}_{N}}$, уносимую N-й компонентой, проинтегрировав плотность потока мощности, выходящего за контрольную окружность радиуса ${{R}_{0}}$, $k{{R}_{0}} \gg 1$. Применяя приближение $H_{n}^{{(1)}}(k{{R}_{0}})$ ≈ ≈ $\sqrt {\frac{2}{{\pi k{{R}_{0}}}}} {\text{exp}}\left[ {ik{{R}_{0}}\, - \,\frac{1}{2}i\pi \left( {n\, + \,\frac{1}{2}} \right)} \right]$, находим

(4.2)

${{W}_{N}} = \left\{ \begin{gathered} \frac{{\rho {{g}^{2}}}}{{4\omega k}}{{a}^{2}},\quad N = 0 \hfill \\ \frac{{\rho {{g}^{2}}}}{{2\pi \omega k}}{{a}^{2}}\int\limits_0^{2\pi } {{{{\cos }}^{2}}N\theta d\theta } ,\quad N \geqslant 1 \hfill \\ \end{gathered} \right.$

Значение интеграла в (4.2) равно π при любых N. Плотность потока мощности (2.7) в падающей волне составляет $J = \frac{{\rho {{g}^{2}}{{a}^{2}}}}{{4\omega }}$, откуда находим максимальное по всем направлениям падающей волны сечение поглощения мультиполя порядка N

Таким образом, максимальное сечение поглощения мультипольного резонатора, начиная с диполя, не зависит от порядка мультипольности. Это характерно для двумерных задач и отлично от трехмерных, в которых сечение поглощения растет с увеличением порядка мультиполя: например, максимальное сечение поглощения звуковой волны мультиполя порядка $N$ в свободном пространстве составляет 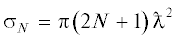[11].

5. РЕЗОНАТОР В КАНАЛЕ

Решим задачу о поглощении резонатором поверхностной волны, распространяющейся в канале шириной L и глубиной H.

В первую очередь найдем поле монополя в прямоугольном канале, для чего решим уравнение

(5.1)

$\Delta \varphi = q\delta (x - {{x}_{0}},y - {{y}_{0}},z + h)$

и дополним граничное условие (2.2), выполняемое на поверхности жидкости, граничными условиями для жестких стенок канала

(5.2)

${{\left. {\frac{{\partial \varphi }}{{\partial y}}} \right|}_{{y = 0,L}}} = 0,\quad {{\left. {\frac{{\partial \varphi }}{{\partial z}}} \right|}_{{z = - H}}} = 0$

Решение системы уравнений (2.2), (5.1), (5.2), найденное методом Фурье, имеет вид

(5.3)

$\varphi = \frac{q}{{2\pi L}}\int\limits_{ - \infty }^{ + \infty } {\frac{{{{F}_{0}}}}{{\xi {{Y}_{0}}}}{{e}^{{i\xi (x - {{x}_{0}})}}}d\xi } + \frac{q}{{\pi L}}\sum\limits_{n = 1}^\infty {\cos {{\kappa }_{n}}y\cos {{\kappa }_{n}}{{y}_{0}}} \int\limits_{ - \infty }^{ + \infty } {\frac{{{{F}_{n}}}}{{{{k}_{n}}{{Y}_{n}}}}{{e}^{{i\xi (x - {{x}_{0}})}}}d\xi } $

где ${{\kappa }_{n}} = \frac{{\pi n}}{L}$, ${{k}_{n}} = + \sqrt {\kappa _{n}^{2} + {{\xi }^{2}}} $

(5.4)

${{Y}_{n}} = ({{D}_{n}}{{e}^{{ - {{k}_{n}}h}}} - {{e}^{{{{k}_{n}}h}}}) - ({{D}_{n}}{{e}^{{ - {{k}_{n}}h}}} + {{e}^{{{{k}_{n}}h}}}){\text{th}}\left( {{{k}_{n}}(H - h)} \right)$

(5.5)

${{F}_{n}} = \left\{ \begin{gathered} {{D}_{n}}{{e}^{{{{k}_{n}}z}}} + {{e}^{{ - {{k}_{n}}z}}},\quad - h < z < 0 \hfill \\ \frac{{{\text{ch}}\left( {H + z} \right)}}{{{\text{ch}}\left( {H - h} \right)}}({{D}_{n}}{{e}^{{ - {{k}_{n}}h}}} + {{e}^{{{{k}_{n}}h}}}),\quad - H < z < - h \hfill \\ \end{gathered} \right.$

(5.6)

${{D}_{n}} = \frac{{{{k}_{n}}g + {{\omega }^{2}}}}{{{{k}_{n}}g - {{\omega }^{2}}}}$

Интегрирование в (5.3) производится по действительной оси, полюсы, лежащие на действительной оси, обходятся снизу.

Упростим задачу, полагая канал достаточно глубоким, чтобы для всех n выполнялось условие

$\left| {{{k}_{n}}(H - h)} \right| \gg 1$

Тогда (5.4) и (5.5) преобразуются к виду

$\frac{{{{F}_{n}}}}{{{{Y}_{n}}}} = - \frac{1}{2}({{D}_{n}}{{e}^{{{{k}_{n}}(z - h)}}} + {{e}^{{ - {{k}_{n}}(z + h)}}}),\quad - h < z < 0$

Найдем сопротивление излучения монополя, расположенного на оси канала, т.е. ${{y}_{0}} = L{\text{/}}2$, для чего вычислим мнимую часть потенциала (5.3) в точке $({{x}_{0}},{{y}_{0}}, - h)$. Поскольку при x = x₀ подынтегральные выражения в (5.3) действительны, а интегрирование также ведется по действительной оси, то мнимая часть потенциала определяется только полувычетами в полюсах, лежащих на действительной оси. Из (5.6) находим полюсы, расположенные в точках

(5.7)

${{\xi }_{n}} = \frac{{{{\omega }^{2}}}}{g}\sqrt {1 - {{{\left( {\frac{{\pi g}}{{L{{\omega }^{2}}}}2n} \right)}}^{2}}} $

При этом на действительной оси лежат только те полюсы, для которых выполняется условие

(5.8)

$\frac{{\pi g}}{{L{{\omega }^{2}}}}2n < 1$

Вычислив вычеты в полюсах (5.7), находим мнимую часть потенциала

$\operatorname{Im} \varphi = - \frac{q}{L}{{e}^{{ - 2{{\omega }^{2}}{h \mathord{\left/ {\vphantom {h g}} \right. \kern-0em} g}}}}\left( {1 + \sum\limits_{n = 1}^{n'} {\frac{2}{{\sqrt {1 - {{{({{2\pi ng} \mathord{\left/ {\vphantom {{2\pi ng} {L{{\omega }^{2}}}}} \right. \kern-0em} {L{{\omega }^{2}}}})}}^{2}}} }}} } \right)$

где $n{\text{'}}$ – максимальное целое число, удовлетворяющее (5.8). Запишем сопротивление излучения монополя в канале $\operatorname{Re} {{Z}_{c}}$ следующим образом

$\frac{{\operatorname{Re} {{Z}_{c}}}}{{\operatorname{Re} Z}} = \frac{2}{{kL}}\left( {1 + \sum\limits_{n = 1}^{n'} {\frac{2}{{\sqrt {1 - {{{\left( {{{2\pi n} \mathord{\left/ {\vphantom {{2\pi n} {kL}}} \right. \kern-0em} {kL}}} \right)}}^{2}}} }}} } \right) = {{\Gamma }_{0}}(kL)$

где $\operatorname{Re} Z$ – сопротивление излучения монополя в свободном пространстве (2.5).

Согласно (2.6), (2.8) сечение поглощения обратно пропорционально сопротивлению излучения, поэтому сечение поглощения монопольного резонатора в канале имеет вид

${{\sigma }_{{0,c}}} = \frac{{{{\sigma }_{0}}}}{{{{\Gamma }_{0}}(kL)}}$

В узком канале $kL \ll 1$ сечение поглощения составляет ${{\sigma }_{{0,c}}} = {{kL{{\sigma }_{0}}} \mathord{\left/ {\vphantom {{kL{{\sigma }_{0}}} 2}} \right. \kern-0em} 2} = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}$, т.е. монопольный резонатор поглощает половину мощности падающей волны. С увеличением ширины канала сечение поглощения увеличивается, достигая максимального значения ${{\sigma }_{{0,c}}} = \pi {{\sigma }_{0}} = {\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right. \kern-0em} 2}$ при $kL \to 2\pi $.

Аналогично находим сечение поглощения дипольного резонатора, момент которого направлен вдоль оси канала, продифференцировав поле монополя (5.3),

${{\sigma }_{{1,c}}} = \frac{{{{\sigma }_{1}}}}{{{{\Gamma }_{1}}(kL)}},\quad {{\Gamma }_{1}}(kL) = \frac{4}{{kL}}\left( {1 + 2\sum\limits_{n = 1}^{n'} {\sqrt {1 - {{{\left( {\frac{{2\pi }}{{kL}}n} \right)}}^{2}}} } } \right)$

В узком канале $kL \ll 1$ сечение поглощения составляет ${{\sigma }_{{1,c}}} = {{kL{{\sigma }_{1}}} \mathord{\left/ {\vphantom {{kL{{\sigma }_{1}}} 4}} \right. \kern-0em} 4} = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}$, т.е. дипольный резонатор также поглощает половину мощности падающей волны.

На рис. 2 представлены сечения поглощения монополя и диполя в канале, нормированные на 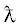, в зависимости от ширины канала $kL$.

Рис. 2.

Сечение поглощения монополя 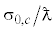(сплошная кривая) и диполя 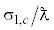(пунктирная кривая) в канале в зависимости от его ширины L.

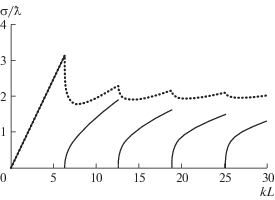
Поля монопольного и дипольного резонатора ортогональны, поэтому при одновременном использовании этих резонаторов их суммарное сечение поглощения равно ${{\sigma }_{{0,c}}} + {{\sigma }_{{1,c}}} = L$ при $kL < 2\pi $, т.е. плоская гравитационная волна, распространяющаяся в канале, ширина которого не превышает длину волны, может быть полностью поглощена при одновременном использовании монопольного и дипольного резонаторов. Аналогичные результаты получены ранее для монопольно-дипольных резонаторов, полностью поглощающих звуковую волну в трубах [16], изгибную волну в стержнях [17] и рэлеевскую волну на поверхности твердого тела [18].

Необходимо отметить, что волны на поверхности жидкости часто бывают нелинейными [19, 20], что требует уточнения расчета резонансного сечения поглощения гравитационных волн.

ЗАКЛЮЧЕНИЕ

Вычислено максимально возможное сечение поглощения гравитационной волны на поверхности жидкости рассеивателем малого волнового размера, расположенного на произвольной глубине. Оно достигается при импедансе рассеивателя, обеспечивающего выполнение резонансных условий поглощения, и поэтому называется резонансным. Резонансное сечение поглощения зависит только от длины гравитационной волны λ. Для монопольного рассеивателя оно составляет ${\lambda \mathord{\left/ {\vphantom {\lambda {2\pi }}} \right. \kern-0em} {2\pi }}$ и не зависит от направления распространения волны. Для мультипольных рассеивателей ненулевого порядка максимальное значение резонансного сечения поглощения по всем направлениям составляет λ/π.

Для полного поглощения гравитационной волны, распространяющейся в канале, ширина которого не превышает длину волны, достаточно двух резонаторов, один из которых является монополем, а другой – диполем.

Список литературы

Pelc R., Fujita R.M. Renewable energy from the ocean // Mar. Policy. 2002. V. 26. № 6. P. 471–479. https://doi.org/10.1016/S0308-597X(02)00045-3
Drew D., Plummer A.R., Sahinkaya M.N. A review of wave energy converter technology // Proc. IMechE. 2009. V. 223. P. 887–902. https://doi.org/10.1243/09576509JPE782
Shami E., Zhang R., Wang X. Point Absorber Wave Energy Harvesters: A Review of Recent Developments // Energies. 2019. V. 12. № 1. P. 47. https://doi.org/10.3390/en12010047
Falnes J. Ocean Waves and Oscillating Systems. Cambridge: University Press, 2004. 275 p.
Zheng S., Porter R., Greaves D. Wave scattering by an array of metamaterial cylinders // J. Fluid Mech. 2020. V. 903. A50. https://doi.org/10.1017/jfm.2020.660
Калиниченко В.А. Подавление интенсивных колебаний жидкости слоем плавающих частиц // Изв. РАН. МЖГ. 2020. № 6. С. 85–97. https://doi.org/10.31857/S0568528120060067
Budal K., Falnes J. A resonant point absorber of ocean waves // Nature. 1975. V. 256. P. 478–479.
Evans D.V. A theory for wave-power absorption by oscillating bodies // J. Fluid Mech. 1976. V. 77. P. 1–25.
Исакович М.А. Общая акустика. М.: Наука, 1973. 436 с.
Канев Н.Г., Миронов М.А. Дипольный резонансный рассеиватель звука // Акуст. журн. 2003. Т. 49. № 3. С. 372–375.
Арабаджи В.В. Поглощение длинных волн линейными структурами // Акуст. журн. 2010. Т. 56. № 6. С. 739–746.
Лапин А.Д. Сечение рассеяния резонатора в многомодовом волноводе // Акуст. журн. 2011. Т. 57. № 3. С. 303–306.
Лапин А.Д. Поперечники рассеяния и поглощения резонатора для продольных и сдвиговых волн в пластинах // Акуст. журн. 1988. Т. 34. № 3. С. 543–545.
Лапин А.Д. Поперечник рассеяния резонатора для поверхностной рэлеевской волны // Акуст. журн. 1991. Т. 37. № 1. С. 202–205.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986. 736 с.
Канев Н.Г., Миронов М.А. Монопольно-дипольный резонансный поглотитель в узком волноводе // Акуст. журн. 2005. Т. 51. № 1. С. 111–116.
Лапин А.Д. Резонатор монопольно-дипольного типа для изгибных волн в стержне // Акуст. журн. 2004. Т. 50. № 1. С. 90–93.
Лапин А.Д. Рассеяние рэлеевской волны монопольно-дипольными резонаторами // Акуст. журн. 2007. Т. 53. № 1. С. 15–19.
Якимов A.Ю. Уравнения для нелинейных волн на мелкой воде // Изв. РАН. МЖГ. 2012. № 6. С. 122–125.
Миндлин И.М. Волны на воде: теории и эксперименты // Изв. РАН. МЖГ. 2020. № 4. С. 69–81. https://doi.org/10.31857/S0568528120030093

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал