1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 5, 2021

Известия РАН. Механика жидкости и газа, 2021, № 5, стр. 61-75

ГИДРОДИНАМИЧЕСКОЕ ДЕМПФИРОВАНИЕ КОЛЕБАНИЙ БАЛОК ВБЛИЗИ ЭКРАНА

А. М. Камалутдинов a, *, А. Н. Нуриев b

a Казанский национальный исследовательский технический университет им. А.Н. Туполева
Казань, Россия

b Казанский (Приволжский) федеральный университет
Казань, Россия

* E-mail: amkamalutdinov@mail.ru

Поступила в редакцию 21.12.2020
После доработки 09.03.2021
Принята к публикации 23.03.2021

Полный текст (PDF)

Аннотация

Проводится исследование гидродинамического воздействия на длинные тонкие балки, совершающие изгибные резонансные колебания в жидкости вблизи плоской жесткой поверхности (экрана). Используется модель квазиплоского взаимодействия между жидкостью и балкой, согласно которой гидродинамическое воздействие, оказываемое на каждое сечение балки, можно считать результатом его плоского обтекания. Движение жидкости в плоскостях ортогональных оси балки моделируется с помощью нестационарной системы уравнений Навье–Стокса, решение которой проводится численно на основе метода конечных объемов. Решения строятся в широком диапазоне изменения управляющих параметров колебательного процесса: безразмерной частоты, амплитуды колебаний и расстояния до экрана. Полученные зависимости для гидродинамических сил используются для оценки влияния эффекта экрана на колебания консолей с реальными физическими параметрами.

Ключевые слова: изгибные колебания балки, гидродинамическое демпфирование, вязкая несжимаемая жидкость, эффект экрана, численное моделирование

Исследования аэро-гидродинамических эффектов, возникающих при упругих колебаниях удлиненных балочных конструкций малого размера стали активно развиваться в последние два десятилетия в связи с появлением целого ряда перспективных технологических решений с применением пьезоактуаторов изгиба. Благодаря своей энергоэффективности и мобильности пьезоактуаторы успешно внедряются в области робототехники, как движители автономных подводных и летательных аппаратов, как охлаждающие системы и харвестеры в микроэлектронике, в качестве элементов насосов в микрофлюидных устройствах и т.д.

Течения жидкости, индуцированные колебаниями балок, проводят к динамическому изменению собственных частот резонанса, к нелинейному демпфированию колебаний, к появлению постоянного силового воздействия (тяги и подъемной силы) и др. эффектам, влияющим на режимы работы таких систем.

С точки зрения теории упругости системы на основе пластинчатых (ленточных) пьезоактуаторов изгиба представляют собой удлиненные балочные конструкции с характерными размерами от десятка микрон до двух-трех десятков сантиметров, которые совершают резонансные колебания, главным образом по первой изгибной моде с частотой от 5 до 200 Гц. Многочисленные исследования (см., например, [1–4]) показывают, что колебания таких конструкций в условиях малости перемещений хорошо описываются классической теорией Эйлера–Бернули при известных параметрах материала и заданной внешней распределенной аэро-гидродинамической нагрузки. В рассматриваемых случаях тонких балок внешняя нагрузка в значительной степени влияет на процесс колебания, а для некоторых материалов (с низким внутренним трением) является абсолютно преобладающей. Аэро-гидродинамические силы, создаваемые течениями (несжимаемой, при рассматриваемых значениях параметров) жидкости, образованными в результате колебаний, даже при относительно малых амплитудах, являются нелинейными функциями нескольких параметров (в том числе параметров колебания), по этой причине их определение является чрезвычайно сложной задачей.

Основой большинства современных моделей гидродинамического воздействия на балку является квазиплоская гипотеза, согласно которой аэро-гидродинамическое воздействие, оказываемое на каждое сечение балки, можно считать результатом его плоского обтекания. Это позволяет использовать результаты обтекания гармонически осциллирующих твердых цилиндрических тел, полученных в ходе численных расчетов или гидродинамических экспериментов, для определения параметров аэродинамического воздействия на балки. Этот метод получил свое развитие в работах [2, 3, 5–11].

Теория обтекания гармонически осциллирующих твердых цилиндрических тел, на которую опирается квазиплоская теория, в свою очередь достаточно хорошо развита для случая колебаний в безграничной жидкости. Ключевые результаты получены в рамках экспериментальных и численных исследований. Экспериментальный блок составляют классические [12–17] и современные работы [8, 9, 18]. В ходе многочисленных экспериментов с цилиндрическими телами различного сечения было установлено, что ключевыми параметрами подобия течений около колеблющихся тел (в безграничной жидкости), имеющих одинаковые геометрические характеристики, являются следующие комплексы

(0.1)
$KC = 2\pi \frac{{{{U}_{0}}}}{{b\omega }} = 2\pi \frac{A}{b},\quad \beta = \frac{{{{b}^{2}}\omega }}{{2\pi \nu }}$

Здесь A, ${{U}_{0}} = A\omega $ – амплитуда колебаний и амплитуда скорости колебаний, b – ширина пластины, ω – угловая частота, $\nu $ – вязкость жидкости. Параметр KC – число Келегана–Карпентера – характеризует безразмерную амплитуду колебаний. Согласно результатам [15] этот параметр практически полностью определят решение задачи при больших амплитудах колебания. Второй параметр (β) часто называют числом Стокса или колебательным числом Рейнольдса, он характеризует безразмерную частоту колебаний. Значительное влияние этого параметра на осциляционный процесс проявляется при малых и умеренных амплитудах.

Наряду с экспериментальными исследованиями достаточно продолжительное время развиваются методы численного решения задачи обтекания гармонически осциллирующей тонкой пластины. Значительных успехов численное моделирование принесло в области малых амплитуд колебания. В работах [1–3] на базе традиционных сеточных моделей проведено решение задачи о колебании прямоугольных пластин в диапазоне изменения параметров $0.1 \leqslant \Delta \leqslant 1$, $0.003 \leqslant KC \leqslant 0.3$. Полученные результаты описывают начало развития нелинейных гидродинамических эффектов около пластины и их влияние на гидродинамические силы. В диапазоне больших амплитуд $0.2 \leqslant KC \leqslant 9$ динамика жидкости около пластин численно исследовалась в работах [19–21]. В ходе этих исследований описаны характерные структуры течений, формирующиеся около пластин, построена карта режимов течения, изучены зависимости гидродинамических сил от формы пластин и от параметров колебания.

Во всех представленных выше работах изучались колебания, происходящие в безграничной вязкой несжимаемой жидкости. В случае колебания тела вблизи другой поверхности (твердой или упругой) аэро-гидродинамика течения меняется (см., например, [22–29]). В частности, наличие жесткого экрана около балки значительно повышает аэро-гидродинамическое воздействие на нее. Несмотря на то что именно эти случаи имеют большое практическое значение, исследований в этой области проведено значительно меньше.

В настоящей работе рассмотрена задача об изгибных колебаниях балки в жидкости параллельно жесткому экрану. Решение этой задачи проводилось ранее в [30] в стоксовском приближении. Результаты этого исследования охватывают лишь диапазон самых малых амплитуд колебания $KC \ll 1$. В рамках настоящего исследования рассмотрено гидродинамическое воздействие на балку в существенно более широком амплитудном диапазоне $0.1 \leqslant KC < 7$. Для учета силового воздействия жидкости проводится численное решение полной нестационарной системы уравнений Навье–Стокса, описывающей движение жидкости, индуцированные колебаниями балки.

1. ПОСТАНОВКА ЗАДАЧИ

1.1. Модель колебания балки

Проведем исследование гидродинамического воздействия на тонкие длинные балки ($L \gg b \gg h$, где $L$, b, $h$ соответственно длина, ширина и толщина балок), совершающие изгибные колебания около жесткого экрана. Рассмотрим случай, когда плоскость изгиба расположена параллельно плоскости экрана. Предполагая справедливость основных положений теории Эйлера–Бернулли, запишем уравнение движения балки в следующем виде

(1.1)
$\rho S\frac{{{{\partial }^{2}}\tilde {w}}}{{\partial {{{\tilde {t}}}^{2}}}} + EJ\frac{{{{\partial }^{4}}\tilde {w}}}{{\partial {{{\tilde {z}}}^{4}}}} = \tilde {H}(\tilde {z},\tilde {t}) + \tilde {F}(\tilde {z},\tilde {t})$
где $\tilde {w}$ – смещение средней линии балки в направлении оси $O\tilde {x}$; S – площадь сечения балки; $\rho $, E – эффективные плотность и модуль Юнга материала балки; J – осевой момент инерции; $\tilde {H}$ – силы внутреннего трения; $\tilde {F}$ – гидродинамические силы, действующие в направлении оси $O\tilde {x}$. Здесь и далее тильдой отмечены размерные переменные.

Рассмотрим свободные и вынужденные колебания консольно защемленных балок. Граничные и начальные условия для этих случаев можно определить следующим образом

(1.2)
$\tilde {w}(0,\tilde {t}) = {{A}_{0}}sin(\omega \tilde {t}),\quad \frac{{\partial{ \tilde {w}}}}{{\partial{ \tilde {z}}}}(0,\tilde {t}) = 0,\quad \frac{{{{\partial }^{2}}\tilde {w}}}{{\partial {{{\tilde {z}}}^{2}}}}(L,\tilde {t}) = 0,\quad \frac{{{{\partial }^{3}}\tilde {w}}}{{\partial {{{\tilde {z}}}^{3}}}}(L,,\tilde {t}) = 0$
$\tilde {w}(\tilde {z},0) = {{A}_{L}}W(\tilde {z}{\text{/}}L)$

Здесь ${{A}_{L}}$ – начальное отклонение свободного конца балки от положения равновесия; A0 – амплитуда колебаний защемленного конца балки; ω – угловая частота колебаний; $W(\xi )$ – профиль резонансных колебаний балки по первой моде в вакууме

$W(\xi ) = \frac{1}{2}\left( {cos(k\xi ) - cosh(k\xi ) + \frac{{sink - sinhk}}{{cosk + coshk}}\left( {sin(k\xi ) - sinh(k\xi )} \right)} \right)$
где $k = 1.875$ наименьший положительный корень характеристического уравнения $coskcoshk$ = = –1. Для свободных колебаний амплитуда колебаний защемленного конца считается равной нулю A0 = 0, для вынужденных колебаний начальное отклонение свободного конца балки от положения равновесия считается равным нулю AL = 0.

1.2. Модель расчета гидродинамического воздействия

Полагаем, что обтекание каждого поперечного сечения балки ($\tilde {z} = {\text{const}}$) происходит независимо от других, т.е. выполняется квазиплоская гипотеза (см., например, [8]). В этом случае задача определения гидродинамического воздействия на балку $\tilde {F}(\tilde {z},\tilde {t})$ сводится к серии однотипных плоских задач определения гидродинамических сил, действующих на двумерный профиль сечения балки.

Пусть двумерный профиль сечения балки совершает гармонические колебания в плоскости $\tilde {x}O\tilde {y}$ со скоростью

${{U}_{p}} = {{U}_{0}}cos(\omega \tilde {t})$

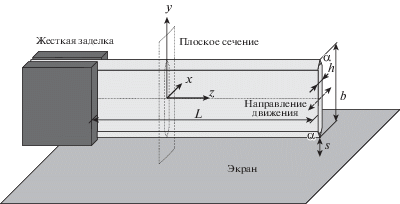
На рис. 1 представлена схема движения такого сечения балки в жидкости. Поперечные сечения балки имеют форму усеченного прямоугольника с соотношением сторон $\Delta = h{\text{/}}b = 1{\text{/}}10$ и углом при вершине α = 60°. Длинная сторона профиля сечения балки b располагается перпендикулярно экрану. Колебания происходят параллельно экрану. Характерное расстояние от балки до экрана определяется как $\sigma = s{\text{/}}b$.

Рис. 1.

Геометрия задачи.

Решение гидродинамической задачи проводится в подвижной декартовой системе координат, жестко связанной с профилем. Направление осей зададим таким образом, чтобы ось колебания совпадала с осью $O\tilde {x}$. Проводя нормировку пространственных координат, времени и скорости на b, $bU_{0}^{{ - 1}}$, –U0 соответственно, запишем систему уравнений движения жидкости в следующем виде

$\begin{gathered} \frac{{\partial {\mathbf{U}}}}{{\partial t}} + {\mathbf{U}} \cdot \nabla {\mathbf{U}} = - \nabla p + \frac{1}{{KC\beta }}{{\nabla }^{2}}{\mathbf{U}} \\ \nabla \cdot {\mathbf{U}} = 0 \\ \end{gathered} $

Здесь ${\mathbf{U}} = (u,{v})$ – безразмерная скорость, p – фиктивное давление, равное сумме истинного давления $\hat {p}$ и инерционной составляющей $\bar {p}$, которая возникает в результате перехода в подвижную систему координат (см., например, [31]) и может быть определена как

(5)
$\bar {p} = x\frac{{2\pi }}{{KC}}sin\left( {\frac{{2\pi }}{{KC}}t} \right)$

Безразмерные параметры $\beta $ и KC определены в соответствии с формулами (0.1).

На профиле в новой системе координат задаются условия прилипания

${{u}_{\Omega }} = {{{v}}_{\Omega }} = 0$

На бесконечном удалении от сечения балки и на экране изменение скорости определяется по следующему гармоническому закону

${{u}_{\infty }} = cos\left( {\frac{{2\pi }}{{KC}}t} \right),\quad {{{v}}_{\infty }} = 0$

Вычисление гидродинамической силы, действующей на сечение балки со стороны жидкости в направлении оси колебания, в представленной безразмерной постановке проводится по формулам

$F = \left( {\int\limits_\Omega p {\mathbf{n}}ds - \int\limits_\Omega {\overline \Sigma } \cdot {\mathbf{n}}ds} \right) \cdot {\mathbf{i}}$
где $\overline \Sigma $ – тензор вязких напряжений, $\Omega $ – граница профиля, n – внутренняя единичная нормаль к границе профиля, i – единичный вектор в направлении оси колебания. Заметим, что вычисленная в подвижной системе координат сила определена по фиктивному давлению и поэтому содержит вклад от инерционной составляющей $\bar {p}$, определенный согласно (1.3). Он может быть вычислен следующим образом

(1.3)
${{F}_{{kf}}} = \frac{{2\pi }}{{KC}}sin\left( {\frac{{2\pi }}{{KC}}t} \right)\int\limits_\Omega x {\mathbf{n}}ds \cdot {\mathbf{i}}$

Эта составляющая известна также как сила Крылова–Фруда.

2. ЧИСЛЕННОЕ РЕШЕНИЕ ГИДРОДИНАМИЧЕСКОЙ ЗАДАЧИ

2.1. Численная модель

Для решения гидродинамической задачи была адаптирована численная модель, разработанная в [21] на базе пакета OpenFOAM. Плоскость течения ограничивалась прямоугольной областью, стороны которой устанавливались параллельно осям координат. Расстояние от центра профиля до удаленных внешних границ (моделируемой бесконечности) задавалось равным 30, что, согласно результатам [21], достаточно для минимизации их влияния. Кроме того, на удаленных границах, расположенных параллельно плоскости колебания, задавались условия проскальзывания.

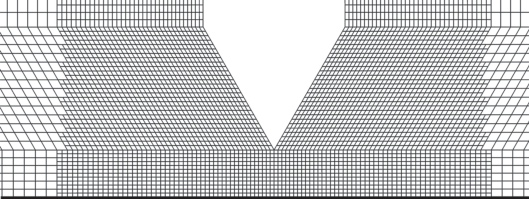
Для дискретизации расчетной области использовались блочные сетки, ячейки которых в плоскости течения имели четырехгранную форму. Разрешающая способность сеток вблизи профиля регулировалась за счет линейного сгущения узлов в направлении нормалей к сторонам профиля, а также последовательного дробления ячеек в окрестности его границы (рис. 2).

Рис. 2.

Структура расчетной сетки в окрестности торца балки, расположенного около экрана.

Основные параметры применяемых стандартных расчетных сеток для разных значений $\sigma $ представлены в табл. 1, где N – общее количество ячеек, Vmin – минимальным объемом ячеек в пограничном слое пластины, Np – количеством ячеек на границе пластины, Vmax – максимальным объемом ячеек в области.

Таблица 1.

Параметры стандартных расчетных сеток $M(h*)$ для разных значений $\sigma $

σ N Vmin Vmax Np
∝ 20 × 104 2.95 × 10–5 1.18 590
0.5 16 × 104 2.95 × 10–5 1.18 590
0.1 13 × 104 2.95 × 10–5 1.18 590

Дискретизация системы уравнений движения жидкости проводилась по методу конечных объемов (FVM) в декартовой системе координат. Дискретные значения составляющих скорости и дискретные давления локализовались в центрах ячеек расчетных сеток. Для вычисления объемных интегралов по контрольному объему использовалась общая процедура Гаусса. Для аппроксимации градиента давления в расчетах применялась линейная интерполяция. В диффузионных слагаемых при дискретизации оператора Лапласа нормальные градиенты скорости на поверхности ячейки аппроксимировались с помощью симметричной схемы второго порядка с поправкой на неортогональность [32].

Для интерполяции переменных в конвективных слагаемых использовалась гибридная схема Спалдинга, предложенная в работах [33, 34] (аналог широко применяемой в конечно-элементной дискретизации схемы SUPG [35]). Она представляет собой комбинацию линейной и противопоточной интерполяций. Линейная интерполяция применяется в области, где сеточное число Рейнольдса (или число Пекле) ${\text{R}}{{{\text{e}}}_{h}} < 2$. В остальных случаях используется противопоточная интерполяция. Как показывают результаты [36–39], для рассматриваемого класса задач, гибридная схема обеспечивает хорошее согласование численных результатов с экспериментальными данными в широком диапазоне чисел Рейнольдса.

Для дискретизации системы уравнений по времени используется неявная схема Эйлера. Шаг по времени во всех расчетах являлся постоянной удовлетворяющей двум условиям: 1) максимальное число Куранта не превышает значения 0.1; 2) минимальное число шагов за период должно быть не менее 500.

Решение дискредитированной задачи проводилось с помощью метода PISO [40, 41]. Решение системы уравнений для давления выполнялось на основе метода сопряженных градиентов (PCG) с геометро-алгебраическим многосеточным предобуславливателем (GAMG). Системы уравнений для компонент скорости решались методом бисопряженных градиентов (PBiCG) с предиктором на основе неполной LU факторизации. Расчеты выполнялись распределенным образом по технологии MPI с применением метода декомпозиции области решения.

2.2. Верификация численной схемы

Для оценки точности проводимых расчетов для случая $\beta = 300$, $KC = 0.5$, $\sigma = 0.1$ был выполнен анализ сеточной сходимости. Для этого в расчетной области были построены две вспомогательные сетки, на одной из которых размеры ячеек были пропорционально уменьшены в $1.25$ раза, на другой увеличены в $1.25$ раза (по каждому направлению) по сравнению со стандартной сеткой. Соответствующие сетки далее будем обозначать $M(h*)$ (стандартная сетка), $M(h{\text{*/}}1.25)$ (точная сетка) и M(1.25h*) (грубая сетка). Результаты сопоставления расчетных данных, полученных на этих сетках, представлены в табл. 2, где отображены локальные максимальные значения силы $F$ на разных периодах.

Таблица 2.

Вычисленные локальных максимальных значений силы F за период ${{T}_{{num}}}$ (${{T}_{{num}}} - 1 < t{\text{/}}T \leqslant {{T}_{{num}}}$) на разных сетках

Tnum 5 10 15 20 30 50 70 100
M(1.25h*) 31.706 31.64 31.63 31.62 31.625 31.64 31.645 31.6
M(h*) 31.79 31.72 31.7 31.695 31.7 31.71 31.72 31.72
M(h*/1.25) 31.82 31.75 31.725 31.72 31.72 31.74 31.745 31.75

Как можно видеть максимальные значения гидродинамической силы, полученные на разных сетках, отличаются менее чем на 3–4%. При этом разница между значениями, вычисленными на сетках $M(h*)$ и $M(h{\text{*/}}1.25)$, меньше чем на сетках $M(h*)$ и $M(1.25h*)$, что свидетельствует о сеточной сходимости решения.

3. СТРУКТУРА ГИДРОДИНАМИЧЕСКИХ СИЛ, ДЕЙСТВУЮЩИХ НА БАЛКУ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ

Решение гидродинамической задачи проводилось в следующем диапазоне параметров: $200 \leqslant \beta \leqslant 500$, $0.05 \leqslant \sigma < \infty $, $0.1 \leqslant KC < 7$. В этом диапазоне наблюдаются хорошо структурированные периодические (и квазипериодические) течения, оказывающие соответственно периодическое (квазипериодическое) воздействие на профиль вдоль оси колебания.

Для анализа продольной составляющей силы (F) будем использовать разложение Морисона [42]. Cила F представляется в виде суммы силы сопротивления (демпфирования), пропорциональной квадрату скорости, и силы инерции, пропорциональной ускорению осцилляционного движения

(3.1)
$F = \frac{\pi }{2}{{C}_{M}}\frac{{d{{u}_{\infty }}}}{{dt}} + {{C}_{D}}\left| {{{u}_{\infty }}} \right|{{u}_{\infty }}$

Вычисление гидродинамических коэффициентов ${{C}_{D}}$, ${{C}_{M}}$ будем проводить на каждом периоде колебания T с помощью интегрирования

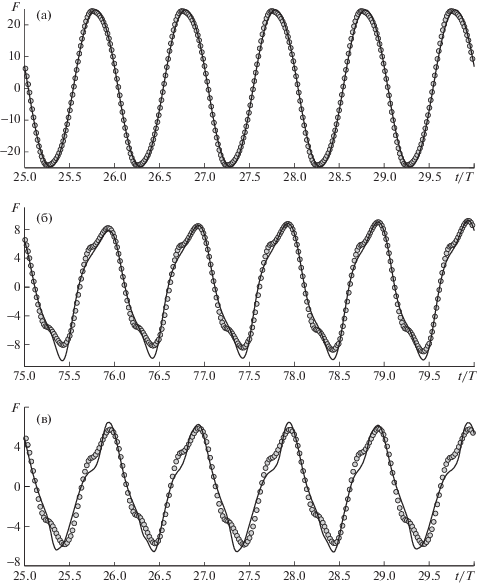
${{C}_{M}} = - \frac{2}{{{{\pi }^{2}}}}\int\limits_{{{t}_{0}}}^{T + {{t}_{0}}} {{{F}_{x}}} sin\left( {\frac{{2\pi }}{{KC}}t} \right)dt,\quad {{C}_{D}} = \frac{{3\pi }}{{4T}}\int\limits_{{{t}_{0}}}^{T + {{t}_{0}}} {{{F}_{x}}} cos\left( {\frac{{2\pi }}{{KC}}t} \right)dt$

На рис. 3 представлены графики изменения гидродинамической силы за несколько периодов, и результаты аппроксимации соответствующих данных. Как можно видеть, при малых значениях безразмерной амплитуды в сигнале F (см. рис. 3, a) в основном присутствует только главная гармоника. Основной вклад дают инерциальные силы, пропорциональные ускорению движения. При $KC = 0.5$ их доля составляет более 80%. С ростом KC вклад инерциальных сил уменьшается, а в сигнале появляются гармоники, отличные от главной.

Рис. 3.

Гидродинамические силы, действующие на балку в сечениях при $\beta = 300$: (а–в) – $KC = 0.5,\;2.5,\;6$. Сплошными линиями изображены результаты расчетов, маркерами – аппроксимация Морисона.

Амплитудный спектр $F$ при больших амплитудах колебания ($KC = 5$) представлен на рис. 4 для разных значений параметра $\sigma $. По горизонтали отложены номера гармоник (m) разложения силы F в ряд Фурье, по вертикали отношение модуля комплексной амплитуды соответствующей гармоники ($Am{{p}_{m}}$) к модулю амплитуды основной гармоники ($Am{{p}_{1}}$), соответствующей частоте колебаний балки. Как можно видеть, на большом расстоянии от экрана гидродинамическая сила содержит в основном нечетные гармоники ($m = 1,3,5$). Это в точности соответствует структуре аппроксимационной зависимости (ее волновому спектру). На малых расстояниях (см. данные для $\sigma = 0.1$) появляется ярко выраженный вклад второй и четвертой гармоник ($m = 2,4$). Для этого случая аппроксимация Морисона работает хуже, поскольку она не может описывать вклады четных гармоник, тем не менее, даже здесь разность между численными данными и аппроксимацией остается невысокой.

Рис. 4.

Амплитудный спектр $F$ при $\beta = 200$, $KC = 5$ для разных значений параметра $\sigma $: 1–4 – $\sigma = \infty ,\;0.5,\;0.1$, $\infty $ (аппроксимация).

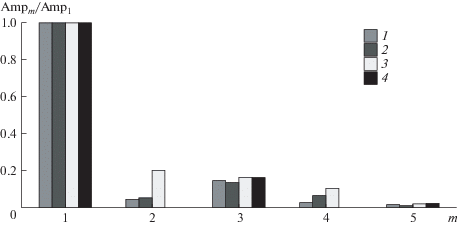
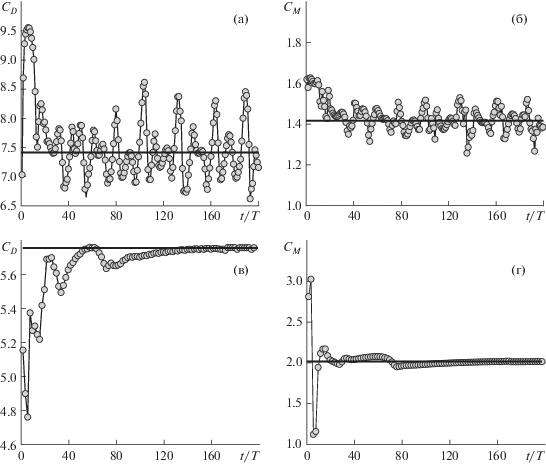
Изменение гидродинамических коэффициентов ${{C}_{D}}$, ${{C}_{M}}$, вычисленных на каждом периоде для разных значений KC, представлено на рис. 5. Показано два характерных случая: 1) полностью периодическое течение, наблюдаемое при $KC = 6$, и 2) квазипериодическое течение, наблюдаемое при $KC = 2.5$. В первом случае ${{C}_{D}}$ и ${{C}_{M}}$ со временем выходят на постоянные значения, которые используются далее для оценки характерного гидродинамического воздействия при соответствующих параметрах колебания. Для квазипериодических режимов течения (характеризуется медленным цикличным преобразованием структуры течения за несколько периодов колебания) значения коэффициентов изменяются от периода к периоду. В этом случае для оценки характерного гидродинамического воздействия проводился расчет осредненных значений коэффициентов за последние 50 периодов колебания (в которые попадают несколько таких циклов).

Рис. 5.

Зависимости коэффициентов сопротивления и инерции от периода колебания при $\beta = 300$, $\sigma = \infty $: (а, б) – KC = 2.5, (в, г) – KC = 6.

4. ЗАВИСИМОСТЬ КОЭФФИЦИЕНТОВ ГИДРОДИНАМИЧЕСКИХ СИЛ ОТ ПАРАМЕТРОВ КОЛЕБАНИЯ И РАССТОЯНИЯ ОТ ЭКРАНА

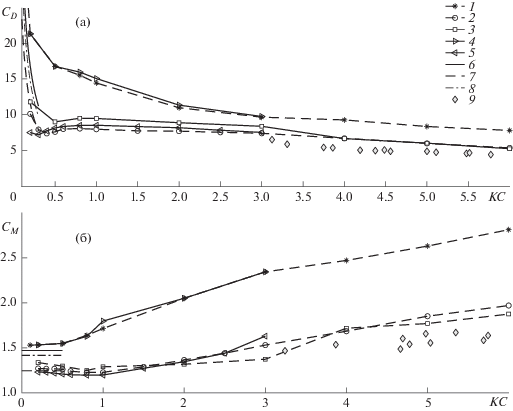
Рассмотрим изменения коэффициентов инерциальных и демпфирующих сил от параметров колебания сечения и расстояния от экрана. Кривые зависимостей ${{C}_{D}}(KC)$, ${{C}_{M}}(KC)$ для разных значений β и $\sigma $ изображены на рис. 6. Помимо результатов настоящей работы, на рисунках показаны известные экспериментальные [14] и аналитико-численные данные [1, 30], полученные в предыдущих исследованиях.

Рис. 6.

Графики зависимостей (а) ${{C}_{D}}(KC)$, (б) ${{C}_{M}}(KC)$ для разных значений параметров $\beta $ и $\sigma $: 1 – $\sigma = 0.1$, $\beta = 200$, 2 – $\sigma = \infty $, $\beta = 200$, 3 – $\sigma = 0.5$, $\beta = 200$, 4 – $\sigma = 0.1$, $\beta = 300$, 5 – $\sigma = \infty $, $\beta = 500$, 6 – $\sigma = 0.1$, $\beta = 200$ [30], 7 – $\sigma = 0.5$, $\beta = 200$ [30], 8 – $\sigma = 0.1$, $\beta = 300$ [30], 9 – $\sigma = \infty $, $\beta \approx 1600$ [14].

В диапазоне малых амплитуд зависимости ${{C}_{D}}(KC,\beta ,\sigma )$, ${{C}_{M}}(KC,\beta ,\sigma )$ хорошо описываются в рамках стоксовской асимптотики. Решение гидродинамической задачи в этом приближении получено в [1, 43] (колебания в безграничной жидкости) и [30] (колебания вблизи экрана). Гидродинамические силы, действующие на колеблющееся тело, в этих исследованиях определены численно с помощью метода граничных элементов, а конечные численные данные обобщены с помощью аппроксимаций. Для безграничной жидкости аппроксимация записывается как

$KC \to 0,\quad \sigma \to \infty {\text{:}}\quad {{C}_{D}} = 28.97{\text{/}}(KC\sqrt \beta ),\quad {{C}_{M}} = 1.02 + 2.45{{\beta }^{{ - 1/2}}}$

Структура аппроксимационной зависимости для случая колебаний около экрана, предложенная [30], имеет существенно более сложную форму

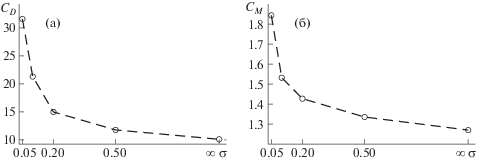
$KC \to 0{\text{:}}\quad {{C}_{D}} = K{{C}^{{ - 1}}}\sum\limits_{i = 0}^5 {\sum\limits_{j = 0}^5 {{{A}_{{ij}}}} } \beta _{l}^{i}\sigma _{l}^{j},\quad {{C}_{M}} = \sum\limits_{i = 0}^5 {\sum\limits_{j = 0}^5 {{{B}_{{ij}}}} } \beta _{l}^{i}\sigma _{l}^{j}$
где ${{A}_{{ij}}}$, ${{B}_{{ij}}}$ – постоянные коэффициенты, ${{\beta }_{l}} = log(\beta )$, ${{\sigma }_{l}} = log(\sigma )$.

Сопоставление этих аппроксимационных зависимостей с данными настоящих расчетов показывает, что стоксовская асимптотика остается валидной для значений $KC \leqslant 0.2$. Обратим внимание на роль параметра $\sigma $ при малых амплитудах. Как можно видеть на рис. 7, где изображены графики зависимостей ${{C}_{D}}(\sigma )$, ${{C}_{M}}(\sigma )$, на границе диапазона при KC = 0.2 для одних и тех же значений параметра $\beta $ коэффициент CD увеличивается при приближении к экрану в области $0.05 < \sigma < 0.5$ практически в три раза, коэффициент CM увеличивается приблизительно на 45%.

Рис. 7.

Графики зависимостей (а) ${{C}_{D}}(\sigma )$, (б) ${{C}_{M}}(\sigma )$ для $\beta = 200$, $KC = 0.2$.

С ростом безразмерной амплитуды $KC > 0.2$ структура зависимостей ${{C}_{D}}(KC)$, ${{C}_{M}}(KC)$ изменяется. Поведение коэффициента CD существенно перестраивается уже в области умеренных значений амплитуд $0.2 < KC < 1$ колебания. В случае $\sigma \geqslant 0.5$ с увеличением $KC$ наблюдается рост CD, при малых $\sigma $ скорость снижения CD существенно уменьшается (по сравнению с $1{\text{/}}KC$). В результате влияние экрана ослабевает. Значения коэффициента CM в диапазоне умеренных амплитуд остаются близки стоксовским.

В диапазоне больших амплитуд $KC > 1$ значения коэффициента CD уменьшаются с ростом KC (при всех значениях σ, $\beta $). Обратим внимание, что для $\sigma \geqslant 0.5$ при $KC > 4$ значения CD совпадают. Влияние экрана на демпфирующие силы на таких расстояниях утрачивается. Заметим, что влияние другого параметра задачи β в этом диапазоне также невелико. Изменение коэффициента при $\sigma \geqslant 0.5$, $200 \leqslant \beta \leqslant 500$ для больших амплитуд $KC \geqslant 4$, достаточно хорошо описывается аппроксимацией

$KC \geqslant 4,\quad \sigma \geqslant 0.5:\quad {{C}_{D}} \approx 4.427{{(KC{\text{/}}2\pi )}^{{ - 0.58}}}$
предложенной в [8] (для случая колебаний балки в безграничной жидкости). Настоящие результаты в этом диапазоне в целом хорошо согласуются и с экспериментальными оценками [14], полученными при исследовании колебаний жестких пластин в безграничной жидкости. Разница между значениями коэффициента CD в диапазоне $0.1 < \sigma < 0.5$ также уменьшается: отличие между максимальным значением коэффициента при $\sigma = 0.1$ и значением CD в безграничной жидкости не превышает 89% при $KC = 1$, в области $KC > 3$ не превышает 32%.

Значения коэффициента CM в диапазоне больших амплитуд $KC > 1$ увеличиваются с ростом KC. Влияние экрана при $\sigma \geqslant 0.5$ на инерциальные силы практически отсутствует, при $\sigma < 0.5$ с ростом KC влияние экрана увеличивается: при $KC = 5$, $\beta = 200$ отличие между CM ($\sigma = 0.5$) и CM ($\sigma = 0.1$) составляет более 48%.

Используя полученные зависимости, проведем расчет параметров колебания балки вблизи экрана.

5. ИЗМЕНЕНИЕ АМПЛИТУДЫ И РЕЗОНАНСНОЙ ЧАСТОТЫ БАЛКИ ПОД ДЕЙСТВИЕМ ГИДРОДИНАМИЧЕСКИХ СИЛ

5.1. Численное решение уравнения колебаний

Для определения параметров движения консольно-закрепленной балки проведем решение одномерного уравнения колебаний (1.1) с граничными и начальными условиями (1.2). Нормируя пространственные переменные на b, время на $\omega _{0}^{{ - 1}}$ запишем уравнения колебаний в следующем виде

(5.1)
$\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} + {{C}_{1}}\frac{{{{\partial }^{4}}w}}{{\partial {{z}^{4}}}} = - {{C}_{2}}\left( {\frac{\pi }{2}C_{M}^{ * }\ddot {w} + {{C}_{D}}KC(z)\left| {\dot {w}} \right|\dot {w}KC{{{(z)}}^{{ - 1}}}} \right)$
${{C}_{1}} = \frac{{EJ}}{{\rho Sb\omega _{0}^{2}}},\quad {{C}_{2}} = \frac{{{{\rho }_{f}}{{b}^{2}}}}{{2\rho S}}$
где C1, C2 – безразмерные коэффициенты, определяющие баланс между упругими и гидродинамическими силами, $C_{M}^{ * }$ – коэффициент инерциальных сил без учета вклада от сил Крылова-Фруда, ρf – плотность жидкости. Если считать профиль балки прямоугольным, то коэффициенты C1, C2 можно выразить в более простом виде

${{C}_{1}} = \mathop {\left( {\frac{L}{b}\frac{1}{k}} \right)}\nolimits^4 ,\quad {{C}_{2}} = \frac{{{{\rho }_{f}}}}{\rho }\frac{b}{{2h}}$

В (5.1) $\tilde {H} = 0$. Хотя этот случай не описывает общую ситуацию, он наглядно демонстрирует относительное влияние гидродинамических сил на колебания в зависимости от расстояния до экрана. Более того, такое предложение справедливо и для некоторых материалов, чье внутреннее демпфирование мало по сравнению с внешним гидродинамическим воздействием. К таким материалам, например, можно отнести алюминий [8].

Поиск решения безразмерной задачи будем проводить численно на основе метода конечных разностей. Для этого на балке строится равномерная сетка с шагом $h = L{\text{/}}(bn)$, в узлах которой определялись дискретные значения переменной $w_{i}^{j}$, где индексы i, j обозначают номер узла расчетной сетки и номер временного слоя (${{t}_{j}} = \tau * j$) соответственно. Применяемая конечно разностная схема может быть записана в следующем виде

$\frac{{2w_{i}^{{j + 1}} - 5w_{i}^{j} + 4w_{i}^{{j - 1}} - w_{i}^{{j - 2}}}}{{{{\tau }^{2}}}} + {{C}_{1}}\frac{{w_{{i - 2}}^{{j + 1}} - 4w_{{i - 1}}^{{j + 1}} + 6w_{i}^{{j + 1}} - 4w_{{i + 1}}^{{j + 1}} + w_{{i + 2}}^{{j + 1}}}}{{{{h}^{4}}}} = $
(5.2)
$ = \; - {{C}_{2}}\left( {{{C}_{D}}(\beta ,KC,\sigma )KC{\text{|}}\dot {w}_{i}^{j}{\text{|}}K{{C}^{{ - 1}}}\dot {w}_{i}^{j} + \frac{\pi }{2}C_{M}^{ * }(\beta ,KC,\sigma )\ddot {w}_{i}^{j}} \right),\quad i = \overline {2,n - 2} $
$w_{0}^{{j + 1}} = {{A}_{0}}{\text{/}}bsin({{t}_{{j + 1}}}),\quad \frac{{ - 3w_{0}^{{j + 1}} + 4w_{1}^{{j + 1}} - w_{2}^{{j + 1}}}}{{2h}} = 0,$
$\frac{{ - w_{{n - 3}}^{{j + 1}} + 4w_{{n - 2}}^{{j + 1}} - 5w_{{n - 1}}^{{j + 1}} + 2w_{n}^{{j + 1}}}}{{{{h}^{2}}}} = 0,\quad \frac{{3w_{{n - 4}}^{{j + 1}} - 14w_{{n - 3}}^{{j + 1}} + 24w_{{n - 2}}^{{j + 1}} - 18w_{{n - 1}}^{{j + 1}} + 5w_{n}^{{j + 1}}}}{{2{{h}^{3}}}} = 0$

Все члены в левой части уравнения движения балки и граничные условия определяются неявным образом, значения гидродинамических сил в правой части уравнения вычисляются по старому временному слою. Алгоритм расчета можно описать следующим образом:

1. Задаются начальные условия (при j = 0).

2. С помощью метода прогонки решается задача (5.2), определяются значения $w_{i}^{{j + 1}}$, $i = \overline {0,\;n} $.

3. Вычисляются значения $\dot {w}_{i}^{{j + 1}}$, $\ddot {w}_{i}^{{j + 1}}$ с помощью конечно-разностных схем второго порядка точности.

4. Если скорость $\dot {w}_{n}^{{j + 1}}$ на новом временном слое меняет свой знак, то производится новый расчет значений KC, ${{C}_{D}}(\beta ,KC,\sigma )KC$ и $C_{M}^{ * }(\beta ,KC,\sigma )$ в каждом узле расчетной сетки. Для этого по новому значению амплитуды колебаний $w_{i}^{{j + 1}}$ вычисляется $KC({{z}_{i}}) = 2\pi w_{i}^{{j + 1}}{\text{/}}b$. Далее для найденного KC вычисляются ${{C}_{D}}KC$ и $C_{M}^{ * }$ путем интерполяции расчетных данных, полученных в разделе 4.

5. Значение $j$ увеличивается на единицу, и осуществляется переход к шагу 2.

В расчетах использовались сетки с числом узлов n = 100, шаг по времени выбирался как $\tau $ = 10–6.

5.2. Свободные колебания балки

Переходя к анализу влияния гидродинамических сил на амплитуду колебания балки, в качестве первого примера рассмотрим случай свободных затухающих колебаний. В первую очередь этот случай интересен с точки зрения апробации расчетной схемы, которую можно провести по экспериментальным данным, представленным в работах [8–10, 44]. В экспериментах колебания возбуждались начальным отклонением свободного конца балки с помощью внешней силы, в расчетах этот случай моделировался с помощью задания начального перемещения по собственной изгибной форме (см. граничные условия (1.2)). Заметим, что начальные профили изгиба в этих случаях геометрически близки.

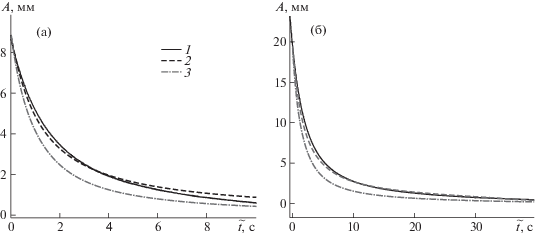
На рис. 8 изображены графики изменения амплитуды колебаний свободного конца балки, полученные в рамках численного моделирования изгибных колебаний на разном расстоянии от экрана, и экспериментальные данные из работ [8–10, 44], полученные для случая колебаний при $\sigma = \infty $ в воздухе. В экспериментах использовались дюралевые образцы со следующими геометрическими характеристиками $L = 300$ мм, b = 20 мм, $h = 0.98$ мм и $L = 170$ мм, b = 10 мм, $h = 0.98$ мм. Как можно видеть, данные моделирования хорошо согласуются с экспериментом для $\sigma = \infty $. Графики изменения амплитуды для случая $\sigma = 0.1$ заметно отличаются,что свидетельствует о значимости наблюдаемых изменений в коэффициенте демпфирования.

Рис. 8.

Изменение амплитуды свободного конца балки при свободных колебаниях безграничной жидкости и вблизи экрана. Данные получены для алюминиевых консолей со следующими параметрами (а) L = 300 мм, $b = 20$ мм, $h = 0.98$ мм; (б) $L = 170$ мм, $b = 10$ мм, $h = 0.98$: 1–3 – эксперимент, моделирование при $\sigma = \infty $, моделирование при $\sigma = 0.1$.

5.3. Вынужденные колебания балки

В качестве второго примера рассмотрим вынужденные колебания балок, когда защемленный конец совершает периодические колебания с заданной амплитудой A0. Все расчеты для заданной частоты ω здесь проводились до установления постоянной амплитуды колебания. На рис. 9 представлены результаты моделирования изменения безразмерной амплитуды колебаний свободного конца балки ($K{{C}_{e}} = KC$ ($x = L{\text{/}}b$)) со временем под действием гидродинамического демпфирования и изменения резонансной частоты колебаний под действием сил инерции (присоединенной массы жидкости). Параметры расчетов, как и в предыдущем разделе, соответствуют колебаниям алюминиевых балок в воздухе.

Рис. 9.

Изменение безразмерной амплитуды свободного конца балки ($K{{C}_{e}}$) при вынужденных колебаниях в безграничной жидкости и вблизи экрана. Графики изображают результаты моделирования колебания алюминиевых образцов $b = 20$ мм, L = 300 мм в воздухе с частотой ω, вызванных колебаниями защемленного конца с различными значениями амплитуды A0. (а) изменение амплитуды со временем при ω = ω0, (б) изменение максимальной амплитуды колебаний в зависимости от ω. 1 – $\sigma = \infty $, 2 – $a = 0.1$.

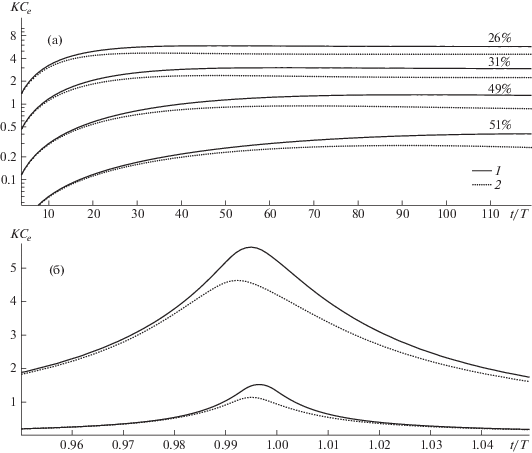
Как можно видеть на рис. 9a, эффект влияния экрана существенно сказывается на амплитуде колебания балки во всех моделируемых ситуациях. Для случаев, когда колебание всех сечений балки происходит в диапазоне малых и умеренных амплитуд, эффект влияния экрана максимален: в представленных расчетах различия в амплитуде свободного конца консоли при одной и той же амплитуде колебания базы (${{A}_{0}}{\text{/}}b = 0.2 \times {{10}^{{ - 3}}},\;1 \times {{10}^{{ - 3}}}$) достигают 51%. С ростом амплитуды колебания балки эффект экрана начинает ослабевать, в расчетных случаях при ${{A}_{0}}{\text{/}}b = 4 \times {{10}^{{ - 3}}}$, 12 × 10–3 различия в амплитуде колебания конца составили соответственно 31 и 26%.

Влияние сил присоединенной массы на колебания алюминиевых балок в воздухе невелико. Как можно видеть на рис. 9б, во всех случаях резонансная частота в воздухе близка к резонансной частоте в вакууме (определенной теоретически). По мере увеличения относительной плотности ρf/ρ эффект присоединенных масс становится более значимым. Так, например, при увеличении ρf/ρ в 250 раз, при аналогичных значениях $K{{C}_{e}}$ и параметрах балки, первая резонансная частота консоли под действиемэффекта присоединенных масс составит приблизительно $0.58{{\omega }_{0}}$ в безграничном объеме и $0.54{{\omega }_{0}}$ при $\sigma = 0.1$.

6. ЗАКЛЮЧЕНИЕ

Основываясь на модели квазиплоского взаимодействия балки с жидкостью, проведены исследования эффекта экрана, возникающего при изгибных колебаниях балок около твердой поверхности. Для определения гидродинамического воздействия на балку в сечениях решена серия однотипных плоских задач обтекания, в рамках которых движение жидкости описывалось нестационарной системой уравнений Навье–Стокса. Используя аппроксимацию Морисона для обработки численных данных, исследованы изменения сил гидродинамического демпфирования и инерциальных сил в зависимости от локальных безразмерной амплитуды, частоты и расстояния до экрана.

Показано, что эффект экрана начинает влиять на параметры гидродинамического воздействия, когда расстояние до экрана меньше половины ширины балки. Влияние экрана на демпфирующие силы наиболее значимо при малых амплитудах колебания (сопротивление выше почти в 3 раза) и постепенно уменьшается с ростом безразмерной амплитуды. Влияние экрана на силы инерции увеличивается с ростом амплитуды колебаний (с 24 до 48%).

Полученные зависимости для гидродинамических сил использованы для оценки влияния эффекта экрана на колебания консолей с реальными характерными физическими параметрами. С помощью разработанной численной модели проведены расчеты свободных и вынужденных колебаний алюминиевых балок в воздухе. Наибольшее влияние экрана на изменение амплитуды колебаний ожидаемо (основываясь на полученных данных о гидродинамических силах) наблюдалось в диапазоне малых и умеренных амплитуд (достигало 51%). В диапазоне больших амплитуд эффект оказался почти в два раза меньше.

Список литературы

  1. Aureli M., Porfiri M. Low frequency and large amplitude oscillations of cantilevers in viscous fluids // Appl. Phys. Lett. 2010. V. 96. № 16. P. 164102.

  2. Aureli M., Porfiri M., Basaran M.E. Nonlinear finite amplitude vibrations of sharp-edged beams in viscous fluids // J. Sound Vib. 2012. V. 331. № 7. P. 1624–1654.

  3. Phan C.N., Aureli M., Porfiri M. Basaran M.E. Finite amplitude vibrations of cantilevers of rectangular cross sections in viscous fluids // J. Fluids Struct . 2013. V. 40. P. 52–69.

  4. Facci A.L., Porfiri M. Nonlinear hydrodynamic damping of sharp-edged cantilevers in viscous fluids undergoing multi-harmonic base excitation // J. Appl. Phys. 2012. V. 112. № 12. P. 124908.

  5. Sader J.E., Porfiri M. Nonlinear hydrodynamic damping of sharp-edged cantilevers in viscous fluids undergoing multi-harmonic base excitation // J. Appl. Phys. 1998. V. 84. № 1. P. 64.

  6. Bidkar R.A., Kimber M., Raman A., Bajaj A.K., Garimella S.V. Nonlinear aerodynamic damping of sharp-edged flexible beams oscillating at low Keulegan–Carpenter numbers // J. Fluid Mech. 2009. V. 634. P. 269–289.

  7. Kopman V., Porfiri M. Design, Modeling, and Characterization of a Miniature Robotic Fish for Research and Education in Biomimetics and Bioinspiration // IEEE ASME Trans. Mechatron. 2013. V. 18. № 2. P. 471–483.

  8. Egorov A.G., Kamalutdinov A.M., Nuriev A.N. Evaluation of aerodynamic forces acting on oscillating cantilever beams based on the study of the damped flexural vibration of aluminium test samples // J. Sound Vib. 2018. V. 421. P. 334–347.

  9. Егоров А.Г., Камалутдинов А.М., Нуриев А.Н., Паймушин В.Н. Экспериментальное определение демпфирования колебаний пластины вязкой жидкостью // Доклады РАН. 2017. Т. 474. № 2. С. 172–176.

  10. Егоров А.Г., Камалутдинов А.М., Паймушин В.Н., Фирсов В.А. Теоретико-экспериментальный метод определения коэффициента аэродинамического сопротивления гармонически колеблющейся тонкой пластины // ПМТФ. 2016. Т. 57. № 2 (336). С. 96–104.

  11. Паймушин В.Н., Фирсов В.А., Гюнал И., Шишкин В.М. Теоретико-экспериментальный метод определения аэродинамической составляющей демпфирования тест-образца ромбовидного поперечного сечения // Вестник ПНИПУ. Механика. 2016. № 4. P. 194–217.

  12. Keulegan G.H., Carpenter L.H. Forces on cylinders and plates in an oscillating fluid // J. Res. Natl. Inst. Stand. Technol. 1958. V. 60. № 5. P. 423–440.

  13. Bearman P.W., Graham J.M.R., Singh S. Forces on Cylinders in Harmonically Oscillating Flow // Proc. Mechanics of Wave-induced Forces on Cylinders: Pitman Advanced Publishing 1979. P. 437–449.

  14. Singh S. Forces on Bodies in Oscillatory Flow: PhD thesis. University of London 1979. 367 p.

  15. Bearman P.W., Downie M.J., Graham J.M.R., Obasaju E.D. Forces on cylinders in viscous oscillatory flow at low Keulegan-Carpenter numbers // J. Fluid Mech. 1985. V. 154. P. 337–356.

  16. Bearman P.W. An investigation of the forces on flat plates normal to a turbulent flow // J. Fluid Mech. 1971. V. 46. № 1. P. 177–198.

  17. Bearman P.W., Obasaju E.D. An experimental study of pressure fluctuations on fixed and oscillating square-section cylinders // J. Fluid Mech. 1982. V. 119. № 1. P. 177–198.

  18. Shrestha B., Ahsan S.N., Aureli M. Experimental study of oscillating plates in viscous fluids: Qualitative and quantitative analysis of the flow physics and hydrodynamic forces // Phys. Fluids 2018. V. 30. № 1. P. 013102.

  19. Egorov A.G., Kamalutdinov A.M., Nuriev A.N., Paimushin V.N. Theoretical-experimental method for determining the parameters of damping based on the study of damped flexural vibrations of test specimens 2. aerodynamic component of damping // Mech. Compos. Mater. 2014. V. 50. № 3. P. 267–278.

  20. Nuriev A.N., Kamalutdinov A.M., Egorov A.G., Zaitseva O.N. Numerical investigation of hydrodynamic influence on long oscillating plates in a viscous fluid // J. Phys.: Conf. Ser 2019. V. 1158. № 3. P. 032040.

  21. Nuriev A.N., Kamalutdinov A.M., Egorov A.G. A numerical investigation of fluid flows induced by the oscillations of thin plates and evaluation of the associated hydrodynamic forces // J. Fluid Mech. 2019. V. 874. P. 1057–1095.

  22. Grimaldi E., Porfiri M., Soria L. Finite amplitude vibrations of a sharp-edged beam immersed in a viscous fluid near a solid surface // J. Appl. Phys. 2012. V. 112. № 10. P. 104907.

  23. Xiong C., Cheng L., Tong F., An H. Oscillatory flow regimes for a circular cylinder near a plane boundary // J. Fluid Mech. 2018. V. 844. P. 127–161.

  24. Green C.P., Sader J.E. Small amplitude oscillations of a thin beam immersed in a viscous fluid near a solid surface // Phys. Fluids 2005. V. 17. № 7. P. 073102.

  25. Hsieh S.-C., Low Y.M., Chiew Y.-M. Flow characteristics around a circular cylinder subjected to vortex-induced vibration near a plane boundary // J. Fluids Struct. 2016. V. 65. P. 257–277.

  26. Munir A., Zhao M., Wu H., Ning D., Lu L. Numerical investigation of the effect of plane boundary on two-degree-of-freedom of vortex-induced vibration of a circular cylinder in oscillatory flow // Ocean Eng. 2018. V. 148. P. 17–32.

  27. Паймушин В.Н., Фирсов В.А., Газизуллин Р.К., Шишкин В.М. Аэродинамическая составляющая демпфирования консольно-закрепленных тест-образцов при колебаниях вблизи жесткого экрана // Вестник ПНИПУ. Механика. 2018. № 2. С. 62–71.

  28. Rozhdestvensky K.V., Ryzhov V.A. Aerohydrodynamics of flapping-wing propulsors // Prog. Aerosp. Sci. 2003. V. 39. № 8. P. 585–633.

  29. Рождественский К.В. Основные результаты асимптотической теории низколетящего крыла (Метод сращиваемых разложений) // Гидромеханика. 1980. № 41. С. 18–28.

  30. Xiu H., Davis R.B., Romeo R.C. Edge clearance effects on the added mass and damping of beams submerged in viscous fluids // J. Fluids Struct. 2018. V. 83. P. 194–217.

  31. Dtsch H., Durst F., Becker S., Lienhart H. Low-Reynolds-number flow around an oscillating circular cylinder at low Keulegan-Carpenter numbers // J. Fluid Mech. 1998. V. 360. P. 249–271.

  32. Jasak H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows: PhD thesis. Department of Mechanical Engineering Imperial College of Science, Technology and Medicine 1996. 394 p.

  33. Spalding D.B. A novel finite difference formulation for differential expressions involving both first and second derivatives // Int. J. Numer. Methods Eng. 1972. V. 4. № 4. P. 551–559.

  34. Patankar S.V., Spalding D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows // Int. J. Heat Mass Transf. 1972. V. 15. № 10. P. 1787–1806.

  35. Brooks A.N., Hughes T.J.R. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations // Comput. Methods Appl. Mech. Eng. 1982. V. 32. № 1. P. 199–259.

  36. Justesen P. A numerical study of oscillating flow around a circular cylinder // J. Fluid Mech. 1991. V. 222. P. 157–196.

  37. Zhao M., Cheng L., Teng B., Dong G. Hydrodynamic forces on dual cylinders of different diameters in steady currents // J. Fluids Struct. 2007. V. 23. № 1. P. 59–83.

  38. An H., Cheng L., Zhao M. Steady streaming around a circular cylinder in an oscillatory flows // Ocean Eng. 2009. V. 36. № 14. P. 1089–1097.

  39. Tang G., Liang C., Lin L., Teng Y., Zhao M., An H. Effect of oscillatory boundary layer on hydrodynamic forces on pipelines // Coast. Eng. 2018. V. 140. P. 114–123.

  40. Issa R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting // J. Comput. Phys. 1986. V. 62. № 1. P. 40–65.

  41. Ferziger J.H., Perich M. Computational Methods for Fluid Dynamics. B.: Springer Berlin Heidelberg, 2002. 596 p.

  42. Morison J.R., Johnson J.W., Schaaf S.A. The Force Exerted by Surface Waves on Piles // J. Pet. Technol. 1950. V. 2. P. 149–154.

  43. Tuck E.O. Calculation of unsteady flows due to small motions of cylinders in a viscous fluid // J. Eng. Math. 1969. V. 3. № 1. P. 29–44.

  44. Камалутдинов М.А. Теоретико-экспериментальное исследование аэродинамических свойств колеблющейся пластины: Дис. … канд. физ.-мат. наук: 01.02.04, 01.02.05 К., 2017. 142 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал