1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 5, 2021

Известия РАН. Механика жидкости и газа, 2021, № 5, стр. 122-137

ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК МНОГОУГОЛЬНОГО ГИДРАВЛИЧЕСКОГО ПРЫЖКА ПРИ НАТЕКАНИИ ЖИДКОЙ СТРУИ НА ПЛОСКУЮ ПОДЛОЖКУ

A. Esmaeeli a, *, M. Passandideh-Fard a, **

a Ferdowsi University of Mashhad
Mashhad, Iran

* E-mail: ali_esmaeeli_67@yahoo.com
** E-mail: mpfard@um.ac.ir

Поступила в редакцию 03.07.2020
После доработки 06.11.2020
Принята к публикации 24.12.2020

Полный текст (PDF)

Аннотация

Неустойчивости, возникающие при натекании жидкой струи на плоскую пластину, рассматриваются с помощью комбинированного численно-аналитического метода. Когда жидкая струя ударяется о подложку, она растекается по подложке и в экспериментах наблюдается круговой гидравлический прыжок, возникающий на некотором расстоянии по радиусу от точки натекания струи. Неустойчивости, развивающиеся в потоке жидкости, при определенных условиях изменяют форму прыжка с круговой на многоугольную. Однако с численной точки зрения моделируемый гидравлический прыжок всегда имеет круговую форму, так как эти неустойчивости игнорируются при численном моделировании. Поскольку число углов многоугольного прыжка представляет собой важную характеристику рассматриваемого явления, цель настоящего исследования состоит в объединении характеристик моделируемого кругового прыжка в некоторую аналитическую модель, имеющуюся в литературе, чтобы получить число углов многоугольного прыжка. Чтобы следить за свободной поверхностью жидкости во время соударения струи с подложкой и дальнейшим деформированием этой поверхности, приводящим к круговому прыжку, используется метод объема жидкости совместно с алгоритмом Юнга. Важными параметрами рассматриваемого явления, которые используются в методе, предложенном в настоящем исследовании, являются высота жидкости выше и ниже по потоку от гидравлического прыжка, а также радиус и кривизна прыжка, которые могут быть извлечены из численных результатов моделирования кругового гидравлического прыжка. Полученное при расчете число углов многоугольного прыжка сравнивается с числом углов в эксперименте для различных случаев, между которыми наблюдается хорошее согласие.

Ключевые слова: натекание жидкой струи, число углов, многоугольный гидравлический прыжок, неустойчивости Рэлея–Плато, метод объема жидкости

СПИСОК ОБОЗНАЧЕНИЙ

Acell Площадь свободной поверхности вычислительной ячейки
B Параметр формы
Bo Число Бонда
C Постоянный коэффициент
f Объемная доля жидкости (дробная функция)
Fb Массовая сила
FST Сила поверхностного натяжения
Fr Число Фруда
G Безразмерный параметр
g Ускорение свободного падения
ho Высота жидкости ниже по течению
hi Высота жидкости выше по течению
lc Капиллярная длина Capillary length
K Число углов многоугольного прыжка
n Нормальный вектор поверхности
P Давление
Q Объемный расход
r0 Характеристический радиус
rj Внутренний радиус прыжка
R Внешний радиус прыжка
R1 Радиус кривизны
Re Число Рейнольдса
t Время
V Вектор скорости
α Отношение высоты потока и внешнего радиуса прыжка
∇ Оператор Гамильтона
Ωcell Объем ячейки
σ Поверхностное натяжение
δ0 Нормализованная ширина бочки (переворачивающегося вала жидкости) кругового гидравлического прыжка
ξ0 Характеристическая высота жидкости
μ Динамическая вязкость
ν Кинематическая вязкость
ρ Плотность
ρ1 Безразмерный радиус кривизны
τ Тензор напряжений
Π Безразмерный параметр
κ Кривизна поверхности

Натекание жидкой струи на плоскую пластину используется во многих приложениях, таких как охлаждение электронных систем и турбинных лопаток [1], обработка листового металла [2], нанесение защитного слоя на поверхность [3], смыв поверхностного слоя [4], производство стекла [5], лазерные зеркала [6] и т.д. Когда жидкая струя с круглым поперечным сечением натекает по нормали на горизонтальную подложку, по поверхности подложки растекается пленка жидкости. В случае присутствия некоторой преграды вниз по потоку от жидкой пленки, можно наблюдать, что на определенном радиальном расстоянии от точки соударения струи с поверхностью толщина жидкого слоя внезапно возрастает. Это приводит к явлению, известному как круговой гидравлический прыжок [7]. Радиус и глубина жидкости вверх по потоку от прыжка меньше, чем эти величины вниз по потоку. По этой причине, чтобы сохранить массовый расход жидкости, скорость жидкости в состоянии вверх по потоку от прыжка должна быть намного больше, чем скорость в состоянии вниз по потоку от прыжка. Это течение с большой скоростью перед прыжком увеличивает касательное напряжение сдвига и коэффициент теплообмена на поверхности [8]. Именно по этой причине следует избегать образования гидравлического прыжка во многих приложениях. В результате очень важным является предсказание положения и формы гидравлического прыжка в этом явлении. В связи с этим, были предприняты многочисленные экспериментальные [9–11], аналитические [9, 12–16] и численные [17–19] исследования, чтобы описать гидравлический прыжок и ввести разные соотношения для предсказания радиуса прыжка [11, 13, 14, 16].

Неустойчивости могут изменить форму потока жидкости. В [20] было изучено влияние неустойчивостей на мелкодисперсное разбрызгивание жидкой струи, натекающей на плоскую пластину перед гидравлическим прыжком. В [21] было экспериментально исследовано разбрызгивание, происходящее во время натекания жидкой струи на твердые мишени. В этом исследовании авторы утверждали, что в присутствии разбрызгивания капиллярная неустойчивость важнее поверхностного натяжения. При изучении круговых гидравлических прыжков [22] было найдено, что когда докритическая жидкая пленка становится толще и эффекты поверхностного натяжения уменьшаются, можно увидеть некоторую последовательность неустойчивостей в структуре прыжка. В недавних исследованиях [23–29] были изучены эффекты неустойчивостей при изменении круговой формы гидравлического прыжка на многоугольную. В настоящем исследовании, с помощью использовании комбинированного численно-аналитического метода, описывается многоугольный гидравлический прыжок, образованный за счет неустойчивостей, развивающихся во время натекания струи жидкости.

В процессе образования гидравлического прыжка, когда жидкость имеет небольшую вязкость (подобно воде), гидравлический прыжок имеет один и тот же радиус при всех углах и на поверхности образуется жидкая пленка круговой формы (рис. 1а). Однако, если струя натекает наклонно или жидкость имеет бóльшую вязкость (приблизительно десятикратную по сравнению с вязкостью воды), форма гидравлического прыжка изменяется на некруговую (овальную или многоугольную) (рис. 1б). Многоугольные прыжки образуются из-за неустойчивостей Рэлея–Плато в высоковязких жидкостях [29].

Рис. 1.

Круговой гидравлический прыжок [23] (а); некоторые многоугольные гидравлические прыжки [30] (б).

Впервые круговой гидравлический прыжок наблюдался в 1914 г. [10]. В этом исследовании автор (лорд Рэлей) отметил, что бóльшая часть необъясненных акустических явлений связана с неустойчивостью струй жидкости. Он классифицировал причины неустойчивости жидких струй, разделив их на две категории. Первая состоит в ускорении струи жидкости высокой плотности в жидкости низкой плотности. Другая категория неустойчивости связана со струей и окружающей средой, состоящих из одного и того же вещества. Рэлей экспериментально исследовал влияние различных факторов на круговой гидравлический прыжок и указал на то, что поверхностное натяжение и объемный расход жидкости представляют собой два важных параметра, действующих на радиус кругового гидравлического прыжка. Одним из наиболее важных результатов в исследовании кругового гидравлического прыжка состоит в возможности предсказания радиуса прыжка и его структуры. Радиус кругового гидравлического прыжка, структура которого зависит от поведения жидкости за прыжком, определяется как расстояние зоны прыжка от точки натекания струи. В [12] была представлена теория невязкого гидравлического прыжка, возникающего в результате воздействия вертикальной струи на горизонтальную пластину. На основе этой теории делается вывод, что гидростатическая сила должна равняться скорости изменений импульса жидкости в месте расположения прыжка. Было показано, что невязкой теории недостаточно для объяснения многих экспериментов, описанных в литературе [16, 29], поскольку в ней пренебрегается эффектом вязкости и существованием вихрей в области прыжка, которые важны в рассматриваемом явлении.

В [16], используя теорию пограничного слоя, было рассмотрено влияние вязкости жидкости на круговой гидравлический прыжок. В этом исследовании было получено неявное соотношение для определения радиуса кругового гидравлического прыжка и выполнены несколько экспериментов с целью проверки и обоснования предложенной модели. Было показано, что результаты предлагаемой теории находятся в хорошем согласии с результатами измерений только в режиме ламинарного течения [16].

В [13] было представлено соотношение подобия для радиуса кругового гидравлического прыжка в зависимости от объемного потока жидкости, кинематической вязкости и ускорения силы тяжести при использовании уравнений мелкой воды. В другом исследовании [31] разные формы гидравлического прыжка были исследованы аналитически и экспериментально. Гидравлические прыжки были отнесены к двум типам по числу вихрей под свободной поверхностью жидкости в области прыжка. У гидравлического прыжка первого типа (I) имеется один вихрь вблизи твердой поверхности, который вызывает внезапный рост высоты жидкости. В гидравлическом прыжке второго типа (II) появляется другой вихрь вблизи свободной поверхности, что приводит к изменениям в ее профиле. В [31] утверждалось, что форма прыжка изменяется с типа I на тип II, когда высота жидкости вниз по потоку от гидравлического прыжка возрастает до определенного значения. В [14] теория Ватсона [16] была модифицирована за счет аналитического рассмотрения поверхностного натяжения в данном явлении и путем сравнения полученного соотношения с экспериментальными результатами.

Круговой гидравлический прыжок был численно моделирован в [17]. Метод объема жидкости и алгоритм Юнга были использованы для отслеживания адвекции свободной поверхности. Было найдено, что при увеличении вязкости устойчивость прыжка растет, а чувствительность положения прыжка к высоте жидкости вниз по потоку от него уменьшается. Было отмечено, что при увеличении высоты жидкости вниз по потоку радиус прыжка уменьшается до определенного предела, после которого устойчивость прыжка начинает снижаться.

В жидкостях с низкой вязкостью это явление очень неустойчиво; по этой причине в [23] был использован этилен-гликоль (в 10 раз более вязкий, чем вода), чтобы получить более устойчивые круговые гидравлические прыжки. Что удивительно, в этом исследовании наблюдалась новая геометрия гидравлических прыжков с некоторыми углами, которую авторы назвали многоугольным гидравлическим прыжком. Кроме того, было исследовано влияние разных параметров на форму образовавшегося многоугольника. Многоугольники наблюдались только в течениях типа II. Это было достигнуто за счет увеличения высоты жидкости ниже по потоку от прыжка, при этом число углов многоугольника уменьшалось [24]. С тех пор многие исследователи изучали многоугольные гидравлические прыжки и представили соотношения для оценки числа углов многоугольника. Круговой гидравлический прыжок был исследован в [32] численно и теоретически. Были представлены два дифференциальных уравнения для радиуса прыжка и высоты свободной поверхности. В [26] эта модель для теоретического расчета высоты свободной поверхности и полей скорости в многоугольном гидравлическом прыжке была модифицирована. Были рассмотрены малые возмущения в окрестности кругового прыжка и получено нелинейное уравнение для многоугольного прыжка. На основе этого исследования было найдено следующее соотношение, которое может быть использовано для оценки числа углов многоугольного прыжка

(0.1)
$k = \sqrt {1 - {{r}_{0}}^{2}\frac{{{\text{Bo}}}}{\alpha } + \frac{{35}}{8}\frac{{{{r}_{0}}^{2}}}{{{{{{\xi }}}_{0}}^{3}}}\frac{{{\text{BoFr}}}}{{{\text{R}}{{{\text{e}}}^{2}}}}} ,$
где ${{\alpha }} = {{h}_{{\text{o}}}}{\text{/}}R$ – отношение высоты потока и внешнего радиуса прыжка, ${\text{Bo}} = \frac{{h_{{\text{o}}}^{2}{{\rho }}{\mathbf{g}}}}{{{\sigma }}}$ – число Бонда, Fr = $\frac{{{{Q}^{2}}}}{{{{{{\pi }}}^{2}}{{R}^{2}}h_{{\text{o}}}^{3}{\mathbf{g}}}}$ – число Фруда, ${\text{Re}} = \frac{{Q{{h}_{o}}}}{{{{\pi }}{{R}^{2}}{{\nu }}}}$ – число Рейнольдса, а r0 и ξ0 – функции Re, α, Fr и Bo. В этих безразмерных числах ho представляет собой высоту свободной поверхности вниз по потоку от прыжка, R – внешний радиус за прыжком, ρ – плотность жидкости, g – ускорение свободного падения, σ – поверхностное натяжение, Q – объемный расход жидкости и ν – кинематическая вязкость.

В [33] круговой гидравлический прыжок был исследован численно с помощью метода объема жидкости. На основе исследования линий тока в жидкости вверх и вниз по потоку была продемонстрирована динамика течения в круговом гидравлическом прыжке. Был проиллюстрирован тот факт, что при достижении некоторого критического предела положительным градиентом давления (нарастание давления по направлению течения) может наблюдаться противоток, что указывает на область прыжка. Этот противоток вызывает циркуляцию в зоне растекания жидкости, которая резко повышает высоту потока жидкости.

В [25] для многоугольного гидравлического прыжка была предложена феноменологическая модель. В этой модели утверждалось, что многоугольное состояние прыжка возникнет с длиной волны порядка ширины “бочки” (закрученного (переворачивающегося) жидкого вала), возникающего вследствие неустойчивости Рэлея–Плато. В этой модели было представлено некоторое безразмерное уравнение для вычисления числа углов многоугольного гидравлического прыжка, полученное посредством рассмотрения закона сохранения массы и баланса сил вверх и вниз по потоку от прыжка. Хотя поверхностное натяжение является одним из важнейших факторов, участвующих в формировании многоугольного гидравлического прыжка, в этом соотношении пренебрегалось поверхностным натяжением из-за отсутствия детальной информации о профиле свободной поверхности прыжка и его кривизне.

В настоящем исследовании кривизны прыжков рассчитаны с помощью численного моделирования профиля высоты кругового гидравлического прыжка. Некоторые геометрические параметры прыжка получены из расчетов, которые далее использованы для вычисления сил поверхностного натяжения на основе модели, представленной в [25]. В результате отсутствует необходимость пренебрегать поверхностным натяжением, что, таким образом, приводит к комбинированному численно-аналитическому методу, предназначенному для более точного определения числа углов.

1. КРАТКОЕ ОПИСАНИЕ МОДЕЛИ МАРТЕНСА [25]

Уравнение количества движения и закон сохранения массы были использованы в [25] для некоторого секторного контрольного объема в области прыжка. Чтобы получить различные члены в уравнении количества движения, были построены балансы сил для разных направлений вокруг прыжка. Что касается радиального направления, были использованы сила гидростатического давления и радиальная компонента силы вязкого трения. Далее, были выведены выражения для гидростатического давления, касательного напряжения сдвига и силы поверхностного натяжения в азимутальном направлении. Наконец, была использована теория возмущений, чтобы получить соотношение для числа углов в многоугольном гидравлическом прыжке в виде:

(1.1)
$k = \sqrt {\frac{1}{{2{{{{\delta }}}_{0}}}}\left( {B - \frac{{{\text{B}}{{{\text{o}}}^{2}}}}{{3{{\alpha }}}} \pm \sqrt G } \right)} ,{\text{\;}}$
(1.2)
$G \equiv {{\left( {B - \frac{{{\text{B}}{{{\text{o}}}^{2}}}}{{3{{\alpha }}}}} \right)}^{2}} + \frac{{2{\text{B}}{{{\text{o}}}^{2}}}}{{3{{\pi \alpha }}}}\left[ {\frac{{{{{{\Pi }}}_{2}}}}{{{{\delta }}_{0}^{2}}} + {{{{\Pi }}}_{3}}\left( {1 - \frac{1}{2}{{{{\delta }}}_{0}}} \right)} \right],$
где ${{{{\Pi }}}_{2}} \equiv {\text{\;}}\frac{{2{{c}_{2}}{{\nu }}Q}}{{{\mathbf{g}}{{R}^{2}}h_{{\text{o}}}^{2}}}$ и ${{{{\Pi }}}_{3}} \equiv \frac{{2{{c}_{3}}{{\nu }}Q}}{{{\mathbf{g}}{{h}_{{\text{i}}}}h_{{\text{o}}}^{3}}}$ – два безразмерных числа, связанные с условиями в жидкости и потоке. В этих безразмерных числах hi – высота свободной поверхности вверх по потоку от прыжка, c2 и c3 – некоторые постоянные порядка единицы [25], $B \equiv \frac{{{{{{\delta }}}_{0}}{{\rho }}_{1}^{'}({{{{\delta }}}_{0}})}}{{{{{[{{{{\rho }}}_{1}}({{{{\delta }}}_{0}})]}}^{2}}}}$ – параметр формы, связанный с кривизной свободной поверхности в области прыжка и ${{{{\delta }}}_{0}} = \frac{{R - {{r}_{{\text{j}}}}}}{R}$ – нормализованная ширина переворачивающегося вала (бочки) кругового гидравлического прыжка при тех же самых условиях.

Из-за отсутствия каких-либо аналитических выражений для профиля высоты прыжка, его безразмерная кривизна ${{{{\rho }}}_{1}} = \frac{{{{R}_{1}}}}{R}$ и производная от ρ1 по δ не могут быть получены аналитически. Мартенс и соавт. [25] заявили, что эта кривизна может привести к неустойчивости. Поэтому, предположив, что поверхностное натяжение имеет пренебрежимо малую величину, авторы [25] пренебрегли числом B. Следовательно, уравнение (1.1) было упрощено и приведено к следующему виду:

(1.3)
$k = \pm \sqrt {\frac{1}{{2{{\pi }}{{{{\delta }}}_{0}}}}\left( {\frac{{{{{{\Pi }}}_{2}}}}{{{{\delta }}_{0}^{2}}} + {{{{\Pi }}}_{3}}\left( {1 - \frac{1}{2}{{{{\delta }}}_{0}}} \right)} \right)} \,.$

Для подтверждения адекватности профиль высоты, полученный из экспериментальных результатов, использовался для расчета числа углов в многоугольном гидравлическом прыжке с помощью уравнения (1.1).

Далее, были рассмотрены зависящие от времени уравнения неразрывности и баланса радиальных и азимутальных сил в окрестности прыжка. Наконец, был сделан вывод, что, если поперечное сечение переворачивающегося вала (бочки) близко к цилиндрическому, длина волны, пропорциональная ширине бочки, как в неустойчивости Рэлея–Плато (k*), обратно пропорциональна нормализованной ширине переворачивающегося вала кругового гидравлического прыжка (δ0) при тех же условиях, т.е.,

(1.4)
$k{\text{*}} = \frac{1}{{{{{{\delta }}}_{0}}}}$

Было показано, что число углов в многоугольном прыжке будет равно округленному (либо с избытком или с недостатком) значению k*, полученному из уравнения (1.4). Для подтверждения адекватности модели, которая приводит к уравнению (1.4), полученные экспериментально значения профиля высоты были использованы для вычисления δ0. Далее, число углов в многоугольном прыжке, наблюдаемом экспериментально, сравнивалось с числом углов, полученным из уравнения (1.4). Как можно видеть, основной недостаток вышеупомянутой модели состоит в вычислении δ0. Хотя уравнение (1.4) представляет собой простое соотношение для оценки числа углов в многоугольном прыжке, никаких аналитических зависимостей для δ0 не было представлено.

В настоящем исследовании параметры в вышеупомянутой теории, для которых нет доступных аналитических значений, оцениваются с помощью численного моделирования. Это было проделано как для уравнения (1.1), так и для уравнения (1.4). При использовании уравнения (1.1) для оценки параметра формы $\left( {B \equiv \frac{{{{{{\delta }}}_{0}}{{\rho }}_{1}^{'}\left( {{{{{\delta }}}_{0}}} \right)}}{{{{{[{{{{\rho }}}_{1}}\left( {{{{{\delta }}}_{0}}} \right)]}}^{2}}}}} \right)$, все величины должны быть извлечены из профиля свободной поверхности кругового гидравлического прыжка. Этот профиль свободной поверхности и кривизна прыжка могут быть получены с помощью результатов численного моделирования кругового гидравлического прыжка. Таким образом, число углов в многоугольном гидравлическом прыжке получается при вычислении числа B и подстановке его в уравнение (1.1). Аналогично, значение нормализованной ширины переворачивающегося вала кругового гидравлического прыжка (δ0) определяется из результатов расчетов, после чего можно вычислить значение k из уравнения (1.4).

2. МОДЕЛИРОВАНИЕ НАТЕКАНИЯ ЖИДКОЙ СТРУИ

2.1. Объяснение численного метода

В настоящем исследовании натекание жидкой струи численно моделируется посредством решения уравнения неразрывности и трехмерных уравнений Навье–Стокса

(2.1)
$\nabla \cdot {\mathbf{V}} = 0,$
(2.2)
$\frac{{\partial {\mathbf{V}}}}{{\partial t}} + {\mathbf{V}} \cdot \nabla {\mathbf{V}} = - \frac{1}{{{\rho }}}\nabla P + \frac{1}{{{\rho }}}\nabla \cdot {\mathbf{\tau }} + {\mathbf{g}} + \frac{1}{{{\rho }}}{{{\mathbf{F}}}_{{\text{b}}}},$
где V – вектор скорости, P – давление, Fb – массовая сила на единицу объема и τ – тензор напряжений, определенный следующим образом:

(2.3)
${\mathbf{\tau }} = {{\mu }}[\left( {\nabla {\mathbf{V}}} \right) + {{\left( {\nabla {\mathbf{V}}} \right)}^{{\text{T}}}}].$

В настоящем исследовании максимальное число Рейнольдса для исходной круглой жидкой струи равно 2000 и режим течения рассматривается как ламинарный. Кроме того, жидкость предполагается ньютоновской и несжимаемой. Благодаря постоянной температуре жидкости, ее физические свойства, включая поверхностное натяжение, плотность и вязкость, считаются постоянными. Чтобы решить уравнение неразрывности и уравнение количества движения, использовался двухшаговый метод проекции [34], в котором вначале явно вычисляется скорость за счет использования конвективных слагаемых и массовых сил

(2.4)
$\frac{{{\mathbf{\tilde {V}}} - {{{\mathbf{V}}}^{n}}}}{{\Delta t}} = - {{\left( {{\mathbf{V}} \cdot \nabla {\mathbf{V}}} \right)}^{n}} + \frac{1}{{{{{{\rho }}}^{n}}}}\nabla \cdot {{{\mathbf{\tau }}}^{n}} + {{{\mathbf{g}}}^{n}} + \frac{1}{{{{{{\rho }}}^{n}}}}{\mathbf{F}}_{{\text{b}}}^{n},$
где верхний индекс n обозначает значение соответствующей величины на предыдущем временнóм слое и Δt равно величине шага по времени. Врéменная скорость (${\mathbf{\tilde {V}}}$) вычисляется на этом шаге посредством использования некоторой явной дискретизации конвективных слагаемых, вязких членов, массовых сил и сил поверхностного натяжения (как будет объяснено позже в этом разделе). Далее, вектор скорости на новом временнóм слое (Vn+ 1) вычисляется с помощью неявного решения уравнения с членом для распределения давления:

(2.5)
$\frac{{{{{\mathbf{V}}}^{{n + 1}}} - {\mathbf{\tilde {V}}}}}{{\Delta t}} = - \frac{1}{{{{{{\rho }}}^{n}}}}\nabla {{P}^{{n + 1}}}$

Вычисление дивергенции уравнения (2.5) с использованием уравнения неразрывности (2.1) дает неявное уравнение Пуассона для давления:

(2.6)
$\nabla \cdot \left[ {\frac{1}{{{{{{\rho }}}^{n}}}}\nabla {{P}^{{n + 1}}}} \right] = \frac{{\nabla {\mathbf{\tilde {V}}}}}{{\Delta t}}$

Для решения уравнения (2.6) используется солвер, основанный на методе Холецкого неполного разложения сопряженнных градиентов [35]. После решения уравнения (2.6) получается распределение давления на следующем временнóм слое, которое может быть использовано, за счет применении уравнения (2.5), для вычисления скорости на следующем временнóм слое (Vn+ 1).

Свободная поверхность жидкости отслеживается с помощью метода объема жидкости, в котором используется скалярный параметр f, называемый объемной долей (дробной функцией). Этот параметр рассматривается в качестве числового критерия, показывающего величину объема, занимаемого жидкостью в каждой вычислительной ячейке:

(2.7)
$f = \left\{ {\begin{array}{*{20}{c}} 0&{{\text{в газе}}} \\ {{\text{Число между }}0{\text{ и }}1}&{{\text{на поверхности контакта газа и жидкости}}} \\ 1&{{\text{в жидкости}}} \end{array}} \right.$

Таким образом, в настоящем исследовании, помимо уравнений неразрывности и количества движения, решается следующее уравнение переноса для адвекции (горизонтального перемещения) дробной функции:

(2.8)
$\frac{{\partial f}}{{\partial t}} + ({\mathbf{V}} \cdot \nabla )f = 0.{\text{\;}}$

В дополнение к вышеизложенному, используется алгоритм Юнга для построения кусочно-линейной границы раздела [36] при реконструкции свободной поверхности на каждом временнóм слое. В этом алгоритме после решения уравнения адвекции для дробной функции делается вывод, что некоторая ячейка принадлежит области свободной границы, если значение дробной функции для этой ячейки находится между нулем и единицей. После этого граница раздела между жидкостью и газом воссоздается приближенно, а затем объемные потоки через грани элементарных ячеек вычисляются геометрически. Для реконструкции границы раздела аппроксимирующая плоскость располагается в каждой ячейке, содержащей границу раздела. Ориентация этой плоскости и ее расположение в каждой ячейке должны удовлетворять дробной функции этой ячейки и сопрягаться с плоскостями в соседних ячейках. Плоскость, разрезающая кубическую ячейку, представляет собой некоторый многоугольник с числом сторон от трех до шести. Далее вычисляются объемные потоки во всех направлениях. Чтобы минимизировать смещение (сдвиг) ориентации плоскостей, порядок адвекции объема в трех направлениях меняется от одного к другому шагу по времени.

Чтобы рассчитать поверхностное натяжение, нужно удовлетворить следующему уравнению на границе раздела жидкость/газ [37]:

(2.9)
$\left( {{{p}_{{\text{l}}}} - {{p}_{{\text{g}}}} - {{\sigma \kappa }}} \right){{n}_{{\text{i}}}} = \left( {{{{{\tau }}}_{{{\text{l}},{\text{ik}}}}} - {{{{\tau }}}_{{{\text{g}},{\text{ik}}}}}} \right){{n}_{{\text{k}}}} + \frac{{\partial {{\sigma }}}}{{\partial {{x}_{{\text{i}}}}}},{\text{\;}}$
где индексы l и g обозначают жидкость и газ соответственно, σ – поверхностное натяжение, κ – кривизна поверхности, ni и nk есть векторы нормали к поверхностям жидкой и газовой фаз, а ${{{{\tau }}}_{{{\text{l}},{\text{ik}}}}}$ и ${{{{\tau }}}_{{{\text{g}},{\text{ik}}}}}$ представляют собой напряжения сдвига в жидкости и газе, которыми можно пренебречь для упрощения этого уравнения. Считая, что поверхностное натяжение постоянно, это граничное условие на поверхности контакта можно свести к уравнению Лапласа

(2.10)
${{P}_{{\text{l}}}} - {{P}_{{\text{g}}}} = {{\sigma к}}{\text{.}}$

Для того, чтобы проинтегрировать это условие на поверхности контакта в численной модели, сила поверхностного натяжения переформулируется в виде массовой силы в уравнении количества движения. Эта модель, представленная в [38], называется непрерывной моделью поверхностных сил, она широко и со всеми деталями используется в литературе [39–41]. Для расчета массовой силы на основе этой модели, в [42] представлено следующее уравнение:

(2.11)
${{F}_{{{\text{ST}}}}} = \frac{{{{A}_{{{\text{cell}}}}}}}{{{{{{\Omega }}}_{{{\text{cell}}}}}}}{{\sigma к}}{\mathbf{n}},$
где Acell есть площадь свободной поверхности жидкости в каждой ячейке на границе раздела жидкость/газ, ${{{{\Omega }}}_{{{\text{cell}}}}}$ – объем ячейки, а ${\text{к}}$ и n представляют собой кривизну поверхности и вектор нормали к поверхности соответственно, вычисленные с помощью значений дробной функции f следующим образом:

(2.12)
${\mathbf{n}} = \frac{{\nabla f}}{{\left| {\nabla f} \right|}},{\text{\;}}$
(2.13)
${\text{к}} = - \nabla \cdot {\mathbf{n}}.$

2.2. Формулировка задачи

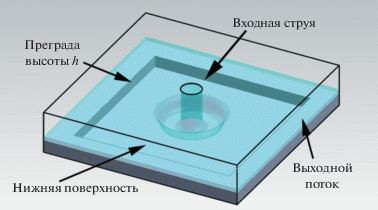
На рис. 2 изображена область вычислений и соответствующие граничные условия. На дне области накладывается условие непротекания и предполагается, что входная струя на верхней границе выходит из круглого сопла в полностью развитом состоянии.

Рис. 2.

Область вычислений при трехмерном моделировании кругового гидравлического прыжка.

Чтобы согласовать высоту течения вниз по потоку, имеются преграды на четырех боковых сторонах области с высотой h. В настоящем моделировании эти преграды моделируются в форме граничных условий. На боковых сторонах области наложено условие непротекания со дна области вплоть до высоты h. Кроме того, выше преград граничное условие есть выходящий поток. В качестве начального условия рассматривается неподвижная пленка жидкости, располагающаяся на нижней поверхности и имеющая толщину h, которая необходима для уменьшения времени вычислений, требуемых для заполнения жидкостью площади, заключенной внутри преград. По этой причине значение дробной функции предполагалась равным единице на дне области вплоть до высоты преграды, а в других ячейках дробная функция считалась равной нулю.

На рис. 3 приведено изометрическое изображение кругового гидравлического прыжка, рассчитанного с помощью предлагаемого численного метода. В этом случае радиус струи a = 5 мм, объемный расход жидкости Q = 31 мл/с и высота преградыt h = 2 мм. Предполагается, что рабочая жидкость есть этилен-гликоль со следующими свойствами: ρ = 1100 кг/м3, ν = 11.8 × 10–6 м2/с и σ = 0.043 Н/м.

Рис. 3.

Пример трехмерного расчета кругового гидравлического прыжка для этилен-гликоля с a = 5 мм, Q = 31 мл/с и h = 2 мм.

3. НЕЗАВИСИМОСТЬ РАСЧЕТОВ ОТ СЕТКИ

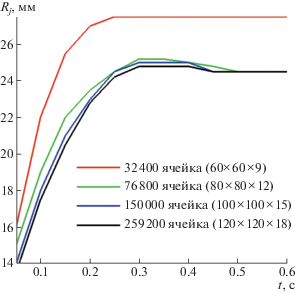
Что касается генерирования сетки, численные расчеты были выполнены на однородной сетке по причине ограничений, связанных с алгоритмом Юнга. Для демонстрации независимости результатов от сетки были использованы четыре размера ячеек для расчета одного случая с одинаковыми условиями, а именно, Q = 47 мл/с, входной радиус струи a = 5 мм и высота жидкости вниз по потоку ho = 4 мм. Преграда вниз по потоку рассматривается в виде твердого квадрата со стороной 160 мм. На рис. 4 изменение радиуса кругового гидравлического прыжка изображено как функция времени для четырех разных размеров сетки. Как можно видеть, когда число ячеек превосходило 76 800, различие между радиусами круговых прыжков уменьшалось, особенно после того, как поток жидкости становился стационарным (приблизительно через 80 с после соударения). По этой причине в настоящем исследовании для моделирования был выбран размер сетки с 150 000 ячейками. В проведенном численном расчете рабочей жидкостью была вода с a = 5 мм, Q = 30 мл/с и h = 2 мм.

Рис. 4.

Зависимость радиуса прыжка от времени для разных размеров сетки. В этих расчетах рабочей жидкостью была вода с a = 5 мм, Q = 30 мл/с и h = 2 мм.

4. ПРОВЕРКА ПРАВИЛЬНОСТИ МОДЕЛИ

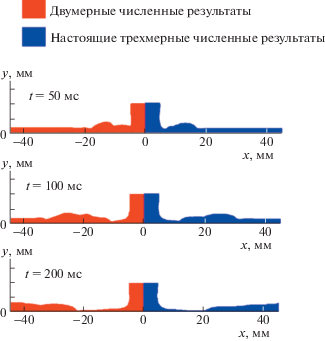
Полученные трехмерные численные результаты сравнивались качественно и количественно с двумерными численными результатами [17] и данными экспериментов [43] с целью проверки правильности предлагаемой модели. На рис. 5 профили свободной поверхности кругового гидравлического прыжка, полученные из настоящего трехмерного численного решения, изображены в три определенные момента времени (справа на рис. 5) и сравнены с двумерными численными результатами [17] (слева на рис. 5). Можно видеть их хорошее согласие. В проведенном численном расчете рабочей жидкостью была вода с a = 5 мм, Q = 30 мл/с и h = 2 мм.

Рис. 5.

Профиль свободной поверхности, полученный из двумерных результатов [17] (слева), в сравнении с трехмерными численными результатами настоящей работы в три разных момента времени. В этих расчетах рабочей жидкостью была вода с a = 5 мм, Q = 30 мл/с и h = 2 мм.

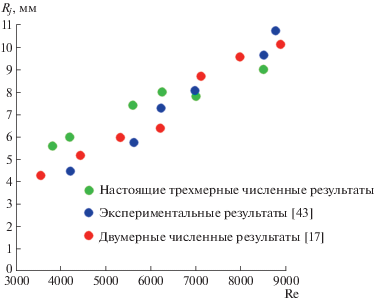
На рис. 6 представлен радиус кругового гидравлического прыжка для разных чисел Рейнольдса, полученный в [17] и [43] и в настоящем исследовании. Из этого рисунка видно хорошее согласие между численными и экспериментальными результатами. Как и ожидалось, радиус прыжка возрастает при увеличении числа Рейнольдса потока.

Рис. 6.

Зависимость радиуса кругового гидравлического прыжка от числа Рейнольдса, полученная из экспериментальных результатов [43] и двумерных численных результатов [17], по сравнению с результатами настоящего трехмерного расчета.

5. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

На рис. 7 изображены линии тока в радиальном сечении струи этилен-гликоля, натекающей на плоскую пластину при Q = 47 мл/с, a = 5.15 мм и ho = 4 мм. При таких условиях наблюдается круговой гидравлический прыжок типа I. Как можно видеть из рис. 7, закрученный жидкий вал, сформировавшийся под свободной поверхностью (“бочка”), вызывает внезапное увеличение высоты свободной поверхности.

Рис. 7.

Линии тока в радиальном сечении кругового гидравлического прыжка типа I; рабочая жидкость – этилен-гликоль с Q = 47 мл/с, a = 5.15 мм и ho = 4 мм.

Из обзора литературы следует, что многоугольный гидравлический прыжок наблюдается как некоторый двухступенчатый прыжок. На рис. 8 изображен шестиугольный гидравлический прыжок [27]. Как показано на рисунке, круговой прыжок наблюдается ниже по потоку от многоугольного гидравлического прыжка. Это означает, что в потоке жидкости имеются две ступени гидравлического прыжка. Форма первого прыжка многоугольная, а второй прыжок – круговой. Таким образом, многоугольный гидравлический прыжок подобен некоторому круговому прыжку типа II в радиальном сечении, где в области течения жидкости существуют два переворачивающихся (закрученных) вала жидкости (две бочки).

Рис. 8.

Результаты наблюдений двухступенчатого прыжка в многоугольном гидравлическом прыжке [27].

Вышеописанное явление также четко прослеживается в численных результатах. На рис. 9 изображены линии тока в струе этилен-гликоля, натекающей на плоскую пластину, с условиями в потоке Q = 55 мл/с, a = 5.15 мм и ho = 5.8 мм. Согласно литературе [31], при увеличении высоты жидкости вниз по потоку форма прыжка изменяется с типа I на тип II.

Рис. 9.

Линии тока в радиальном сечении кругового гидравлического прыжка типа II для этилен-гликоля с условиями в потоке Q = 55 мл/с, a = 5.15 мм и ho = 5.8 мм.

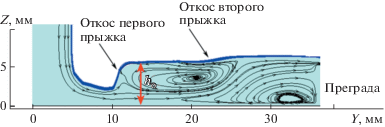
К этому можно добавить, что в области течения жидкости имеются два переворачивающихся (закрученных) вала жидкости (две бочки), одна около твердой поверхности, а другая вблизи свободной поверхности. Эти бочки образуют структуру свободной поверхности в форме двойного прыжка. Как можно видеть из этого рисунка, второй прыжок имеет меньший наклон по сравнению с первым прыжком. В [25] был рассмотрен прыжок типа I и были выведены уравнения для прыжка этого типа. Было предположено, что присутствует тонкий радиальный поток, который продолжается ниже по течению под закрученной бочкой. В настоящем исследовании это предположение о тонкой жидкой пленке наблюдается только вплоть до второй бочки. По этой причине считается, что параметр высоты жидкости вниз по течению (ho), фигурирующий в модели Мартенса [25], является высотой свободной поверхности между первым и вторым прыжками.

На следующем шаге, используя численное решение для получения профиля свободной поверхности жидкости, можно провести оценку числовых значений параметров, используемых в модели Мартенса [25]. Для определения rj и R исследуется наклон высоты свободной поверхности. По мере роста радиуса, отсчитываемого от оси натекающей исходной струи, наблюдается отрицательный наклон, который далее становится равным нулю. При r = rj наклон свободной поверхности начинает возрастать. В настоящем исследовании значение радиуса, при котором наклон превышает 0.1, полагается равным rj. При большем радиусе наклон свободной поверхности растет до некоторого значения, после чего наклон убывает. В этой области, когда наклон становится меньше 0.1, то соответствующий радиус рассматривается как R.

На рис. 10 изображено, что если поперечное сечение кругового прыжка предполагается имеющим форму части круга, то радиус круга может быть получен как функция высоты и ширины прыжка.

Рис. 10.

Радиальное сечение натекания жидкой струи на плоскую пластину. Кривизна прыжка рассматривается как часть круга.

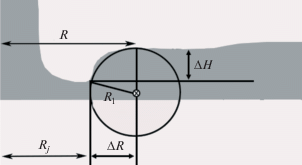
Согласно рассмотрению сил поверхностного натяжения, приложенных к балансу радиальных сил в [25], такое предположение может быть принято. По этой причине на основе рис. 10 можно задать радиус кривизны прыжка R1 следующим образом:

(5.1)
$R_{1}^{2} = \Delta {{R}^{2}} + {{({{R}_{1}} - \Delta H)}^{2}} \to {{R}_{1}} = \frac{{\Delta {{R}^{2}} + \Delta {{H}^{2}}}}{{2\,{\text{*}}\,\Delta H}}.$

Кроме того, поскольку высота и ширина прыжка одного порядка ($\Delta R\sim \Delta H$), можно получить:

(5.2)
${{R}_{1}} \propto \frac{{\Delta {{R}^{2}} + \Delta {{R}^{2}}}}{{2\,{\text{*}}\,\Delta R}} = \Delta R$

Можно сделать вывод, что безразмерный радиус кривизны прыжка порядка δ, т.е.,

(5.3)
${{{{\rho }}}_{1}} = \frac{{{{R}_{1}}}}{R} \propto \frac{{\Delta R}}{R} = {{\delta }}$

Отсюда вытекает, что слагаемое ${{\rho }}_{1}^{'}({{\delta }})$, т.е. производная величины ρ1 по δ в соотношении для параметра формы (B), постоянно для всех значений R и δ. Это означает, что при моделировании различных сценариев развития кругового гидравлического прыжка наклон графика ρ1 как функции δ должен быть почти постоянным и равным ${{\rho }}_{1}^{'}({{{{\delta }}}_{0}})$. Как показано на рис. 11, зависимость безразмерного радиуса кривизны ρ1 от нормализованной ширины бочки δ линейная и наклон свободной поверхности приблизительно равен двум для двух разных диаметров струи (8 и 10 мм).

Рис. 11.

Зависимость безразмерного радиуса кривизны от нормализованной ширины бочки для кругового гидравлического прыжка в случае двух разных диаметрах сопла.

В настоящей работе, чтобы оценить число углов многоугольного прыжка, значение ${{\rho }}_{1}^{'}({{{{\delta }}}_{0}})$ считается равным двум при различных условиях. Следовательно, вычисляется число В, с помощью которого производится оценка числа углов многоугольного прыжка.

В табл. 1 представлена оценка числа углов многоугольных гидравлических прыжков, полученная из комбинированного численно-аналитического метода, представленного в данной работе. Данный комбинированный метод был использован для различных аналитических моделей, представленных уравнениями (1.1), (1.3) и (1.4). В табл. 1 представлены также результаты, полученные по аналитическому методу [26]. Кроме того, представлены экспериментальные результаты [24, 28, 29] для 10 случаев с разными условиями течения. В этих десяти случаях Q лежит в диапазоне 37–70 мл/с, h в диапазоне от 3.52 до 5.86 мм и a на интервале от 5 до 5.15 мм. Следует отметить, что параметры, полученные из численных расчетов и использованные в уравнении (1.1), есть R, rj, ρ1, ${{\rho }}_{1}^{'}({{{{\delta }}}_{0}})$, hi и ho; параметры, полученные из численных расчетов и использованные в уравнении (1.3), есть R, rj, hi и ho; и, наконец, параметры, полученные из численных расчетов и использованные в уравнении (1.4) есть R и rj. Из табл. 1 видно, что уравнение (1.1) дает более точные оценки для числа углов многоугольных гидравлических прыжков по сравнению с другими аналитическими моделями. Важным обстоятельством является то, что уравнение (1.3), в котором пренебрегается поверхностным натяжением, приводит к нежелательным ошибкам. Таким образом, на основе детального сравнения, выполненного в табл. 1, поверхностное натяжение и кривизна поверхности прыжка оказывают сильное воздействие на формирование многоугольных гидравлических прыжков. Кроме того, можно видеть, что уравнение (1.4) и модель, представленная в [26], предсказывают число углов более точно, чем уравнение (1.3) для многоугольника с числом углов меньше шести.

Таблица 1.

Параметры потока и оценка числа углов многоугольного прыжка, полученная из комбинированной численно-аналитической модели, базирующейся на уравнениях (1.1), (1.3) и (1.4). Представлены также значения числа углов прыжка, полученные по модели [26] и измеренные экспериментально

Случай № Параметры потока Оценка числа углов многоугольного прыжка Эксперимен-тальные результаты (ссылка)
Q (мл/с) h (мм) a (мм) Уравнение (1.3) (R, rj, hi и ho получены из расчета) Уравнение (1.4) (R и rj, получены из расчета) Модель Рохаса (R и ho получены из расчета) Уравн. (1.1) (R, rj, ${{{{\rho }}}_{1}}$, ${{\rho }}_{1}^{'}\left( {{{{{\delta }}}_{0}}} \right)$, hi и ho получены из расчета)
1 37 5.67 5.15 0.69 3.63 3.68 3.64 4 [29]
2 60 4.5 5 1.15 7.32 5.84 3.87 4 [28]
3 41.6 4.94 5 0.69 4.16 3.89 4.25 4 [24]
4 49.2 4.97 5 0.71 4.38 4.51 4.12 4 [24]
5 45.5 5.72 5.15 1.14 5.67 3.61 5.55 6 [29]
6 47.1 5.73 5.15 1.04 4.94 4.1 5.57 6 [29]
7 53 4.82 5 0.95 5.46 4.85 5.57 6 [24]
8 63.7 5.86 5.15 1.50 7.9 5.0 7.63 8 [29]
9 48 3.52 5 1.87 9.86 5.99 8.33 8 [28]
10 70 4.65 5 1.49 10.53 6.27 8.25 8 [28]

ВЫВОДЫ

Когда жидкая струя натекает на подложку по нормали, наблюдается круговой гидравлический прыжок. При определенных условиях развитие неустойчивостей во время натекания жидкой струи приводит к изменению структуры течения и формы прыжка от круговой к многоугольной. В настоящей работе используется комбинированный численно-аналитический метод, позволяющий охарактеризовать эффекты этих неустойчивостей и оценить число углов многоугольных гидравлических прыжков. Предлагаемый метод представляет собой некоторую модификацию модели, представленной в [25], в которой пренебрегается поверхностным натяжением из-за отсутствия аналитических выражений для кривизны прыжка и профиля высоты свободной поверхности. Следует отметить, что в аналитической модели, представленной в [25], такие параметры, как отношение высот жидкости вверх/вниз по потоку, отношение внутреннего и внешнего радиусов прыжка, и кривизна прыжка вычисляются на основании некоторого предположения о круговом гидравлическом прыжке. По этой причине в настоящей работе эти необходимые параметры были получены из численной модели кругового гидравлического прыжка. При численном моделировании используется метод объема жидкости вместе с алгоритмом Юнга, чтобы проследить за поведением свободной поверхности жидкости. Оцениваемое число углов многоугольника, полученное на основе комбинированной численно-аналитической модели применительно к десяти разным случаям, доступным в литературе, сравнивается со значениями, полученными экспериментально. Делается вывод, что комбинированная модель, использованная в данном исследовании, приводит к более точному значению числа углов для многоугольных гидравлических прыжков по сравнению с другими моделями, доступными в литературе. Результаты настоящего исследования могут быть использованы в будущих расчетах многоугольных гидравлических прыжков, для которых число углов многоугольника может интегрироваться в круговой гидравлический прыжок, при использовании некоторой модели возмущений.

Список литературы

  1. Mahmoudi S.R., Adamiak K., Castle G.P. Two-phase cooling characteristics of a saturated free falling circular jet of HFE7100 on a heated disk: Effect of jet length // International Journal of Heat and Mass Transfer. 2012. V. 55. P. 6181–6190.

  2. Gradeck M., Kouachi A., Dani A., Arnoult D., Borean J.L. Experimental and numerical study of the hydraulic jump of an impinging jet on a moving surface // Experimental Thermal and Fluid Science. 2006. V. 30. P. 193–201.

  3. Hsu T.T., Walker T.W., Frank C.W., Fuller G.G. Instabilities and elastic recoil of the two-fluid circular hydraulic jump // Experiments in Fluids. 2014. V. 55. P. 1645.

  4. Wilson D.I., Atkinson P., Köhler H., Mauermann M., Stoye H., Suddaby K., Wang T., Davidson J.F., Majschak J.P. Cleaning of soft-solid soil layers on vertical and horizontal surfaces by stationary coherent impinging liquid jets // Chemical Engineering Science. 2014. V. 109. P. 183–196.

  5. Kate R., Das P., Chakraborty S. Hydraulic jumps due to oblique impingement of circular liquid jets on a flat horizontal surface // Journal of Fluid Mechanics. 2007. V. 573. P. 247–263.

  6. Avedisian C., Zhao Z. The circular hydraulic jump in low gravity // Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences. 2000. V. 456. P. 2127–2151.

  7. Craik A., Latham R., Fawkes M., Gribbon P. The circular hydraulic jump // Journal of Fluid Mechanics. 1981. V. 112. P. 347–362.

  8. Baonga J.B., Louahlia-Gualous H., Imbert M. Experimental study of the hydrodynamic and heat transfer of free liquid jet impinging a flat circular heated disk // Applied Thermal Engineering. 2006. V. 26. P. 1125–1138.

  9. Brechet Y., Neda Z. On the circular hydraulic jump // American Journal of Physics. 1999. V. 67. P. 723–731.

  10. Rayleigh L. On the theory of long waves and bores // Proceedings of the Royal Society of London, Series A, Containing Papers of a Mathematical and Physical Character. 1914. V. 90. P. 324–328.

  11. Tani I. Water jump in the boundary layer // Journal of the Physical Society of Japan. 1949. V. 4. P. 212–215.

  12. Биркгоф Г., Сарантонелло Э. Струи, следы и каверны. Москва: Мир, 1964.

  13. Bohr T., Dimon P., Putkaradze V. Shallow-water approach to the circular hydraulic jump // Journal of Fluid Mechanics. 1993. V. 254. P. 635–648.

  14. Bush J.W., Aristoff J.M. The influence of surface tension on the circular hydraulic jump // Journal of Fluid Mechanics. 2003. V. 489. P. 229–238.

  15. Kasimov A.R. A stationary circular hydraulic jump, the limits of its existence and its gas dynamic analogue // Journal of Fluid Mechanics. 2008. V. 601. P. 189–198.

  16. Watson E. The radial spread of a liquid jet over a horizontal plane // Journal of Fluid Mechanics. 1964. V. 20. P. 481–499.

  17. Passandideh-Fard M., Teymourtash A.R., Khavari M. Numerical study of circular hydraulic jump using volume-of-fluid method // Journal of Fluids Engineering. 2011. V. 133. P. 011401.

  18. Yokoi K., Xiao F. A numerical study of the transition in the circular hydraulic jump // Physics Letters A. 1999. V. 257. P. 153–157.

  19. Yokoi K., Xiao F. Mechanism of structure formation in circular hydraulic jumps, Numerical studies of strongly deformed free-surface shallow flows // Physica D: Nonlinear Phenomena. 2002. V. 161. P. 202–219.

  20. Ashgriz N., Washburn R., Barbat T. Segregation of drop size and velocity in jet impinging splash-plate atomizers // International journal of heat and fluid flow. 1996. V. 17. P. 509–516.

  21. Bhunia S.K., Lienhard J.H. Splattering during turbulent liquid jet impingement on solid targets // Journal of Fluids Engineering. 1994. V. 116. № 2. P. 338–344.

  22. Liu X., Lienhard J. The hydraulic jump in circular jet impingement and in other thin liquid films // Experiments in Fluids. 1993. V. 15. P. 108–116.

  23. Ellegaard C., Hansen A.E., Haaning A., Hansen K., Marcussen A., Bohr T., Hansen J.L., Watanabe S. Creating corners in kitchen sinks // Nature. 1998. V. 392. P. 767.

  24. Ellegaard C., Hansen A.E., Haaning A., Hansen K., Marcussen A., Bohr T., Hansen J.L., Watanabe S. Cover illustration: Polygonal hydraulic jumps // Nonlinearity. 1999. V. 12. P. 1.

  25. Martens E.A., Watanabe S., Bohr T. Model for polygonal hydraulic jumps // Physical Review E. 2012. V. 85. P. 036316.

  26. Rojas N., Tirapegui E. Harmonic solutions for polygonal hydraulic jumps in thin fluid films // Journal of Fluid Mechanics. 2015. V. 780. P. 99–119.

  27. Soukhtanlou E., Teymourtash A.R., Mahpeykar M.R. The effects of target plate roughness on the parameters of circular hydraulic jumps: An experimental investigation // Journal of Applied Fluid Mechanics. 2018. V. 11. № 6. P. 1691–1701.

  28. Soukhtanlou E., Teymourtash A.R., Mahpeykar M.R. Proposal of experimental relations for determining the number of sides of polygonal hydraulic jumps // Modares Mechanical Engineering. 2018. V. 18. P. 273–280.

  29. Teymourtash A.R., Mokhlesi M. Experimental investigation of stationary and rotational structures in non-circular hydraulic jumps // Journal of Fluid Mechanics. 2015. V. 762. P. 344–360.

  30. Bush J.W., Aristoff J.M., Hosoi A. An experimental investigation of the stability of the circular hydraulic jump // Journal of Fluid Mechanics. 2006. V. 558. P. 33–52.

  31. Bohr T., Ellegaard C., Hansen A.E., Hansen K., Haaning A., Putkaradze V., Watanabe S. Separation and pattern formation in hydraulic jumps // Physica A: Statistical Mechanics and its Applications. 1998. V. 249. P. 111–117.

  32. Rojas N., Argentina M., Tirapegui E. A progressive correction to the circular hydraulic jump scaling // Physics of Fluids. 2013. V. 25. P. 042105.

  33. Singh D., Das A.K. Computational simulation of radially asymmetric hydraulic jumps and jump–jump interactions // Computers & Fluids. 2018. V. 170. P. 1–12.

  34. Pasandideh-Fard M., Chandra S., Mostaghimi J. A three-dimensional model of droplet impact and solidification // International Journal of Heat and Mass Transfer. 2002. V. 45. P. 2229–2242.

  35. Kershaw D.S. The incomplete Cholesky – conjugate gradient method for the iterative solution of systems of linear equations // Journal of Computational Physics. 1978. V. 26. P. 43–65.

  36. Youngs D.L. Time-dependent multi-material flow with large fluid distortion, in: Numerical Methods for Fluid Dynamics. Oxford: Oxford University Press, 1985.

  37. Ландау Л.Д., Лифшиц Е.М. Теоретическая Физика. Т. 6. Гидродинамика. М.: Наука, 1986.

  38. Brackbill J.U., Kothe D.B., Zemach C. A continuum method for modeling surface tension // Journal of computational physics. 1992. V. 100. P. 335–354.

  39. Bussmann M., Mostaghimi J., Chandra S. On a three-dimensional volume tracking model of droplet impact // Physics of Fluids. 1999. V. 11. P. 1406–1417.

  40. Iranmanesh A., Passandideh-Fard M. A three-dimensional numerical approach on water entry of a horizontal circular cylinder using the volume of fluid technique // Ocean Engineering. 2017. V. 130. P. 557–566.

  41. Mirzaii I., Passandideh-Fard M. Modeling free surface flows in presence of an arbitrary moving object // International Journal of Multiphase Flow. 2012. V. 39. P. 216–226.

  42. Aleinov I., Puckett E. Computing surface tension with high-order kernels // Proceedings of the 6th International Symposium on Computational Fluid Dynamics. 1995. P. 13–18.

  43. Errico M. A study of the interaction of liquid jets with solid surfaces (Impingement, cleaning). Ph.D. Thesis. San Diego: University of California, 1987.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал