Известия РАН. Механика жидкости и газа, 2021, № 5, стр. 138-150

ДЕФОРМАЦИЯ КАПЛИ НЕВЯЗКОЙ НАМАГНИЧИВАЮЩЕЙСЯ ЖИДКОСТИ В НЕСТАЦИОНАРНОМ МАГНИТНОМ ПОЛЕ

А. Н. Тятюшкин^a, *

^a Московского государственного университета им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия

^* E-mail: tan@imec.msu.ru

Поступила в редакцию 30.11.2020
После доработки 13.04.2021
Принята к публикации 23.04.2021

DOI: 10.31857/S0568528121050145

Полный текст (PDF)

Аннотация

Теоретически исследуется изменение формы капли намагничивающейся жидкости, взвешенной в несмешивающейся с ней другой намагничивающейся жидкости, в нестационарном однородном магнитном поле при больших числах Рейнольдса. Система уравнений состоит из уравнения неразрывности для несжимаемой жидкости, уравнения движения для идеальной несжимаемой жидкости, уравнений Максвелла в квазистационарном приближении и приближении феррогидродинамики. Для решения задачи используется представление напряженности магнитного поля и скорости жидкости в виде мультипольного разложения, выраженного через неприводимые тензоры. При таком подходе напряженность магнитного поля и скорость ищутся в виде рядов с векторными и тензорными коэффициентами, для которых получаются соотношения, позволяющие их определить. С использованием этих соотношений коэффициенты ищутся в виде асимптотических разложений по параметру, малость которого обеспечивает малость деформаций капли. Скорость течения и напряженность магнитного поля и форма капли найдены с точностью до членов первого порядка по малому параметру. Решены задачи о вынужденных и собственных колебаниях капли, вызванных мгновенным включением приложенных гармонически колеблющихся и вращающихся полей.

Ключевые слова: феррогидродинамика, вязкость, капля намагничивающейся жидкости, переменное магнитное поле

Под действием приложенного переменного магнитного поля капля намагничивающейся жидкости, взвешенная в несмешивающейся с ней намагничивающейся жидкости с другой магнитной проницаемостью, деформируется. При этом, поскольку поле переменное, ее форма меняется. Изменение формы капли вызывает течение в жидкостях внутри и вне капли.

Работы по исследованию формы капли намагничивающейся жидкости в однородном магнитном поле начали проводиться после изобретения магнитных жидкостей. Магнитная жидкость представляет собой дисперсию твердого материала с сильными магнитными свойствами (ферромагнитного или ферримагнитного) в жидкой среде. Вследствие наличия составляющей с сильными магнитными свойствами такая среда обладает настолько сильными магнитными свойствами, что ее взаимодействие с магнитным полем можно наблюдать в экспериментах с обычными (не сверхсильными) магнитными полями.

В работе [1] выведена система уравнений, определяющая форму капли в постоянном однородном магнитном поле. Система решена аналитически для двух случаев, когда некоторые безразмерные параметры, входящие в систему уравнений, малы. Проведено исследование системы уравнений для произвольных значений этих параметров методами численного анализа, которое показало, что при увеличении напряженности магнитного поля капля вытягивается с образованием шейки. В работах [2, 3] описаны теоретические и экспериментальные исследования формы капли намагничивающейся жидкости в постоянном магнитном поле. Основной вывод теоретического исследования работы [2] заключается в том, что как капля магнитной жидкости в немагнитной, так и капля немагнитной жидкости в магнитной вытягиваются вдоль силовых линий приложенного однородного поля. Проведен эксперимент по изучению поведения капли магнитной жидкости в немагнитной, подтвердивший этот теоретический вывод. В работе [3] выведены формулы, позволяющие определить магнитную восприимчивость, плотность и поверхностное натяжение магнитной жидкости по результатам экспериментального исследования изменения ее формы и положения равновесия в осесимметричном неоднородном магнитном поле, и описаны результаты соответствующих экспериментов. В работе [4] описаны теоретическое и экспериментальное исследования влияния приложенного однородного магнитного поля на форму капли концентрированной магнитной жидкости, взвешенной в магнитной жидкости с меньшей концентрацией магнитной фазы. Проведено экспериментальное исследование зависимости отношения максимальных размеров капли поперек вектора напряженности приложенного поля и вдоль него от абсолютной величины напряженности. В предположении, что капля имеет форму вытянутого сфероида, а коэффициенты магнитной проницаемости концентрированной и разреженной фаз и объем капли не зависят от напряженности, эта зависимость получена теоретически. Сравнивая теоретически полученную зависимость и экспериментальные данные, авторы получили экспериментальное значение поверхностного натяжения. Экспериментально обнаружен гистерезис зависимости отношения размеров капли от напряженности. Предложено теоретическое объяснение этого явления, которое связывает его с тем, что эта зависимость неоднозначна в некотором интервале изменения напряженности, и с тем, что на этом интервале один из трех участков кривой, представляющей эту зависимость, соответствует состояниям неустойчивого равновесия капли. Влияние зависимости поверхностного натяжения от параметров магнитного поля на изменение формы капли намагничивающейся жидкости в постоянных магнитных полях исследовалось в работах [5, 6].

Результаты экспериментального и теоретического исследования поведения капель магнитной жидкости в переменных магнитных полях представлены в работах [7–15]. Изучалось также и поведение в переменном магнитном поле капель обычной жидкости, взвешенных в магнитной жидкости [16]. В работе [7] выведены уравнения движения малой капли намагничивающейся идеальной жидкости в предположении о том, что капля имеет форму эллипсоида вращения. Решена осесимметричная задача о колебаниях капли, помещенной в немагнитную жидкость, в окрестности устойчивого положения равновесия в переменном магнитном поле. Описаны резонансные свойства колебаний центра и формы капли. В работах [7, 10, 11, 13, 15] для теоретического описания поведения капли магнитной жидкости в переменном однородном магнитном поле использовались модели, основанные на предположении о форме капли. В работах [8, 9, 12, 14] для определения формы капли использовались асимптотические методы.

В данной работе задача о форме капли и течении в переменном однородном магнитном поле решается при помощи асимптотических методов без использования предположения о форме капли. В рамках такого подхода форма капли, напряженность магнитного поля, скорость и давление в течении определяются из системы уравнений и граничных условий, описывающих магнитное поле и течение. При этом для того, чтобы асимптотические методы можно было применять, деформации капли считаются малыми. Данный подход использовался также в работах [17–19], в которых теоретически исследовалось поведение капли вязкой магнитной жидкости в переменных полях в пренебрежении ее инерции. В данной работе неустановившееся течение внутри и вне капли намагничивающейся жидкости, взвешенной в несмешивающейся с ней другой намагничивающейся жидкости в переменном магнитном поле, исследуется в пренебрежении вязкости жидкостей.

1. ПОСТАНОВКА ЗАДАЧИ

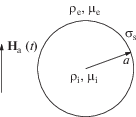
Рассмотрим каплю однородной, несжимаемой и намагничивающейся жидкости, окруженную несмешивающейся с ней однородной, несжимаемой и намагничивающейся жидкостью, к которой приложено однородное переменное магнитное поле с напряженностью ${{{\mathbf{H}}}_{{\text{a}}}} = {{{\mathbf{H}}}_{{\text{a}}}}(t)$, где $t$ – время. Пусть a – радиус капли в отсутствие приложенного поля. Будем считать, что капля настолько крупная, что числа Рейнольдса достаточно высоки, чтобы пренебречь вязкостью и считать жидкости идеальными. Коэффициенты электропроводности жидкостей считаются достаточно малыми, чтобы выполнялось приближение феррогидродинамики (см. [20]). Пусть ${{\rho }_{{\text{i}}}}$ и ${{\mu }_{{\text{i}}}}$ и ${{\rho }_{{\text{e}}}}$ и ${{\mu }_{{\text{e}}}}$ – плотности и магнитные проницаемости жидкости капли и окружающей ее жидкости соответственно, ${{\sigma }_{{\text{s}}}}$ – поверхностное натяжение границы раздела жидкостей. Влиянием силы тяжести в данной задаче пренебрегается, так что результаты ее решения можно использовать либо для капли в невесомости, либо при ${{\rho }_{{\text{i}}}} = {{\rho }_{{\text{e}}}}$.

Для того, чтобы найти форму капли, а также напряженность магнитного поля H, скорость v и давление p как функции радиус-вектора ${\mathbf{r}}$ и времени $t$ при сделанных выше предположениях, будем использовать систему уравнений феррогидродинамики (см. [20]), записанную для магнитных полей в квазистационарном приближении и для течений идеальных жидкостей. Эта система состоит из уравнения неразрывности для несжимаемой жидкости

(1.1)

$\nabla \cdot {\mathbf{v}} = 0$

уравнения движения

(1.2)

$\rho \frac{{\partial {\mathbf{v}}}}{{\partial t}} + \rho {\mathbf{v}} \cdot \nabla {\mathbf{v}} = \nabla \cdot \left( { - p{\mathbf{I}} + {{\sigma }_{{\text{m}}}}} \right)$

уравнений Максвелла в приближениях феррогидродинамики и квазистационарного поля

(1.3)

$\nabla \cdot {\mathbf{B}} = 0,\quad \nabla \times {\mathbf{H}} = 0$

и материального соотношения

(1.4)

${\mathbf{B}} = \mu {\mathbf{H}}$

Здесь формулы записаны для гауссовой системы единиц, символы “$ \cdot $”и “×” обозначают скалярное и векторное произведения; ${\mathbf{B}}$ – магнитная индукция, $\rho = {{\rho }_{{\text{i}}}}$ и $\mu = {{\mu }_{{\text{i}}}}$ внутри капли, $\rho = {{\rho }_{{\text{e}}}}$ и $\mu = {{\mu }_{{\text{e}}}}$ вне ее; $\nabla $ – оператор набла, ${\mathbf{I}}$ – единичный тензор, ${{\sigma }_{{\text{m}}}}$ – тензор магнитных напряжений, выраженный следующим образом:

${{\sigma }_{{\text{m}}}} = \frac{1}{{4\pi }}{\mathbf{BH}} - \frac{1}{{8\pi }}{\mathbf{B}} \cdot {\mathbf{HI}}$

где AB обозначает диадное произведение векторов A и B, $\nabla {\mathbf{f}}$ обозначает диадное произведение оператора набла и векторного поля ${\mathbf{f}} = {\mathbf{f}}({\mathbf{r}})$, ${{{\mathbf{T}}}^{{\text{S}}}}$ обозначает симметричную часть тензора T.

Будем предполагать, что числа Рейнольдса не настолько высоки, чтобы происходил переход к турбулентности. Таким образом, течение в жидкостях является ламинарным и потенциальным. Тогда уравнение неразрывности с учетом выражения для скорости течения через потенциал

(1.5)

${\mathbf{v}} = \nabla \Phi $

дает уравнение Лапласа для потенциала

(1.6)

$\Delta \Phi = 0$

где Δ – лапласиан. Отметим, что формула (1.5) определяет потенциал $\Phi = \Phi ({\mathbf{r}},t)$ с точностью до некоторой функции времени.

Используя уравнение неразрывности (1.1) и уравнения Максвелла (1.3) и учитывая, что магнитная проницаемость постоянна, уравнение движения (1.2) можно переписать в виде уравнения Эйлера (см. [20])

$\rho \frac{{\partial {\mathbf{v}}}}{{\partial t}} + \rho {\mathbf{v}} \cdot \nabla {\mathbf{v}} = - \nabla p$

Оно с учетом потенциальности движения дает следующее уравнение:

$\nabla \left( {\rho \frac{{\partial \Phi }}{{\partial t}} + \rho \frac{{{{{v}}^{2}}}}{2}} \right) = - \nabla p$

Из этого уравнения следует выражение для давления через потенциал скорости

(1.7)

$p = - \rho \frac{{\partial \Phi }}{{\partial t}} - \frac{1}{2}\rho \mathop {\left| {\nabla \Phi } \right|}\nolimits^2 + {{C}_{p}}(t)$

где ${{C}_{p}}(t)$ – некоторая функция времени, определяемая из граничных условий. Таким образом, скорость и давление в течении определяются потенциалом скорости при помощи формул (1.5) и (1.7), а сам потенциал является решением уравнения Лапласа (1.6).

Граничные условия на границе раздела жидкостей включают в себя условие непроницаемости

(1.8)

$\mathop {\left. {\mathbf{v}} \right|}\nolimits_{\text{e}} \cdot {\mathbf{n}} = \mathop {\left. {\mathbf{v}} \right|}\nolimits_{\text{i}} \cdot {\mathbf{n}} = {{v}_{{{\text{s}}n}}}$

условия для скачков нормальной и тангенциальной составляющих вектора напряжений ${{\sigma }_{n}}\, = \,{\mathbf{n}}\, \cdot \,( - p{\mathbf{I}}\, + \,{{\sigma }_{{\text{m}}}})$

(1.9)

${\mathbf{n}} \cdot \mathop {[ - p{\mathbf{I}} + {{\sigma }_{{\text{m}}}}]}\nolimits_{\text{s}} \cdot {\mathbf{n}} = - {{\sigma }_{{\text{s}}}}K$

(1.10)

${\mathbf{n}} \times \mathop {[{{\sigma }_{{\text{m}}}}]}\nolimits_{\text{s}} \cdot {\mathbf{n}} = 0$

условие непрерывности для тангенциальной составляющей напряженности магнитного поля

(1.11)

$\mathop {\left[ {\mathbf{H}} \right]}\nolimits_{\text{s}} \times {\mathbf{n}} = 0$

и для нормальной составляющей индукции магнитного поля

(1.12)

$\mathop {\left[ {\mathbf{B}} \right]}\nolimits_{\text{s}} \cdot {\mathbf{n}} = 0$

Здесь $\mathop {\left. A \right|}\nolimits_{\text{i}} $ и $\mathop {\left. A \right|}\nolimits_{\text{e}} $ обозначают значения величины $A$ на границе раздела между жидкостями, достигаемые изнутри и снаружи капли соответственно, ${{[A]}_{{\text{s}}}} = \mathop {\left. A \right|}\nolimits_{\text{e}} - \mathop {\left. A \right|}\nolimits_{\text{i}} $ обозначает скачок величины A на границе раздела жидкостей при движении изнутри наружу, n – вектор внешней единичной нормали на данной точке границы раздела, ${{{v}}_{{{\text{s}}n}}}$ – нормальная составляющая скорости поверхности капли в данной точке, K – средняя кривизна поверхности капли. Определение средней кривизны, используемое в данной работе – такое, что она принимает отрицательные значения на поверхности выпуклой области. Предполагается, что выполняются условия для того, чтобы можно было считать поверхностное натяжение не зависящим от магнитного поля (см. [5, 6]).

Условия непрерывности для тангенциальных компонент скорости и напряженности магнитного поля и нормальных компонент скорости и магнитной индукции поля позволяют ввести следующие векторные и скалярные поля, определенные на поверхности капли:

${{{\mathbf{v}}}_{{{\text{s}}\tau }}} = {\mathbf{n}} \times \left( {\mathop {\left. {\mathbf{v}} \right|}\nolimits_{\text{i}} \times {\mathbf{n}}} \right) = {\mathbf{n}} \times \left( {\mathop {\left. {\mathbf{v}} \right|}\nolimits_{\text{e}} \times {\mathbf{n}}} \right)$

(1.13)

${{{\mathbf{H}}}_{{{\text{s}}\tau }}} = {\mathbf{n}} \times \left( {\mathop {\left. {\mathbf{H}} \right|}\nolimits_{\text{i}} \times {\mathbf{n}}} \right) = {\mathbf{n}} \times \left( {\mathop {\left. {\mathbf{H}} \right|}\nolimits_{\text{e}} \times {\mathbf{n}}} \right)$

(1.14)

${{{v}}_{{{\text{s}}n}}} = \mathop {\left. {\mathbf{v}} \right|}\nolimits_{\text{i}} \cdot {\mathbf{n}} = \mathop {\left. {\mathbf{v}} \right|}\nolimits_{\text{e}} \cdot {\mathbf{n}}$

(1.15)

${{B}_{{{\text{s}}n}}} = \mathop {\left. {\mathbf{B}} \right|}\nolimits_{\text{i}} \cdot {\mathbf{n}} = \mathop {\left. {\mathbf{B}} \right|}\nolimits_{\text{e}} \cdot {\mathbf{n}}$

Отметим, что вследствие пренебрежения вязкостью жидкостей условие непрерывности тангенциальной составляющей вектора напряжений (1.10) следует из граничных условий (1.11) и (1.12), а также из материального соотношения (1.4). Кроме того, используя эти условия и материальное соотношение, условия для нормальной составляющей вектора напряжений (1.9) с использованием введенных обозначений (1.13) и (1.15) можно преобразовать к виду

(1.16)

$ - \mathop {\left[ p \right]}\nolimits_{\text{s}} + \frac{1}{{8\pi }}\left( {\frac{1}{{{{\mu }_{{\text{e}}}}}} - \frac{1}{{{{\mu }_{{\text{i}}}}}}} \right)B_{{{\text{s}}n}}^{2} - \frac{1}{{8\pi }}\left( {{{\mu }_{{\text{e}}}} - {{\mu }_{{\text{i}}}}} \right)H_{{{\text{s}}\tau }}^{2} = - {{\sigma }_{{\text{s}}}}K$

Граничные условия на бесконечности имеют вид

(1.17)

${\mathbf{v}}({\mathbf{r}},t) \to 0,\quad p({\mathbf{r}},t) \to {{p}_{\infty }},\quad {\mathbf{H}}({\mathbf{r}},t) \to {{{\mathbf{H}}}_{{\text{a}}}}\quad {\text{при}}\quad r \to \infty $

где ${{p}_{\infty }}$ – давление на бесконечности.

Кроме того, ${\mathbf{v}}({\mathbf{r}},t)$, $p({\mathbf{r}},t)$ и ${\mathbf{H}}({\mathbf{r}},t)$ должны быть ограниченными для всех ограниченных значений ${\mathbf{r}}$.

Из граничных условий (1.17) с учетом формул, определяющих потенциал скорости (1.5) и давление (1.7), следует соотношение, определяющее функцию ${{C}_{p}}(t)$

${{p}_{\infty }} = - \rho \mathop {lim}\limits_{r \to \infty } \frac{{\partial \Phi }}{{\partial t}} + {{C}_{p}}(t) = - \rho \frac{\partial }{{\partial t}}\mathop {lim}\limits_{r \to \infty } \Phi + {{C}_{p}}(t)$

Для однозначного определения потенциала скорости установим для него следующее граничное условие на бесконечности:

(1.18)

$\Phi ({\mathbf{r}},t) \to 0,\quad r \to \infty $

Тогда ${{C}_{p}}(t) = {{p}_{\infty }}$ и давление

(1.19)

$p = {{p}_{\infty }} - \rho \frac{{\partial \Phi }}{{\partial t}} - \frac{1}{2}\rho \mathop {\left| {\nabla \Phi } \right|}\nolimits^2 $

Рассмотрим деформации капли. Ее поверхность зададим следующим уравнением:

(1.20)

$r = a + h\left( {\frac{{\mathbf{r}}}{r},t} \right)$

где $h\left( {{\mathbf{r}}{\text{/}}r,t} \right) = h\left( {{{{\mathbf{n}}}_{0}},t} \right)$ – некоторая функция векторного и скалярного аргументов ${{{\mathbf{n}}}_{0}} = {\mathbf{r}}{\text{/}}r$ и t. Функция $h\left( {{{{\mathbf{n}}}_{0}},t} \right)$ может быть представлена в виде

$h = h\left( {{{{\mathbf{n}}}_{0}},t} \right) = \sum\limits_{n = 0}^\infty {{{{\mathbf{h}}}_{n}}} \cdot {{\,}^{n}}{\mathbf{n}}_{0}^{n}$

Это однозначно определяет форму капли.

Здесь ${{{\mathbf{h}}}_{n}} = {{{\mathbf{h}}}_{n}}(t)$ – некоторые зависящие от времени тензоры, каждый из которых – либо произвольный скаляр при n = 0, либо произвольный вектор при n = 1, либо при $n > 1$ произвольный неприводимый тензор n-го порядка, т.е. тензор симметричный по отношению к любой паре индексов и такой, что его свертка по любой паре индексов равна нулю. Здесь и далее ${{{\mathbf{b}}}^{n}}$ обозначает n-ю диадную степень вектора ${\mathbf{b}}$ (т.е. $(n - 1)$-кратное диадное произведение вектора ${\mathbf{b}}$ на себя), ${{ \cdot }^{n}}$ обозначает n-кратную свертку тензоров по смежным индексам.

Из условия непроницаемости следует соотношение между функцией $h\left( {{{{\mathbf{n}}}_{0}},t} \right)$ и ${{{v}}_{{{\text{s}}n}}}$

(1.21)

${\mathbf{n}} \cdot {{{\mathbf{n}}}_{0}}\frac{{\partial h}}{{\partial t}} = {{{v}}_{{{\text{s}}n}}}$

2. РЕШЕНИЕ

Ищем напряженность магнитного поля в виде

${\mathbf{H}} = \nabla \psi $

где потенциал магнитного поля

(2.1)

$\psi = \left\{ \begin{gathered} {{{\mathbf{H}}}_{{\text{a}}}} \cdot {\mathbf{r}} - \sum\limits_{n = 1}^\infty {{{{\mathbf{M}}}_{{{\text{e}}n}}}} {{ \cdot }^{n}}\frac{{{{{\mathbf{r}}}^{n}}}}{{{{r}^{{2n + 1}}}}},\quad r > a + h \hfill \\ {{{\mathbf{H}}}_{{\text{a}}}} \cdot {\mathbf{r}} - \sum\limits_{n = 1}^\infty {{{{\mathbf{M}}}_{{{\text{i}}n}}}} {{ \cdot }^{n}}\frac{{{{{\mathbf{r}}}^{n}}}}{{{{a}^{{2n + 1}}}}},\quad r \leqslant a + h \hfill \\ \end{gathered} \right.$

Здесь ${{{\mathbf{M}}}_{{{\text{e}}n}}} = {{{\mathbf{M}}}_{{{\text{e}}n}}}(t)$ и ${{{\mathbf{M}}}_{{{\text{i}}n}}} = {{{\mathbf{M}}}_{{{\text{i}}n}}}(t)$ – тензоры, каждый из которых – либо некоторый вектор для n = 1 или для $n > 1$ – некоторый неприводимый тензор n-го порядка. Для поля, заданного в таком виде, уравнения Максвелла (1.3) с материальным соотношением (1.4), условие на бесконечности (1.17) для H и условие ограниченности H удовлетворяются автоматически.

Условие непрерывности тангенциальной составляющей напряженности магнитного поля (1.11) равносильно условию непрерывности магнитного потенциала

(2.2)

$\mathop {\left[ \psi \right]}\nolimits_{\text{s}} = 0$

Используя (2.1), получим из граничных условий (2.2) и (1.12) два соотношения для определения ${{{\mathbf{M}}}_{{{\text{i}}n}}}$, ${{{\mathbf{M}}}_{{{\text{e}}n}}}$ и $h = h\left( {{{{\mathbf{n}}}_{0}},t} \right)$.

Скорость и давления в течении определяются через потенциал скорости при помощи формул (1.5) и (1.19), а сам потенциал является решением уравнения Лапласа (1.6) с граничным условием на границе раздела

(2.3)

${\mathbf{n}} \cdot \mathop {\left[ {\nabla \Phi } \right]}\nolimits_{\text{s}} = 0$

которое следует из условия непроницаемости (1.8), и с условием на бесконечности (1.18). Из условий ограниченности скорости и давления следует условие ограниченности потенциала скорости. Скалярное поле на поверхности капли ${{{v}}_{{{\text{s}}n}}}$, определенное формулой (1.14), выражается через потенциал скорости следующим образом:

${{{v}}_{{{\text{s}}n}}} = \mathop {\left. {\left( {\nabla \Phi } \right)} \right|}\nolimits_{\text{i}} \cdot {\mathbf{n}} = \mathop {\left. {\left( {\nabla \Phi } \right)} \right|}\nolimits_{\text{e}} \cdot {\mathbf{n}}$

Будем искать потенциал скорости в виде

(2.4)

$\Phi = \left\{ \begin{gathered} \sum\limits_{n = 1}^\infty {{{\Phi }_{{{\text{e}}n}}}} {{ \cdot }^{n}}\frac{{{{{\mathbf{r}}}^{n}}}}{{{{r}^{{2n + 1}}}}},\quad r > a + h \hfill \\ \sum\limits_{n = 1}^\infty {{{\Phi }_{{{\text{i}}n}}}} {{ \cdot }^{n}}\frac{{{{{\mathbf{r}}}^{n}}}}{{{{a}^{{2n + 1}}}}},\quad r \leqslant a + h \hfill \\ \end{gathered} \right.$

Здесь ${{\Phi }_{{{\text{e}}n}}} = {{\Phi }_{{{\text{e}}n}}}(t)$ и ${{\Phi }_{{{\text{i}}n}}} = {{\Phi }_{{{\text{i}}n}}}(t)$ – тензоры, каждый из которых – либо некоторый вектор для n = 1 или для $n > 1$ – некоторый неприводимый тензор n-го порядка, ${{p}_{0}} = {{p}_{0}}(t)$ – подлежащее определению давление в центре капли. Для потенциала скорости, заданного в таком виде, уравнения Лапласа (1.6), условие на бесконечности (1.18) и условие ограниченности $\Phi $ удовлетворяются автоматически.рис. 1

Рис. 1.

Постановка задачи.

Используя (2.4), получим из граничных условий (2.3), (1.21) и (1.16) три соотношения для определения ${{\Phi }_{{{\text{i}}n}}}$, ${{\Phi }_{{{\text{e}}n}}}$ и $h = h\left( {{{{\mathbf{n}}}_{0}},t} \right)$ при известных M_in и M_en.

Таким образом, для того, чтобы решить поставленную выше задачу, необходимо найти неизвестные векторные и тензорные функции ${{{\mathbf{M}}}_{{{\text{e}}n}}}(t)$, ${{\Phi }_{{{\text{e}}n}}}(t)$, ${{{\mathbf{M}}}_{{{\text{i}}n}}}(t)$, и ${{\Phi }_{{{\text{i}}n}}}(t)$ ($n = 1,\;2,\; \ldots $), а также $h({{{\mathbf{n}}}_{0}},t)$ и ${{p}_{0}}(t)$, воспользовавшись соотношениями, полученными из граничных условий (2.2), (1.12), (2.3), (1.21) и (1.16).

Обезразмерим полученные из граничных условий соотношения, введя безразмерные неизвестные векторные, тензорные и скалярные функции ${\mathbf{M}}_{{{\text{e}}n}}^{ * }(t*)$, $\Phi _{{{\text{e}}n}}^{ * }(t*)$, ${\mathbf{M}}_{{{\text{i}}n}}^{ * }(t*)$, $\Phi _{{{\text{i}}n}}^{*}(t*)$ ($n = 1,2, \ldots $), $h{\text{*}}({{{\mathbf{n}}}_{0}},t*)$ и $p_{0}^{ * }(t*)$ следующим образом:

$\begin{gathered} {{{\mathbf{M}}}_{{{\text{e}}n}}}(t) = \frac{{{{\mu }_{{\text{i}}}} - {{\mu }_{{\text{e}}}}}}{{{{\mu }_{{\text{e}}}}}}{{a}^{{n + 2}}}{{H}_{{am}}}{\mathbf{M}}_{{{\text{e}}n}}^{*}(t*),\quad {{\Phi }_{{{\text{e}}n}}}(t) = \sqrt {\frac{{{{\sigma }_{{\text{s}}}}a}}{{{{\rho }_{{\text{e}}}}}}} {{a}^{{n + 1}}}\Phi _{{{\text{e}}n}}^{*}(t*) \\ {{{\mathbf{M}}}_{{{\text{i}}n}}}(t) = \frac{{{{\mu }_{{\text{i}}}} - {{\mu }_{{\text{e}}}}}}{{{{\mu }_{{\text{e}}}}}}{{a}^{{n + 2}}}{{H}_{{am}}}{\mathbf{M}}_{{{\text{i}}n}}^{*}(t*),\quad {{\Phi }_{{{\text{i}}n}}}(t) = \sqrt {\frac{{{{\sigma }_{{\text{s}}}}a}}{{{{\rho }_{{\text{e}}}}}}} {{a}^{{n + 1}}}\Phi _{{{\text{i}}n}}^{*}(t*) \\ h({{{\mathbf{n}}}_{0}},t) = ah{\text{*}}({{{\mathbf{n}}}_{0}},t*),\quad {{p}_{0}}(t) = \frac{{\left( {{{\mu }_{{\text{i}}}} - {{\mu }_{{\text{e}}}}} \right)H_{{am}}^{2}}}{{4\pi }}p_{0}^{*}(t*) + {{p}_{\infty }} + \frac{{2{{\sigma }_{{\text{s}}}}}}{a},\quad t = \sqrt {\frac{{{{\rho }_{{\text{e}}}}{{a}^{3}}}}{{{{\sigma }_{{\text{s}}}}}}} {\kern 1pt} {\kern 1pt} t{\text{*}} \\ \end{gathered} $

Обезразмеренные соотношения содержат следующие безразмерные величины:

${\mathbf{H}}_{{\text{a}}}^{*} = {\mathbf{H}}_{{\text{a}}}^{*}(t{\text{*}}) = \frac{{{{{\mathbf{H}}}_{{\text{a}}}}}}{{{{H}_{{am}}}}},\quad \mu _{{\text{i}}}^{*} = \frac{{{{\mu }_{{\text{i}}}}}}{{{{\mu }_{{\text{e}}}}}},\quad \rho _{{\text{i}}}^{*} = \frac{{{{\rho }_{{\text{i}}}}}}{{{{\rho }_{{\text{e}}}}}},\quad \alpha = \frac{{\left( {{{\mu }_{{\text{i}}}} - {{\mu }_{{\text{e}}}}} \right)aH_{{am}}^{2}}}{{4\pi {{\sigma }_{{\text{s}}}}}}$

где ${{H}_{{am}}}$ – максимальное значение модуля вектора напряженности приложенного магнитного поля.

Будем искать неизвестные векторы, тензоры и скаляры ${\mathbf{M}}_{{{\text{e}}n}}^{*}$, $\Phi _{{{\text{e}}n}}^{*}$, ${\mathbf{M}}_{{{\text{i}}n}}^{*}$, $\Phi _{{{\text{i}}n}}^{*}$ ($n = 1,\;2,\; \ldots $), $h{\text{*}}$ и $p_{0}^{*}$ в виде асимптотических разложений

(2.5)

$\begin{gathered} {\mathbf{M}}_{{{\text{e}}n}}^{*} \sim \sum\limits_{j = 0}^\infty {{{\alpha }^{j}}} {\mathbf{M}}_{{{\text{e}}n,j}}^{*}\quad {\text{при}}\quad \alpha \to 0,\quad \Phi _{{{\text{e}}n}}^{*} \sim \sum\limits_{j = 1}^\infty {{{\alpha }^{j}}} \Phi _{{{\text{e}}n,j}}^{*}\quad {\text{при}}\quad \alpha \to 0 \\ {\mathbf{M}}_{{{\text{i}}n}}^{*} \sim \sum\limits_{j = 0}^\infty {{{\alpha }^{j}}} {\mathbf{M}}_{{{\text{i}}n,j}}^{*}\quad {\text{при}}\quad \alpha \to 0,\quad \Phi _{{{\text{i}}n}}^{*} \sim \sum\limits_{j = 1}^\infty {{{\alpha }^{j}}} \Phi _{{{\text{i}}n,j}}^{*}\quad {\text{при}}\quad \alpha \to 0 \\ {{h}^{ * }} \sim \sum\limits_{j = 1}^\infty \,{{\alpha }^{j}}h_{j}^{ * }\;{\text{при}}\;\alpha \to 0,\quad p_{0}^{ * } \sim \sum\limits_{j = 0}^\infty \,{{\alpha }^{j}}p_{{0,j}}^{ * }\;{\text{при}}\;\alpha \to 0 \\ \end{gathered} $

Предельному случаю $\alpha \to 0$, т.е. основному приближению данной задачи, соответствует намагниченная недеформированная сферическая капля. Условие $\alpha \ll 1$ соответствует условию малых деформаций капли $maxh* \ll 1$.

Функции $h_{j}^{*} = h_{j}^{*}({{{\mathbf{n}}}_{0}},t{\text{*}})$ ($j = 1,\;2,\; \ldots $) можно представить в виде

(2.6)

$h_{j}^{*} = h_{j}^{*}\left( {{{{\mathbf{n}}}_{0}},t} \right) = \sum\limits_{n = 0}^\infty {{\mathbf{h}}_{{n,j}}^{*}} {{ \cdot }^{n}}{\mathbf{n}}_{0}^{n}$

где ${\mathbf{h}}_{{n,j}}^{*} = {\mathbf{h}}_{{n,j}}^{*}(t*)$ – зависящие от безразмерного времени скаляры при n = 0, векторы при n = 1 или при $n > 1$ неприводимые тензоры $n$-го порядка.

Рассмотрим основное приближение и поправки первого порядка. Подставив (2.5) в обезразмеренные соотношения, полученные из граничных условий (2.2), (1.12), (2.3), (1.21) и (1.16), и устремляя $\alpha $ к нулю, получим уравнения

(2.7)

$\sum\limits_{n = 1}^\infty {{\mathbf{M}}_{{{\text{e}}n,0}}^{*}} {{ \cdot }^{n}}{\mathbf{n}}_{0}^{n} = \sum\limits_{n = 1}^\infty {{\mathbf{M}}_{{{\text{i}}n,0}}^{*}} {{ \cdot }^{n}}{\mathbf{n}}_{0}^{n}$

(2.8)

${\mathbf{H}}_{{\text{a}}}^{ * } \cdot {{{\mathbf{n}}}_{0}} + \sum\limits_{n = 1}^\infty {(n + 1)} {\mathbf{M}}_{{{\text{e}}n,0}}^{ * }{{ \cdot }^{n}}{\mathbf{n}}_{0}^{n} + \mu _{{\text{i}}}^{ * }\sum\limits_{n = 1}^\infty n {\mathbf{M}}_{{{\text{i}}n,0}}^{ * }{{ \cdot }^{n}}{\mathbf{n}}_{0}^{n} = 0$

(2.9)

$ - \sum\limits_{n = 1}^\infty {(n + 1)} \Phi _{{{\text{e}}n,1}}^{ * }{{ \cdot }^{n}}{\mathbf{n}}_{0}^{n} - \sum\limits_{n = 1}^\infty n \Phi _{{{\text{i}}n,1}}^{ * }{{ \cdot }^{n}}{\mathbf{n}}_{0}^{n} = 0$

(2.10)

$\frac{{\partial h_{1}^{ * }}}{{\partial t{\text{*}}}} = \sum\limits_{n = 1}^\infty n \Phi _{{{\text{i}}n,1}}^{ * }{{ \cdot }^{n}}{\mathbf{n}}_{0}^{n}$

(2.11)

$\begin{gathered} p_{{0,0}}^{ * } + \sum\limits_{n = 1}^\infty {\frac{{d\Phi _{{{\text{e}}n,1}}^{ * }}}{{dt{\text{*}}}}} {{ \cdot }^{n}}{\mathbf{n}}_{0}^{n} - \rho _{{\text{i}}}^{ * }\sum\limits_{n = 1}^\infty {\frac{{d\Phi _{{{\text{i}}n,1}}^{ * }}}{{dt{\text{*}}}}} {{ \cdot }^{n}}{\mathbf{n}}_{0}^{n} + \\ + \;\frac{1}{2}[(\mu _{{\text{i}}}^{ * } - 1){\mathbf{n}}_{0}^{2} - {\mathbf{I}}]{{ \cdot }^{2}}{\mathbf{H}}_{{\text{a}}}^{{ * 2}} - [(\mu _{{\text{i}}}^{ * } - 1){\mathbf{n}}_{0}^{2} - {\mathbf{I}}]{{ \cdot }^{2}}{\mathbf{H}}_{{\text{a}}}^{ * }\sum\limits_{n = 1}^\infty n (\mu _{{\text{i}}}^{ * } - 1){\mathbf{M}}_{{{\text{i}}n,1}}^{ * }{{ \cdot }^{{n - 1}}}{\mathbf{n}}_{0}^{{n - 1}} + \\ + \;\frac{1}{2}[(\mu _{{\text{i}}}^{ * } - 1){\mathbf{n}}_{0}^{2} - {\mathbf{I}}]{{ \cdot }^{2}}\sum\limits_{k = 1}^\infty k (\mu _{{\text{i}}}^{ * } - 1){\mathbf{M}}_{{{\text{i}}k,1}}^{ * }{{ \cdot }^{{k - 1}}}{\mathbf{n}}_{0}^{{k - 1}}\sum\limits_{m = 1}^\infty m (\mu _{{\text{i}}}^{ * } - 1){\mathbf{M}}_{{{\text{i}}m,1}}^{ * }{{ \cdot }^{{m - 1}}}{\mathbf{n}}_{0}^{{m - 1}} = \\ = \; - ({\mathbf{I}} - {{{\mathbf{n}}}_{0}}{{{\mathbf{n}}}_{0}}){{ \cdot }^{2}}\frac{{{{\partial }^{2}}h_{1}^{ * }}}{{\partial \mathop {{{{\mathbf{n}}}_{0}}}\nolimits^2 }} + 2{{{\mathbf{n}}}_{0}} \cdot \frac{{\partial h_{1}^{ * }}}{{\partial {{{\mathbf{n}}}_{0}}}} - 2h_{1}^{ * } \\ \end{gathered} $

Из уравнений (2.7) и (2.8) получаем

(2.12)

${\mathbf{M}}_{{{\text{e}}1,0}}^{ * } = {\mathbf{M}}_{{{\text{i}}1,0}}^{ * } = \frac{{{\mathbf{H}}_{{\text{a}}}^{ * }}}{{2 + \mu _{{\text{i}}}^{ * }}},\quad {\mathbf{M}}_{{{\text{e}}n,0}}^{ * } = {\mathbf{M}}_{{{\text{i}}n,0}}^{ * } = 0\quad (n > 1)$

Из уравнений (2.9) и (2.10) с учетом представления (2.6) следует:

(2.13)

$\Phi _{{{\text{i}}n,1}}^{ * } = \frac{1}{n}\frac{{d{\mathbf{h}}_{{n,1}}^{ * }}}{{dt{\text{*}}}},\quad \Phi _{{{\text{e}}n,1}}^{ * } = - \frac{1}{{n + 1}}\frac{{d{\mathbf{h}}_{{n,1}}^{ * }}}{{d{{t}^{ * }}}}\quad (n = 1,\;2,\;3,\; \ldots )$

Подставив (2.12) и (2.13) в (2.11) и используя для $h_{1}^{ * }$ представление (2.6), получим уравнение, из которого следует

(2.14)

$p_{{0,0}}^{ * } = - \frac{3}{2}\frac{{H_{{\text{a}}}^{{ * 2}}}}{{2 + \mu _{{\text{i}}}^{ * }}}$

(2.15)

$\frac{{{{d}^{2}}{\mathbf{h}}_{{1,1}}^{ * }}}{{d{{t}^{{ * 2}}}}} = 0$

(2.16)

$\frac{{2 + 3\rho _{{\text{i}}}^{ * }}}{6}\frac{{{{d}^{2}}{\mathbf{h}}_{{2,1}}^{ * }}}{{d{{t}^{{ * 2}}}}} + 4{\mathbf{h}}_{{2,1}}^{ * } = \frac{9}{2}\frac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}\left( {{\mathbf{H}}_{{\text{a}}}^{{ * 2}} - \frac{1}{3}{\mathbf{I}}H_{{\text{a}}}^{{ * 2}}} \right)$

(2.17)

$\frac{{n + \rho _{{\text{i}}}^{ * }(n + 1)}}{{(n + 1)n}}\frac{{{{d}^{2}}{\mathbf{h}}_{{n,1}}^{ * }}}{{d{{t}^{{ * 2}}}}} + (n + 2)(n - 1){\mathbf{h}}_{{n,1}}^{ * } = 0\quad (n > 2)$

Уравнения (2.17) описывают незатухающие собственные деформационные колебания капли. Решение уравнения (2.16) представляет собой суперпозицию вынужденных и незатухающих собственных колебаний капли. Уравнение (2.15) описывает равномерное прямолинейное движение капли. В силу симметрии постановки задачи собственные деформационные колебания капли, описываемые уравнениями (2.17), не возбуждаются, и капля остается неподвижной, т.е. ${\mathbf{h}}_{{n,1}}^{ * } = 0$ при $n \ne 2$ и ${\mathbf{h}}_{{1,1}}^{ * } = 0$.

Уравнение поверхности капли (1.20) можно переписать в виде

(2.18)

${{r}^{2}}\mathop {\left[ {{{a}^{2}} + 2ah\left( {\frac{{\mathbf{r}}}{r},t} \right) + {{h}^{2}}\left( {\frac{{\mathbf{r}}}{r},t} \right)} \right]}\nolimits^{ - 1} = 1$

С точностью до членов первого порядка по $\alpha $ уравнение (2.18) эквивалентно уравнению

(2.19)

$\frac{{{{r}^{2}}}}{{{{a}^{2}}}} - \frac{{2{{{\mathbf{h}}}_{{2,1}}}}}{{{{a}^{3}}}}{{ \cdot }^{2}}{{{\mathbf{r}}}^{2}} = 1$

Это уравнение является уравнением эллипсоида с полуосями

${{a}_{1}} = \frac{a}{{\sqrt {1 - 2{{h}_{{2,1,1}}}{{a}^{{ - 1}}}} }},\quad {{a}_{2}} = \frac{a}{{\sqrt {1 - 2{{h}_{{2,1,2}}}{{a}^{{ - 1}}}} }},\quad {{a}_{3}} = \frac{a}{{\sqrt {1 - 2{{h}_{{2,1,3}}}{{a}^{{ - 1}}}} }}$

где ${{h}_{{2,1,1}}}$, ${{h}_{{2,1,2}}}$ и ${{h}_{{2,1,3}}}$ – собственные значения тензора ${{{\mathbf{h}}}_{{2,1}}} = {{{\mathbf{h}}}_{{2,1}}}(t)$. С точностью до членов первого порядка по $\alpha $ выражения для полуосей имеют вид:

(2.20)

${{a}_{1}} = a\left( {1 + \frac{{{{h}_{{2,1,1}}}}}{a}} \right),\quad {{a}_{2}} = a\left( {1 + \frac{{{{h}_{{2,1,2}}}}}{a}} \right),\quad {{a}_{3}} = a\left( {1 + \frac{{{{h}_{{2,1,3}}}}}{a}} \right)$

Для гармонически колеблющегося приложенного магнитного поля с напряженностью ${{{\mathbf{H}}}_{{\text{a}}}} = {{H}_{{{\text{am}}}}}{\mathbf{k}}{\text{cos}}(\omega t)$ имеем следующее решение уравнения (2.16) в виде вынужденных колебаний:

${\mathbf{h}}_{{2,1}}^{ * } = \frac{3}{{16}}\frac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}( - {{{\mathbf{i}}}^{2}} - {{{\mathbf{j}}}^{2}} + 2{{{\mathbf{k}}}^{2}})\left[ {1 + \frac{{\omega _{{2,1}}^{{ * 2}}cos(2\omega {\text{*}}t{\text{*}})}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}}} \right]$

$\omega _{{2,1}}^{ * } = \sqrt {\frac{{24}}{{2 + 3\rho _{{\text{i}}}^{ * }}}} ,\quad \omega * = \sqrt {\frac{{{{\sigma }_{{\text{s}}}}}}{{{{\rho }_{{\text{e}}}}{{a}^{3}}}}} \omega $

где i, j и k образуют правую тройку ортонормированных векторов. Согласно (2.19) и (2.20) с точностью до членов первого порядка в таком приложенном поле капля является вытянутым сфероидом с осью, направленной вдоль k, и с полуосями

$\begin{gathered} {{a}_{1}} = {{a}_{2}} = a\left\{ {1 - \frac{{3\alpha }}{{16}}\frac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}\left[ {1 + \frac{{\omega _{{2,1}}^{{ * 2}}cos(2\omega {\text{*}}t{\text{*}})}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}}} \right]} \right\} \\ {{a}_{3}} = a\left\{ {1 + \frac{{3\alpha }}{8}\frac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}\left[ {1 + \frac{{\omega _{{2,1}}^{{ * 2}}cos(2\omega {\text{*}}t{\text{*}})}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}}} \right]} \right\} \\ \end{gathered} $

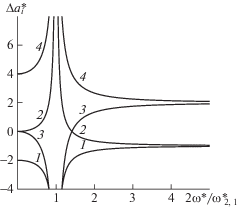
Таким образом, капля совершает деформационные колебания с угловой частотой 2ω так, что при $\omega * < \omega _{{2,1}}^{ * }{\text{/}}2$ она максимально удлиняется вдоль вектора напряженности приложенного поля в тот момент, когда его модуль максимален, а при $\omega * > \omega _{{2,1}}^{ * }{\text{/}}2$ – тогда, когда напряженность приложенного поля равна нулю. При $\omega \to \infty $ капля стремится принять форму неизменяющегося вытянутого сфероида. При $\omega * = \omega _{{2,1}}^{ * }$ имеет место резонанс: амплитуда деформационных колебаний капли равномерно возрастает до бесконечности. Решение с возрастающей до бесконечности амплитудой не выписано, поскольку оно не реализуется вследствие наличия вязкости. На рис. 2 представлены зависимости максимального и минимального значений длин полуосей колеблющегося эллипсоида как удлинений относительно радиуса недеформированной капли

$\Delta a_{i}^{ * } = \frac{{16}}{{3\alpha }}\frac{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}{{\mu _{{\text{i}}}^{ * } - 1}}\frac{{{{a}_{i}} - a}}{a}$

от угловой частоты колебаний напряженности приложенного магнитного поля. Удлинения и частота при помощи умножения на не зависящие от частоты величины приведены к такому виду, который позволяет построить графики, не зависящие от параметров задачи $\mu _{{\text{i}}}^{ * }$, $\rho _{{\text{i}}}^{ * }$ и α.

Рис. 2.

Установившиеся колебания капли в гармонически колеблющемся магнитном поле: 1 – ${{a}_{i}} = {{a}_{{1{\text{min}}}}} = {{a}_{{2{\text{min}}}}}$, 2 – ${{a}_{i}} = {{a}_{{1{\text{max}}}}} = {{a}_{{2{\text{max}}}}}$, 3 – ${{a}_{i}} = {{a}_{{3{\text{min}}}}}$, 4 – ${{a}_{i}} = {{a}_{{3{\text{max}}}}}$.

Для вращающегося приложенного магнитного поля с напряженностью H_a = H_amicos(ωt) + + ${{H}_{{{\text{am}}}}}{\mathbf{j}}{\text{sin}}(\omega t)$ уравнение (2.16) имеет решение в виде вынужденных колебаний, которое может быть записано следующим образом:

${\mathbf{h}}_{{2,1}}^{ * } = \frac{3}{{16}}\frac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}({\mathbf{i}}{\kern 1pt} {{'}^{2}} + {{j}^{{'2}}} - 2{{{\mathbf{k}}}^{2}}) + \frac{9}{{16}}\frac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}\frac{{\omega _{{2,1}}^{{ * 2}}}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}}({\mathbf{i}}{\kern 1pt} {{'}^{2}} - {\mathbf{j}}{\kern 1pt} {{'}^{2}})$

${\mathbf{i}}{\text{'}} = cos(\omega {\text{*}}t{\text{*}}){\mathbf{i}} + sin(\omega {\text{*}}t{\text{*}}){\mathbf{j}},\quad {\mathbf{j}}{\text{'}} = sin\left( {\omega {\text{*}}t{\text{*}}} \right){\mathbf{i}} - cos\left( {\omega {\text{*}}t{\text{*}}} \right){\mathbf{j}}$

Согласно (2.19) и (2.20) с точностью до членов первого порядка в таком приложенном поле капля является трехосным эллипсоидом с полуосями

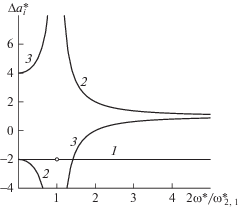
$\begin{gathered} {{a}_{1}} = a\left[ {1 - \frac{{3\alpha }}{8}\frac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}} \right] \\ {{a}_{2}} = a\left[ {1 + \frac{{3\alpha }}{{16}}\frac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}\left( {1 - \frac{{3\omega _{{2,1}}^{{ * 2}}}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}}} \right)} \right] \\ {{a}_{3}} = a\left[ {1 + \frac{{3\alpha }}{{16}}\frac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}\left( {1 + \frac{{3\omega _{{2,1}}^{{ * 2}}}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}}} \right)} \right] \\ \end{gathered} $

Эллипсоид вращается вокруг своей малой оси, направленной вдоль ${\mathbf{k}} = {\mathbf{i}} \times {\mathbf{j}}$ с угловой скоростью $\omega $ так, что при $\omega * < \omega _{{2,1}}^{ * }{\text{/}}2$ вдоль H_a направлена его большая ось, а при $\omega * > \omega _{{2,1}}^{ * }{\text{/}}2$ – средняя. При $\omega \to \infty $ капля стремится принять форму неизменяющегося сплюснутого сфероида. При $\omega * = \omega _{{2,1}}^{ * }$ имеет место резонанс: большая ось равномерно возрастает до бесконечности. Решение с возрастающей до бесконечности амплитудой не выписано. На рис. 3 представлены зависимости значений длин полуосей вращающегося эллипсоида как приведенных удлинений $\Delta a_{i}^{ * }$ относительно радиуса недеформированной капли от приведенной угловой частоты колебаний напряженности приложенного магнитного поля.

Рис. 3.

Вращение капли во вращающемся магнитном поле: 1 – ${{a}_{i}} = {{a}_{1}}$, 2 – ${{a}_{i}} = {{a}_{2}}$, 3 – ${{a}_{i}} = {{a}_{3}}$.

Отметим, что с точностью до членов первого порядка во вращающемся магнитном поле частицы жидкости не совершают вращение вокруг оси, проходящей через центр капли, т.е. жидкость не вовлекается во вращение вращающимся полем.

Пусть капля вначале была неподвижна, а в момент t = 0 прикладывается однородное магнитное поле так, что его напряженность имеет вид

${{{\mathbf{H}}}_{{\text{a}}}} = \left\{ \begin{gathered} 0,\quad t \leqslant 0 \hfill \\ {{H}_{{{\text{am}}}}}{\mathbf{k}}cos\left( {\omega t + {{\phi }_{0}}} \right),\quad t > 0 \hfill \\ \end{gathered} \right.$

Тогда кроме описанных выше вынужденных колебаний возбуждаются собственные деформационные колебания. При этом в любой момент времени капля представляет собой вытянутый сфероид с осью, направленной вдоль k и с полуосями

$\begin{gathered} {{a}_{1}} = {{a}_{2}} = a\left\{ {1 - \tfrac{{3\alpha }}{{16}}\tfrac{{\mu _{{\text{i}}}^{ * } - 1}}{{{{{(2 + \mu _{{\text{i}}}^{ * })}}^{2}}}}\left[ {1 + \tfrac{{\omega _{{2,1}}^{{ * 2}}cos\left( {2\omega {\text{*}}t{\text{*}}} \right)}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}} - {{\delta }_{{\text{m}}}}cos(\omega _{{2,1}}^{ * }t{\text{*}} + \phi )} \right]} \right\} \\ {{a}_{3}} = a\left\{ {1 + \tfrac{{3\alpha }}{8}\tfrac{{\mu _{{\text{i}}}^{ * } - 1}}{{{{{(2 + \mu _{{\text{i}}}^{ * })}}^{2}}}}\left[ {1 + \tfrac{{\omega _{{2,1}}^{{ * 2}}cos\left( {2\omega {\text{*}}t{\text{*}}} \right)}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}} - {{\delta }_{{\text{m}}}}cos(\omega _{{2,1}}^{ * }t{\text{*}} + \phi )} \right]} \right\} \\ {{\delta }_{{\text{m}}}} = \mathop {\left\{ {\mathop {\left[ {1 + \tfrac{{\omega _{{2,1}}^{{ * 2}}cos\left( {2{{\phi }_{0}}} \right)}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}}} \right]}\nolimits^2 + \mathop {\left[ {\tfrac{{2\omega {\text{*}}}}{{\omega _{{2,1}}^{ * }}}\tfrac{{\omega _{{2,1}}^{{ * 2}}sin\left( {2{{\phi }_{0}}} \right)}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}}} \right]}\nolimits^2 } \right\}}\nolimits^{1/2} \\ \phi = \left[ {\tfrac{{2\omega {\text{*}}}}{{\omega _{{2,1}}^{ * }}}\tfrac{{\omega _{{2,1}}^{{ * 2}}sin\left( {2{{\phi }_{0}}} \right)}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}} + \omega _{{2,1}}^{{ * 2}}cos\left( {2{{\phi }_{0}}} \right)}}} \right] \\ \end{gathered} $

Пусть к неподвижной капле при t = 0 прикладывается вращающееся однородное магнитное поле

${{{\mathbf{H}}}_{{\text{a}}}} = \left\{ \begin{gathered} 0,\quad t \leqslant 0 \hfill \\ {{H}_{{{\text{am}}}}}{\mathbf{i}}cos\left( {\omega t} \right) + {{H}_{{{\text{am}}}}}{\mathbf{j}}sin\left( {\omega t} \right),\quad t > 0 \hfill \\ \end{gathered} \right.$

Тогда при t > 0 капля представляет собой трехосный эллипсоид, главные оси которого направлены вдоль векторов k, $cos\theta {\mathbf{i}} + sin\theta {\mathbf{j}}$ и $sin\theta {\mathbf{i}} - cos\theta {\mathbf{j}}$, а соответствующие полуоси равны

$\begin{gathered} {{a}_{1}} = a\left\{ {1 - \tfrac{{3\alpha }}{8}\tfrac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}[1 - cos(\omega _{{2,1}}^{ * }t{\text{*}})]} \right\} \\ {{a}_{2}} = a\left[ {1 + \tfrac{{3\alpha }}{{16}}\tfrac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}{{\Lambda }_{1}}} \right] \\ {{a}_{3}} = a\left[ {1 + \tfrac{{3\alpha }}{{16}}\tfrac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}{{\Lambda }_{2}}} \right] \\ \theta = \theta (t*) = \tfrac{1}{2}{\text{arctg}}\left\{ {[ - cos(2\omega {\text{*}}t{\text{*}}) + cos(\omega _{{2,1}}^{ * }t{\text{*}})]{\kern 1pt} {\kern 1pt} \mathop {\left[ {sin(2\omega {\text{*}}t{\text{*}}) - \tfrac{{2\omega {\text{*}}}}{{\omega _{{2,1}}^{ * }}}sin(\omega _{{2,1}}^{ * }t{\text{*}})} \right]}\nolimits^{ - 1} } \right\} + \tfrac{\pi }{4} \\ {{\Lambda }_{{1,2}}} = 1 - cos(\omega _{{2,1}}^{ * }t{\text{*}}) \pm \left| {\tfrac{{3\omega _{{2,1}}^{{ * 2}}}}{{\omega _{{2,1}}^{{ * 2}} - 4{{\omega }^{{ * 2}}}}}\left[ {sin(2\omega {\text{*}}t{\text{*}}) - \tfrac{{2\omega {\text{*}}}}{{\omega _{{2,1}}^{ * }}}sin(\omega _{{2,1}}^{ * }t{\text{*}})} \right]\mathop {\left[ {sin\left( {2\theta } \right)} \right]}\nolimits^{ - 1} } \right| \\ \end{gathered} $

Вышеизложенные результаты имеют место для достаточно малых значений параметра α, который характеризует отношение магнитных сил, стремящихся деформировать каплю, к капиллярным силам, препятствующим деформации. Для магнитной жидкости на основе магнетита в керосине с олеиновой кислотой в качестве стабилизатора, окруженной водой, для которой можно считать ${{\sigma }_{{\text{s}}}}$ = 20 дин/см и ${{\mu }_{{\text{i}}}} = 5$, получим, что для капель, радиус которых в недеформированном состоянии a = 1 мм, напряженность магнитного поля не должна быть выше 25 Э, чтобы параметр $\alpha $ был меньше 0.1.

3. УЧЕТ ЗАВИСИМОСТИ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ОТ МАГНИТНОГО ПОЛЯ

Согласно работе [5] зависимость поверхностного натяжения от магнитного поля имеет место при наличии поверхностной намагниченности. При постоянных коэффициентах поверхностной магнитной восприимчивости $\beta $ и $\gamma $ для того, чтобы учесть эту зависимость, необходимо заменить граничные условия (2.2), (1.12) и (1.16) на условия

$\mathop {\left[ \psi \right]}\nolimits_{\text{s}} = - 4\pi \beta {{B}_{{\Sigma n}}}$

$\mathop {\left[ {\mathbf{B}} \right]}\nolimits_{\text{s}} \cdot {\mathbf{n}} = - 4\pi \gamma {{\nabla }_{\Sigma }} \cdot {{{\mathbf{H}}}_{{\Sigma \tau }}}$

${\mathbf{n}} \cdot \mathop {[ - p{\mathbf{I}} + {{\sigma }_{{\text{m}}}}]}\nolimits_{\text{s}} \cdot {\mathbf{n}} = - \left( {{{\sigma }_{{\text{s}}}} + \frac{1}{2}\beta B_{{\Sigma n}}^{2} - \frac{1}{2}\gamma H_{{\Sigma \tau }}^{2}} \right)K + \gamma {{{\mathbf{H}}}_{{\Sigma \tau }}} \cdot {{{\mathbf{b}}}_{\Sigma }} \cdot {{{\mathbf{H}}}_{{\Sigma \tau }}}$

Здесь ${{{\mathbf{b}}}_{\Sigma }}$ – тензор внешней кривизны поверхности капли, ${{\nabla }_{\Sigma }}$ – поверхностный оператор набла,

${{B}_{{\Sigma n}}} = \frac{1}{2}\left( {\mathop {\left. {\mathbf{B}} \right|}\nolimits_{\text{e}} \cdot {\mathbf{n}} + \mathop {\left. {\mathbf{B}} \right|}\nolimits_{\text{i}} \cdot {\mathbf{n}}} \right)$

${{{\mathbf{H}}}_{{\Sigma \tau }}} = \frac{1}{2}\left\{ {\left[ {{\mathbf{n}} \times \left( {\mathop {\left. {\mathbf{H}} \right|}\nolimits_{\text{e}} \times {\mathbf{n}}} \right)} \right] + \left[ {{\mathbf{n}} \times \left( {\mathop {\left. {\mathbf{H}} \right|}\nolimits_{\text{i}} \times {\mathbf{n}}} \right)} \right]} \right\}$

Проводя соответствующие вычисления, получаем вместо (2.12), (2.14) и (2.16) следующее решение:

${\mathbf{M}}_{{{\text{e}}1,0}}^{ * } = \frac{{{{\chi }_{e}}}}{{\mu _{{\text{i}}}^{ * } - 1}}{\mathbf{H}}_{{\text{a}}}^{ * },\quad {\mathbf{M}}_{{{\text{i}}1,0}}^{ * } = \frac{{{{\chi }_{i}}}}{{\mu _{{\text{i}}}^{ * } - 1}}{\mathbf{H}}_{{\text{a}}}^{ * },\quad {\mathbf{M}}_{{{\text{e}}n,0}}^{ * } = {\mathbf{M}}_{{{\text{i}}n,0}}^{ * } = 0\quad (n > 1)$

$\begin{gathered} p_{{0,0}}^{ * } = - \frac{1}{{6(\mu _{{\text{i}}}^{ * } - 1)}}[3{{\chi }_{{\text{e}}}}\left( {2 + {{\chi }_{{\text{e}}}}} \right) - {{\left( {1 - {{\chi }_{{\text{e}}}}} \right)}^{2}} + \mu _{{\text{i}}}^{ * }{{\left( {1 - {{\chi }_{{\text{i}}}}} \right)}^{2}}]H_{{\text{a}}}^{{ * 2}} + \\ + \;\frac{{2\beta {\text{*}}}}{{3(\mu _{{\text{i}}}^{ * } - 1)}}\mathop {\left( {\frac{{\mu _{{\text{i}}}^{ * } + 1}}{2} + \frac{{2{{\chi }_{{\text{e}}}} - \mu _{{\text{i}}}^{ * }{{\chi }_{{\text{i}}}}}}{2}} \right)}\nolimits^2 H_{{\text{a}}}^{{ * 2}} \\ \end{gathered} $

$\frac{{2 + 3\rho _{{\text{i}}}^{ * }}}{6}\frac{{{{d}^{2}}{\mathbf{h}}_{{2,1}}^{ * }}}{{dt{{{\text{*}}}^{2}}}} + 4{\mathbf{h}}_{{2,1}}^{ * } = \frac{9}{2}\mu {\text{**}}\left( {{\mathbf{H}}_{{\text{a}}}^{{ * 2}} - \frac{1}{3}{\mathbf{I}}H_{{\text{a}}}^{{ * 2}}} \right)$

$\begin{gathered} \mu {\text{**}} = \frac{1}{{9(\mu _{{\text{i}}}^{ * } - 1)}}[3{{\chi }_{{\text{e}}}}\left( {2 + {{\chi }_{{\text{e}}}}} \right) + 2{{\left( {1 - {{\chi }_{{\text{e}}}}} \right)}^{2}} - 2\mu _{{\text{i}}}^{ * }{{\left( {1 - {{\chi }_{{\text{i}}}}} \right)}^{2}}] - \\ - \;\frac{{2\beta {\text{*}}}}{{\mu _{{\text{i}}}^{ * } - 1}}\mathop {\left( {\frac{{\mu _{{\text{i}}}^{ * } + 1}}{2} + \frac{{2{{\chi }_{{\text{e}}}} - \mu _{{\text{i}}}^{ * }{{\chi }_{{\text{i}}}}}}{2}} \right)}\nolimits^2 \\ \end{gathered} $

${{\chi }_{{\text{e}}}} = \frac{{(1 + \mu _{{\text{i}}}^{ * }\beta {\text{*}})(\mu _{{\text{i}}}^{ * } - 1 + 4\gamma {\text{*}}) - (\mu _{{\text{i}}}^{ * } + 1)\beta {\text{*}}(\mu _{{\text{i}}}^{ * } + 2\gamma {\text{*}})}}{{(1 + 2\beta {\text{*}})(\mu _{{\text{i}}}^{ * } + 2\gamma {\text{*}}) + (1 + \mu _{{\text{i}}}^{ * }\beta {\text{*}})(2 + 2\gamma {\text{*}})}}$

${{\chi }_{{\text{i}}}} = \frac{{\left( {1 + 2\beta {\text{*}}} \right)(\mu _{{\text{i}}}^{ * } - 1 + 4\gamma {\text{*}}) + (\mu _{{\text{i}}}^{ * } + 1)\beta {\text{*}}\left( {2 + 2\gamma {\text{*}}} \right)}}{{\left( {1 + 2\beta {\text{*}}} \right)(\mu _{{\text{i}}}^{ * } + 2\gamma {\text{*}}) + (1 + \mu _{{\text{i}}}^{ * }\beta {\text{*}})\left( {2 + 2\gamma {\text{*}}} \right)}}$

$\beta * = 2\pi {{\mu }_{{\text{e}}}}\frac{\beta }{a},\quad \gamma * = \frac{{2\pi }}{{{{\mu }_{{\text{e}}}}}}\frac{\gamma }{a}$

При $\beta = 0$ и $\gamma = 0$ имеем

$\mu {\text{**}} = \frac{{\mu _{{\text{i}}}^{ * } - 1}}{{\mathop {(2 + \mu _{{\text{i}}}^{ * })}\nolimits^2 }}$

Таким образом, все вышеизложенное остается в силе и при учете зависимости поверхностного натяжения от магнитного поля, если в соответствующих формулах заменить комбинацию $(\mu _{{\text{i}}}^{ * } - 1){\text{/}}{{(2 + \mu _{{\text{i}}}^{ * })}^{2}}$ на μ**. Из полученных формул следует, что влиянием зависимости поверхностного натяжения от магнитного поля можно пренебречь при выполнении условия $max\left( {\left| {\beta {\text{*}}} \right|,\left| {\gamma {\text{*}}} \right|} \right) \ll 1$. Отметим, что подобное условие следует также из результатов работы [5]. На основании экспериментов, описанных в [5], для магнитной жидкости на основе магнетита в керосине с олеиновой кислотой в качестве стабилизатора в воде были получены следующие значения для коэффициентов поверхностной восприимчивости: $\beta = - (4 \pm 2) \times {{10}^{{ - 4}}}$ см, $\gamma = (4 \pm 2) \times {{10}^{{ - 4}}}$ см. Таким образом, влияние зависимости поверхностного натяжения от магнитного поля становится заметным для такой магнитной жидкости уже при размерах капли порядка 100 мкм и возрастает при ее уменьшении.

ЗАКЛЮЧЕНИЕ

Проведено теоретическое исследование поведения капли намагничивающейся жидкости, взвешенной в несмешивающейся с ней другой намагничивающейся жидкости, в переменном однородном магнитном поле при больших числах Рейнольдса. В первом приближении по безразмерному малому параметру, малость которого обеспечивает малость деформаций капли, получены уравнения, описывающие изменение формы капли в произвольно меняющемся магнитном поле. Найдены решения этих уравнений для вынужденных колебаний капли в гармонически колеблющемся и вращающемся приложенных магнитных полях, а также решения для случаев, когда приложенные колеблющееся и вращающееся поля включаются в некоторый начальный момент времени.

Работа выполнена при частичной поддержке РФФИ (проект № 19-01-00056-а).

Список литературы

Тарапов И.Е. Некоторые вопросы гидростатики намагничивающихся и поляризующихся сред // Изв. АН СССР. Сер. МЖГ. 1974. № 5. С. 141–144.
Архипенко В.И., Барков Ю.Д., Баштовой В.Г. Исследование формы капли намагничивающейся жидкости в однородном магнитном поле // Магнитная гидродинамика. 1978. № 3. С. 131–134.
Голубятников А.Н. Определение магнитной восприимчивости, плотности и поверхностного натяжения магнитной жидкости. Отчет НИИ механики МГУ № 2238. М.: МГУ, 1979. 21 с.
Bacri J.C., Salin D. Instability of ferrofluid magnetic drop under magnetic field // J. Phys. (Lett.) 1982. V. 43. № 17. P. L649–L654.
Голубятников А.Н., Субханкулов Г.И. О поверхностном натяжении магнитной жидкости // Магнитная гидродинамика. 1986. № 1. С. 73–78.
Голубятников А.Н., Субханкулов Г.И. Поверхностные магнитные свойства магнитных жидкостей // 12-е Рижское совещание по магнитной гидродинамике. Тезисы докладов. Т. 3. Магнитные жидкости. Саласпилс: Ин-т физики АН Латв. ССР, 1987. С. 87–90.
Голубятников А.Н. Колебание капли магнитной жидкости в переменном поле. Отчет НИИ механики МГУ № 2438. М.: МГУ, 1980. 22 с.
Субханкулов Г.И. Динамика малых деформируемых капель магнитной жидкости // Магнитная гидродинамика. 1984. № 4. С. 49–55.
Субханкулов Г.И. Динамика капель и твердых тел в магнитной жидкости: Дис. … канд. физико-математических наук: 01.02.05. М., 1986. 130 с.
Лебедев А.В., Морозов К.И. Динамика капли магнитной жидкости во вращающемся магнитном поле // Письма в ЖЭТФ. 1997. Т. 65. № 2. С. 150–154.
Морозов К.И. Вращение капли в вязкой жидкости // ЖЭТФ. 1997. Т. 112. Вып. 4 (10). С. 1340–1350.
Братухин Ю.К., Лебедев А.В., Пшеничников А.Ф. Движение деформируемой капли магнитной жидкости во вращающемся магнитном поле // Изв. РАН. МЖГ. 2000. № 1. С. 22–30.
Морозов К.И., Лебедев А.В. Бифуркации формы капли магнитной жидкости во вращающемся магнитном поле // ЖЭТФ. 2000. Т. 118. Вып. 5. С. 1188–1192.
Братухин Ю.К., Лебедев А.В. Вынужденные колебания капли магнитной жидкости // ЖЭТФ. 2002. Т. 121. Выпуск 6. С. 1298–1305.
Lebedev A.V., Engel A., Morozov K.I., Bauke H. Ferrofluid drops in rotating magnetic fields // New J. Phys. 2003. V. 5. P. 57.1–57.20.
Диканский Ю.И., Закинян А.Р. Динамика немагнитной капли, взвешенной в магнитной жидкости, во вращающемся магнитном поле // Журнал технической физики. 2010. Т. 80. Вып. 8. С. 8–12.
Tyatyushkin A.N. Deformation of a magnetic liquid drop in an applied non-stationary uniform magnetic field // EPJ Web of Conferences. 2018. V. 185. P. 09006-1–09006-4.
Tyatyushkin A.N. Drop of viscous magnetic liquid in a non-stationary magnetic field // Magnetohydrodynamics. 2018. V. 54. № 1–2. P. 151–154.
Тятюшкин А.Н. Намагничивание и деформация капли магнитной жидкости в переменном магнитном поле // Изв. РАН. Серия физическая. 2019. Т. 83. № 7. С. 885–887.
Rosensweig R.E. Ferrohydrodynamics. Cambridge: Cambridge University Press, 1985. 344 p.
Ламб Г. Гидродинамика. М.: ОГИЗ, 1947. 929 с.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал