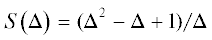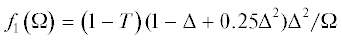Известия РАН. Механика жидкости и газа, 2021, № 5, стр. 103-121
ОСОБЕННОСТИ ПОЛЯ ТЕЧЕНИЯ ОКОЛО НАВЕТРЕННОЙ ПОВЕРХНОСТИ ТРЕУГОЛЬНОГО КРЫЛА МАЛОГО УДЛИНЕНИЯ В ГИПЕРЗВУКОВОМ ПОТОКЕ
a Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Жуковский, Россия
* E-mail: vngolubkin@mail.ru
Поступила в редакцию 20.02.2021
После доработки 06.03.2021
Принята к публикации 23.03.2021
Аннотация
Рассмотрено существенно неоднородное течение газа около нижней поверхности плоского треугольного крыла, находящегося под углом атаки в гиперзвуковом потоке. В аналитическом решении задачи асимптотическим методом тонкого ударного слоя исследован наиболее общий случай узкого крыла, с головным скачком уплотнения, присоединенным к передней кромке или отошедшим от нее. В решении с присоединенным скачком выявлены перпендикулярные крылу “особые сечения” с изломами поверхностей тока под действием сосредоточенных сил, оценен их вклад в аэродинамические характеристики. При обтекании с отсоединенным скачком особенность решения связана с образованием на поверхности крыла тонкого энтропийного слоя, в котором течение формируется под влиянием бокового градиента давления. Построены примеры универсальных решений, пригодных для сквозного описания “внешнего” потока в основной части ударного слоя и “внутреннего” течения в энтропийном слое.
При обтекании тонкого крыла гиперзвуковым потоком под углом атаки α его подветренная (верхняя) сторона находится в так называемой аэродинамической тени с практически нулевым давлением. Аэродинамическое воздействие потока приходится, главным образом, на наветренную (нижнюю) сторону крыла. Около нее формируется интенсивный головной скачок уплотнения, в котором газ претерпевает сильное сжатие, и дальнейшее его течение происходит в достаточно тонком слое между скачком и наветренной поверхностью. В предположении, что его толщина равна нулю при бесконечной степени сжатия газа, простейшая оценка коэффициента давления на плоскость крыла проводится по формуле Ньютона [1, 2] ${{c}_{p}} = 2{\text{si}}{{{\text{n}}}^{2}}\alpha $. Уточнение этой зависимости требует учесть ненулевую толщину и структуру течения в этой области, которую естественно рассмотреть методом тонкого ударного слоя [1], удерживая следующие члены вслед за ньютоновскими. С современной точки зрения, условия применимости данного метода физически адекватны проявлению высокотемпературных реальных свойств воздуха [3]. При этом наибольший интерес представляет случай, когда удлинение крыла произвольной формы в плане (или угол при вершине треугольного крыла) малы и по порядку величины совпадают с углом Маха в сжатом слое [4]. Тогда возмущенное течение оказывается пространственным (коническим), и возможны два различных режима обтекания, когда присоединенный к острой вершине головной скачок присоединен также к передней кромке или отсоединен от нее. Задача пространственного 3D-обтекания в следующем приближении к ньютоновскому допускает общее аналитическое решение [5, 6]. Наиболее часто рассматривались 2D конические течения около треугольного крыла [4, 6]. Полученные для обоих режимов обтекания асимптотические решения не относятся к равномерно пригодным, поскольку содержат особенности [6–8], появление которых в течениях газа большой плотности является скорее правилом, чем исключением [9].
В настоящей работе кратко воспроизводятся и дополняются полученные решения и приводятся результаты анализа указанных особенностей с применением метода сращиваемых асимптотических разложений и построением универсального решения.
1. ФОРМУЛИРОВКА И ОБЩЕЕ РЕШЕНИЕ ЗАДАЧИ
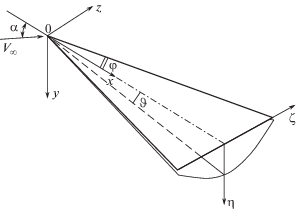
Пусть плоское треугольное крыло малого удлинения установлено под углом атаки в равномерном гиперзвуковом потоке со скоростью V∞ (рис. 1). При конечных углах атаки α ($\cos {{\alpha }}\sim 1$) головной скачок уплотнения имеет с крылом, по крайней мере, одну общую точку, будучи присоединенным к его острой вершине, и течение в тонком слое между скачком и нижней поверхностью крыла коническое. Для его анализа используем метод тонкого ударного слоя (МТУС) [1, 4], в котором малым параметром служит отношение плотностей на сильном косом скачке уплотнения, наклоненном под углом α к набегающему гиперзвуковому потоку газа с числом Маха ${{{\text{M}}}_{\infty }} \gg 1$ и близким к единице показателем адиабаты γ
Как это впервые принято в [4], считаем угол при вершине крыла асимптотически малым и имеющим по параметру ε тот же порядок величины, что и угол Маха в ударном слое: $\varphi \sim {{\varepsilon }^{{1/2}}}{\text{tg}}\alpha $. В этом случае для плоского треугольного крыла имеется единственный параметр подобия ${{\Omega }} = \varphi {\text{/}}{{\varepsilon }^{{1/2}}}~{\text{tg}}\alpha $. Малый угол $~\vartheta $ между скачком и крылом в плоскости симметрии, служащий мерой относительной толщины слоя, имеет порядок $\vartheta \sim \varepsilon {\text{tg}}\alpha $. Как следует из соотношений Рэнкина–Гюгонио [8], наклон присоединенного к передней кромке головного скачка уплотнения пропорционален величине $T = ({{\Omega }} - \sqrt {{{{{\Omega }}}^{2}} - 4} ){\text{/}}2$, поэтому такой скачок реализуется, если ${{\Omega }} \geqslant 2$. При ${{\Omega }} < 2$ скачок является отошедшим от передней кромки, как показано на рис. 1. То есть такой случай обтекания охватывает оба характерных режима обтекания и на этом основании считается наиболее общим.
В связанной с крылом декартовой системе координат $Oxyz~$ (рис. 1), используя принятые выше вертикальный и боковой масштабы течения разного порядка малости, введем конические переменные, имеющие порядок единицы в ударном слое
(1.1)
$\eta = y{\text{/}}x\varepsilon {\text{tg}}\alpha ,\quad \zeta = z{\text{/}}x{{\varepsilon }^{{1/2}}}{\text{tg}}\alpha $(1.2)
${v} = \varepsilon ~{\text{sin}}\alpha ~{{{v}}_{1}}(\eta ,\zeta ) + \ldots ,\quad ~w = {{\varepsilon }^{{1/2}}}{\text{sin}}\alpha ~{{w}_{1}}(\eta ,\zeta ) + \ldots $Здесь члены нулевого порядка по параметру ε даются предельной теорией Ньютона для плоской пластины с углом наклона α. Подставляя (1.1), (1.2) в уравнения конического течения [8], соотношения на скачке уплотнения $\eta = {{\eta }_{s}}\left( \zeta \right)$ и условие непротекания на крыле η = 0, в следующем приближении к ньютоновскому имеем нелинейные уравнения и краевые условия (без индексов)
(1.3)
$D{v} = - {{p}_{\eta }},\quad Dw = 0,\quad {{{v}}_{\eta }} + {{w}_{\zeta }} = 0,\quad D\sigma = 0,\quad D = \left( {{v} - \eta } \right)\frac{\partial }{{\partial \eta }} + \left( {w - \zeta } \right)\frac{\partial }{{\partial \zeta }}$(1.4)
$\eta = {{\eta }_{s}}\left( \zeta \right):{{{v}}_{s}} = {{\eta }_{s}} - \zeta \eta _{s}^{'} - 1 - ~\eta {{_{s}^{'}}^{2}},\quad {{w}_{s}} = - \eta _{s}^{'},\quad {{p}_{s}} = {{{v}}_{s}} + {{\eta }_{s}} - \zeta \eta _{s}^{'}$Отход скачка в плоскости симметрии, коэффициент давления на крыле cp и коэффициент нормальной силы cN подчиняются следующим законам подобия по параметру Ω [4]
(1.6)
$\frac{{{\text{tg}}\vartheta }}{{\varepsilon ~{\text{tg}}\alpha }} = {{{{\Delta }}}_{0}}\left( {{\Omega }} \right),\quad \frac{{{{c}_{p}} - 2{\text{si}}{{{\text{n}}}^{2}}\alpha }}{{2\varepsilon {\text{\;si}}{{{\text{n}}}^{2}}\alpha }} = {{p}_{b}}\left( {\zeta ,{{\Omega }}} \right)$В задаче (1.3)–(1.5) перейдем к новым переменным $\zeta ,\psi $, где функция тока ψ постоянна вдоль поверхности тока поперечного конического течения $\left( {D\psi = 0} \right)$ и равна координате ζ точки ее пересечения со скачком уплотнения $~\psi = {{\zeta }_{s}}$. Тогда получаем первый интеграл преобразованных уравнений, выражающий постоянство боковой компоненты скорости на поверхностях тока
В результате дальнейшего интегрирования этих уравнений получается общее аналитическое решение [4, 10], которое выражает все искомые газодинамические функции через основную функцию, описывающую форму скачка уплотнения $\eta = {{\eta }_{s}}\left( \zeta \right).$ Она удовлетворяет приведенным далее уравнениям, которые будет удобно записать по-разному применительно к режимам обтекания крыла с присоединенным и отошедшим скачком.
В новых переменных на обтекаемой плоскости крыла имеем $\zeta = {{\zeta }_{b}}\left( \psi \right)$ или ψ = ψb(ζ). Удовлетворяя условию непротекания (1.5), получаем альтернативу: либо
а) $\psi _{b}^{'}\left( \zeta \right)$ = 0, тогда функция тока постоянна на плоскости крыла, и она является регулярной изоэнтропической поверхностью тока; либо
б) функция тока на крыле переменна и является обратной по отношению к функции $w\left( \psi \right),~$ или с учетом (1.7)
По-другому, в данном случае на крыле ${{\zeta }_{b}}\left( \psi \right) = w\left( \psi \right)$, а это означает, что его поверхность является огибающей конических проекций поверхностей тока, которые пересекают искривленный скачок, подходят по касательной и оканчиваются на ней в точках с координатами ${{\zeta }_{b}}$, равными постоянным вдоль них значениям бокового скоса w. Каждая из них приносит свое значение энтропии, делая энтропию на огибающей поверхности крыла переменной.
2. ОБТЕКАНИЕ С ПРИСОЕДИНЕННЫМ СКАЧКОМ
Основное интегро-дифференциальное функциональное уравнение для формы присоединенного скачка, генерируемого плоским крылом, удобно взять в форме [10], и после двукратного дифференцирования оно приобретает вид
(2.1)
$\eta _{s}^{{''}}\left( \zeta \right)\left[ {1 - \frac{1}{{{{{(\eta _{s}^{'} + \zeta )}}^{2}}}}} \right] = \frac{{\psi _{b}^{'}\left( \zeta \right)}}{{{{{\left( {{{\psi }_{b}} - \zeta } \right)}}^{2}}}}~$При отсутствии скольжения течение симметрично относительно вертикальной плоскости ζ = 0, поэтому уравнение (2.1) совместно с обеими вышеуказанными альтернативами в определении функции ${{\psi }_{b}}\left( \zeta \right)$ решается на отрезке [0, Ω]. Граничными условиями на его концах являются условие симметрии и соотношения на передней кромке
(2.2)
$\eta _{s}^{'}\left( 0 \right) = 0;\quad {{\eta }_{s}}\left( {{\Omega }} \right) = 0,\quad \eta _{s}^{'}\left( {{\Omega }} \right) = - T$После нахождения формы скачка и скоростей ${v},w$ форма проекций поверхностей тока $\eta = {{\eta }_{t}}\left( \zeta \right)\left( {\psi = {\text{const}}} \right)$ определяется из уравнения
(2.3)
$\eta _{t}^{'}\left( \zeta \right) = \frac{{{v}\left( {\zeta ,\psi } \right) - \eta \left( {\zeta ,\psi } \right)}}{{w\left( \psi \right) - \zeta }}$В решении классической задачи обтекания плоского треугольного крыла с присоединенным к передней кромке скачком уплотнения (при ${{\Omega }} \geqslant 2$) [11] основная по протяженности консольная часть крыла, прилежащая к кромке, совпадает с поверхностью тока, а в сравнительно узкой корневой части имеется последовательность чередующихся зон с переменной и постоянной функцией тока. Полученные формы скачка и конических проекций поверхностей тока для значения Ω = 3 показаны на рис. 2.
Рис. 2.
Присоединенный скачок уплотнения, области с постоянной (I–III) и переменной (IV–V) функцией тока, ${{\zeta }_{*}}$, ${{\zeta }_{2}}$ – координаты “особых сечений”.
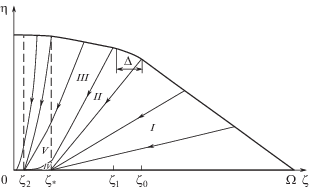
Начинающийся от передней кромки присоединенный скачок над основной частью крыла ${{\zeta }_{*}} = T < \zeta \leqslant {{\Omega }}$ с постоянной функцией тока ${{\psi }_{b}} = {\text{const}} = {{\Omega }}$, описывается простыми аналитическими решениями уравнения (2.1), которое здесь переходит в однородное. Эти решения соответствуют обращению в нуль двух сомножителей в левой части данного уравнения и дают соответственно плоский или искривленный, параболический скачки с постоянным $\eta _{s}^{'} = {\text{const}}$ или линейно уменьшающимся $\eta _{s}^{'} = \pm 1 - \zeta $ наклоном. Форма присоединенного головного скачка определяется, начиная от передней кромки, и состоит из двух плоских участков разного наклона $\eta _{s}^{'}~$ =–T и $\eta _{s}^{'} = {{\Delta }} - T.$ Они сопрягаются гладким образом (так что функция наклона $\eta _{s}^{'}$ непрерывна) посредством промежуточного искривленного параболического скачка. Первое, начиная от передней кромки, искривление скачка начинается в критическом сечении ${{\zeta }_{0}} = 1 + T$, где плоский скачок от кромки с сохранением непрерывности наклона переходит в параболический, а поперечная скорость потока равна скорости звука, и заканчивается при ${{\zeta }_{1}} = 1 + T - {{\Delta }}$. Отмеченная гладкость имеет принципиальное значение, ибо излом скачка, введенный над крылом с ${{\psi }_{b}} = {\text{const}}$, например в [12], влечет за собой и излом поверхностей тока, что невозможно, ибо одной из них является плоская по условию поверхность крыла.
В областях I–III над прилежащей к передней кромке основной частью крыла ${{\zeta }_{*}} < \zeta \leqslant {{\Omega }}$ с постоянной функцией тока реализуется простая структура течения с прямолинейными проекциями поверхностей тока$,{\text{\;}}$однако она весьма сложна в достаточно узкой корневой части $0 < \zeta < {{\zeta }_{*}}$. Параболический скачок оказывает определяющее влияние на формирование этой центральной части поля течения. В самом деле, прошедшие через него поверхности тока формируют на крыле зону ζ2 = $T - {{\Delta }} < \zeta \leqslant {{\zeta }_{*}} = T$ (рис. 2) с переменной функцией тока, определяемой из уравнения (1.8) путем обращения функции $ - \eta _{s}^{'} = \zeta - $ 1 на параболическом участке: $~{{\psi }_{b}}\left( \zeta \right) = \zeta + 1$. Над этой частью крыла форма искривленного скачка находится численным интегрированием неоднородного уравнения (2.1) с правой частью, равной единице, и определяет функцию тока на следующем интервале интегрирования и т.д. Однако при этом нужно учитывать еще одно обстоятельство. В особых сечениях, проходящих через границы этих интервалов, начиная с первого ${{\zeta }_{*}} = T$, действуют вертикально направленные сосредоточенные силы, необходимые для разворота вдоль поверхности крыла “струй” газа большой плотности, идущих со скачка (первая из них представляет собой область II на рис. 2). Они вызывают соответствующие изломы поверхностей тока и скачка, что соответствует идеям монографии [7] о невозможности решения с присоединенным скачком гладкой формы. Например, каждая поверхность тока области II (III) при переходе в область IV (V) претерпевает уменьшение наклона на $\Delta \eta _{t}^{'} = 1 - T$. Наклон скачка после излома, необходимый как начальное условие при численном решении уравнения (2.1), находится из условия совпадения наклонов предельных поверхностей тока, начинающихся на скачке до и после излома. В первом особом сечении получаются следующие значения наклона скачка по разные стороны от излома
Скорость $w = - \eta _{s}^{'}$ принимает разные значения вдоль поверхностей тока, начинающихся по разные стороны от точки излома скачка. Поэтому, хотя они и совпадают в поле течения, но на крыле оканчиваются в разных точках с координатами ζ2, $\zeta _{2}^{'} = - \eta _{s}^{'}({{\zeta }_{*}} - 0)$. Между ними (как и на каждом следующем отрезке интегрирования), образуется зона с ${{\psi }_{b}} = {\text{const}}$, к которой слева примыкает остальная часть ${{\zeta }_{3}} = - \eta _{s}^{'}\left( {{{\zeta }_{2}} - 0} \right) \leqslant \zeta \leqslant \zeta _{2}^{'}$ с переменной ψb. Над первой из них скачок уплотнения будет плоским, над второй – искривленным. Таким образом, вблизи плоскости симметрии форма скачка определяется на ряде интервалов, длина которых быстро стремится к нулю, и состоит из чередующихся искривленных и плоских участков. В результате такого быстро сходящегося процесса решения находится форма скачка, причем основная в данной задаче величина параметра Δ определяется методом пристрелки из условия симметрии (2.2). Как видно на рис. 3, значения Δ(Ω) почти везде, за исключением непосредственной окрестности Ω = 2, достаточно близки к величине наклона присоединенного к кромке скачка T(Ω), поэтому основное уменьшение наклона скачка при перемещении к плоскости симметрии происходит в пределах параболической зоны. При ${{\Omega }} \gg 1$ оно сопровождается уменьшением порядка величины, поскольку $T\sim {{\Delta }}\sim {{{{\Omega }}}^{{ - 1}}}$.
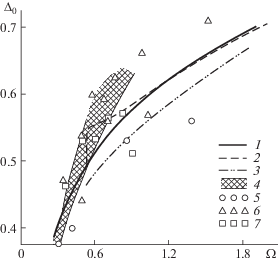
Рис. 3.
Зависимости ${{{{\Delta }}}_{0}}({{\Omega }}),T({{\Omega }}),{{\Delta }}({{\Omega }})$; асимптотика при ${{\Omega }} \gg 1$ показана пунктирной линией.

Затем находятся и все остальные газодинамические функции в следующем приближении к ньютоновскому для рассматриваемого режима обтекания. В частности, получим отход скачка в плоскости симметрии ${{{{\Delta }}}_{0}} = {{\eta }_{s}}\left( 0 \right)$ с графиком на рис. 3 и распределение давления по крылу ${{p}_{b}}\left( \zeta \right)$ (при умножении на ε оно дает добавку первого прядка к основному ньютоновскому значению давления), причем в диапазоне $T < \zeta \leqslant {{\Omega }}$ давление на крыле такое же, как сразу за скачком, и содержит два изобарических участка с уровнями $T{{\Omega }}$ и $T{{\Omega }} - 2{{\Delta }}$ (см. далее рис. 7).
В итоге приходим к решению, описывающему достаточно сложную структуру поля течения за присоединенным скачком, состоящую из перемежающихся областей вихревого (за искривленными участками скачка) и безвихревого (за плоскими скачками) течения. Функция подобия $F\left( {{\Omega }} \right)$ для коэффициента нормальной силы и приведенный отход скачка в плоскости симметрии из законов подобия (1.6), рассчитанные с помощью полученного решения в случае присоединенного скачка, аппроксимируются простыми зависимостями:
(2.4)
$F\left( {{\Omega }} \right) = 2(1 - 0.607{\text{\;}}{{{{\Omega }}}^{{ - 1.869}}}),~\quad {{\Delta }_{0}}\left( {{\Omega }} \right) = 1 - 0.545{\text{\;}}{{{{\Omega }}}^{{ - 0.785}}}$При этом в соотношении для F учтен вклад сосредоточенных сил в первом особом сечении по приведенной далее формуле (3.2).
3. ОСОБЫЕ СЕЧЕНИЯ И СОСРЕДОТОЧЕННЫЕ СИЛЫ
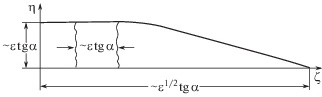
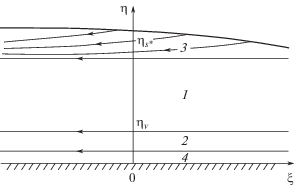
Как установлено выше, поле течения около крыла за присоединенным скачком характеризуется наличием особенностей, которые можно назвать “вертикальными” – это особые сечения ${{\zeta }} = {\text{const}}$ с изломами поверхностей тока под действием вертикально направленных сосредоточенных сил, которые означают сингулярное поведение давления в виде δ-функций. Отметим, что в появлении сосредоточенных сил в течениях газа большой плотности чего-либо необычного нет (см., например, книгу [9]). Проведенный в данной задаче c целью выяснения их природы анализ методом сращиваемых асимптотических разложений [13] показал, что в исходном поле течения в окрестности особых сечений вблизи плоскости симметрии возникают “квадратные” (имеющие одинаковые масштабы $\sim {{\varepsilon tg\alpha }}$ в обоих направлениях) внутренние области локального повышения давления (рис. 4). Для их рассмотрения нужно ввести дополнительно растянутую внутреннюю переменную, например, для первого особого сечения ${{\xi }} = ({{\zeta }} - {{{{\zeta }}}_{{\text{*}}}}){\text{/}}{{{{\varepsilon }}}^{{1/2}}}$. Структура во внутренней области оказывается неоднородной по вертикали и состоит из следующих подобластей или слоев (рис. 5): два основных по толщине слоя почти горизонтального течения 1 – безвихревое течение из области III в область V, образованное поверхностями тока за вторичным плоским скачком (рис. 2); 2 – отделенное от него линией слабого разрыва ${{\eta }} = {{{{\eta }}}_{{v}}} = {{\Delta }^{2}}{\text{/}}2$ вихревое течение из области II в область IV, образованное поверхностями тока за параболическим скачком (рис. 2); а также тонкие слои 3 – зона ${{{{\eta }}}_{s}}_{{\text{*}}} - {{\eta }}\sim {{{{\varepsilon }}}^{{1/2}}}({{{{\eta }}}_{s}}_{{\text{*}}} = 1 - \Delta + {{{{\eta }}}_{{v}}})$ с поверхностями тока, вошедшими в ударный слой в пределах внутренней области; 4 – тонкий вихревой слой, рассматриваемый ниже.
Рис. 5.
Внутренняя область в окрестности особого сечения: 1 – безвихревое течение из области III в область V; 2 – вихревое течение из области II в область IV; 3 – узкая зона с искривленными поверхностями тока; 4 – тонкий вихревой слой.
Во внутренней области главный член поправки к ньютоновскому значению давления в квадратных скобках разложения (1.2) по порядку превышает ε и имеет вид ${{\varepsilon }^{{1/2}}}P.$ Его вертикальный градиент необходим для обеспечения плавного поворота течения сильно сжатого газа, представляющегося во внешнем течении изломом поверхностей тока под действием сосредоточенных сил (δ – функций давления εp), в которые трансформируется это повышенное давление. Вводя нормированные координаты $X = \xi {\text{/}}h,~\;Y = 1 - \eta {\text{/}}{{\eta }_{{s*}}}$, где $h = {{\eta }_{{s*}}}\sqrt {1 - {{\Delta }^{2}}} $, в подобласти 1 для функции ${{P}_{1}}\left( {X,Y} \right)$ получим краевую задачу с уравнением Лапласа, условиями сращивания и интегральным условием, следующим из связи погонной интенсивности сосредоточенных сил с постоянным вдоль особого сечения перепадом наклона поверхностей тока [13]
С помощью косинус-преобразования Фурье находится решение указанной задачи
(3.1)
${{P}_{1}}\left( {X,Y} \right) = \frac{a}{\pi }\ln \frac{{{\text{ch}}\left( {\pi cX} \right) + \sin \left( {\pi cY} \right)}}{{{\text{ch}}\left( {\pi cX} \right) - \sin \left( {\pi cY} \right)}}$Рис. 6.
Эпюра давления – 1 и наклон скачка – 2 во внутренней области; 3 – предельные значения наклона скачка слева и справа от излома.
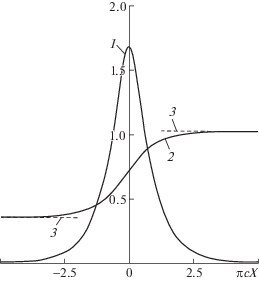
При неравномерном растяжении по осям (1.1) указанные “квадратные” внутренние области (рис. 4) превращаются в вертикальные особые сечения $\zeta = {\text{const}}$ c сосредоточенными силами и изломами скачка и поверхностей тока. Следует отметить, что вклад в поправку к ньютоновскому значению коэффициента нормальной силы от повышенного давления $p\sim {{\varepsilon }^{{1/2}}}$ в окрестности особых сечений $\Delta \zeta \sim {{\varepsilon }^{{1/2}}}$ по порядку такой же, как от его непрерывного распределения $p\sim \varepsilon ~~$ на основной части крыла $~\Delta \zeta \sim 1$. Однако максимальное численное значение приращения функции подобия $F\left( {{\Omega }} \right)$, равного для первого особого сечения
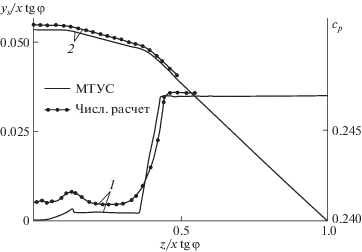
не превышает 1%. Вклад сосредоточенных сил в других особых сечениях еще меньше, и им можно пренебречь.Полученное немонотонное поведение давления вблизи плоскости симметрии в результате действия сосредоточенных сил представлялся неожиданным и потому весьма спорным даже после вскрытия его физической природы методом сращиваемых асимптотических разложений. Для окончательного его обоснования получено подтверждение сравнением с точным численным расчетом гиперзвукового обтекания треугольного крыла при близких к единице значениях γ на основе полных уравнений Эйлера, выполненным А.А. Голубинским при M∞ = 19.3, $\alpha = 20^\circ ,~\varphi = 13.6^\circ $, γ = 1.05.
В месте расположения первого особого сечения и еще ближе к плоскости симметрии действительно обнаружены, по крайней мере, два локальных максимума коэффициента давления (рис. 7 с использованием исходных декартовых координат (рис. 1)). Остальные немонотонности его величины, видимо, настолько малы, что расчетом уже не обнаруживаются, да и теоретически они ничтожны. Полученная в том же расчете форма скачка практически полностью воспроизвела его конфигурацию согласно полученному точному решению (рис. 7).
4. ОБТЕКАНИЕ С ОТСОЕДИНЕННЫМ ОТ КРОМКИ СКАЧКОМ
В отличие от предыдущего случая, для данного режима течения ситуация с граничным условием однозначная: функция тока на крыле может быть только переменной. Поэтому на скачке $\zeta = \psi $, на крыле ${{\zeta }_{b}}\left( \psi \right) = w\left( \psi \right),$ и основное интегро-дифференциальное функциональное уравнение для формы скачка берется в виде [4]. Оно сводится к нелинейному функционально-дифференциальному уравнению относительно функции $w(\psi ){\text{:}}$
(4.1)
$w{\kern 1pt} '\left[ {w\left( \psi \right)} \right]w{\kern 1pt} '\left( \psi \right)\left( {\frac{1}{{{{{\left\{ {w\left[ {w\left( \psi \right)} \right] - w\left( \psi \right)} \right\}}}^{2}}}} - 1} \right) = \frac{1}{{{{{\left[ {w\left( \psi \right) - \psi } \right]}}^{2}}}}$Для первой схемы точка окончания проекции поверхности тока на крыле лежит дальше от плоскости симметрии, чем точка ее входа в ударный слой на скачке ${{\zeta }_{b}} = w\left( \psi \right) = b\psi + \cdots > {{\zeta }_{s}} = \psi $. Значит, в корневой части происходит растекание потока. Дальнейшее численное решение задачи (4.1), (4.4) в данном случае не вызывает затруднений, и такое расходящееся поведение поверхностей тока оказывается присущим течению в целом [14] – это схема D.
Для второй схемы, наоборот, в плоскости симметрии расположена линия стекания, поскольку ${{\zeta }_{b}} < {{\zeta }_{s}}$. Она образуется при некотором значении параметра ${{\Omega }} = {{{{\Omega }}}_{*}}$, начиная с которого находившаяся там до этого линия растекания сдвигается по направлению к передней кромке в некоторое сечение $\zeta = {{\zeta }_{d}}$. Таким образом, в консольной части крыла образуется дополнительная вертикальная линия растекания, после которой поток приобретает нужное направление для перетекания через переднюю кромку. Численное решение для этой схемы CD, начатое от плоскости симметрии, потребовало преодоления проблем, связанных с переходом через эту вертикальную поверхность тока, для чего оно осуществлялось в три этапа: интегрирование в центральной зоне стекания, экстраполяция через дополнительную линию растекания и интегрирование в зоне растекания вплоть до передней кромки. Попутно определялось значение координаты дополнительной линии растекания ${{\zeta }_{d}}$.
Долгое время не было ясности с точной величиной граничного значения параметра ${{\Omega }} = {{{{\Omega }}}_{*}}$, разделяющего схемы течения D и CD. В книге [8] со ссылкой на [15] приведена оценочная величина ${{{{\Omega }}}_{*}} \approx 1,~$ в работе [16] получено другое приближение ${{{{\Omega }}}_{*}} \approx 0.5.$ И лишь в [14] с высокой степенью точности найдено лежащее между ними пограничное значение ${{{{\Omega }}}_{*}} = 0.5648$. График фундаментальной для данной задачи зависимости кривизны скачка в плоскости симметрии от приведенного полуразмаха $b\left( {{\Omega }} \right)$, полученной путем систематических расчетов на основе (4.2)–(4.4), приведен на рис. 8. Эта кривая для ${{\Omega }} \geqslant 0.24$ близка к гиперболе и аппроксимируется аналитически как
Рис. 8.
Зависимости кривизны скачка в плоскости симметрии $b\left( {{\Omega }} \right)$ (1 – данная работа, 2 – [16]) и на дополнительной линии растекания ${{b}_{d}}\left( {{\Omega }} \right)$, 3 – от параметра подобия.
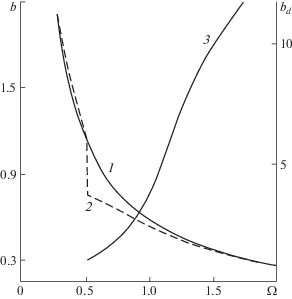
Она является гладкой, тогда как приближенное решение [16] имеет ступенчатый разрыв при определенном в ней граничном значении ${{\Omega }} = {{{{\Omega }}}_{*}}$ (штриховая линия на рис. 8). В случае ${{\Omega }} < 0.24$ результаты расчетов хорошо совпадают с гиперболической зависимостью $b(\Omega ) = \frac{1}{{2\Omega }}$, полученной в [4] из аналитического решения при $\Omega \ll 1$. Отметим, что кривизна скачка в центре крыла стремится к бесконечности при приближении приведенного полуразмаха Ω к нулю и монотонно убывает до $b \approx 0.3$ с ростом этого параметра до его граничного значения Ω = 2.
Найдя численное решение задачи (4.2)–(4.4), конфигурацию головного скачка определяем интегрированием
(4.6)
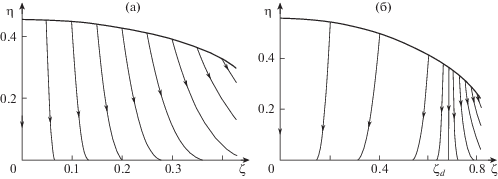
${{\eta }_{s}}\left( \zeta \right) = {{\Delta }_{0}} - \mathop \smallint \limits_0^\zeta w\left( z \right)dz,\quad {{{{\Delta }}}_{0}} = \frac{{1 - b + b\ln b}}{{{{{\left( {1 - b} \right)}}^{2}}}}$Форма скачка (4.6) и проекций поверхностей тока, найденная далее интегрированием из (2.3), показаны на рис. 9, а (схема D) и рис. 9, б (схема CD).
Рис. 9.
Возможные схемы конического течения за отошедшим скачком (а) – схема D при ${{\Omega }} = 0.4285$, (б) – схема CD при ${{\Omega }} = 0.8168$.
В промежуточном случае $b = 1,~~{{\Omega }} = {{{{\Omega }}}_{*}}$ получается течение c вертикальными поверхностями тока, и в формуле (4.6) для Δ0 возникает неопределенность 0/0, раскрывая которую находим пограничное значение $~{{\Delta }_{0}} = 1{\text{/}}2$.
Давление на поверхности крыла из формулировки второго закона подобия (1.6) вычисляется по формуле, содержащей в качестве нижнего предела интегрирования переменную функцию тока на крыле, обратную к w:
(4.7)
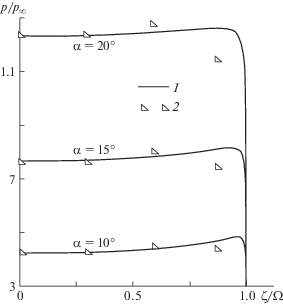
$~{{p}_{b}}\left( \zeta \right) = {{p}_{s}}\left( \zeta \right) - \{ 1 - {{\left[ {w\left( \zeta \right) - \zeta } \right]}^{{ - 2}}}\} w'\left( \zeta \right)\mathop \smallint \limits_{{{w}^{{ - 1}}}\left( \zeta \right)}^\zeta \frac{{{{{\left[ {w\left( z \right) - \zeta } \right]}}^{3}}}}{{{{{\left[ {w\left( z \right) - z} \right]}}^{2}}}}dz$Как видно на рис. 10, распределения суммарной величины давления, найденной по формулам (1.2), (4.7) и отнесенной к ${{p}_{\infty }}$, для разных углов атаки удовлетворительно согласуются с экспериментальными данными.
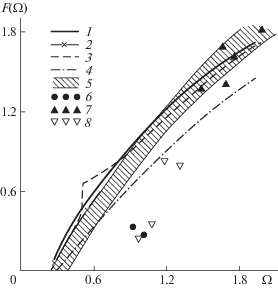
Рассмотрим некоторые другие интегральные и локальные характеристики, определенные расчетным путем. Кривые приведенного отхода скачка уплотнения в плоскости симметрии $~{{\Delta }_{0}}\left( {{\Omega }} \right)$ и функции подобия $F\left( {{\Omega }} \right)$ для коэффициента нормальной силы и из первого и третьего законов подобия (1.6), полученные для обеих схем обтекания, на рис. 11, 12 сравниваются с результатами других работ по МТУС, а также с данными экспериментов и прямых численных расчетов на основе уравнений Эйлера.
Наряду с (2.4) для присоединенного скачка, результаты эталонных расчетов по МТУС в случае отошедшего скачка аппроксимируются формулами
(4.8)
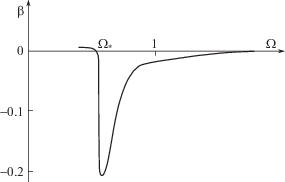
$F\left( {{\Omega }} \right) = 0.667~{{\left( {{\text{ln}}\frac{{{\Omega }}}{{0.24}}} \right)}^{{1.219}}}~,~\quad {{\Delta }_{0}}\left( {{\Omega }} \right) = 1.1 - 0.497{{{{\Omega }}}^{{ - 0.271}}}$Первая из них при достаточно малых Ω дает отрицательные значения F, которые получены и в эксперименте [26], но не показаны на рис. 12. Оказалось, что со второй, кинематической величиной Δ0 линейно связана динамическая характеристика – давление в плоскости симметрии: ${{p}_{c}} = 1.4~{{\Delta }_{0}} - 0.45.$ Поведение параметра $\beta \left( {{\Omega }} \right) = - {{p}_{{\zeta \zeta }}}\left( {0,\zeta } \right){\text{/}}2,$ который пропорционален взятой с обратным знаком кривизне эпюры давления на поверхности крыла, иллюстрируется на рис. 13. Как видно, знак этого параметра, важного для дальнейшего рассмотрения энтропийного слоя, меняется при смене схемы обтекания (когда ${{\Omega }} = {{{{\Omega }}}_{*}}$) одновременно с направлением боковой силы, действующей на газ вблизи стенки.
Для схемы течения CD приведем новые результаты эталонных расчетов методом [14] параметров, относящихся к дополнительной линии растекания. При ${{\Omega }} = {{{{\Omega }}}_{*}}\left( {b = 1} \right)$ эта вертикальная линия, на которой
совпадает с центральной ${{\zeta }_{d}} = 0~.$ Если b несколько меньше единицы, то, как нетрудно показать, ее координата быстро возрастает ${{\zeta }_{d}} = {{\left( {1 - b} \right)}^{{0.5}}}$, а с дальнейшим ростом Ω и уменьшением b (рис. 8) она приближается к передней кромке (рис. 14). Согласно равенствам (1.4) и (4.2), кривая ${{\zeta }_{d}}\left( {{\Omega }} \right)$ показывает также поведение величины наклона скачка на дополнительной линии растекания $\eta _{s}^{'}({{\zeta }_{d}})~$ =–ζd. Здесь же показана зависимость приведенного отхода скачка в этом месте ${{{{\Delta }}}_{d}}(\Omega )$ = ηs(ζd). Для этих величин получены новые формулы аппроксимации(4.10)
${{\zeta }_{d}}\left( {{\Omega }} \right) = 1.553{{\left( {{{\Omega }} - 0.565} \right)}^{{0.647}}},\quad {{\Delta }_{d}}\left( {{\Omega }} \right) = 0.3{{\left( {2 - {{\Omega }}} \right)}^{{1.38}}}$Рис. 14.
Координата дополнительной линии растекания ${{\zeta }_{d}}\left( {{\Omega }} \right)$ и отход скачка ${{{{\Delta }}}_{d}}\left( {{\Omega }} \right)$.
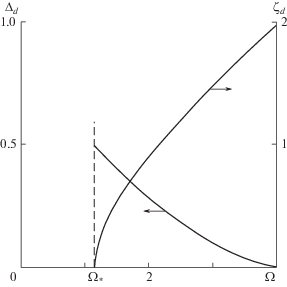
В диапазоне ${{{{\Omega }}}_{*}} < \Omega < 2$ на рис. 8 нанесена зависимость величины кривизны скачка на дополнительной линии растекания ${{b}_{d}}\left( {{\Omega }} \right)$, которая стремится к бесконечности, когда эта линия приближается к передней кромке ${{\zeta }_{d}} \to {{\Omega }}$ при ${{\Omega }} \to 2.$ На другом краю этого диапазона имеем ${{b}_{d}}({{{{\Omega }}}_{*}}) = b({{{{\Omega }}}_{*}})$ = 1, хотя на рис. 8 слияние кривых в этой точке отсутствует по причине разных масштабов по вертикальным осям.
5. ЭНТРОПИЙНЫЙ СЛОЙ
В разделе 2 в подтверждение особого характера решения, описывающего режим обтекания с присоединенным к кромке скачком, рассмотрены вертикальные особые сечения с изломами скачка уплотнения и поверхностей тока под действием сосредоточенных сил, предварительно проанализированные в [13].
Вместе с тем полученным в рамках МТУС решениям для обоих режимов обтекания, которые должны рассматриваться как внешние, относящиеся к основной части ударного слоя, свойственны и “горизонтальные” особенности, которые обусловлены тем, что на всей поверхности крыла или некоторых ее частях функция тока оказывается переменной. Изоэнтропические поверхности тока здесь подходят к крылу по касательной и оканчиваются на нем в точках, где поперечная коническая компонента скорости $w - \zeta $ обращается в нуль. Следовательно, при подходе к ним $\left( {w - \zeta } \right) \to 0.$ Согласно четвертому уравнению (1.3), внепорядковое влияние боковой составляющей градиента давления ${{p}_{\zeta }},$ которая в уравнении импульсов по оси ζ умножается на $\varepsilon \ll 1$, пренебрежимо мало в основной части сжатого слоя и не учитывается в системе уравнений (1.3) для этой “внешней” области, где $\left( {w - \zeta } \right)\sim 1$. Однако боковой градиент давления оказывается существенным и его необходимо учитывать в пристеночной “внутренней” области, где разность $\left( {w - \zeta } \right)$ мала. Эту область можно назвать вихревым или энтропийным слоем. Здесь полученные в разделах 2, 4 внешние решения непригодны, так как дают искаженную картину поверхностей тока. Далее выполняется дополнительное исследование, позволяющее уточнить характер пристеночного поведения поверхностей тока путем построения универсального равномерно пригодного решения [27], применимого во всей возмущенной области. Для этой цели наиболее подходит режим обтекания плоского треугольного крыла с отошедшим скачком (см. раздел 4), когда функция тока на нем переменна (1.8), и энтропийный слой примыкает ко всей поверхности крыла. Чтобы получить решение в обозримом аналитическом виде, рассмотрим течения вблизи плоскости симметрии и в окрестности дополнительной линии растекания на консоли крыла.
6. УНИВЕРСАЛЬНОЕ РЕШЕНИЕ В ОКРЕСТНОСТИ ПЛОСКОСТИ СИММЕТРИИ
Это решение будет справедливо для обеих схем обтекания D и CD с отсоединенным от кромки скачком. Чтобы оценить толщину вихревого слоя и разницу между точным и внешним решениями, построим универсальное решение, пригодное вплоть до поверхности крыла. Поскольку в рассматриваемой задаче источник неравномерной пригодности внешнего решения очевиден, можно получить универсальное решение, просто сохраняя малый член с производной ${{p}_{\zeta }}$ в правой части четвертого уравнения (1.3). В окрестности плоскости симметрии такого “планарного тела”, как плоское крыло, при $\left| \zeta \right| \ll 1,$ учитывая свойства четности функций, входящих в разложения (1.2), представим их в виде
(6.1)
$f\left( {\eta ,\zeta } \right) = {{f}^{{\left( 0 \right)}}}\left( Y \right) - {{f}^{{\left( 2 \right)}}}\left( Y \right){{\zeta }^{2}} + \ldots ,\quad f = \left\{ {{{{v}}_{1}},{{p}_{1}},~{{\rho }_{0}},{{\sigma }_{2}}} \right\}$Подставим эти представления в исходные уравнения МТУС и краевые условия (1.3)–(1.5). Тогда, отбрасывая индексы и обозначая штрихом полные производные по приведенной координате Y, получим следующую систему обыкновенных дифференциальных уравнений и краевые условия, которым удовлетворяют главные члены (6.1):
(6.2)
$\begin{gathered} {{v}^{{(0)}}}{\kern 1pt} '\, + {{\Delta }_{0}}W = 0,\quad v{{\sigma }^{{(0)}}}{\kern 1pt} '\,\, = 0 \hfill \\ v = {{\Delta }_{0}}Y - {{v}^{{(0)}}},\quad W = {{W}^{{(1)}}} - 1 \hfill \\ \end{gathered} $(6.3)
$Y = 1:~{{{v}}^{{\left( 0 \right)}}} = {{\Delta }_{0}} - 1,\quad {{w}^{{\left( 1 \right)}}} = b,\quad {{p}^{{\left( 0 \right)}}} = 2{{\Delta }_{0}} - 1,\quad {{p}^{{\left( 2 \right)}}} = \left( {b - 1} \right)b$В правой части второго уравнения (6.2) в соответствии с отмеченным выше оставлен член, существенный лишь в тонком пристеночном слое, где $Y,~W \ll 1$, поэтому аналогично [3] имеем право положить в нем ${{p}^{{\left( 2 \right)}}}\left( Y \right) \approx {{p}^{{\left( 2 \right)}}}\left( 0 \right) = \beta $. Определенные из глобального внешнего решения с учетом условия (4.3) на передней кромке формулы для $b\left( {{\Omega }} \right),{{\Delta }_{0}}\left( {{\Omega }} \right),\beta \left( {{\Omega }} \right)$ приведены в разделе 4 и изображены графически на рис. 8, 11, 13.
После перехода от координаты Y к новой переменной r, задаваемого уравнением
уравнения и граничные условия для вертикальной и боковой составляющих скорости поперечного конического течения V, W из (6.2) записываются в видеНайдем сначала предельное внешнее решение ${{W}_{0}},~{{V}_{0}}$, которое фактически представляет собой разложение найденного в разделе 4 решения при $\zeta \ll 1$. Интегрируя последовательно уравнения (6.5) при ε = 0 и (6.6), получаем
(6.8)
${{W}_{0}}\left( t \right) = \frac{{\left( {b - 1} \right)r}}{{b - \left( {b - 1} \right)r}},\quad {{V}_{0}}\left( t \right) = \frac{{{{r}^{2}}}}{{b - \left( {b - 1} \right)r}}$Последующее интегрирование обеих частей (6.4) приводит к трансцендентному соотношению между параметрами b и Δ0, совпадающему с формулой (4.7).
Внешнее решение (6.8) дает ${{W}_{0}} = 0$ на крыле при r = 0, как и ранее. Исследуем теперь поведение энтропийной функции и поверхностей тока. Главный член ${{\sigma }^{{\left( 0 \right)}}} = {\text{const}}$ согласно четвертому уравнению системы (6.2), а для следующего члена разложения (6.1) из уравнений (1.3) имеем: $rd{{\sigma }^{{(2)}}}{\text{/}}dr = 2{{\sigma }^{{(2)}}}W(r).~$ Подставляя сюда $W = {{W}_{0}}\left( r \right)$ из (6.8), во внешней области находим
(6.9)
$\sigma _{0}^{{\left( 2 \right)}}\left( r \right) = \frac{{\sigma _{0}^{{\left( 2 \right)}}\left( 1 \right)}}{{{{{\left[ {b - \left( {b - 1} \right)r} \right]}}^{2}}}},\quad \sigma _{0}^{{\left( 2 \right)}}\left( 0 \right) \ne 0$Следовательно, внешнее решение дает переменную энтропию на поверхности:
Теперь, сохраняя в (6.5) последнее слагаемое, существенное в тонком пристеночном слое, найдем универсальное решение
(6.10)
$W\left( r \right) = \frac{{{{\lambda }_{1}}{{\omega }_{2}} - {{\lambda }_{2}}{{\omega }_{1}}{{r}^{\mu }}}}{{{{\omega }_{2}} - {{\omega }_{1}}{{r}^{\mu }}}},\quad V\left( r \right) = \frac{{\mu {{r}^{\nu }}}}{{{{\omega }_{2}} - {{\omega }_{1}}{{r}^{\mu }}}}$В основной части сжатого слоя (r ~ 1) универсальное (6.10) и внешнее (6.8) решения совпадают с точностью до членов порядка ε, однако в тонком слое вблизи стенки при $t \ll 1$ найденные решения для боковой компоненты скорости значительно различаются, а представления ее вертикальной компоненты совпадают и имеют вид
(6.11)
$~W = 2\beta \varepsilon + \ldots ,\quad {{W}_{0}} = \left( {b - 1} \right)r{\text{/}}b + \ldots ,\quad V = {{V}_{0}} = ~~{{r}^{2}}{\text{/}}b + ~ \ldots $Как видно отсюда, ${{W}_{0}} \to 0$, если r → 0, но, согласно универсальному решению, скорость W при этом отлична от нуля и вместе с параметром β имеет знак, противоположный градиенту давления вдоль размаха. Приравняв по порядку величины слагаемые в числителе (6.10), получим в энтропийном слое оценку координаты $r\sim \varepsilon $, или его толщины
Она является величиной второго порядка малости по сравнению с толщиной основной части сжатого слоя $~{{\Delta }_{0}}\sim 1$. С использованием универсального решения (6.10) получаем, что в отличие от (6.9) энтропия на крыле постоянна $\sigma \left( {0,\zeta } \right) = {{\sigma }^{{\left( 0 \right)}}} = {\text{const}}$, поскольку
Форма проекций поверхностей тока находится из уравнения (2.3), которое в переменных $r,\zeta $ приобретает вид
куда нужно подставить W0 из (6.8) или W из (6.10). Во внешней области для поверхности тока, входящей в сжатый слой на скачке при $\zeta = {{\zeta }_{s}}$ и приходящей в точку $\zeta = {{\zeta }_{b}}$ на крыле, это дает линейную зависимость(6.13)
${{r}_{0}}\left( \zeta \right) = \frac{{{{\zeta }_{b}} - \zeta }}{{\left( {b - 1} \right){{\zeta }_{s}}}}{\text{,}}\quad {{\zeta }_{b}} = b{{\zeta }_{s}}$В исходных конических переменных соответствующее уравнение поверхности тока $Y = {{Y}_{{t0}}}\left( \zeta \right)$ найдем, используя связь координат r и Y (6.4), а также решения (6.8), (6.13):
(6.14)
${{Y}_{{t0}}}\left( \zeta \right) = \frac{{b - \zeta {\text{/}}{{\zeta }_{s}} + b\ln \left( {\zeta {\text{/}}{{\zeta }_{b}}} \right)}}{{b - 1 - b\ln b}}$Универсальный вид внешних проекций поверхностей тока в окрестности плоскости симметрии показан на рис. 15 штриховыми линиями для двух случаев: (а) $b$ = 1.5 > 1 (стекание) и (б) $b$ = = 0.5 < 1 (растекание). Здесь по горизонтальной оси отложена положительная приведенная координата $\zeta {\text{/}}{{\zeta }_{s}}$, хотя те же кривые, зеркально отраженные от вертикальной оси, относятся и к левой полуплоскости $\zeta < 0.$ В универсальном решении форма поверхностей тока определяется из (6.12), (6.10) в параметрическом виде:
(6.15)
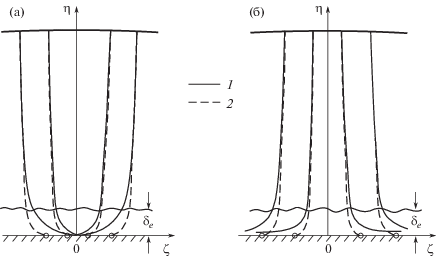
${{Y}_{t}}\left( r \right) = \frac{{{{\omega }_{2}}F\left( r \right) - r}}{{{{\omega }_{2}}F\left( 1 \right) - 1}},\quad \frac{\zeta }{{{{\zeta }_{s}}}} = {{r}^{{{{\lambda }_{1}}}}}{{\left( {\frac{{{{\lambda }_{1}} - {{\lambda }_{2}}}}{{{{\omega }_{2}} - {{\omega }_{1}}t{{r}^{\mu }}}}} \right)}^{{{{\omega }_{2}}}}},\quad F\left( r \right) = \mathop \smallint \limits_0^r \frac{{dx}}{{{{\omega }_{2}} - {{\omega }_{1}}{{x}^{\mu }}}}$Рис. 15.
Универсальные формы поверхностей тока вблизи плоскости симметрии: 1 – универсальное решение, 2 – внешнее решение.
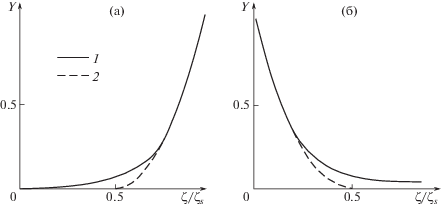
Она показана на рис. 15 сплошными линиями. Внешние и универсальные формы поверхностей тока (6.14) и (6.15) совпадают в основной части сжатого слоя (внешней области), но сильно различаются в пристеночном (внутреннем) слое ввиду отличия решений (6.11). Под действием существенного здесь бокового градиента давления происходит резкий разворот поверхностей тока вдоль плоскости крыла. Действительно, для $\left| {{{\zeta }_{b}} - \zeta } \right| \ll 1$ из (6.14) и (6.15) имеем во внешнем и универсальном решениях
Координата точки входа ζs может быть как положительной, так и отрицательной. Поэтому если кривые на рис. 15 построить в зависимости не от отношения $\zeta {\text{/}}{{\zeta }_{s}}$, а от координаты ζ при значениях ζs обоих знаков, то они покажут картину поверхностей тока в двусторонней окрестности плоскости симметрии (рис. 16). В зависимости от характера течения и соответствующих параметров $b,~\,\beta ~$ во внешней области поток направлен к плоскости симметрии, если $b > 1,\,\,\beta > 0$ (рис. 16, а), либо от нее, если $b < 1,~\,\beta < 0$ (рис. 16, б). Соответственно особая точка $\eta = \zeta = 0$ (точка Ферри [8]) для проекций поверхностей тока, показанных на рис. 16, в пределах внутренней области является либо узловой, либо седловой. Существующий поперек нее градиент энтропии порождает здесь сильно завихренное течение, вследствие чего рассмотренный пристеночный слой и называется энтропийным или вихревым.
7. ОКРЕСТНОСТЬ ДОПОЛНИТЕЛЬНОЙ ЛИНИИ РАСТЕКАНИЯ
Как отмечалось в разделе 4, в начале диапазона ${{{{\Omega }}}_{*}} < \Omega < 2$, в котором реализуется схема течения с дополнительной линией растекания, отход скачка составляет ${{{{\Delta }}}_{d}} = {{\Delta }_{0}} = 1{\text{/}}2,$ и далее он монотонно убывает до 0 (рис. 14). Основное отличие от предыдущего случая состоит в том, что когда эта вертикальная линия $\zeta = {{\zeta }_{d}}$ отходит от центра, в точке ее начала касательная к скачку уже не горизонтальна, а с учетом (4.9) ее наклон равен ${{\delta }_{d}} = \eta _{s}^{'}\left( {{{\zeta }_{d}}} \right) = - {{\zeta }_{d}} < 0$ (рис. 14). Тогда в окрестности этой линии форма скачка представима в виде:
(7.1)
${{\eta }_{s}} = {{{{\Delta }}}_{d}} - {{\zeta }_{d}}{{\zeta }_{1}} - {{b}_{d}}\zeta _{1}^{2}{\text{/}}2 + \ldots ,\quad {{\zeta }_{1}} = \zeta - {{\zeta }_{d}}$(7.2)
$f\left( {\eta ,\zeta } \right) = {{f}^{{\left( 0 \right)}}}\left( Y \right) + {{f}^{{\left( 1 \right)}}}\left( Y \right){{\zeta }_{1}} + \ldots ,\quad f = \left\{ {{{{v}}_{1}},{{w}_{1}},{{\sigma }_{2}}} \right\}$Вводя аналогично (6.2) функции $V\left( Y \right) = {{\Delta }_{d}}Y - {{{v}}^{{\left( 0 \right)}}},\,\,W\left( Y \right) = {{w}^{{\left( 1 \right)}}} - 1,$ получим те же уравнения и граничные условия, что и (6.5)–(6.7) с использованием параметров ${{b}_{d}},~{{\Delta }_{d}},~{{\beta }_{d}} = {{p}^{{\left( 2 \right)}}}(0),$ вместо $b,~{{\Delta }_{0}},~\beta $. На тех же условиях остаются в силе внешнее и универсальное решения (6.8), (6.10). Параметры Δd и bd будут связаны друг с другом таким же соотношением (4.6), которое имеется между Δ0 и b. Тогда, зная аппроксимацию (4.10) для ${{\Delta }_{d}}\left( {{\Omega }} \right) \leqslant 0.5$, найдем и зависимость ${{b}_{d}}\left( {{\Omega }} \right)$ (рис. 8). Поскольку в отличие от параметра b (рис. 8) всегда имеем ${{b}_{d}} \geqslant 1$, то в окрестности $\zeta = {{\zeta }_{d}}$ возможна лишь схема течения с линией растекания, для которой форма поверхностей тока соответствует рис. 15, б и рис. 16, б с той лишь разницей, что при $\zeta = {{\zeta }_{d}}$ скачок имеет конечный угол наклона, а не нулевой, как в центре. С приближением линии растекания к передней кромке кривизна скачка bd стремится к бесконечности, как и должно быть при выполнении условия (4.3). Относительная толщина энтропийного слоя здесь также ${{\delta }_{e}}\sim {{\varepsilon }^{2}}$. Вместе с аналогичным результатом для окрестности центральной линии $\left| \zeta \right| \ll 1$ это дает основание предположить, что такая оценка выполняется равномерно на всей поверхности крыла. Таким образом, показано, что энтропийный слой на “планарном” крыле оказывается более толстым, чем на круговом конусе, где он экспоненциально тонкий [8].
По той же причине, что для обтекания с отошедшим скачком, тонкий энтропийный слой аналогичной природы образуется на узких участках поверхности крыла с переменной функцией тока в центральной части течения с присоединенным скачком (разд. 2).
ЗАКЛЮЧЕНИЕ
Применительно к задаче гиперзвукового обтекания плоского треугольного крыла малого удлинения под конечным углом атаки в рамках закона подобия по параметру подобия Ω методом тонкого ударного слоя получены решения и приведена дополненная классификация, которая включает в себя основные режимы обтекания по форме головного скачка уплотнения, присоединенного к передней кромке (${{\Omega }} \geqslant 2$) или отсоединенного от нее (${{\Omega }} < 2$), и во втором случае – две схемы обтекания по характеру поведения поверхностей тока (течение с линией растекания в центральной плоскости симметрии при ${{\Omega }} < {{{{\Omega }}}_{*}}$ и течение с линией стекания в центре и дополнительными линиями растекания на консолях при ${{{{\Omega }}}_{*}} < \Omega < 2$). Это позволяет априори судить о реализации того или иного режима и/или схемы обтекания на основе исходных параметров задачи. Даны приближенные формулы, аппроксимирующие результаты расчетов на основе аналитико-численных решений. Они характерны тем, что пространственное возмущенное течение обладает свойством коничности во всем сжатом слое между скачком уплотнения и поверхностью крыла, включая окрестности особых сечений (за присоединенным скачком) и тонкий пристеночный энтропийный слой (для обоих режимов обтекания). Наличие таких особенностей, обусловленных большой плотностью газа в ударном слое, служит подтверждением мнения М. Ван-Дайка [27] о том, что особое поведение и неравномерная пригодность решений в механике жидкости являются скорее правилом, чем исключением. С применением асимптотических методов построены равномерно пригодные (универсальные) решения, которые характеризуются заметными (локализованными) отличиями в поведении некоторых параметров течения и конических поверхностей тока вблизи этих особенностей от основной части сжатого слоя.
Приведенные решения получены в рамках приближенной модели без учета вязкости, и их следует рассматривать как внешние по отношению к вязкому пограничному слою.
Список литературы
Чёрный Г.Г. Течения газа с большой сверхзвуковой скоростью. М.: Физматгиз, 1959. 220 с.
Хейз У.Д., Пробстин Р.Ф. Теория гиперзвуковых течений. М.: Изд-во иностр. лит., 1962. 607 с.
Лунёв В.В. Гиперзвуковая аэродинамика. М.: Машиностроение, 1975. 327 с.
Месситер A. Подъемная сила тонких треугольных крыльев по ньютоновской теории // Ракетная техника и космонавтика. 1963. № 4. С. 31–41.
Голубинский А.И., Голубкин В.Н. О пространственном обтекании тонкого крыла гиперзвуковым потоком газа // Докл. АН СССР. 1977. Т. 234. № 5. С. 1032–1034.
Голубкин В.Н. Пространственное обтекание крыльев гиперзвуковым потоком газа // Изв. РАН. МЖГ. 1992. № 5. С. 148–161.
Hayes W.D., Probstein R.F. Hypersonic flow theory / 2nd ed. V. 1. Inviscid flows. N.Y.–London: Acad. Press, 1966. 602 p.
Буллах Б.М. Нелинейные конические течения. М.: Наука, 1970. 344 с.
Ладыженский М.Д. Пространственные гиперзвуковые течения газа. М.: Машиностроение, 1968. 120 с.
Голубинский А.И. Обтекание гиперзвуковым потоком треугольных крыльев определенного класса, установленных под углом атаки, с присоединенным скачком уплотнения // Изв. АН СССР. МЖГ. 1968. № 5. С. 73–78.
Голубкин В.Н. Обтекание плоского треугольного крыла гиперзвуковым потоком газа // Учен. зап. ЦАГИ. 1976. Т. VII. № 6. С. 1–10.
Woods B.A. Hypersonic flow with attached shock waves over delta wing // Aeronaut. Quart. 1970. V. 21. № 4. P. 319–325.
Голубинский А.И., Голубкин В.Н. Анализ особенностей в решении задачи гиперзвукового обтекания треугольного крыла малого удлинения // Учен. зап. ЦАГИ. 1987. Т. XVIII. № 6. С. 20–29.
Голубкин В.Н., Негода В.В. К расчету обтекания треугольных крыльев в приближении тонкого ударного слоя // ЖВМ МФ. 1989. № 10. С. 1530–1537.
Hida K. Thickness effect on the force of slender delta wings in hypersonic flow // AIAA J. 1965. № 3. P. 427–433.
Shanbhag V.V. Numerical studies on hypersonic delta wings with detached shock waves // ARC Current Paper. 1974. № 1277.
Johnson C.B., Marcum D.C. A parametric study of effect of forebody shape on flow angularity at Mach 8 // NASA TN D–7768, 1974.
Squire L.C. Calculated pressure distributions and shock shapes on thick conical wings at high supersonic speeds // Aeronaut. Quart. 1967. № 2. P. 185–206.
Базжин А.П. Две новые корреляционные зависимости для параметров течения на плоском треугольном крыле // Учен. зап. ЦАГИ. 1976. № 4. С. 111–114.
Башкин В.А. Экспериментальное исследование обтекания плоских крыльев при числах М = 3 и 5 в диапазоне углов атаки от нуля до 90° // Тр. ЦАГИ. 1970. Вып. 1175. С. 124–162.
Bertram M.H., Henderson A. Recent hypersonic studies of wings and bodies // ARS J. 1961. V. 31. № 8. P. 1129–1139.
Coleman G.T. Force measurements on caret and delta wings at high incidence // Imperial Coll., London. Dept. of Aeronautics Rept. 1972. № 16–76.
Минайлос А.Н. Подобие аэродинамических характеристик треугольных крыльев при сверхзвуковых скоростях // Учен. зап. ЦАГИ. 1979.Т. X. № 3. С. 16–26.
Sorrels R.S., Landrum E.J. Theoretical and experimental study of twisted and cambered delta wings designed for a Mach number of 3.5 // 1976. NASATN.D-8247.
Жданов А.В. Экспериментальное исследование интерференции крыла и корпуса при гиперзвуковых скоростях // Тр. ЦАГИ. 1982. Вып. 2161. С. 3–7.
Stallings R.L., Lamb M. Wing-alone aerodynamic characteristics at high angles of attack // J. Spacecraft. 1982. V. 19. № 2. P. 145–149.
Ван-Дайк М. Методы возмущений в механике жидкости. М.: Мир, 1967. 310 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа