Известия РАН. Механика жидкости и газа, 2021, № 4, стр. 63-72

ДВИЖЕНИЕ НАГРУЗКИ ПО ЛЕДЯНОМУ ПОКРОВУ С НЕРАВНОМЕРНЫМ СЖАТИЕМ

И. В. Стурова^a, *

^a Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

Поступила в редакцию 24.12.2020
После доработки 21.01.2021
Принята к публикации 24.01.2021

DOI: 10.31857/S0568528121040125

Аннотация

Рассмотрена линейная гидроупругая задача о движении прямоугольной области внешнего давления по безграничному ледяному покрову, плавающему на поверхности жидкости. Ледовый покров моделируется тонкой упругой пластиной с учетом продольных, поперечных и сдвиговых сжимающих усилий. Внешняя нагрузка описывает движение судна на воздушной подушке. Построено решение нестационарной задачи о мгновенном старте нагрузки и последующем прямолинейном движении с постоянной скоростью. Исследовано установившееся волновое движение, возникающее при больших значениях времени. Определены вертикальные прогибы и деформации ледяного покрова, а также волновые силы, действующие на судно.

Ключевые слова: плавающая упругая пластина, изгибно-гравитационные волны, сжимающие усилия, движущаяся нагрузка, волновые силы, деформации

В настоящее время достаточно полно исследована задача о генерации изгибно-гравитационных волн (ИГВ) при движении локализованной области внешнего давления по ледяному покрову, плавающему на поверхности жидкости. Движущаяся нагрузка может представлять собой обычный автомобиль, самолет на режимах взлета или посадки, а также судно на воздушной подушке. Подробно исследовано прямолинейное движение нагрузки как в стационарном, так и в нестационарном случаях. Богатую библиографию можно найти в работах [1–3]. Ледяной покров обычно моделировался изначально ненапряженной, однородной изотропной тонкой упругой пластиной. Однако ледяной покров может подвергаться сжатию или растяжению под воздействием ветра, течений или температурных деформаций [4, 5]. Кинематические свойства ИГВ, возникающих от периодических и импульсных возмущений в условиях равномерного и неравномерного сжатия, подробно исследованы в [5].

В данной работе представлено решение линейной трехмерной нестационарной задачи гидроупругости о развитии волнового движения, возникающего при мгновенном старте и последующем равномерном прямолинейном движении области внешней нагрузки по ледяному покрову. Предполагается, что нагрузка распределена равномерно в прямоугольной области, что моделирует движение судна на воздушной подушке (СВП). Для ледяного покрова учитываются продольные, поперечные и сдвиговые сжимающие усилия. Определены волновые силы, действующие на судно, и деформации, возникающие в ледяном покрове.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается бесконечно протяженный ледяной покров постоянной толщины и плотности, плавающий на поверхности идеальной несжимаемой жидкости глубины $H$. Ледяной покров моделируется тонкой упругой пластиной. Предполагается, что в упругой пластине существуют сжимающие усилия (продольные, поперечные и сдвиговые) [6]. Жидкость и пластина первоначально являются невозмущенными. Начиная с момента времени t = 0, на пластину действует заданное локализованное внешнее давление, которое затем движется прямолинейно с постоянной скоростью U. Вводится система координат x, $y$, $z$, связанная с движущимся давлением, где x и $y$ – горизонтальные координаты, а $z$ – вертикальная координата, направленная вверх. Ось x совпадает с направлением движения нагрузки. Возникающее течение жидкости полагается потенциальным, а скорость частиц жидкости и прогиб пластины – малыми. Предполагается, что во все моменты времени жидкость находится в контакте с пластиной.

Задача о поведении пластины и жидкости сводится к решению уравнения Лапласа для потенциала скоростей частиц жидкости $\varphi (x,y,z,t)$

(1.1)

$\Delta \varphi + {{\partial }^{2}}\varphi {\text{/}}\partial {{z}^{2}} = 0\left( {\left| x \right|,\left| y \right| < \infty , - H \leqslant z \leqslant 0} \right),\quad \Delta \equiv {{\partial }^{2}}{\text{/}}\partial {{x}^{2}} + {{\partial }^{2}}{\text{/}}\partial {{y}^{2}}$

с граничными условиями

$D{{\Delta }^{2}}w + {{Q}_{1}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + {{Q}_{2}}\frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + 2{{Q}_{3}}\frac{{{{\partial }^{2}}w}}{{\partial x\partial y}} + M{{\left( {\frac{\partial }{{\partial t}} - U\frac{\partial }{{\partial x}}} \right)}^{2}}w + \rho gw + $

(1.2)

$ + \;\rho \left( {\frac{\partial }{{\partial t}} - U\frac{\partial }{{\partial x}}} \right)\varphi = - P(x,y,t)\quad (z = 0)$

(1.3)

$\frac{{\partial w}}{{\partial t}} - U\frac{{\partial w}}{{\partial x}} = \frac{{\partial \varphi }}{{\partial z}}\quad (z = 0),\quad \frac{{\partial \varphi }}{{\partial z}} = 0\quad (z = - H)$

(1.4)

$\mathop {lim}\limits_{r \to \infty } \nabla \varphi = 0\quad (t \geqslant 0)\quad ({{r}^{2}} = {{x}^{2}} + {{y}^{2}})$

и начальными условиями

(1.5)

$\varphi (x,y,z,0) = w(x,y,0) = 0$

Здесь $w(x,y,t)$ – нормальный прогиб упругой пластины, ее цилиндрическая жесткость равна D = ${{Eh_{1}^{3}} \mathord{\left/ {\vphantom {{Eh_{1}^{3}} {[12(1 - {{\nu }^{2}})]}}} \right. \kern-0em} {[12(1 - {{\nu }^{2}})]}}$, $M = {{\rho }_{1}}h$; $E$, ${{\rho }_{1}}$, $h$, $\nu $ – модуль Юнга, плотность, толщина и коэффициент Пуассона пластины; ${{Q}_{1}}$, ${{Q}_{2}}$, ${{Q}_{3}}$ – продольные, поперечные и сдвиговые напряжения (сжатие при положительных значениях и растяжение при отрицательных значениях) по соответствующим направлениям; $\rho $ – плотность жидкости, $P(x,y,t)$ – внешнее давление, g – ускорение свободного падения. Далее будет рассматриваться действие только сжимающих усилий, т.е. ${{Q}_{j}} \geqslant 0$ (j = 1, 2, 3).

Предполагается для простоты, что аналогично [7] функция $P(x,y,t)$ в (1.2) отлична от нуля только при $t \geqslant 0$ в прямоугольнике длиной 2a и шириной 2b. Внутри этого прямоугольника давление постоянно

(1.6)

$P(x,y,t) = {{P}_{0}}\quad \left( {\left| x \right| \leqslant a,\left| y \right| \leqslant b,t \geqslant 0} \right)$

Для решения задачи (1.1)–(1.6) используется двойное преобразование Фурье

(1.7)

$W(\lambda ,\mu ,t) = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty w } (x,y,t)exp[ - i(\lambda x + \mu y)]dxdy$

Функция $W(\lambda ,\mu ,t)$ удовлетворяет обыкновенному дифференциальному уравнению

(1.8)

$\ddot {W} - 2i\lambda U\dot {W} + TW = - kFB$

с нулевыми начальными условиями. Здесь точкой обозначена производная по времени $t$,

$T(k,\theta ) = {{\omega }^{2}}(k,\theta ) - {{(kUcos\theta )}^{2}},\quad k = \sqrt {{{\lambda }^{2}} + {{\mu }^{2}}} ,\quad \theta = {\text{arctg}}(\mu {\text{/}}\lambda )$

(1.9)

$\omega (k,\theta ) = \sqrt {kB(k)[D{{k}^{4}} - Q(\theta ){{k}^{2}} + \rho g]} ,\quad B(k) = {{\left[ {Mk + \rho {\text{cth}}(kH)} \right]}^{{ - 1}}}$

$Q(\theta ) = {{Q}_{1}}co{{s}^{2}}\theta + {{Q}_{2}}si{{n}^{2}}\theta + {{Q}_{3}}sin(2\theta )$

$F(k,\theta ) = {{P}_{0}}\int\limits_{ - a}^a {{{e}^{{ - i\lambda x}}}} dx\int\limits_{ - b}^b {{{e}^{{ - i\mu y}}}} dy = \frac{{4{{P}_{0}}}}{{{{k}^{2}}}}C(k,\theta )$

$C(k,\theta ) = \frac{{sin(akcos\theta )sin(bksin\theta )}}{{sin\theta cos\theta }}$

Решение уравнения (1.8) имеет вид

$W = - \frac{{kFB}}{{2\omega }}\left\{ {\frac{{1 - cos[(\omega + \lambda U)t]}}{{\omega + \lambda U}}} \right. + \frac{{1 - cos[(\omega - \lambda U)t]}}{{\omega - \lambda U}} - $

$ - \;i\left. {\left[ {\frac{{sin[(\omega + \lambda U)t]}}{{\omega + \lambda U}} - \frac{{sin[(\omega - \lambda U)t]}}{{\omega - \lambda U}}} \right]} \right\}$

После выполнения обратных преобразований Фурье получим

(1.10)

$w(x,y,t) = - \frac{{{{P}_{0}}}}{{{{\pi }^{2}}}}\int\limits_0^\infty B (k)\int\limits_0^{\pi /2} C (k,\theta )[{{G}_{ + }}(k,\theta ,t) + {{G}_{ - }}(k,\theta ,t)]d\theta dk$

где

${{G}_{ \pm }} = \frac{1}{{{{\omega }_{ \pm }}}}\left\{ {\Lambda _{1}^{ \pm }cos[k(xcos\theta \pm ysin\theta )] + \Lambda _{2}^{ \pm }sin\left[ {k(xcos\theta \pm ysin\theta )} \right]} \right\}$

$\Lambda _{1}^{ \pm } = \frac{{1 - cos[({{\omega }_{ \pm }} + kUcos\theta )t]}}{{{{\omega }_{ \pm }} + kUcos\theta }} + \frac{{1 - cos[({{\omega }_{ \pm }} - kUcos\theta )t]}}{{{{\omega }_{ \pm }} - kUcos\theta }}$

(1.11)

$\Lambda _{2}^{ \pm } = \frac{{sin\left[ {({{\omega }_{ \pm }} + kUcos\theta )t} \right]}}{{{{\omega }_{ \pm }} + kUcos\theta }} - \frac{{sin\left[ {({{\omega }_{ \pm }} - kUcos\theta )t} \right]}}{{{{\omega }_{ \pm }} - kUcos\theta }},\quad {{\omega }_{ \pm }} = \omega (k, \pm \theta )$

Функция $\omega (k,\theta )$ в (1.9) представляет собой дисперсионное соотношение для ИГВ, возникающих в системе жидкость–упругая пластина [5, 8]. Для существования вещественного значения частоты $\omega $ необходимо, чтобы при всех возможных значениях $\theta $ подкоренное выражение в (1.9) было неотрицательным. Это условие гарантирует устойчивость плавающей упругой пластины и выполняется при условии, что $Q(\theta ) \leqslant 2\sqrt {g\rho D} $ для $0 \leqslant \theta \leqslant \pi $ [4].

При движении СВП по ледяному покрову на него действуют волновые силы в направлении горизонтальных осей x и y: волновое сопротивление ${{R}_{x}}$ и боковая сила ${{R}_{y}}$. Аналогично движению судна по свободной поверхности жидкости эти силы для нагрузки (1.6) вычисляются по формулам [9]

(1.12)

${{R}_{{x,y}}}(t) = - {{P}_{0}}\int\limits_{ - a}^a {\int\limits_{ - b}^b {\left( {\frac{{\partial w}}{{\partial x}},\frac{{\partial w}}{{\partial y}}} \right)} } dydx$

Используя решение (1.10), получим

${{R}_{x}} = - \frac{{4P_{0}^{2}}}{{{{\pi }^{2}}}}\int\limits_0^\infty B (k)\int\limits_0^{\pi /2} {{{C}_{x}}} (k,\theta )\left[ {\frac{{\Lambda _{2}^{ + }}}{{{{\omega }_{ + }}}} + \frac{{\Lambda _{2}^{ - }}}{{{{\omega }_{ - }}}}} \right]d\theta dk$

${{R}_{y}} = - \frac{{4P_{0}^{2}}}{{{{\pi }^{2}}}}\int\limits_0^\infty B (k)\int\limits_0^{\pi /2} {{{C}_{y}}} (k,\theta )\left[ {\frac{{\Lambda _{2}^{ + }}}{{{{\omega }_{ + }}}} - \frac{{\Lambda _{2}^{ - }}}{{{{\omega }_{ - }}}}} \right]d\theta dk$

где

(1.13)

${{C}_{x}}(k,\theta ) = \frac{{si{{n}^{2}}(akcos\theta )si{{n}^{2}}(bksin\theta )}}{{ksi{{n}^{2}}\theta cos\theta }}$

(1.14)

${{C}_{y}}(k,\theta ) = \frac{{si{{n}^{2}}(akcos\theta )si{{n}^{2}}(bksin\theta )}}{{ksin\theta co{{s}^{2}}\theta }}$

Согласно (1.11) боковая сила равна нулю при отсутствии сдвиговых напряжений в упругой пластине, т.к. в этом случае ${{\omega }_{ + }} = {{\omega }_{ - }}$.

2. УСТАНОВИВШЕЕСЯ ВОЛНОВОЕ ДВИЖЕНИЕ

Рассмотрим поведение волнового движения в установившемся режиме, т.е. при $t \to \infty $. В этом случае в подвижной системе координат задача становится стационарной за исключением некоторых значений скоростей, называемых критическими, о которых будет сказано ниже. Для простоты ограничимся рассмотрением случая бесконечно глубокой жидкости ($H \to \infty $). Потенциал скоростей движения жидкости $\varphi (x,y,z)$ удовлетворяет уравнению Лапласа (1.1) с граничными условиями

(2.1)

$D{{\Delta }^{2}}w + {{Q}_{1}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + {{Q}_{2}}\frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + 2{{Q}_{3}}\frac{{{{\partial }^{2}}w}}{{\partial x\partial y}} + M{{U}^{2}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \rho gw - \rho U\frac{{\partial \varphi }}{{\partial x}} = - P(x,y)\quad (z = 0)$

(2.2)

$\frac{{\partial \varphi }}{{\partial z}} + U\frac{{\partial w}}{{\partial x}} = 0\quad (z = 0),\quad \frac{{\partial \varphi }}{{\partial z}} \to 0\quad (z \to - \infty )$

В дальнем поле требуется выполнение условия излучения, которое означает, что распространяющиеся вверх по потоку волны могут быть только в том случае, когда их групповая скорость больше скорости движения нагрузки, в противном случае волновые движения существуют только вниз по потоку.

Для решения задачи (1.1), (2.1), (2.2) также используется двойное преобразование Фурье (1.7). Образ Фурье функции $w(x,y)$, описывающей вертикальные прогибы упругой пластины в стационарном случае, имеет вид

$W(k,\theta ) = - \frac{{kF(k,\theta )B(k)}}{{{{\omega }^{2}}(k,\theta ) - {{{(kUcos\theta )}}^{2}}}}$

После выполнения обратных преобразований Фурье решение для функции $w(x,y)$ можно представить в виде

(2.3)

$w(x,y) = - \frac{{2{{P}_{0}}}}{{{{\pi }^{2}}}}\int\limits_0^{\pi /2} {\int\limits_0^\infty {\frac{{C(k,\theta )}}{k}\left\{ {\frac{{cos\left[ {k(xcos\theta + ysin\theta )} \right]}}{{{{Z}_{ + }}(k,\theta )}} + \frac{{cos\left[ {k(xcos\theta - ysin\theta )} \right]}}{{{{Z}_{ - }}(k,\theta )}}} \right\}} } dkd\theta $

где

${{Z}_{ \pm }}(k,\theta ) = D{{k}^{4}} - {{Q}_{ \pm }}{{k}^{2}} + g\rho - k{{U}^{2}}co{{s}^{2}}\theta (\rho + kM),\quad {{Q}_{ \pm }} = Q( \pm \theta )$

Функции ${{Z}_{ \pm }}(k,\theta )$ являются полиномами 4-й степени по k и для некоторых значений $\theta $ могут обращаться в нуль при $k_{1}^{ \pm }(\theta )$ и $k_{2}^{ \pm }(\theta )$ $(k_{1}^{ \pm } < k_{2}^{ \pm })$. В этих случаях внутренний интеграл в (2.3) вычисляется в смысле главного значения и для учета условия излучения в дальнем поле следует добавить вычеты в особых точках. Известно [1, 4], что групповая скорость ИГВ больше их фазовой скорости для коротких волн и меньше для длинных волн. Короткие волны соответствуют упругой ветви дисперсионной кривой, а длинные волны – гравитационной ветви. Поэтому для первого слагаемого во внутреннем интеграле (2.3), например, следует вычислять

$\begin{gathered} p{v}\int\limits_0^\infty {\frac{{C(k,\theta )cos\left[ {k(xcos\theta + ysin\theta )} \right]}}{{k{{Z}_{ + }}(k,\theta )}}} dk + \\ + \;\pi \left\{ {\frac{{C(k_{1}^{ + },\theta )sin[k_{1}^{ + }(xcos\theta + ysin\theta )]}}{{k_{1}^{ + }\partial {{Z}_{ + }}{\text{/}}{{{\left. {\partial k} \right|}}_{{k = k_{1}^{ + }}}}}} - \frac{{C(k_{2}^{ + },\theta )sin[k_{2}^{ + }(xcos\theta + ysin\theta )]}}{{k_{2}^{ + }\partial {{Z}_{ + }}{\text{/}}{{{\left. {\partial k} \right|}}_{{k = k_{2}^{ + }}}}}}} \right\} \\ \end{gathered} $

где символы $p{v}$ обозначают интеграл в смысле главного значения. Аналогичные выражения имеют место и для второго слагаемого в (2.3) для тех значений θ, при которых полином ${{Z}_{ - }}(k,\theta )$ имеет два положительных корня.

Максимальная скорость движения нагрузки U, при которой обе функции ${{Z}_{ \pm }}(k,\theta )$ не имеют положительных корней при всех значениях $0 \leqslant \theta \leqslant \pi {\text{/}}2$, называется критической скоростью U_c. При движении нагрузки со скоростью $U < {{U}_{c}}$ в дальнем поле не возникает волновых движений. Стационарного решения линейной задачи о равномерном движении нагрузки с критической скоростью по поверхности упругой пластины не существует [2, 10]. Для нахождения ограниченного решения при критической скорости необходимо применять нелинейные модели или учитывать структурное демпфирование пластины [11–13].

Формула для определения критической скорости U_c в жидкости конечной глубины дана в [5, 8]. Для бесконечно глубокой жидкости эта формула имеет вид

(2.4)

${{U}_{c}} = \Psi ({{k}_{c}}),\quad {{\left. {d\Psi (k){\text{/}}dk} \right|}_{{k = {{k}_{c}}}}} = 0$

где

(2.5)

$\Psi (k) = \sqrt {\frac{1}{{k(\rho + kM)}}\left[ {D{{k}^{4}} - {{Q}_{1}}{{k}^{2}} + \rho g - \frac{{Q_{3}^{2}{{k}^{4}}}}{{D{{k}^{4}} - {{Q}_{2}}{{k}^{2}} + \rho g}}} \right]} $

Определение ${{k}_{c}}$ сводится к вычислению положительного корня полинома 13-й степени

(2.6)

$\begin{gathered} \text{[}2\bar {M}\bar {k}(\bar {D}{{{\bar {k}}}^{4}} - 1) + {{{\bar {k}}}^{2}}(3\bar {D}{{{\bar {k}}}^{2}} - \mathop {\bar {Q}}\nolimits_1 ) - 1]{{[1 + {{{\bar {k}}}^{2}}(\bar {D}{{{\bar {k}}}^{2}} - \mathop {\bar {Q}}\nolimits_2 )]}^{2}} + \\ + \;\mathop {\bar {Q}}\nolimits_3^2 {{{\bar {k}}}^{4}}[2\bar {M}\bar {k}(\bar {D}{{{\bar {k}}}^{4}} - 1) + {{{\bar {k}}}^{2}}(\bar {D}{{{\bar {k}}}^{2}} + \mathop {\bar {Q}}\nolimits_2 ) - 3] = 0 \\ \end{gathered} $

где введены безразмерные переменные

(2.7)

$\bar {D} = \frac{D}{{g\rho {{a}^{4}}}},\quad \bar {M} = \frac{M}{{\rho a}},\quad \mathop {\bar {Q}}\nolimits_j = \frac{{{{Q}_{j}}}}{{g\rho {{a}^{2}}}}\quad (j = 1,\;2,\;3),\quad \bar {k} = ka$

Волновые силы, действующие в стационарной задаче на нагрузку, вычисляются по формулам, аналогичным (1.12). Эти силы отличны от нуля только при движении нагрузки со скоростью $U > {{U}_{c}}$, так как определяются вкладами от вычетов в особых точках внутреннего интеграла в (2.3). Обозначим интервал значений угловой координаты θ для особых точек функции ${{Z}_{ + }}(k,\theta )$ как $\gamma _{1}^{ + } < \theta < \gamma _{2}^{ + }$, а для функции ${{Z}_{ - }}(k,\theta )$ как $\gamma _{1}^{ - } < \theta < \gamma _{2}^{ - }$. Тогда

${{R}_{x}} = \frac{{8P_{0}^{2}}}{\pi }\left\{ {\int\limits_{\gamma _{1}^{ + }}^{\gamma _{2}^{ + }} {\left[ {\frac{{{{C}_{x}}(k_{1}^{ + },\theta )}}{{{{{\left. {k_{1}^{ + }\partial {{Z}_{ + }}{\text{/}}\partial k} \right|}}_{{k = k_{1}^{ + }}}}}} - \frac{{{{C}_{x}}(k_{2}^{ + },\theta )}}{{{{{\left. {k_{2}^{ + }\partial {{Z}_{ + }}{\text{/}}\partial k} \right|}}_{{k = k_{2}^{ + }}}}}}} \right]} } \right.d\theta + \left. {\int\limits_{\gamma _{1}^{ - }}^{\gamma _{2}^{ - }} {\left[ {\frac{{{{C}_{x}}(k_{1}^{ - },\theta )}}{{{{{\left. {k_{1}^{ - }\partial {{Z}_{ - }}{\text{/}}\partial k} \right|}}_{{k = k_{1}^{ - }}}}}} - \frac{{{{C}_{x}}(k_{2}^{ - },\theta )}}{{{{{\left. {k_{2}^{ - }\partial {{Z}_{ - }}{\text{/}}\partial k} \right|}}_{{k = k_{2}^{ - }}}}}}} \right]} d\theta } \right\}$

${{R}_{y}} = \frac{{8P_{0}^{2}}}{\pi }\left\{ {\int\limits_{\gamma _{1}^{ + }}^{\gamma _{2}^{ + }} {\left[ {\frac{{{{C}_{y}}(k_{1}^{ + },\theta )}}{{{{{\left. {k_{1}^{ + }\partial {{Z}_{ + }}{\text{/}}\partial k} \right|}}_{{k = k_{1}^{ + }}}}}} - \frac{{{{C}_{y}}(k_{2}^{ + },\theta )}}{{{{{\left. {k_{2}^{ + }\partial {{Z}_{ + }}{\text{/}}\partial k} \right|}}_{{k = k_{2}^{ + }}}}}}} \right]} } \right.d\theta - $

$ - \;\left. {\int\limits_{\gamma _{1}^{ - }}^{\gamma _{2}^{ - }} {\left[ {\frac{{{{C}_{y}}(k_{1}^{ - },\theta )}}{{k_{1}^{ - }\partial {{Z}_{ - }}{\text{/}}\partial k{{{\text{|}}}_{{k = k_{1}^{ - }}}}}} - \frac{{{{C}_{y}}(k_{2}^{ - },\theta )}}{{k_{2}^{ - }\partial {{Z}_{ - }}{\text{/}}\partial k{{{\text{|}}}_{{k = k_{2}^{ - }}}}}}} \right]} d\theta } \right\}$

где использованы значения ${{C}_{x}}(k,\theta )$, ${{C}_{y}}(k,\theta )$, приведенные в (1.13), (1.14).

Аналогично нестационарной задаче, изложенной в п. 1, боковая сила R_y тождественно равна нулю при отсутствии сдвиговых напряжений в упругой пластине.

Согласно линейной теории упругости деформации пластины изменяются по толщине по линейному закону. Тензор максимальных деформаций имеет вид

$\varepsilon (x,y) = - \frac{h}{2}\left( {\begin{array}{*{20}{c}} {{{\partial }^{2}}w{\text{/}}\partial {{x}^{2}}}&{{{\partial }^{2}}w/\partial x\partial y} \\ {{{\partial }^{2}}w{\text{/}}\partial x\partial y}&{{{\partial }^{2}}w{\text{/}}\partial {{y}^{2}}} \end{array}} \right)$

Главные значения деформаций определяются как собственные числа этой матрицы для каждой точки на упругой пластине. Необходимо, чтобы деформации не превышали предельных значений, при которых начинаются пластические деформации и разрушение. Экспериментально полученные в [14] критические значения максимальных деформаций для морского льда составляют $4.4 \times {{10}^{{ - 5}}}{\kern 1pt} - {\kern 1pt} 8.5 \times {{10}^{{ - 5}}}$. В [15] использовано критическое значение максимальных деформаций ${{\varepsilon }_{ * }} = 8 \times {{10}^{{ - 5}}}$. В данной работе также используется это значение.

При движении нагрузки по упругой пластине под углом β к оси x задачу следует рассматривать в новой системе координат $x{\text{'}}$, $y{\text{'}}$, $z$, где

(2.8)

$x{\text{'}} = xcos\beta + ysin\beta ,\quad y{\text{'}} = ycos\beta - xsin\beta $

В новой системе координат величины продольного, поперечного и сдвигового усилий примут значения [5, 8]

(2.9)

$Q_{1}^{'} = {{Q}_{1}}co{{s}^{2}}\beta + {{Q}_{2}}si{{n}^{2}}\beta + {{Q}_{3}}sin(2\beta )$

(2.10)

$Q_{2}^{'} = {{Q}_{1}}si{{n}^{2}}\beta + {{Q}_{2}}co{{s}^{2}}\beta - {{Q}_{3}}sin(2\beta )$

(2.11)

$Q_{3}^{'} = ({{Q}_{2}} - {{Q}_{1}})sin(2\beta ){\text{/}}2 + {{Q}_{3}}cos(2\beta )$

Анализ волнового движения в новой системе координат проводится также, как и в исходной задаче.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Для численных расчетов использованы следующие параметры ледяного покрова и внешней нагрузки:

$E = 5 \times {{10}^{9}}\;{\text{Па}},\quad \rho = 1025\;{\text{кг/}}{{{\text{м}}}^{3}},\quad {{\rho }_{1}} = 922.5\;{\text{кг/}}{{{\text{м}}}^{3}},\quad \nu = 0.3$

${{P}_{0}} = {{10}^{3}}\;{\text{Па}},\quad a = 20\;{\text{м}},\quad b = 10\;{\text{м}}$

Для данных параметров и глубины жидкости $H = 350$ м значения критической скорости ИГВ для ледяного покрова без сжатия равны ${{U}_{c}} = 15.496,\;20.011$ м/с для h = 1 м и h = 2 м соответственно. Дальнейшее увеличение глубины жидкости практически не меняет эти значения. Критическая скорость U_c и соответствующее ей волновое число k_c определяются в этом случае из решения системы уравнений

(3.1)

$\bar {U}_{с}^{2} = \frac{{1 + \bar {D}\bar {k}_{c}^{4}}}{{{{{\bar {k}}}_{c}}[{\text{cth}}({{{\bar {k}}}_{c}}\bar {H}) + \bar {M}{{{\bar {k}}}_{c}}]}}$

(3.2)

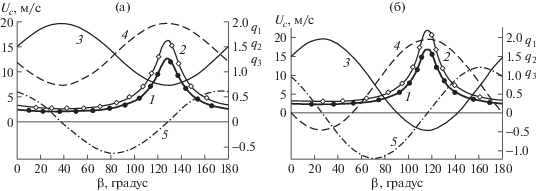
$\bar {U}_{c}^{4}\bar {k}_{c}^{2}({{\bar {M}}^{2}}\bar {k}_{c}^{2} - \bar {M} - 1) + \bar {U}_{c}^{2}\{ \bar {k}_{c}^{2}[\bar {D}\bar {k}_{c}^{2}(3 - 2\bar {M}\bar {k}_{c}^{2}) - 2\bar {M}] - 1\} + \bar {D}\bar {k}_{c}^{4}(\bar {D}\bar {k}_{c}^{4} + 2) + 1 = 0$

где в дополнение к безразмерным переменным (2.7) добавлены значения ${{\bar {U}}_{c}} = {{U}_{c}}{\text{/}}\sqrt {ga} $, $\bar {H} = H{\text{/}}a$. Система трансцендентных уравнений (3.1), (3.2) несколько упрощается в случае M = 0 и приведена в [16]. Для бесконечно глубокой жидкости значение k_c определяется как положительный корень полинома 5-го порядка [17].

Влияние сжимающих усилий и угловой координаты $\beta $ движения внешней нагрузки показано на рис. 1 для двух наборов значений параметров сжатия: ${{q}_{1}} = 1.5$, ${{q}_{2}} = 1.2$, ${{q}_{3}} = 0.6$ (рис. 1а) и ${{q}_{1}} = 1.5$, ${{q}_{2}} = 0$, ${{q}_{3}} = 0.95$ (рис. 1б), где безразмерные значения ${{q}_{j}} \equiv {{Q}_{j}}{\text{/}}\sqrt {g\rho D} $ (j = 1, 2, 3). Представлены значения ${{q}_{j}}(\beta )$, вычисленные согласно (2.9)–(2.11), и величины критической скорости ${{U}_{c}}(\beta )$, определенные из соотношений (2.4)–(2.6), для двух толщин ледяного покрова: $h = 1$ м и $h = 2$ м. На рис. 1 кривые 1, 2 показывают значения критической скорости при $h = 1$ м и $h = 2$ м, соответственно, а кривые 3, 4, 5 – значения ${{q}_{j}}(\beta )$ ($j = 1,\;2,\;3$). В диапазоне $0 \leqslant \beta \leqslant 180^\circ $ значения критической скорости имеют локальный минимум и максимум при значениях β, которые соответствуют нулевому сдвиговому напряжению $({{q}_{3}} = 0)$. Минимальное значение ${{U}_{c}}(\beta )$ имеет место при том значении $\beta $, при котором значение ${{q}_{1}}(\beta )$ максимально, а ${{q}_{2}}(\beta )$ – минимально. Противоположная картина имеет место для максимального значения ${{U}_{c}}(\beta )$. Экстремальные значения критической скорости отличаются более, чем в 6 раз для параметров рис. 1а и более, чем в 7 раз – для рис. 1б.

Рис. 1.

Зависимости критической скорости ${{U}_{c}}$ и безразмерных параметров сжатия ${{q}_{j}}$ ($j = 1,\;2,\;3$) от угла поворота $\beta $ при начальных значениях (${{q}_{1}}$, ${{q}_{2}}$, ${{q}_{3}}$): а, б – ($1.5,\;1.2,\;0.6$), ($1.5,\;0,\;0.95$). Кривые 1 и 2 соответствуют значениям ${{U}_{c}}(\beta )$ при h = 1 м и 2 м, а кривые 3, 4, 5 – значениям ${{q}_{j}}(\beta )$ ($j = 1,\;2,\;3$).

На рис. 2а–г показаны изолинии вертикальных прогибов в ледяном покрове в различные моменты времени $\bar {t} \equiv t\sqrt {g{\text{/}}a} = 2,\;5,\;10,\;20$ для h = 1 м, $H = 350$ м, $U = 10$ м/с, ${{q}_{1}} = 1.5$, ${{q}_{2}} = 1.2$, ${{q}_{3}} = 0.6$. Изолинии функции $w(x,y,t)$ представлены на рис. 2, 3 с шагом 1 см. Нулевые изолинии на этих рисунках показаны более жирными линиями, а области положительных и отрицательных значений функции $w(x,y,t)$ знаками “+” и “–” соответственно. Максимальные прогибы возникают под нагрузкой и составляют примерно 7, 11, 10, 9 см при $\bar {t}$ = 2, 5, 10, 20 соответственно.

Рис. 2.

Изолинии вертикальных прогибов $w(x,y,t)$ в зависимости от времени для нестационарной задачи при $h = 1$ м, $H = 350$ м, $U = 10$ м/с, $({{q}_{1}},{{q}_{2}},{{q}_{3}})$ = $(1.5,\;1.2,\;0.6)$: а–г – $\bar {t} = 2,\;5,\;10,\;20$.

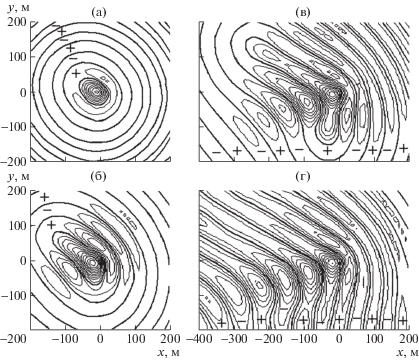
Рис. 3.

Изолинии вертикальных прогибов $w(x,y)$ в стационарной задаче для параметров рис. 2: а,б – $\beta = 0,\;{{130}^{ \circ }}$.

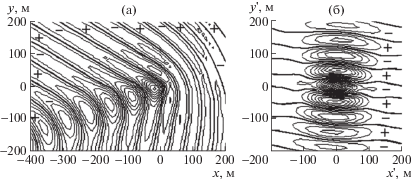
Решение стационарной задачи при тех же параметрах, но для бесконечно глубокой жидкости, представлено на рис. 3а. Максимальный прогиб составил 9 см. Из сравнения рис. 2г и рис. 3а видно, что решение нестационарной задачи при $\bar {t}$ = 20 довольно близко к установившемуся движению. Скорость движения нагрузки $U = 10$ м/с при используемых параметрах сжатия является сверхкритической и возникающие ИГВ распространяются как вниз, так и вверх по потоку. На рис. 3б показаны результаты решения стационарной задачи при движении нагрузки со скоростью $U = 10$ м/с под углом $\beta = 130^\circ $ к исходной системе координат. Картина волнового поля показана в системе координат (2.8). Значения параметров сжатия в этих координатах согласно (2.9)–(2.11) равны $q_{1}^{'} = 0.733$, $q_{2}^{'} = 1.97$, $q_{3}^{'} = 0.044$. Максимальный прогиб упругой пластины составил 18 см. Скорость движения нагрузки $U = 10$ м/с является в этом случае докритической (см. рис. 1а) и волновые движения в дальнем поле не возникают. Однако в силу достаточно большого поперечного сжатия заметные прогибы возникают не только вблизи действия нагрузки, но и в окрестности линии $x{\text{'}} = 0$ вдали от нагрузки.

Безразмерные значения волнового сопротивления и боковой силы, действующие на подвижную нагрузку в стационарной задаче, показаны соответственно на рис. 4а,б для h = 1 м, ${{q}_{1}} = 1.5$, ${{q}_{2}} = 1.2$, ${{q}_{3}} = 0.6$ и различных углов $\beta = 0,\;45^\circ $ ($1.95,\;0.75$), –0.15), 90° ($1.2,\;1.5,\; - {\kern 1pt} 0.6$), 135° ($0.75,\;1.95,\;0.15$) (кривые 1–4). В скобках указаны значения ${{q}_{j}}(\beta )$ (j = 1, 2, 3) для конкретных значений угла β. Использованы безразмерные значения

$(\mathop {\bar {R}}\nolimits_x ,\mathop {\bar {R}}\nolimits_y ) = - \frac{{g\rho }}{{2bP_{0}^{2}}}({{R}_{x}},{{R}_{y}})$

Рис. 4.

Зависимость волнового сопротивления (а) и боковой силы (б) от скорости движения нагрузки для стационарной задачи при h = 1 м, $({{q}_{1}},{{q}_{2}},{{q}_{3}})$ = $(1.5,\;1.2,\;0.6)$. Кривые 1–4 соответствуют значениям угла $\beta = 0,\;45,\;90$, 135°. Кривая 5 – волновое сопротивление при нулевых значениях параметров сжатия.

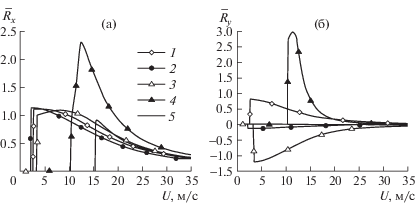
Максимальные значения волновых сил в рассмотренных случаях имеют место при движении внешней нагрузки под углом β = 135° к исходной системе координат. Значение знака боковой силы совпадает со знаком сдвигового сжатия. Кривая 5 на рис. 4а показывает волновое сопротивление при движении нагрузки по ледяному покрову без сжатия ${{q}_{j}} = 0$ (j = 1, 2, 3). В этом случае критическая скорость ИГВ больше, а максимальное значение волнового сопротивления меньше, чем при наличии сжатия. Однако с ростом скорости движения нагрузки влияние сжатия уменьшается.

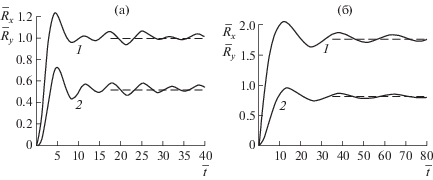
Зависимость волновых сил от времени в нестационарной задаче представлена на рис. 5а,б для h = 1 м, $H = 350$ м. Для рис. 5а использованы значения $U = 10$ м/с, ${{q}_{1}} = 1.5$, ${{q}_{2}} = 1.2$, ${{q}_{3}} = 0.6$, а для рис. 5б – $U = 15$ м/с, ${{q}_{1}} = 0.75$, ${{q}_{2}} = 1.95$, ${{q}_{3}} = 0.15$. Кривые 1 соответствуют ${{\bar {R}}_{x}}$, а кривые 2 – ${{\bar {R}}_{y}}$. Штриховыми прямыми показаны значения волновых сил для соответствующей стационарной задачи. Видно, что с ростом времени значения волновых сил выходят на установившейся режим.

Рис. 5.

Зависимость волнового сопротивления (1) и боковой силы (2) от времени в нестационарной задаче при h = 1 м, $H = 350$ м: (а) – $U = 10$ м/с, $({{q}_{1}},{{q}_{2}},{{q}_{3}})$ = $(1.5,\;1.2,\;0.6)$, (б) – $U = 15$ м/с, $({{q}_{1}},{{q}_{2}},{{q}_{3}})$ = $(0.75,\;1.95,\;0.15)$. Штриховыми прямыми показаны значения волновых сил для соответствующей стационарной задачи.

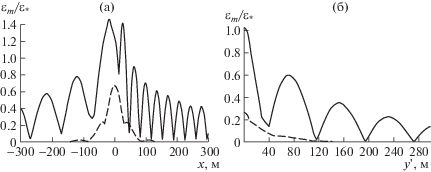
Деформации упругой пластины максимальны в области действия нагрузки. На рис. 6 показано отношение максимальных деформаций ε_m к критическому значению ${{\varepsilon }_{ * }}$. Сплошными кривыми представлены значения ${{\varepsilon }_{m}}{\text{/}}{{\varepsilon }_{ * }}$ для пластины толщиной h = 1 м (рис. 6а) и h = 2 м (рис. 6б) при параметрах сжатия ${{q}_{1}} = 1.5$, ${{q}_{2}} = 1.2$, ${{q}_{3}} = 0.6$. Нагрузка движется со скоростью $U = 10$ м/с. Для рис. 6а движение происходит в направлении оси $x\;(\beta = 0)$ и показана зависимость деформаций от $x$ при $y = 0$. Для рис. 6б нагрузка движется в направлении оси $x{\text{'}}$ в системе координат, повернутой на угол β = 128°, и показано распределение деформаций вдоль оси $y{\text{'}}$ при $x{\text{'}} = 0$. В этом случае волновое движение является докритическим и практически симметрично относительно оси $x{\kern 1pt} '$. Штриховыми линиями на рис. 6 представлены деформации при нулевых сжимающих усилиях ${{q}_{j}} = 0$ (j = 1, 2, 3). Видно, что сжимающие усилия существенно увеличивают деформации ледяного покрова и приводят к значениям максимальных деформаций ${{\varepsilon }_{m}} > {{\varepsilon }_{ * }}$, как при сверхкритическом, так и при докритическом движении нагрузки. Это свидетельствует о более вероятном разрушении ледяного покрова при наличии сжимающих усилий.

Рис. 6.

Значения ${{\varepsilon }_{m}}{\text{/}}{{\varepsilon }_{ * }}$ при $U = 10$ м/с, $({{q}_{1}},{{q}_{2}},{{q}_{3}})$ = $(1.5,\;1.2,\;0.6)$: а – h = 1 м, $\beta = 0$, $y = 0$, б – h = 2 м, β = 128°, $x{\text{'}} = 0$ (сплошные кривые). Штриховые кривые – соответствующие деформации при нулевых сжимающих усилиях.

ЗАКЛЮЧЕНИЕ

Выполненные исследования показали, что наличие неравномерного сжатия в ледяном покрове оказывает существенное влияние на волновые возмущения, возникающие при движении внешней нагрузки. Волновой след может быть несимметричным относительно курса движения нагрузки.

Волновые силы, действующие на судно на воздушной подушке, при наличии сжимающих усилий в ледяном покрове зависят от направления его движения относительно исходной системы координат. Максимальные деформации ледяного покрова появляются в области действия нагрузки и при наличии сжатия могут существенно превышать соответствующие значения, возникающие в его ненапряженном состоянии. Волновое движение в нестационарной задаче достаточно быстро выходит на установившийся режим, как это было ранее отмечено в [2].

Список литературы

Squire V.A., Hosking R.J., Kerr A.D., Langhorne P.J. Moving loads on ice plates. Dordrecht: Kluwer, 1996. 230 p.
Nugroho W.S., Wang K., Hosking R.J., Milinazzo F. Time-dependent response of a floating flexible plate to an impulsively started steadily moving load // J. Fluid Mech. 1999. V. 381. P. 337–355.
Погорелова А.В., Козин В.М., Матюшина А.А. Исследование напряженно-деформированного состояния ледяного покрова при взлете и посадке на него самолета // ПМТФ. 2015. Т. 56. № 5. С. 214–221. https://doi.org/10.15372/PMTF20150520
Хейсин Д.Е. Динамика ледяного покрова. Л.: Гидрометеоиздат. 1967. 215 с.
Букатов А.Е. Волны в море с плавающим ледяным покровом. Севастополь: ФГБУН МГИ, 2017. 360 с.
Timoshenko S., Woinowsky-Krieger S. Theory of plates and shells. 2nd ed., New York a.o., Mc Graw-Hill, 1959. 580 p. = Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки. М.: Книжный дом “ЛИБРОКОМ”, 2009. 640 с.
Milinazzo F., Shinbrot M., Evans N.W. A mathematical analysis of the steady response of floating ice to the uniform motion of a rectangular load // J. Fluid Mech. 1995. V. 287. P. 173–197.
Букатов А.Е., Жарков В.В., Завьялов Д.Д. Трехмерные изгибно-гравитационные волны при неравномерном сжатии // ПМТФ. 1991. № 6. С. 51–57.
Haussling H.J., VanEseltine R.T. Unsteady air-cushion vehicle hydrodynamics using Fourier series // J. Ship Research. 1976. V. 20. № 2. P. 79–84.
Yeung R.W., Kim J.W. Effects of a translating load on a floating plate – structural drag and plate deformation // J. Fluids and Structures. 2000. V. 14. P. 993–1011. https://doi.org/10.1006/jfls.2000.0307
Wang K., Hosking R.J., Milinazzo F. Time-dependent response of a floating viscoelastic plate to an impulsively started moving load // J. Fluid Mech. 2004. V. 521. P. 295–317. https://doi.org/10.1017/S002211200400179X
Погорелова А.В. Особенности волнового сопротивления СВПА при нестационарном движении по ледяному покрову // ПМТФ. 2008. Т. 49. № 1. С. 89–99.
Dinvay E., Kalisch H., Părău E.I. Fully dispersive models for moving loads on ice sheets // J. Fluid Mech. 2019. V. 876. P. 122–149. https://doi.org/10.1017/jfm.2019.530
Squire V., Martin A. A field study of the physical properties, response to swell, and subsequent fracture of a single ice floe in the winter Bering sea. Technical report 18, Univ Washington, 1980.
Brocklehurst P., Korobkin A.A., Pru E.I. Interaction of hydro-elastic waves with a vertical wall // J. Eng. Math. 2010. V. 68. P. 215–231. https://doi.org/10.1007/s10665-010-9386-8
Li Z.F., Wu G.X., Shi Y.Y. Interaction of uniform current with a circular cylinder submerged below an ice sheet // Appl. Ocean Research. 2019. V. 86. P. 310–319. https://doi.org/10.1016/j.apor.2018.12.007
Sturova I.V. Unsteady three-dimensional sources in deep water with an elastic cover and their applications // J. Fluid Mech. 2013. V. 730. P. 392–418. https://doi.org/10.1017/jfm.2013.303

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал