Известия РАН. Механика жидкости и газа, 2021, № 4, стр. 52-62

1. ПОСТАНОВКА ЗАДАЧИ

В общем случае система уравнений динамики несжимаемой степенной неньютоновской жидкости может быть записана в виде [1, 6]

Здесь ${{{v}}^{i}}$ – компоненты вектора скорости, p – давление, ρ – плотность, ${{\tau }^{{ij}}}$ – компоненты тензора вязких напряжений, e_ij – компоненты тензора скоростей деформаций, $\mu $ – коэффициент консистенции, $\beta $ – показатель степени неньютоновской модели.

Если перейти к уравнению живых сил, то получается

Рассматривается сферически-симметричная задача о динамике газовой полости внутри неограниченного объема жидкости. Пусть радиус полости обозначен через $R(t)$, в начальный момент времени $t = 0$ он равен ${{R}_{0}}$. Давление внутри полости принимается однородным p_cav(R) = = ${{p}_{0}}{{({{R}_{0}}{\text{/}}R(t))}^{{3\gamma }}}$, где $\gamma $ – показатель адиабаты, ${{p}_{0}}$ – начальное давление [2]. Давление в жидкости на бесконечности, вообще говоря, зависит от времени, ${{p}_{\infty }}(t)$.

В этом случае уравнение неразрывности в (1.1) c использованием кинематического условия на границе приводит к выражению скорости через радиус полости

Кинетическая энергия жидкости, в свою очередь, принимает вид

Свертка тензора скоростей деформаций также вычисляется через $R(t)$

Уравнение (1.2) интегрируется по всему объему жидкости. С использованием динамических граничных условий получается

Уравнение (1.4) является основным в рамках исследований, приведенных в настоящей работе. Важно заметить, что при сжатии $dR(t){\text{/}}dt < 0$.

С помощью задания функции $R(t)$ в уравнении (1.4) можно определить необходимый вид ${{p}_{\infty }}(t)$, обеспечивающий реализацию заданной динамики границы полости.

При выборе конкретных физических величин в данной работе используется система единиц измерения СГС.

2. ЗАДАЧА О СОХРАНЕНИИ ЭНЕРГИИ

Рассматривается задача о сохранении кинетической энергии $E(t) \equiv {{E}_{0}}$ в процессе сжатия. На основе соотношения (1.3) получается, что

при этом процесс схлопывания длится конечный промежуток времени $t \in [0,T]$, где

Необходимая для реализации соответствующего процесса зависимость давления на бесконечности от времени имеет вид

Видно, что для осуществления данного схлопывания необходимо преодолевать не только растущее давление внутри газовой полости за счет ее сжатия (первое слагаемое), но и растущую величину, связанную с диссипацией (второе слагаемое, обозначается через ${{p}_{{dis}}}$ ниже). Стоит отметить, что оба члена справа в формуле (2.2) не ограничены при $t \to T$. В случае если $\gamma < (5{\text{/}}3)\beta $, второе слагаемое растет асимптотически быстрее.

Однако рассматриваемое сжатие имеет смысл осуществлять до значений плотности внутри газовой полости равных по величине плотности жидкости, т.е. во многих случаях до одного порядка по радиусу, так как далее необходимо учитывать явление сжимаемости жидкости [4]. Схлопывание полости до радиуса $R = {{R}_{ * }}$ происходит за время

при этом давление ${{p}_{\infty }}({{T}_{ * }})$ является максимальным.

Давление внутри газовой полости тем больше, чем больше показатель адиабаты. В случае с диссипативным членом и показателем степени неньютоновской модели жидкости ситуация иная. Наименьшего значения обезразмеренная величина ${{T}^{{2\beta }}}{{p}_{{{\text{dis}}}}}({{T}_{*}},\beta ){\text{/}}\mu $ достигает при

Неравенство ${{R}_{ * }}{\text{/}}{{R}_{0}} < {{(24{\text{/}}25)}^{{1/5}}}$ обеспечивает условие ${{\beta }_{ * }} > 0$. В частности, при ${{R}_{ * }}{\text{/}}{{R}_{0}} = {{10}^{{ - 1}}}$ получается ${{\beta }_{ * }} = 0.087$. При $1 > {{R}_{ * }}{\text{/}}{{R}_{0}} \geqslant {{(24{\text{/}}25)}^{{1/5}}}$ значение величины ${{T}^{{2\beta }}}{{p}_{{{\text{dis}}}}}({{T}_{ * }},\beta ){\text{/}}\mu $ уменьшается с ростом показателя β.

3. ЗАДАЧА О ПОСТОЯННОЙ СКОРОСТИ ДИССИПАЦИИ

Рассматривается задача о постоянстве в процессе сжатия величины скорости диссипации. В этом случае

На основе соотношения (3.1) получается степенной закон динамики полости, аналогичный формуле (2.1)

Таким образом,

Для псевдопластической жидкости с показателем нелинейности $\beta = 1{\text{/}}10$ можно в процессе сжатия полости одновременно с постоянством величины скорости диссипации дополнительно добиться сохранения кинетической энергии. При $\beta < 1{\text{/}}10$ кинетическая энергия жидкости неограниченно растет при схлопывании.

Необходимое внешнее давление при произвольном $\beta $ имеет вид

Первое и третье слагаемые в правой части формулы (3.2) растут неограниченно при $t \to T$ для любых β, в то время как множитель ${{(1 - t{\text{/}}T)}^{{ - 2(1 - \lambda )}}}$ во втором слагаемом (которое с точностью до знака равно отношению изменения кинетической энергии жидкости к изменению объема полости в процессе сжатия) меняет режим неограниченного возрастания на убывание к нулю при переходе параметра β через 1.

4. УТОЧНЕНИЕ ЛИНЕЙНО-РЕЗОНАНСНЫХ РЕШЕНИЙ В РАМКАХ НЕЛИНЕЙНОЙ ПОСТАНОВКИ ЗАДАЧИ

Пусть рассматривается некоторое возмущение равновесного внешнего давления в виде периодической функции времени

Возмущения радиуса полости при этом предполагаются относительно малыми

Известно [6], что в случае ньютоновской жидкости (β = 1/2) уравнение (1.4) с учетом соотношений (4.1) и (4.2) допускает линеаризацию вида

Уравнение (4.3) с учетом резонансного условия $\Omega = \omega $ имеет решение

С помощью уравнения (1.4) можно определить вид функции ${{p}_{\infty }}(t)$, необходимый для сохранения динамики границы полости, соответствующей линейному резонансу (4.4), в рамках нелинейной постановки задачи для произвольной степенной неньютоновской жидкости. В этом случае внешнее давление определяется выражением

где R(t) представлен формулой (4.4). Относительная малость возмущений уже не требуется.

Важно заметить, что ${{p}_{\infty }}(t)$ – это внешнее усилие, создаваемое для реализации того или иного режима динамики полости, поэтому для него в рамках модели несжимаемой жидкости допускаются отрицательные значения.

Пусть параметры задачи имеют вид $\rho = 1$ г/см³, $\mu = {{10}^{{ - 2}}}$ г/(см$ \cdot $с), $\beta = 1{\text{/}}2$ (вода), $\gamma = 1.4$ (воздух), ${{p}_{0}} = {{10}^{6}}$ г/(см$ \cdot $с²), ${{R}_{0}} = {{10}^{{ - 2}}}$ см. В этом случае коэффициент затухания $\delta = 2 \times {{10}^{2}}$ с^–1, собственная частота $\omega = 2 \times {{10}^{5}}$ с^–1. Пусть также ${{p}_{1}}{\text{/}}{{p}_{0}} = {{10}^{{ - 2}}}$ и $a = - A{\text{/}}(2\delta \omega )$. Последний параметр фактически определяет величину $dR{\text{/}}dt(0)$.

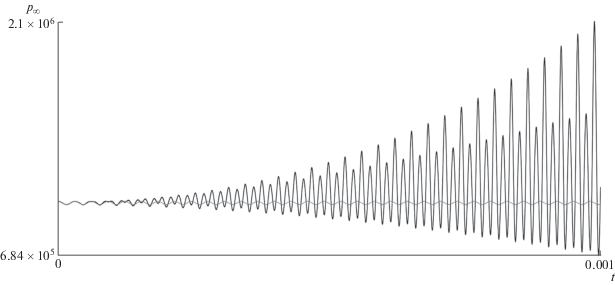
Со временем амплитуда колебаний радиуса полости растет все сильнее, до тех пор пока при $t = 0.00859$ с полость не схлопнется в точку. На рис. 1 представлены сравнительные графики необходимых внешних давлений от времени в случае нелинейной (черная кривая) и линейной (серая кривая) постановок задач. Видно, что данные функции с течением времени отличаются все сильнее, внешнее давление для нелинейного случая перестраивается на принципиально новый режим. В момент схлопывания полости внешнее давление в рамках нелинейной постановки задачи обращается в бесконечность.

Уменьшение отношения p₁/p₀ до, например, 10^–4 при неизменных остальных параметрах обеспечивает выполнение условия $R(t) > 0$ для любого момента времени, нелинейный вариант давления на бесконечности также становится ограниченным.

На уравнение живых сил можно посмотреть и с обратной стороны. Пусть ${{p}_{\infty }}(t)$ в уравнении (4.5) задано в виде (4.1) с учетом выполнения резонансного условия $\Omega = \omega $. В этом случае уравнение (4.5) фактически является нелинейным дифференциальным уравнением второго порядка для нахождения R(t). Таким образом решается задача об уточнении закона динамики газовой полости при переходе от линеаризованной постановки задачи к точной нелинейной. Для построения решения R(t) используются математический пакет Maple и его встроенная функция dsolve. В качестве численного метода выбирается метод Рунге–Кутты–Фельберга четвертого-пятого порядка (RKF45) с интерполянтом четвертой степени – стандартный метод в dsolve.

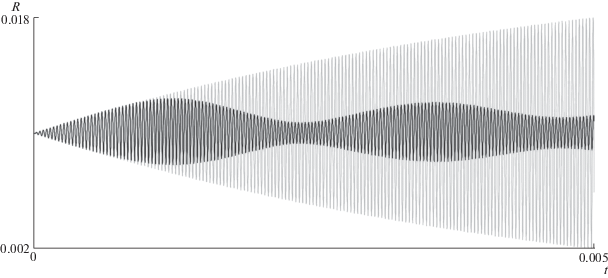
Пусть параметры задачи имеют тот же вид, что и для примера на рис. 1. На рис. 2 представлены графики зависимости радиуса полости от времени для нелинейного (черная кривая) и линейного (серая кривая) решений. Как и в прошлом примере, кривые совпадают на малых временах, но с ростом t появляются принципиальные расхождения. Особенно важно отметить тот факт, что в рамках нелинейного решения полость не схлопывается, у R(t) появляется огибающая, которая совершает затухающие колебания.

В приведенном примере возмущение давления на 1% дает рост и уменьшение радиуса полости в рамках нелинейного решения на более чем 20% в процессе колебаний, влияние центра пузырька сказывается не очень сильно. При увеличении отношения p₁/p₀ до, например, 1 при неизменных остальных параметрах наблюдаются такие колебания нелинейного решения, при которых полость расширяется по радиусу более чем в два раза и сжимается более чем в три раза относительно начального значения ${{R}_{0}}$. При этом существенно сказывается влияние центра.

5. ЗАДАЧА О СЖАТИИ ПУЗЫРЬКА СКАЧКОМ ВНЕШНЕГО ДАВЛЕНИЯ

Рассмотрим традиционную задачу о схлопывании полости в жидкости скачком внешнего давления [3, 4].

Пусть в начальный момент времени давление на бесконечности скачком растет от значения p₀ до некоторого значения ${{p}_{\infty }}$ и далее продолжает сохраняться постоянным. Необходимо определить величину кинетической энергии жидкости при сжатии полости из состояния покоя до размеров $R = {{R}_{ * }}$.

Для решения указанной задачи в уравнении (1.4) совершается переход от переменной $t$ к переменной $V = (4{\text{/}}3)\pi {{R}^{3}}(t)$. При этом скорость схлопывания границы $dR(t){\text{/}}dt$ выражается через кинетическую энергию жидкости и радиус полости на основе соотношения (1.3). В результате получается нелинейное дифференциальное уравнение, описывающее изменение энергии в процессе сжатия

где K – постоянная, зависящая от физических параметров жидкости.

При использовании переменной V начальным условием для уравнения (5.1) выступает равенство $E({{V}_{0}}) = 0$, при этом ${{V}_{ * }} \leqslant V \leqslant {{V}_{0}}$. Соответственно, ${{V}_{0}} = V({{R}_{0}})$ и ${{V}_{ * }} = V({{R}_{ * }})$. В точке V = 0 уравнение сингулярно и требует специального исследования в ее окрестности.

Уравнение (5.1) обезразмеривается. Для этого вводятся следующие замены: $V = {{V}_{0}}z$ и E = ${{p}_{\infty }}{{V}_{0}}y$. В этом случае уравнение (5.1) переписывается в виде

где $\nu = \mu {\text{/}}\rho $.

При β = 1/2 параметр σ связан с числом Рейнольдса ${\text{Re}} = ({{R}_{0}}{\text{/}}\nu )\sqrt {{{p}_{\infty }}{\text{/}}\rho } $ соотношением σ = = $(4{\text{/Re}})\sqrt {2{\text{/}}3} $. Таким образом, в данной работе величина σ играет роль обобщенного числа Рейнольдса.

Переход от переменной z к переменной $x = 1{\text{/}}z$ позволяет избавиться от сингулярности в правой части уравнения (5.2) при z = 0

где $C = {{V}_{0}}{\text{/}}{{V}_{ * }}$.

Следует отметить, что уравнение (5.3) содержит $4$ безразмерных параметра: $\beta $, $\sigma $, $\theta $ и $\gamma $, от значений которых зависит поведение решения. Ниже будет приведен анализ типичных ситуаций.

Для дилатантной жидкости с параметром β = 1 уравнение (5.3) линеаризуется и его аналитическое решение находится стандартными методами.

Величина полной диссипации энергии может быть представлена в виде

где ${{T}_{ * }}$ – время, за которое сжатие полости осуществляется вплоть до радиуса ${{R}_{ * }}$. Следовательно, для вычисления полной диссипации необходимо найти величину y(C) – чем больше ее значение, тем меньше энергии теряется в процессе схлопывания.

Задача Коши (5.3) допускает следующее качественное исследование. Во-первых, $y{\text{'}}(1) = 1 - \theta $ > 0, но с ростом x величина $y{\text{'}}(x)$ становится отрицательной, функция y(x) допускает максимум в некоторой точке. Во-вторых, в любом экстремуме ${{x}_{0}} > 1$ справедливо соотношение

при использовании которого

Следовательно, максимум в x₀ является единственным экстремумом. Особенный интерес представляет изучение характера поведения решения при $x > {{x}_{0}}$.

Задача (5.3) может быть представлена в интегральном виде

Соотношение (5.5) позволяет заключить, что y(x) ограничена сверху значением 1. За счет члена $\theta {{x}^{{\gamma - 1}}}$ функция y(x) убывает неограниченно, что говорит о существовании некоторой точки ${{x}_{1}} > {{x}_{0}}$, в которой $y({{x}_{1}}) = 0$, точки остановки. Таким образом, сжатие газовой полости в принципе может быть осуществлено лишь до некоторого предельного значения, после которого нужно рассматривать ее расширение. Простейшую верхнюю оценку координаты ${{x}_{1}}$ можно получить в виде

Пусть числа $\theta $ и $\gamma $ заданы. Если определить $C = {{\theta }^{{ - 1/\gamma }}}$, то ${{x}_{1}} > C$, иначе $y{\text{'}}({{x}_{1}}) \geqslant 0$, что невозможно. Следовательно, при $\theta = {{C}^{{ - \gamma }}}$ гарантирована возможность сжатия газовой полости с показателем адиабаты $\gamma $ до размеров ${{V}_{ * }} = {{V}_{0}}{\text{/}}C$.

Далее рассматривается частный случай вакуумной полости (θ = 0), при условии, что обратное не оговорено отдельно. Здесь особенно интересным является изучение вопроса о концентрации кинетической энергии жидкости, т.е. исследование величины $y(\infty )$.

Если предположить, что существует точка ${{x}_{1}} > 1$, в которой $y({{x}_{1}}) = 0$, то отсюда, опять же, будет следовать тот факт, что $y{\text{'}}({{x}_{1}}) > 0$, приводящий к противоречию. Таким образом, можно считать, что при $x \gg 1$ справедлива асимптотика

Подставляя (5.7) в (5.3) и проводя элементарные преобразования, получается соотношение

Если предположить, что параметр α равен нулю, то формула (5.8) преобразуется к виду

Отсутствие стремления к нулю с ростом x второго слагаемого в правой части (5.9) при $\beta \geqslant 3{\text{/}}5$ приводит к противоречию. Для таких β параметр α должен быть строго положительным, что говорит об отсутствии концентрации кинетической энергии жидкости при схлопывании вакуумной полости, $y(\infty ) = 0$.

Область значений безразмерного параметра σ весьма широка. Пусть, например, заданы ${{p}_{\infty }} = {{10}^{6}}$ г/(см · с²) и ${{R}_{0}} = {{10}^{{ - 2}}}$ см. В этом случае σ выражается через плотность $\rho $, коэффициент консистенции $\mu $ и показатель степени нелинейности $\beta $ неньютоновской жидкости следующим образом:

Для воды параметр $\sigma $ имеет порядок $3 \times {{10}^{{ - 3}}}$. Раствор цементного камня в воде 54.3% концентрации является псевдопластической жидкостью с параметрами $\beta = 0.077$ и $\mu = 18.715$ г/(см · с) [1], а также $\rho = 2$ г/см³ [7]. В этом случае параметр $\sigma $ получается порядка 10^–3. Несмотря на то что показатель $\beta $ данного раствора сильно отличается от показателя $\beta $ воды, безразмерные числа $\sigma $ для них совпадают по порядку.

В работе [8] рассмотрены реологические свойства дилатантной жидкости – смеси кукурузного крахмала с этиленгликолем в различных концентрациях, для которой предложена эмпирическая формула связи параметра консистенции с показателем нелинейности ($0.55 \leqslant \beta \leqslant 1.46$)

где ${{k}_{0}} = 13.8$ г/(см · с). Таким образом, при $\beta $, равных 0.8, 1 и 1.2, получаются $\sigma $ порядка $7 \times {{10}^{4}}$, $5 \times {{10}^{5}}$ и $4 \times {{10}^{7}}$ соответственно. Такие $\beta $ соответствуют концентрациям крахмала порядка 35–40%, что дает значение плотности смеси около $\rho = 1.25$ г/см³ [7].

При произвольном $\beta $ решение уравнения (5.3) строится численно. Для этого используются математический пакет Maple и его встроенная функция dsolve. В качестве численного метода выбирается неявный метод Рунге–Кутты–Розенброка третьего-четвертого порядка с интерполянтом третьей степени – стандартный метод в dsolve для жестких систем.

Пусть безразмерный параметр β = 1. На рис. 3 представлен график зависимости численного значения $y$ при $x = {{10}^{9}}$ от показателя β.

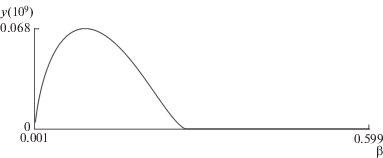
В окрестности точки $\beta = 0.09$ наблюдается максимум концентрации кинетической энергии, ее значение достигает порядка 6.8% от работы постоянного внешнего давления на схлопывании вакуумной полости в идеальной жидкости из состояния покоя в точку. При $\beta > 0.27$ концентрация кинетической энергии отсутствует.

Характер решения уравнения (5.3) сильно зависит от обобщенного числа Рейнольдса. На рис. 4 представлены графики значений $y({{10}^{9}})$ при различных $\beta $ и $\sigma $. На рис. 4а изображен график поверхности, на рис. 4б показан контурный график. Цифрами обозначены линии, соответствующие следующим значениям $y({{10}^{9}})$: 1 – 0.8, 2 – 0.7, 3 – 0.6, 4 – 0.5, 5 – 0.4, 6 – 0.3, 7 – 0.2, 8 – 0.1, 9 – 0.01.

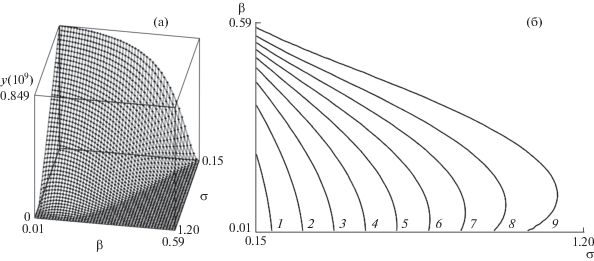
Видно, что для каждого $\beta $ существует критическое значение ${{\sigma }_{{{\text{crit}}}}}(\beta )$, при превышении которого концентрация энергии исчезает. При $\beta = 0.116$ наблюдается максимум ${{\sigma }_{{{\text{crit}}}}} = 1.16$. Зависимость режима схлопывания вакуумной полости от $\sigma $ согласуется с результатами для ньютоновских жидкостей в [4] ($\mathop {{\text{Re}}}\nolimits_{{\text{crit}}} = 8.4$, что дает ${{\sigma }_{{{\text{crit}}}}} = 0.39$).

В случае полости, заполненной газом, величина $y(C)$, для которой $\theta = {{C}^{{ - \gamma }}}$, зависит от $\beta $ и $\sigma $ аналогичным образом. Это позволяет дать соответствующие рекомендации относительно минимизации величины полной диссипации энергии (5.4).

На рис. 5 представлен график полной диссипации (отнесенный к ${{p}_{\infty }}{{V}_{0}}$) при $\sigma = 1$, $\gamma = 1.4$ и $C = {{10}^{3}}$ для разных показателей степени неньютоновской модели жидкости. Минимальное значение достигается при $\beta = 0.093$.

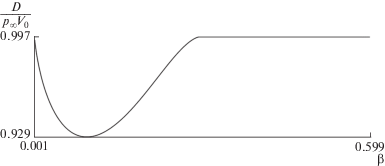
На рис. 6 представлены графики значений $D{\text{/}}({{p}_{\infty }}{{V}_{0}})$ для $\gamma = 1.4$ и $C = {{10}^{3}}$ при различных параметрах $\beta $ и $\sigma $. Как и на рис. 4, на рис. 6 изображены график поверхности (6а) и контурный график (6б). Цифрами обозначены кривые, соответствующие значениям $D{\text{/}}({{p}_{\infty }}{{V}_{0}})$: 0 – 0.1, 1 – 0.2, 2 – 0.3, 3 – 0.4, 4 – 0.5, 5 – 0.6, 6 – 0.7, 7 – 0.8, 8 – 0.9, 9 – 0.99.

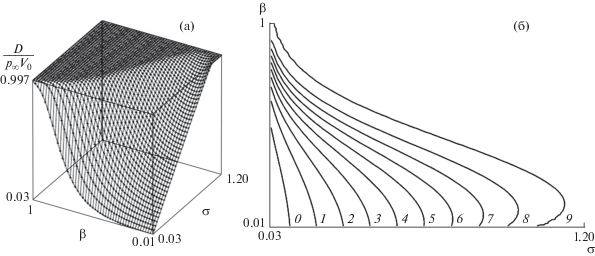
Видно, что величина полной диссипации энергии меньше в области псевдопластических жидкостей, достаточно близких к предельной чисто пластической модели.

Для пузырька воздуха в воде при параметрах ${\text{Re}} = {{10}^{3}}$ (${{p}_{\infty }} = {{10}^{6}}$ г/(см · с²) и ${{R}_{0}} = {{10}^{{ - 2}}}$ см) и $\theta = 0.1$ максимум кинетической энергии достигается в точке ${{x}_{0}} = 5.1$ и равен ${{y}_{{{\text{max}}}}} = 0.571$. В данном случае сжатие осуществляется вплоть до точки остановки ${{x}_{1}} = C = 53.2$, т.е. до ${{R}_{ * }} = 0.266{{R}_{0}}$. При этом оценка (5.6) дает ${{x}_{1}} < {{5}^{{5/2}}} = 55.9$, т.е. работает достаточно точно. Полагая θ = 0 и переходя к рассмотрению вакуумной полости, получается $y({{10}^{9}}) = 0.983$, что говорит о величине концентрации энергии, близкой к предельно допустимой.

Согласно теории сильного взрыва в несжимаемой жидкости [5] концентрация энергии ${{E}_{0}}$ приводит к последующему взрыву, в результате чего $(4{\text{/}}25){{E}_{0}}$ превращается в кинетическую энергию расширяющейся жидкости.

ЗАКЛЮЧЕНИЕ

Рассмотрена серия задач о динамике сферического газового пузырька с однородно распределенным давлением внутри в неограниченном объеме несжимаемой степенной неньютоновской жидкости. Отдельное внимание уделено изучению поведения решений в зависимости от показателя степени неньютоновской модели и установлению их экстремальных свойств. Решены задачи об определении необходимого внешнего давления, приводящего к сохранению величины кинетической энергии в процессе схлопывания, а также обеспечивающего постоянную скорость диссипации. Построены решения, представляющие собой реализацию резонансного поведения полости в рамках нелинейной формулировки задачи. Дано уточнение (по отношению к линеаризованному решению) закона динамики полости при заданном гармоническом внешнем давлении с резонансной частотой. С помощью аналитических и численных методов установлен закон зависимости величины концентрации кинетической энергии жидкости от показателя степени неньютоновской модели и обобщенного числа Рейнольдса при кусочно-постоянном внешнем давлении в частном случае вакуумной полости. Показано, что для части степеней концентрация энергии вообще отсутствует. Для остальных показателей степени вычислены критические значения обобщенного числа Рейнольдса, при котором концентрация энергии также исчезает. Изучена возможность минимизации величины полной диссипации энергии при наличии газа. Введение степенной нелинейности указывает на разнообразие физических свойств динамики сжимающихся пузырьков внутри жидкости в различных режимах, а также выявляет новые эффекты.