Известия РАН. Механика жидкости и газа, 2021, № 4, стр. 73-99
ВТОРИЧНЫЕ ТЕЧЕНИЯ ПРАНДТЛЯ 2-ГО РОДА. ПРОБЛЕМЫ ОПИСАНИЯ, ПРЕДСКАЗАНИЯ, МОДЕЛИРОВАНИЯ
Н. В. Никитин a, *, Н. В. Попеленская a, **, A. Stroh b, ***
a МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия
b Institute of Fluid Mechanics, Karlsruhe Institute of Technology
Karlsruhe, Germany
* E-mail: nvnikitin@mail.ru
** E-mail: aero.natap@mail.ru
*** E-mail: alexander.stroh@kit.edu
Поступила в редакцию 23.03.2021
После доработки 25.03.2021
Принята к публикации 25.03.2021
Аннотация
Наличие турбулентных пульсаций в прямых трубах некруглого поперечного сечения приводит к тому, что в осредненном поле скорости появляется не только продольная компонента, но и поперечные компоненты, образующие вторичное течение. Обнаруженное в 20-е годы прошлого столетия (И. Никурадзе, Л. Прандтль), это гидродинамическое явление остается объектом активных исследований вплоть до наших дней. Интенсивность турбулентных вторичных течений невысока, и не превышает, как правило, 2–3% от характерной скорости потока. Тем не менее их вклад в процессы поперечного переноса импульса и тепла сопоставим со вкладом турбулентных пульсаций. В работе дается обзор экспериментальных, теоретических и численных исследований вторичных течений в прямых трубах и каналах. Особое внимание уделяется вопросу выявления физических механизмов формирования вторичных течений, построения моделей априорной оценки их формы. Затрагиваются вопросы специфики развития вторичных течений в открытых каналах и каналах с неоднородно шероховатыми стенками. Обсуждаются подходы полуэмпирического моделирования турбулентных потоков при наличии вторичных течений.
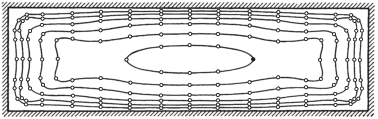
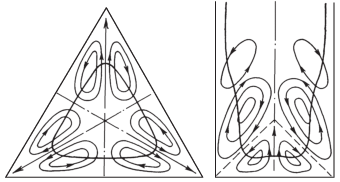
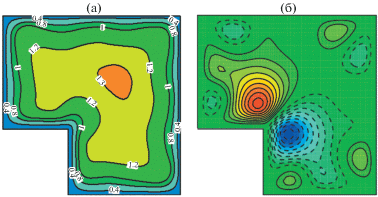
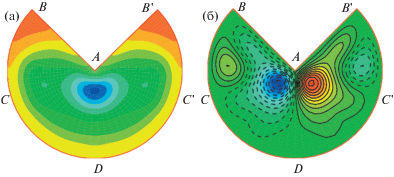
Одно из интересных и важных с практической точки зрения проявлений турбулентности, это способность вызывать так называемые вторичные течения, т.е. организованные движения жидкости в плоскости, перпендикулярной направлению основного потока. Наиболее известны в этом отношении течения в прямых трубах некруглого поперечного сечения. В ламинарных течениях скорость жидкости в любой точке на достаточном удалении от входа направлена вдоль трубы. А вот в турбулентных режимах в осредненном поле скорости появляются ненулевые поперечные составляющие. Первые экспериментальные свидетельства возникновения турбулентных вторичных течений были получены И. Никурадзе в трубах прямоугольного и треугольного сечения [1]. Он обнаружил, что изотахи (изолинии средней продольной скорости в плоскости поперечного сечения) имеют необычные выпуклости, направленные в сторону углов (рис. 1). Л. Прандтль предположил, что характерные искажения изотах вызываются вторичными течениями, возникающими под действием турбулентных пульсаций. Жидкость двигается вдоль биссектрисы в сторону угла и растекается в обе стороны вдоль стенок. Таким образом, частицы жидкости с большим импульсом из ядра потока переносятся к стенкам в угловую область, чем и обусловлено аномальное повышение скорости в этой части трубы [2–4] (рис. 2). Предположение Прандтля о наличии вторичных течений в прямых некруглых трубах было подтверждено в [5] измерениями средней скорости и визуализацией турбулентных течений в трубах различных сечений. Интенсивность вторичных течений не могла быть надежно измерена в то время. Первые непосредственные измерения вторичных течений в прямоугольных трубах были выполнены лишь 30 годами позже [6]. Вторичные течения в прямых трубах возникают только в турбулентных потоках. Прандтль [7, 8] предложил называть подобные течения вторичными течениями 2-го рода, в отличие от вторичных течений 1-го рода, возникающих в искривленных потоках под действием центробежных эффектов как в турбулентных, так и в ламинарных течениях. Интенсивность вторичных течений 1-го рода может достигать больших значений в десятки процентов от скорости потока. Характерные скорости вторичных течений 2-го рода существенно меньше. В трубах они, как правило, не превышают величины в 2–3%. Тем не менее их вклад в процессы поперечного переноса сопоставим со вкладом турбулентных пульсаций [9].
В [10] предложен несколько другой принцип классификации вторичных течений. К первому типу относятся течения, в которых продольная компонента средней завихренности образуется в результате изменения направления вектора средней завихренности. Это возникает, в частности, в изгибах труб, независимо от характера течения, ламинарного или турбулентного. В турбулентных течениях рейнольдсовы напряжения вносят свой вклад в образование средней завихренности, но их воздействие в таких случаях сводится к ослаблению вторичного течения за счет турбулентной диффузии. В течениях второго типа именно напряжения Рейнольдса являются причиной возникновения средней продольной завихренности. В [10] дан краткий обзор вторичных течений первого и второго типа. В [11, 12] описаны особенности вторичных течений в трехмерных турбулентных потоках в угловых областях, включая случаи развивающихся и переходных течений. В настоящей работе приводится обзор и анализ результатов исследований вторичных течений, возникающих в прямых длинных трубах некруглого сечения. Кроме оригинальных результатов различных авторов, в статье представляются некоторые результаты, полученные авторами настоящего обзора.
1. ВТОРИЧНЫЕ ТЕЧЕНИЯ В ТРУБАХ РАЗЛИЧНОГО СЕЧЕНИЯ
Множество работ посвящено выявлению физических механизмов и объяснению причин возникновения вторичных течений 2-го рода. Прандтль предположил, что турбулентные пульсации в угловой области поперечного сечения трубы происходят не только в направлении градиента средней скорости, но и, с большей интенсивностью, в поперечном направлении, т.е. вдоль изотах. При движении частиц жидкости вдоль искривленных изотах возникает сила, направленная в сторону их выпуклости, что приводит в конечном итоге к возникновению вторичного течения. Позже в монографии [13] он сформулировал принцип, согласно которому вторичные течения в некруглых трубах направлены от стенки внутрь потока в местах повышенного напряжения трения на стенке, и наоборот, из потока к стенке в местах пониженного трения, в частности, в угловых областях поперечного сечения. Таким образом достигается выравнивание трения по периметру сечения трубы. В эксперименте [6] исследованы вторичные течения в трубах прямоугольного сечения при нескольких соотношениях длин сторон прямоугольника. Показано, что изменение трения вдоль границы согласуется с направлением вторичных течений, что подтверждает выводы [13]. В [14, 15] предложен другой принцип, основанный на анализе членов уравнения баланса кинетической энергии турбулентности. Если в некотором локальном месте потока производство кинетической энергии существенно превышает вязкую диссипацию, возникает вторичное течение, переносящее частицы жидкости с большой кинетической энергией из этой области, в сторону областей, где производство энергии уступает ее диссипации.
Вторичное течение в плоскости поперечного сечения однозначно определяется по распределению продольной компоненты завихренности среднего течения ${{\Omega }_{x}} = \partial W{\text{/}}\partial y - \partial V{\text{/}}\partial z$. Здесь и далее (x, y, z) – декартовы координаты (ось x направлена вдоль трубы), ($u$, ${v}$, $w$) и (${{\omega }_{x}}$, ${{\omega }_{y}}$, ${{\omega }_{z}}$) – соответствующие компоненты вектора скорости ${\mathbf{u}}$ и завихренности $\nabla \times {\mathbf{u}}$. Заглавными буквами обозначаются средние величины, а штрихами – пульсации: $q(t,x,y,z) = Q(y,z) + q{\text{'}}(t,x,y,z)$ для произвольной величины q; статистическое осреднение обозначается угловыми скобками $Q = \left\langle q \right\rangle $. Уравнение для ${{\Omega }_{x}}$ в турбулентном потоке выведено в [16]
(1.1)
$V\frac{{\partial {{\Omega }_{x}}}}{{\partial y}} + W\frac{{\partial {{\Omega }_{x}}}}{{\partial z}} - \nu \left( {\frac{{{{\partial }^{2}}{{\Omega }_{x}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{\Omega }_{x}}}}{{\partial {{z}^{2}}}}} \right) = S$Жидкость считается несжимаемой, а течение предполагается установившимся по времени и однородным в продольном направлении. Таким образом, средние величины не зависят от времени и продольной координаты. Первые два слагаемых в левой части (1.1) описывают конвекцию продольной завихренности вторичным течением. Их действие состоит в выравнивании значений завихренности вдоль траектории. Третье слагаемое отвечает вязким эффектам, сглаживающим градиенты ${{\Omega }_{x}}$. За производство продольной завихренности отвечает источниковый член в правой части (1.1), который выражается через градиенты напряжений Рейнольдса
(1.2)
$S = \frac{{{{\partial }^{2}}}}{{\partial y\partial z}}(\langle {{{v}}^{{'2}}}\rangle - \langle {{w}^{{'2}}}\rangle ) + \left( {\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}} - \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)\left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle \equiv {{S}_{1}} + {{S}_{2}}$В [17, 18] доказано, что (1.1) с нулевой правой частью и условиями прилипания на неподвижных стенках не имеет решений, отличных от тривиального. Следовательно, в установившихся ламинарных течениях в прямых трубах вторичные течения возникать не могут. С другой стороны, очевидно, что при $S \ne 0$ невозможно отсутствие вторичного течения. В [16] показано, что источниковый член в (1.1) отличен от нуля в угловых областях труб прямоугольного сечения, что объясняет возникновение вторичного течения. Из соображений симметрии следует, что $S$ меняет знак на противоположный на каждой из линий симметрии. Таким образом, линии симметрии в поперечном сечении трубы разделяют области противоположной циркуляции [19].
Два слагаемых в (1.2) представляют собой крутящие моменты, действующие на жидкость. Для их оценки в эксперименте [19] измерены все три компоненты скорости и шесть компонент тензора напряжений Рейнольдса в трубе квадратного сечения. Сделан вывод о том, что при расположении осей координат (y, z) параллельно стенкам первое слагаемое S1, содержащее разность нормальных напряжений $\langle {{{v}}^{{'2}}}\rangle - \langle {{w}^{{'2}}}\rangle $, доминирует над вторым слагаемым S2, содержащим производные от сдвигового напряжения $\left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle $. Таким образом, продольная завихренность производится слагаемым S1 и конвектируется в те места, где диссипирует под действием вязкости. Замечание об ориентации осей координат существенно, потому что S1 и ${{S}_{2}}$ не инвариантны по отношению к изменению системы координат. В частности, при повороте осей (y, z) на 45° значения S1 и S2 меняются местами. В [20] предложена другая интерпретация того, что вторичные течения в квадратной трубе вызываются градиентами нормальных напряжений. Показано, что уравнения Рейнольдса в плоскости поперечного сечения трубы с отброшенными градиентами сдвиговых напряжений имеют решение только при наличии вторичного течения, в котором движение направлено вдоль стенок в стороны от угла. То, что пренебрежение сдвиговым напряжением Рейнольдса $\left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle $ приводит к выводу об обязательном наличии вторичного течения в трубе квадратного сечения можно увидеть и из (1.2). Легко показать, что S1 не равно тождественно нулю, а значит, при отсутствии компенсирующего второго слагаемого, S также не равно тождественно нулю, и (1.1) имеет ненулевое решение. В [21] утверждается, что $\langle {{{v}}^{{'2}}}\rangle - \langle {{w}^{{'2}}}\rangle \ne 0$ является достаточным условием возникновения вторичного течения в трубах некруглого сечения. С одной стороны, действительно, и указанное неравенство, и вторичные течения имеют место в большинстве некруглых труб. С другой стороны, в круглых трубах или, например, в трубах кольцевого сечения, вторичные течения отсутствуют, несмотря на неравенство нормальных напряжений, а приведенные в [21] рассуждения не используют условие некруглости сечения трубы.
Точность результатов и выводы о доминировании ${{S}_{1}}$ в (1.2), сделанные в [19], подвергнуты сомнению в [22]. Показано, что ошибки на уровне 1% в сигнале термоанемометра при использованной системе измерений может приводить к 100% погрешности при оценке сдвиговых напряжений $\left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle $. Более точные измерения [23] показали, что градиенты напряжений Рейнольдса, порождающие слагаемые ${{S}_{1}}$ и ${{S}_{2}}$ в (1.2), близки по величине, тогда как конвективные и вязкие члены имеют величину на два порядка меньшую. Сделан вывод, что вторичное течение возникает под действием малой разности между градиентами давления и рейнольдсовых напряжений. На основе анализа экспериментальных работ в прямоугольных трубах, выполненных в 1960–1970 годы, в [24] сделаны следующие выводы. Слагаемые в (1.2) имеют близкие значения и противоположные знаки. Их амплитуда существенно превышает величину конвективных членов (1.1). Вязкие члены пренебрежимо малы всюду, за исключением непосредственной близости к углу. Таким образом, производство продольной завихренности описывается малой разностью относительно больших по величине ${{S}_{1}}$ и ${{S}_{2}}$.
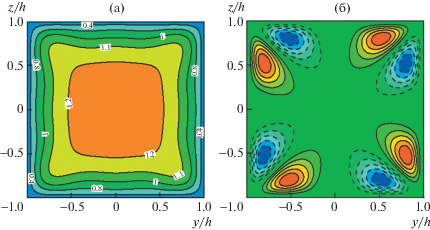
С конца 1980-х годов численное моделирование становится равноправным инструментом исследования турбулентности. Для расчетов вторичных течений используются вихреразрешающие методы решения уравнений Навье–Стокса: LES (Large Eddy Simulation) и DNS (Direct Numerical Simulation). В первом подходе расчет производится на относительно грубой сетке, а для учета мелкомасштабных составляющих используются определенные модели описания малых (подсеточных) масштабов. Во втором подходе предполагается разрешение на расчетной сетке всех существенных масштабов турбулентного движения. Первые подробные расчеты турбулентных течений в трубе квадратного сечения были выполнены в [25] (LES) и [26, 27] (DNS). Хотя числа Рейнольдса в численных расчетах, как правило, заметно ниже, чем в большинстве экспериментов, результаты вычислений позволили существенно расширить знания о свойствах течений в некруглых трубах вообще и углубить понимание механизмов возникновения вторичных течений в частности. В [26] проведен расчет при числе Рейнольдса ${\text{Re}} = 4410$, определенном через среднюю скорость Ub и ширину трубы $2h$. Впервые с высокой точностью получены распределения средних и пульсационных характеристик по сечению трубы. Распределение средней скорости и линии тока вторичного течения при этом числе Рейнольдса, полученные в [28], представлены на рис. 3. На этих рисунках и всюду далее синий цвет соответствует малым, а красный – большим значениям представляемых величин. Изолинии с отрицательными значениями изображаются прерывистыми линиями. Сплошные линии тока вторичного течения отвечают движению жидкости против часовой стрелки, штриховые – по часовой стрелке. В окрестности каждого из четырех углов поперечного сечения трубы частицы жидкости переносятся вторичным течением из центра трубы к углам вдоль биссектрисы и растекаются в обе стороны вдоль стенок. Максимальная скорость во вторичном течении (на биссектрисах углов и в пристенной области) составляет $0.02{{U}_{b}}$. Проявлением вторичных течений являются характерные выпуклости изолиний средней скорости, направленные в сторону угловых точек. На рис. 4 показаны распределения средней продольной завихренности ${{\Omega }_{x}}(y,z)$ и источникового члена $S(y,z)$ в правой части (1.1), определяющего производство ${{\Omega }_{x}}$. Представлена четверть сечения трубы. Все величины здесь нормируются на вязкие масштабы скорости ${{U}_{\tau }} = \sqrt {{{\tau }_{w}}{\text{/}}\rho } $ и длины ${{l}_{\tau }} = \nu {\text{/}}{{U}_{\tau }}$, где ${{\tau }_{w}}$ – среднее трение на стенке трубы, $\rho $, $\nu $ – плотность и вязкость жидкости. Нормировка на вязкие (пристенные) масштабы обозначается верхним индексом ‘+’. Число Рейнольдса ${\text{R}}{{{\text{e}}}_{\tau }} = {{U}_{\tau }}h{\text{/}}\nu \equiv {{h}^{ + }}$. Производство завихренности сосредоточено в пристенном районе угловой области. Максимум $\left| S \right|$ достигается в симметричных относительно биссектрисы угла точках $({{y}^{ + }},{{z}^{ + }}) \approx (35,10)$ и (10, 35). Результаты расчетов [26] положили конец дискуссиям об относительной важности слагаемых ${{S}_{1}}$ и ${{S}_{2}}$ в выражении (1.2) для источникового члена $S$ уравнения (1.1). Распределения ${{S}_{1}}$, ${{S}_{2}}$ приведены на рис. 5. В точках максимума $\left| S \right|$ источниковый член на 90% определяется слагаемым ${{S}_{1}}$, однако ближе к стенке модули каждого из слагаемых вдвое превышают значения максимума $\left| S \right|$ и на 90% нейтрализуют друг друга. Таким образом, подтверждено существенное значение обоих членов, входящих в выражение (1.2). Вопреки выводам [24], в [26] показано, что конвективные члены в (1.1) пренебрежимо малы по сравнению с вязкими членами, которые уравновешивают члены производства ${{\Omega }_{x}}$.
Рис. 4.
Распределения средней продольной завихренности $\Omega _{x}^{ + } = \pm 0.01n$, $n = 1{\kern 1pt} - {\kern 1pt} 6$ (а), и источникового члена в (1.1) ${{S}^{ + }} = \pm 0.0001n$, $n = 1{\kern 1pt} - {\kern 1pt} 7$ (б), в поперечном сечении трубы квадратного сечения при ${\text{Re}} = 4410$ (${\text{R}}{{{\text{e}}}_{\tau }} = 150$) [26, 28].
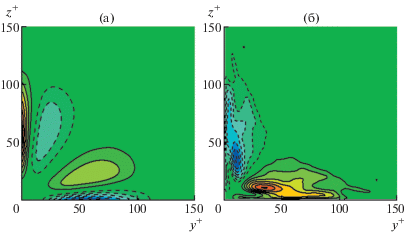
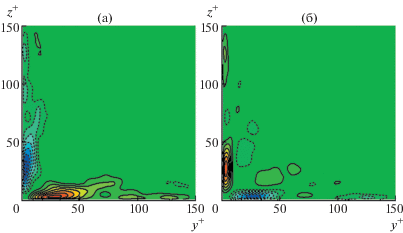
Рис. 5.
Распределения величин ${{S}_{1}}$, ${{S}_{2}}$ (1.2) в поперечном сечении трубы квадратного сечения при ${\text{Re}} = 4410$ (${\text{R}}{{{\text{e}}}_{\tau }} = 150$) [26, 28]. $S_{1}^{ + } = \pm 0.0002n$, $n = 1{\kern 1pt} - {\kern 1pt} 7$ (а), $S_{2}^{ + } = \pm 0.0002n$, $n = 1{\kern 1pt} - {\kern 1pt} 6$ (б).
Аналогичные выводы были сделаны в [27] при ${\text{Re}} \approx {{10}^{4}}$. В этой работе также проведен квадрантный анализ сдвиговых напряжений Рейнольдса $\left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle $. Сделана попытка связать появление вторичного течения с взаимодействием интенсивных турбулентных выплесков (ejections) между соседними стенками в угловой области. В [29] уточнены некоторые детали статистических характеристик при изменении числа Рейнольдса. Показано, что профили средней скорости на разных расстояниях от угла удовлетворяют закону стенки при нормировке на местное пристенное трение. В [30] обнаружено, что координаты локальных экстремумов ${{\Omega }_{x}}$ и функции тока вторичного течения $\Psi $ в плоскости поперечного сечения, примерно совпадая при самых малых значениях числаРейнольдса ${\text{Re}} \sim 2000$, расходятся при больших ${\text{Re}}$. При этом координаты локальных экстремумов ${{\Omega }_{x}}$ с ростом ${\text{Re}}$ перестают меняться, будучи выраженными в вязких единицах. Наоборот, координаты экстремумов $\Psi $ постоянны в глобальных масштабах. Наблюдается определенная статистическая связь между вторичным течением и пристенными турбулентными структурами, такими, как полосчатые структуры, возникающие в пристенной области турбулентного пограничного слоя. Ближайшие к углу полосчатые структуры преобладающе имеют повышенную скорость и образуются на расстоянии 50 вязких длин. При этом квазипродольные вихри в пристенной области преобладающе имеют знак, совпадающий со знаком ${{\Omega }_{x}}$. В [31], где проведены LES расчеты при трех числах Рейнольдса, ${\text{R}}{{{\text{e}}}_{\tau }} = 190,\;300,\;550$ (${\text{Re}} \approx 6000{\kern 1pt} - {\kern 1pt} 20{\kern 1pt} {\kern 1pt} 000$), сделан вывод, что при нормировке на вязкие масштабы величины и распределения членов, отвечающих вязкой диффузии и производству продольной завихренности в (1), не меняются при изменении ${\text{Re}}$. DNS расчеты вплоть до ${\text{R}}{{{\text{e}}}_{\tau }} = 600$ (${\text{Re}} \approx 21{\kern 1pt} {\kern 1pt} 400$) проведены в [32]. Основное внимание уделено уточнению распределений компонент средней скорости и интенсивностей пульсаций. Расчеты до еще больших значений ${\text{Re}} \approx 40{\kern 1pt} {\kern 1pt} 000$ проведены в [33]. Показано, что за пределами угловой области вторичные течения с хорошей точностью аппроксимируются собственными функциями оператора Лапласа. Сделан вывод, что при больших числах Рейнольдса вторичные течения оказывают незначительное влияние на интегральные свойства течения.
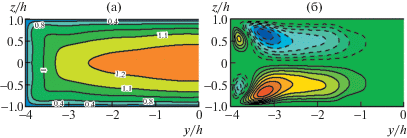
Скорости вторичных течений в трубах прямоугольного сечения впервые были измерены в экспериментах [6]. В трех трубах с соотношением длин сторон прямоугольника в поперечном сечении $b:a = $ 1:1, 2:1 и 3:1 максимальные значения оказались примерно одинаковыми в 1.5% от скорости в центре трубы. Максимум скорости вторичного течения всюду достигается вблизи стенки. На биссектрисах углов скорость не превышает 1%. В каждом углу вторичное течение имеет вид пары вихрей противоположного знака, разделенных биссектрисой. Вихрь малого размера расположен вдоль короткой стороны прямоугольника, больший вихрь – вдоль длинной. В отличие от [2], где предполагалось наличие нескольких вихрей вдоль длинной стороны прямоугольника, во всех исследованных вариантах наблюдался только один вихрь, интенсивность движения в котором уменьшается по мере удаления от угла. Распределение средней скорости и линии тока вторичного течения в прямоугольной трубе с соотношением сторон 4:1, полученные в численных расчетах [34] при ${\text{Re}} = 4410$ (${\text{R}}{{{\text{e}}}_{\tau }} = 150$), изображены на рис. 6. Показаны только левые половины сечения трубы. Форма изолиний скорости качественно совпадает с результатами Никурадзе [1], представленными на рис. 1. Отличительная особенность распределения скорости – характерные выпуклости изолиний в сторону углов. Форма линий тока вторичного течения согласуется с результатами [6] и опровергает предположение Прандтля [2] о наличии нескольких циркуляционных ячеек вдоль длинной стороны прямоугольника (рис. 2).
Рис. 6.
Распределение средней скорости U/Ub (а), линии тока вторичного течения (изолинии функции тока $\Psi h{\text{/}}{{U}_{b}} = \pm 0.0005n$, $n = 1{\kern 1pt} - {\kern 1pt} 8$) (б), в поперечном сечении трубы прямоугольного сечения с соотношением сторон 4:1 при ${\text{Re}} = 4410$ [34].
Расчеты турбулентных течений в трубах прямоугольного сечения проводились в [35] (${\text{R}}{{{\text{e}}}_{\tau }} \approx 300$, $b{\text{/}}a = 3.33$), [36] (LES, ${\text{R}}{{{\text{e}}}_{\tau }} \approx 150$, $b{\text{/}}a = 1{\kern 1pt} - {\kern 1pt} 4$), а также в серии работ Р. Винуесы и соавт. [37–40] в диапазоне ${\text{R}}{{{\text{e}}}_{\tau }} = 180{\kern 1pt} - {\kern 1pt} 360$, $b{\text{/}}a = 1 - 14.4$. Исследованы изменения в форме вторичного течения, происходящие с ростом b/a, и влияние боковых стенок трубы на течение в центральной части. Результаты этих работ подытожены в [40]. Влияние вторичного течения простирается на большие расстояния от угла. Профиль скорости в максимально удаленном от угла сечении выходит на асимптотический вид только при $b{\text{/}}a > 10$. С целью возможного ослабления вторичного течения А. Видал и соавт. [41–43] исследовали течения в прямоугольных трубах с закругленными углами. Вопреки ожиданиям, закругление углов не приводит к ослаблению вторичного течения, а в ряде случаев, наоборот, приводит к его усилению. Вихри формируются вблизи сопряжений закруглений и прямых участков. В вариантах, когда прямая боковая стенка в прямоугольной трубе заменяется полукруглой вместо обычных четырех вихрей (по паре вблизи каждого угла) образуется лишь по одному вихрю вблизи сопряжения полукруга с прямолинейными длинными стенками.
В [9] рассчитаны турбулентные течения в трубах эллиптического сечения. Расчеты проведены в декартовой системе координат. Для удовлетворения условий прилипания на криволинейных границах использован метод виртуальных границ [44]. Исследованы течения при ${\text{Re}} = 6000$ в трубах с отношением полуосей эллипса $b{\text{/}}a = 2{\text{/}}3$ и 1/2. Обнаружено, что вторичные течения в обоих случаях имеют вид двух пар вихрей противоположного знака. Жидкость из центра трубы двигается к стенкам вдоль больших полуосей, растекается вдоль стенок в обе стороны и возвращается от стенок к центру трубы вдоль коротких полуосей. В ядре потока максимальная скорость вторичного течения имеет величину менее 1% от средней скорости, у стенок – 1 и 1.4%, в широкой и узкой трубе соответственно. Несмотря на столь незначительную интенсивность, вторичные течения оказывают существенное влияние на распределение средней скорости по сечению трубы, сопоставимое с воздействием турбулентных напряжений. Вторичные течения и турбулентные напряжения обладают противоположным эффектом – вторичные течения стремятся растянуть линии равной скорости вдоль больших полуосей эллипса, а турбулентные напряжения, наоборот, сжимают их к центру трубы. Для более аккуратного воспроизведения деталей течения в пристенной области расчеты в эллиптической трубе были выполнены в [45, 46]. В этих работах уравнения Навье–Стокса решались в эллиптической цилиндрической системе координат, в которой стенка трубы совпадает с координатной поверхностью. Использовался метод решения уравнений Навье–Стокса в произвольной ортогональной криволинейной системе координат [47]. Подтверждены и уточнены выводы [9], оценены величины членов уравнения для продольной завихренности (1.1). Источниковый член $S$ в правой части (1.1) имеет заметные ненулевые значения только в узком пристенном слое, где он может быть представлен аналогично (1.2) в виде суммы двух слагаемых, первое из которых, ${{S}_{1}}$, есть вторая смешанная производная от разности нормальных напряжений Рейнольдса, а второе, ${{S}_{2}}$ – разность вторых производных от сдвигового напряжения Рейнольдса. Элементарные оценки показывают, что ${{S}_{1}}$ действует как источник, а ${{S}_{2}}$ – как сток продольной завихренности. Распределения ${{S}_{1}}$ и $ - {{S}_{2}}$ по сечению трубы оказываются удивительно похожими по форме, при этом $\left| {{{S}_{2}}} \right|$ составляет около 30% от $\left| {{{S}_{1}}} \right|$.
В трубах круглого сечения вторичные течения не возникают по причине центральной симметрии потока. Очевидно, что по той же причине вторичные течения не возникают и в трубах кольцевого сечения. Вторичные течения в трубах с эксцентрическим кольцевым сечением изучались экспериментально в [48, 49]. Согласно измерениям [48], вторичное течение имеет вид пары противоположных по знаку вихрей, расположенных симметрично относительно линии симметрии в плоскости поперечного сечения. Циркуляционные ячейки по большей части прижаты к внутреннему цилиндру. Жидкость перемещается из области узкого зазора в сторону широкого зазора вдоль внутреннего цилиндра и возвращается обратно примерно посередине между цилиндрами. В самой широкой части зазора скорость вторичного течения направлена от внутреннего цилиндра к внешнему. В [49] получено противоположное направление вторичного течения. Кроме того, в узкой части зазора отмечена еще одна пара вихрей меньшей интенсивности. Отметим, что достоверность и тех и других результатов весьма невысока, в чем признаются сами авторы. Кроме того, измерения в двух цитированных экспериментах проводились при заметно различающихся геометрических параметрах и числах Рейнольдса. В [50, 51] проведены прямые расчеты турбулентных течений в эксцентрических кольцевых трубах при двух значениях ${\text{Re}} = 4000$ и 8000. Применялся алгоритм [47] в бицилиндрической системе координат, в которой обе стенки трубы являются координатными поверхностями. Полученная картина вторичных течений напоминает результаты [48] – частицы жидкости двигаются вдоль внутреннего цилиндра со стороны узкого зазора к широкому и возвращаются обратно в средней части сечения. Ближе к внешнему цилиндру со стороны широкого зазора имеется менее интенсивная циркуляционная ячейка с противоположным направлением вращения. Топологически эквивалентная картина вторичных течений с двумя вихрями разного знака в каждой половине поперечного сечения получена численно в [52]. Однако, в отличие от [50, 51], менее интенсивный вихрь расположен не в широкой, а в узкой части зазора. Такие различия в виде вторичных течений могут объясняться существенным различием геометрических параметров труб, рассмотренных в [50, 51] и [52].
Вторичные течения вдоль внешних углов изучены менее подробно. Можно отметить лишь эксперименты, проведенные в Мельбурнском университете [53–55], и численные расчеты [56, 57]. В эксперименте изучалось течение вдоль ребра, образованного двумя плоскими пластинами, состыкованными под прямым углом. В расчетах рассматривалось течение в зазоре между вложенными одна в другую трубами квадратного сечения, в котором имеется 4 внутренних и 4 внешних угла в 90°. Хотя числа Рейнольдса в расчете и эксперименте различались значительно, результаты, касающиеся особенностей вторичного течения в окрестности внешнего угла, качественно совпадают. На рис. 7 приведены распределение средней скорости и линии тока вторичного течения в трубе, в сечении которого имеется внешний угол [58]. Вторичное течение в окрестности внешнего угла имеет вид пары вихрей, симметрично расположенных относительно биссектрисы угла. Направление движения жидкости во вторичном течении – от угла в сторону потока вдоль биссектрисы и к углу вдоль стенок, т.е. противоположное случаю внутреннего угла. Соответственно линии равной скорости имеют характерные выпуклости, направленные от угла в сторону потока. Интенсивность вторичного течения в окрестности внешнего угла достигает 5.25% от ${{U}_{b}}$, что заметно превышает аналогичную интенсивность вблизи внутренних углов с максимальным значением около 2%. В [57] рассчитаны распределения слагаемых ${{S}_{1}}$, ${{S}_{2}}$, выражения для производства продольной завихренности (1.2). Как и в окрестностях внутренних углов, ${{S}_{1}}$, ${{S}_{2}}$ оказываются близкими по значению и противоположными по знаку. Их роль в генерации завихренности меняется в разных частях окрестности угла.
Рис. 7.
Распределение средней скорости U/Ub (а), линии тока вторичного течения (изолинии функции тока $\Psi h{\text{/}}{{U}_{b}} = \pm 0.0004n$, $n = 1{\kern 1pt} - {\kern 1pt} 9$) (б), в поперечном сечении трубы с внешним углом при ${\text{Re}} = 4000$ [58].
Вторичные течения в каналах со свободной поверхностью интенсивно изучаются в связи с очевидной геофизической важностью. С вторичными течениями связаны зоны подъема и опускания жидкости, охватывающие всю толщину потока. В натурных условиях вторичные течения значительно влияют на газо- и теплообмен, на самоаэрацию на свободной поверхности. Благодаря переносу донных отложений вторичными течениями изменяется форма дна, возникает неоднородность шероховатости дна с образованием продольных гребней и впадин, что усиливает вторичные течения и приводит в конечном итоге к образованию цепочки продольных вихрей с чередующимся по ширине канала направлением вращения. По этой причине наибольшее внимание уделяется изучению течений в каналах с шероховатым дном при наличии разного рода неоднородностей в распределении донной шероховатости [59–64].
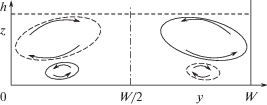
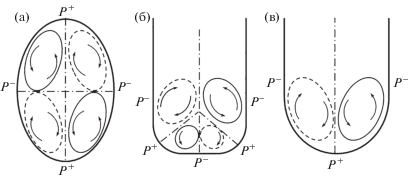
Считается, что на начальном этапе развития вторичные течения возникают в угловых областях, где боковые стенки сопрягаются с горизонтальным дном. Согласно устоявшейся точке зрения, угловые вторичные течения в гладком канале имеют форму двух ячеек, нижней и верхней с противоположным направлением вращения жидкости (рис. 8) [60]. Движение в верхней ячейке направлено от боковой стенки вдоль свободной поверхности, оно более интенсивное, чем течение в нижней ячейке. При удалении от боковой стенки интенсивность угловых вторичных течений ослабляется и полностью пропадает на расстоянии в ∼$3h$ ($h$ – глубина канала) [65]. Отметим, что описанная картина углового вторичного течения в открытом канале отличается от вторичного течения в трубе прямоугольного сечения. В последней наблюдается не одна, а две пары вихрей у каждой из боковых стенок. Подробное экспериментальное и численное исследование области сопряжения свободной границы и твердой стенки [66] выявило наличие менее интенсивного “внутреннего” вторичного вихря, движение в котором направлено в сторону угла вдоль свободной границы. Исследование механизмов переноса импульса и энергии в этой области выполнено в [67].
2. ФИЗИЧЕСКИЙ МЕХАНИЗМ ФОРМИРОВАНИЯ ВТОРИЧНЫХ ТЕЧЕНИЙ В НЕКРУГЛЫХ ТРУБАХ
Несмотря на большое количество экспериментальных, теоретических и вычислительных работ, посвященных изучению вторичных течений Прандтля 2-го рода, вопрос о физическом механизме их формирования продолжает обсуждаться в литературе. Во многих работах рассуждения базируются на анализе источниковых членов (1.2) уравнения для средней продольной завихренности (1.1). Оценивается относительная важность двух членов: члена с разницей нормальных напряжений ${{S}_{1}}$ и члена со сдвиговыми напряжениями ${{S}_{2}}$. Такое разделение источникового члена было введено в [16] для труб прямоугольного сечения, когда оси координат параллельны стенкам трубы. Это обстоятельство зачастую упускается из вида, и членам ${{S}_{1}}$, ${{S}_{2}}$ приписывается особый физический смысл при анализе течений в трубах произвольного сечения [21]. А между тем, их значения изменяются при повороте системы координат в плоскости (y, z), и, в частности, меняются местами при повороте осей на 45° [19]. Другими словами, если ${{{v}}_{1}}$, w1, пульсации компонент скорости, отвечающие повернутой на 45° системе координат ${{y}_{1}}$, z1, то
Поэтому использование источникового члена в виде (1.2) для описания вторичных течений в трубах с сечением, отличным от прямоугольного, представляется не очень продуктивным. Величины ${{S}_{1}}$, ${{S}_{2}}$, будучи отличными от нуля по отдельности, могут полностью нейтрализовывать друг друга, как происходит, например, в круглых трубах. Да и в прямоугольных трубах ${{S}_{1}}$, ${{S}_{2}}$ имеют близкие по форме распределения и противоположные по знаку значения, нейтрализуя друг друга на 90% [26].
В [28] предложено альтернативное представление источникового члена
(2.1)
$S = \left( {\left\langle {\omega _{x}^{'}\frac{{\partial u{\text{'}}}}{{\partial x}}} \right\rangle - \left\langle {u{\text{'}}\frac{{\partial \omega _{x}^{'}}}{{\partial x}}} \right\rangle } \right) + \left( {\left\langle {\omega _{y}^{'}\frac{{\partial u{\text{'}}}}{{\partial y}}} \right\rangle + \left\langle {\omega _{z}^{'}\frac{{\partial u{\text{'}}}}{{\partial z}}} \right\rangle - \left\langle {{v}{\text{'}}\frac{{\partial \omega _{x}^{'}}}{{\partial y}}} \right\rangle - \left\langle {w{\text{'}}\frac{{\partial \omega _{x}^{'}}}{{\partial z}}} \right\rangle } \right) \equiv S_{1}^{'} + S_{2}^{'}$В такой записи каждое из слагаемых, ограниченных круглыми скобками, инвариантно относительно выбора системы координат в плоскости (y, z). В однородных по x течениях $ - \langle u{\text{'}}\partial \omega _{x}^{'}{\text{/}}\partial x\rangle $ = = $\langle \omega _{x}^{'}\partial u{\text{'/}}\partial x\rangle $, так что
(2.2)
$S_{1}^{'} = 2\left\langle {\omega _{x}^{'}\frac{{\partial u{\text{'}}}}{{\partial x}}} \right\rangle $Эта величина описывает эффект изменения продольной завихренности под действием пульсационного сжатия/растяжения вихревых трубок. Оказывается, что в области концентрации Ωx в прямоугольных трубах производство средней продольной завихренности в значительной степени описывается членом $S_{1}^{'}$. Это значит, в частности, что пульсации продольных компонент скорости и завихренности происходят согласованным образом, так что корреляции $\omega _{x}^{'}$ и $\partial u{\text{'/}}\partial x$ по величине и по знаку согласованы со значением Ωx. В [28] предложено объяснение причины возникновения такого согласования.
Начиная с работы [27], предпринимаются попытки связать вторичные течения с особенностями крупномасштабных турбулентных структур (пристенные полосы, квазипродольные вихри) и явлений (sweepings, ejections), наблюдающихся в пристенном слое турбулентных течений [30, 39, 43, 68–70] и др. На наш взгляд, подобные наблюдения лишь указывают на существование определенных особенностей турбулентных структур в областях возникновения вторичных течений, но не выявляют механизмы возникновения вторичных течений. В пользу такой точки зрения говорит и то, что вторичные течения могут наблюдаться и в отсутствие основного турбулентного потока [71].
В [72] проведен теоретический анализ развития турбулентного пограничного слоя при течении вдоль внутреннего угла в 90°. Течение рассматривается на достаточном удалении от передней кромки, где справедливо погранслойное приближение. Считается, что вторичные течения отсутствуют. Уравнения Рейнольдса в этом случае дают связь среднего давления и напряжений Рейнольдса. Пусть биссектриса угла в плоскости поперечного сечения пересекается с внешней границей пограничного слоя в точке $A$, а точки $B$, $C$ – проекции точки $A$ на боковые стенки. При некоторых дополнительных предположениях получается, что давление $P(O)$ в угловой точке O превышает давление на стенке в точках $B$, $C$. Отсюда делается вывод, что жидкость под действием разности давления должна двигаться вдоль стенки в обе стороны от угловой точки и подтекать к углу вдоль биссектрисы. Таким образом получается известная картина вторичного течения внутри угла. В [72] также сделано предположение, что в развивающемся пограничном слое возникает цепочка вторичных вихрей, характерный размер которых увеличивается по мере увеличения толщины погранслоя. В экспериментах [73] эта модель не была подтверждена. Более того, было обнаружено, что на этапе пространственного развития первичные напряжения Рейнольдса $\left\langle {u{\text{'}}{v}{\text{'}}} \right\rangle $, $\left\langle {u{\text{'}}w{\text{'}}} \right\rangle $ дают более существенный вклад в образование вторичного течения, чем напряжения Рейнольдса, связанные с пульсациями в плоскости (y, z).
Рассуждения [72] повторяются с минимальными коррекциями в [74] для случая установившегося течения в трубе квадратного сечения. В качестве точки $A$ берется центр поперечного сечения трубы. В результате получается, что давление в вершине угла $P(O)$ превышает давление $P(B)$, $P(C)$ в серединах боковых стенок поперечного сечения, откуда делается вывод о том, что градиент давления приводит к растеканию жидкости вдоль стенок в сторону от угла. Отметим, что в обеих цитированных работах на основании неравенства $P(O) > P(B)$ делается вывод, что в угловой точке достигается локальный максимум давления. Теоретически возможна ситуация, когда давление от значения $P(O)$ сначала увеличивается при удалении от угла вдоль стенки до некоторого еще большего значения, а затем уже уменьшается до $P(B)$. В этом случае направление вторичного течения вблизи угла должно быть противоположным известному. Кроме того, результаты [72, 74] относятся исключительно к углу в 90° и не дают представления о поведении вторичных течений в других геометрических конфигурациях.
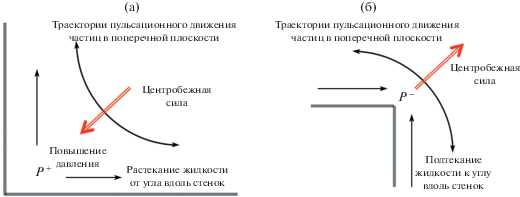
Изменение среднего давления в угловых точках поперечного сечения можно объяснить исходя из простых качественных соображений, описываемых ниже на примерах течений вдоль внутреннего и внешнего углов в 90°. В пристенном слое тангенциальные пульсации скорости превышают нормальные пульсации, так что жидкие частицы двигаются преимущественно параллельно стенкам, а в угловой области поперечного сечения – по дугообразным траекториям, сопрягающим направления вдоль касательных к смежным границам (рис. 9). Возникающая при этом центробежная сила (сила инерции) направлена в сторону выпуклости траектории. Она вызывает изменение среднего давления в углу и градиент давления, действующий радиально во все стороны. На твердых стенках трубы напряжения Рейнольдса и их градиенты равны нулю, поэтому действие градиента давления вдоль стенок может быть нейтрализовано только силами вязкого трения. Это диктует необходимость движения жидкости вдоль стенок от большего давления к меньшему. В окрестности внутреннего угла центробежная сила направлена в сторону угла, где возникает повышение давления (рис. 9 (a)). В окрестности внешнего угла, наоборот, центробежная сила направлена в сторону от угла, что вызывает разряжение в угловой точке (рис. 9 (б)). Соответственно, во внутренних углах жидкость растекается вдоль стенок в сторону от угла, что компенсируется подтеканием жидкости вдоль биссектрисы. А в окрестности внешних углов жидкость подтекает вдоль стенок к углу и вытекает наружу в направлении биссектрисы.
3. СВЯЗЬ ДАВЛЕНИЯ НА СТЕНКЕ С КРИВИЗНОЙ ГРАНИЦЫ
Предсказание вторичных течений на основе анализа правых частей уравнений (1.1) затруднительно. В большинсте случаев распределения напряжений Рейнольдса по сечению трубы трудно оценить заранее, не прибегая к численному или лабораторному эксперименту. Единственное надежное априорное знание относится к их поведению вблизи твердой гладкой стенки, где в силу условий прилипания все компоненты тензора напряжений Рейнольдса, а также их градиенты равны нулю. Поэтому, если вдоль периметра поперечного сечения трубы действует градиент давления, то неминуемо должно возникнуть вторичное течение с направлением движения жидкости вдоль стенки от большего давления к меньшему, компенсирующее силу давления силой вязкого трения. Вопрос о связи среднего давления на стенке с кривизной границы подробно проанализирован в [75]. Приведем здесь основные элементы этого анализа.
Влияние кривизны границы на пристенное давление можно оценить из следующих простых рассуждений. Рассмотрим три типичных варианта формы границы: вогнутую, плоскую и выпуклую (рис. 10(а)–(в)). Зафиксируем некоторую точку на границе и введем систему координат (y, z) с осями, направленными по нормали и по касательной к границе в выбранной точке. Уравнение Рейнольдса в направлении $y$ при пренебрежении вторичным течением дает связь градиента среднего давления и напряжений Рейнольдса:
(3.1)
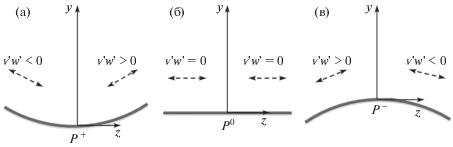
$ - \frac{{\partial P}}{{\partial y}} = \frac{{\partial \langle {{{v}}^{{'2}}}\rangle }}{{\partial y}} + \frac{{\partial \left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle }}{{\partial z}}$Вблизи твердой стенки первое слагаемое в правой части (3.1) всегда положительно и стремится увеличить среднее давление на стенке. Знак второго слагаемого определяется знаком кривизны границы. Доминирующее направление пульсаций в пристенной области параллельно направлению касательной к ближайшей точке границы, поэтому в случае вогнутой стенки (рис. 10(а)) сдвиговое напряжение Рейнольдса $\left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle < 0$ при z < 0 и $\left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle > 0$ при z > 0. Таким образом, второе слагаемое в правой части (3.1) тоже положительно, что обеспечивает дополнительное (по сравнению с эффектом первого слагаемого) увеличение давления на границе. Этот факт отражен обозначением ${{P}^{ + }}$ на рис. 10(а). Аналогичные рассуждения для окрестности выпуклой границы (рис. 10(в)) приводят к выводу, что $\partial \left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle {\text{/}}\partial z < 0$ в этом случае, т.е. эффект сдвиговых напряжений Рейнольдса на пристенное давление отрицателен. Наконец, на плоском участке границы можно считать, что $\left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle \approx 0$ с обеих сторон от линии z = 0, так что вклад второго члена в правой части (3.1) несущественен.
Рис. 10.
Доминирующие направления пульсаций скорости и значения произведений ${v}{\text{'}}w{\text{'}}$ в пристенной области трех типов границы: вогнутой, плоской и выпуклой, (а), (б) и (в). Обозначения ${{P}^{ + }}$, ${{P}^{ - }}$ и ${{P}^{0}}$ отражают положительный, отрицательный и нейтральный эффект второго слагаемого в правой части (3.1) на давление на стенке.
Изложенным качественным оценкам можно придать более формальное звучание. Для этого в [75] вводится определение траектории пульсаций, как линии в поперечном сечении, направление касательной к которой в каждой точке совпадает с главным направлением тензора напряжений Рейнольдса, отвечающим большему главному напряжению. Если ${v}_{\tau }^{'}$ и ${v}_{n}^{'}$ – тангенциальная и нормальная компоненты пульсаций скорости на траектории, то $\langle {v}_{\tau }^{{'2}}\rangle > \langle {v}_{n}^{{'2}}\rangle $ и $\langle {v}_{\tau }^{'}{v}_{{}}^{'}\rangle = 0$. Доказано, что в каждой точке траектории
(3.2)
$ - \frac{{\partial P}}{{\partial n}} = \frac{{\partial \langle {v}_{n}^{{'2}}\rangle }}{{\partial n}} + \frac{{\langle {v}_{\tau }^{{'2}}\rangle - \langle {v}_{n}^{{'2}}\rangle }}{R}$Здесь n – главная нормаль, а $R$ – радиус кривизны траектории. Первое слагаемое в правой части (3.2) указывает, что изменение давления вдоль нормали обратно изменению нормального напряжения в этом направлении и не зависит от кривизны траектории пульсаций. Второе слагаемое всегда положительно, откуда получается вывод: пульсационное движение вдоль искривленной траектории увеличивает давление в направлении выпуклости траектории. Это увеличение пропорционально кривизне траектории.
Искривление траекторий пульсаций возникает вблизи искривленных стенок, где $\langle {v}_{\tau }^{{'2}}\rangle \sim {{d}^{2}}$, $\langle {v}_{n}^{{'2}}\rangle \sim {{d}^{4}}$, d – расстояние до стенки. При $d \to 0$ $\langle {v}_{\tau }^{{'2}}\rangle \gg \langle {v}_{n}^{{'2}}\rangle $ и можно считать, что кривизна траектории пульсаций близка к кривизне стенки. Разумно предполагать, что кривизна траекторий пульсаций сохраняет свой знак и на некотором удалении от стенки, так что действие второго слагаемого в правой части (3.2) приводит к конечному изменению давления на стенке. Таким образом, при изменении кривизны стенки на соседних участках периметра сечения трубы можно ожидать пропорциональное изменение давления: на вогнутых стенках давление увеличивается с увеличением кривизны стенки, а на выпуклых – уменьшается. Как уже было отмечено выше, напряжения Рейнольдса не могут уравновешивать действие силы давления вдоль стенки, поэтому должно возникать вторичное течение. В соответствии со сказанным, вдоль вогнутых стенок движение во вторичном течении направлено от большей кривизны в сторону меньшей кривизны, а вдоль выпуклых стенок – наоборот.
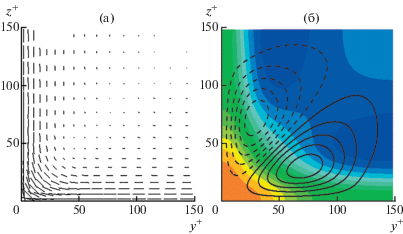
Очевидно, что искривление траекторий пульсаций возникает также в угловых областях. Семейство траекторий пульсаций в трубе квадратного сечения при ${\text{R}}{{{\text{e}}}_{\tau }} = 150$ [28] представлено на рис. 11(а). Радиус кривизны траекторий пульсаций равен нулю непосредственно в угловой точке и увеличивается с удалением от нее. Заметное искривление траекторий наблюдается в области ${{y}^{ + }},{{z}^{ + }} < 50$. Здесь же имеется значительная анизотропия нормальных напряжений, вносящая вклад во второе слагаемоев правой части (3.2). На рис. 11(б) изображены поле давления и линии тока вторичного течения. Именно в области искривления траекторий пульсаций наблюдается дополнительное повышение давления на стенке по сравнению с более удаленными от угла участками границы. За пределами этой области траектории пульсаций параллельны стенкам, и единственным вкладом в увеличение давления на стенке является первое слагаемое в правой части (3.2). Во внутренних углах оба слагаемых правой части (3.2) положительны и их действие складывается. В окрестности внешних углов траектории пульсаций направлены выпуклостями в сторону от угла, так что второе слагаемое в правой части (6) стремится уменьшить давление в углу. Это приводит к разряжению (относительно окружающих участков периметра) в угловой области и вторичному течению, направленному вдоль стенок к углу и вдоль биссектрисы от угла наружу.
Рис. 11.
Направления касательных к траекториям пульсаций в квадратной трубе (а) и поле среднего давления и линии тока вторичного течения (б); ${\text{R}}{{{\text{e}}}_{\tau }} = 150$. Длина векторов на панели (а) пропорциональна степени анизотропии нормальных напряжений $(\langle {v}_{\tau }^{{'2}}\rangle - \langle {v}_{n}^{{'2}}\rangle ){\text{/}}(\langle {v}_{\tau }^{{'2}}\rangle + \langle {v}_{n}^{{'2}}\rangle )$. Показана четверть сечения трубы.
4. ПРЕДСКАЗАНИЕ И ОБЪЯСНЕНИЕ ФОРМЫ ВТОРИЧНЫХ ТЕЧЕНИЙ В НЕКРУГЛЫХ ТРУБАХ
Аргументы и оценки предыдущего раздела о связи кривизны границы поперечного сечения трубы с величиной среднего давления и направлением возникающего вторичного течения можно сформулировать в виде следующего принципа. Вторичное течение вдоль стенок трубы направлено от точек локального максимума давления к точкам локального минимума. Следствием этого является подтекание жидкости к стенкам из внешнего потока к точкам локальных максимумов давления, и наоборот, возвращение жидкости от стенок во внешний поток в точках локального минимума давления. Линии тока в окрестности каждого экстремума имеют вид, изображенный на рис. 12. В точках локальных экстремумов кривизны границы достигаются экстремумы давления того же типа на вогнутых стенках и противоположного типа на выпуклых стенках.
Рис. 12.
Форма линий тока вторичного течения в окрестности точек локального минимума ${{P}^{ - }}$ и локального максимума ${{P}^{ + }}$ среднего давления на стенке.

Изложенный принцип можно использовать для примерной оценки и предсказания формы вторичных течений, возникающих в том или ином конкретном варианте поперечного сечения трубы. Для этого следует попытаться определить точки локальных экстремумов давления на границе поперечного сечения трубы, исходя из анализа кривизны границы, условий симметрии или иных соображений. Два экстремума одного типа не могут находиться рядом на участке границы и обязательно должны быть разделены хотя бы одним экстремумом противоположного типа.
Попробуем применить изложенный рецепт к некоторым конкретным случаям. На рис. 13 и рис. 14 приведены распределения давления и линии тока вторичных течений в трубах с сечением в виде кругового сектора с углом при вершине в 90° и 270°, полученные в DNS расчетах при ${\text{Re}} = {{U}_{b}}{{D}_{h}}{\text{/}}\nu \approx 2800$ [76]. Здесь Ub – средняя скорость, ${{D}_{h}}$ – гидравлический диаметр.
Рис. 13.
Распределение среднего давления (а) и линии тока вторичного течения (б) в трубе с сечением в виде кругового сектора с углом при вершине в 90° [76].
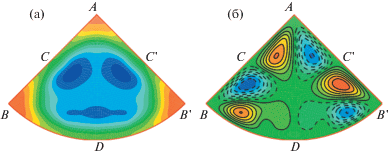
Рис. 14.
Распределение среднего давления (а) и линии тока вторичного течения (б) в трубе с сечением в виде кругового сектора с углом при вершине в 270° [76].
Априорный анализ сечения трубы с углом при вершине в 90° (рис. 13) позволяет сделать следующие выводы. В трех внутренних углах A, $B$, $B{\text{'}}$ давление по описанным выше причинам больше, чем на окружающих участках периметра. На прямолинейных участках $AB$ и $AB{\text{'}}$ должны иметься точки локального минимума давления, обозначим их $C$ и $C{\text{'}}$. На этих участках отсутствует изменение кривизны границы или иные обстоятельства, указывающие на наличие других экстремумов. Посередине дуги $BB{\text{'}}$ в точке $D$ в силу симметрии должен располагаться экстремум. Поскольку эта точка находится между двумя локальными максимумами, то это, вероятно, локальный минимум. Остается соединить точки экстремумов давления в соответствии с правилом, показанным на рис. 12 без взаимных пересечений линий внутри трубы, чтобы получить примерную картину линий тока вторичного течения. В данном случае предполагаемое вторичное течение качественно эквивалентно течению в трубе треугольного сечения [2], показанного на рис. 2. Жидкость из центральной области трубы двигается к точкам локальных максимумов давления, расположенным в вершинах трех углов $B$, $B{\text{'}}$ и $A$. Из углов жидкость растекается вдоль стенок в сторону точек $C$, $C{\text{'}}$ и $D$. От этих точек жидкость уходит обратно в сторону центра трубы. Результаты DNS в целом подтверждают сделанный прогноз и в части распределения давления по периметру сечения (рис. 13(а)), и по форме линий тока вторичного течения (рис. 13(б)). Небольшие отклонения от предсказанной формы вторичных течений, имеющиеся в нижней части рис. 13(б), не могут быть получены на основании относительно грубого анализа.
Обратимся теперь к трубе с углом при вершине в 270°, рис. 14. В угловых точках предполагаем экстремумы давления – во внутренних углах $B$ и $B{\text{'}}$ имеем локальные максимумы, а во внешнем углу A – локальный минимум. Отметим, что поведение давления рассматривается в данном случае только вдоль периметра. Локальный минимум в точке A означает, что на окружающих участках границы давление больше, но не означает обязательное увеличение давления в окружающих точках внутри трубы. На середине $D$ дуги $BB{\text{'}}$ в силу симметрии должен находиться локальный экстремум. Тип этого экстремума в данном случае не очевиден. Поведение давления в этой точке в меньшей степени определяется удаленными углами $B$, $B{\text{'}}$, чем углом A. Выпуклости траекторий в окрестности точки $A$ направлены в сторону точки $D$, что может проявиться в некотором увеличении давления в окрестности этой точки по сравнению с окружающими участками дуги $BB{\text{'}}$. Таким образом, можно предполагать локальный максимум давления в точке $D$, а значит, появления локальных минимумов в некоторых промежуточных точках $C$, $C{\text{'}}$ на дугах $BD$ и $B{\text{'}}D$. В таком случае вторичное течение вдоль границы имеет направление от углов $B$, $B{\text{'}}$ к углу $A$ и к точкам $C$, $C{\text{'}}$, а также от точки $D$ к точкам $C$, $C{\text{'}}$. От точек локального минимума $C$, $C{\text{'}}$ и $A$ жидкость движется внутрь трубы, а затем в направлении точек $B$, $B{\text{'}}$ и $D$ соответственно.
Описанная картина распределения давления по периметру и вытекающая из него топология вторичного течения подтверждаются результатами численного расчета, представленными на рис. 14. Отметим, что она была получена на основании лишь одного предположения, что давление в точке $D$ имеет локальный максимум. Альтернативное предположение о локальном минимуме давления в этой точке дает другую картину. В этом случае вторичное течение вдоль дуг $BD$ и $B{\text{'}}D$ направлено в сторону точки $D$, а от нее – внутрь трубы, где оно встречается со вторичным потоком из точки A, после чего оба потока растекаются в сторону углов $B$, $B{\text{'}}$. Хотя такая картина в данном случае не подтверждается результатами DNS, она может реализовываться при других значениях числа Рейнольдса или величины угла при вершине A.
На рис. 14(а) обращает на себя внимание характерное распределение давления вдоль радиуса $AD$ с минимумом не в точке A, а в некоторой промежуточной точке. Объяснение этому факту состоит в том, что нормальные пульсации скорости в окрестности особой точки A имеют весьма значительную величину, так что отрицательное первое слагаемое в правой части (3.2) перевешивает положительное значение второго слагаемого, связанного с эффектом кривизны траекторий пульсаций. Отметим, что главная нормаль вдоль радиуса $AD$, ориентированная в сторону вогнутости траекторий пульсаций, направлена в данном случае в сторону угловой точки от центральной области трубы, а не наоборот, как это имеет место во внутренних углах.
Рассмотрим еще несколько случаев, известных из литературы.
i) Эллиптическая труба [9, 45, 46], рис. 15(а). Максимальная кривизна стенки достигается на концах большего диаметра, поэтому там возникает относительное повышение давления ${{P}^{ + }}$. Наоборот, минимальная кривизна стенки и пониженное давление ${{P}^{ - }}$ отвечают концам меньшего диаметра. Таким образом, на каждой четверти периметра движение жидкости вдоль стенки направлено от точки максимального давления к точке минимального, т.е. от концов большего диаметра к концам малого. Жидкость собирается к центру эллипса вдоль малых полуосей и растекается обратно к стенкам вдоль больших полуосей.
Рис. 15.
Схематическая картина вторичных течений в трубе эллиптического сечения [9, 45, 46] (а), прямоугольной трубе с закругленными углами [41] (б) и трубе с полукруглой стенкой [41, 43] (в). Штриховые линии тока соответствуют вращению по часовой стрелке, сплошные – против часовой стрелки. Дополнительно направление вращения жидкости во вторичных течениях отмечено стрелками. Области повышенного давления на стенке обозначены ${{P}^{ + }}$, а пониженного – ${{P}^{ - }}$.
ii) Прямоугольная труба с закругленными углами [41], рис. 15(б). В угловых областях, где кривизна границы максимальна, возникает повышение давления ${{P}^{ + }}$. До тех пор, пока радиус закругления углов меньше полуширины канала, на нижней стенке имеется прямолинейный участок с пониженным давлением ${{P}^{ - }}$. Так что картина вторичного течения качественно совпадает со случаем незакругленных углов: жидкость из основного потока двигается к точкам повышенного давления в угловой части трубы, откуда растекается вдоль стенок в обе стороны к зонам пониженного давления.
iii) Труба с полукруглой стенкой [41, 43], рис. 15(в). При исчезновении плоского участка на нижней стенке пропадает и область пониженного давления. Соответственно, пропадает участок вторичного течения вдоль стенки в сторону вертикальной линии симметрии и вместо четырехвихревой картины вторичного течения возникает двухвихревая.
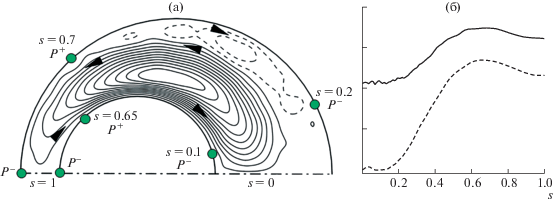
iv) Кольцевая эксцентрическая труба [50, 51], рис. 16. Прогноз формы вторичного течения в эксцентрической кольцевой трубе не столь очевиден. Относительно распределения давления по стенкам трубы априори с большой долей уверенности можно утверждать лишь, что на вогнутой поверхности внешнего цилиндра давление больше, чем в ближайшей точке на выпуклой поверхности внутреннего цилиндра. Распределения давления вдоль периметра внутреннего и внешнего цилиндра, полученные в DNS расчете [51], изображены на рис. 16(б). Положение локальных максимумов давления на каждой границе отмечено на рис. 16(а). Направление движения жидкости вдоль стенок согласуется с распределением давления. Отметим, что диапазон изменения давления вдоль стенки внутреннего цилиндра вдвое превышает аналогичное изменение вдоль внешнего цилиндра. Учитывая, что и длина внутреннего периметра вдвое меньше наружного, характерный градиент давления вдоль внутренней стенки вчетверо больше, чем вдоль внешней. Это отражается заметно большей интенсивностью вторичного течения вдоль поверхности внутренней границы на отрезке $0.1 < s < 0.65$, где жидкость двигается от узкого зазора к широкому. В том же направлении происходит слабое движение и вдоль внешнего цилиндра. В самой широкой части зазора $s < 0.2$ изменение давления вдоль внешней границы останавливается, исчезает и вторичное течение. В узкой части зазора $s > 0.7$ давление падает с ростом s на обеих границах. В этой части трубы жидкость вдоль стенок должна двигаться в сторону узкого зазора. На внешнем цилиндре это отчетливо видно на рис. 16(а), на внутреннем это проявляется в виде отрыва ближайшей к стенке линии тока от поверхности цилиндра. Вероятно, ближе к стенке в этом месте имеется не отмеченное на рисунке слабое движение с обратным направлением.
Рис. 16.
Течение в кольцевой эксцентрической трубе [51]. Показана верхняя половина поперечного сечения. Линии тока вторичного течения (а) и распределения среднего давления по периметру внутреннего (прерывистая линия) и внешнего (сплошная линия) цилиндра (б). Стрелки указывают направление движения во вторичном течении. Координата s = 0 соответствует широкой части зазора, s = 1 – узкому. Точки на стенках цилиндров – положение локальных экстремумов среднего давления ${{P}^{ + }}$ и ${{P}^{ - }}$.
5. ТЕЧЕНИЕ В КАНАЛАХ СО СВОБОДНЫМИ ГРАНИЦАМИ
Описанный в предыдущих разделах механизм формирования вторичных течений основан на предположении об отсутствии сил напряжений Рейнольдса на твердых границах трубы. В этих условиях изменение давления вдоль границы должно непременно сопровождаться движением жидкости от большего давления к меньшему. Условия образования вторичных течений в каналах со свободной границей отличаются от случая канала с твердыми стенками тем, что на свободной поверхности имеются тангенциальные пульсации скорости, отсутствующие на твердой стенке. Таким образом, направление движения определяется конкуренцией сил давления и сил напряжений Рейнольдса. Анализ условий образования вторичных течений в угловых областях, образованных твердой и свободной стенками, проведен в [75].
Рассмотрено течение в прямоугольном канале, три стенки которого являются твердыми, а одна (верхняя) – плоской, но свободной от касательных напряжений. В силу причин, изложенных выше, в каждом из четырех углов поперечного сечения должны возникать зона повышенного давления и градиент давления, вытесняющий жидкость вдоль стенок канала. Вблизи твердых стенок, где отсутствуют напряжения Рейнольдса, которые могли бы противодействовать силе давления, обязательно возникает движение жидкости в сторону от угла. Однако на свободной поверхности направление движения, вообще говоря, может быть разным и определяется конкуренцией градиентов давления и напряжений Рейнольдса. Если в результате этой конкуренции побеждает сила давления, то возникнет вторичное течение, аналогичное течению в углу с твердыми стенками – жидкость растекается вдоль стенок в обе стороны от угла. В случае, если сила давления уступает, то жидкость во вторичном течении будет двигаться вдоль свободной поверхности в сторону угла и уноситься вниз вдоль твердой стенки, т.е. в верхнем углу возникает одновихревая картина вторичного течения. В любом из двух возможных сценариев, в окрестности верхних углов жидкость должна двигаться вниз вдоль твердой боковой стенки, что противоречит картине вторичного течения, согласно которой жидкость подтекает к верхнему углу вдоль боковой стенки и уносится к центру канала вдоль свободной границы (рис. 8) [60].
Для изучения деталей вторичного течения в области сопряжения свободной поверхности с твердой стенкой в [75] проведены прямые расчеты турбулентного течения в прямоугольном канале с сечением 4:1 со свободной границей. Линии тока вторичного течения вместе с полем среднего давления в поперечном сечении канала представлены на рис. 17(а). Изображена левая из двух симметричных половин канала. Как и предсказывалось, в каждом из углов поперечного сечения, включая верхний, имеется зона повышенного давления. На свободной поверхности вблизи стенки действие напряжений Рейнольдса направлено в сторону стенки и превосходит действие градиента давления, благодаря чему жидкость на этом участке двигается в сторону угла. Здесь образуется единичный верхний угловой вихрь, т.е. из двух перечисленных сценариев реализуется второй, согласующийся с результатами [66, 67] о формировании в этой области “внутреннего вихря”. В остальном картина вторичного течения согласуется с традиционным представлением: большая часть сечения канала оккупирована двумя мощными вихрями, рождающимися в нижнем углу и проникающими внутрь потока на большое расстояние. Интенсивность вторичного течения оказывается существенно больше, чем в прямоугольной трубе с твердыми стенками. Вблизи твердых стенок она достигает 2.5%, а на свободной поверхности доходит до 5% от Ub. Столь большая скорость вторичного течения объясняется тем, что за пределами пристенной области и градиент давления, и сила напряжений Рейнольдса на свободной поверхности действуют в одном направлении – в сторону от угла. В отсутствие трения на стенке здесь и возникает интенсивное вторичное движение, которое передается и в другие части канала.
Рис. 17.
Поле давления и линии тока вторичного течения в поперечном сечении канала со свободной верхней границей (а); изолинии средней продольной скорости $U{\text{/}}{{U}_{b}}$ (б).
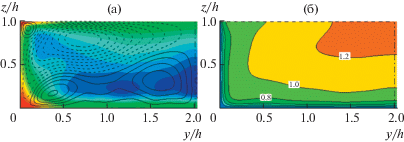
Изолинии средней продольной скорости U, изображенные на рис. 17(б), имеют характерные особенности, отражающие воздействие вторичных течений. В нижнем и верхнем углах – это характерные выпуклости в сторону углов. Главная особенность, свойственная течению в открытых каналах, – повышение скорости под свободной поверхностью в центральной части канала. Объяснение этому эффекту – поверхностный перенос жидкости с низким импульсом из прибрежных зон в сторону центра канала, осуществляемый вторичным течением.
Исследование течения в канале со свободной границей [75] выявило несколько интересных свойств вторичных течений. В частности, исходя из сформулированного принципа формирования вторичных течений, была предсказана возможность возникновения вторичного течения в виде одиночного вихря в области сопряжения твердой стенки и свободной поверхности в плоскости поперечного сечения [66, 67]. Факт возникновения вторичного вихря в этом месте обусловлен наличием стенки с прилипанием, а возникновение лишь одного вихря, а не двух – отличительная особенность взаимодействия твердой стенки и свободной границы. Выглядит интересным вопрос о возможности и особенностях возникновения вторичных течений в углах сопряжения двух свободных границ, где твердая стенка, как важный элемент механизма возникновения вторичного течения, отсутствует. Канал с двумя свободными стенками трудно реализуем в эксперименте, однако не сложен для численного моделирования. В [75] проведены прямые расчеты турбулентных течений в канале квадратного сечения, две смежные стенки которого являются твердыми, а другие две – плоскими и свободными. Влиянием нормальных пульсаций на свободных границах пренебрегается. В расчетах при нескольких числах Рейнольдса от ${\text{Re}} = 2000$ до ${\text{Re}} = 16{\kern 1pt} {\kern 1pt} 000$ обнаружено, что в угловой области вблизи сопряжения двух свободных границ силы напряжений Рейнольдса оказываются потенциальными с точностью до погрешностей вычислений. Таким образом, эти силы нейтрализуются градиентом давления и не производят вторичного течения. Вторичное течение сохраняется здесь лишь благодаря конвекции из удаленных областей.
6. ВТОРИЧНЫЕ ТЕЧЕНИЯ ВБЛИЗИ ШЕРОХОВАТЫХ ПОВЕРХНОСТЕЙ
Вторичные течения второго рода могут вызываться неоднородностью шероховатости обтекаемой поверхности в поперечном к потоку направлении (направлении размаха). Образование вторичных течений в таких условиях имеет большое значение, так как турбулентные потоки в большинстве инженерных приложений и природных экосистем происходят именно вдоль шероховатых поверхностей, в то время как гладкие поверхности скорее являются редкостью. Это явление особенно актуально в условиях пространственно неоднородного образования шероховатости, известным примером которого являются потоки вдоль лопаток турбомашин [77]. Экспериментальное исследование турбулентного потока над поврежденной лопаткой турбины с неравномерной шероховатостью поверхности в [78, 79] отчетливо показало образование вторичных течений. Другое важное проявление вторичных течений этого типа наблюдается в речных потоках, где перенос донных отложений в направлении размаха может создавать и поддерживать изменения донной поверхности в русле реки [80].
Впервые образование вторичных течений над неоднородно шероховатой стенкой показано в [14, 15]. Направленные вдоль потока полосы шероховатости в трубе прямоугольного сечения приводят к образованию восходящего потока над гладким участком стенки и нисходящих потоков над шероховатыми областями (рис. 18). Для объяснения этого явления в [14] предлагается сравнение локального производства турбулентной кинетической энергии с вязкой диссипацией: дисбаланс между этими величинами определяет топологию и направление движения во вторичном течении. Делается вывод, что жидкость из менее турбулентных областей переносится в области, где производство турбулентной кинетической энергии превышает вязкую диссипацию и наоборот. Исходя из этого, во многих последующих работах направление и топология вторичного течения связываются с распределением турбулентной кинетической энергии или величиной трения на стенке, которые используются для локализации областей с большей/меньшей турбулентной активностью.
Рис. 18.
Искривление изолиний средней скорости в прямоугольной трубе с неоднородно шероховатой стенкой [15].
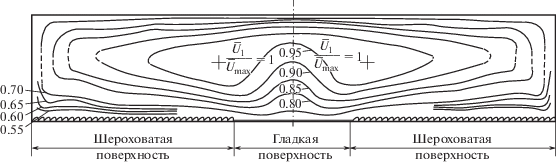
Рис. 19.
Вторичное течение над шероховатостью ленточного типа (слева) и выступного типа (справа) [80].
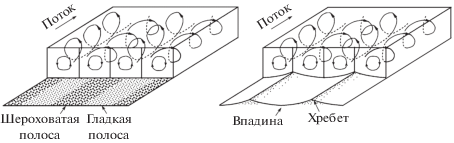
Как отмечено в [81], термин “шероховатость” иногда используется разными исследовательскими группами в разных значениях. Под понятием “шероховатость” одновременно понимаются два разных типа структурирования стенки: мелкомасштабные (около 10% толщины пограничного слоя) однородные в направлении потока гладкие структуры, создаваемые исключительно поперечным изменением высоты стенки (например, продольные ребра различной формы на гладкой стенке), и нерегулярные шероховатые поверхности с разнонаправленным изменением высоты поверхности (например, полосы шероховатости). Решающим различием между этими двумя видами поверхностей является отсутствие сопротивления давления для первого типа поверхностей (иногда называемых “продольной шероховатостью”) из-за их однородности в направлении потока. Все поверхностные напряжения в такой конфигурации возникают под действием вязких сил. Для второго типа поверхностей, нерегулярных шероховатостей, напротив, сопротивление давления является доминирующим. Это различие является существенным и для механизма образования вторичных течений. Образование вторичных течений при наличии продольно однородной структурированной поверхности может быть объяснено описанными выше механизмами для внутренних и внешних углов в трубах. В случаях шероховатых поверхностей с неоднородностью вдоль потока следует учитывать дополнительные эффекты, связанные с сопротивлением давления. Несмотря на большое разнообразие возможных конфигураций поперечной неоднородности стенок, в последние десятилетия были хорошо изучены две основные конфигурации: шероховатые участки стенок, возникшие в результате изменения сдвигового напряжения на стенке, и поперечное изменение локальной возвышенности стенки. В [80] предложено разделение на два типа шероховатости: при преобладании эффекта изменения сдигового напряжения шероховатость именуется как “шероховатость ленточного типа” (strip-type roughness), а при преобладании эффекта возвышении стенки, как “шероховатость выступного типа” (ridge-type roughness). Экспериментально исследовано формирование вторичного движения в открытом канале путем размещения шероховатых поверхностей обоих типов. Показано, что шероховатости генерируют крупномасштабные вторичные течения при условии, когда величина поперечного интервала неоднородности сопоставима с толщиной пограничного слоя (рис. 19). При этом наблюдается восходящее и нисходящее течение над шероховатостью ленточного типа, возникающее над гладкой и шероховатой поверхностью, в то время как для шероховатости выступного типа восходящее и нисходящее движение наблюдалось над приподнятой и утопленной поверхностью стенки соответственно.
Для шероховатости ленточного типа характерно попеременное изменение сдвигового напряжения на стенке в направлении размаха, при этом изменение высоты стенки отсутствует или пренебрежимо мало. В [82] и [83] проведены численные исследования шероховатости ленточного типа (DNS, LES) в канале с полосами “малой” и “большой” шероховатости, которые реализованы с помощью изменения граничных условий на стенке, обеспечивающего меньшее или большее локальное трение. Обе группы сообщают о вторичном течении, аналогичном наблюдавшемся в [14, 15], т.е. восходящем над областью с меньшим трением и с нисходящем над областью с большим трением. Полученная структура вторичных вихрей согласуется с экспериментальными наблюдениями течения над поврежденными лопатками турбин [78, 79]. В этих работах обнаружены полосы с низкой и высокой скоростью течения, что может быть связано с наличием крупномасштабных вторичных течений [68, 84]. В [82] показано, что расположение областей противоположного направления движения во вторичном течении (подъем или спуск) может меняться в зависимости от ширины полосы шероховатости. В [79] и [85] численно изучена похожая конфигурация в плоском канале с чередующимися продольными полосами с условиями проскальзывания и прилипания на стенках. Обнаружена смена топологии и направления вторичного течения при изменении ширины области с проскальзыванием.
В [86] экспериментально изучены вторичные течения над неоднородными поверхностями, изготовленными из чередующихся по размаху полос картона и наждачной бумаги. Полученные результаты можно резюмировать следующим образом: при ширине полос меньше толщины пограничного слоя размер вторичных вихрей ограничивается этой шириной (в том числе и по направлению от стенки). Если ширина полосы имеет порядок толщины пограничного слоя, то вторичное движение заполняет весь пограничный слой и демонстрирует максимальную интенсивность. Для полос шире, чем толщина пограничного слоя, вторичное движение остается локализованным на краю между шероховатой и гладкой полосой и сохраняет размер, сопоставимый с толщиной пограничного слоя.
Шероховатость выступного типа также подробно изучалась различными исследовательскими группами. В целом наблюдается, что длина интервала между приподнятыми элементами влияет на топологию и интенсивность вторичных течений, аналогично шероховатости ленточного типа. Несмотря на незначительную интенсивность, вторичные течения над шероховатостью выступного типа заметно меняют свойства основного потока, что приводит, в частности, к значительному увеличению трения и теплообмена [87]. В [88] представлено численное исследование вторичного течения над треугольными продольными ребрами. Образование вторичного течения связывается с локальным перенаправлением турбулентных пульсаций в направлении размаха вблизи верхнего угла ребра в сторону от стенки, т.е. с появлением ненулевой корреляции $\left\langle {v{\text{'}}w{\text{'}}} \right\rangle $. В [89, 70 ] экспериментально и численно изучалось турбулентное течение над рядами блоков детского конструктора Lego. Несмотря на почти десятикратную разницу в ${\text{R}}{{{\text{e}}}_{\tau }}$, в расчете и эксперименте были получены схожие результаты: вторичное течение состоит из мгновенных крупномасштабных вихрей с преимущественно положительной и отрицательной завихренностью справа и слева от возвышающегося элемента соответственно. Аналогичные эксперимены были проведены для различной геометрии ребер в [90, 91]. Обе исследовательские группы наблюдали восходящее движение над выступающими поверхностями. В [92] представлены результаты численного исследования развивающегося турбулентного пограничного слоя над продольными прямоугольными ребрами. Специфическое направление вторичных течений объясняется сильным локальным дисбалансом турбулентной кинетической энергии, обусловленным высоким турбулентным переносом, происходящим над шероховатостями выступного типа, что не было замечено в шероховатостях ленточного типа. Направление вращения во вторичных течениях связывается с активным переносом турбулентной кинетической энергии в область над ребром (отсутствующим в случаях шероховатостей ленточного типа), что вызывается отклонением вверх поперечных турбулентных пульсаций на боковых стенках элементов шероховатости. В [87] показано, что геометрия и высота ребра могут существенно влиять на интенсивность генерируемого вторичного движения: остроугольные треугольные ребра высотой в 16% полувысоты канала в этом случае приводят к интенсивности вторичного потока в 6% от средней скорости, что значительно превышает обычно наблюдаемую интенсивность вторичного течения в углах труб или при шероховатости полосового типа.
Разделение неоднородной шероховатости стенки на два типа (шероховатости ленточного или выступного типа) облегчает физическое понимание явления, изолируя эффекты изменения сдвигового напряжения на стенке от эффектов, связанных с возвышением стенки. Следует отметить, однако, что четкое разделение между этими двумя категориями невозможно для реалистичной шероховатости, поскольку наличие шероховатости всегда сопровождается изменением высоты поверхности. Так, например, в [93] численно изучено вторичное течение в турбулентном плоском канале над шероховатой поверхностью, состоящей из продольных рядов пирамид, при изменении расстояния между рядами. В работе обнаружен эффект смены направления движения во вторичном течении при увеличении интервала между рядами шероховатости сверх размера высоты канала. При меньших интервалах восходящее движение происходит над элементами шероховатости, что согласуется со вторичными течениями над шероховатостями выступного типа, а при больших расстояниях над элементами возникает нисходящее движение. Недавно в [94] было показано, что направление вращения вторичных течений над стенкой с полосой шероховатости зависит от относительной высоты среднего уровня полосы шероховатости (выступающей или утопленной шероховатости). В исследовании рассмотрены три различных уровня средней высоты полосы шероховатости, соответствующие выступающей (вызванной отложениями), утопленной (из-за эрозии или коррозии) и промежуточной высоты шероховатости. В зависимости от этого параметра направление вторичного течения соответствует либо ленточному, либо выступному типу шероховатости.
7. RANS-МОДЕЛИРОВАНИЕ ВТОРИЧНЫХ ТЕЧЕНИЙ
Большинство численных исследований вторичных течений Прандтля 2-го рода выполнено с использованием прямого численного моделирования (DNS) или крупно-вихревого моделирования (LES). Вторичные течения становятся видимыми в расчете только в результате осреднения поля скоростей на значительном временном отрезке. Такие исследования являются вычислительно дорогостоящими даже при низких числах Рейнольдса, поскольку для получения надежного осреднения при наличии лишь одного однородного пространственного направления, расчет потока должен проводиться в течение длительного периода времени. Применение более экономичных вычислительных подходов, основанных на решении уравнений Рейнольдса (RANS-моделирование) с использованием полуэмпирических моделей замыкания для прогнозирования вторичных течений, оказывается нетривиальным из-за отсутствия универсальных моделей. Кроме того, образование вторичных течений по своей сути является результатом анизотропии напряжений Рейнольдса, что не улавливается широко используемыми классическими моделями, основанными на предположении линейной турбулентной вязкости [95, 96]. Следовательно, для описания вторичных течений необходимы специализированные модели турбулентности с более высокой сложностью. Эта сложность, в свою очередь, ограничивает применение и принятие таких моделей для решения технических задач. Вычисления становятся более дорогостоящими, а повышенная численная жесткость из-за нелинейности снижает надежность моделей, что приводит к ухудшению сходимости [97].
Как видно из (1.1), (1.2), вторичное движение возникает при появлении разности градиентов нормальных напряжений Рейнольдса $\langle {{{v}}^{{'2}}}\rangle - \langle {{w}^{{'2}}}\rangle $ и градиентов поперечного сдвигового напряжения $\left\langle {{v}{\text{'}}w{\text{'}}} \right\rangle $ [7]. Следовательно, способность модели турбулентности предсказывать вторичное течение Прандтля второго рода напрямую связана с ее способностью улавливать анизотропию напряжений Рейнольдса. Во всех моделях замыкания, основанных на линейном соотношении Буссинеска, предполагается, что напряжения Рейнольдса определяются локальными средними скоростями деформации:
где ${{\nu }_{t}}$ – вихревая вязкость, k – кинетическая энергия турбулентности, Sij – тензор скоростей деформации среднего течения и ${{\delta }_{{ij}}}$ – тензор Кронекера [95]. При таком допущении (2.1), (2.2) не имеют ненулевых решений, так что правильное описание вторичного течения невозможно. Таким образом, наиболе популярные модели, такие как Spalart–Allmaras [98], $k - \varepsilon $ [99], $k - \omega $ [100] или $k - \omega $ SST [101], не могут описывать генерацию вторичного движения [102].Анизотропия тензора напряжений Рейнольдса может быть учтена с помощью соответствующей модификации приближения Буссинеска. Пример такой модификации представлен в [97], где стандартная ${{{v}}^{2}}$–$f$ модель [103], основанная на предположении линейной турбулентной вязкости, расширена с неизотропным вкладом в соотношение Буссинеска. Расширенная модель успешно апробирована на примере течений в трубах квадратного и треугольного сечения, для которых получено разумное согласие с известными данными по распределению турбулентных напряжений и топологии вторичного течения. Следует отметить, что предлагаемая модификация имеет специфический вид для конкретных наборов условий [96], что может значительно сократить диапазон ее применимости [95]. Модели турбулентности, разрешающие анизотропию, такие как модели переноса напряжений Рейнольдса (RSTM), введенные в [104], представляют собой более точный и принципиально более полный способ замыкания уравнений Рейнольдса [96]. В этих моделях решается система уравнений переноса отдельных компонент тензора напряжений Рейнольдса, дополненная уравнением для длины или временного масштаба турбулентности, что полностью исключает гипотезу турбулентной вязкости [95]. RST модели автоматически разрешают анизотропию напряжений Рейнольдса и способны описывать образование вторичного течения. Основная проблема RSTM заключается в замыкании члена деформации давления и диффузионного члена в уравнениях переноса напряжений Рейнольдса, к которым по-разному подходят в разных формулировках. Следует также отметить, что RST модели относятся к вычислительно более дорогим RANS моделям из-за более высокой сложности и большего набора уравнений, необходимых для решения: решение RSTM требует вдвое большего времени по сравнению с решением нелинейной $k - \varepsilon $ модели [95]. Впервые RST подход был применен при численном моделировании течения в квадратном канале [105], с разумным согласием профилей скорости и турбулентных характеристик с экспериментальными данными. В [106] для исследования развивающихся и развитых течений в замкнутых и открытых каналах использовалась RST модель Лаундера, Риса и Роди (так называемая LRR модель). В различных конфигурациях получено хорошее согласие вторичного течения с экспериментальными данными [1, 107] и предыдущими расчетами [105, 108]. В другой известной RST модели, так называемой SSG модели [109], использовалась расширенная квадратичная корреляционная модель давления-деформации (вместо линейной зависимости давления-деформации в LRR [110]). Показано, что SSG модель превосходит LRR модель [109] и проще в численной реализации [111]. SSG модель была испытана в [112] на примере течения в прямоугольном открытом канале. Показано, что SSG успешно предсказывает не только среднее течение, но и особенности пульсационных характеристик. Эта модель применялась для исследования свойств турбулентного течения в прямоугольном [111] и трапециевидном каналах [113], извилистых потоков в открытых каналах [114] и ограниченных по глубине потоках в прямоугольном открытом канале с донной растительностью [115].
С целью снижения вычислительных усилий при решении уравнений переноса отдельных компонент тензора напряжений Рейнольдса на основе RST подхода был разработан новый класс моделей турбулентности с упрощенными алгебраическими соотношениями для расчета напряжений Рейнольдса – так называемые алгебраические модели переноса напряжений (ASTM). Первая попытка использовать ASTM для расчета течений в некруглых трубах была предпринята в [108] на основе AST-формулировки, предложенной в [116]. Модель обеспечивает приемлемое представление вторичного течения, несмотря на то, что турбулентная анизотропия недооценивается на порядок [117, 118]. Кроме того, некоторые коэффициенты модели должны были быть настроены так, чтобы уменьшить интенсивность вторичного движения до более низких, и следовательно, более физических значений. Позже аналогичная реализация ASTM, предложенная в [119], применялась в [120, 121] в расчетах течений в прямоугольных и эллиптических каналах. Получены правильные тенденции деформации основного потока вторичным течением, несмотря на ошибки в деталях распределений средней скорости и трения на стенке. В [122] ASTM, предложенная в [108], была расширена дополнительным уравнением для турбулентной кинетической энергии с анизотропным подходом к определению турбулентной вязкости. Модель использована при расчете течений в квадратной трубе и открытых прямоугольных каналах различной формы. Получено хорошее согласие во всех особенностях среднего и вторичного течения, включая модификацию турбулентных характеристик вблизи свободной поверхности. В дальнейшей модификации модели [24] учтен вклад скорости вторичного течения при расчете напряжений Рейнольдса (которым пренебрегали [108] или который упрощали [121, 105 ] в предыдущих исследованиях). Проведены расчеты в квадратной трубе и в прямоугольном канале с частично шероховатыми стенками. Сопоставления с экспериментом [15] показали, что модель работает лучше, чем [108] и [122], но все же страдает от некоторой недооценки деформации первичного потока и интенсивности вторичного движения. Аналогичный ASTM класс моделей развился из RST анализа, основанного на нелинейной зависимости напряжение–деформация [123]. Этот класс моделей называют нелинейными (или анизотропными) моделями турбулентной вязкости [95]. Нелинейные реализации $k - \varepsilon $ и $k - l$ моделей, предложенные в [123], были применены для расчета течения в прямоугольных прямых каналах [124] и криволинейных каналах [125]. Показано, что в отличие от своих линейных аналогов, нелинейные модели способны более успешно предсказывать турбулентное вторичное течение и его воздействие на первичный поток.
В [126, 127] приводится сравнение нелинейной $k - \varepsilon $ модели с LRR моделью на основе RST [110] для различных геометрий в конфигурациях труб и открытых каналов. В целом обе модели способны достаточно точно предсказать формирование вторичного течения и его детальные особенности. Однако деформация профиля скорости за счет вторичного течения лучше улавливается RST подходом, в то время как влияние вторичного течения на трение на стенке более точно воспроизводится нелинейной $k - \varepsilon $ моделью. Сравнение результатов моделирования течения в трапециевидном канале между $k - \varepsilon $, $k - \omega $, SST, LRR и SSG моделями, представленных в [128], подчеркивает превосходство формулировки SSG. Линейные модели турбулентной вязкости, как и ожидалось, не воспроизводят вторичное течение. LRR модель показывает неполную топологию вторичного потока. SSG модель является единственной, демонстрирующей подробные и точные характеристики вторичного течения. Подводя итог, можно сказать, что RST модели обеспечивают наиболее полное и точное описание вторичного течения в рамках RANS моделирования. При этом SSG модель дает более точные результаты, чем LRR модель и демонстрирует производительность, сравнимую с вычислительно менее дорогими моделями, такими как ASTM и нелинейными моделями турбулентной вязкости.
8. ЗАКЛЮЧЕНИЕ
В данном обзоре представлены работы по изучению вторичных течений Прандтля 2-го рода, возникающих в турбулентных потоках под действием напряжений Рейнольдса. Образование вторичных течений в прямых трубах является одним из интересных проявлений турбулентности. Изучение условий их возникновения, особенностей проявления и влияния на основное течение является важным как в фундаментальном, так и в прикладном плане. Кроме обзора теоретических, экспериментальных и вычислительных работ в данной статье сформулирован принцип, позволяющий объяснять, а в некоторых случаях и предсказывать форму вторичных течений, возникающих в гладких трубах различного поперечного сечения. Теоретически предсказано и дано объяснение причины образования так называемых внутренних вихрей в углах сопряжения твердых стенок и свободной поверхности в открытых каналах. Впервые дан обзор исследований вторичных течений, вызванных неоднородностью шероховатости стенки, темы, особенно активно изучающейся в последние годы. Затронуты вопросы полуэмпирического моделирования турбулентных потоков при наличии вторичных течений.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-11-50031 с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ им. М.В. Ломоносова и с использованием вычислительных ресурсов ОВК НИЦ Курчатовский институт, http://computing.nrcki.ru/.
Acknowledgments: the reported study was funded by RFBR, project number 20-11-50031.
Список литературы
Nikuradse J. Untersuchung über die Geschwindigkeitsverteilung in turbulenten Strömungen // V.D.I. Forschungsheft. 1926. V. 70. P. 1229–1230.
Prandtl L. Über die ausgebildete Turbulenz // Verh. des II. Int. Kong. für Tech. Mech., 1926, P. 62–75.
Prandtl L. Turbulent flow // NACA TM-435. 1927.
Шлихтинг Г. Теория пограничного слоя.Москва: Наука, 1974.
Nikuradse J. Turbulente strömung in nicht-kreisförmigen rohren // Ing.-Arch. 1930. V. 1. P. 306–332.
Hoagland L.C. Fully developed turbulent flow in straight rectangular ducts – secondary flow, its cause and effect on the primary flow // PhD thesis, Department of Mechanical Engineering, Massachusetts Institute of Technology. 1960.
Prandtl L. Einführung in die Grundbegriffe der Strömungslehre // Akademische Verlagsgesellschaft, 1931.
Прандтль Л. Гидроаэромеханика. Ижевск: НИЦ РХД, 2000.
Nikitin N., Yakhot A. Direct numerical simulation of turbulent flow in elliptical ducts // J. Fluid Mech. 2005. V. 532. P. 141–164.
Bradshaw P. Turbulent secondary flows // Annu. Rev. Fluid Mech. V. 19. № 1. P. 53–74.
Корнилов В.И. Пространственные пристенные турбулентные течения в угловых конфигурациях. Новосибирск: Издательство СО РАН, 2013.
Kornilov V.I. Three-dimensional turbulent near-wall flows in streamwise corners: Current state and questions // Progress in Aerospace Sciences. 2017. V. 94. P. 46–81.
Prandtl L. Essentials of Fluid Dynamics. Hafner, 1952.
Hinze J. Secondary currents in wall turbulence // Phys. Fluids (Suppl). 1967. V. 10. P. S122–S125.
Hinze J.O. Experimental imvestigation of secondary currents in the turbulent flow through a straight conduit // Appl. Sci. Res. 1973. V. 28. P. 453–465.
Einstein H.A., Li H. Secondary currents in straight channels // Trans. Am. Geophys. Union. 1958. V. 39. № 6. P. 1085–1088.
Moissis R. Secondary flow in rectangular ducts // Master’s Thesis, Massachusetts Institute of Technology. 1957.
Maslen S.H. Transverse velocities in fully-developed flows // Quart. Appl. Math. 1958. V. 16. P. 173–175.
Brundrett E., Baines W.D. The production and diffusion of vorticity in duct flow // J. Fluid Mech. 1964. V. 19. № 3. P. 375–394.
Townsend A.A. Turbulence // In Handbook of Fluid Dynamics, ed. V. L. Streeter. McGraw-Hill, 1961.
Speziale C.G. On turbulent secondary flows in pipes of noncircular cross-section // Int. J. Engng Sci. 1982. V. 20. № 7. P. 863–872.
Perkins H.J. The formation of streamwise vorticity in turbulent flow // J. Fluid Mech. 1970. V. 44. P. 721–740.
Gessner F.B., Jones J.B. On some aspects of fully-developed turbulent flow in rectangular channels // J. Fluid Mech. 1965. V. 23. № 4. P. 689–713.
Demuren A.O., Rodi W. Calculation of turbulence-driven secondary motion in non-circular ducts // J. Fluid Mech. 1984. V. 140. P. 189–222.
Madabhushi R.K., Vanka S.P. Large eddy simulation of turbulence-driven secondary flow in a square duct // Phys. Fluids A. 1991. V. 3. P. 2734–2745.
Gavrilakis S. Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct // J. Fluid Mech. 1992. V. 244. P. 101–129.
Huser A., Biringen S. Direct numerical simulation of turbulent flow in a square duct // J. Fluid Mech. 1993. V. 257. P. 65–95.
Никитин Н.В., Пиманов В.О., Попеленская Н.В. К вопросу об образовании вторичных течений Прандтля 2-го рода // ДАН. 2019. Т. 484. № 4. С. 1–5.
Никитин Н.В. Численное моделирование турбулентных течений в трубе квадратного сечения // ДАН. 1997. Т. 353. № 3. С. 338–342.
Pinelli A., Uhlmann M., Sekimoto A., Kawahara G. Reynolds number dependence of mean flow structure in square duct turbulence // J. Fluid Mech. 2010. V. 644. P. 107–122.
Kim M., You D. Reynolds number effect on turbulent secondary flow in a duct // J. Mech. Sci. Technol. 2014. V. 28. P. 1311–1318.
Zhang H., Trias F.X., Gorobets A., Tan Y., Oliva A. Direct numerical simulation of a fully developed turbulent square duct flow up to ${\text{R}}{{{\text{e}}}_{\tau }} = 1200$ // Int. J. Heat Fluid Flow. 2015. V. 54. P. 258–267.
Pirozzoli S., Modesti D., Orlandi P., Grasso F. Turbulence and secondary motions in square duct flow // J. Fluid Mech. 2018. V. 840. P. 631–655.
Никитин Н.В., Попеленская Н.В. Основные характеристики турбулентных вторичных течений в прямых трубах // Ломоносовские чтения. Научная конференция. Секция механики. 17–26 апреля 2017 года. Тезисы докладов. М.: Издательство Московского университета, 2017.
Ohlsson J., Schlatter P., Fischer P.F., Henningson D. Direct numerical simulation of separated flow in a three-dimensional diffuser // J. Fluid Mech. 2010. V. 650. P. 307–318.
Choi H.S., Park T.S. The influence of streamwise vortices on turbulent heat transfer in rectangular ducts with various aspect ratios // Int. J. Heat Fluid Flow. 2013. V. 40. P. 1–14.
Vinuesa R., Noorani A., Lozano-Duran A., El Khoury G.K., Schlatter P., Fischer P.F., Nagib H.M. Aspect ratio effects in turbulent duct flows studied through direct numerical simulation // J. Turbul. 2014. V. 15. P. 677–706.
Vinuesa R., Schlatter P., Nagib H.M. On minimum aspect ratio for duct flow facilities and the role of side walls in generating secondary flows // J. Turbul. 2015. V. 16. P. 588–606.
Vinuesa R., Prus C., Schlatter P., Nagib H.M. Convergence of numerical simulations of turbulent wall-bounded flows and mean cross-flow structure of rectangular ducts // Meccanica. 2016. V. 51. P. 3025–3042.
Vinuesa R., Schlatter P., Nagib H.M. Secondary flow in turbulent ducts with increasing aspect ratio // Phys. Rev. Fluids. 2018. V. 3. P. 054606.
Vidal A., Vinuesa R., Schlatter P., Nagib H.M. Impact of corner geometry on the secondary flow in turbulent ducts // In Proceedings of the 10th International Symposium on Turbulence and Shear Flow Phenomena, TSFP-10, Chicago, USA. 2017.
Vidal A., Vinuesa R., Schlatter P., Nagib H.M. Influence of corner geometry on the secondary flow in turbulent square ducts // Int. J. Heat Fluid Flow. 2017. V. 67. P. 69–78.
Vidal A., Vinuesa R., Schlatter P., Nagib H.M. Turbulent rectangular ducts with minimum secondary flow // Int. J. Heat Fluid Flow. 2018. V. 72. P. 317–328.
Kim J., Kim D., Choi H. An immersed-boundary finite-volume method for simulations of flow in complex geometries // J. Comput. Phys. 2001. V. 171. P. 132–150.
Воронова Т.В., Никитин Н.В. Прямой расчет турбулентного течения в трубе эллиптического сечения // ЖВМ и МФ. 2006. Т. 46. № 8. С. 1477–1485.
Воронова Т.В., Никитин Н.В. Результаты прямого расчета турбулентного течения в трубе эллиптического сечения // Изв. РАН. МЖГ. 2007. № 2. С. 59–70.
Nikitin N. Finite-difference method for incompressible Navier–Stokes equations in arbitrary orthogonal curvilinear coordinates // J. Comput. Phys. 2006. V. 217. P. 759–781.
Kacker S.C. Some aspects of fully developed turbulent flow in non-circular ducts // J. Fluid Mech. 1973. V. 57. P. 583–602.
Nouri J.M., Umur H., Whitelaw J.H. Flow of Newtonian and non-Newtonian fluids in concentric and eccentric annuli // J. Fluid Mech. 1993. V. 253. P. 617–641.
Никитин Н.В. Прямой расчет турбулентных течений в эксцентрических трубах // ЖВМ и МФ. 2006. Т. 46. № 3. P. 509–525.
Nikitin N., Wang H., Chernyshenko S. Turbulent flow and heat transfer in eccentric annulus // J. Fluid Mech. 2009. V. 638. P. 95–116.
Kanaris N., Albets-Chico X., Kassinos S.C. Numerical simulations of turbulent flow in an eccentric annulus of unit eccentricity // In: 9th International Symposium on Turbulence and Shear Flow Phenomena, TSFP 2015. V. 3. TSFP-9. 2015.
Panchapakesan N.R., Joubert P.N. Turbulent boundary layer development along a streamwise edge (Chine) – mean flow // 13th Australasian Fluid Mechanics Conference, Monash. 1998. P. 373–376.
Panchapakesan N.R., Joubert P.N. Turbulence measurements in the boundary layer over a streamwise edge (Chine) // Turbulence and Shear flow Phenomena, Santa Barbara. 1999.
Moinuddin K.A.M., Joubert P.N., Chong M.S. Experimental investigation of turbulence-driven secondary motion over a streamwise external corner // J. Fluid Mech. 2004. V. 511. P. 1–23.
Xu H., Pollard A. Large eddy simulation of turbulent flow in a square annular duct // Phys. Fluids. 2001. V. 13. № 11. P. 3321–3337.
Xu H. Direct numerical simulation of turbulence in a square annular duct // J. Fluid Mech. 2009. V. 621. P. 23–57.
Никитин Н.В., Попеленская Н.В. Турбулентное течение вдоль внешнего угла // Ломоносовские чтения. Научная конференция. Секция механики. Октябрь 2020 года. Тезисы докладов. Москва : Издательство Московского университета, 2020.
Tominaga A., Nezu I., Ezaki K., Nakagawa H. Threedimensional turbulent structure in straight open-channel flows // J. Hydraul. Res. 1989. V. 27. P. 149–173.
Nezu I., Nakagawa H. Turbulence in Open-Channel Flows // Monograph of IAHR; Balkema: Rotterdam, The Netherlands. 1993.
Pan Y., Banerjee S. Numerical investigation of free-surface turbulence in open-channel flows // Phys. Fluids. 1995. V. 7. P. 1649–1664.
Albayrak I., Lemmin U. Secondary currents and corresponding surface velocity patterns in a turbulent open-channel flow over a rough bed // J. Hydraul. Eng. 2011. V. 137. № 11. P. 1318–1334.
Yang S.-Q., Tan S.K., Wang X.-K. Mechanism of secondary currents in open channel flows // J. Geophys. Res. 2012. V. 117. P. F04014.
Stoesser T., McSherry R., Fraga B. Secondary currents and turbulence over a non-uniformly roughened open-channel bed // Water. 2015. V. 7. № 9. P. 4896–4913.
Nezu I., Rodi W. Experimental study on secondary currents in open channels flow // Proc. 21st Congress of IAHR. 2. Melbourne. Australia. 1985. P. 19–23.
Grega L.M., Wey T., Leighton R.I., Neves J.C. Turbulent mixed-boundary flow in a corner formed by a solid wall and a free-surface // J. Fluid Mech. 1995. V. 294. P. 17–46.
Broglia R., Pascarelli A., Piomelli U. Large-Eddy simulations of ducts with a free surface // J. Fluid Mech. 2003. V. 484. P. 223–253.
Anderson W., Barros J., Christensen K., Awasthi A. Numerical and experimental study of mechanisms responsible for turbulent secondary flows in boundary layer flows over spanwise heterogeneous roughness // J. Fluid Mech. 2015. V. 768. P. 316–347.
Marin O., Vinuesa R., Obabko A.V., Schlatter P. Characterization of the secondary flow in hexagonal ducts // Phys. Fluids. 2016. V. 28. P. 125101.
Vanderwel C., Stroh A., Kriegseis J., Frohnapfel B., Ganapathisubramani B. The instantaneous structure of secondary flows in turbulent boundary layers // J. Fluid Mech. 2019. V. 862. P. 845–870.
Nagata K., Hunt J.C.R., Sakai Y., Wong H. Distorted turbulence and secondary flow near right-angled plates // J. Fluid Mech. 2011. V. 668. P. 446–479.
Eichelbrenner E.A., Preston J.H. On the role of secondary flow in turbulent boundary layers in corners (and salients) // J. Méanique. 1971. V. 10. P. 91–112.
Gessner F.B. The origin of secondary flow in turbulent flow along a corner // J. Fluid Mech. 1973. V. 58. P. 1–25.
Dai Yi-Jun, Xu Chun-Xiao. Wall pressure and secondary-flow origination in a square duct // Phys. Fluids. 2019. V. 31. P. 085104.
Nikitin N. Turbulent secondary flows in channels with no-slip and shear-free boundaries // J. Fluid Mech. 2021. V. 917. A24.
Пивоваров Д.Е., Попеленская Н.В., Никитин Н.В. Прямое численное моделирование турбулентного течения вдоль внешнего угла // Тезисы докладов, представленных на XXIV Международную конференцию Нелинейные задачи теории гидродинамической устойчивости и турбулентность. Ответственные редакторы – Н.В. Никитин, Н.В. Попеленская. М.: Издательство Московского Университета, 2020.
Bons J., Taylor R., McClain S., Rivir R. The many faces of turbine surface roughness // In ASME Turbo Expo 2001: Power for Land, Sea, and Air. 2001. P. V003T01A042–V003T01A042. American Society of Mechanical Engineers.
Mejia-Alvarez R., Christensen K.T. Wall-parallel stereo particle image velocimetry measurements in the roughness sublayer of turbulent flow over-lying highly irregular roughness // Phys. Fluids. 2013. V. 25. № 11. P. 115109.
Barros J.M., Christensen K.T. Observations of turbulent secondary flows in a rough-wall boundary layer // J. Fluid Mech. 2014. V. 748. P. R1.
Wang Z.-Q., Cheng N.-S. Time-mean structure of secondary flowsin open channel with longitudinal bedforms // Adv. Water Resour. 2006. V. 29. № 11. P. 1634–1649.
Castro I., Kim J., Stroh A., Lim H. Channel flow with large longitudinal ribs // J. Fluid Mech. 2021. V. 915. A92.
Chung D., Monty J.P., Hutchins N. Similarity and structure of wall turbulence with lateral wall shear stress variations // J. Fluid Mech. 2018. V. 847. P. 591–613.
Willingham D., Anderson W., Christensen K.T., Barros J.M. Tur-bulent boundary layer flow over transverse aerodynamic roughness transitions: Induced mixing and flow characterization // Phys. Fluids. 2014. V. 26. № 2. P. 025111.
Zheng Y., Anderson W. Flow-roughness heterogeneity: critical obliquity and salient parameters // J. Fluid Mech. 2021. V. 913. P. A12.
Türk S., Daschiel G., Stroh A., Hasegawa Y., Frohnapfel B. Turbulent flow over superhydrophobic surfaces with streamwise grooves // J. Fluid Mech. 2014. V. 747. P. 186–217.
Wangsawijaya D.D., Baidya R., Chung D., Marusic I., Hutchins N. The effect of spanwise wavelength of surface heterogeneity on turbulent secondary flows // J. Fluid Mech. 2020. V. 894. P. A7.
Stroh A., Schäfer K., Forooghi P., Frohnapfel B. Secondary flow and heat transfer in turbulent flow over streamwise ridges // Int. J. Heat Fluid Flow. 2020. V. 81. P. 108518.
Goldstein D.B., Tuan T.-C. Secondary flow induced by riblets // J. Fluid Mech. 1998. V. 363. P. 115–151.
Vanderwel C., Ganapathisubramani B. Effects of spanwise spacing on large-scale secondary flows in rough-wall turbulent boundary layers // J. Fluid Mech. 2015. V. 774. P. 1–12.
Medjnoun T., Vanderwel C., Ganapathisubramani B. Characteristics of turbulent boundary layers over smooth surfaces with spanwise heterogeneities // J. Fluid Mech. 2018. V. 838. P. 516–543.
Zampiron A., Cameron S., Nikora V. Secondary currents and very-large-scale motions in open-channel flow over streamwise ridges // J. Fluid Mech. 2020. V. 887. P. A17.
Hwang H., Lee J. Secondary flows in turbulent boundary layers over longitudinal surface roughness // Phys. Rev. Fluids. 2018. V. 3. P. 014608.
Yang J., Anderson W. Numerical study of turbulent channel flow over surfaces with variable spanwise heterogeneities: Topographically-driven secondary flows affect outer-layer similarity of turbulent length scales // Flow Turbul. Combust. 2018. V. 100. № 1. P. 1–17.
Stroh A., Schäfer K., Frohnapfel B., Forooghi P. Rearrangement of secondary flow over spanwise heterogeneous roughness // J. Fluid Mech. 2020. V. 885. P. R5.
Pope S. Turbulent flows. Cambridge, 2001.
Leschziner M., Drikakis D. Turbulence modelling and turbulent-flow computation in aeronautics // Aeronaut. J. 2002. V. 106. P. 349–384.
Pecnik R., Iaccarino G. Predictions of turbulent secondary flows using the ${{{v}}^{2}}$–$f$ model // In 38th Fluid Dynamics Conference and Exhibit. 2008. P. 3852.
Spalart P., Allmaras S. A one-equation turbulence model for aerodynamic flows // In 30th aerospace sciences meeting and exhibit. 1992. P. 439.
Jones W., Launder B. The prediction of laminarization with a two-equation model of turbulence // Int. J. Heat Mass Transf. 1972. V. 15. № 2. P. 301–314.
Wilcox D. Turbulence modeling for CFD, volume 2 // DCW industries La Canada. CA. 1993.
Menter F. Two-equation eddy-viscosity turbulence models for engineering applications // AIAA Journal. 1994. V. 32. № 8. P. 1598–1605.
Alfonsi G. Reynolds-averaged Navier–Stokes equations for turbulence modeling // Appl. Mech. Rev. 2009. V. 62. № 4. P. 040802.
Durbin P. Near-wall turbulence closure modeling without “damping functions” // Theor. Comput. Fluid Dyn. 1991. V. 3. № 1. P. 1–13.
Rotta J. Statistische theorie nichthomogener turbulenz // Zeitschrift für Physik. 1951. V. 129. № 6. P. 547–572.
Naot D., Savit A., Wolfshtin M. Numerical calculation of Reynolds stresses in a square duct with secondary flow // Wärme-und Stoffübertragung. 1974. V. 7. № 3. P. 151–161.
Reece G. Development and application of a generalized Reynolds-stress model of turbulence // PhD thesis. University of London. 1977.
Leutheusser H. Turbulent flow in rectangular ducts // J. Hydraul. Eng. 1963. V. 89. № 3. P. 1–19.
Launder B., Ying W. Prediction of flow and heat transfer in ducts of square cross-section // Proceedings of the Institution of Mechanical Engineers. 1973. V. 187. № 1. P. 455–461.
Speziale C., Sarkar S., Gatski T. Modelling the pressure-strain correlation of turbulence: an invariant dynamical systems approach // J. Fluid Mech. 1991. V. 227. P. 245–272.
Launder B., Reece G., Rodi W. Progress in the development of a Reynolds-stress turbulence closure // J. Fluid Mech. 1975. V. 68. № 3. P. 537–566.
De Cacqueray N., Hargreaves D., Morvan H. A computational study of shear stress in smooth rectangular channels // J. Hydraul. Res. 2009. V. 47. № 1. P. 50–57.
Kang H., Choi S. Reynolds stress modelling of rectangular open channel flow // Int. J. Numer. Methods Fluids. 2006. V. 51. № 11. P. 1319–1334.
Ansari K., Morvan H.P., Hargreaves D.M. Numerical investigation into secondary currents and wall shear in trapezoidal channels // J. Hydraul. Eng. 2011. V. 137. № 4. P. 432–440.
Jing H., Guo Y., Li C., Zhang J. Three-dimensional numerical simulation of compound meandering open channel flow by the Reynolds stress model // Int. J. Numer. Methods Fluids. 2009. V. 59. № 8. P. 927–943.
Choi S., Kang H. Characteristics of mean flow and turbulence statistics of depth-limited flows with submerged vegetation in a rectangular open channel // J. Hydraul. Res. 2016. V. 54. № 5. P. 527–540.
Hanjalic K., Launder B. A Reynolds stress model of turbulence and its application to thin shear flows // J. Fluid Mech. 1972. V. 52. № 4. P. 609–638.
Kacker S. Discussion of ‘prediction of flow and heat transfer in ducts of square cross-section’ // Proceedings of the Institution of Mechanical Engineers. 1973. V. 187. P. D147–D148.
Nakayama A., Chow W., Sharma D. Calculation of fully developed turbulent flows in ducts of arbitrary cross-section // J. Fluid Mech. 1983. V. 128. P. 199–217.
Tatchell D. Convection processes in confined three-dimensional boundary layers // PhD thesis. Imperial College London. 1975.
Gosman A., Rapley C. Fully-developed flow in passages of arbitrary cross-section // Recent Advances in Numerical Methods in Fluids. 1980. V. 1. P. 335–399.
Rapley C. The simulation of secondary flow effects in turbulent noncircular passage flows // Int. J. Numer. Methods Fluids. 1982. V. 2. № 4. P. 331–347.
Naot D., Rodi W. Calculation of secondary currents in channel flow // J. Hydraul. Eng. 1982. V. 108. № 8. P. 948–968.
Speziale C. On nonlinear $k - l$ and $k - \varepsilon $ models of turbulence // J. Fluid Mech. 1987. V. 178. P. 459–475.
Younis B., Abdellatif O. Modeling sediment transport in rectangular ducts with a two-equation model of turbulence // In Sediment Transport Modeling. P. 197–202. ASCE, 1989.
Hur N., Thangam S., Speziale C. Numerical study of turbulent secondary flows in curved ducts // J. Fluid Eng. 1990. V. 112. P. 205–211.
Cokljat D. Turbulence models for non-circular ducts and channels // PhD thesis. City University London. 1993.
Cokljat D., Younis B. Second-order closure study of open-channel flows // J. Hydraul. Eng. 1995. V. 121. № 2. P. 94–107.
Tajnesaie M., Nodoushan E.J., Barati R., Moghadam M.A. Performance comparison of four turbulence models for modeling of secondary flow cells in simple trapezoidal channels // J. Hydraul. Eng. 2020. V. 26. № 2. P. 187–197.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа