Известия РАН. Механика жидкости и газа, 2021, № 4, стр. 41-51

1. СТРУКТУРА ПОЛЯ ПУЛЬСАЦИЙ В ТУРБУЛЕНТНОЙ СТРУЕ

На основе известных к настоящему времени экспериментальных, теоретических и численных результатов [14–16] в турбулентной дозвуковой струе с достаточно большим числом Рейнольдса (обычно более 10⁵ при использовании диаметра сопла в качестве характерного размера) можно выделить три характерные области (рис. 1). Это, во-первых, область с ненулевой завихренностью, в которой и сосредоточено собственно турбулентное движение газа (область A на рис. 1). Далее, это область, в которой движение газа потенциально, но при этом в нем доминируют неакустические пульсации, характеризующиеся дозвуковой скоростью распространения и экспоненциальным затуханием по радиальному направлению (область B на рис. 1). И наконец, область чисто акустических пульсаций, простирающаяся от области B в бесконечность (область C на рис. 1). Отметим, что поле пульсаций в осесимметричной (в среднем) струе удобно представлять в виде разложения по азимутальным модам вида $\cos (n\theta )$, $\sin (n\theta )$, n = 0, 1, …, где θ – азимутальный угол (рис. 1).

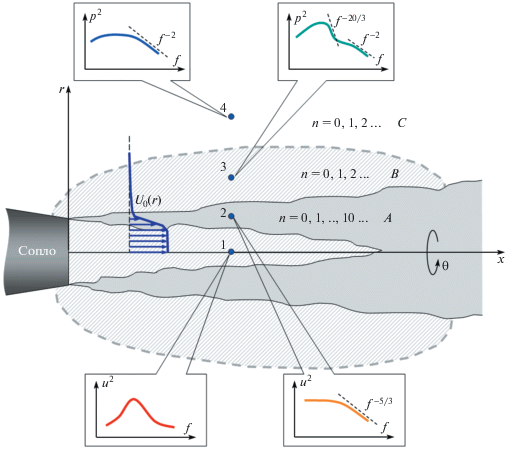
Наиболее сложной структурой обладают пульсации в области турбулентного движения газа – в слое смешения струи. Они, кроме наличия завихренности, характеризуются также богатым модальным составом (существенный вклад в пульсации могут вносить до десяти мод и более) и сравнительно малыми пространственными масштабами корреляции [22]. Подобные возмущения несут основную энергию турбулентного движения. В данной области течения, ввиду наличия среднего потока, обычно проводятся измерения пульсаций скорости (с помощью термоанемометров или бесконтактных методов типа PIV). Типичный вид частотного спектра пульсаций скорости u в области А приведен на рис. 1 (точка 2). Он характеризуется равномерно наполненной низкочастотной областью и монотонным спаданием в области высоких частот по закону “–5/3”, характерному для развитого турбулентного течения [24].

Область C наиболее подробно изучена в работах акустической направленности [4–13]. В экспериментах в данной области обычно с помощью микрофонов регистрируются акустические пульсации давления p. Типичный частотный спектр таких пульсаций для излучения звука в боковом направлении также показан на рис. 1 (точка 4). Спектр отличается большой шириной, сравнительно слабовыраженным максимумом в области средних частот и высокочастотным спаданием по закону “–2” [6]. В азимутальном составе звукового поля круглой струи доминируют три моды низших порядков: n = 0, 1, 2 [6, 9, 10, 16].

В настоящей работе нас будет интересовать область В. Именно в ней доминируют пульсации, связанные с развитием в слое смешения когерентных структур [14–16, 25]. В той части области B, которая находится вне слоя смешения, средний поток, возникающий за счет эжекции внешнего газа в струю, достаточно мал, и в экспериментах измеряются, как и в акустическом поле C, пульсации давления $p{\text{'}}$ [14, 15, 25]. На рис. 1 изображен типичный для этой зоны спектр пульсаций давления (точка 3), который отличается от чисто акустического спектра (точка 4) наличием ярко выраженного максимума в области низких частот, который и является “следом” волн неустойчивости в ближнем поле струи [20, 25]. Правый склон этого максимума имеет характерный наклон “–20/3”, свойства этой части спектра подробно исследованы в [25]. Основной вклад в пульсации также дают первые три азимутальные моды [14–16, 20, 25], причем фазовые скорости соответствующих возмущений лежат (в зависимости от частоты) в диапазоне 20–80% скорости истечения струи U_j [20], т.е. заведомо ниже скорости звука. Таким образом, данные возмущения не являются акустическими, поэтому регистрируемые микрофонами соответствующие пульсации давления обычно называют “псевдозвуковыми”.

В той зоне области B, которая лежит внутри потенциального ядра струи, в эксперименте обычно измеряются пульсации скорости, поскольку присутствует мощный средний поток, препятствующий измерению пульсаций давления. В спектре пульсаций наблюдается ярко выраженный максимум (рис. 1, точка 1), который, также как и для ближнего поля (рис. 1, точка 3), ассоциируется с волнами неустойчивости [22].

Отметим, что указанные когерентные структуры присутствуют, разумеется, и внутри слоя смешения (область А), неустойчивость которого является причиной их возникновения, однако в этой области они не являются доминирующими и могут быть маскированы более мощными мелкомасштабными возмущениями [17, 22].

В том случае, когда регистрируемые в области В пульсации действительно являются проявлением одного и того же объекта – волны неустойчивости, следует ожидать, что спектры пульсаций, измеренные в одной точке, можно пересчитывать в другие точки, если известна пространственная структура волн неустойчивости. Построению упрощенной процедуры такого пересчета посвящена настоящая работа.

Необходимо также отметить, что, как уже упоминалось, в слое смешения развиваются волновые пакеты, соответствующие различным азимутальным модам, поэтому упомянутый пересчет можно реализовать лишь для каждой моды по отдельности. Таким образом, для пересчета, например, пульсаций скорости из потенциального ядра струи в пульсации давления в ближнее поле вне струи требуется знание азимутальных компонент рассматриваемых пульсаций. В то время как разложение на азимутальные моды вне струи является сравнительно простой экспериментальной задачей, требующей размещения в интересующем сечении струи азимутальной решетки с достаточным числом микрофонов [10, 14, 15], разложение на азимутальные моды поля пульсаций скорости представляет значительные сложности. Для получения такого разложения можно, аналогично решетке микрофонов ближнего поля, использовать азимутальную решетку термоанемометров [26], однако это слишком громоздкий метод, к тому же являющийся существенно “инвазивным”, т.е. возмущающим поток. Неинвазивной альтернативой решетке термоанемометров является использование нестационарной стерео-PIV системы, позволяющей регистрировать спектральные свойства пульсаций скорости в заданной плоскости. Такой способ применялся в работе [22], однако подобные системы не являются пока распространенными и к тому же требуют тщательной калибровки.

В упомянутой работе [22] было отмечено, что измерения пульсаций продольной компоненты скорости на оси струи соответствуют осесимметричной моде неустойчивости, т.к. высшие моды не дают вклада в пульсации данной компоненты на оси. Таким образом, измерения лишь одним датчиком на оси струи достаточны для идентификации осесимметричной моды. Поскольку именно осесимметричные возмущения аккумулируют существенную долю энергии пульсаций ближнего поля, в настоящей работе мы сосредоточим внимание именно на анализе азимутальной моды n = 0.

2. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

В настоящей работе будет проведен анализ экспериментальных данных, полученных для дозвуковой струи, истекающей из круглого профилированного сопла диаметром D = 40 мм. Число Маха истечения струи, вычисленное по скорости звука в окружающей среде, равно M_j = 0.53. Число Рейнольдса, рассчитанное по диаметру сопла и скорости истечения струи, составляло около 4.8 × 10⁵.

Для указанной струи ранее [15, 23] были проведены измерения двух типов: измерения пульсаций давления многомикрофонной решеткой (пять колец по шесть микрофонов в каждом) вблизи внешней границы слоя смешения (рис. 2а), измерения скорости термоанемометром на оси струи и в нескольких поперечных сечениях (рис. 2б).

Параметры использованных микрофонов и термоанемометра, а также детальное описание точек измерений и методов обработки данных приведены в работах [15, 23]. На рис. 3 представлена сводная информация по имеющимся данным.

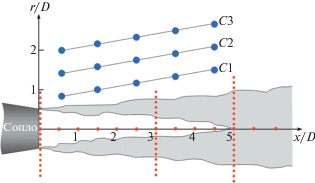
С помощью микрофонной решетки были измерены пульсации давления в точках, лежащих на трех конических поверхностях C1, С2 и С3 с углом полураствора 10.5°, выбранного так, чтобы микрофоны гарантированно находились вне слоя смешения. Кольца располагались вдоль оси струи с расстоянием между соседними кольцами D (рис. 3). Первое кольцо в конфигурации С1 располагалось на расстоянии x/D = 0.5 от плоскости среза сопла, радиус кольца был r/D = 0.8.

При испытаниях временные реализации пульсаций давления синхронно записывались на каждом микрофоне. В каждом сечении струи проводилось разложение измеренного поля давления P(x, r, θ, t) на азимутальные компоненты с учетом лишь первых трех мод, вносящих основной вклад в сигнал [15]:

Измерения термоанемометром проводились вдоль оси струи с шагом 0.5D, а также в поперечных сечениях с координатами x/D = 0.075, 3, 5 (рис. 3). Нить термоанемометра располагалась перпендикулярно основному потоку, и преимущественно регистрировала продольную компоненту скорости, которая представлялась в виде осредненного по времени значения и пульсаций: $U = {{U}_{0}} + u$.

Как было отмечено в [22], пульсации продольной компоненты скорости, регистрируемые на оси круглой струи, соответствуют осесимметричной моде неустойчивости. Задачей настоящей работы является демонстрация того факта, что частотные спектры пульсаций скорости u, измеренные на оси в области начального участка ($x{\text{/}}D < 5$), могут быть в каждом сечении пересчитаны в частотные спектры осесимметричной моды пульсаций давления A₀ с помощью сравнительно простой процедуры решения линейной задачи устойчивости для цилиндрического слоя смешения.

3. РЕШЕНИЕ ЗАДАЧИ УСТОЙЧИВОСТИ ДЛЯ СЛОЯ СМЕШЕНИЯ

Волны неустойчивости в круглой струе рассматриваются на фоне осесимметричного среднего течения, которое, вообще говоря, неоднородно по продольному направлению х. Для описания волн неустойчивости используются линеаризованные уравнения, причем предполагается, что вязкость и теплопроводность не играют существенной роли в их развитии. На основании указанных допущений из полных уравнений Навье–Стокса выводятся уравнения для малых возмущений [8, 27].

Аксиальная симметрия среднего течения позволяет искать решения этих уравнений в виде отдельных азимутальных гармоник вида $\exp (in\theta )$ в цилиндрических координатах (x, r, θ) (рис. 1). Решение ищется в частотной области в виде $\exp ( - i\omega t)$. Предположим также, что средние значения плотности ${{\rho }_{0}}$ и давления p₀ одинаковы во всем пространстве, что вполне справедливо для дозвуковых ненагретых струй.

Благодаря тому, что среднее течение в струе характеризуется сравнительно медленным изменением параметров в продольном направлении, уравнения для возмущений могут быть упрощены. Самый простой вариант (так называемое, локально-параллельное приближение) заключается в пренебрежении изменением по х параметров среднего потока и, соответственно, переходе к решению задачи для параллельного течения, параметры которого выбираются в соответствии с представляющим интерес поперечным сечением струи. В этом случае для возмущений давления, которые представляются в виде разложения по продольным и азимутальным гармоникам ${{p}_{n}}(\alpha ,r){{e}^{{ - i\alpha x + in\theta - i\omega t}}}$, можно получить известное уравнение

где c₀ – скорость звука, функция ${{U}_{0}}(r)$ описывает профиль скорости среднего течения, соответствующего некоторому поперечному сечению х струи.

Решением спектральной задачи (3.1), которое будет описано ниже несколько подробнее, являются локальное волновое число $\alpha $ и собственная функция ${{p}_{n}}(\alpha ,r)$. В этом случае продольная координата входит в уравнение в качестве параметра, определяя вид функции ${{U}_{0}}(r)$.

Данный подход позволяет найти радиальную структуру собственного решения в заданном сечении, однако не пригоден для описания продольного развития волны неустойчивости, которая существенно зависит от соответствующей эволюции среднего течения. Учет продольной неоднородности потока может быть выполнен аналитически, с помощью введения малого параметра ε, характеризующего медленное изменение течения с координатой х. Тогда решение исходных уравнений для возмущений можно искать в виде разложения по параметру ε [8, 27]. В таком подходе решение уравнения (3.1) дает главное приближение, а неоднородность по х учитывается в следующем приближении по ε.

Альтернативный вариант упрощенного учета неоднородности среднего течения состоит в решении так называемых параболизованных уравнений устойчивости [28], которые получаются из исходных уравнений для возмущений путем представления искомого решения в виде произведения медленно меняющейся функции (по сути – огибающей волнового пакета) и быстро меняющейся функции, описывающей волнообразный характер возмущений. Получившиеся уравнения решаются численно маршевым методом по продольной координате, что существенно проще численного решения исходных уравнений.

В настоящей работе мы сосредоточим внимание на решении простейшего уравнения (3.1) для моды n = 0. Как уже упоминалось, локально-параллельное приближение позволяет определить радиальную структуру волны неустойчивости в заданном сечении. Таким образом, предполагая, что пульсации скорости на оси струи и пульсации осесимметричной моды давления в ближнем поле являются проявлением одного и того же объекта – осесимметричной волны неустойчивости, можно ожидать, что решение уравнения (3.1) позволит осуществить пересчет экспериментальных данных с оси струи в ближнее поле в каждом сечении струи. Поскольку измерения на оси струи доступны в нескольких точках, нет необходимости аналитического восстановления продольной эволюция волны неустойчивости – эта информация будет доступна из эксперимента. Причем можно ожидать, что точность пересчета в целом при этом повысится, поскольку в дозвуковых струях угол расширения слоя смешения является не слишком малой величиной (около 20°), и количественное согласие решений параболизованных уравнений с данными экспериментов не всегда удовлетворительно, особенно для сравнительно низких частот [22, 23].

Уравнение (3.1) для осесимметричной моды решалось численно методом, описанным в [28]. Решение искалось для граничных условий ${{p}_{0}}\sim {{I}_{0}}(\beta r)$ при $r \to 0$ и ${{p}_{0}}\sim {{K}_{0}}(\gamma r)$ при $r \to \infty $, где I₀ и K₀ – модифицированные функции Бесселя, соответственно первого и второго рода, порядка 0, $\gamma = \sqrt {{{\alpha }^{2}} - {{k}^{2}}} $, β = $\sqrt {(\alpha - (k + M\alpha ))(\alpha + (k + M\alpha ))} $. Разрезы для функций $\gamma $ и $\beta $ определяются таким образом, что их действительная часть была положительной на всем листе римановой поверхности [27].

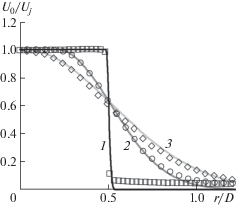
Профиль средней скорости в пределах начального участка струи задавался с использованием аналитических выражений [8]:

где U_j – скорость на оси струи, в потенциальном ядре равная скорости истечения струи, B(x) – полуширина слоя смешения, H(x) – поперечный размер потенциального ядра струи. Зависимость функций B и H от х была взята аналогично работе [27]: где величины δ и $L$ (длина потенциального ядра) подбирались из условия наилучшего совпадения модельных профилей скорости с экспериментально измеренными. Для рассмотренной струи были взяты значения $\delta = 1.23$, $L = 5.1D$. Результаты сравнения модельных профилей с данными измерений приведены на рис. 4.

Уравнение (3.1) решалось для 90 значений параметра x/D, равномерно распределенных на отрезке 0.01–5.1, интегрирование по r проводилось в пределах от $2 \times {{10}^{{ - 4}}}D$ до $3D$. Решение проводилось для набора чисел Струхаля (${\text{St}} = \omega D{\text{/}}(2\pi {{U}_{j}})$) в диапазоне 0.1–0.8. В результате для каждого значения x/D и каждого St находилось собственное волновое число ${{\alpha }_{0}}(x{\text{/}}D)$, соответствующее неустойчивости Кельвина–Гельмгольца, и собственная функция давления ${{p}_{0}}(r)$. Траектории волновых чисел α₀, нормированных на $k = \omega {\text{/}}{{c}_{0}}$, при изменении x/D от 0.01 до 5.1 показаны на рис. 5.

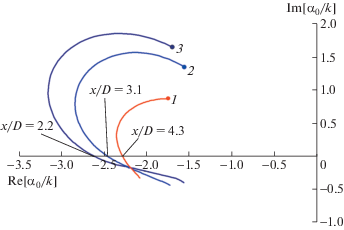
Отметим, что при некотором значении x/D волна становится нейтрально устойчивой ($\operatorname{Im} [{{\alpha }_{0}}]$ = 0). В этом случае в уравнении (3.1) возникает критический слой, и решение при бóльших значениях x/D ищется как аналитическое продолжение решения при меньших x/D, для чего контур интегрирования по r деформируется вблизи корня уравнения $\omega + \alpha {{U}_{0}} = 0$ таким образом, чтобы сохранить обход логарифмической точки ветвления сверху [8, 27, 28]. Значение x/D, при котором достигается нейтральная устойчивость, характеризует положение максимума волнового пакета и его характерный продольный масштаб. Как видно из рис. 5, при повышении частоты (числа Струхаля) продольный масштаб пакета уменьшается, что качественно соответствует данным измерений [14–16].

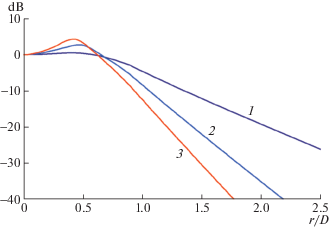
На рис. 6 для значения x/D = 3.5 показаны соответствующие собственные функции давления. Функции показаны в логарифмическом масштабе (в дБ), нормировка выбрана так, чтобы на оси струи модуль функции равнялся единице.

Отметим также, что хотя параметры волновых пакетов зависят от частоты возмущений, суммарные спектры пульсаций ближнего поля все равно являются широкополосными, т.е. нет возможности указать на некую точку ближнего поля и сказать, что в ней доминируют пульсации на конкретной частоте. Волновые пакеты различных частот не являются локализованными в пространстве возмущениями и перекрываются друг с другом, что в итоге приводит к формированию широкополосного спектра в ближнем поле.

4. ПЕРЕСЧЕТ ДАННЫХ С ОСИ СТРУИ В БЛИЖНЕЕ ПОЛЕ

Для пересчета пульсаций с оси струи на пульсации во вне струи с помощью найденных выше функций ${{p}_{0}}(r)$ необходимо сначала пересчитать измеренные на оси пульсации скорости в пульсации давления. Для этого воспользуемся уравнением импульса в проекции на ось х. В данном уравнении присутствуют и играют значимую роль производные функций по продольной координате, поэтому локально-параллельное приближение для связи p и u, вообще говоря, не годится. Учтем тот факт, что на оси струи возмущения давления и скорости могут быть для заданной частоты представлены в виде произведения сравнительно плавной огибающей и бегущей волны: $p = {{p}_{m}}(x){{e}^{{i\omega (x/{{U}_{c}} - t)}}}$, $u = {{u}_{m}}(x){{e}^{{i\omega (x/{{U}_{c}} - t)}}}$, где U_c – фазовая скорость возмущений. Тогда уравнение импульса примет вид

Безразмерные продольные производные давления и скорости являются величинами одного порядка: ${{U}_{c}}{\text{/}}{{u}_{m}} \times u_{m}^{'}{\text{/}}\omega \sim {{U}_{c}}{\text{/}}{{p}_{m}} \times p_{m}^{'}{\text{/}}\omega $. Измерения скорости на оси струи в интересующем нас частотном диапазоне $St\sim 0.2{\kern 1pt} - {\kern 1pt} 0.6$ показывают (рис. 7), что характерная величина $u_{m}^{'}{\text{/}}{{u}_{m}}$ имеет порядок D^–1, тогда при типичном значении ${{U}_{c}}\sim 0.7{{U}_{j}}$ [20] получим ${{U}_{c}}{\text{/}}{{u}_{m}} \times u_{m}^{'}{\text{/}}\omega \sim 0.7{\text{/}}(2\pi St)$. Для не слишком малых чисел Струхаля пренебрежение этой величиной по сравнению с единицей в правой части (4.1) вполне допустимо, учитывая, что спектры пульсаций давления выражаются с логарифмической точностью. Однако в левой части такое упрощение невозможно, поскольку второе слагаемое ${{U}_{c}} - {{U}_{j}}\sim - 0.3{{U}_{j}}$ имеет тот же порядок, что и ${{U}_{j}}({{U}_{c}}{\text{/}}{{u}_{m}} \times u_{m}^{'}{\text{/}}\omega )$. Таким образом, приближенно можно выразить спектральную плотность L_p пульсаций давления на оси струи через соответствующую спектральную плотность пульсаций скорости L_u следующим образом:

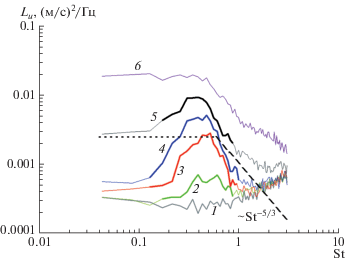
Характерные спектры пульсаций скорости, измеренные воль оси струи в области начального участка, показаны на рис. 7. В области средних частот (St ∼ 0.2–0.8) при 1 < x/D < 5 явно виден максимум, который связывают с волнами неустойчивости [22]. При меньших значениях x/D сигнал становится слабым, и плохо различим на фоне собственных шумов датчика (кривая 1 на рис. 7). В области конца потенциального ядра и далее ниже по потоку в сигнале начинают доминировать пульсации, связанные с собственно турбулентным вихревым движением в слое смешения и имеющие типичный спектр с “полочкой” в области низких частот и спаданием по закону “–5/3” [22] – в области высоких частот (штриховая линия и кривая 6 на рис. 7). Учитывая указанные факторы, сигнал, связанный с волнами неустойчивости, можно выделить лишь в ограниченном частотном интервале, зависящем к тому же от положения точки измерения x/D. На кривых 2–5 на рис. 7 жирными участками показаны частотные области, в которых пик, связанный с волнами неустойчивости, заведомо превышает уровни пульсаций, связанные с другими факторами (будь то фоновый шум датчика или широкополосный спектр мелкомасштабной турбулентности).

Результаты пересчета пульсаций скорости на оси струи в пульсации осесимметричной моды давления вне струи с помощью решения уравнения (3.1) и соотношения (4.2) приведены на рис. 8. В расчетах по (4.2) было принято, в соответствии с данными [20], что конвективная скорость возмущений U_c линейно растет с ростом x/D от $0.6{{U}_{j}}$ при x/D = 1 до $0.8{{U}_{j}}$ при x/D = 4.5. Эта зависимость в целом соответствует поведению действительной части волнового числа ${{\alpha }_{0}}$ при увеличении x/D (рис. 5), однако локально-параллельное приближение дает несколько завышенные абсолютные значения конвективной скорости и затянутый участок ее снижения при малых x/D.

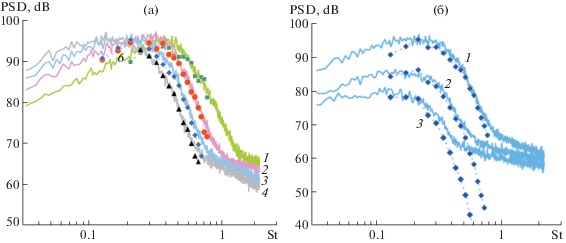
Результаты, показанные на рис. 8, в целом демонстрируют приемлемое согласование измеренных в ближнем поле спектров пульсаций осесимметричной моды давления и спектров, полученных пересчетом из пульсаций скорости на оси струи. Отметим еще раз, что в соответствии с соображениями, высказанными выше, пересчет данных с оси струи во внешнюю область возможен лишь для ограниченного частотного диапазона, зависящего от значения x/D, и не позволяет полностью восстановить низкочастотные и высокочастотные склоны спектра для x/D, близких к срезу сопла и к концу потенциального ядра. Полученные результаты косвенно подтверждают исходные предположения о том, что гидродинамические пульсации в областях потенциального течения вблизи слоя смешения (зона B на рис. 1) в основном связаны с волнами неустойчивости слоя, развивающимися в струе вследствие неустойчивости слоя смешения.

ЗАКЛЮЧЕНИЕ

В работе построена упрощенная процедура, связывающая пульсации продольной компоненты скорости на оси струи (в зоне потенциального ядра) и пульсации осесимметричной моды давления в ближнем поле вне слоя смешения. Предлагаемый подход основан на допущении о том, что указанные пульсации в области средних частот (St ∼ 0.2–0.8) являются проявлением пакетов волн неустойчивости, развивающихся в струе за счет неустойчивости Кельвина–Гельмгольца. В отличие от подходов, использовавшихся в работах [21, 28] и основанных на решении параболизованных уравнений устойчивости, в настоящей работе использовано собственное решение для пульсаций давления, полученное в простейшем локально-параллельном приближении, а учет эволюции течения и, соответственно, структуры волновых пакетов по продольной координате, выполнен с использованием экспериментальных данных, полученных в нескольких точках на протяжении начального участка.

В результате показано, что с помощью предложенной процедуры пульсации скорости, измеренные на оси, могут быть с достаточной точностью пересчитаны в пульсации осесимметричной моды давления. Это, во-первых, косвенно подтверждает исходное допущение о том, что гидродинамические пульсации в потенциальном ядре струи и в области вне струи вблизи границы слоя смешения связаны именно с волнами неустойчивости.

Во-вторых, подобная процедура определения структуры осесимметричных пульсаций давления по измерениям скорости может быть полезна с точки зрения оценок шума струи в компоновке, для которых требуется знание поля давления, падающего на кромку крыла, в том числе при наличии спутного потока. Кроме того, возможность восстановления параметров осесимметричного волнового пакета по измерениям скорости может быть использована при разработке систем активного управления волнами неустойчивости с целью снижения шума струи [15] и, возможно, позволит повысить эффективность и реализуемость таких систем за счет приближения датчика к соплу и замене многомикрофонных систем регистрации давления в ближнем поле [29] одноточечными измерениями скорости.

Работа выполнена при финансовой поддержке РНФ (грант 19-71-10064).