Известия РАН. Механика жидкости и газа, 2021, № 4, стр. 100-113

1. МОДЕЛЬНЫЕ УРАВНЕНИЯ ТЕЧЕНИЙ ВОЛНОВЫХ ПЛЕНОК

Течение тонких слоев вязкой жидкости по твердой поверхности под воздействием сил тяжести, вязкости и поверхностного натяжения описывается краевой задачей [2], которая включает уравнения Навье–Стокса

Уравнения (1.1), (1.2) записаны в безразмерной форме. Нижний индекс обозначает частную производную по переменной. Использованы масштабы длины h₀ и $\frac{{{{h}_{0}}}}{\kappa }$ для переменных y, x, масштабы скорости ${{U}_{0}}$, $\kappa {{U}_{0}}$ для скоростей u, ${v}$, динамический напор $\rho U_{0}^{2}$ для давлений p и p₁. Характерные значения толщины слоя h₀ и скорости жидкости U₀, а также коэффициент $\kappa $ растяжения по продольной переменной x должны быть заданы дополнительно.

Краевая задача (1.1), (1.2) содержит безразмерные параметры Рейнольдса ${\text{Re}} = \frac{{{{U}_{0}}{{h}_{0}}}}{\nu }$, Вебера We = $\frac{{\rho {{h}_{0}}U_{0}^{2}}}{\sigma }$, Фруда ${\text{Fr}} = \frac{{U_{0}^{2}}}{{g{{h}_{0}}}}$. Будем рассматривать такие гравитационно-капиллярные течения вязких несжимаемых жидкостей, в которых силы вязкости, тяжести, поверхностного натяжения имеют одинаковый порядок, задаваемый величиной δ, в соответствии с соотношениями [2, 3]

Отсюда находим безразмерные критерии и масштабирующие множители h₀, U₀, характерные для рассматриваемого класса течений,

Теперь задача (1.1), (1.2) полностью определяется парой внешних управляющих параметров математической модели δ, κ.

Существенное значение масштабирования (1.3) и введения параметра $\delta $ для успешного решения задачи о нелинейных волнах в пленках отмечено в [4, 5].

В работе [1.3] представлен вывод следующей модельной системы уравнений

Члены правой части (1.5) с множителем κ² отражают более точный учет влияния вязкости в исходной краевой задаче (1.1), (1.2). При малых значения κ, пренебрегая членами с множителем κ², из (1.5) получаем модельную систему $(h - q)$, выведенную в [2]. Эта система при больших γ (малой вязкости) управляется одним параметром δ и приводится к виду

Система (1.6) явилась основой интегрального метода для расчетов нелинейных волн в пленках маловязких жидкостей в длинном ряде работ, представленных в [4, 6]. Полная ${{(h - q)}_{1}}$ система (1.5) содержит два внешних параметра δ, κ и предназначена для исследования волн в жидкостях с произвольной вязкостью.

В [7, 8] представлена история построения системы эволюционных уравнений Шкадова (1.6) с момента ее создания в 1967 г. [2], а также ее частного асимптотического случая – слабонелинейного уравнения интегрального метода теории волновых пленок, которое впервые было выведено в [2] и исследовано в [7]

Исследование по данному уравнению было продолжено и впервые опубликовано в форме (1.7) в [9] со ссылкой: “отметим, что уравнение вида (1.7) может быть получено также из уравнений, выведенных в [2], если сохранить в них только главные члены по k_m”. Достаточно подробное исследование волновых решений слабонелинейного уравнения (1.7) было проведено в [10].

Уравнение (1.7) представляет предельную асимптотическую форму модельной системы (1.6) при стремлении расхода к нулю. При конечных значениях $\delta $ система (1.6) описывает физические волны, которые можно сравнить с экспериментами. Асимптотическому уравнению (1.7) соответствуют математические волны бесконечной длины и бесконечно малой амплитуды и оно не содержит параметры, которые можно связать с экспериментальными условиями. Отметим, что математическая модель нестационарных нелинейных волн в пленках сводится к одному уравнению только при условии $\delta \to 0$. Для конечных значений δ нестационарные волновые течения пленки описывается системой двух уравнений (1.6).

Полезное применение предельного при $\delta \to 0$ слабонелинейного уравнения теории стекающих волновых пленок (1.7) связано с возможностью использовать его решения для расчета начальных данных в итерационных вычислениях при $\delta \ne 0$. Этот подход применялся в [11] для численного решения системы (1.6) и в [1] – для расчета решений системы (1.5).

Отметим, что в [12, 13] предпринимались попытки дополнить $(h - q)$ модель членами, квадратичными по волновому числу α, а в [14] рассматриваются модификации системы $(h - q)$ (1.6) путем введения весовых множителей при интегрировании первого уравнения (1.1) по y.

Задача (1.5) определяется парой внешних управляющих параметров математической модели $\delta $ и $\kappa $. В экспериментальных работах часто используются параметры $R = 3{\text{Re}}$ и $\gamma = \frac{\sigma }{\rho }\mathop {({{\nu }^{4}}g)}\nolimits^{ - 1/3} $, которые, на основании (1.4), связаны с $\delta $, $\kappa $ соотношениями:

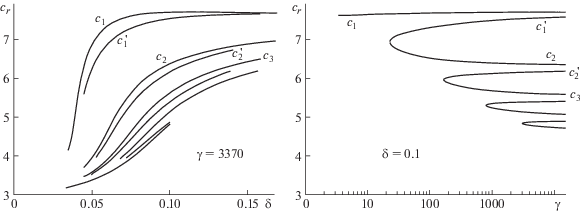
На рис. 1 представлены в плоскостях $(R,\gamma )$ и $(\delta ,\kappa )$ области значений управляющих параметров, при которых проводились эксперименты по волновым пленкам. Линии 1, 2 ограничивают область $A$ больших значений $\gamma $, соответствующих маловязким жидкостям. Сюда отнесены классические эксперименты работы [15] и многих других последующих работ, результаты которых собраны в [16]. Кривая $\kappa = 0.2$ проходит через центральную часть этой области, поэтому при решении задачи (1.1), (1.2) можно принять допущение ${{\kappa }^{2}} \ll 1$. Соответствующая теория, включая вывод приближенной модельной задачи $(h - q)$ с одним внешним управляющим параметром $\delta $ и исследование решений для периодических и уединенных волн, построена в [2, 3]. Она позволила истолковать основные экспериментальные результаты, получила дальнейшее развитие и обобщение путем учета процессов тепло- и массообмена в пленках и успешно применяется до настоящего времени [6].

Рис. 1.

Области существования волновых режимов течения пленок в плоскостях ($R,\gamma $) и ($\delta ,\kappa $): 1, 2 – линии, ограничивающие область A, соответствующую маловязким жидкостям; 3, 4 – линии, ограничивающие область B течений волновых пленок при больших и малых значениях $\gamma $; 5 – бифуркационный перевал, разделяющий области C и D.

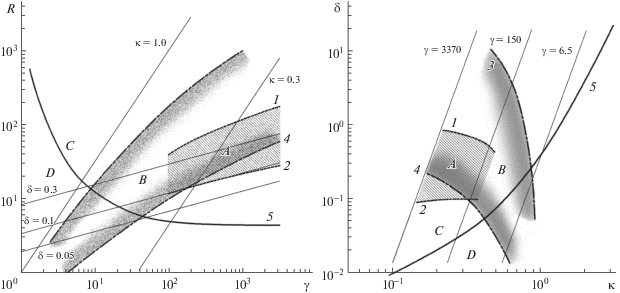
Линии 3, 4 ограничивают обширную область $B$ новых экспериментов [12, 13] с течениями волновых пленок при больших и малых значениях γ. Видно, что для указанного множества экспериментальных точек выполняются неравенства $0.1 < \kappa < 1$, причем значения $\kappa $ возрастают с уменьшением γ. В табл. 1 в качестве примера приведены значения γ, $\kappa $ при $\delta = 0.15$. С возрастанием вязкости уменьшается γ и растет $\kappa $, достигая значения $\kappa \sim 1$ ($\kappa = 0.15$ при $\gamma = 3750$; κ = 1 при $\gamma = 3.572$). Особый интерес представляет область малых значений γ для жидкостей с повышенной вязкостью. Волны в этой области пока изучены недостаточно и требуется как развитие теории, так и проведение новых более детальных расчетов.

2. БИФУРКАЦИОННЫЙ БАРЬЕР

Основное состояние системы (1.5) соответствует динамически возможному течению пленки постоянной толщины и постоянного расхода h = 1, q = 1. Рассмотрим условия, при которых вследствие гидродинамической неустойчивости происходит мягкая бифуркация от основного состояния волнового режима течения с волновым числом α

Линеаризуя систему (1.5) относительно малых амплитуд $\hat {h}$, $\hat {q}$, получаем дисперсионное соотношение для определения в области неустойчивости $0 < \alpha \leqslant {{\alpha }_{n}}$ собственного числа c = $c(\alpha ,\delta ,{{\kappa }^{2}})$.

Полагая в (2.1) ${{c}_{i}} = 0$, выводим уравнения для α_n и c_r на нейтральной кривой

Вычислим $\frac{{d{{c}_{r}}}}{{d\alpha }}$ для дисперсионного уравнения (2.1) в точках нейтральной кривой. Из условия $\frac{{d{{c}_{r}}}}{{d\alpha }} = 0$ получим

На рис. 1 линия 5 представляет множество точек, в которых на плоскости $(\kappa ,\delta )$ выполняются одновременно соотношения (2.2), (2.3). В каждой точке области C, выше линии 5, на нейтральной кривой выполняется условие $\frac{{d{{c}_{r}}}}{{d\alpha }} > 0$, а в каждой точке области D – условие $\frac{{d{{c}_{r}}}}{{d\alpha }} < 0$. Перемена знака $\frac{{d{{c}_{r}}}}{{d\alpha }}$ приводит к изменению характера мягкой бифуркации волнового режима. Мягкая бифуркация происходит вблизи нейтральной кривой, при смещении $\alpha $ в область неустойчивости $\alpha = {{\alpha }_{n}} + \delta \alpha $, $\delta \alpha < 0$. Следовательно, в области C на нейтральной кривой ответвляются медленные волны с фазовой скоростью, меньшей фазовой скорости нейтральных волн ${{c}_{r}} < {{c}_{{rn}}}$. Соответственно, в области $D$ на нейтральной кривой мягко ответвляются быстрые волны с фазовой скоростью ${{c}_{r}} > {{c}_{{rn}}}$. Линия 5 представляет бифуркационный перевал, разделяющий пленочные течения типа I в области C и типа II в области $D$.

В течениях типа I, при достаточно больших значениях γ, на нейтральной кривой $\alpha = {{\alpha }_{n}}$ ответвляется семейство медленных волн γ₁. При уменьшении волнового числа достигается критическое значение $\alpha = {{\alpha }_{ * }}$, при котором от семейства γ₁ происходит жесткая бифуркация семейства быстрых волн γ₂, которое продолжается по внутреннему параметру α к точке α = 0.

При переходе через бифуркационный перевал в область D к течениям типа II бифуркации первого семейства ${{\gamma }_{1}}$ исчезают. На нейтральной кривой ответвляется сразу семейство быстрых волн ${{\gamma }_{2}}$, которое по внутреннему параметру α продолжается до точки α = 0.

Понятие медленных и быстрых волн с внутренним параметром α при малых значениях $\delta $ впервые введено в [11]. Также в [11] были сформулированы основные принципиальные свойства регулярных волн при конечных значениях $\delta $. В дальнейшем было показано [17], что при $\delta > 0.09$ возникают жесткие бифуркации промежуточных семейств медленных волн, количество которых возрастает с ростом величины $\delta $. Соответственно в сторону малых значений α сдвигается точка жесткой бифуркации семейства ${{\gamma }_{2}}$.

На рис. 1 кривая бифуркационного перевала 5 делит в плоскости $(\kappa ,\delta )$ множество экспериментальных точек [13] на две большие группы. Свойства нелинейных волн, вызываемых гидродинамической неустойчивостью, для них существенно различаются, но тем и другим соответствуют волновые решения системы ${{(h - q)}_{1}}$. Некоторые значения управляющих параметров для точек, расположенных на бифуркационном перевале, представлены в табл. 2.

3. РЕГУЛЯРНЫЕ ПЕРИОДИЧЕСКИЕ ВОЛНЫ

В случае пространственно-периодических волн для каждой пары внешних независимых параметров $R$, $\gamma $ (или $\delta $, $\kappa $) существует также внутренний параметр – волновое число α такое, что при $0 < \alpha \leqslant {{\alpha }_{n}}$ малые возмущения неустойчивы и развиваются в нелинейные регулярные волны, и ${{\alpha }_{n}}$ – точка на нейтральной кривой. С изменением α от точки $\alpha = {{\alpha }_{n}}$ до точки $\alpha = 0$ изменяется характер волновых решений (1.5) от гармонических волн (медленных или быстрых) к быстрым уединенным волнам — солитонам. В [1] установлено фундаментальное свойство системы (1.5). В плоскости управляющих параметров существует линия (линия 5 на рис. 1), разделяющая множество регулярных волновых решений на два подмножества: в области A в каждой точке любой нейтральной кривой от стационарного течения ответвляются медленные волны (фазовая скорость c_r меньше фазовой скорости нейтральной волны), в области B ответвляются быстрые волны. Линии $\gamma = {\text{const}}$ на рис. 1 пересекают линию 5 бифуркационного перевала [1], причем точка пересечения зависит от значения γ. При переходе через точку пересечения с уменьшением $\kappa $ изменяется структура волновых решений, в частности, исчезает мелкомасштабная рябь на переднем фронте волны. Ниже приводятся результаты прямого численного решения двухпараметрической модели для периодических и уединенных волн.

В общем случае, для произвольной формы поверхности пленки жидкости, решения находились численно методом установления по времени с использованием фурье-представлений по пространственной координате $x$

Подставив (3.1) в (1.5), получим соответствующую динамическую систему обыкновенных нелинейных дифференциальных уравнений для коэффициентов разложений ${{h}_{n}}(t)$ и ${{q}_{n}}(t)$, которая численно интегрируется по времени с использованием прямого и обратного преобразований Фурье. В качестве начальных условий для коэффициентов ${{h}_{0}}$ и ${{q}_{0}}$ задавались значения для невозмущенного потока, а малые значения для ${{h}_{1}}$ и ${{q}_{1}}$ использовались в качестве начальных возмущений.

Для периодических волн с длиной волны $2\pi {\text{/}}\alpha $ использовались следующие граничные условия

Для каждого расчета задавались значения управляющих параметров δ, $\kappa $, α (или $R$, $\gamma $, α).

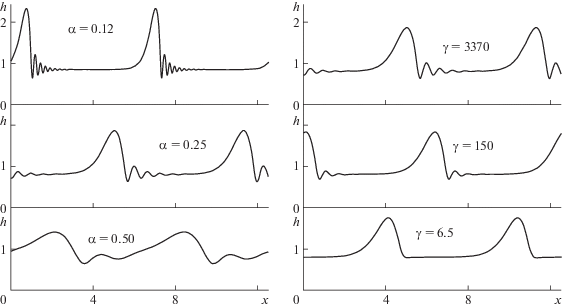
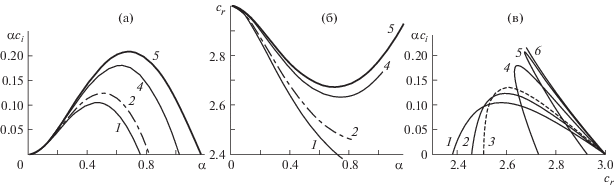
На рис. 2а,б представлена зависимость коэффициента нарастания $\alpha {{c}_{i}}$ и фазовой скорости ${{c}_{r}}$ от волнового числа α, полученная на основе анализа линеаризованной задачи. При различных значениях $\gamma $ результаты представлены для значений α из интервала неустойчивости. Для больших значений $\gamma $ = 3370, 150 от нейтральной кривой сначала происходит бифуркация к медленным волнам, лишь затем переход к быстрым. При меньших значениях $\gamma $ = 12.6, 6.5 формирование быстрых волн происходит сразу. Зависимость коэффициента нарастания $\alpha {{c}_{i}}$ от фазовой скорости ${{c}_{r}}$ для различных значений $\gamma $ показана на рис. 2в. Для величины $\gamma \approx 19$ выполняется условие $\mathop {\left. {\tfrac{{d\alpha {{c}_{i}}}}{{d{{c}_{r}}}}} \right|}\nolimits_{{{\alpha }_{0}}} = \infty $. При больших значениях $\gamma $ зависимость коэффициента нарастания $\alpha {{c}_{i}}$ от фазовой скорости ${{c}_{r}}$ не является однозначной: значение $\alpha $, при котором выполняется условие $\tfrac{{d\alpha {{c}_{i}}}}{{d{{c}_{r}}}} = \infty $, находится внутри интервала неустойчивости, и для одного значения фазовой скорости c_r в интервале ${{\alpha }_{{{\text{max}}}}} < \alpha < {{\alpha }_{0}}$ существуют два различных значения коэффициента нарастания $\alpha {{c}_{i}}$, где α_max – волновое число для максимального коэффициента нарастания $\alpha {{c}_{i}}$, ${{\alpha }_{0}}$ – волновое число нейтральных колебаний. При $\gamma \to 0$, ${{c}_{r}}({{\alpha }_{0}}) \to 3$. Тогда мы получаем случай (6), когда каждой точке кривой соответствуют два различных значения α из интервала линейной неустойчивости.

Рис. 2.

Зависимость коэффициента нарастания $\alpha {{c}_{i}}$ и фазовой скорости ${{c}_{r}}$ в области линейной неустойчивости для $\delta = 0.1$ и различных значений $\gamma $: 6.5 (1), 12.6 (2), 19 (3), 150 (4), 3370 (5), $\infty $ (6).

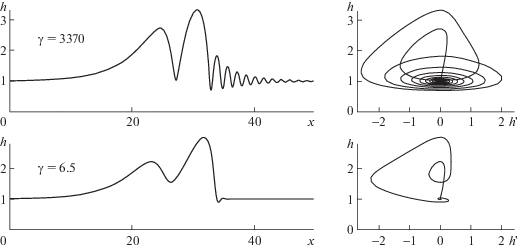
Предельные решения системы эволюционных уравнений, при $t \to \infty $ и фиксированном $\alpha = {\text{const}}$, представляют собой доминирующие волны. Для каждого заданного $\delta $ множество доминирующих волн, из интервала неустойчивости ($0 < \alpha < {{\alpha }_{n}}$), образуют глобальный аттрактор [6].

Различия сценариев бифуркаций в течениях типа I и II можно видеть на рис. 3, где показаны результаты прямого численного решения (1.5) предельных волн глобального аттрактора для областей C и D при $\delta = 0.1$ (1 – $\gamma = 3370$, 2 – γ = 6.5). В первом случае имеется ряд бифуркаций медленных волн до перехода на семейство быстрых волн ${{\gamma }_{2}}$, им соответствуют локальные максимумы на кривых ${{q}_{0}} = {{q}_{0}}(\alpha )$ и ${{c}_{r}} = {{c}_{r}}(\alpha )$; во втором случае имеется единственная бифуркация семейства быстрых волн ${{\gamma }_{2}}$ от основного состояния на нейтральной кривой при $\alpha = {{\alpha }_{n}}$.

Рис. 3.

Глобальный аттрактор при $\delta = 0.1$: а – проекция на плоскость $({{q}_{0}},\alpha )$; б – проекция на плоскость (${{c}_{r}},\alpha $); 1 – $\gamma = 3370$; 2 – $\gamma = 6.5$.

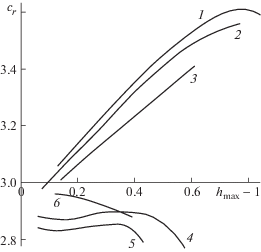
Диапазон изменения значений фазовой скорости c_r для сильновязкой жидкости проиллюстрирован рис. 4. Здесь показана зависимость c_r от приведенного значения максимальной толщины пленки ${{h}_{{max}}} - 1$ для случая $\alpha = 0.15$, $\gamma = 22$ (1), $\gamma = 13$ (2), $\gamma = 6.5$ (3) и для $\alpha = {{\alpha }_{m}}$, где α_m соответствует максимальному значению коэффициента нарастания $\alpha {{c}_{i}}$, $\gamma = 22$ (4), $\gamma = 13$ (5), γ = 6.5 (6).

Рис. 4.

Зависимость фазовой скорости ${{c}_{r}}$ от приведенного значения максимальной толщины пленки ${{h}_{{max}}} - 1$ для случая $\alpha = 0.15$ (1 – $\gamma = 22$, 2 – 13, 3 – 6.5) и для $\alpha = {{\alpha }_{m}}$, соответствующего максимальному значению коэффициента нарастания $\alpha {{c}_{i}}$ (4 – $\gamma = 22$, 5 – 13, 6 – 6.5).

Волновые решения модельной системы $(h - q)$ работы [2] при ${{\kappa }^{2}} \ll 1$ характеризуются наличием капиллярной ряби на переднем фронте быстрых волн большой амплитуды. Как было показано выше, включение членов порядка κ² в ${{(h - q)}_{1}}$ модели создает эффект сглаживания передних фронтов, особенно заметный для сильно вязких жидкостей.

Для $\delta = 0.1$ и $\gamma = 3370$, на рис. 5 приведено сравнение профилей волн при различных значениях волнового числа α. Из расчетов видно, как в результате последовательности бифуркаций перед фронтом волны с максимальной амплитудой происходит формирование мелкомасштабной ряби. Сравнение профилей волн при $\delta = 0.1$, $\alpha = 0.25$ для жидкостей с различными значениями числа Капицы $\gamma $ представлено на рис. 5. При малых значениях $\gamma $ рябь отсутствует.

Рис. 5.

Формы профиля волны для различных волновых чисел $\alpha $ и чисел Капицы $\gamma $.

4. ОТ ПЕРИОДИЧЕСКИХ УЕДИНЕННЫХ ВОЛН К СОЛИТОНАМ

При стремлении волнового числа α к нулю периодические решения системы эволюционных уравнений переходят в солитоны – регулярные уединенные волны. Для установившегося режима бегущей со скоростью c волны имеем ${{q}_{x}} = c{{h}_{x}}$. Исключая из системы уравнений расход q, можем получить уравнение третьего порядка относительно толщины пленки h:

Краевые условия в данном случае будут следующие:

Для малых возмущений формы поверхности пленки $h = 1 + h{\text{'}}$ имеем линеаризованное уравнение:

Рассмотрим возмущения вида $h{\text{'}}(\eta ) = \hat {h} \cdot exp(\sigma \eta )$, $\hat {h}$ – амплитуда возмущений, $\eta = x - ct + {{x}_{0}}$. Тогда получим следующее дисперсионное соотношение

Решением данного уравнения являются три корня, один из которых – действительный, а два – сопряженных комплексных. В случае положительных солитонов (когда $c > 3$) имеем:

В этом случае асимптотическое поведение при $\eta \to \mp \infty $ заднего и переднего фронтов движущейся уединенной волны (солитона) дается формулами

Волновые решения модельной системы $(h - q)$ работы [2] при ${{\kappa }^{2}} \ll 1$ характеризуются наличием капиллярной ряби на переднем фронте быстрых волн большой амплитуды типа уединенных волн и солитонов. Включение членов порядка κ² в ${{(h - q)}_{1}}$ модели создает эффект сглаживания передних фронтов, что согласуется с экспериментальными наблюдениями волн, особенно в сильно вязких жидкостях. С приближением пары режимных параметров $\gamma $, $\kappa $ к линии бифуркационного перевала амплитуда капиллярной ряби на переднем фронте волны быстро уменьшается. Например, для $\delta = 0.15$ и c = 4, при уменьшении числа Капицы с $\gamma = 3750$ до $\gamma = 3.572$ (табл. 1), показатель экспоненты $a < 0$, обеспечивающий затухание амплитуды волн ряби при $\eta \to \infty $, возрастает по модулю в 11–16 раз. В то же время длина волн ряби увеличивается в два раза, а форма заднего фронта практически не изменяется.

Область существования положительных солитонов для однопараметрической модельной системы $(h - q)$ представляет собой счетное множество сегментов, вне которых ограниченных решений нет. В случае использования двухпараметрической модельной системы ${{(h - q)}_{1}}$, для заданных ограниченных значениях числа Капицы $\gamma $, количество данных сегментов становится конечным. Например (рис. 6), при $\delta = 0.1$, $\gamma = 3370$ их – пять, а при $\delta = 0.1$, $\gamma = 160$ – два. При $\delta = 0.1$, $\gamma < 22.8$ конечные сегменты, внутри которых нет ограниченных решений задачи, не существуют.

Рис. 6.

Области существования положительных солитонов для модельной системы ${{(h - q)}_{1}}$.

На рис. 7 показаны формы и фазовые портреты положительного двугорбого солитона $C_{1}^{'}$ для $\delta = 0.1$ и чисел Капицы $\gamma = 3370$, $\gamma = 6.5$. Как и в случае регулярных периодических волн, уменьшение числа Капицы для сильно вязких жидкостей и соответствующее увеличение значения параметра $\kappa $ приводят к сглаживанию осцилляций на переднем фронте солитона, форма же задней части изменяется слабо.

Рис. 7.

Формы и фазовые портреты положительного двугорбого солитона $C_{1}^{'}$ для $\delta = 0.1$.

На рис. 8, 9 представлено сравнение результатов настоящих расчетов и экспериментальных данных для различных режимов течения пленки жидкости.

Рис. 8.

Сравнение результатов расчетов ($\gamma = 6.5$) с экспериментальными данными [13]: 1 – зависимость ${{h}_{{{\text{max}}}}} - 1$ от ${\text{We}}$ при максимальном значении фазовой скорости ${{c}_{{r{\text{max}}}}}$; 2 – зависимость ${{h}_{{{\text{max}}}}} - 1$ от ${\text{We}}$ при максимальном значении среднего расхода ${{q}_{{0{\text{max}}}}}$ (оптимальный режим [2]); точками отмечены данные серии экспериментов [13] в диапазоне изменений чисел Капицы $2 < \gamma < 130$.

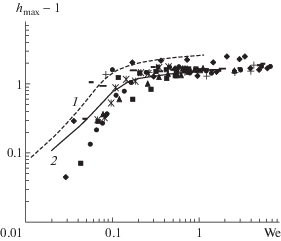
Рис. 9.

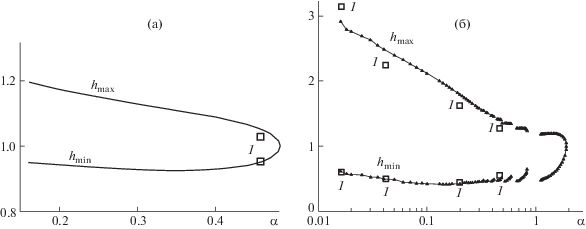
Сравнение результатов расчетов и данных экспериментов: а – проекции глобального аттрактора для тонкого слоя сильновязкой жидкости ($\delta $ = 0.0202, $\gamma $ = 5.9) на плоскость (${{h}_{{{\text{max}}}}},\alpha $), (${{h}_{{{\text{min}}}}},\alpha $), 1 – экспериментальные данные [21]; б – проекции глобального аттрактора на плоскость (${{h}_{{{\text{max}}}}},\alpha $), (${{h}_{{{\text{min}}}}},\alpha $) для $\delta $ = 2.75, $\gamma = 200$, 1 – экспериментальные данные [13].

На рис. 8 приведены данные серии экспериментов работы [13] для случая сильновязких жидкостей (область B на рис. 1) в диапазоне изменений чисел Капицы $\gamma $ от 2 до 130. Проведенные расчеты при $\gamma = 6.5$ и для оптимального режима (максимальное значение среднего расхода ${{q}_{{0{\text{max}}}}}$) показали, что в области ${\text{We}} > 0.1$ наблюдается хорошее согласование зависимости значений максимальной амплитуды волны h_max от безразмерного числа Вебера We.

В работе [18], на основе использования преобразования подобия, был проведен сравнительный анализ методов расчета нелинейных волн, формирующихся в пленке при пространственном и временном развитии возмущений основного стационарного течения. Использование инвариантных свойств эволюционных уравнений позволило провести сравнение свойств волновых режимов и полученных характеристик регулярных волн с данными численного решения соответствующей пространственной краевой задачи [19], в том числе и для формы волны возникающего пленочного течения.

В [20], для численного решения системы уравнений Навье–Стокса, использовался расширенный метод конечных элементов. В работе было показано хорошее соответствие полученных характеристик предельных волновых режимов и данных [18] для оптимального режима множества доминирующих волн — глобального аттрактора.

Следующие численные исследования течений пленки производились для режимов постоянного расхода ${{q}_{0}} = 1$ [18].

Результаты расчетов для тонкой пленки сильновязкой жидкости при $\delta $ = 0.0202, $\gamma $ = 5.9 показаны на рис. 9а. В работе [21] приведены экспериментальные данные для течения пленки жидкости при Re = 0.5. В плоскости (${{h}_{{{\text{max}}}}},\alpha $), (${{h}_{{{\text{min}}}}},\alpha $) представлены расчеты настоящей работы для тонкого слоя сильновязкой жидкости ($\delta $ = 0.0202, $\gamma $ = 5.9). Данные расчетов вблизи нейтральной кривой показывают хорошее соответствие значений максимальной h_max и минимальной h_min толщин пленки при заданном волновом числе α.

Проекции глобального аттрактора на плоскость (${{h}_{{{\text{max}}}}},\alpha $), (${{h}_{{{\text{min}}}}},\alpha $) для случая пленки большой толщины ($\delta $ = 2,75, $\gamma $ 0) представлены на рис. 9б. Расхождение h_max с данными экспериментов [13] в данном случае не превышают 7–10%.

5. БИФУРКАЦИИ ВОЛНОВЫХ СТРУКТУР СИЛЬНО ВЯЗКОЙ ЖИДКОСТИ ПРИ МАЛЫХ ЗНАЧЕНИЯХ ВОЛНОВОГО ЧИСЛА (ОБРАТНАЯ БИФУРКАЦИЯ)

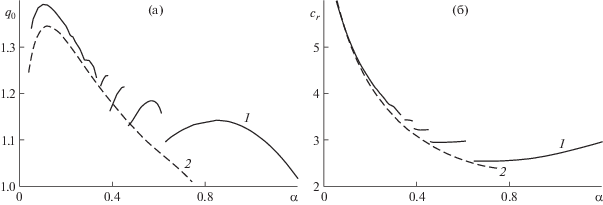
В пределе, при уменьшении волнового числа, регулярная периодическая волна переходит в уединенную волну. При этом для быстрых решений уравнений на переднем фронте возникают и усиливаются осцилляции, возрастает количество локальных максимумов. Увеличение вязкости приводит к сглаживанию этих осцилляций и снижению числа локальных максимумов вплоть до их исчезновения. Прямые численные расчеты уравнения (1.5) и граничных условий (3.2) показали, что при малых значенях числа Капицы ($\gamma = 6.5$) уменьшение волнового числа и последующая бифуркация решения не ведут к возрастанию числа локальных максимумов, а приводят к распаду волны с образованием соответствующего количества одногорбных структур. Их характеристики полностью совпадают с параметрами волны с соответствующим кратным увеличением волнового числа. Например, для случая ${\text{We}} = 0.02$, $\gamma = 6.5$, ($\delta = 0.01336$) “одногорбные” решения существуют до $\alpha \approx 0.09$. При меньших значения волнового числа мы наблюдаем образование двух идентичных друг другу волновых решений, которые существуют соответственно до $\alpha \approx 0.045$. Дальше, до $\alpha \approx 0.03$, можно наблюдать три идентичных друг другу волновых решения и т.д. Этот результат можно получить, решая эволюционные уравнения (1.5) или (1.6), но с граничными условиями, которые обобщают условия (3.2)

Анализ свойств глобального аттрактора показывает (рис. 10), что переход с решения n = 1 на решение $n = 2$ в области $\alpha \approx 0.09$ связан с тем, что локальный расход решения n = 2 в точке $\alpha = 0.1$ принимает свое максимальное значение ${{q}_{0}} = 1.0055$, в то время как для решения n = 1 локальный расход ${{q}_{0}} = 1.004$. В дальнейшем, с уменьшением волнового числа до $\alpha \approx 0.045$ ситуация повторяется и происходит переход на решение n = 3.

Рис. 10.

Глобальный аттрактор при ${\text{We}} = 0.02$, $\gamma = 6.5$ ($\delta = 0.01336$): а – проекция на плоскость (${{q}_{0}},\alpha $), б – проекции на плоскости (${{h}_{{{\text{max}}}}},\alpha $) и (${{h}_{{{\text{min}}}}},\alpha $), в – проекция на плоскость (${{c}_{r}},\alpha $), г – проекция на плоскость (${{c}_{r}},{{h}_{{{\text{max}}}}}$).

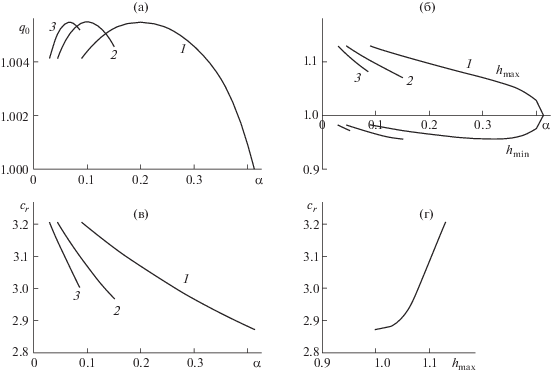
Как показано в [18], наряду с вынужденной частотой колебаний, на формирование волны может оказывать влияние частота с наибольшей скоростью роста, которая близка частоте оптимального режима. В результате чего наблюдаются перестройка течения и изменение частоты колебаний. Тогда, вследствие каких-либо особенностей возбуждения частоты на начальном участке при проведении экспериментов возможно формирование наряду с волновой структурой “основной частоты” также волн с кратным увеличением длины волны. Наблюдаемые при этом “первичные” и “вторичные” волновые течения, возникающие вследствие кратного увеличения длины волны, в проекции глобального аттрактора на плоскость (${{c}_{r}},{{h}_{{{\text{max}}}}}$) представляются единой кривой рис. 10г. Возможные решения с кратным увеличением длины волны, представляемые как решения с меньшими волновыми числами ${{\alpha }_{2}} = \alpha {\text{/}}2$, ${{\alpha }_{3}} = \alpha {\text{/}}3$ и т.д., будут иметь меньшее значение фазовой скорости ${{c}_{r}}$ и максимальной толщины пленки h_max (рис. 10а,б,в). Предельное значение волнового числа, при котором происходит обратная бифуркация, для $\gamma = 6.5$ имеет значение ${{\alpha }_{ * }} = 0.09$, а для γ = 40 примерно равно ${{\alpha }_{ * }} = 0.12$. Эти величины близки предельному значению волнового числа ${{\alpha }_{ * }} = 0.14$, при котором в экспериментах наблюдаются регулярные волны [16]. Отметим, что при ${{\alpha }_{ * }} = 0.09$ коэффициент нарастания $\alpha {{c}_{i}}$ для n = 2 примерно в 3.5 раза больше $\alpha {{c}_{i}}$ для n = 1, a $\alpha {{c}_{i}}$ для n = 3 при данном волновом числе принимает свое максимальное значение. Таким образом, при $\alpha < 0.09$, на формирование “предельного решения” эволюционной системы уравнений начинают влиять решения n = 2 и n = 3, что и приводит к возникновению “обратной бифуркации”.

6. ЗАКЛЮЧЕНИЕ

Исследована модельная система ${{(h - q)}_{1}}$ с двумя внешними параметрами $\delta $, $\kappa $, которая обобщает классическую $(h - q)$ модель [2] с одним параметром $\delta $ на течения вязких жидкостей в широком диапазоне значений числа Капицы $\gamma $. В модельной системе (1.5) работы [1] сохранены основные диссипативные члены, входящие в исходную краевую задачу для уравнений Навье–Стокса. При возрастании вязкости жидкости и соответствующем уменьшении $\gamma $ проявляются новые свойства волновых решений. Установлен механизм подавления мелкомасштабной ряби и сглаживания волновых фронтов при уменьшении $\gamma $. Показано, что с уменьшением $\gamma $ меняется характер бифуркаций нелинейных волн от состояния равновесия на нейтральной кривой. В пространстве режимных параметров $\delta $, $\kappa $ построена линия, разделяющая бифуркации к медленным и быстрым нелинейным волнам. Проведено сравнение с экспериментальными данными. Показано, что для заданного $\delta $ характеристики регулярных волн, образующихся при пространственном развитии, можно описать на основе использования расчетов глобального аттрактора. Проведено исследование явления обратной бифуркации при переходе уединенных периодических волн в солитоны.

Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта 18-01-00762 и 19-11-50105.