1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 4, 2021

Известия РАН. Механика жидкости и газа, 2021, № 4, стр. 114-124

О МОДЕЛИРОВАНИИ ЭНЕРГОВЫДЕЛЕНИЯ ФРАГМЕНТИРОВАННОГО МЕТЕОРОИДА В АТМОСФЕРЕ

М. Д. Брагин a, b, И. Г. Брыкина c, *

a Институт прикладной математики РАН им. М.В. Келдыша
Москва, Россия

b Московский физико-технический институт (государственный университет)
Долгопрудный, Россия

c МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия

* E-mail: shantii@mail.ru

Поступила в редакцию 24.12.2020
После доработки 18.01.2021
Принята к публикации 20.01.2021

Полный текст (PDF)

Аннотация

Рассматривается проблема моделирования абляции и энерговыделения космических тел, входящих в атмосферу Земли с большими скоростями и разрушающихся на множество фрагментов. На первом этапе фрагменты движутся с общей ударной волной, прежде чем разойтись на расстояние, достаточное для образования индивидуальных ударных волн. Исследуются модели облака фрагментов, моделирующие разрушение метеороида на этом этапе: двухпараметрическая модель, учитывающая изменения формы и плотности облака, и простые модели, не учитывающие эти эффекты. Проведено сопоставление моделей применительно к возможности воспроизведения с их помощью энерговыделения Челябинского болида. Показано влияние коэффициента теплопередачи на результаты расчета энерговыделения и бокового расширения облака при использовании разных моделей фрагментации и на применимость самих моделей. Найдена оптимальная простая модель, дающая наилучшее согласование с наблюдательной кривой энерговыделения Челябинского болида в зависимости от значения коэффициента теплопередачи.

Ключевые слова: метеороид, большие скорости, коэффициент теплопередачи, энерговыделение

Основными процессами, существенно влияющими на взаимодействие астероидов и комет с атмосферой Земли, являются разрушение и абляция. Разрушение космических тел вызывается действием аэродинамических сил, возрастающих по мере их проникновения в более плотные слои атмосферы. Интенсивный нагревкосмических объектов под дейтвием тепловых потоков, главным образом радиационных в случае крупных тел, ведет к значительному уносу их массы вследствие плавления и испарения. Одна из задач моделирования взаимодействия метеороида с атмосферой заключается в том, чтобы, разработав подходящий сценарий разрушения и модель абляции, воспроизвести траекторию, унос массы и энерговыделение (световую кривую) и таким образом оценить его неизвестные начальные массу и размер.

Когда астероид разрушается на большое количество фрагментов, на первом этапе они движутся с общей ударной волной, прежде чем разойтись на достаточное расстояние, чтобы иметь свои собственные ударные волны, и затем, после полного отделения, двигаться независимо. В настоящем исследовании рассматривается первая стадия разрушения метеороида на множество фрагментов, когда они движутся с общей ударной волной как единое тело. Григорян [1] первым разработал модель распада метеороида на мелкие осколки, когда раздробленное тело, обладающее значительной деформируемостью и пластичностью, сжимается в направлении полета и расширяется в боковом направлени из-за разницы давлений на лобовой и боковой частях тела. Позднее аналогичные модели сплющенного облака фрагментов, называемые “pancake” [2] и “жидкостными” [3] моделями, разрабатывались [2, 4–6] и использовались [3, 7–12] во многих исследованиях и продолжают использоваться до настоящего времени. Они отличаются, по существу, уравнениями для скорости бокового расширения облака, и наиболее популярной, применяемой в большинстве работ, является модель Хиллза и Годы [5]. Модели облака фрагментов могут применяться к моделированию разрушения космических объектов размером более нескольких метров, которые интенсивно дробятся. Они используются также в гибридных моделях разрушения, включающих независимое движение фрагментов [13–15].

Моделирование абляции космических объектов, входящих в атмосферу Земли со скоростями, намного превышающими скорости космических аппаратов, является очень сложной проблемой. Большинство исследований по радиационной газовой динамике относится к теплообмену возвращаемых космических аппаратов и зондов, поэтому рассматриваемый в них диапазон параметров обтекания ограничен значениями скоростей и размеров, характерными для данной задачи. Для решения уравнений движения, абляции и траектории космических тел, определяющих их торможение, обусловленное аэродинамическим сопротивлением, и унос массы вследствие сильного нагрева, надо не только знать тепловой поток к поверхности, но и представить его в виде аналитической зависимости от скорости и размера тела и плотности атмосферы. Обзор имеющихся в литературе корреляционных формул и их применение к расчету радиационных тепловых потоков в диапазоне параметров, характерном для космических аппаратов – при скоростях, меньших 12 км/c, даны в статьях [16, 17]. В более широком диапазоне параметров обтекания аппроксимационные формулы для радиационного теплового потока в точке торможения на неразрушающейся поверхности даны вработе [18]. В последние годы, в связи с актуализацией проблемы астероидно-космической опасности после Челябинского события, стали разрабатываться численные подходы к расчету радиационного теплового потока для параметров обтекания, характерных для входа в атмосферу крупных метеороидов, с учетом влияния абляции на поле течения в ударном слое, например [19–21]; численная модель [21] применялась к моделированию радиационного потока, достигающего поверхности Земли, в случае Тунгусского события [22]. Отметим, что результаты расчета радиационного потока разными авторами в случае больших скоростей и размеров и низких высот сильно отличаются друг от друга [21]. Существует неопределенность в результатах расчетов радиационного нагрева вследствие наличия многих неучтенных и неизвестных факторов (см. раздел 3); так, оценки статьи [23] показали значительную неопределенность в расчетах радиационного теплового потока в точке торможения для входа в атмосферу Земли космического аппарата со скоростью 15 км/с. В связи с недостаточностью данных по тепловому потоку в метеорном диапазоне параметров и его неопределенностью почти во всех работах, в которых решаются уравнения физической теории метеоров, коэффициент теплопередачи полагается постоянным (или ступенчатой функцией) и подбирается так, чтобы результаты расчетов соответствовали данным наблюдений за полетом и свечением космических тел.

В данной работе рассматриваются абляция и энерговыделение космических тел в атмосфере с учетом их разрушения на множество фрагментов. Для моделирования разрушения применяются модели облака фрагментов, движущихся с общей ударной волной: двухпараметрическая модель, разработанная авторами [6], учитывающая изменения формы и плотности облака, и простые модели, не учитывающие эти эффекты, в том числе, используемые в литературе [1, 5, 7]. Оценивается способность моделей воспроизвести наблюдательную кривую энерговыделения Челябинского болида путем численного решения для каждой из них уравнений метеорной физики и сравнения результатов расчета с наблюдательными данными. При моделировании абляции метеороида для коэффициента радиационной теплопередачи используется аппроксимационное выражение, зависящее от скорости и размера тела и плотности атмосферы, в которое вводится фактор неопределенности; также используется постоянное его значение. Изучается влияние неопределенности значения коэффициента теплопередачи на характеристики взаимодействия метеороида с атмосферой и на применимость моделей фрагментации.

1. МОДЕЛИРОВАНИЕ ФРАГМЕНТАЦИИ

Рассмотрим вход в атмосферу метеорного тела с большой скоростью V под углом θ по отношению к горизонтальной поверхности Земли. По мере увеличения плотности атмосферы ρ напряжение, возникающее под действием силы аэродинамического давления ρV2, начинает превышать прочность тела σ, что приводит к его разрушению. Предполагается, что до начала разрушения метеороид имеет форму шара, затем он продолжает свой полет как облако фрагментов и паров, объединенных общей ударной волной, движущееся как единое тело, которое под действием сил давления сжимается в направлении полета и расширяется в боковом направлении. При этом шар трансформируется в сплюснутый сфероид с отношением полуосей b/a = k ≥ 1. В двухпараметрической модели [6] вводятся два параметра: параметр сплющивания k и параметр γ, характеризующий уменьшение плотности раздробленного метеороида δ из-за увеличения промежутков между фрагментами: δ = δe/γ3, δe – его начальная плотность.

В двухпараметрической модели уравнение для скорости увеличения радиуса миделя облака фрагментов RS, характеризующее боковое расширение облака, имеет вид:

(1.1)
$\begin{gathered} \frac{{\operatorname{d} {{R}_{S}}}}{{\operatorname{d} t}} = {{\left( {\frac{{{{\gamma }^{3}}}}{k}} \right)}^{{1/2}}}{{\left( {\frac{\rho }{{{{\delta }_{e}}}}} \right)}^{{1/2}}}V,\quad k = \frac{{4\pi {{\delta }_{e}}}}{3}\frac{{R_{S}^{3}}}{{M{{\gamma }^{3}}}} \\ \gamma = 1 + \frac{{{{\rho }^{{1/2}}} - \rho _{f}^{{1/2}}}}{{\rho _{m}^{{1/2}} - \rho _{f}^{{1/2}}}}({{\gamma }_{m}} - 1) \\ \end{gathered} $

Здесь t – время, V и M – скорость и масса метеороида, индексы f и m соответствуют значениям величин на высотах начала фрагментации hf и максимальной яркости болида hm. Уравнение для RS получено при задании распределения давления по поверхности сфероида по формуле Ньютона. Уравнение для γ получено в предположении, что скорость увеличения расстояния между фрагментами пропорциональна ρ1/2 [24, 25], и записано в виде, удобном для определения свободного параметра γm путем приравнивания расчетной высоты hm и наблюдаемой, когда она известна. Полагается, что γ не превышает 3, так как при γ > 3 надо учитывать взаимодействие между фрагментами, при γ > 7 – их независимое движение [26].

В простых моделях облака фрагментов уравнения для радиуса миделя RS имеют одинаковую структуру и отличаются только значением коэффициента c, который считается постоянным

(1.2)
$\frac{{d{{R}_{S}}}}{{dt}} = c{{\left( {\frac{\rho }{{{{\delta }_{e}}}}} \right)}^{{1/2}}}V$

В модели Григоряна [2, 7] c = 1, в модели Хиллза и Годы [5] c = (7/2)1/2 ≈ 1.87.

Уравнение (1.2) имеет аналитическое решение в случае прямолинейной траектории и изотермической атмосферы, которое находится с использованием равенства d/dt = ρVsinθ/h* ⋅ d/dρ, где h* = 7 км – шкала высот

(1.3)
${{R}_{S}} = {{R}_{f}}\left( {1 + \frac{{2ch{\text{*}}}}{{\sin \theta \delta _{e}^{{1/2}}{{R}_{f}}}}({{\rho }^{{1/2}}} - \rho _{f}^{{1/2}})} \right)$

Здесь Rf – радиус тела на высоте hf. Из выражения (1.3) следует, что значение радиуса миделя RS в простых моделях определяется только параметрами на высоте начала фрагментации: θ, ρf, Rf и δe, и нет влияния на RS изменения массы и скорости метеороида вдоль траектории.

Отметим основные отличия моделей фрагментации. В двухпараметрической модели учитывается изменение плотности (влияние параметра γ) и формы (влияние параметра k) облака фрагментов, а в простых моделях – нет. В статье [5] и в последующих работах, использующих модель [5], говорится об облаке осколков и промежутках между ними, однако при этом плотность облака принимается постоянной и равной плотности тела до начала дробления. В двухпараметрической модели скорость роста RS зависит от массы тела M, которая меняется вдоль траектории из-за абляции, поэтому, чтобы найти RS и M, надо решать совместную задачу фрагментации, абляции и торможения метеороида. В простых моделях RS определяется не текущими, а начальными параметрами, таким образом, задача фрагментации фактически отделена от задачи абляции и движения.

2. МОДЕЛИРОВАНИЕ АБЛЯЦИИ И ЭНЕРГОВЫДЕЛЕНИЯ

Для моделирования взаимодействия метеорного тела с атмосферой используются уравнения метеорной физики [27], определяющие изменение его скорости и массы вдоль траектории. Уравнения торможения, абляции и траектории, и уравнение, задающее плотность изотермической атмосферы в зависимости от высоты полета h, имеют вид:

(2.1)
$\begin{gathered} M\frac{{dV}}{{dt}} = - \frac{\pi }{2}R_{s}^{2}{{C}_{D}}\rho {{V}^{2}},\quad Q\frac{{\operatorname{d} M}}{{\operatorname{d} t}} = - \frac{\pi }{2}R_{s}^{2}{{C}_{H}}\rho {{V}^{3}} \\ \frac{{dh}}{{dt}} = - V\sin \theta ,\quad \rho = {{\rho }_{0}}\exp \left( { - \frac{h}{{h{\text{*}}}}} \right) \\ \end{gathered} $

Здесь CD и CH – коэффициенты сопротивления и теплопередачи на единицу площади миделя, Q – эффективная теплота уноса массы, ρ0 = 1.29 × 10–3 г/см3. Траектория метеороида считается прямолинейной (θ = const), учет криволинейности траектории, как было показано ранее [28], оказывает слабое влияние на изменение его массы и энерговыделения.

Интенсивность свечения метеорного тела I, наблюдаемая при его движении в атмосфере, определяется в зависимости от изменения его кинетической энергии E в единицу времени и коэффициента эффективности излучения τ [29]

(2.2)
$I = \tau J,\quad J = - \frac{{dE}}{{dt}} = - \left( {\frac{{{{V}^{2}}}}{2}\frac{{dM}}{{dt}} + MV\frac{{dV}}{{dt}}} \right)$

Рассматривается также энерговыделение метеорного тела на единицу высоты

(2.3)
$\frac{{dE}}{{dh}} = \frac{J}{{V\sin \theta }}$

Для расчета абляции и торможения раздробленного метеороида с применением простых моделей фрагментации уравнения (2.1) надо решать вместе с уравнением (1.2). При применении двухпараметрической модели уравнения (2.1) решаются соместно с уравнениями (1.1), до начала дробления полагается γ = 1 и k = 1.

Основные определяющие параметры, входящие в уравнения (2.1), – это коэффициент сопротивления CD и коэффициент теплопередачи CH. В литературе коэффициент сопротивления обычно полагается постоянным, при использовании простой модели облака фрагментов – равным 1 или 1.5. Однако очевидно, что по мере сплющивания облака коэффициент сопротивления должен меняться. В работе [6] получено аналитическое решение для коэффициента лобового сопротивления сфероида в зависимости от параметра k при задании распределения давления вдоль поверхности по формуле Ньютона

(2.4)
$C_{D}^{{}} = \frac{{2{{k}^{2}}}}{{{{k}^{2}} - 1}}\left( {1 - \frac{{\ln {{k}^{2}}}}{{{{k}^{2}} - 1}}} \right),\quad \mathop {\lim }\limits_{k \to 1} = 1,\quad \mathop {\lim }\limits_{k \to \infty } = 2$

Это решение с точностью до 5% аппроксимируется простой формулой

(2.5)
$C_{D}^{{}} = 2 - \frac{1}{k}$

Формула (2.5) согласуется с точностью до 12% с формулой, полученной путем аппроксимации численных расчетов [30] гиперзвукового обтекания диссоциированным воздухом космических аппаратов со сфероидальной лобовой поверхностью

(2.6)
${{C}_{D}} = 1.78 - \frac{{0.85}}{k}$

Коэффициент радиационной теплопередачи на единицу площади миделя для сфероида представим в виде

(2.7)
${{C}_{H}} = \psi \varphi \beta {{C}_{{H0}}}$

Здесь параметр β характеризует зависимость теплового потока в точке торможения сфероида от параметра k, для него использовалась аппроксимационная формула работы [31]

(2.8)
$\beta = \frac{1}{{0.956 + 0.036k}},\quad k \leqslant 6,\quad \beta = 0.85,\quad k > 6$
СН0 – коэффициент теплопередачи в точке торможения сферы, зависящий от плотности атмосферы ρ, скорости тела V и радиуса кривизны его затупленной части R. Для него использовалась модификация аппроксимационной формулы работы [18]
(2.9)
$\begin{gathered} {{C}_{{H0}}} = \frac{{2 \times {{{10}}^{{ - 5}}}q}}{{\rho {{V}^{3}}}},\quad q = 0.5({{q}_{1}} + {{q}_{2}})\left( {1 - 0.17{{{\left| {\lg \frac{\rho }{{\rho {\text{*}}}}} \right|}}^{{1.5}}}} \right) \times \\ \times \;\left( {1 - 0.22{{{\lg }}^{2}}\frac{R}{{1.5}}} \right)\left( {1 - 7\lg \frac{V}{{17}}{{{\left| {\lg \frac{V}{{17}}} \right|}}^{{0.7}}}} \right) \\ {{q}_{1}} = {{\varphi }_{1}}(V){{\rho }^{{{{n}_{1}}(V)}}}{{R}^{{{{m}_{1}}(V)}}},\quad {{q}_{2}} = {{\varphi }_{2}}(V){{\rho }^{{{{n}_{2}}}}}{{R}^{{{{m}_{2}}(\rho ,V)}}} \\ \end{gathered} $
где [ρ] = кг/м3, [R] = м, [V] = км/с, [q] = Вт/см2, ρ* – плотность атмосферы на высоте 50 + + 15(V – 12)/V км, функции φ1, n1, m1 и φ2, n2, m2 приведены в статье [18]. Выражение (2.9) для коэффициента теплопередачи в точке торможения основано на комбинации формул работ [31] и [32] (q1 и q2), аппроксимирующих результаты численных расчетов радиационного теплового потока. Эти формулы были получены для ограниченного диапазона параметров обтекания, поэтому при расширении этого диапазона они дают неверные результаты, например, при скоростях V выше 17 км/с. В связи с этим были сделаны корреляции по параметрам V, R и ρ [18], которые позволили достичь адекватного согласования с имеющимися в литературе численными расчетами радиационного теплового потока для некоторого диапазона параметров, соответствующего участку траектории Челябинского метеороида с наиболее интенсивным энерговыделением. В формуле (2.9), по сравнению с работой [18], сделаны уточняющие поправки по скорости V и по плотности атмосферы ρ для расширения диапазона ее применимости на меньшие скорости и более низкие высоты. При радиусе затупления R более 10 м зависимость СН0 от R становится слабой, поэтому мы полагали R равным 10 в выражении (2.9). Параметр φ отражает тот факт, что тепловой поток к поверхности тела снижается по мере удаления от точки торможения, поэтому коэффициент теплопередачи на единицу площади миделя будет меньше, чем коэффициент теплопередачи в точке торможения. В данном исследовании φ полагался равным 0.7.

Параметр ψ введен в выражение (2.7) для того, чтобы учесть существующую неопределенность в значении радиационного потока к телу, которая связана со многими факторами: с неучетом влияния излучения воздуха перед ударной волной, турбулентности, экранирования парами метеороида; с неопределенностью в оптических свойствах горячего воздуха и паров, в моделях переноса излучения и поля течения; с неизвестностью реальной формы тела. В исследовании [23] отмечалось, что такая неопределенность радиационного потока в точке торможения составляет примерно от +81 до –52% для входа в атмосферу Земли со скоростью 15 км/с. Для изучения влияния неопределенности коэффициента теплопередачи CH на характеристики взаимодействия метеороида с атмосферой и на применимость разных моделей облака фрагментов параметр ψ варьировался при проведении расчетов. Расчеты также проводились с принятым в литературе постоянным значением CH.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Модели фрагментации, описанные в первом разделе, применялись для моделирования взаимодействия с атмосферой Челябинского астероида, вошедшего в атмосферу Земли 15 февраля 2013 г., с целью сопоставить возможности моделей воспроизвести наблюдательную кривую его энерговыделения [33]. Другая цель состояла в оценке влияния значения коэффициента теплопередачи на энерговыделение болида, боковое расширение облака фрагментов и применимость рассматриваемых моделей.

Отметим, что разрушение Челябинского астероида – очень сложное явление, и модели облака фрагментов не дают о нем полного представления. Отдельные фрагменты отделялись от облака и вели себя независимо, мелкие фрагменты тормозились и падали на землю. Однако, согласно наблюдениям [34], крупные фрагменты начали отделяться от облака на высотах ниже 25 км, и это дает основание использовать модели облака фрагментов при моделировании взаимодействия Челябинского метеороида с атмосферой выше этой высоты.

Для каждой модели фрагментации решалась соответствующая система обыкновенных дифференциальных уравнений методом Рунге–Кутты. В качестве начальных параметров, соответствующих входу Челябинского астероида в атмосферу, брались результаты обработки наблюдательных данных [34]: Ve = 19 км/с, θ = 18°, δe = 3.3 г/см3, высота начала фрагментации hf полагалась равной 45 км, что соответствует начальной прочности метеороида σ ≈ 0.75 МПа; эффективная теплота уноса массы Q полагалась равной 6 км2/c2. Неизвестная начальная масса метеороида Me для каждой модели и каждого расчетного случая находилась таким образом, чтобы максимальное значение энерговыделения на единицу высоты dE/dh соответствовало данным наблюдений [33] и составляло ∼82 кт ТНТ/км. (1 кт ТНТ (тротилового эквивалента) = 4.184 × 1012 Дж = = 4.184 ТДж. Тротиловый эквивалент – это мера энерговыделения высокоэнергетических событий; в таких едиицах принято оценивать и энерговыделение крупных метеороидов, в частности, Челябинского.) Для двухпараметрической модели параметр γm подбирался так, чтобы расчетная высота, где достигается максимум энерговыделения, совпала с высотой, определенной из наблюдений [33]. При расчете коэффициентов сопротивления и теплопередачи по формулам (2.5)–(2.9) параметр формы k, который непосредственно не входит в простые модели (хотя в модели [5] облако фрагментов также рассматривалось как сфероид), вычислялся из второго соотношения (1.1), связывающего массу и радиус миделя сфероида.

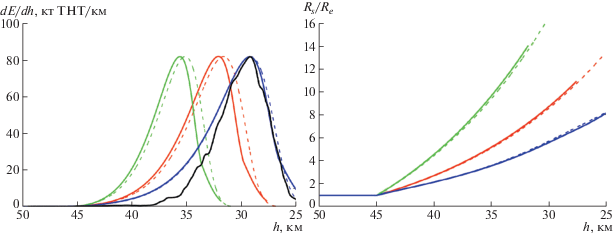
Результаты расчетов энерговыделения раздробленного метеороида и радиуса миделя, отнесенного к его значению Re при входе в атмосферу, для двухпараметрической модели и простых моделей с c = 1 [2, 7] и c = 1.87 [5] при переменном коэффициенте теплопередачи CH с ψ = 1 и постоянном CH = 0.1 (наиболее часто используемом в литературе) приведены на рис. 1 в зависимости от высоты полета h. Видно, что при использовании для CH формулы (2.7) с ψ = 1 и при CH = = 0.1 результаты расчетов довольно близки друг к другу. (При ψ = 1 значение CH постепенно увеличивается вдоль траектории до 0.1 на высоте ∼50 км, достигает максимума 0.11 на высоте ∼43 км, затем уменьшается). Простые модели с c = 1 и c = 1.87 дают высоту, где достигается пик яркости болида, на несколько километров выше наблюдаемой. Для двухпараметрической модели кривая энерговыделения хорошо согласуется с наблюдательной кривой [33], также приведенной на рис. 1.

Рис. 1.

Результаты расчета энерговыделения болида и радиуса миделя для двухпараметрической (синие линии) и простых моделей [2, 7] (красные) и [5] (зеленые) при переменном CH с ψ = 1 (сплошные линии) и при CH = = 0.1 (штриховые). Черная кривая – наблюдательные данные [33].

Рисунок 1 показывает также, что двухпараметрическая модель дает значительно меньшие значения радиуса миделя, т.е. значительно меньшее боковое расширение облака фрагментов, чем простые модели. Физически нереальное возрастание радиуса миделя в модели [5] в литературе принято ограничивать некоторым значением RS/Re, обычно не превышающим 7–8 [9, 10, 15]. Влияние такого обрезания радиуса миделя в разных моделях фрагментации на результаты моделирования энерговыделения болида изучалось ранее [12].

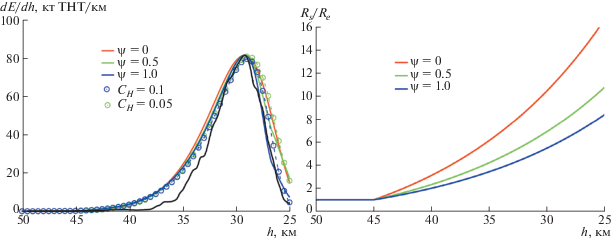
Влияние коэффициента теплопередачи на моделирование энерговыделения болида и радиус миделя облака фрагментов для двухпараметрической модели демонстрирует рис. 2. С увеличением параметра ψ и, соответственно, CH, абляция возрастает, что приводит к уменьшению массы метеороида, его радиуса миделя и степени расширения облака осколков в боковом направлении. Меньшее влияние величина CH оказывает на энерговыделение, особенно перед пиком яркости. Варьирование параметра ψ ведет только к изменению формы кривой энерговыделения, делая ее немного шире при уменьшении значения коэффициента теплопередачи. Наилучшее согласование с наблюдательной кривой энерговыделения [33] достигается при ψ = 1 (ψ от 0.8 до 1.2) и при CH = 0.1. Значение CH оказывает слабое влияние на оценку начальной массы метеороида Me при входе в атмосферу: при ψ = 1.2, 1, 0.8, 0.5 масса Me равна соответственно 1.318, 1.325, 1.337, 1.355 × × 1010 г; Me = 1.325 × 1010 г при CH = 0.1. Двухпараметрическая модель дает значение начальной массы, близкое к наиболее вероятным значениям 1.2 и 1.3 × 1010 г по оценкам работ [34] и [35].

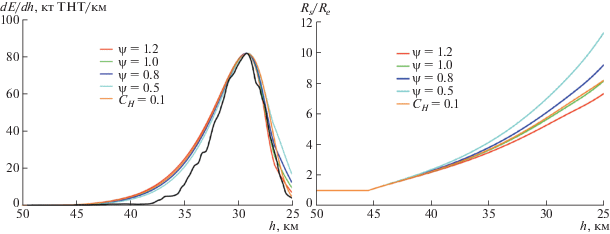
Рис. 2.

Влияние коэффициента теплопередачи на результаты расчета энерговыделения болида и радиуса миделя для двухпараметрической модели. Черная кривая – наблюдательные данные [33].

Отметим, что в простых моделях, в отличие от двухпараметрической, варьирование параметра ψ почти не влияет на радиус миделя, так как в этих моделях, как упоминалось выше, задача фрагментации практически отделена от задачи абляции (почти незаметное влияние происходит через значение радиуса Rf на высоте начала фрагментации (формула (1.3)). В этом заключено некоторое противоречие: абляция влияет на массу раздробленного метеороида и не влияет на его радиус миделя.

Для простых моделей коэффициент теплопередачи оказывает сильное влияние на расчетную высоту, где достигается максимум яркости болида. (В отличие от двухпараметрической модели, где корректирование параметра γm позволяет достичь совпадения расчетной высоты максимума с наблюдаемой). При ψ = 1 в формуле (2.7) модель [2, 7] дает высоту достижения пика яркости болида примерно на 3 км выше высоты ∼29.5 км, соответствующей наблюдениям, а модель [5] – на 6 км выше (рис. 1). Это объясняется очень быстрым боковым расширением облака фрагментов в этих моделях и, как следствие, слишком ранним ростом кривой энерговыделения. Уменьшая коэффициент теплопередачи, можно сдвинуть вниз высоту пика яркости. Так, уменьшение СН в два раза (ψ = 0.5) сдвигает высоту пика до ∼30.5 км для модели [2, 7] и до ∼34 км для модели [5].

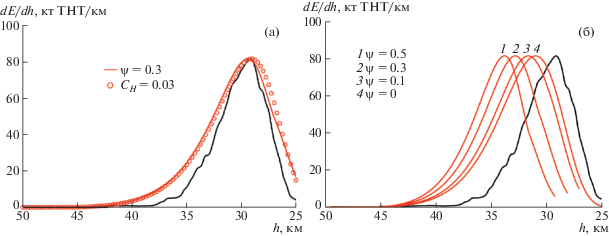
Для модели [2, 7] с c = 1 удовлетворительное согласие с наблюдательной кривой энерговыделения болида достигается при ψ = 0.3 и при CH = 0.03, что демонстрирует рис. 3а. Для модели [5] с c = 1.87 уменьшение CH вплоть до 0 (отсутствие абляции) не позволяет достичь согласия с данными наблюдений, что демонстрирует рис. 3б. При любом значении ψ высота, где достигается пик яркости болида, остается выше наблюдаемой, что связано с очень сильным возрастанием радиуса миделя облака фрагментов из-за большого параметра c, почти в два раза превышающего параметр c в модели [2, 7]. Как показано в работе [12], обрезание радиуса миделя в модели [5] позволяет сдвинуть высоту достижения пика яркости вниз вплоть до совпадения с наблюдаемой, однако при этом расчетная кривая энерговыделения оказывается намного шире наблюдательной, и значение начальной массы Me = 2.5 × 1010 г примерно в два раза превышает наиболее вероятные значения [34, 35]. Таким образом, при использовании модели [5] не удается получить согласование с данными наблюдений.

Рис. 3.

Результаты расчета энерговыделения болида для простых моделей: c = 1 [2, 7] (а) и c = 1.87 [5] (б) при разных коэффициентах теплопередачи. Черная кривая – наблюдательные данные [33].

На основании многочисленных расчетов, проведенных для простых моделей при разных значениях параметра ψ в формуле для коэффициента теплопередачи и параметра с в уравнении для радиуса миделя, найден оптимальный параметр c, при котором достигается наилучшее согласование с наблюдательной кривой энерговыделения Челябинского болида [33] при заданном значении параметра ψ. В таблице приведены значения параметров c и Me в зависимости от значений ψ, при которых достигается совпадение максимумов расчетной и наблюдательной кривых энерговыделения для простых моделей фрагментации.

Таким образом, при c > 1.39 невозможно получить совпадение с данными наблюдений для Челябинского события ни при каких значениях коэффициента теплопередачи. Зависимость c (ψ) из табл. 1 аппроксимируется простой формулой

$c(\psi ) = {{(\psi + 0.7)}^{{ - 0.92}}}$
Таблица 1
Ψ 0 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
c 1.39 1.31 1.24 1.11 1.00 0.92 0.85 0.79 0.74 0.69 0.65 0.615
Me, 1010 г 1.45 1.472 1.477 1.477 1.460 1.434 1.407 1.380 1.352 1.329 1.306 1.285

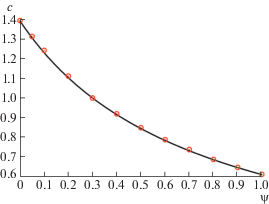
Зависимости c(ψ), определяемые таблицей и формулой (3.1), приведены на рис. 4.

Рис. 4.

Зависимость c (ψ). Красные маркеры – данные таблицы, черная линия – формула (3.1).

Анализ расчетов показал, что для моделей облака фрагментов, моделирующих разрушение крупных метеорных тел (с радиусом более нескольких метров), результаты расчетов с постоянным коэффициентом теплопередачи CH = 0.1 ψ близки к результатам, полученным с переменным коэффициентом, определяемым формулой (2.7) (отметим, что это не относится к случаю движения независимых фрагментов и тел меньших размеров). Таким образом, если использовать постоянное значение CH, то параметр c, определяющий оптимальную простую модель, находится по формуле

$c({{C}_{H}}) = {{(10{{C}_{H}} + 0.7)}^{{ - 0.92}}}$

В уравнение абляции коэффициент теплопередачи входит в комбинации CH/Q = Cab, которую назовем, как и в статье [10], параметром абляции. (В литературе принято называть коэффициентом абляции комбинацию CH/(QCD) и полагать ее, как и коэффициент CD, постоянной). Поэтому имеет смысл представить параметр c оптимальной модели фрагментации как функцию параметра абляции Cab. Учитывая, что в проведенных расчетах Q полагалось равным 6 км2/c2, получим в случае постоянного CH

$c({{C}_{{ab}}}) = {{(60{{C}_{{ab}}} + 0.7)}^{{ - 0.92}}},\quad \left[ {{{C}_{{ab}}}} \right] = {{{\text{с}}}^{2}}{\text{/к}}{{{\text{м}}}^{2}}$

В случае расчета CH по формуле (2.7)

$c({{\psi }_{{ab}}}) = {{(6{{\psi }_{{ab}}} + 0.7)}^{{ - 0.92}}},\quad {{\psi }_{{ab}}} = \psi {\text{/}}Q,\quad [{{\psi }_{{ab}}}] = {{{\text{с}}}^{2}}{\text{/к}}{{{\text{м}}}^{2}}$

Результаты моделирования энерговыделения и радиуса миделя облака фрагментов для оптимальных простых моделей при разном задании коэффициента теплопередачи показаны на рис. 5. Видно, что наилучшее согласование с наблюдательной кривой энерговыделения получается при ψ = 1 и при CH = 0.1 (при ψab = 0.167 с2/км2 и при Cab = 0.0167 с2/км2), как и для двухпараметрической модели. Параметр c в этом случае равен 0.615, а радиус миделя в этой оптимальной простой модели принимает вдоль траектории вполне допустимые значения (RS/Re не превышает 8).

Рис. 5.

Влияние коэффициента теплопередачи на результаты расчета энерговыделения болида и радиуса миделя для оптимальных простых моделей. Черная кривая – наблюдательные данные [33].

ЗАКЛЮЧЕНИЕ

Показано, что коэффициент теплопередачи сильно влияет на результаты расчета энерговыделения метеороида с использованием простых моделей фрагментации, особенно на высоту, где достигается максимум энерговыделения. Предложен оптимальный коэффициент с в уравнении для радиуса миделя в зависимости от коэффициента теплопередачи (параметра абляции), при котором достигается совпадение расчетной высоты пика яркости Челябинского болида с наблюдательной [33]. При значениях с более 1.39 невозможно достичь согласия с данными наблюдений при любых значениях коэффициента теплопередачи (Q = 6 км2/c2).

Наилучшее согласование с наблюдательной кривой энерговыделения Челябинского болида [33] получается, когда используется двухпараметрическая модель или оптимальная простая модель с c = 0.615 при параметре ψ = 1 в выражении для коэффициента теплопередачи (2.7) и при CH = 0.1, Q = 6 км2/c2. Эти две модели фрагментации дают оценки массы метеороида при входе в атмосферу 1.325 × 1010 г и 1.285 × 1010 г, очень близкие к оценкам исследований [34, 35] по анализу данных наблюдений Челябинского события.

Список литературы

  1. Григорян С.С. О движении и разрушении метеоритов в атмосферах планет // Космич. исслед. 1979. Т. 17. № 6. С. 875–893.

  2. Melosh H.J. Atmospheric breakup of terrestrial impactors // Proc. Lunar Planet. Sci. 1981. V. 12A. P. 29–35.

  3. Svetsov V.V., Nemtchinov I.V., Teterev A.V. Disintegration of large meteoroids in Earth’s atmosphere: Theoretical models // Icarus. 1995. V. 116. P. 131–153.

  4. Chyba C.F., Thomas P.J., Zahnle K.J. The 1908 Tunguska explosion – Atmospheric disruption of a stony asteroid // Nature. 1993. V. 361. P. 40–44.

  5. Hills J.G., Goda M.P. The fragmentation of small asteroids in the atmosphere // Astron. J. 1993. V. 105. № 3. P. 1114–1144.

  6. Брыкина И.Г. О модели фрагментации крупного метеороида: моделирование взаимодействия Челябинского метеороида с атмосферой // Астрон. вестн. 2018. Т. 52. № 5. С. 437–446.

  7. Григорян С.С., Ибодов Ф.С., Ибадов С.И. Челябинский суперболид: к физике взрыва // Астрон. вестн. 2013. Т. 47. № 4. С. 292–298.

  8. Register P.J., Mathias D.L., Wheeler L.F. Asteroid fragmentation approaches for modeling atmospheric energy deposition // Icarus. 2017. V. 284. P. 157–166.

  9. Collins G.S., Lynch E., McAdam R., Davison T.M. A numerical assessment of simple airblast models of impact airbursts // Meteorit. & Planet. Sci. 2017. V. 52. P. 1542–1560.

  10. McMullan S., Collins G.S. Uncertainty Quantification in Continuous Fragmentation Airburst Models // Icarus. 2019. V. 327. P. 19–35.

  11. Brykina I.G., Bragin M.D. On models of meteoroid disruption into the cloud of fragments // Planetary & Space Sci. 2020. V. 187. № 104942.

  12. Брыкина И.Г., Брагин М.Д. Об ограничении бокового расширения облака фрагментов разрушенного метеороида // Физико-химическая кинетика в газовой динамике. 2020. Т. 21. Вып. 1. http://chemphys.edu.ru/issues/2020-21-1/articles/894/

  13. Wheeler L.F., Mathias D.L., Stokan E., Brown P.G. Atmospheric energy deposition modeling and inference for varied meteoroid structures // Icarus. 2018. V. 315. P. 79–91.

  14. Wheeler L.F., Mathias D.L. Probabilistic assessment of Tunguska-scale asteroid impacts // Icarus. 2019. V. 327. P. 83–96.

  15. Borovička J., Popova O., Spurný P. The Maribo CM2 meteorite fall – Survival of weak material at high entry speed // Meteorit. & Planet. Sci. 2019. V. 54. P. 1024–1041.

  16. Суржиков С.Т., Шувалов М.П. Тестирование расчетных данных по радиационному и конвективному нагреву спускаемых космических аппаратов нового поколения // Теплофизика высоких температур. 2013. Т. 51. № 3. С. 456–470.

  17. Суржиков С.Т., Шувалов М.П. Анализ радиационно-конвективного нагрева четырех типов спускаемых космических аппаратов // Физико-химическая кинетика в газовой динамике. 2014. Т. 15. № 4. С. 1–18.

  18. Брыкина И.Г., Егорова Л.А. Аппроксимационные формулы для радиационного теплового потока при больших скоростях // Изв. РАН. МЖГ. 2019. № 4. С. 123–134.

  19. Park C. Inviscid-flow approximation of radiative ablation of asteroidal meteoroids by line-by-line method // AIAA Paper 2016–0506. 2016. 18 p.

  20. Park C. Inviscid-flow approximation of radiative ablation of cometary meteoroids // AIAA Paper 2016–4430. 2016. 17 p.

  21. Johnston C.O., Stern E.C., Wheeler L.F. Radiative heating of large meteoroids during atmospheric entry // Icarus. 2018. V. 309. P. 25–44.

  22. Johnston C.O., Stern E.C. A model for thermal radiation from the Tunguska airburst // Icarus. 2019. V. 327. P. 48–59.

  23. Johnston C.O., Mazaheri A., Gnoffo P., Kleb B., Sutton K., Prabhu D., Brandis A.M., Bose D. Radiative heating uncertainty for hyperbolic Earth entry, part 1: flight simulation modeling and uncertainty // J. Spacecraft & Rockets. 2013. V. 50. № 1. P. 19–38.

  24. Artemieva N., Shuvalov V. Motion of a fragmented meteoroid through the planetary atmosphere // J. Geophys. Res. Planets. 2001. V. 106. E2. P. 3297–3309.

  25. Лукашенко В.Т., Максимов Ф.А. Математическая модель разлета осколков метеорного тела после разрушения // Инженерный журнал: наука и инновации. 2017. Т. 9 (69).

  26. Максимов Ф.А. Сверхзвуковое обтекание системы тел // Компьютерные исследования и моделирование. 2013. № 5. С. 969–980.

  27. Бронштэн В.А. Физика метеорных явлений. М.: Наука, 1981. 416 с.

  28. Брыкина И.Г., Егорова Л.А. Моделирование движения, абляции и энерговыделения метеороида в атмосфере с учетом криволинейности траектории // Физико-химическая кинетика в газовой динамике. Т. 21. Вып. 2. http://chemphys.edu.ru/issues/2020-21-2/articles/903/

  29. Ceplecha Z., Borovička J., Elford W.G., ReVelle D.O., Hawkes R.L., Porubcan V.Í., Šimek M. Meteor phenomena and bodies // Space Sci. Rev. 1998. V. 84. P. 327–471.

  30. Голомазов М.М., Литвинов И.А., Литвинов Л.А., Иванков А.А., Финченко В.С. Численное моделирование обтекания спускаемых аппаратов при входе в атмосферу планеты // Вестн. МГТУ им. Н.Э. Баумана. Сер. “Машиностр.” 2011. № 4. С. 42–53.

  31. Suttles J.T., Sullivan E.M., Margolis S.B. Curve fits of predicted inviscid stagnation-point radiative heating rates, cooling factors, and shock standoff distances for hyperbolic earth entry // NASA CR-1548. 1974. 45 p.

  32. Brandis A.M., Johnston C.O. Characterization of Stagnation-Point Heat Flux for Earth Entry // AIAA 2014–2374. 2014. 20 p.

  33. Brown P.G., Assink J.D., Astiz L., Blaauw R., Boslough M.B., Borovička J., Brachet N., Brown D., Campbell-Brown M., Ceranna L., Cooke W., de Groot-Hedlin C., Drob D.P., Edwards W., Evers L.G., Garces M., Gill J., Hedlin M., Kingery A., Laske G., Le Pichon A., Mialle P., Moser D.E., Saffer A., Silber E., Smets P., Spalding R.E., Spurny P., Tagliaferri E., Uren D., Weryk R.J., Whitaker R., Krzeminski Z. A 500-kiloton airburst over Chelyabinsk and an enhanced hazard from small impactors // Nature. 2013. V. 503. P. 238–241.

  34. Borovička J., Spurný P., Brown P., Wiegert P., Kalenda P., Clark, D., Shrbený L. The trajectory, structure and origin of the Chelyabinsk asteroidal impactor // Nature. 2013. V. 503. P. 235–237.

  35. Popova O.P., Jenniskens P., Emel’yanenko V., Kartashova A., Biryukov E., Khaibrakhmanov S., Shuvalov V., Rybnov Yu., Dudorov A., Grokhovsky V.I., Badyukov D.D., Yin Q.-Z., Gural P.S., Albers J., Granvik M., Evers L.G., Kuiper J., Kharlamov V., Solovyov A., Rusakov Yu.S., Korotkiy S., Serdyuk I., Korochantsev A.V., Larionov M.Yu., Glazachev D., Mayer A.E., Gisler G., Gladkovsky S.V., Wimpenny J., Sanborn M.E., Yamakawa A., Verosub K.L., Rowland D.J., Roeske S., Botto N.W., Friedrich J.M., Zolensky M.E., Le L., Ross D., Ziegler K., Nakamura T., Ahn I., Lee J.I., Zhou Q., Li X.-H., Li Q.-L., Liu Yu, Tang G.-Q., Hiroi T., Sears D., Weinstein I.A., Vokhmintsev A.S., Ishchenko A.V., Schmitt-Kopplin Ph., Hertkorn N., Nagao K., Haba M.K., Komatsu M., Mikouchi T. Chelyabinsk airburst, damage assessment, meteorite recovery, and characterization // Science. 2013. V. 342. Iss. 6162. P. 1069–1073.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал