Известия РАН. Механика жидкости и газа, 2021, № 2, стр. 52-62

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И ПОСТАНОВКА ЗАДАЧИ

Вязкость водных растворов солей увеличивается с ростом их концентрации. Для описания такой закономерности наиболее часто используются экспоненциальная (формула Франк-Каменецкого) или линейная зависимости динамической вязкости раствора μ от концентрации примеси:

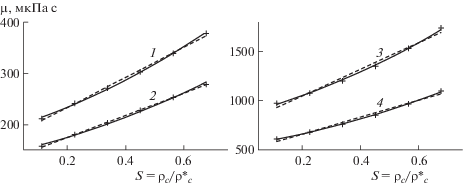
Здесь μ₀ – вязкость чистой воды, $S = {{\rho }_{c}}{\text{/}}\rho _{c}^{ * }$ – безразмерная плотность растворенной примеси; ρ_c, $\rho _{c}^{ * }$ – плотность примеси (масса примеси в единичном объеме раствора) текущая и соответствующая насыщенному раствору. Верхним индексом “$ * $” отмечен насыщенный раствор. Величину ρ_c называют также концентрацией. Константы ${{\Gamma }_{e}}$ и ${{\Gamma }_{l}}$ – параметры изменения вязкости. Использована работа [15], в которой собран и обработан большой объем экспериментальных данных о значениях динамической вязкости водного раствора хлорида натрия (NaCl) в широком диапазоне температур и давлений. На рис. 1 маркерами отмечены значения [15], соответствующие условиям на глубине в несколько километров (слева) и в почве на глубине в несколько десятков метров (справа). По этим данным методом наименьших квадратов построены оптимальные кривые, заданные экспоненциальной и линейной функциями. Найдены константы ${{\Gamma }_{e}} = 1.02$, 1.00, 1.03, 1.04 (1–4) и ${{\Gamma }_{l}} = 1.68$, 1.62, 1.74, 1.76 (1–4). Видно, что ${{\Gamma }_{e}}$ и ${{\Gamma }_{l}}$ меняются несущественно, поэтому можно использовать единые значения

Рис. 1.

Зависимость вязкости водного раствора соли NaCl от ее относительной плотности. Маркеры – данные [15] при $P = 10$ МПа и $T = 423$ (1), $473$ K (2); $P = 0.1$ МПа и $T = 298$ (3), $323$ K (4). Сплошная и пунктирная линии – аппроксимирующие кривые, соответствующие экспоненциальной и линейной функциям.

Как экспоненциальная функция, так и линейная описывают экспериментальные данные с хорошей точностью. Далее для определенности будет использоваться экспоненциальная зависимость $\mu $ от S.

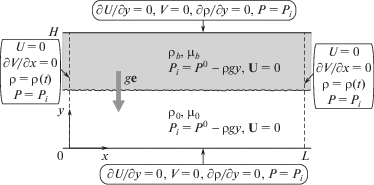
Рассматривается прямоугольная двумерная пористая область (часть бесконечного горизонтального слоя), заполненная двухслойной жидкостью так, что граница между слоями проходит по середине области (рис. 2). В нижней половине находится чистая вода с плотностью ρ₀ и вязкостью ${{\mu }_{0}}$, верхняя половина заполнена водным раствором соли с плотностью ρ_b и вязкостью ${{\mu }_{b}}$. В начальный момент система неподвижна. Соль диффундирует из верхней части области в нижнюю, при этом переходная зона между слоями расширяется со временем. Полагается, что ${{\rho }_{b}} > {{\rho }_{0}}$, т.е. состояние жидкости неустойчиво в поле силы тяжести и со временем развивается концентрационная конвекция.

Рис. 2.

Постановка задачи.

Конвективное движение и массоперенос описываются в рамках гидродинамической модели, которая включает уравнения неразрывности, движения (уравнение Дарси) и переноса примеси [2, 7]

Здесь ${\mathbf{U}} = (U,V)$, $\rho $, $P$, $k$, ϕ, $D$, $g$, ${\mathbf{e}}$ – скорость фильтрации, плотность раствора, давление, проницаемость, пористость, коэффициент диффузии, модуль ускорения силы тяжести и единичный вектор, сонаправленный с вектором силы тяжести. Пористость, проницаемость и коэффициент диффузии считаются постоянными. Плотность раствора и его вязкость варьируются в диапазонах от ${{\rho }_{0}}$ до ${{\rho }_{b}}$ и от ${{\mu }_{0}}$ до ${{\mu }_{b}}$ соответственно. Уравнение состояния, связывающее $\rho $ с плотностью растворенной примеси ρ_c, имеет вид

В уравнение (1.6) входит константа $\alpha = 0.85$.

Границы области непроницаемы для воды. Примесь тоже не проходит через горизонтальные границы. Однако некоторая доля вещества может диффундировать через вертикальные границы, поскольку на них поддерживается определенное распределение плотности примеси, которое в безразмерной форме приводится в следующем разделе. Давление стратифицировано в поле силы тяжести, его начальное распределение ${{P}_{i}}$ находится при интегрировании гидростатического уравнения $\nabla P = \rho g{\mathbf{e}}$. Начальные и граничные условия показаны на рис. 2; P⁰ – давление на уровне y = 0.

Уравнения (1.3)–(1.5) преобразуются к безразмерному виду. Масштабами длины, скорости и времени являются величины $H$, $D{\text{/}}H$, ${{H}^{2}}{\text{/}}D$, включающие высоту области H. От абсолютных значений давления и плотности следует перейти к относительным переменным $P - {{P}_{0}}$ и $\rho - {{\rho }_{0}}$, которые затем приводятся к безразмерной форме делением на масштабы $\alpha \rho _{c}^{ * }gH$ и $\alpha \rho _{c}^{ * }$ соответственно. Масштаб вязкости – μ₀. Получаются следующие уравнения в безразмерных переменных:

В уравнениях (1.7)–(1.9) содержатся переменные: скорость фильтрации u, давление $\Pi $, плотность растворенной примеси S. Вязкость ${{f}_{\mu }}$ меняется по пространству. Безразмерные параметры, определяющие поведение жидкости, – это число Рэлея–Дарси и контраст вязкости

Исходно верхняя часть области заполнена стратифицированным раствором; изменение давления $\Pi $ с высотой получается при интегрировании гидростатического уравнения, написанного для раствора. Начальные условия принимают вид

Плотность на границе между слоями жидкости подвержена флуктуациям, они описаны в следующем разделе.

Для определенности рассматриваются условия на глубине в несколько километров, где находятся глубинные геологические образования и функционируют геотермальные системы. Используются следующие параметры [16]: ${{\mu }_{0}} = 1.21 \times {{10}^{{ - 4}}}$ Па ⋅ с, ${{\rho }_{0}} = 843$ кг ⋅ м^–3, $D = 3 \times {{10}^{{ - 9}}}$ м² ⋅ с^–1, $\rho _{c}^{ * } = 400$ кг ⋅ м^–3, $\varphi = 0.1$. Имеются два сильно меняющихся параметра: проницаемость (варьируется от 10^–17 до 10^–12 м²) и геометрический масштаб H (варьируется от десятков сантиметров до километров). Взяты значения $k = 3.63 \times {{10}^{{ - 15}}}$ м², $H = 10$ м и рассчитано число Рэлея–Дарси

Поскольку $k$ и H могут меняться на несколько порядков, то и значение $Ra$ может быть очень разным. Выбор H не диктуется условиями задачи и довольно произволен, поэтому принятое значение Ra (1.10) подходит для широкого диапазона реальных условий. Поскольку число Ra представляет собой отношение конвективной скорости к диффузионной скорости, то для моделирования процессов с ведущей ролью конвекции следует брать $Ra \gg 1$. В представленных далее результатах высота зоны перемешивания всегда меньше H, так что можно считать, что конвекция развивается в вертикально бесконечной области.

2. ЧИСЛЕННЫЙ МЕТОД

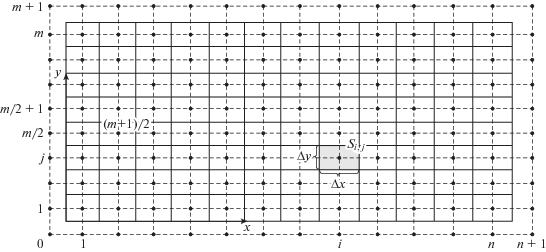
Уравнения (1.7)–(1.9) с начальными и граничными условиями решались численно с помощью авторского кода, разработанного для задач о концентрационной конвекции в пористой среде и успешно применяющегося в течение ряда лет [16–20]. Код основан на конечно-разностном методе, реализованном на разнесенной прямоугольной сетке (рис. 3). Уравнения неразрывности и Дарси решаются совместно с помощью алгоритма типа SIMPLE [21]. Затем интегрируется уравнение переноса примеси, переход на новый временной слой производится по схеме Рунге–Кутты второго порядка, пространственные производные аппроксимируются по схеме QUICK [22].

Рис. 3.

Пространственная сетка; ${{S}_{{i,j}}}$ – дискретная плотность примеси.

В настоящей работе граничные условия для плотности на вертикальных границах меняются со временем – задается диффузионное распространение примеси из верхнего слоя в нижний, чтобы избежать нефизических эффектов около границ. Решение уравнения диффузии имеет вид [23]:

Функция ошибок $erf(\zeta )$ варьируется от –1 при $\zeta \to - \infty $ до 1 при $\zeta \to \infty $. Брались табличные значения $erf(\zeta )$ с шагом переменной $\zeta $, равным 0.01. Граничная плотность $S(y,t)$ (2.1) рассчитывалась заново на каждом временном слое, при этом значение $erf((0.5 - y){\text{/}}(2{{t}^{{1/2}}}))$ определялось с помощью линейной интерполяции между $erf(\zeta )$ и $erf(\zeta + 0.01)$ при условии $\zeta \leqslant (0.5 - y){\text{/}}(2{{t}^{{1/2}}}) \leqslant \zeta $ + 0.01. Такое задание граничных условий не влияет на скорость роста зоны перемешивания и основные закономерности течения.

Точность численного решения контролировалась по выполнению баланса массы. На всех временных слоях вычислялось изменение массы $\Delta M(t) = M(t) - {{M}^{0}}$, где $M(t)$ – суммарная масса примеси в области в текущий момент $t$, а ${{M}^{0}}$ – это $M(t)$ при $t = 0$. Рассчитывался также суммарный диффузионный поток примеси через вертикальные границы M_J. В идеальном случае должно выполняться $\Delta M = {{M}_{J}}$, однако, численное решение дает погрешность, которую можно оценить, как

Во всех расчетах величина $\delta M$ не превосходила десятых долей процента, что свидетельствует о высокой точности численного решения.

Чтобы конвекция начала развиваться, в системе должны присутствовать флуктуации физических величин. В начальный момент задаются флуктуации плотности на границе между слоями жидкости, которая располагается между узлами сетки при $j = m{\text{/}}2$ и $j = m{\text{/}}2 + 1$ (рис. 3). Начальные условия в невозмущенной среде имели бы вид: ${{S}_{{i,j}}} = 0$ при $j \leqslant m{\text{/}}2$ и ${{S}_{{i,j}}} = 1$ при $j \geqslant m{\text{/}}2 + 1$. Для возмущения границы между слоями задаются условия

Здесь $\sigma $ – амплитуда флуктуаций ($\sigma \ll 1$), $D(i)$ – ряд случайных чисел, принимающих значения в диапазоне от 0 до 1. В остальных узлах сетки плотность остается невозмущенной.

При проведении численного моделирования определяются два характерных времени начала конвекции: критическое время ${{\tau }_{1}}$ и видимое время ${{\tau }_{2}}$. Первое по смыслу близко к времени начала конвекции в аналитических исследованиях, так как ассоциируется с ростом малых возмущений. Второе близко к определению времени начала конвекции в экспериментах, так как связывается с видимыми отклонениями от диффузионного режима массопереноса. Для определения ${{\tau }_{1}}$ находится максимальная скорость движения жидкости в расчетной области ${{{v}}_{{max}}} = {{\left| {\mathbf{v}} \right|}_{{max}}}$; скорость жидкости v и скорость фильтрации u связаны между собой равенством ${\mathbf{u}} = \phi {\mathbf{v}}$. Момент ${{\tau }_{1}}$ соответствует началу роста ${{{v}}_{{max}}}$. Величина ${{\tau }_{2}}$ – это момент, когда высота зоны перемешивания ${{h}_{c}}$, полученная при моделировании, начинает превосходить высоту диффузионной зоны ${{h}_{d}}$ на 1%, т.е. достигается условие ${{h}_{c}}{\text{/}}{{h}_{d}} = 1.01$. Чтобы найти ${{h}_{c}}$, сначала рассчитывается средняя масса примеси ${{Q}_{m}}(y)$ на высоте $y$.

Уровень $y$ соответствует ячейкам пространственной сетки с номером $j$; $l = L{\text{/}}H$ – безразмерная длина области. Далее определяются нижняя координата ${{y}_{l}}$ и верхняя координата ${{y}_{u}}$ зоны перемешивания: $y = {{y}_{l}}$ при ${{Q}_{m}}(y) = 0.01$ и $y = {{y}_{u}}$ при ${{Q}_{m}}(y) = 0.99$. Затем находится высота зоны перемешивания ${{h}_{c}} = {{y}_{u}} - {{y}_{l}}$. Высота диффузионной зоны ${{h}_{d}}$ определяется аналогичным способом по плотности, вычисленной по уравнению (2.1).

Основные расчеты проведены в областях 12 × 1 и 10 × 6, покрытых равномерной пространственной сеткой. Шаги сетки составляли $\Delta x = 1.67 \times {{10}^{{ - 3}}}$, $3.0 \times {{10}^{{ - 3}}}$; $\Delta y = 2.0 \times {{10}^{{ - 3}}}$, $2.5 \times {{10}^{{ - 3}}}$. Использован шаг интегрирования по времени $\Delta t = 3.13 \times {{10}^{{ - 8}}}$.

3. РЕЗУЛЬТАТЫ

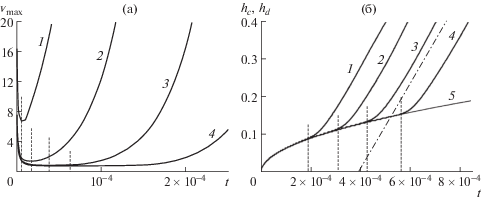
Сначала рассматривается жидкая система постоянной вязкости (${{F}_{\mu }} = 1$) и исследуется влияние начальных флуктуаций на возникновение конвекции. Критическое и видимое времена обозначаются здесь как ${{\tau }_{{01}}}$ и ${{\tau }_{{02}}}$; индекс “0” указывает на отсутствие контраста вязкости (вся жидкость имеет вязкость чистой воды). На рис. 4 (a) приведены временные зависимости максимальной скорости ${{{v}}_{{max}}}$ на начальном этапе. Флуктуации плотности на границе раздела между слоями инициируют слабые неупорядоченные движения, которые со временем перестраиваются в согласованное конвективное движение. Перестройка движения ассоциируется с уменьшением ${{{v}}_{{max}}}$. Когда скорость ${{{v}}_{{max}}}$ становится минимальной, фиксируется ${{\tau }_{{01}}}$. Видно, что величина ${{\tau }_{{01}}}$ существенно зависит от амплитуды начальных флуктуаций $\sigma $; чем меньше $\sigma $, тем позднее начинается рост ${{{v}}_{{max}}}$. Первоначально имеет место диффузионный массоперенос – соль диффундирует из верхнего слоя в нижний. При развитии конвекции перемешивание слоев усиливается, зона перемешивания увеличивается быстрее, чем это происходило бы в чисто диффузионном режиме. Изменения в массопереносе за счет конвекции начинают проявляться значительно позже момента ${{\tau }_{{01}}}$. Влияние конвекции становится заметным, когда высота зоны перемешивания ${{h}_{c}}$ начинает превосходить высоту диффузионной зоны ${{h}_{d}}$ (рис. 4 (б)). В диффузионном режиме зона перемешивания увеличивается как ${{h}_{d}} \sim {{t}^{{1/2}}}$, а в конвективном режиме как ${{h}_{c}} \sim t$. Видимое время ${{\tau }_{{02}}}$ становится больше при уменьшении σ, что аналогично с поведением ${{\tau }_{{01}}}$. Для вариантов, показанных на рис. 4, отношение ${{\tau }_{{02}}}{\text{/}}{{\tau }_{{01}}}$ меняется в диапазоне от 9 до 35.

Рис. 4.

Временные зависимости максимальной скорости жидкости ${{{v}}_{{max}}}$ (a) и высоты зоны перемешивания ${{h}_{c}}$ (б) при задании начальных флуктуаций плотности с амплитудой $\sigma = {{10}^{{ - 2}}}$ (1), 10^–3 (2), 10^–4 (3), 10^–5 (4). Временная зависимость высоты диффузионной зоны ${{h}_{d}}$ (5) (б). Вертикальными пунктирными линиями отмечены значения критического времени ${{\tau }_{{01}}}$ (a) и видимого времени ${{\tau }_{{02}}}$ (б). Штрихпунктирная линия показывает наклон кривых ${{h}_{c}}$ (б).

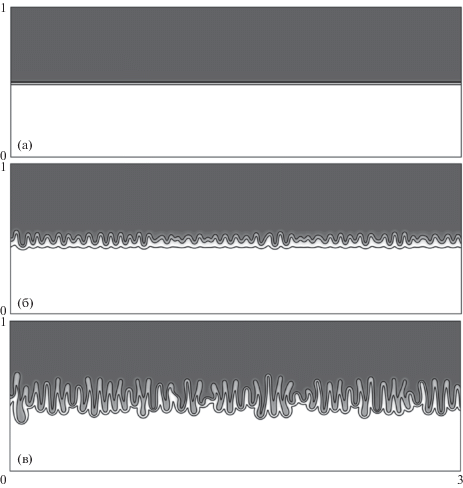
На рис. 4 (a) показано, что при $\sigma = {{10}^{{ - 4}}}$ скорость ${{{v}}_{{max}}}$ начинает расти с величины, которая меньше 1. Это значит, что во всей расчетной области в начале роста вклад конвекции в массообмен меньше, чем диффузии и поэтому возмущения можно считать малыми. Для случая с $\sigma = {{10}^{{ - 4}}}$ на рис. 5 продемонстрированы поля плотности; моменты времени на фрагментах (а) и (б) соответствуют ${{\tau }_{{01}}}$ и ${{\tau }_{{02}}}$. Плотность возрастает от светлого тона к темному. Показана часть расчетной области 3 × 1. Граница раздела между жидкостями выглядит прямой на рис. 5 (a), а на рис. 5 (б) уже видно образование квазипериодических конвективных пальцев, которые в дальнейшем удлиняются (рис. 5 (в)). Максимальная скорость движения составляет ${{{v}}_{{max}}} = 0.83$ (a), $9.92 \times {{10}^{2}}$ (б), $1.29 \times {{10}^{3}}$ (в).

Рис. 5.

Поле плотности примеси в моменты времени $t = 3.83 \times {{10}^{{ - 5}}}$ (a), $4.27 \times {{10}^{{ - 4}}}$ (б), $6.00 \times {{10}^{{ - 4}}}$ (в).

Возвращаясь к рис. 4 (б), следует отметить, что в конвективном режиме высота зоны перемешивания ${{h}_{c}}$ увеличивается примерно с одинаковой скоростью независимо от размера начальных флуктуаций. По штрихпунктирной прямой линии, которая показывает наклон кривых ${{h}_{c}}$, можно найти производную $d{{h}_{c}}{\text{/}}dt \simeq 1.2 \times {{10}^{3}}$. Очевидно, что скорость роста зоны перемешивания $d{{h}_{c}}{\text{/}}dt$ – это параметр, который действительно характеризует физический процесс и не зависит от деталей численного моделирования.

Как продемонстрировано выше, критическое и видимое времена начала конвекции зависят от начальных флуктуаций. Поэтому при изучении влияния контраста вязкости на начало конвективного движения будут рассматриваться не абсолютные значения времени ${{\tau }_{1}}$, ${{\tau }_{2}}$, а отношения ${{\tau }_{1}}{\text{/}}{{\tau }_{{01}}}$ и ${{\tau }_{2}}{\text{/}}{{\tau }_{{02}}}$, показывающие, во сколько раз меняется характерное время при ${{F}_{\mu }} \ne 1$ по сравнению с аналогичной величиной при ${{F}_{\mu }} = 1$. Численные параметры в сопоставляемых вариантах одинаковые. Проведены три серии расчетов с различными амплитудами флуктуаций и на разных пространственных сетках. Константа изменения вязкости варьировалась в диапазоне ${{\Gamma }_{e}} \in [0,1.5]$, что по уравнению (1.1) дает контраст вязкости ${{F}_{\mu }} \in [1,\;4.48]$. Зависимости ${{\tau }_{1}}{\text{/}}{{\tau }_{{01}}}$ и ${{\tau }_{2}}{\text{/}}{{\tau }_{{02}}}$ от ${{F}_{\mu }}$ показаны на рис. 6 (a).

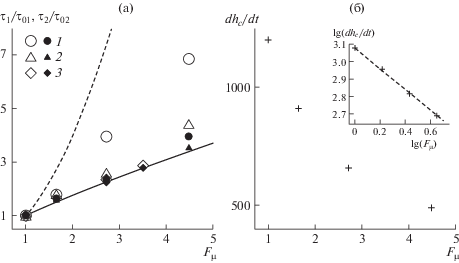
Рис. 6.

Значения относительного критического ${{\tau }_{1}}{\text{/}}{{\tau }_{{01}}}$ (крупные незакрашенные маркеры) и видимого ${{\tau }_{2}}{\text{/}}{{\tau }_{{02}}}$ (мелкие закрашенные маркеры) времени; сплошная и пунктирная линии – зависимости (3.1) и (3.2) соответственно. Расчетная область 1 × 12 (1, 2) и 6 × 10 (3), амплитуда начальных флуктуаций $\sigma = {{10}^{{ - 2}}}$ (1), ${{10}^{{ - 4}}}$ (2, 3) (а). Скорость роста зоны перемешивания в линейных (б) и логарифмических (б, врезка) шкалах.

Для сравнения приводятся результаты линейного анализа устойчивости диффузионного слоя, образующегося в пористой среде под горизонтальной границей – источником примеси [24]; зависимость вязкости от концентрации описывается формулой Франк-Каменецкого. В [24] отмечено, что в случае переменной вязкости получить аналитическое решение не удается, однако, приводится численное решение задачи на собственные значения в виде графической зависимости логарифма критического времени ${{\tau }_{c}}$ (обозначенного в настоящей работе как ${{\tau }_{1}}$) от параметра $\Gamma $ (обозначенного как $ - {{\Gamma }_{e}}$; константы $\Gamma $ и $ - {{\Gamma }_{e}}$ противоположны друг другу). Видно, что зависимость ${\text{lg}}({{\tau }_{c}})$ от $\Gamma $ является практически линейной (рис. 5 в [24]); из нее можно получить следующее выражение

В экспериментах [14] регистрировалось время начала конвекции Рэлея–Тейлора в пористом цилиндре в случае различных пар жидкостей; это время будет обозначено как ${{\tau }_{2}}$. Обработав экспериментальные данные, авторы получили зависимость ${{\tau }_{2}} \sim {{(Ra{\text{/}}{{F}_{\mu }})}^{{ - 2}}}$. Поскольку число Рэлея в [14] строится по меньшему значению вязкости, т.е. $Ra \sim {{({{\mu }_{0}})}^{{ - 1}}}$, то можно прийти к другой зависимости: ${{\tau }_{2}} \sim (\mu _{0}^{2}){{({{\mu }_{b}}{\text{/}}{{\mu }_{0}})}^{2}} \sim \mu _{b}^{2}$. Из полученного следует, что только более вязкая жидкость определяет время начала конвекции ${{\tau }_{2}}$, в то время как менее вязкая жидкость на начало конвекции не влияет. Такой результат в применении к реальным жидкостям вызывает вопросы, однако, его можно рассматривать как предельный случай. Найденную зависимость можно записать также в виде

Кривые, соответствующие уравнениям (3.1) и (3.2), нанесены на рис. 6 (a). Заметно, что все маркеры, представляющие значения ${{\tau }_{1}}{\text{/}}{{\tau }_{{01}}}$ и ${{\tau }_{2}}{\text{/}}{{\tau }_{{02}}}$ в численном моделировании, располагаются между теоретической и экспериментальной кривыми, причем находятся ближе к теоретической кривой (некоторые попадают на нее). На экспериментальную кривую маркеры не попадают, наглядно демонстрируя, что не только более вязкая, но и менее вязкая жидкость влияет на начало конвекции.

На рис. 6 (б) дана скорость роста высоты зоны перемешивания $d{{h}_{c}}{\text{/}}dt$ в зависимости от ${{F}_{\mu }}$. Обнаружено, что величина $d{{h}_{c}}{\text{/}}dt$ уменьшается с возрастанием ${{F}_{\mu }}$, что соответствует ожиданиям, поскольку с более вязким верхним слоем система в целом становится менее мобильной. На врезке, представляющей данные в логарифмических шкалах, продемонстрировано, что зависимость ${\text{lg}}(d{{h}_{c}}{\text{/}}dt)$ от ${\text{lg}}({{F}_{\mu }})$ близка к линейной. Исходя из представленных данных можно получить аппроксимирующую функцию

Чтобы продемонстрировать, какие изменения вносит учет контраста вязкости в реальных условиях, проведено моделирование начального этапа конвекции в жидкой системе с константой ${{\Gamma }_{e}} = 1.0$, взятой в соответствии с оценкой (1.2). Контраст вязкости, рассчитанный по (1.1), составляет ${{F}_{\mu }} = 2.72$. На рис. 7 показано поле плотности в различные моменты времени, причем времена на рис. 7 (а, б) совпадают с ${{\tau }_{1}}$, ${{\tau }_{2}}$ для рассматриваемой пары жидкостей. Максимальная скорость движения жидкости в порах имеет значение ${{{v}}_{{max}}} = 0.62$ (a), $6.43 \times {{10}^{2}}$ (б), $1.20 \times {{10}^{3}}$ (в). В общем, картина течения качественно повторяет картину, представленную на рис. 5, но имеет количественные отличия. При ${{F}_{\mu }} = 2.72$ масштаб образующейся конвективной структуры становится больше, чем при ${{F}_{\mu }} = 1$. Например, сравнивая фрагменты (б), можно увидеть, что если изменение вязкости не учитывать, то на показанном участке образуются 43 конвективных пальца (рис. 5), в то время как при учете переменной вязкости их становится только 29 (рис. 7). Амплитуда начальных флуктуаций σ оказывает некоторое влияние на наиболее опасную длину волны возмущения $\lambda $, а значит, на количество формирующихся конвективных пальцев: с уменьшением σ возмущения начинают расти позже, когда диффузионная зона стала шире, следовательно, $\lambda $ будет больше. Однако этот эффект слабый, им можно пренебречь и считать, что величина $\lambda $ определяется значениями Ra и ${{F}_{\mu }}$ как и в аналитическом исследовании [24].

Рис. 7.

Поле плотности примеси в моменты времени $t = 1.00 \times {{10}^{{ - 4}}}$ (a), $1.05 \times {{10}^{{ - 3}}}$ (б), $1.52 \times {{10}^{{ - 3}}}$ (в).

Кроме того, при ${{F}_{\mu }} = 2.72$ конвекция появляется позже, чем при ${{F}_{\mu }} = 1$. Относительные значения критического ${{\tau }_{1}}{\text{/}}{{\tau }_{{01}}}$ и видимого ${{\tau }_{2}}{\text{/}}{{\tau }_{{02}}}$ времени лежат в диапазоне от 2.26 до 7.40, который рассчитан по (3.1), (3.2).Конвективное перемешивание между слоями становится менее интенсивным, скорость роста высоты перемешанной зоны уменьшается в 1.8 раза от $d{{h}_{c}}{\text{/}}dt = 1.20 \times {{10}^{3}}$ до $d{{h}_{c}}{\text{/}}dt = 6.58 \times {{10}^{2}}$, как следует из (3.3).

ЗАКЛЮЧЕНИЕ

Проведено численное исследование развития неустойчивости Рэлея–Тейлора в пористой среде; рассмотрены двухслойные жидкие системы постоянной и переменной вязкости. Предложено оценивать два характерных времени возникновения конвекции: критическое время находится по началу роста скорости движения и по смыслу близко к моменту потери устойчивости в аналитических исследованиях, видимое время определяется по отклонению высоты зоны конвективного перемешивания от высоты диффузионной зоны, что ассоциируется с обнаружением конвекции в экспериментах. Показано, что обе величины зависят от начальных флуктуаций, при этом видимое время всегда существенно больше критического (вплоть до нескольких десятков раз).

Найден параметр, который не зависит от начальных флуктуаций, задаваемых в численном моделировании, и поэтому является характеристикой реального процесса. Это скорость роста зоны перемешивания.

Изучено влияние контраста вязкости на начало конвективного движения и массопереноса. Рассмотрены значения критического и видимого времени, приведенные к соответствующим величинам в жидкой системе постоянной вязкости. Обнаружено, что при увеличении контраста вязкости конвективное движение появляется позже. Относительные характерные времена локализуются между двумя кривыми, построенными по имеющимся в литературе данным, таким образом, определен диапазон их возможных значений. Найдено, что скорость роста зоны перемешивания уменьшается с возрастанием контраста вязкости, что описывается полученной степенной зависимостью.

Проведено сравнение жидких систем с одинаковой вязкостью слоев и с контрастом вязкости, соответствующим геологическим условиям. Учет переменной вязкости, как продемонстрировано, приводит к заметным количественным изменениям в характеристиках начала конвекции, что имеет практическую значимость.

Автор благодарит Г.Г. Цыпкина за полезные обсуждения. Работа выполнена при финансовой поддержке Российского научного фонда (грант 16-11-10195).