Известия РАН. Механика жидкости и газа, 2021, № 2, стр. 63-71
ВЛИЯНИЕ НЕРАВНОМЕРНОГО СЖАТИЯ УПРУГОЙ ПЛАСТИНЫ, ПЛАВАЮЩЕЙ НА ПОВЕРХНОСТИ ЖИДКОСТИ, НА РАЗВИТИЕ НЕСТАЦИОНАРНЫХ ИЗГИБНО-ГРАВИТАЦИОННЫХ ВОЛН
a Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия
* E-mail: sturova@hydro.nsc.ru
Поступила в редакцию 04.09.2020
После доработки 01.10.2020
Принята к публикации 01.10.2020
Аннотация
В линейной постановке получено решение трехмерной нестационарной гидроупругой задачи о колебаниях тонкой упругой пластины, плавающей на поверхности весомой жидкости конечной глубины, под действием нестационарного внешнего давления. Изучено влияние продольного, поперечного и сдвигового сжатия пластины на развитие изгибно-гравитационных волн. В качестве примеров рассмотрено периодическое и импульсное воздействие нагрузки.
Задача о развитии волновых движений в жидкости, на верхней границе которой плавает тонкая упругая пластина, активно рассматривается в последнее время в связи с изучением волновых процессов в море с плавающим ледяным покровом или искусственными плавающими платформами больших размеров [1]. Значительное количество работ посвящено исследованию изгибно-гравитационных волн (ИГВ), вызванных нестационарным воздействием внешней нагрузки на плавающую пластину (см., например, [2, 3] и указанную в них библиографию). Как правило, используется модель не напряженной упругой пластины Кирхгофа–Лява, в которой пластина характеризуется только ее изгибной жесткостью и инерцией. Однако в пластине могут существовать также растягивающие или сжимающие усилия, которые в ледяном покрове возникают под воздействием ветра, течений или температурных деформаций [4]. В трехмерном случае возможны усилия трех типов: продольные, поперечные и сдвиговые [5]. Поведение свободных ИГВ при наличии неравномерного сжатия изучено в [6], а поведение установившегося волнового движения при воздействии внешней нагрузки – в [7]. Обе эти работы отражены также в монографии [8].
В данной работе исследованы допустимые значения параметров сжатия, которые обеспечивают неразрушающее воздействие на пластину, и определены области существования ИГВ с положительной групповой скоростью. Используя интегральные преобразования Фурье и Лапласа, построено решение начально-краевой задачи о воздействии на плавающую пластину локализованной области внешнего давления. Подробно исследовано воздействие периодической и импульсной нагрузки.
1. ПОСТАНОВКА ЗАДАЧИ
Рассматривается слой идеальной несжимаемой весомой жидкости толщиной $H$, который занимает область $\left| x \right| < \infty $, ${\text{|}}y{\text{|}} < \infty $, $ - H \leqslant z \leqslant 0$, где $x$ и $y$ – горизонтальные координаты, а $z$ – вертикальная координата, направленная вверх. Плавающая на верхней границе жидкости тонкая упругая пластина описывается моделью Кирхгофа–Лява с учетом продольных, поперечных и сдвиговых сжимающих усилий [7, 8]. Первоначально жидкость и пластина покоятся, но начиная с момента времени $t = 0$ на пластину действует нестационарное внешнее давление $P(x,y,t)$, которое является заданным. Возникающее течение жидкости полагается потенциальным, а скорость частиц жидкости и прогиб пластины – малыми. Предполагается, что во все моменты времени жидкость находится в контакте с пластиной.
Задача о поведении пластины и жидкости сводится к решению уравнения Лапласа для потенциала скоростей частиц жидкости $\varphi (x,y,z,t)$
(1.1)
$\Delta \varphi + {{\partial }^{2}}\varphi {\text{/}}\partial {{z}^{2}} = 0\left( {\left| x \right|,\;\left| y \right| < \infty ,\; - H \leqslant z \leqslant 0} \right),\quad \Delta \equiv {{\partial }^{2}}{\text{/}}\partial {{x}^{2}} + {{\partial }^{2}}{\text{/}}\partial {{y}^{2}}$(1.2)
$D{{\Delta }^{2}}w + {{Q}_{x}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + {{Q}_{y}}\frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + 2{{Q}_{{xy}}}\frac{{{{\partial }^{2}}w}}{{\partial x\partial y}} + M\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} + \rho gw + \rho \frac{{\partial \varphi }}{{\partial t}} = - P\quad (z = 0)$(1.3)
$\frac{{\partial w}}{{\partial t}} = \frac{{\partial \varphi }}{{\partial z}}(z = 0),\quad \frac{{\partial \varphi }}{{\partial z}} = 0\quad (z = - H)$Здесь $w(x,y,t)$ – нормальный прогиб упругой пластины, $D = Eh_{1}^{3}{\text{/}}[12(1 - {{\nu }^{2}})]$, $M = {{\rho }_{1}}h$; E, ${{\rho }_{1}}$, $h$, $\nu $ – модуль Юнга, плотность, толщина и коэффициент Пуассона пластины, ${{Q}_{x}}$${{Q}_{y}}$, ${{Q}_{{xy}}}$ – продольные, поперечные и сдвиговые напряжения (сжатие при положительных значениях и растяжение при отрицательных значениях) по соответствующим направлениям, $\rho $ – плотность жидкости, $g$ – ускорение свободного падения. Далее будет рассматриваться действие только сжимающих усилий, т.е. ${{Q}_{x}},{{Q}_{y}},{{Q}_{{xy}}} \geqslant 0$.
Предполагается для простоты, что давление $P(x,y,t)$ в (1.2) имеет вид
где $a$ – множитель, имеющий размерность длины, а безразмерные функции $f(r)$ и $Z(t)$ являются заданными.Для решения задачи (1.1)–(1.4) используется двойное преобразование Фурье
Функция $W(\lambda ,\mu ,t)$ удовлетворяет обыкновенному дифференциальному уравнению
(1.6)
$\ddot {W} + {{\Omega }^{2}}W = - \gamma (k)Z(t),\quad \gamma (k) = \frac{{a\rho gk{\text{th}}(kH)F(k)}}{{\rho + kM{\text{th}}(kH)}}$(1.7)
${{\Omega }^{2}}(k,\theta ) = \frac{{k[D{{k}^{4}} - Q(\theta ){{k}^{2}} + \rho g]{\text{th}}(kH)}}{{\rho + kM{\text{th}}(kH)}},\quad k = \sqrt {{{\lambda }^{2}} + {{\mu }^{2}}} ,\quad \theta = {\text{arctg}}\frac{\mu }{\lambda }$(1.8)
$Q(\theta ) = {{Q}_{x}}co{{s}^{2}}\theta + {{Q}_{y}}si{{n}^{2}}\theta + {{Q}_{{xy}}}sin(2\theta )$После выполнения обратных преобразований Фурье получим
(1.10)
$\begin{gathered} w(x,y,t) = \frac{1}{{2{{\pi }^{2}}}}\int\limits_0^\infty {\int\limits_0^{\pi /2} k } \left\{ {{{W}_{ + }}cos[k(xcos\theta + ysin\theta )]} \right. + \\ + \;{{W}_{ - }}cos\left. {[k(xcos\theta - ysin\theta )]} \right\}d\theta dk \\ \end{gathered} $2. ДИСПЕРСИОННОЕ СООТНОШЕНИЕ
Зависимость $\Omega (k,\theta )$ в (1.7) устанавливает связь между волновым числом k и частотой Ω при различных значениях угловой координаты θ. Согласно (1.8) при отсутствии сдвиговых сжимающих усилий (${{Q}_{{xy}}} = 0$) достаточно рассмотреть диапазон $0 \leqslant \theta \leqslant \pi {\text{/}}2$, а при ${{Q}_{{xy}}} \ne 0$ – диапазон $0 \leqslant \theta \leqslant \pi $.
В безразмерных переменных
(2.1)
$\bar {\Omega } = \sqrt {\frac{{\bar {k}(\bar {D}{{{\bar {k}}}^{4}} - \bar {Q}{{{\bar {k}}}^{2}} + 1){\text{th}}(\bar {k}\bar {H})}}{{1 + \bar {k}\bar {M}{\text{th}}(\bar {k}\bar {H})}}} $Для существования вещественного значения частоты $\bar {\Omega }$ необходимо, чтобы при всех возможных значениях $\theta $ подкоренное выражение в (2.1) было неотрицательным. Это условие гарантирует устойчивость плавающей упругой пластины и выполняется при $\bar {Q} \leqslant {{Q}_{ * }} \equiv 2\sqrt {\bar {D}} $ [9]. При наличии сжимающих усилий существует также значение ${{Q}_{0}} < {{Q}_{ * }}$ такое, что при $\bar {Q} < {{Q}_{0}}$ групповая скорость ИГВ ${{c}_{g}} = d\bar {\Omega }{\text{/}}d\bar {k}$ положительна для всех волновых чисел $\bar {k} \geqslant 0$ во всем диапазоне значений угловой координаты $\theta $ [4, 8]. Этот случай назовем нормальной дисперсией в отличие от случая аномальной дисперсии при ${{Q}_{0}} < \bar {Q}(\theta ) < {{Q}_{ * }}$, который характеризуется наличием для некоторых значений $\theta $ области волновых чисел, при которых групповая скорость ИГВ становится отрицательной. Значение Q0 и соответствующее ему волновое число k0 определяются из совместного решения двух уравнений ${{c}_{g}}({{k}_{0}}) = 0$ и ${{\left. {d{{c}_{g}}(\bar {k}){\text{/}}d\bar {k}} \right|}_{{\bar {k} = {{k}_{0}}}}} = 0$. Для дисперсионного соотношения (2.1) это сводится к определению вещественного корня трансцендентного уравнения
(2.2)
$\begin{gathered} 2\bar {M}{{{\bar {k}}}^{3}}(2\bar {D}{{{\bar {k}}}^{2}} - \bar {Q}){\text{t}}{{{\text{h}}}^{2}}\left( {\bar {k}\bar {H}} \right) + [1 + {{{\bar {k}}}^{2}}(5\bar {D}{{{\bar {k}}}^{2}} - 3\bar {Q})]{\text{th}}\left( {\bar {k}\bar {H}} \right) + \\ + \;\bar {k}\bar {H}[1 + {{{\bar {k}}}^{2}}(\bar {D}{{{\bar {k}}}^{2}} - \bar {Q})]{\text{c}}{{{\text{h}}}^{{ - 2}}}\left( {\bar {k}\bar {H}} \right) = 0 \\ \end{gathered} $(2.3)
$\bar {Q} = \frac{{10\bar {M}\bar {D}{{{\bar {k}}}^{4}}{\text{t}}{{{\text{h}}}^{2}}(\bar {k}\bar {H}) + 2\bar {D}{{{\bar {k}}}^{3}}(2\bar {H}\bar {M}{{{\bar {k}}}^{2}} + 5){\text{th}}(\bar {k}\bar {H}) + \bar {H}(1 + 5\bar {D}{{{\bar {k}}}^{4}})}}{{\bar {k}[3\bar {M}\bar {k}{\text{t}}{{{\text{h}}}^{2}}(\bar {k}\bar {H}) + (3 + 2\bar {H}\bar {M}{{{\bar {k}}}^{2}}){\text{th}}(\bar {k}\bar {H}) + 3\bar {H}\bar {k}]}}$После определения k0 значение Q0 вычисляется из соотношения (2.3) при $\bar {k} = {{k}_{0}}$. В случае бесконечно глубокой жидкости соотношения (2.2) и (2.3) существенно упрощаются и приведены в работе [10].
В табл. 1 даны значения k0 и ${{q}_{0}} \equiv {{Q}_{0}}{\text{/}}\sqrt {\bar {D}} $ для различных значений толщины упругой пластины $h = 0.5$, 1, 2 м и глубины жидкости $H = 40,100,350$ м, а также бесконечно глубокой жидкости. Исходные параметры имеют следующие значения
(2.4)
$E = 5 \times {{10}^{9}}\;{\text{Па}},\quad \rho = 1025\;{\text{кг/}}{{{\text{м}}}^{3}},\quad {{\rho }_{1}} = 922.5\;{\text{кг/}}{{{\text{м}}}^{3}},\quad \nu = 0.3,\quad a = 20\;{\text{м}}$Таблица 1
| h1, м | H = 40 м | H = 100 м | H = 350 м | H = ∞ | ||||
|---|---|---|---|---|---|---|---|---|
| k0 | q0 | k0 | q0 | k0 | q0 | k0 | q0 | |
| 0.5 | 1.553 | 1.487 | 1.533 | 1.477 | 1.533 | 1.477 | 1.533 | 1.477 |
| 1 | 0.961 | 1.537 | 0.912 | 1.476 | 0.911 | 1.475 | 0.911 | 1.475 |
| 2 | 0.594 | 1.615 | 0.552 | 1.489 | 0.541 | 1.472 | 0.541 | 1.472 |
Из табл. 1 видно, что с увеличением толщины пластины $h$ существенно уменьшается значение волнового числа k0, однако коэффициент q0 меняется слабо. При глубине жидкости $H = 350$ м значения ${{k}_{0}}$ и ${{q}_{0}}$ полностью совпали со случаем бесконечно глубокой жидкости $H = \infty $.
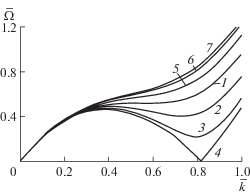
На рис. 1 представлены дисперсионные зависимости $\bar {\Omega }(\bar {k},\theta )$ при ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$, где ${{q}_{i}} = {{\bar {Q}}_{i}}{\text{/}}\sqrt {\bar {D}} $ ($i = 1,2,3$) для различных значений угловой координаты $\theta $ в диапазоне $0 \leqslant \theta \leqslant \pi $ с шагом $\pi {\text{/}}12$. Использованы параметры (2.4), глубина жидкости составляет $H = 100$ м, а толщина упругой пластины $h = 2$ м. В силу равенства значений ${{q}_{1}}$ и ${{q}_{2}}$ при $0 \leqslant \theta \leqslant \pi {\text{/}}2$ выполняется $\bar {\Omega }(\bar {k},\theta ) = \bar {\Omega }(\bar {k}$, π/2 – θ), а при $\pi {\text{/}}2 \leqslant \theta \leqslant \pi $ – $\bar {\Omega }(\bar {k},\theta ) = \bar {\Omega }(\bar {k},3\pi {\text{/}}2 - \theta )$. Кривые 5–7 соответствуют нормальной дисперсии, так как для них значение $q \equiv \bar {Q}{\text{/}}\sqrt {\bar {D}} < {{q}_{0}}$, а кривые 1–4, для которых $q > {{q}_{0}}$, – аномальной дисперсии. В этом случае имеется область значений частоты $\bar {\Omega }$, при которой возникают ИГВ с отрицательной групповой скоростью. Из рис. 1 следует, что в случае нормальной дисперсии для каждого значения частоты $\Omega $ существует единственное значение волнового числа k, характеризующего пространственное распределение ИГВ заданной частоты. При аномальной дисперсии для некоторых значений угла $\theta $ возможно существование трех различных вещественных положительных корней уравнения $\Omega (k,\theta ) = 0$, что означает генерацию при заданной частоте трех волн с различными волновыми числами.
Рис. 1.
Дисперсионные зависимости $\bar {\Omega }(\bar {k},\theta )$ при различных значениях $\theta = \pi n{\text{/}}12$: 1 – $n = 0,\;6,\;12$; 2 – $n = 1,\;5$; 3 – $n = 2,\;4$; 4 – $n = 3$; 5 – $n = 7,\;11$; 6 – $n = 8,\;10$; 7 – $n = 9$.
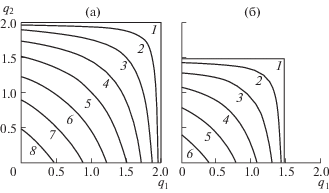
Согласно условию устойчивости упругой пластины все значения qi ($i = 1,\;2,\;3$) не должны превышать 2. На рис. 2а представлены кривые для ряда значений ${{q}_{3}} = 0.25(j - 1)$ при $j = 1, \ldots ,8$, которые ограничивают область устойчивости упругой пластины, т.е. для значений q1 и q2 ниже этих кривых при указанном q3 величина $maxq(\theta ) < 2$ при всех значениях $0 \leqslant \theta \leqslant \pi $, где q(θ) = = ${{q}_{1}}{\text{co}}{{{\text{s}}}^{2}}(\theta ) + {{q}_{2}}{\text{si}}{{{\text{n}}}^{2}}(\theta )$ + q3sin(2θ). Рисунок 2б показывает области значений q1 и q2 при указанном q3, которые ограничивают области ИГВ с нормальной дисперсией. Рассмотрен случай бесконечно глубокой жидкости, толщина упругой пластины равна h = 2 м. Согласно табл. 1 в этом случае ${{q}_{0}} = 1.472$ и, следовательно, для значений ${{q}_{1}}$ и ${{q}_{2}}$, попадающих в область ниже кривой для заданной величины q3, $maxq(\theta ) < {{q}_{0}}$ при всех значениях $0 \leqslant \theta \leqslant \pi $. При ${{q}_{3}} > {{q}_{0}}$ для всех допустимых значений ${{q}_{1}}$ и ${{q}_{2}}$ возбуждаются волны с аномальной дисперсией.
3. ДЕЙСТВИЕ НЕСТАЦИОНАРНОЙ НАГРУЗКИ
Рассмотрено два типа нагрузки: периодическая и импульсная. Для обоих типов нагрузки функция $f(r)$ в (1.5) имеет вид
Двойное преобразование Фурье для этой функции в (1.9) равно
Результаты численных расчетов, представленные ниже, выполнены при h = 2 м, $H = 100$ м, $L = 25$ м.
Для периодической нагрузки в (1.5) используется зависимость $Z(t) = sin(\omega t)$. Вертикальные прогибы упругой пластины определяются выражением (1.10), в котором
Особенность, которая возникает при интегрировании (1.10), в случае $\Omega \to \omega $ легко устраняется, так как
Результаты численных расчетов для периодической нагрузки представлены на рис. 3, 4. На рис. 3а–в показаны безразмерные значения прогиба ледяного покрова $\bar {w} = w{\text{/}}a$ в центре области давления r = 0 в зависимости от безразмерного времени $\bar {t} = t\sqrt {g{\text{/}}a} $ соответственно для трех значений частоты колебания нагрузки $\omega = 0.25,\;0.5,\;0.75$ с–1. Этим значениям частоты соответствуют следующие значения периода колебаний $T = 2\pi {\text{/}}\omega $: 25.13 с (17.60), 12.57 с (8.801), 8.378 с (5.867). В скобках указаны безразмерные значения периода $\bar {T} = T\sqrt {g{\text{/}}a} $. Рассмотрены следующие значения параметров сжатия: ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$ (кривая 1), ${{q}_{1}} = 1$, ${{q}_{2}} = 0$, ${{q}_{3}} = 0.5$ (кривая 2), ${{q}_{1}} = {{q}_{2}} = {{q}_{3}} = 0$ (кривая 3). Видно, что колебания пластины достаточно быстро (примерно через 2–3 периода) выходят на установившийся периодический режим при всех сочетаниях параметров сжатия. Наибольшие прогибы возникают при низкочастотных колебаниях для ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$. С увеличением частоты внешней нагрузки амплитуды колебаний пластины уменьшаются и слабо зависят от параметров сжатия.
Рис. 3.
Прогибы упругой пластины в зависимости от времени при $r = 0$: (а–в) – $\omega = 0.25$, $0.5$, $0.75$ с–1; 1 – ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$; 2 – ${{q}_{1}} = 1$, ${{q}_{2}} = 0$, ${{q}_{3}} = 0.5$; 3 – ${{q}_{1}} = {{q}_{2}} = {{q}_{3}} = 0$.
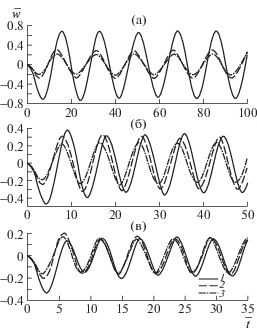
Рис. 4.
Прогибы упругой пластины: (а) в зависимости от времени в различных точках окружности $r = 2L$ при $\theta {{(}^{ \circ }}) = 0,\;15,\;45,\;105,\;135$ (кривые 1–5); (б) в зависимости от расстояния до центра области давления при $\bar {t} = 60$ при различных значениях угла $\theta {{(}^{ \circ }}) = 0,\;15,\;45$ (кривые 1–3).
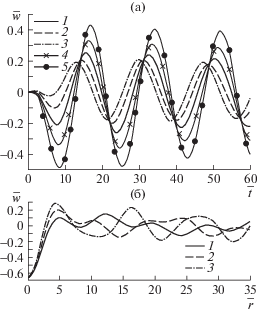
Для рис. 4 использованы значения $\omega = 0.25$ с–1 и ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$. На рис. 4а показаны зависимости от времени безразмерного прогиба ледяного покрова, вычисленного в различных точках на окружности $r = 2L$ при значениях угла $\theta {{(}^{ \circ }}) = 0,\;15,\;45,\;105,\;135$ (кривые 1–5). Видно, что периодическое поведение по времени устанавливается также достаточно быстро и амплитуды вертикальных прогибов существенно зависят от угла $\theta $. Зависимость прогибов пластины от расстояния до центра пятна давления представлена на рис. 4б для различных значений угла $\theta {{(}^{ \circ }}) = 0,\;15,\;45$ (кривые 1–3) при $\bar {t} = 60$. Видно, что с ростом расстояния $r$ значения прогибов уменьшаются, но зависимость $w(r,\theta )$ не имеет выраженного периода по переменной r, так как используемые значения параметров сжатия согласно рис. 2 находятся в области, соответствующей аномальной дисперсии.
Для исследования импульсного воздействия на ледовый покров в выражении (1.5) функция $Z(t)$ имеет вид
(3.1)
$Z(t) = \left\{ \begin{gathered} t{\text{/}}b\quad (t \leqslant b) \hfill \\ 2 - t{\text{/}}b\quad (b \leqslant t \leqslant 2b) \hfill \\ 0\quad (t > 2b) \hfill \\ \end{gathered} \right.$Вертикальные прогибы ледяного покрова для импульсного возмущения определяются соотношением (1.10), в котором
Поведение вязкоупругой пластины под действием треугольного импульса (3.1), равномерно распределенного по круговой области, без учета сжимающих усилий в пластине рассмотрено в [3].
Результаты для импульсной нагрузки представлены на рис. 5–7 при $b = 0.5$ с или в безразмерных переменных $\bar {b} = b\sqrt {g{\text{/}}a} = 0.35$. На рис. 5 показаны вертикальные прогибы пластины в центре пятна давления в зависимости от времени при различных параметрах сжатия: ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$; ${{q}_{1}} = 1$; ${{q}_{2}} = 0$, ${{q}_{3}} = 0.5$; ${{q}_{1}} = {{q}_{2}} = {{q}_{3}} = 0$ (кривые 1–3). Видно, что наличие сжатия влияет как на максимальный прогиб упругой пластины, так и на скорость затухания колебаний после окончания действия нагрузки ($\bar {t} > 2\bar {b} = 0.7$). Наиболее быстрое восстановление начального невозмущенного положения пластины происходит при отсутствии сжимающих усилий.
Рис. 5.
Зависимость от времени вертикальных прогибов пластины в центре пятна давления $r = 0$ для $b = 0.5$ с–1 при различных параметрах сжатия: 1 – ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$; 2 – ${{q}_{1}} = 1$, ${{q}_{2}} = 0$, ${{q}_{3}} = 0.5$; 3 – ${{q}_{1}} = {{q}_{2}} = {{q}_{3}} = 0$.
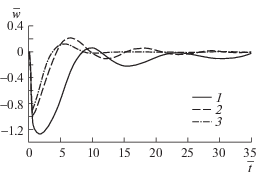
Рис. 6.
Зависимость от времени вертикальных прогибов пластины в различных точках окружности $r = 2L$ при $b = 0.5$ с–1 и ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$: 1–5 – $\theta = 0,\;15,\;45,\;105,\;135$°.
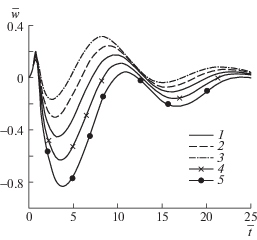
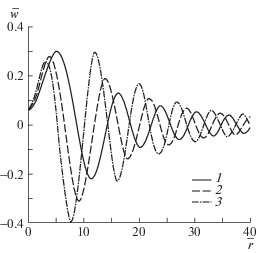
Рис. 7.
Зависимость вертикальных прогибов пластины от расстояния до центра области давления при $\bar {t} = 60$, ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$: 1–3 – $\theta = 0,\;15,\;45$°.
На рис. 6 показаны прогибы пластины в зависимости от времени в различных точках окружности $r = 2L$ при ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$. Кривые 1–5 соответствуют следующим значениям угла $\theta {{(}^{ \circ }}) = 0,\;15,\;45,\;105,\;135$. Видно, что в первые моменты времени картина волнового движения близка к осесимметричной, но с ростом времени осевая симметрия нарушается.
Поведение вертикальных прогибов пластины при фиксированном значении времени $\bar {t} = 10$ в зависимости от расстояния до центра области давления показано на рис. 7 при ${{q}_{1}} = {{q}_{2}} = 1.5$, ${{q}_{3}} = 0.5$. К указанному моменту времени внешнее воздействие уже прекратилось и происходит затухание волновых возмущений как по времени, так и по пространству. Однако в отличие от периодического поверхностного давления (ср. рис. 4) поведение функции $w(r,\theta )$ носит характер затухающих колебаний, амплитуда и период которых зависят от угла $\theta $.
ЗАКЛЮЧЕНИЕ
Исследовано влияние неравномерных сжимающих усилий (продольных, поперечных и сдвиговых) в плавающей на поверхности жидкости упругой пластине на ее поведение при нестационарной внешней нагрузке. На основе анализа дисперсионного соотношения для изгибно-гравитационных волн определены границы параметров сжатия, которые обеспечивают устойчивые колебания упругой пластины и гарантируют отсутствие волновых движений с аномальной дисперсией, т.е. с отрицательными значениями групповой скорости. Рассмотрены случаи периодического и импульсного воздействия поверхностного давления. Показано, что при осесимметричной внешней нагрузке наличие неравномерного сжатия приводит к неосесимметричному поведению волнового движения.
Список литературы
Squire V.A. Synergies between VLFS hydroelsticity and sea-ice research // J. Offshore Polar Eng. 2008. V. 18. P. 1–13.
Погорелова А.В., Козин В.М., Матюшина А.А. Исследование напряженно-деформированного состояния ледяного покрова при взлете и посадке на него самолета// ПМТФ. 2015. Т. 56. № 5. С. 214–221. https://doi.org/10.15372/PMTF20150520
Ху М.-Й., Чзан Ч.-Х. Колебания льдины под действием импульса треугольной формы // ПМТФ. 2017. Т. 58. № 4. С. 163–170. https://doi.org/10.15372/PMTF20170416
Schulkes R.M.S.M., Hosking R.J., Sneyd A.D. Waves due to a steadily moving source on a floating ice plate. Pt. 2 // J. Fluid Mech. 1987. V. 180. P. 297–318.
Timoshenko S., Woinowsky-Krieger S. Theory of plates and shells. 2d ed., New York a.o., Mc Graw-Hill, 1959. 580 p. = Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки. М.: Книжный дом “ЛИБРОКОМ”, 2009. 640 с.
Букатов А.Е., Гончаров А.М. Изгибно-гравитационные волны при неравномерном сжатии // Морской гидрофизический журнал. 1989. № 4. С. 35–39.
Букатов А.Е., Жарков В.В., Завьялов Д.Д. Трехмерные изгибно-гравитационные волны при неравномерном сжатии // ПМТФ. 1991. № 6. С. 51–57.
Букатов А.Е. Волны в море с плавающим ледяным покровом. Севастополь: ФГБУН МГИ. 2017. 360 с.
Хейсин Д.Е. Динамика ледяного покрова. Л.: Гидрометеоиздат. 1967. 215 с.
Sturova I.V. Unsteady three-dimensional sources in deep water with an elastic cover and their applications // J. Fluid Mech. 2013. V. 730. P. 392–418. https://doi.org/10.1017/jfm.2013.303
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа