Известия РАН. Механика жидкости и газа, 2021, № 2, стр. 40-51

КАСАТЕЛЬНОЕ НАПРЯЖЕНИЕ ПРИ ПЕРИОДИЧЕСКОМ ДВИЖЕНИИ ВЯЗКОУПРУГОЙ ЖИДКОСТИ В ЦИЛИНДРИЧЕСКОЙ ТРУБЕ

Ж. А. Акилов^a, *, М. С. Джаббаров^a, **, Б. Х. Хужаёров^b, ***

^a Самаркандский государственный архитектурно-строительный институт
Самарканд, Узбекистан

^b Самаркандский государственный университет
Самарканд, Узбекистан

^* E-mail: jaxon.akilov@mail.ru
^** E-mail: m.s.jabborov1954@mail.ru
^*** E-mail: b.khuzhayorov@mail.ru

Поступила в редакцию 13.05.2020
После доработки 10.06.2020
Принята к публикации 27.08.2020

DOI: 10.31857/S0568528121020018

Полный текст (PDF)

Аннотация

Рассмотрена задача исследования нестационарного касательного напряжения при периодическом ламинарном движении вязкоупругой жидкости в цилиндрической трубе на основе модели Максвелла. Получены формулы для передаточной и частотной функций, численными экспериментами изучено влияние частоты колебаний, ускорения и релаксационных свойств жидкости на касательное напряжение. Показано, что вязкоупругие свойства жидкости, как и ускорение движения жидкости, действуют как лимитирующий фактор использования квазистационарного подхода.

Ключевые слова: касательное напряжение, вязкоупругая жидкость, передаточная и частотная функции, частота колебаний

Вязкоупругие свойства неньютоновских жидкостей оказывают существенное влияние на гидравлические характеристики потока. При транспортировке высоковязких и тяжелых нефтей и нефтепродуктов на большие расстояния, циркуляции буровых растворов в скважине одной из важных задач является разработка эффективных способов снижения гидравлического сопротивления потоков. Экспериментальными исследованиями показано, что буровые растворы, обработанные высокомолекулярными полимерами, и нефти с высоким содержанием асфальтено-смолистых веществ обладают релаксационными свойствами и относятся к вязкоупругим жидкостям [1–4]. Во многих технологических процессах поток жидкости является пульсирующим или осциллирующим, характеристики которого существенно могут отличаться от обычных потоков. В них режим изменения давления или потока жидкости имеет колебательный характер. Такие потоки широко используются в различных технологических процессах, наряду с отмеченными выше, в химической технологии, пищевой промышленности, физиологии, акустике.

Математическое описание процессов течения неньютоновских жидкостей непосредственно связано с выбором реологической модели, адекватно описывающей течение этих жидкостей. Исходя из сказанного выше, наиболее важной характеристикой течения жидкостей при исследовании различных технологических процессов является гидродинамическое сопротивление. Для неньютоновских жидкостей гидродинамическое сопротивление, при сдвиговых течениях – касательное напряжение, для различных реологических моделей определяется различным образом. При этом касательное напряжение может иметь специфические особенности, не характерные для обычных вязких жидкостей. Поэтому наряду с другими характеристиками течения изучение касательного напряжения при течении неньютоновских жидкостей имеет важное значение [5–7].

Пульсирующему движению неньютоновских жидкостей, в частности вязкоупругих, в трубах посвящено большое количество исследований. В [8] экспериментально изучено поле скорости жидкости при колебательном ламинарном течении в длинной круглой трубе под влиянием периодического градиента давления. Для случая ньютоновской жидкости результаты эксперимента показывают, что амплитуда периодической продольной скорости как функция радиальной координаты и частоты хорошо согласуется с теоретическими. Показано, что при низких частотах распределение скорости приблизительно параболическое с максимумом на оси трубы. В более высоких частотах максимальная скорость достигается между осью и стенкой трубы, и этот пик перемещается в сторону стенки с увеличением частоты. Некоторые исследования периодических потоков рассмотрены также в [9, 10].

Движение вязкоупругой жидкости в длинной трубе при колебательном градиенте давления изучено в [11] и показаны отличительные особенности от соответствующего случая движения ньютоновской жидкости.

Мгновенные профили скорости по круглому поперечному сечению трубы и соответствующие продольные градиенты давления при безынерционном колеблющемся и пульсирующем течении нелинейного вязкоупругого полимерного раствора исследованы в [12]. Показано, что в колеблющемся потоке продольные скоростные профили симметричны и существует значительный фазовый сдвиг между градиентом давления и скоростью. В пульсирующих потоках фазовый сдвиг фактически отсутствовал и осевая скорость изменяется асимметрично относительно среднего ее значения за период.

В [13] изучен ламинарный колебательный поток вязкоупругих жидкостей Максвелла и Олдройд-B. Колебательное поведение потока классифицировано в двух широких классах, соответствующих “широким” и “узким” системам.

В течении Пуазейля вязкоупругой жидкости Максвелла со спектром времен релаксации мгновенные скорости потока значительно могут увеличиться в определенных частотах колеблющегося градиента давления [14]. Довольно большие повышения могут быть достигнуты на резонансных частотах, даже если амплитуда дополнительного колебательного градиента давления очень мала.

Пульсирующий поток жидкости Грина-Ривлина в прямых трубах произвольного поперечного сечения исследовался в [15]. Главное заключение статьи состоит в том, что эффекты скоростного усиления в трубах произвольной формы не могут быть предсказаны с помощью анализа первого порядка. Неустановившийся продольный поток вязкоупругой жидкости Олдройд-B вдоль бесконечной трубы кругового сечения анализирован в [16]. Жидкость двигается под действием зависящего от времени градиента давления в следующих трех случаях: 1) изменяется по экспоненциальному закону со временем, 2) пульсирующий и 3) постоянный. Получены распределения скорости жидкости, имеющие пульсирующее поведение.

В теории вязкоупругости в последнее время стали использоваться дифференциальные реологические модели дробного порядка [17–19], что естественно можно рассматривать как обобщение классических моделей. В [20] отмечено, что очень хорошее описание экспериментальных данных было достигнуто с использованием модели Максвелла дробного порядка. Некоторые точные аналитические решения получены для класса неустановившихся потоков для обобщенной жидкости второго порядка с дробными производными между двумя параллельными пластинами [21]. Неустойчивые потоки созданы импульсивным движением или периодическим колебанием одной из пластин. В [22] описывается нестационарное течение вязкоупругой жидкости для максвелловской модели с дробными производными. Анализировано влияние дробных параметров и констант материала на поле скорости и касательное напряжение.

Следует отметить, что изучение пульсирующего нестационарного движения неньютоновских жидкостей в трубах и каналах имеет важное значение в исследовании устойчивости течения и самой трубы [23, 24]. При этом не меньшее значение имеет установление критериев устойчивости и абсолютной неустойчивости в зависимости от реологических свойств жидкости и материала трубы, а также от режимов течения.

В отмеченных выше статьях в основном изучается поле скоростей жидкости при различных режимах изменения давления. Поле напряжений, касательные и нормальные напряжения при движении вязкоупругих жидкостей исследовались сравнительно мало. В гидродинамических моделях нестационарных течений жидкости в большинстве случаев реальные потоки заменяются последовательностью потоков с квазистационарным распределением гидродинамических величин [25]. Однако структура нестационарных потоков отличается от квазистационарных, и такая замена потока должна быть обоснована для каждого конкретного случая. На сегодняшний день до конца не решен вопрос правомерности использования квазистационарного подхода при определении поля касательных напряжений даже для нестационарных потоков обычной вязкой жидкости, не говоря уже вязкоупругих. Естественно, при таких условиях необходимо использовать гидродинамические модели нестационарных процессов, учитывающие изменение характеристик течения и гидродинамических параметров в зависимости от времени. В частности, сопротивление трения при нестационарном течении жидкости в трубе в общем случае нельзя определить по характеристикам, соответствующим стационарным условиям течения.

В настоящей работе предлагается теоретический способ определения обобщенного закона сопротивления при периодическом движении вязкоупругой максвелловской жидкости в цилиндрической трубе. Строится передаточная функция, выражающая обобщенный закон сопротивления трения, выводятся формулы для частотной функции и с их помощью исследуется зависимость нестационарного касательного напряжения на стенке трубы от частоты колебания, ускорения и релаксационных свойств жидкости. Оценивается роль нестационарности потока на закон сопротивления, показано отличие результатов от полученных на основе квазистационарного подхода.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается задача определения касательного напряжения ${{\tau }_{{оns}}}(t) = \tau (R,t)$ на стенке круглой цилиндрической трубы радиуса R при периодическом движении жидкости. Реологическое уравнение состояния жидкости принимаем в виде [5, 7]

(1.1)

$\left( {1 + \lambda \frac{\partial }{{\partial t}}} \right)\tau \left( {r,t} \right) = - \mu \frac{{\partial u}}{{\partial r}}$

где $r$ – радиальная координата, отсчитываемая от оси трубы, $0 \leqslant r \leqslant R$; $t$ – время; $u$ – скорость жидкости; $\mu $ – динамическая вязкость; $\tau $ – касательное напряжение; $\lambda $ – время релаксации. В (1.1) при λ = 0 получается закон вязкого трения Ньютона, а при λ > 0 – модель вязкоупругой среды Максвелла. Подставляя (1.1) в уравнение движения

$\rho \frac{{\partial u}}{{\partial t}} = - \frac{{\partial p}}{{\partial z}} - \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\tau } \right)$

относительно скорости жидкости u(r, t), получим

(1.2)

$\rho \left( {1 + \lambda \frac{\partial }{{\partial t}}} \right)\frac{{\partial u}}{{\partial t}} = - \left( {1 + \lambda \frac{\partial }{{\partial t}}} \right)\frac{{\partial p}}{{\partial z}} + \mu \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial u}}{{\partial r}}} \right)$

где $\partial p{\text{/}}\partial z$ – градиент давления $p$ вдоль оси Oz, совпадающей с осью трубы, $\rho $ – плотность жидкости. Считается, что в начальный момент жидкость покоится, в соответствии с условием прилипания скорость на стенке трубы равна нулю. Тогда начальные и граничные условия имеют вид

(1.3)

$u(r,0) = 0,\quad \frac{{\partial u(r,0)}}{{\partial t}} = 0,\quad 0 \leqslant r \leqslant R;\quad u(0,t) < + \infty ,\quad u(R,t) = 0,\quad \tau (R,0) = 0$

Уравнения (1.1), (1.2) и условия (1.3) выражают математическую модель исследуемого процесса.

Введем следующие безразмерные величины:

(1.4)

$r{\text{'}} = \frac{r}{R},\quad t{\text{'}} = \frac{U}{R}t,\quad \lambda {\text{'}} = \frac{U}{R}\lambda ,\quad u{\text{'}} = \frac{u}{U}$

где U – некоторое характерное значение скорости.

В безразмерных переменных (1.4) уравнения (1.1), (1.2) принимают вид

(1.5)

$\left( {1 + \lambda {\text{'}}\frac{\partial }{{\partial{ \bar {t}}}}} \right)\tau {\text{'}} = - \frac{{\partial u{\text{'}}}}{{\partial r{\text{'}}}}$

(1.6)

$\frac{1}{{\operatorname{Re} }}\frac{1}{{r{\text{'}}}}\frac{\partial }{{\partial r{\text{'}}}}\left( {r{\text{'}}\frac{{\partial u{\text{'}}}}{{\partial r{\text{'}}}}} \right) - \left( {1 + \lambda {\text{'}}\frac{\partial }{{\partial t{\text{'}}}}} \right)\frac{{\partial u{\text{'}}}}{{\partial t{\text{'}}}} = \left( {1 + \lambda {\text{'}}\frac{\partial }{{\partial t{\text{'}}}}} \right){{P}_{z}}(t{\text{'}})$

где Re = $UR\rho {\text{/}}\mu $; τ' = $\tau R{\text{/}}(U\mu )$ – безразмерное касательное напряжение; P_z(t') = $\partial p{\text{'/}}\partial z{\text{'}}$ = = $R(\partial p{\text{/}}\partial z){\text{/}}(\rho {{U}^{2}})$ – безразмерный градиент давления; $p{\text{'}} = p{\text{/}}(\rho {{U}^{2}})$; $z = Rz{\text{'}}$.

Начальные и граничные условия в безразмерных величинах имеют вид

(1.7)

$\begin{gathered} \hfill u{\text{'}}(r{\text{'}},t{\text{'}}) = 0,\quad \frac{{\partial u{\text{'}}(r{\text{'}},0)}}{{\partial t{\text{'}}}} = 0,\quad 0 \leqslant r{\text{'}} \leqslant 1; \\ \hfill u{\text{'}}(0,t{\text{'}}) < + \infty ,\quad u{\text{'}}(1,t{\text{'}}) = 0,\quad \tau {\text{'}}(1,t') = 0 \\ \end{gathered} $

2. РЕШЕНИЕ ЗАДАЧИ

Для решения уравнений (1.5), (1.6) с краевыми условиями (1.7), применяя интегральное преобразование Лапласа [26]

${{u}_{ * }}(r{\text{'}},s) = \int\limits_0^{ + \infty } {u{\text{'}}{{e}^{{ - st{\text{'}}}}}dt{\text{'}},\quad {{\tau }_{ * }}\left( {r{\text{'}},s} \right) = \int\limits_0^{ + \infty } {\tau {\text{'}}{{e}^{{ - st{\text{'}}}}}dt{\text{'}},\quad {{P}_{{z * }}}\left( s \right) = \int\limits_0^{ + \infty } {{{P}_{z}}(t{\text{'}}){{e}^{{ - st{\text{'}}}}}dt{\text{'}}} } } $

получим

(2.1)

$\frac{1}{{r{\text{'}}}}\frac{d}{{dr{\text{'}}}}\left( {r{\text{'}}\frac{{d{{u}_{ * }}}}{{dr{\text{'}}}}} \right) - \operatorname{Re} {{k}^{2}}{{u}_{ * }} = \frac{{{{k}^{2}}\operatorname{Re} }}{s}{{P}_{{z*}}}(s)$

(2.2)

${{u}_{ * }}(1,s) = 0,\quad {{u}_{ * }}(0,s) < + \infty $

(2.3)

$\left( {1 + \lambda {\text{'}}s} \right){{\tau }_{ * }} = - \frac{{d{{u}_{ * }}}}{{dr{\text{'}}}}$

Решение уравнения (2.1) с граничными условиями (2.2) имеет вид

(2.4)

${{u}_{ * }}\left( {r{\text{'}},s} \right) = - \frac{{{{P}_{{z*}}}(s)}}{s}\left[ {1 - \frac{{{{J}_{0}}(iakr{\text{'}})}}{{{{J}_{0}}(iak)}}} \right]$

Подставляя (2.4) в (2.3), получим формулу для касательного напряжения

(2.5)

${{\tau }_{ * }}(r{\text{'}},s) = - \frac{{\operatorname{Re} }}{{iak}}\frac{{{{J}_{1}}(iakr{\text{'}})}}{{{{J}_{0}}(iak)}}$

где $k = \sqrt {s(1 + \lambda {\text{'}}s)} $; $\,a = \sqrt {\operatorname{Re} } $; ${{J}_{0}}(x)$, J₁(x) – функции Бесселя первого рода нулевого и первого порядков.

Сопротивление трения на стенке трубы определяется касательным напряжением ${{\tau }_{{оns}}}(t)$ = = τ(R, t), безразмерный вид которого для данного случая имеет вид

$\tau _{{ons}}^{'}(t{\text{'}}) = \frac{R}{{U\mu }}{{\tau }_{{ons}}}(t)$

Положив в (2.5) $r{\text{'}} = 1$, найдем изображение по Лапласу безразмерного нестационарного касательного напряжения на стенке трубы

(2.6)

${{\tau }_{{ons*}}}(s) = {{\tau }_{ * }}(1,s) = - \frac{{\operatorname{Re} }}{{iak}}\frac{{{{J}_{1}}(iak)}}{{{{J}_{0}}(iak)}}{{P}_{{z*}}}(s)$

При квазистационарном распределении скорости касательное напряжение на стенке трубы ${{\tau }_{{oks}}}$ определяется как [27, 28]

(2.7)

${{\tau }_{{оks}}} = \frac{4}{R}\mu {{{v}}_{{ks}}}$

в безразмерной форме

(2.8)

$\tau _{{оks}}^{'} = 4{v}_{{ks}}^{'}$

где ${{{v}}_{{ks}}}$ – средняя по сечению трубы квазистационарная скорость; $\tau _{{оks}}^{'} = R{{\tau }_{{oks}}}{\text{/}}(U\mu )$, ${v}_{{ks}}^{'} = {{{v}}_{{ks}}}{\text{/}}U$.

Согласно (2.7) квазистационарное касательное напряжение на стенке трубы ${{\tau }_{{оks}}}$ является функцией средней по сечению трубы скорости. Чтобы найти зависимость нестационарного касательного напряжения на стенке трубы от средней по сечению трубы скорости ${v}(t)$ нестационарного потока в безразмерных величинах, исключим из формулы (2.6) изображение безразмерного градиента давления ${{P}_{{z*}}}(s)$. С этой целью умножим уравнение (1.6) на $2\pi r{\text{'}}$ и проинтегрируем на промежутке [0, 1]

$2\pi \int\limits_0^1 {\frac{\partial }{{\partial r{\text{'}}}}\left( {r{\text{'}}\frac{{\partial u{\text{'}}}}{{\partial r{\text{'}}}}} \right)dr{\text{'}}} - 2\pi {\text{Re}}\int\limits_0^1 {\left( {1 + \lambda {\text{'}}\frac{\partial }{{\partial t{\text{'}}}}} \right)\frac{{\partial u{\text{'}}}}{{\partial t{\text{'}}}}r{\text{'}}dr{\text{'}} = 2\pi \operatorname{Re} \left( {1 + \lambda {\text{'}}\frac{\partial }{{\partial t'}}} \right){{P}_{z}}(t{\text{'}})\int\limits_0^1 {r{\text{'}}dr{\text{'}}} } $

откуда

(2.9)

$2{{\left. {\left[ {\frac{{\partial u{\text{'}}}}{{\partial r{\text{'}}}}} \right]} \right|}_{{\bar {r} = 1}}} - {\text{Re}} \cdot \left( {1 + \lambda {\text{'}}\frac{d}{{dt{\text{'}}}}} \right)\frac{{d{v}{\text{'}}}}{{dt{\text{'}}}} = \operatorname{Re} \left( {1 + \lambda {\text{'}}\frac{d}{{dt{\text{'}}}}} \right){{P}_{z}}(t{\text{'}})$

Переходя к изображению в (2.9) c учетом (2.3), получим

${{P}_{{z*}}}(s) = - 2{{\tau }_{{ons*}}}(s){\text{/}}\operatorname{Re} - s{{{v}}_{ * }}(s)$

где ${v}{\text{'}}(t{\text{'}}) = 2\int_0^1 {u{\text{'}}r{\text{'}}dr{\text{'}}} $ – безразмерная средняя по сечению трубы скорость, ${{{v}}_{ * }}(s) = \int_0^{ + \infty } {{v}{\text{'}}{{e}^{{ - st'}}}dt{\text{'}}} $ – ее изображение по Лапласу. Подставляя найденное выражение ${{P}_{{z*}}}(s)$ в (2.6), используя свойство $2{{J}_{1}}(x){\text{/}}x - {{J}_{0}}(x) = {{J}_{2}}(x)$ функций Бесселя, получим

(2.10)

${{\tau }_{{ons*}}}(s) = - s{{{v}}_{ * }}(s) \cdot \frac{{\operatorname{Re} {{J}_{1}}(iak)}}{{iak{{J}_{2}}(iak)}}$

где J₂(x) – функции Бесселя первого рода второго порядка.

Соотношение (2.10) устанавливает связь между безразмерными значениями изображения по Лапласу касательного напряжения на стенке трубы и средней по сечению трубы скоростью жидкости при нестационарном течении жидкости. В терминах теории автоматического управления его можно представить в виде передаточной функции

(2.11)

$W(s) = \frac{{{{\tau }_{{ons*}}}(s)}}{{{{{v}}_{ * }}(s)}} = - s\frac{{\operatorname{Re} {{J}_{1}}(iak)}}{{iak{{J}_{2}}(iak)}}$

В общем случае передаточная функция определяется отношением “силового” фактора (электрического напряжения, силы, давления) к “скоростному” фактору (электрическому току, скорости, объемному расходу) в комплексной форме. Механическая передаточная функция (2.11) выражает отношение комплексных величин, описывающих законы изменения касательного напряжения на стенке трубы и средней по сечению трубы скорости. Она справедлива для любых возмущений, вызывающих нестационарное ламинарное движение жидкости в трубе, и поэтому описывает обобщенный закон сопротивления трения. Частный случай этого закона – зависимость касательного напряжения на стенке трубы от скорости при стационарном движении жидкости, которая известна в гидравлике в форме соотношения (2.7). Функция $W(i\omega )$, где ω – частота колебаний, называется частотной функцией. Построению передаточной и частотной функций для касательного напряжения на стенке трубы при ламинарном периодическом движении вязкой жидкости посвящены [25, 27, 28].

Для того чтобы выяснить характер изменения нестационарного касательного напряжения на стенке трубы, рассмотрим определение безразмерного касательного напряжения на стенке трубы $\tau _{{ons}}^{'}(t{\text{'}})$ при гармонических колебаниях жидкости

(2.12)

${v}{\text{'}}(t') = {{a}_{{v}}}{\text{sin}}\omega {\text{'}}t{\text{'}}$

где ${{a}_{{v}}}$ – амплитуда безразмерной средней по сечению трубы скорости жидкости; $\omega {\text{'}} = \omega R{\text{/}}U$ – безразмерная угловая частота колебаний жидкости.

Рассматривая установившиеся гармонические колебания, $\tau _{{ons}}^{'}(t{\text{'}})$ представим в виде следующей функции:

(2.13)

$\tau _{{оns}}^{'}(t{\text{'}}) = {{a}_{\tau }}\sin (\omega {\text{'}}t{\text{'}} + {{\varphi }_{\tau }})$

где a_τ – амплитуда безразмерного касательного напряжения на стенке трубы; ${{\varphi }_{\tau }}$ – смещение по фазе между величинами $\tau _{{ons}}^{'}(t{\text{'}})$ и ${v}{\text{'}}(t{\text{'}})$. С учетом (2.12 ) равенство (2.13) приведем к виду

(2.14)

$\tau _{{ons}}^{'}(t{\text{'}}) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}{v}{\text{'}}\cos {{\varphi }_{\tau }} + \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\frac{1}{{\omega {\text{'}}}}\sin {{\varphi }_{\tau }}\frac{{d{v}{\text{'}}}}{{dt{\text{'}}}}$

Применяя к (2.14) преобразование Лапласа, имеем

${{\tau }_{{ons*}}}(s) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}{{{v}}_{ * }}(s)\cos {{\varphi }_{\tau }} + \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\frac{s}{{\omega {\text{'}}}}{{{v}}_{ * }}(s)\sin {{\varphi }_{\tau }}$

Отсюда и из (2.11) следует

(2.15)

$W(s) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}{\text{cos}}{{\varphi }_{\tau }} + \frac{s}{{\omega {\text{'}}}}\frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}{\text{sin}}{{\varphi }_{\tau }}$

частотная функция, соответствующая к (2.15), имеет вид

$W(i\bar {\omega }) = \operatorname{Re} \left( {W(i\omega {\text{'}})} \right) + i\operatorname{Im} \left( {W(i\omega {\text{'}})} \right) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\cos {{\varphi }_{\tau }} + i\frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\sin {{\varphi }_{\tau }}$

где $\operatorname{Re} \left( {W(i\omega {\text{'}})} \right)$ и $\operatorname{Im} \left( {W(i\omega {\text{'}})} \right)$ – реальная и мнимая части выражения $W(i\omega {\text{'}})$.

Отсюда следует

$\operatorname{Re} \left( {W(i\omega {\text{'}})} \right) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\cos \varphi ,\quad \operatorname{Im} \left( {W(i\omega {\text{'}})} \right) = \frac{{{{a}_{\tau }}}}{{{{a}_{{v}}}}}\sin {{\varphi }_{\tau }}$

С учетом этого (2.15) можно представить в виде

(2.16)

$\tau _{{ons}}^{'}(t{\text{'}}) = \operatorname{Re} \left( {W(i\omega {\text{'}})} \right){v}{\text{'}}(t{\text{'}}) + \frac{1}{{\omega {\text{'}}}}\operatorname{Im} \left( {W(i\omega {\text{'}})} \right)\frac{{d{v}{\text{'}}}}{{dt{\text{'}}}}$

Функция (2.16) определяет в безразмерных переменных нестационарное касательное напряжение на стенке трубы в любой момент времени при установившихся гармонических колебаниях жидкости. Она раскрывает основную особенность его нестационарности, состоящую в том, что его значение изменяется в зависимости как от скорости, так и от ускорения жидкости, причем на его значения влияют еще частота колебаний жидкости в трубе и вязкоупругие свойства жидкости. Такой характер изменения касательного напряжения на стенке трубы при нестационарном движении среды не будет учитываться, если исходить из квазистационарного распределения скоростей по живому сечению потока. В последнем случае значение напряжения на стенке трубы определяется соотношением (2.7), которое в безразмерной форме имеет вид (2.8).

Использование формулы (2.16) связано с задачей определения действительной и мнимой частей частотной функции $W(i\omega {\text{'}})$. Для вязкой жидкости соответствующие формулы с помощью функций Кельвина получены в [27]. Для “больших” значений $\omega {\text{'}}$ использованы асимптотические формулы. Выведем формулы $\operatorname{Re} \left( {W(i\omega {\text{'}})} \right)$, $\operatorname{Im} \left( {W(i\omega {\text{'}})} \right)$ для рассматриваемой здесь вязкоупругой жидкости, справедливые при любых $\omega {\text{'}}$. С этой целью введем функцию комплексного переменного

$f(z) = \frac{{{{J}_{1}}(z)}}{{z{{J}_{2}}(z)}}.$

Можно показать, что ${{z}^{2}}f(z) \to 4$ при $z \to 0$. Ввиду этого для функции

(2.17)

$F(z) = f(z) - \frac{4}{{{{z}^{2}}}}$

точка z = 0 – устранимая особая точка. При $z \ne 0$ эта функция ограничена и имеет простые полюсы в точках $ \pm {{z}_{1}},\; \pm {{z}_{2}},\; \ldots ,\; \pm {{z}_{n}},\; \ldots $, где z_n – положительные корни уравнения ${{J}_{2}}(z) = 0$, $n = 1,2, \ldots $. Следовательно, F(z) удовлетворяет всем условиям теоремы Коши о разложении мероморфной функции на простые дроби [29]. Следовательно, имеет место формула

$F(z) = \sum\limits_{n = 1}^\infty {\left[ {\frac{1}{{{{z}_{n}}(z - {{z}_{n}})}} + \frac{1}{{{{z}_{n}}(z + {{z}_{n}})}}} \right] = 2\sum\limits_{n = 1}^\infty {\frac{1}{{{{z}^{2}} - z_{n}^{2}}}} } .$

Отсюда, с учетом (2.17) получим

(2.18)

$\frac{{{{J}_{1}}(z)}}{{z{{J}_{2}}(z)}} = \frac{4}{{{{z}^{2}}}} + 2\sum\limits_{n = 1}^\infty {\frac{1}{{{{z}^{2}} - z_{n}^{2}}}} $

Используя формулу (2.18), разложим функцию W(s) в ряд

$W(s) = \frac{{4s}}{{{{k}^{2}}}} + 2s\sum\limits_{n = 1}^\infty {\frac{1}{{{{k}^{2}} + z_{n}^{2}}} = } \frac{4}{{1 + \lambda {\kern 1pt} '{\kern 1pt} s}} + 2s{\text{Re}}\sum\limits_{n = 1}^\infty {\frac{1}{{s{\text{Re}}(1 + \lambda {\text{'}}s) + z_{n}^{2}}}} $

Положив здесь $s = i\omega {\text{'}}$, найдем выражение для частотной функции

$W(i\omega {\text{'}}) = \frac{{4(1 - \lambda {\text{'}}\omega {\text{'}}i)}}{{1 + {{\lambda }^{{'2}}}{{\omega }^{{'2}}}}} + 2{\text{Re}}\omega {\text{'}}\sum\limits_{n = 1}^\infty {\frac{{{\text{Re}}\omega {\text{'}} + i(z_{n}^{2} - \lambda {\text{'}}{{\omega }^{{'2}}}{\text{Re}})}}{{{{{(z_{n}^{2} - \lambda {\text{'}}{{\omega }^{{'2}}}{\text{Re}})}}^{2}} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} $

Отсюда получим следующие формулы для действительной и мнимой частей частотной функции:

(2.19)

$\operatorname{Re} \left( {W(i\omega {\text{'}})} \right) = \frac{4}{{1 + {{\lambda }^{{'2}}}{{\omega }^{{'2}}}}} + 2{\text{R}}{{{\text{e}}}^{2}}{{\omega }^{{'2}}}\sum\limits_{n = 1}^\infty {\frac{1}{{{{{(z_{n}^{2} - \lambda {\text{'}}{{\omega }^{{'2}}}{\text{Re}})}}^{2}} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} $

(2.20)

$\operatorname{Im} \left( {W(i\omega {\text{'}})} \right) = - \frac{{4\omega {\text{'}}\lambda {\text{'}}}}{{1 + {{\lambda }^{{'2}}}{{\omega }^{{'2}}}}} + 2{\text{Re}}\omega {\text{'}}\sum\limits_{n = 1}^\infty {\frac{{z_{n}^{2} - \lambda {\text{'}}{{\omega }^{{'2}}}{\text{Re}}}}{{{{{(z_{n}^{2} - \lambda {\text{'}}{{\omega }^{{'2}}}{\text{Re}})}}^{2}} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} $

В частности, для вязкой жидкости имеем

$\operatorname{Re} \left( {W(i\omega {\text{'}})} \right) = 4 + 2{{\operatorname{Re} }^{2}}{{\omega }^{{'2}}}\sum\limits_{n = 1}^\infty {\frac{1}{{z_{n}^{4} + {{\omega }^{{'2}}}{{{\operatorname{Re} }}^{2}}}}} ,\quad \operatorname{Im} \left( {W(i\omega {\text{'}})} \right) = 2\operatorname{Re} \omega {\text{'}}\sum\limits_{n = 1}^\infty {\frac{{z_{n}^{2}}}{{z_{n}^{4} + {{\omega }^{{'2}}}{{{\operatorname{Re} }}^{2}}}}} $

Для сравнения $\tau _{{ons}}^{'}$ и $\tau _{{oks}}^{'}$ в одинаковые моменты времени примем ${v} = {{{v}}_{{ks}}}$ и, разделив (2.15) почленно на $\tau _{{oks}}^{'} = 4{v}_{{ks}}^{'}$, найдем отношение

(2.21)

$\frac{{\tau _{{ons}}^{'}}}{{\tau _{{oks}}^{'}}} = \frac{1}{4}\operatorname{Re} \left( {W(i\omega {\text{'}})} \right) + \frac{1}{{4\omega {\text{'}}}}{{K}_{n}}\operatorname{Im} \left( {W(i\omega {\text{'}})} \right)$

Здесь параметр ${{K}_{n}} = (1{\text{/}}{v}{\text{'}})d{v}{\text{'/}}dt{\text{'}}$ служит критерием, отражающим влияние ускорения жидкости на значения нестационарного касательного напряжения на стенке трубы в рассматриваемый момент времени. Подставляя (2.18), (2.19) в (2.20), получим

(2.22)

$\frac{{\tau _{{ons}}^{'}}}{{\tau _{{oks}}^{'}}} = \frac{{{{\tau }_{{ons}}}}}{{{{\tau }_{{oks}}}}} = \frac{{1 - {{K}_{n}}\lambda {\text{'}}}}{{1 + {{\lambda }^{{'2}}}{{\omega }^{{'2}}}}} + \frac{{\operatorname{Re} }}{2}\sum\limits_{n = 1}^\infty {\frac{{{{\omega }^{{'2}}}{\text{Re}} + {{K}_{n}}(z_{n}^{2} - \lambda {\text{'}}{{\omega }^{{'2}}}{\text{Re}})}}{{{{{(z_{n}^{2} - \lambda {\text{'}}{{\omega }^{{'2}}}{\text{Re}})}}^{2}} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} $.

В частности, для вязкой жидкости

(2.23)

$\frac{{\tau _{{оns}}^{'}}}{{\tau _{{оks}}^{'}}} = \frac{{{{\tau }_{{оns}}}}}{{{{\tau }_{{оks}}}}} = 1 + \frac{{\operatorname{Re} }}{2}\sum\limits_{n = 1}^\infty {\frac{{{\text{Re}}\omega {{'}^{2}} + {{K}_{n}}z_{n}^{2}}}{{z_{n}^{4} + {{\omega }^{{'2}}}{\text{R}}{{{\text{e}}}^{2}}}}} $

Из формул (2.22), (2.23) видно, что с ростом ускорения (параметра K_n) нестационарное касательное напряжение возрастает для вязкой жидкости, для вязкоупругой жидкости зависит еще и от параметра релаксации $\lambda $.

3. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ И ВЫВОДЫ

С помощью полученных формул проведены численные эксперименты по исследованию влияния частоты колебаний, ускорения (критерия K_n) и вязкоупругих свойств жидкости на распределение нестационарного касательного напряжения на стенке трубы при периодическом движении жидкости. В расчетах использованы следующие размерные значения для исходных данных задачи: $R = 0.08$ м, $U = 0.2$ м/с, $0 \leqslant \omega \leqslant 2.5$ с^–1; $\lambda = 0;\;0.5;\;1;\;2$ с. Соответствующими безразмерными значениями частоты колебаний и параметра релаксации будут: $0 \leqslant \omega {\text{'}} \leqslant 1$; $\lambda {\text{'}} = 0$; 1.25; 2.50; 5. Значение параметра $\operatorname{Re} = \rho RU{\text{/}}\mu $ при плотности $\rho = 1200$ кг/м³ и вязкости $\mu = 0.030$ Па ⋅ с будет $\operatorname{Re} = 640$.

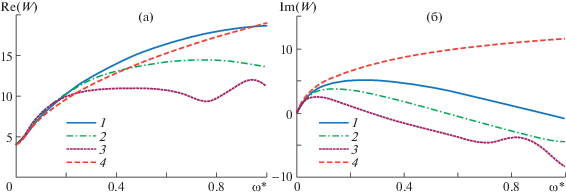
На рис. 1 приведены графики зависимости действительной и мнимой частей частотной функции от безразмерной частоты $\omega {\text{'}}$. Видно, что с ростом безразмерной частоты для вязкой жидкости обе части возрастают. Для вязкоупругой жидкости при больших частотах они могут уменьшаться. С усилением упругих свойств жидкости (с ростом $\lambda {\text{'}}$) графики приобретают колебательный характер.

Рис. 1.

Графики зависимости действительной (a) и мнимой (б) частей частотной функции от безразмерной частоты колебаний при Re = 640: 1–4 – $\lambda {\text{'}} = 1.25;\;2.5;\;5;\;0$.

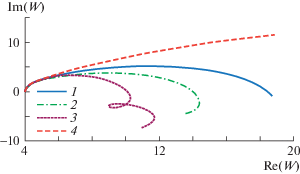
Графики амплитудно-фазовой частотной характеристики колебательного движения при возрастании безразмерной частоты $\omega {\text{'}}$ от 0 до 1 (рис. 2) показывают, что при гармонических колебаниях жидкости в трубе касательное напряжение на стенке для вязкоупругой жидкости принципиально отличается от случая вязкой жидкости, особенно с усилением релаксационных свойств. При больших значениях времени релаксации могут образоваться возвратные течения, что характерно для вязкоупругих жидкостей.

Рис. 2.

Амплитудно-фазовая частотная характеристика касательного напряжения на стенке трубы при ламинарном движении вязкоупругой жидкости при возрастании безразмерной частоты колебаний от 0 до 1 при Re = 640 и 1–4 как на рис. 1.

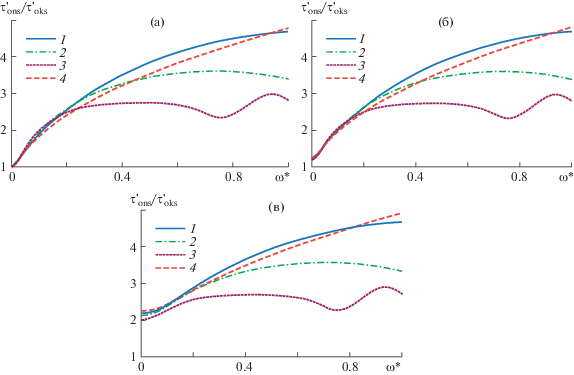
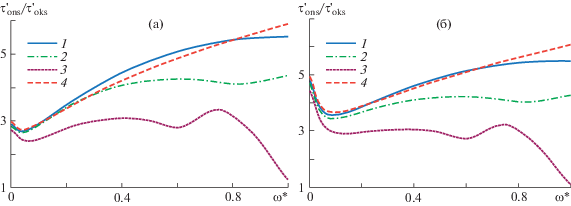
На рис. 3 показаны графики зависимости безразмерного нестационарного касательного напряжения на стенке трубы $\tau _{{ons}}^{'}{\text{/}}\tau _{{oks}}^{'}$ от безразмерной частоты $\omega {\text{'}}$ при $\operatorname{Re} = 640$ и значениях критерия K_n: 0; 0.01; 0.05. Видно, что с ростом ускорения (параметра K_n) при $\omega {\text{'}} = 0$ и малых частотах ($0 \leqslant \omega {\text{'}} \leqslant 0.2$) наблюдается резкий рост касательного напряжения. При больших частотах профили заметно не отличаются. С ростом $\lambda {\text{'}}$ (например, при $\lambda {\text{'}} = 5$) график имеет колебательный характер.

Рис. 3.

Изменение нестационарного касательного напряжения на стенке трубы в зависимости от безразмерной частоты при Re = 640: а–в – K_n = 0; 0.01; 0.05 и 1–4 как на рис. 1.

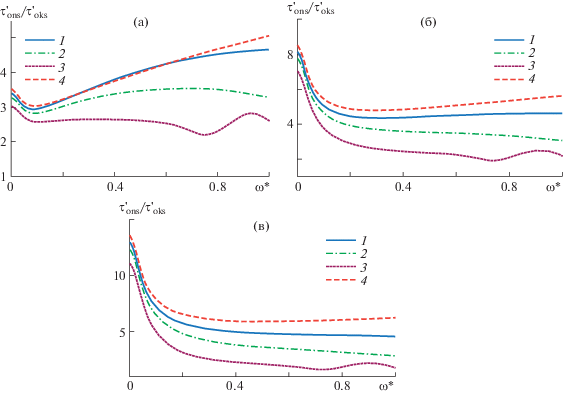
При малых частотах с ростом ускорения происходит перестройка профилей. При дальнейшем увеличении параметра K_n = 0.1; 0.3 (рис. 4a, б) при малых частотах в графике образуется минимум. С усилением релаксационных свойств этот минимум смещается вправо по оси частот. С дальнейшим ростом ускорения (параметра K_n) профили выравниваются, минимум исчезает (рис. 4в).

Рис. 4.

Изменение нестационарного касательного напряжения на стенке трубы в зависимости от безразмерной частоты при Re = 640: а–в – K_n = 0.1; 0.3; 0.5 и 1–4 как на рис. 1.

Графики зависимости $\tau _{{ons}}^{'}{\text{/}}\tau _{{oks}}^{'}$ от $\omega {\text{'}}$ при увеличении числа Re (Re = 1000) показывают (рис. 5), что нестационарное касательное напряжение на стенке трубы при малых частотах возрастает, минимум в графиках проявляется уже при ${{K}_{n}} = 0.05$ (рис. 5a). C ростом ускорения (при K_n = 0.1) существенное изменение в профилях происходит в основном при малых частотах $0 \leqslant \omega {\text{'}} \leqslant 0.4$. При больших частотах колебаний для $\lambda {\text{'}} = 5$ касательное напряжение резко уменьшается.

Рис. 5.

Изменение нестационарного касательного напряжения на стенке трубы в зависимости от безразмерной частоты при Re = 1000: a и б – K_n = 0.05; 0.1 и 1–4 как на рис. 1.

Отметим, что при использовании формулы (2.22) нельзя получить очевидный результат об увеличении нестационарного касательного напряжения на стенке трубы с увеличением вязкости, так как в ${{\tau }_{{оns}}}{\text{/}}{{\tau }_{{оks}}}$ как числитель, так и знаменатель зависят от вязкости. Кроме того, с возрастанием вязкости это отношение уменьшается, что на первый взгляд может привести к противоречивому выводу о снижении нестационарного касательного напряжения на стенке трубы с увеличением вязкости. Действительно, пусть ${{\tau }_{{оns}}}$, ${{\tau }_{{оks}}}$ – значения нестационарного и квазистационарного касательного напряжения при вязкости $\mu $, а $\tau _{{оns}}^{*}$, $\tau _{{оks}}^{*}$ – их значения при вязкости $\mu {\text{*}} = 2\mu $. Из равновесной связи (2.7) следует, что при увеличении вязкости в два раза, квазистационарное касательное напряжение также возрастает в два раза. Из-за неравновесности соотношения (1.1) нестационарное касательное напряжение (за счет запаздывания) увеличивается меньше чем два раза в различные моменты времени переходного периода, например в α раз, где $1 < \alpha < 2$. Тогда

$\tau _{{оks}}^{*} = \frac{{4\mu {\text{*}}}}{R}{{{v}}_{{кs}}} = 2 \cdot \frac{{4\mu }}{R}{{{v}}_{{кs}}} = 2{{\tau }_{{оks}}};\quad \tau _{{оns}}^{*} = \alpha {{\tau }_{{оns}}};\quad \frac{{\tau _{{оns}}^{*}}}{{\tau _{{оks}}^{*}}} = \frac{\alpha }{2} \cdot \frac{{{{\tau }_{{ons}}}}}{{{{\tau }_{{oks}}}}} < \frac{{{{\tau }_{{ons}}}}}{{{{\tau }_{{oks}}}}}$

т.е. с ростом вязкости отношение ${{\tau }_{{оns}}}{\text{/}}{{\tau }_{{оks}}}$ уменьшается.

По-видимому, при исследовании влияния вязкости на нестационарное касательное напряжение лучше использовать формулу

(3.1)

${{\tau }_{{оns}}} = \frac{{4\mu {{{v}}_{{кs}}}}}{R} \cdot \frac{{\tau _{{ons}}^{'}}}{{\tau _{{oks}}^{'}}}$

где второй множитель в правой части вычисляется по формуле (2.22). Расчеты, произведенные по формуле (3.1), показали, что увеличение вязкости жидкости приводит к значительному росту касательного напряжения повсюду. Существенное изменение в профилях происходит только для вязкоупругой жидкости, особенно с ростом времени релаксации.

ЗАКЛЮЧЕНИЕ

Установлено, что с ростом ускорения движения жидкости нестационарное касательное напряжение на стенке трубы возрастает, особенно при малых частотах колебания, наблюдается существенная зависимость от релаксационного параметра вязкоупругой жидкости. Различие между профилями при увеличении релаксационного параметра возрастает с увеличением частоты колебания скорости движения жидкости. При определенных значениях ускорения жидкости нестационарное касательное напряжение при малых частотах имеет минимум. С ростом ускорения этот минимум смещается вправо по оси частот, различие между профилями вязкой и вязкоупругой жидкостей увеличивается. Для вязкоупругой жидкости этот минимум зависит еще и от параметра релаксации. При увеличении параметра $\operatorname{Re} $ минимум на графиках проявляется при относительно малом ускорении, колебательный характер усиливается. С ростом ускорения минимум исчезает, профили принимают убывающий характер.

В целом увеличение времени релаксации уменьшает как относительное, так и само напряжение на стенке трубы. Колебательный характер напряжения обусловлен как с заданным колебательным режимом скорости жидкости, так и релаксационными свойствами жидкости, которые приводят к неравномерному колебательному распределению поля скорости жидкости по поперечному сечению трубы даже при не колебательном режиме движения жидкости. Последний факт известен из многих работ, посвященных движению вязкоупругих жидкостей в трубах. Полученные результаты показывают, что релаксационные свойства жидкости служат лимитирующим фактором использования квазистационарного подхода при определении нестационарного касательного напряжения на стенке трубы, как и ускорение движения жидкости.

Авторы выражают благодарность рецензентам и редактору статьи за полезные замечания.

Список литературы

Акилов Ж.А. Нестационарные движения вязкоупругих жидкостей. Ташкент: Фан, 1982. 104 с.
Хужаёров Б.Х. Реологические свойства смесей. Самарканд: Согдиана, 2000. 216 с.
Мирзаджанзаде А.Х., Караев А.К., Ширинзаде С.А. Гидравлика в бурении и цементировании нефтяных и газовых скважин. М.: Недра, 1977. 230 с.
Аметов И.М., Байдиков Ю.Н., Рузин Л.М. и др. Добыча тяжелых и высоковязких жидкостей. М.: Недра, 1985. 205 с.
Astarista G., Marrucci G. Principles of Non-Newtonian Fluid Mechanics. New York: McGraw-Hill, 1974. 289 p.
Siginer D.A. Developments in the Flow of Complex Fluids in Tubes. Springer, 2015.
Chhabra R.P., Richardson J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications. Butterworth-Heinemann/IChemE. 2nd Ed. 2008.
Harris J., Peev G., Wilkinson W.L. Velocity profiles in laminar oscillatory flow in tubes // Journal of Scientific Instruments (Journal of Physics E). 1969. Ser. 2. V. 2. P. 913–916.
Sergeev S. Fluid oscillations in pipes at moderate Reynolds numbers // Fluid Dyn. 1966. V. 1. № 1. P. 121–122.
Ahn K.H., Ibrahim M.B. Laminar/turbulent oscillating flow in circular pipes // Int. J. Heat Fluid Flow. 1992. V. 13. № 4. P. 340–346.
Jones J.R., Walters T.S. Flow of Elastico-Viscous Liquids in Channels under the Influence of a Periodic Pressure Gradient, Part 1 // Rheol. Acta. 1967. V. 6. 240 p.
Khabakhpasheva E., Popov V., Kekalov A., Mikhailova E. Pulsating flow of viscoelastic fluids in tubes // J. Non-Newtonian Fluid Mech. 1989.V. 33. № 3. P. 289–304.
Casanellas L., Ortıґn J. Laminar oscillatory flow of Maxwell and Oldroyd-B fluids: Theoretical analysis // Journal of Non-Newtonian Fluid Mechanics. 2011. V. 166. P. 1315–1326.
Andrienko Yu.A., Siginer D.A., Yanovsky Yu.G. Resonance behavior of viscoelastic fluids in Poiseuille flow and application to flow enhancement // International Journal of Non-Linear Mechanics. 2000. V. 35. P. 95–102.
Letelier M.F., Siginer D.A., Caceres C. Pulsating flow of viscoelastic fluids in straight tubes of arbitrary cross-section. Part I: Longitudinal field // International Journal of Non-Linear Mechanics. 2002. V. 37. P. 369–393.
Rheology – new concepts, applications and methods. Edited by Rajkumar Durairaj. Published by InTech. 2013. Chapter 6. A. Abu-El Hassan and E.M. El-Maghawry. Unsteady Axial Viscoelastic Pipe Flows of an Oldroyd B Fluid. 91-106. Chr. Friedrich. Relaxation and retardation functions of the Maxwell model with fractional derivatives // Rheol. Acta. 1991. V. 30. P. 151–158.
Friedrich Chr. Relaxation and retardation functions of the Maxwell model with fractional derivatives // Rheol. Acta. 1991. V. 30. P. 151–158.
Mainardi F., Goren R. Time-fractional derivatives in relaxation processes: a tutorial survey // Fractional Calculus and Applied Analysis. 2007. V. 10. № 3. P. 269–308.
Hilfer R. Applications of Fractional Calculus in Physics. Singapore: World Scientific Press, 2000.
Makris N., Dargush G.F., Constantinou M.C. Dynamic Analysis of Generalized Viscoelastic Fluids // Journal of Engineering Mechanics. 1993. V. 119. № 8. P. 1663–1679.
Wenchang T., Mingyu X. Unsteady flows of a generalized second grade fluid with the fractional derivative model between two parallel plates // Acta Mechanica Sinica. 2004. V. 20. № 5. P. 471–476.
Абдулла М., Раза Н., Шахид И. Гибридный метод решения для нестационарной модели максвелловской жидкости с дробными производными, обусловленными касательными сдвиговыми напряжениями // Изв. РАН. МЖГ. 2017. № 6. С. 3–12.
Юшутин В.С. Устойчивость деформируемых каналов при течении по ним нелинейно-вязких сред со степенным законом упрочнения // Вестн. Моск. ун-та. Сер. 1, Математика. Механика. 2012. № 4. С. 67–70.
Веденеев В.В., Порошина А.Б. Устойчивость упругой трубки, содержащей текущую неньютоновскую жидкость и имеющей локально ослабленный участок // Тр. Математического ин-та им. В.А. Стеклова. 2018. Т. 300. С. 42–64.
Попов Д.Н. Обобщенное уравнение для определения касательных напряжений на стенке трубы при неустановившемся движении вязкой жидкости // Изв. вузов. Сер. Машиностроение. 1967. № 5. С. 52–57.
Диткин В.А., Прудников А.П. Операционное исчисление. М.: Наука, 1975. 256 с.
Попов Д.Н. Нестационарные гидромеханические процессы. М.: Машиностроение, 1982. 240 с.
Ричардсон Э. Динамика реальных жидкостей. М.: Мир, 1965. 238 с.
Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука, 1987. 688 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал