Известия РАН. Механика жидкости и газа, 2021, № 2, стр. 29-39

УСТОЙЧИВОСТЬ КАПИЛЛЯРНЫХ ВОЛН ПРОИЗВОЛЬНОЙ СИММЕТРИИ НА СТРУЕ В ПЕРПЕНДИКУЛЯРНОМ ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

А. И. Григорьев^a, *, С. О. Ширяева^a

^a Ярославский государственный университет им. П.Г. Демидова
Ярославль, Россия

Поступила в редакцию 18.03.2020
После доработки 22.06.2020
Принята к публикации 20.07.2020

DOI: 10.31857/S0568528121020043

Аннотация

Получено дисперсионное уравнение для капиллярных волн с произвольной азимутальной симметрией на струе эллиптического сечения в перпендикулярном ее оси симметрии однородном электростатическом поле. Исследована устойчивость первых трех азимутальных мод. Показано, что по мере увеличения напряженности внешнего электростатического поля и связанного с ним эксцентриситета поперечного сечения струи, а также поляризационного заряда на поверхности струи, устойчивость капиллярных волн на струе снижается. Проведено сравнение со струей в радиальном электростатическом поле. Оказалось, что инкременты неустойчивости капиллярных волн любой симметрии на поверхности струи в случае поперечного электростатического поля существенно выше, чем для случая радиального.

Ключевые слова: струя, электростатическое поле, капиллярные волны, устойчивость, симметрия

Явление электродиспергирования жидкости широко используется в академических, технических и технологических целях (см., например, обзоры [1–3]). При электродиспергировании жидкости формирующаяся струя находится в существенно неоднородном электрическом поле, которое в общем случае можно считать суперпозицией продольного, радиально симметричного и поперечного полей [4–8]. Величина поперечной составляющей напряженности поля в реальных установках для электродиспергирования невелика. Если устойчивость капиллярных волн на струе в продольном и радиально симметричном полях на настоящий момент времени теоретически детально исследована [9, 10], то капиллярные волны на струе в поперечном электростатическом поле не рассматривались. В этой связи решение задачи об устойчивости капиллярных волн на струе эллиптического сечения в перпендикулярном ее оси симметрии однородном электростатическом поле представляется вполне актуальным. Строго говоря, вопрос об устойчивости капиллярных волн на струе эллиптического сечения поднимался в [11, 12], но лишь в связи со старыми экспериментами Савара, Магнуса, Плато, Бидона и др. [13]. В них экспериментально исследовались струи, вытекающие под напором через отверстия разной формы: эллиптические, треугольные, четырехугольные и т.п. Эти эксперименты легли в основу теоретического изучения струй, проведенного Рэлеем в конце позапрошлого века [14, 15].

В данной работе исследуется устойчивость струи, помещенной в перпендикулярное ее оси однородное электростатическое поле, в котором поперечное сечение струи принимает примерно эллиптическую форму. На верхней и нижней половинках струи образуются индукционные заряды, изменяющие ее устойчивость по сравнению со струями в радиальном [9] или продольном [10] электрических полях.

1. ФИЗИЧЕСКАЯ МОДЕЛЬ

Пусть дана бесконечно длинная цилиндрическая струя с круговым поперечным сечением радиуса R идеальной, идеально проводящей несжимаемой жидкости плотности ρ с коэффициентом поверхностного натяжения $\sigma $. Влиянием внешней среды пренебрегаем, полагая, что струя находится в вакууме. В окружающем струю пространстве создадим поперечное оси струи однородное электростатическое поле напряженностью E₀, в котором струя примет примерно эллиптическую в поперечном сечении форму [16], уравнение ее равновесной поверхности примет вид: $r = r(\varphi )$, где r и φ – радиальная и угловая координаты соответственно. Поле E₀ будет причиной появления на поверхности струи индуцированного заряда. На половине поверхности струи, обращенной к полю E₀, индуцируется отрицательный заряд, а на противоположной половине – положительный. Будем исследовать устойчивость капиллярных волн на такой струе.

Задача рассматривается в цилиндрической системе координат $(r,\varphi ,z)$, орт e_z которой совпадает с осью симметрии невозмущенной капиллярным волновым движением струи и направлен в направлении движения так, что ${{{\mathbf{Е}}}_{0}} \bot {{{\mathbf{е}}}_{z}}$. Поместим начало системы координат в произвольной точке на оси и примем, что оно движется со скоростью U.

Поверхность реальной струи всегда возмущена капиллярным волновым движением бесконечно малой (тепловой) амплитуды. Капиллярные волны теплового происхождения генерируются тепловым движением молекул жидкости и имеют амплитуды порядка ∼$\sqrt {{{\kappa T} \mathord{\left/ {\vphantom {{\kappa T} \sigma }} \right. \kern-0em} \sigma }} $, где $\kappa $ – постоянная Больцмана, $T$ – абсолютная температура жидкости [17]. Для большинства жидкостей эти амплитуды не превышают одной десятой нанометра.

Уравнение поверхности струи, возмущенной волновым движением, будем описывать формулой

$~r = r\left( \varphi \right) + \xi \left( {\varphi ,z,t} \right)$

где $\xi \left( {\varphi ,z,t} \right)$ малое возмущение равновесной поверхности так, что отношение $\varepsilon \equiv \left( {{{\max \left| \xi \right|} \mathord{\left/ {\vphantom {{\max \left| \xi \right|} R}} \right. \kern-0em} R}} \right) \ll 1$ будет служить малым параметром задачи, решение которой будем искать в первом приближении по ε.

2. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ

В предположении, что гидродинамическая скорость движения частицы жидкости много меньше релятивистских скоростей, запишем математическую формулировку задачи

${\text{div}}\,{\mathbf{V}}\left( {{\mathbf{r}},t} \right) = 0;\quad {{\partial }_{t}}{\mathbf{V}}\left( {{\mathbf{r}},t} \right) + \left( {{\mathbf{V}}\left( {{\mathbf{r}},t} \right) \times \nabla } \right){\mathbf{V}}\left( {{\mathbf{r}},t} \right) = - \frac{1}{\rho }\nabla p\left( {{\mathbf{r}},t} \right)$

$rot{\mathbf{Е}}({\mathbf{r}},t) = 0;\quad {\text{div}}{\mathbf{Е}}({\mathbf{r}},t) = 0$

$r \to \infty {\text{:}}\,\,{\mathbf{E}}\left( {{\mathbf{r}},t} \right) \to {{{\mathbf{E}}}_{0}};\quad r \to 0\,\,\,{\mathbf{V}}({\mathbf{r}},t) \to 0$

$~r = r(\varphi ) + \xi (\varphi ,z,t){\text{:}}$

$\frac{{{\text{d}}F(r,\varphi ,z,t)}}{{{\text{d}}t}} = 0;\quad F(r,\varphi ,z,t) \equiv r - {\text{r}}(\varphi ) - \xi (\varphi ,z,t)$

(2.1)

$p({\mathbf{r}},t) + {{p}_{E}}({\mathbf{r}},t) - {{p}_{\sigma }}({\mathbf{r}},t) = 0$

где ${\mathbf{V}}({\mathbf{r}},t)$ и $p({\mathbf{r}},t)$ – поля скорости и давления в струе; ${\mathbf{Е}}({\mathbf{r}},t)$ – напряженность электрического поля у поверхности возмущенной струи; ${{p}_{E}}({\mathbf{r}},t) \equiv {{{\mathbf{Е}}{{{({\mathbf{r}},t)}}^{2}}} \mathord{\left/ {\vphantom {{{\mathbf{Е}}{{{({\mathbf{r}},t)}}^{2}}} {8\pi }}} \right. \kern-0em} {8\pi }}$ – давление электрического поля на возмущенную поверхность струи; ${{p}_{\sigma }}({\mathbf{r}},t) \equiv \sigma \times {\text{div}}\,{\mathbf{n}}({\mathbf{r}},t)$ – давление сил поверхностного натяжения; ${\mathbf{n}}({\mathbf{r}},t)$ – орт нормали к возмущенной поверхности струи

$~r = r(\varphi ) + \xi (\varphi ,z,t,){\text{:}}\,\,{\mathbf{n}}({\mathbf{r}},t) \equiv \frac{{\nabla F\left( {r,\varphi ,z,t} \right)}}{{\left| {\nabla F\left( {r,\varphi ,z,t} \right)} \right|}}$

Граничное условие для электрического поля на поверхности струи заключается в отсутствии касательной компоненты вектора напряженности

${\mathbf{\tau }}({\mathbf{r}},t) \times {\mathbf{Е}}({\mathbf{r}},t) = 0$

где ${\mathbf{\tau }}({\mathbf{r}},t)$ – орт касательной к поверхности струи.

Дополним задачу интегральными условиями постоянства объема участка струи длиной, равной длине капиллярной волны λ

$~r = r(\varphi ) + \xi (\varphi ,z,t){\text{:}}\,\,\int\limits_a^{a + \lambda } {\int\limits_0^{2\pi } {\int\limits_0^{r(\varphi ) + \xi (\varphi ,z,t)} {rdrd\varphi dz = \pi {{R}^{2}}\lambda } } } $

и сохранения заряда участка струи длиной λ

(2.2)

$~r = r(\varphi ) + \xi (\varphi ,z,t){\text{:}}\int\limits_a^{a + \lambda } {\int\limits_0^{2\pi } {\chi dS = 0} } $

здесь a – фиксированная координата вдоль оси струи; $\chi ({\mathbf{r}},t)$ – поверхностная плотность заряда

3. СКАЛЯРИЗАЦИЯ ЗАДАЧИ

Поскольку жидкость идеальная, несжимаемая и при анализе устойчивости ее поверхности рассматриваются колебания малой амплитуды, то можно ввести гидродинамический потенциал $\psi ({\mathbf{r}},t)$, удовлетворяющий уравнению Лапласа

$\Delta \psi \left( {{\mathbf{r}},t} \right) = 0$

с граничным условием на оси струи

$r \to 0{\text{:}}\quad \psi \to 0$

с которым скорость течения связана соотношением

${\mathbf{V}}({\mathbf{r}},t) = \nabla \psi ({\mathbf{r}},t)$

Вектор напряженности электрического поля также представим через градиент электрического потенциала $\Phi ({\mathbf{r}},t)$ [18]

${\mathbf{E}}({\mathbf{r}},t) = - \nabla \Phi ({\mathbf{r}},t)$

причем $\Phi ({\mathbf{r}},t)$ удовлетворяет уравнению Лапласа ${\Delta \Phi }({\mathbf{r}},t) = 0$; с граничным условием на бесконечности

$r \to \infty {\text{:}}\quad \Phi \to - {{E}_{0}}r \times {\text{cos}}\varphi $

Из уравнения Эйлера легко получить выражение для гидродинамического давления внутри струи

$p({\mathbf{r}},t) = {{p}_{0}} - \rho \left( {{{\partial }_{t}}\psi ({\mathbf{r}},t) + \frac{1}{2}{{{\left( {\nabla \psi ({\mathbf{r}},t)} \right)}}^{2}}} \right)$

где p₀ – константа интегрирования.

Граничные условия на поверхности струи для гидродинамического и электрического потенциалов примут вид

$~r = r(\varphi ) + \xi (\varphi ,z,t){\text{:}}\,\,\,{{\partial }_{t}}F\left( {{\mathbf{r}},t} \right) + \nabla \psi \left( {{\mathbf{r}},t} \right) \times \nabla F\left( {{\mathbf{r}},t} \right) = 0$

${{p}_{0}} - \rho \left( {{{\partial }_{t}}\psi ({\mathbf{r}},t) + \frac{1}{2}{{{\left( {\nabla \psi ({\mathbf{r}},t)} \right)}}^{2}}} \right) + {{p}_{E}}({\mathbf{r}},t) - {{p}_{\sigma }}({\mathbf{r}},t) = 0$

где давление электрического поля ${{p}_{E}}({\mathbf{r}},t)$ выразится через электрический потенциал

${{p}_{E}}({\mathbf{r}},t) = {{{{{\left( {\nabla \Phi ({\mathbf{r}},t)} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {\nabla \Phi ({\mathbf{r}},t)} \right)}}^{2}}} {8\pi }}} \right. \kern-0em} {8\pi }}$

а условие эквипотенциальности струи примет вид

$~r = r(\varphi ) + \xi (\varphi ,z,t){\text{:}}\,\,\Phi ({\mathbf{r}},t) = {\text{const}}$

Интегральное условие (2.2) запишется в виде

$~r = r(\varphi ) + \xi (\varphi ,z,t){\text{:}}\,\,\int\limits_a^{a + \lambda } {\int\limits_0^{2\pi } {\left. {\frac{{n(r,t) \times \nabla \Phi (r,t)}}{{({{e}_{r}} \times n(r,t))}}} \right|} } d\varphi dz = 0$

где ${{{\mathbf{e}}}_{r}}$ – радиальный орт.

Будем решать задачу в безразмерных переменных, положив $R = \sigma = \rho = 1$.

Так как движение жидкости в струе вызывается капиллярными волнами теплового происхождения, то в безразмерных переменных потенциал поля скоростей $\psi (r,\varphi ,z,t)$ должен иметь тот же порядок величины, что и возмущение равновесной поверхности $\xi (\varphi ,z,t)$.

Искомые функции $\xi (\varphi ,z,t)$, $\psi (r,\varphi ,z,t)$ и $\Phi (r,\varphi ,z,t)$ представим в виде разложения по малому параметру ε [19]

$\xi (\varphi ,z,t) = \varepsilon \cdot {{\xi }_{1}}(\varphi ,z,t);\quad \psi (r,\varphi ,z,t) = \varepsilon \cdot {{\psi }_{1}}(r,\varphi ,z,t)$

$\Phi (r,\varphi ,z,t) = {{\Phi }_{0}}(r,\varphi ) + \varepsilon \cdot {{\Phi }_{1}}(r,\varphi ,z,t).$

Нижние индексы в обозначениях функций соответствуют порядку малости по ε величины соответствующей компоненты.

Подставляя разложения в исходную задачу и раскладывая полученные выражения в ряд по ε, сгруппируем слагаемые с одинаковыми степенями малого параметра. В результате получим краевые задачи различных порядков малости.

4. ЗАДАЧА НУЛЕВОГО ПОРЯДКА МАЛОСТИ. РАВНОВЕСНАЯ ФОРМА СТРУИ

Задача нулевого порядка малости имеет вид

$\Delta {{\Phi }_{0}}(r,\varphi ) = 0$

$r \to \infty {\text{:}}\,\,{{\Phi }_{0}}(r,\varphi ) \to - {{E}_{0}} \cdot r \cdot {\text{cos}}\varphi $

$r = r{\text{(}}\varphi {\text{):}}\quad {{{\Phi }}_{{\text{0}}}}\left( {r,\varphi } \right) = 0$

${{p}_{0}} - \left[ {{{\left( {1 + 2\frac{{r{\text{'}}{{{\left( \varphi \right)}}^{2}}}}{{{{r}^{2}}}} - \frac{{r{\text{''}}\left( \varphi \right)}}{r}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + 2\frac{{r{\text{'}}{{{\left( \varphi \right)}}^{2}}}}{{{{r}^{2}}}} - \frac{{r{\text{''}}\left( \varphi \right)}}{r}} \right)} {r{{{\left( {1 + \frac{{r{\text{'}}{{{\left( \varphi \right)}}^{2}}}}{{{{r}^{2}}}}} \right)}}^{{3/2}}}}}} \right. \kern-0em} {r{{{\left( {1 + \frac{{r{\text{'}}{{{\left( \varphi \right)}}^{2}}}}{{{{r}^{2}}}}} \right)}}^{{3/2}}}}}} \right] + $

$ + \;\frac{1}{{8\pi }}\left( {\frac{1}{{{{r}^{2}}}}{{{\left( {{{\partial }_{\varphi }}{{\Phi }_{0}}\left( {r,\varphi } \right)} \right)}}^{2}} + {{{\left( {{{\partial }_{r}}{{\Phi }_{0}}\left( {r,\varphi } \right)} \right)}}^{2}}} \right) = 0$

$\int\limits_a^{a + \lambda } {\int\limits_0^{2\pi } {\frac{{r{{{\left( \varphi \right)}}^{2}}}}{2}d\varphi dz = \pi \lambda } } $

(4.1)

$\mathop \smallint \limits_a^{a + \lambda } \mathop \smallint \limits_0^{2\pi } {{\left. {\left( {\frac{{r{\text{'}}(\varphi )}}{r}{{\partial }_{\varphi }}{{\Phi }_{0}}(r,\varphi ) + r{{\partial }_{r}}{{\Phi }_{0}}(r,\varphi )} \right) \cdot r} \right|}_{{r = r(\varphi )}}}d\varphi dz = 0$

Штрихом обозначено дифференцирование функции по аргументу.

Равновесную форму струи будем искать в виде разложения в ряд Фурье

$r = r\left( \varphi \right) = {{a}_{0}} + \mathop \sum \limits_{n = 1}^\infty \left( {{{a}_{n}}\cos \left( {n\varphi } \right) + {{b}_{n}}\sin \left( {n\varphi } \right)} \right) = $

(4.2)

$ = \;{{a}_{0}}\left( {1 + \mathop \sum \limits_{n = 1}^\infty \left( {\frac{{{{a}_{n}}}}{{{{a}_{0}}}}\cos \left( {n\varphi } \right) + \frac{{{{b}_{n}}}}{{{{a}_{0}}}}\sin \left( {n\varphi } \right)} \right)} \right)$

где a_n и b_n – постоянные коэффициенты разложения, имеющие один порядок малости при $n \geqslant 1$, ${{a}_{0}}\sim 1$.

Полагая, что деформация цилиндрической формы струи мала, примем, что

$\left| {\frac{{{{a}_{n}}}}{{{{a}_{0}}}}} \right|\sim \left| {\frac{{{{b}_{n}}}}{{{{a}_{0}}}}} \right| \ll 1\quad (n \geqslant 1)$

Подставим выражение (4.2) в условие постоянства объема и получим

${{a}_{0}} \equiv \left( {1 + {\rm O}\left( {{{{\left( {\frac{{{{a}_{n}}}}{{{{a}_{0}}}}} \right)}}^{2}}} \right)} \right)$

здесь ${\rm O}$ – символ порядка малости [19].

Таким образом, в линейном по ${{a}_{n}}{\text{/}}{{a}_{0}}$ и ${{b}_{n}}{\text{/}}{{a}_{0}}$ приближении запишем выражение для искомой равновесной формы поверхности струи в виде

(4.3)

$r = r\left( \varphi \right) = 1 + \mathop \sum \limits_{n = 1}^\infty \left( {{{a}_{n}}\cos \left( {n\varphi } \right) + {{b}_{n}}\sin \left( {n\varphi } \right)} \right) + O{{\left( {\frac{{{{a}_{n}}}}{{{{a}_{0}}}}} \right)}^{2}}$

Поскольку отличие равновесной формы струи от цилиндрической вызвано электрическим полем на ее поверхность, то безразмерное искажение цилиндрической поверхности ${{{{a}_{n}}} \mathord{\left/ {\vphantom {{{{a}_{n}}} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}$ и безразмерное давление p_E имеют одинаковый порядок величины. Следовательно, при рассмотрении электрической части равновесной задачи для определения p_E, оставаясь в рамках линейного по ${{{{a}_{n}}} \mathord{\left/ {\vphantom {{{{a}_{n}}} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}$ приближения, искажение цилиндрической формы струи учитывать не следует. Задачу определения электрического потенциала в равновесном состоянии достаточно рассматривать в окрестности цилиндрической поверхности

$\Delta {{\Phi }_{0}}\left( {r,\varphi } \right) = 0$

${{\left. {{{\Phi }_{0}}(r,\varphi )} \right|}_{{r \to \infty }}} = - {{E}_{0}}r \cdot {\text{cos}}\varphi ;\quad {{\left. {{{\Phi }_{0}}(r,\varphi )} \right|}_{{r = 1}}} = 0$

${{\left. {\mathop \smallint \limits_а^{а + \lambda } \mathop \smallint \limits_0^{2\pi } {{\partial }_{r}}{{\Phi }_{0}}\left( {r,\varphi } \right)} \right|}_{{r = 1}}}d\varphi dz = 0$

Решение задачи для электростатического потенциала имеет вид

(4.4)

${{\Phi }_{0}} = - {{E}_{0}}\left( {r - \frac{1}{r}} \right)\cos \varphi + {\rm O}{{\left( {\frac{{{{a}_{n}}}}{{{{a}_{0}}}}} \right)}^{{3/2}}}$

Отметим, что интегральное условие сохранения заряда выполняется тождественно.

Подставим (4.3), (4.4) в динамическое граничное условие задачи нулевого порядка и ограничиваясь линейным по ${{a}_{n}}{\text{/}}{{a}_{0}}$ и ${{b}_{n}}{\text{/}}{{a}_{0}}$ приближением, получим следующее равенство

${{p}_{0}} - 1 + \frac{{E_{0}^{2}}}{{4\pi }} + \frac{{E_{0}^{2}}}{{4\pi }}\cos \left( {2\varphi } \right) = \mathop \sum \limits_{n = 1}^\infty ({{n}^{2}} - 1)\left( {{{a}_{n}}\cos \left( {n\varphi } \right) + {{b}_{n}}\sin \left( {n\varphi } \right)} \right)$

Это соотношение будет выполняться для произвольного значения угла $\varphi $ только в случае, когда равны коэффициенты при одинаковых тригонометрических функциях. Равенство нулю суммы слагаемых, не зависящих от угла φ, в левой части полученного соотношения, позволяет определить величину гидродинамического давления в равновесном состоянии ${{p}_{0}} = 1 - {{E_{0}^{2}} \mathord{\left/ {\vphantom {{E_{0}^{2}} {4\pi }}} \right. \kern-0em} {4\pi }}$.

Приравнивая коэффициенты при одинаковых тригонометрических функциях, получим выражения для коэффициентов a_n и b_n

${{b}_{n}} = 0,\quad \left( {\forall n \ne 1} \right);\quad {{a}_{2}} = \frac{{E_{0}^{2}}}{{12\pi }};\quad {{a}_{n}} = 0\quad \left( {\forall n \ne 1,\;2} \right)$

Учтем, что слагаемые в разложении (4.3), пропорциональные $\cos (\varphi )$ и $\sin \left( \varphi \right)$, описывают смещение струи как целого в направлениях, перпендикулярных ее оси. Поэтому из физических соображений соответствующие слагаемые из разложения (4.3) следует исключить, приняв: ${{a}_{1}} = {{b}_{1}}$ = 0. В итоге выражение для равновесной формы струи принимает вид

(4.5)

$r = r\left( \varphi \right) \approx 1 + h\left( \varphi \right) = 1 + \frac{{E_{0}^{2}}}{{12\pi }}\cos \left( {2\varphi } \right)$

Сравним форму поперечного сечения струи с эллипсом. Для этого разложим уравнение эллипса, записанное в полярных координатах, в ряд по квадрату эксцентриситета $e$

$r = \frac{{{{{(1 - {{e}^{2}})}}^{{\frac{1}{4}}}}}}{{\sqrt {1 - {{e}^{2}}{{{\cos }}^{2}}\varphi } }} \approx 1 + {{e}^{2}}\frac{1}{4}\cos (2\varphi ) + О({{e}^{4}})$

Сравнивая полученное разложение с выражением (4.5), несложно заметить, что форму поперечного сечения струи приближенно можно считать эллипсом с эксцентриситетом, величина которого определяется величиной внешнего электрического поля ${{e}^{2}} = {{E_{0}^{2}} \mathord{\left/ {\vphantom {{E_{0}^{2}} {3\pi }}} \right. \kern-0em} {3\pi }}$.

5. ЗАДАЧА ПЕРВОГО ПОРЯДКА МАЛОСТИ

Линеаризованная по величине равновесного искажения $h\left( \varphi \right)$ цилиндрической формы струи задача первого порядка малости по $\varepsilon $ имеет вид

${\Delta }{{{\psi }}_{{\text{1}}}}\left( {r,\varphi ,z,t} \right) = 0;\quad {\Delta }{{{\Phi }}_{{\text{1}}}}\left( {r,\varphi ,z,t} \right) = 0$

$r \to \infty {\text{:}}\,\,{{\Phi }_{1}}\left( {r,\varphi ,z,t} \right) \to 0;\quad r \to 0{\text{:}}\,\,{{\psi }_{1}}\left( {r,\varphi ,z,t} \right) \to 0$

(5.1)

$r = 1{\text{:}}\,\, - {\kern 1pt} {{\partial }_{t}}{{\xi }_{1}}\left( {\varphi ,z,t} \right) + \left( {{{\partial }_{r}}{{\psi }_{1}}\left( {r,\varphi ,z,t} \right)} \right. - $

$ - \;\left. {h{\text{'}}\left( \varphi \right){{\partial }_{\varphi }}{{\psi }_{1}}\left( {r,\varphi ,z,t} \right) + h\left( \varphi \right){{\partial }_{{r,r}}}{{\psi }_{1}}\left( {r,\varphi ,z,t} \right)} \right) = 0$

${{\partial }_{{z,z}}}{{\xi }_{1}}(\varphi ,z,t) - h{\text{'}}(\varphi ){{\partial }_{\varphi }}{{\xi }_{1}}(\varphi ,z,t) - 2h{\text{''}}(\varphi ){{\xi }_{1}}(\varphi ,z,t) + $

$ + \;\left( {1 - 2h(\varphi )} \right)\left( {{{\xi }_{1}}(\varphi ,z,t) + {{\partial }_{{\varphi ,\varphi }}}{{\xi }_{1}}(\varphi ,z,t)} \right) - {{\pi }^{{ - 1}}}E_{0}^{2} \cdot {\text{co}}{{{\text{s}}}^{2}}\varphi \cdot {{\xi }_{1}}(\varphi ,z,t) - $

$ - \;[{{\partial }_{t}}{{\psi }_{1}}(r,\varphi ,z,t) + {{(2\pi )}^{{ - 1}}}{\text{cos}}\varphi \cdot {{E}_{0}} \cdot {{\partial }_{r}}{{\Phi }_{1}}(r,\varphi ,z,t) + h(\varphi ){{\partial }_{{r,t}}}{{\psi }_{1}}(r,\varphi ,z,t)] = 0$

(5.2)

${{\Phi }_{1}}\left( {r,\varphi ,z,t} \right) - 2{{E}_{0}}\cos \varphi \cdot {{\xi }_{1}}(\varphi ,z,t) = 0$

$\int\limits_a^{a + \lambda } {\int\limits_0^{2\pi } {\left( {1 + h(\varphi )} \right)} } {{\xi }_{1}}(\varphi ,z,t)d\varphi dz = 0;\quad \int\limits_a^{a + \lambda } {\int\limits_0^{2\pi } {{{\partial }_{r}}} } {{\Phi }_{1}}(r,\varphi ,z{{\left. {,t)} \right|}_{{r = 1}}}dzd\varphi = 0$

Решения уравнений Лапласа для функций ${{\psi }_{1}}(r,\varphi ,z,t)$ и ${{\Phi }_{1}}(r,\varphi ,z,t)$, гармонические по координатам $\varphi $ и $z$, удовлетворяющие условиям ограниченности, будем искать в виде

(5.3)

${{\Phi }_{1}}\left( {r,\varphi ,z,t} \right) = \mathop \sum \limits_{m = 0}^\infty \mathop \smallint \limits_0^\infty \left( {{{B}_{{m,k}}}\left( t \right) \cdot {\text{exp(}}im\varphi {\text{)}} \cdot {\text{exp(}}ikz{\text{)}} \cdot {{K}_{m}}\left( {kr} \right)} \right){\text{d}}k$

(5.4)

${{\psi }_{1}}\left( {r,\varphi ,z,t} \right) = \mathop \sum \limits_{m = 0}^\infty \mathop \smallint \limits_0^\infty \left( {{{A}_{{m,k}}}(t) \cdot {\text{exp(}}i{\text{ }}m\varphi {\text{)}} \cdot {\text{exp(}}ikz{\text{)}} \cdot {{I}_{m}}\left( {kr} \right)} \right)dk$

где ${{I}_{m}}\left( {kr} \right)$и ${{K}_{m}}\left( {kr} \right)$ – модифицированные функции Бесселя первого и второго рода [20]; k и m – волновое и азимутальное числа; ${{A}_{{m,k}}}$ и ${{B}_{{m,k}}}$ – неизвестные зависящие от времени коэффициенты.

Поскольку функция ${{\xi }_{1}}\left( {\varphi ,z,t} \right)$ связана с ${{\psi }_{1}}\left( {\varphi ,z,t} \right)$ кинематическим граничным условием, будем искать выражение для нее в виде

(5.5)

${{\xi }_{1}}\left( {\varphi ,z,t} \right) = \mathop \sum \limits_{m = 0}^\infty \mathop \smallint \limits_0^\infty {{С}_{{m,k}}}(t) \cdot {\text{exp(}}im\varphi {\text{)}} \cdot {\text{exp(}}ikz{\text{)}}dk$

где ${{С}_{{m,k}}}(t)$ – неизвестные, зависящие от времени, коэффициенты.

Подставляя выражения (5.3)–(5.5) в условия (5.1) и (5.2), выразим ${{A}_{{m,k}}}(t)$ и ${{B}_{{m,k}}}(t)$ через ${{С}_{{m,k}}}(t)$. Результаты подставим в динамическое граничное условие первого порядка и получим

(5.6)

$С_{{m,k}}^{{''}}\left( t \right) + W(С_{{m + 2,k}}^{{''}}\left( t \right) \cdot {{{\rm A}}_{m}}\left( k \right) + С_{{m - 2,k}}^{{''}}\left( t \right) \cdot {{{\rm X}}_{m}}\left( k \right)) + $

$ + \;{{С}_{{m,k}}}\left( t \right)({{G}_{m}}\left( k \right)({{m}^{2}} + {{k}^{2}} - 1) + W{{{\text{F}}}_{m}}\left( k \right)) + $

$ + \;W{{С}_{{m + 2,k}}}\left( t \right){{\Gamma }_{m}}\left( k \right) + W{{С}_{{m - 2,k}}}\left( t \right){{{\rm N}}_{m}}\left( k \right) = 0$

${{H}_{j}}\left( k \right) = \frac{{kK_{j}^{'}\left( k \right)}}{{{{K}_{j}}\left( k \right)}};\quad {{G}_{j}}\left( k \right) = \frac{{kI_{j}^{'}\left( k \right)}}{{{{I}_{j}}\left( k \right)}}$

${{A}_{m}}\left( k \right) = \frac{1}{6}\left( {{{G}_{m}}\left( k \right) - ({{k}^{2}} + m\left( {m + 2} \right))\frac{1}{{{{G}_{{m + 2}}}\left( k \right)}} + 1} \right)$

${{X}_{m}}\left( k \right) = \frac{1}{6}\left( {{{G}_{m}}\left( k \right) - ({{k}^{2}} + m\left( {m - 2} \right))\frac{1}{{{{G}_{{m - 2}}}\left( k \right)}} + 1} \right)$

${{F}_{m}}\left( k \right) = {{G}_{m}}\left( k \right)\left( {{{H}_{{m + 1}}}\left( k \right) + {{H}_{{m - 1}}}\left( k \right) + 2} \right)$

${{\Gamma }_{m}}\left( k \right) = {{G}_{m}}\left( k \right)\left( {{{H}_{{m + 1}}}\left( k \right) - \frac{{\left( {m + 1} \right)\left( {m + 2} \right)}}{3}} \right)$

${{N}_{m}}\left( k \right) = {{G}_{m}}\left( k \right)\left( {{{H}_{{m - 1}}}\left( k \right) - \frac{{\left( {m - 2} \right)\left( {m - 1} \right)}}{3}} \right)$

где введен безразмерный полевой параметр $W \equiv {{E_{0}^{2}} \mathord{\left/ {\vphantom {{E_{0}^{2}} {4\pi }}} \right. \kern-0em} {4\pi }}$, принимаемый за второй малый параметр задачи.

Система (5.6) является связанной системой обыкновенных дифференциальных уравнений второго порядка относительно неизвестных функций ${{С}_{{m,k}}}\left( t \right)$, описывающих временную эволюцию возмущения свободной поверхности струи.

6. ДИСПЕРСИОННОЕ СООТНОШЕНИЕ

Будем решать систему (5.6) методом последовательных приближений, используя тот факт, что согласно сделанным выше предположениям напряженность внешнего электрического поля, а следовательно, и полевой параметр W являются величинами малыми. Заметим, что слагаемые, ответственные за связанность системы уравнений (5.6), пропорциональны W. Поэтому в нулевом приближении по W ими можно пренебречь, получив систему несвязанных уравнений, решения которой легко находятся.

Пренебрегая в системе (5.6) слагаемыми, пропорциональными $W \cdot С_{{m \pm 2,k}}^{{''}}\left( t \right)$ и $W \cdot {{C}_{{m \pm 2,k}}}\left( t \right)$, получим систему несвязанных гармонических уравнений

(6.1)

$С_{{m,k}}^{{''}}\left( t \right) + {{С}_{{m,k}}}\left( t \right)({{G}_{m}}\left( k \right)({{m}^{2}} + {{k}^{2}} - 1) + W{{F}_{m}}\left( k \right)) = 0$

Решениями этих уравнений являются гармонические функции времени

(6.2)

${{С}_{{m,k}}}\left( t \right) = {{\alpha }_{{m,k}}} \cdot {\text{exp(}}i{{\omega }_{{m,k}}}t{\text{)}}$

где ${{\alpha }_{{m,k}}}$ – это константы, имеющие смысл амплитуд, а ${{\omega }_{{m,k}}}$ – частоты капиллярных волн, определяемые дисперсионным уравнением, которое следует из (6.1) при подстановке туда (6.2)

(6.3)

$\omega _{{m,k}}^{2} = {{G}_{m}}\left( k \right)({{m}^{2}} + {{k}^{2}} - 1) + W{{F}_{m}}\left( k \right)$

7. ЧИСЛЕННЫЙ АНАЛИЗ

Проведем анализ устойчивости возмущений поверхности струи различной симметрии – для первых трех мод: осесимметричной (m = 0), изгибной (m = 1) и деформационной (m = 2).

Осесимметричные волновые возмущения

Рассмотрим осесимметричные (m = 0) волновые возмущения на поверхности струи. На рис. 1 показаны зависимости квадрата частоты $\omega _{{m,k}}^{2}$ от волнового числа $k$, рассчитанные по (6.3) для различных значений полевого параметра W. Неустойчивыми являются капиллярные волны в диапазоне значений волновых чисел, где квадрат частоты отрицателен: $\omega _{{m,k}}^{2} < 0$ (т.е. там, где частота ${{\omega }_{{m,k}}}$ будет мнимой, и фактически определит инкремент неустойчивости ${{\gamma }_{{m,k}}}$ [21]). Как видно из рис. 1а, длинные осесимметричные волны (с малыми значениями волнового числа k) неустойчивы даже в отсутствие электрического поля (см. кривую 1). Из рис. 1а видно, что с ростом величины напряженности внешнего электростатического поля диапазон значений волновых чисел неустойчивых волн расширяется.

Рис. 1.

(a) Зависимость квадрата частоты $\omega _{{m,k}}^{2}$ осесимметричных (m = 0) волн от волнового числа $k$: 1–3; (б) зависимость инкрементов ${{\gamma }_{{m,k}}}$ осесимметричных (m = 0) волн от волнового числа $k$: 1–3 – поперечное однородное электростатическое поле; 4–6 – радиальное электростатическое поле; (1, 4), (2, 5), (3, 6) –$W = 0.5,\;1,\;1.5$.

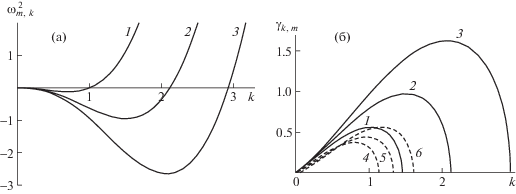
На рис. 1б приведены зависимости инкрементов ${{\gamma }_{{m,k}}}$ неустойчивых осесимметричных волн на поверхности струи от волнового числа для двух ситуаций: когда внешнее однородное электростатическое поле перпендикурно оси струи (кривые 1–3, рассчитанные по (6.3)), и когда электростатическое поле радиально оси струи (рассчитанные по результатам работы [22] кривые 4–6)). Фактически во втором случае имеем заряженную струю.

Следует отметить, что в [22] рассматривались осцилляции и устойчивость капиллярных волн произвольной симметрии на поверхности заряженной струи вязкой электропроводной жидкости, а потому для расчета инкрементов неустойчивости для идеальной жидкости в дисперсионном уравнении, полученном в [22], был совершен переход к идеальной жидкости. В итоге получено дисперсионное уравнение для капиллярных волн на поверхности заряженной струи идеальной несжимаемой электропроводной жидкости

(7.1)

$\omega _{{m,k}}^{2} = \left[ {m + \frac{{k{{I}_{{m + 1}}}\left( k \right)}}{{{{I}_{m}}\left( k \right)}}} \right]\left[ {{{m}^{2}} + {{k}^{2}} - 1 + W\left( {1 + m - \frac{{k{{K}_{{m + 1}}}\left( k \right)}}{{{{K}_{m}}\left( k \right)}}} \right)} \right]$

где полевой параметр $W \equiv 4\pi \chi _{{}}^{2} \equiv \frac{{{{E}^{2}}}}{{4\pi }}$, а χ – плотность поверхностного заряда на струе, т.е. определяется так же, как и в поперечном поле. Кривые 4–6 рассчитаны по (7.1).

Из рис. 1б видно, что при одинаковых значениях полевых параметров струя в поперечном однородном поле более неустойчива, чем в радиальном. Зоны неустойчивости капиллярных волн в первой ситуации шире и инкременты имеют большие значения, чем во второй.

Изгибные волновые возмущения

В отсутствие внешнего электрического поля изгибные капиллярные волны (m = 1) всегда устойчивы. Однако наличие сколь угодно малого отличного от нуля поля приводит к изгибной неустойчивости.

На рис. 2a, б представлены зависимости квадрата частоты $\omega _{{m,k}}^{2}$ и инкремента ${{\gamma }_{{m,k}}}$ от волнового числа $k$, аналогичные изображенным на рис. 1a, б. Из рис. 2 следует, что влияние внешнего электростатического поля на устойчивость изгибных капиллярных волн аналогично его влиянию на осесимметричные капиллярные волны: увеличение полевого параметра увеличивает как ширину диапазона неустойчивых волн, так и инкремент развития их неустойчивости.

Рис. 2.

(a) Зависимость квадрата частоты $\omega _{{m,k}}^{2}$ изгибных (m = 1) волн от волнового числа $k$: 1–3 – $W = 0.5,\;1,\;1.5$; (б) зависимость инкрементов ${{\gamma }_{{m,k}}}$ изгибных (m = 1) волн от волнового числа $k$: 1–3 – поперечное электростатическое однородное поле, 4–6 – радиальное электростатическое поле; (1, 4), (2, 5), (3, 6) – $W = 0.5,\;1,\;1.5$.

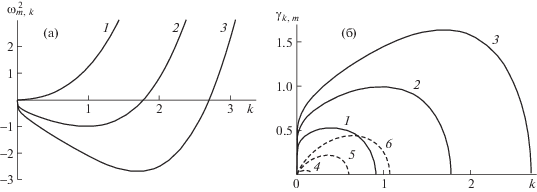
На рис. 2б показано сравнение значений инкрементов изгибных волн для случаев поперечного однородного и радиального электрических полей. Видно, что так же, как и в случае осесимметричных волн, при одинаковых значениях полевого параметра изгибные волны в поперечном однородном поле обладают существенно большими инкрементами, нежели в радиальном поле, т.е. струя менее устойчива.

Деформационные волновые возмущения

В отличие от двух предыдущих случаев неустойчивость капиллярных волновых возмущений с азимутальным числом m = 2 является пороговой, т.е. возможность реализации такой неустойчивости появляется при превышении значением полевого параметра определенной пороговой величины.

На рис. 3a показана зависимость квадрата частоты $\omega _{{m,k}}^{2}$ от волнового числа, из которой следует, что область неустойчивых волн появляется лишь при значении полевого параметра, большем некоторой конечной величины (кривая 3). Данный тип неустойчивости можно назвать изгибно-деформационной неустойчивостью. В результате ее развития на боковой поверхности струи формируются выступы, с вершин которых эмитируются дочерние тонкие струйки.

Рис. 3.

(a) Зависимость квадрата частоты $\omega _{{m,k}}^{2}$ деформационных (m = 2) волн от волнового числа $k$: 1–3 – $W = 0,1,1.5$; (б) зависимость инкрементов ${{\gamma }_{{m,k}}}$ деформационных (m = 2) волн от волнового числа $k$: 1–3 – поперечное электростатическое однородное поле, 4–6 – радиальное электростатическое поле; (1, 4), (2, 5), (3, 6) – $W = 3,3.3,3.5$.

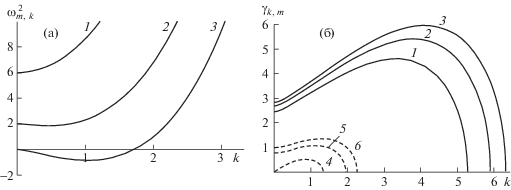
На рис. 3б представлена зависимость величины инкремента изгибно-деформационной неустойчивости от волнового числа: ${{\gamma }_{{m,k}}}$. На рис. 3б кривые 1–3 относятся к поперечному однородному полю, кривые 4–6 – к радиальному. Увеличение полевого параметра как в поперечном однородном электростатическом поле, так и в радиальном приводит к расширению диапазонов неустойчивых волн, а так же к увеличению инкрементов нарастания капиллярных волн. Как и в предыдущих случаях, величины инкрементов неустойчивости в поперечном электростатическом поле существенно превышают величины инкрементов в радиальном поле.

8. ВОЛНОВОЕ ЧИСЛО НАИБОЛЕЕ НЕУСТОЙЧИВОЙ ВОЛНЫ

Как видно из рис. 1б, рис. 2б и рис. 3б, зависимости инкрементов от волнового числа имеют максимумы. Неустойчивость волны с волновым числом $k = {{k}_{{\max }}}$, соответствующим максимуму инкремента, нарастает с наибольшей скоростью и оказывает преимущественное влияние на картину распада всей струи [21]. На рис. 4 представлены зависимости волнового числа ${{k}_{{\max }}}$, соответствующего наиболее неустойчивой волне, от величины полевого параметра W и разных значений азимутального числа $m$, для поперечного однородного (сплошные линии) и радиального (пунктирные линии) полей.

Рис. 4.

Зависимость значений волнового числа наиболее неустойчивой волны ${{k}_{{\max }}}$ от величины зарядового параметра $W$: 1–3 – поперечное электростатическое однородное поле; 4–6 – радиальное электростатическое однородное поле; (1, 4), (2, 5), (3, 6) – m = 0, 1, 2.

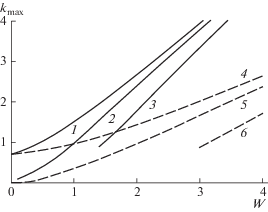
Видно, что с увеличением напряженности электрического поля картина распада струи определяется неустойчивостью все более коротких волн. Отметим, что кривая, соответствующая m = 2, появляется при достижении полевым параметром W фиксированного значения, поскольку, как отмечалось выше, неустойчивость изгибно-деформационных волн имеет пороговый по W характер.

Отметим, что пороговое значение параметра W ниже в случае поперечного однородного поля.

ЗАКЛЮЧЕНИЕ

Найдена равновесная форма сечения струи в поперечном ее оси однородном электростатическом поле, которая может быть представлена эллипсом с эксцентриситетом, величина которого определяется величиной внешнего электростатического поля.

Получено дисперсионное уравнение для капиллярных волн на поверхности струи в поперечном ее оси однородном электростатическом поле. Построены зависимости квадрата частоты от волнового числа для волн различной азимутальной симметрии: осесимметричных, изгибных и изгибно-деформационных. Для всех случаев определено положение зон неустойчивости и показано, что с увеличением напряженности электростатического поля зоны неустойчивости расширяются. Оказалось, что величина инкрементов неустойчивости возрастает с ростом напряженности поля и имеет максимум при некотором значении волнового числа k_max. Показано, что с ростом напряженности электрического поля k_max растет, т.е. характер распада струи определяется все более короткими волнами.

Проведено сравнение решаемой задачи с аналогичной задачей о заряженной струе с круговым поперечным сечением, т.е. когда напряженность электрического поля у поверхности струи направлена радиально ее оси симметрии. Как оказалось, инкременты неустойчивости капиллярных волн на поверхности струи в случае поперечного однородного электростатического поля существенно выше, чем для случая радиального.

Список литературы

Коженков В.И., Фукс Н.А. Электрогидродинамическое распыление жидкости (обзор) // Успехи химии. 1976. Т. 45. № 12. С. 2274–2284.
Bailey A.G. Electrostatic atomization of liquids (revue) // Atomization and Spray Technology. 1986. V. 2. P. 95–134.
Fenn J.B., Mann M., Meng C.K. Electrospray ionization for mass spectrometry of large biomolecules (revue) // Science. 1989. V. 246. № 4926. P. 64–71.
Cloupeau M., Prunet Foch B. Electrostatic spraying of liquids: main functioning modes // J. Electrostatics. 1990. V. 25. P. 165–184.
Cloupeau M., Prunet Foch B. Electrohydrodynamic spraying functioning modes: a critical review // J. Aerosol Sci. 1994. V. 25. № 6. P. 1021–1035.
Jaworek A., Krupa A. Classification of the Modes of EHD Spraying // J. Aerosol Sci. 1999. V. 30. № 7. P. 873–893.
Kim O.V., Dunn P.F. Control Production by in-flight Electrospraying // Langmuir. 2010. V. 26. P. 15807–15813. https://doi.org/10.1021/la102793j
Verdoolda S., Agostinhoc L.L.F., Yurterib C.U., Marijnissenb J.C.M. A generic electrospray classification // J. Aerosol Sci. 2014. V. 67. P. 87–103.
Григорьев А.И., Петрушов Н.А., Ширяева С.О. Нелинейный анализ закономерностей реализации волнового движения на поверхности заряженной струи, движущейся относительно материальной среды // Изв. РАН. МЖГ. 2012. № 1. С. 68–79.
Григорьев А.И., Петрушов Н.А., Ширяева С.О., Полянцев Н.А. Нелинейный анализ волнового движения на поверхности струи в продольном электрическом поле, движущейся в диэлектрической среде // ЖТФ. 2012. С. 82. № 8. С. 35–41.
Amini G., Dolatabadi A. Capillary instability of elliptic liquid jets // Physics of Fluids. 2011. V. 23. № 084109. P. 1–9. https://doi.org/10.1063/1.3626550
Amini G., Yu Lv, Dolatabadi A., Ihme M. Instability of elliptic liquid jets: Temporal linear stability theory and experimental analysis // Physics of fluids. 2014. V. 26. № 114105 P. 1–22. https://doi.org/10.1063/1.4901246
Стретт Дж.В. (Лорд Рэлей). Теория звука. Т. 2. М.: Гостехиздат, 1955. 475 с.
Strutt J.W. (Lord Rayleigh). On the instability of jets // Proc. London Math. Soc. 1878. V. 10. P. 4–13.
Strutt J.W. (Lord Rayleigh) On the instability cylindrical fluid surfaces // Phil. Mag. 1892. V. 34. Ser. 5. P. 145–154.
Cheng K.J. Capillary oscillations of a drop in an electric field // Phys. Lett. 1985. V. A112. № 11. P. 392–396.
Френкель Я.И. К теории Тонкса о разрыве поверхности жидкости постоянным электрическим полем в вакууме // ЖЭТФ. 1936. Т. 6. № 4. С. 348–350.
Ландау Л.Д., Лифшиц Е.М. Теория поля. М.: Наука, 1973. 504 с.
Найфе А.Х. Методы возмущений. М.: Мир, 1976. 455 с.
Справочник по специальным функциям / Под ред. Абрамовиц М., Стиган И. М.: Наука, 1979. 831 с.
Левич В.Г. Физико-химическая гидродинамика. М.: Физматгиз, 1959. 700 с.
Ширяева С.О., Григорьев А.И., Левчук Т.В., Рыбакова М.В. Об устойчивости неосесимметричной заряженной струи вязкой электропроводной жидкости // ЖТФ. 2003. Т. 73. Вып. 4. С. 5–12.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал