1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 2, 2021

Известия РАН. Механика жидкости и газа, 2021, № 2, стр. 15-28

МОДЕЛИРОВАНИЕ ТЕЧЕНИЯ ЖИДКОСТИ В ТРЕЩИНЕ ГИДРОРАЗРЫВА НЕОДНОРОДНО ТРЕЩИНОСТОЙКОГО ПЛАСТА В ПЛОСКО-ТРЕХМЕРНОЙ ПОСТАНОВКЕ

А. Б. Киселев a, b, Ли Кайжуй a, Н. Н. Смирнов a, b, *, Д. А. Пестов b

a МГУ им. М.В. Ломоносова, Механико-математический факультет
Москва, Россия

b ФНЦ НИИСИ РАН
Москва, Россия

* E-mail: N.N.Smirnov@niisi.ru

Поступила в редакцию 04.08.2020
После доработки 01.10.2020
Принята к публикации 30.10.2020

Полный текст (PDF)

Аннотация

Построена плоская квази-трехмерная модель распространения трещины гидроразрыва в пласте, характеризующемся неоднородной трещиностойкостью, для исследования течения жидкости и эволюции трещины. Для моделирования неоднородного слоистого пласта с различными трещиностойкостями рассмотрены три его типичных случая: с ослабленными зонами, однородный и с зонами повышенной прочности. Результаты показывают, что неоднородная трещиностойкость пласта сильно влияет на форму трещины, течение жидкости и общее раскрытие трещины по сравнению с однородным пластом, в котором реализуется радиальный рост трещины. Кроме того, влияние неоднородной трещиностойкости пласта на рост трещины отмечается в основном на ранней стадии. После определенного момента трещина распространяется в различных направлениях с приблизительно равной скоростью.

Ключевые слова: трещина гидроразрыва, плоско-трехмерная модель, неоднородный пласт, трещиностойкость

Моделирование гидроразрыва в неоднородных средах начиналось с двухмерной плоско-деформированной модели PKN [1, 2], в которой трещина ограничена в продуктивном слое, не может расти в высоту из-за земных напряжений на смежных слоях пласта, намного превышающих земное напряжение на продуктивном слое. Такое явление, отражающее неоднородность земного напряжения в пласте, называется “барьером напряжений” [3, 4]. В дальнейшем, помимо учета неоднородности земного напряжения, в моделях трещины гидроразрыва учитывались также неоднородность горных материалов (модуля Юнга и коэффициента Пуассона) в различных слоях пласта [5–12] для исследования влияния неоднородности материала и геологических условий на эволюцию роста трещины, а также исследовалось влияние естественных трещин и разломов [13], или фильтрация жидкости в пласт [14].

Однако следует отметить, что материал горной породы состоит из различных видов минеральных частиц и содержит множество естественных стратификаций и мелких естественных трещин [15], поэтому в дополнение к модулю Юнга и коэффициенту Пуассона, трещиностойкость горных пород также характеризуется сильной неоднородностью. Тем не менее исследований по неоднородности трещиностойкости пласта очень мало: в статьях [16, 17] основное внимание уделялось изучению неоднородности модуля Юнга и коэффициента Пуассона, а неоднородность трещиностойкости пласта была лишь кратко описана.Это связано с тем, что трещиностойкость материала трудно измерить при практическом проектировании, особенно для горных материалов. В [18] был дан метод определения направления роста трещины в плоскости при условии анизотропии трещиностойкости пласта. В соответствии с этим методом было исследовано влияние анизотропии трещиностойкости пласта на распространение плоско-трехмерной трещины гидроразрыва, но влияние неоднородной трещиностойкости рассмотрено не было. В статье [19] исследован рост трещины в поперечно изотропной среде, с учетом анизотропии как трещиностойкости, так и упругих свойств материала. Неоднородная трещиностойкость также не была рассмотрена.

Фактически, согласно механике линейного упругого разрушения трещиностойкость материала – основной параметр, определяющий рост трещины, поэтому неоднородность трещиностойкости породы может существенно влиять как на геометрию трещины, так и на течение гидравлической жидкости.

1. ПОСТАНОВКА ЗАДАЧИ

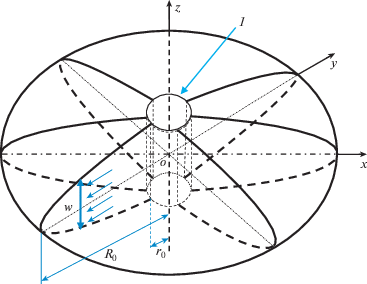
На начальной стадии ГРП (гидравлический разрыв пласта) образуется одна мелкая трещина в пласте, плоскость которой перпендикулярна к скважине, см. рис. 1. Для упрощения модели сделано следующее предположение: начальная трещина имеет круглый профиль в плоскости xoy, где ось z совпадает с осью скважины, а R0, r0 – радиусы трещины и скважины, поэтому описание модели производится в цилиндрической системе координат ozrθ, w – раскрытие трещины.

Рис. 1.

Трехмерная геометрия начальной трещины и скважины: 1 – скважина.

Неоднородность пласта обеспечивается за счет неоднородной прочности среды, т.е. трещиностойкости материала KIC. Модуль Юнга E и коэффициент Пуассона $\nu $ среды предполагаются однородными. Гидравлическая жидкость представляет собой несжимаемый ньютоновский флюид с вязкостью µ, не содержащий в себе примеси твердых частиц проппанта. Зоной отставания жидкости и утечками жидкости в пласт в этой модели пренебрегаем, т.е. фронт гидравлической жидкости совпадает с фронтом трещины.

1.1. Определяющие уравнения

Для линейной упругой модели пласта с одной трещиной имеется соотношение между избыточным давлением p и раскрытием трещины w [20]

(1.1)
$p(x,y) = {{p}_{f}}(x,y) - {{\sigma }_{0}} = - \frac{{E{\kern 1pt} '}}{{8\pi }}\int\limits_{A(t)}^{} {\frac{{w(x{\kern 1pt} ',y{\kern 1pt} ',t)dA(x{\kern 1pt} ',y{\kern 1pt} ')}}{{{{{[{{{(x{\kern 1pt} {\text{'}} - x)}}^{2}} + {{{(y{\kern 1pt} '\, - y{\kern 1pt} ')}}^{2}}]}}^{{3/2}}}}}} $
где pf  – давление гидравлической жидкости в трещине, σ0 – земное напряжение, перпендикулярное к плоскости трещины, E' = E/(1 – ν), A(t) – область трещины.

Обобщенное уравнение непрерывности без учета утечки жидкости получается в соответствии с теорией смазки и законом Пуазейля [21]

(1.2)
$\frac{{\partial w}}{{\partial t}} + {\text{div}}(w{\mathbf{u}}) = 0,\quad {\mathbf{u}} = - \frac{{{{w}^{2}}}}{{12\mu }}\nabla p$
где u представляет собой вектор скорости жидкости в трещине. В цилиндрической системе u = ur + uθ, поэтому ur, uθ имеют следующий вид:
(1.3)
${{u}_{r}} = - \frac{{{{w}^{2}}}}{{\mu {\kern 1pt} '}}\frac{{\partial p}}{{\partial r}},\quad {{u}_{\theta }} = - \frac{{{{w}^{2}}}}{{\mu {\kern 1pt} '}}\frac{1}{r}\frac{{\partial p}}{{\partial \theta }}$
где μ' = 12μ. Совместив уравнения (1.2) и (1.3), получаем уравнение движения жидкости в трещине

(1.4)
$\frac{{\partial w}}{{\partial r}} - \frac{1}{{\mu {\kern 1pt} '}}\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{w}^{3}}\frac{{\partial p}}{{\partial r}}} \right) - \frac{1}{{\mu {\kern 1pt} '}}\frac{1}{r}\frac{\partial }{{\partial \theta }}\left( {r{{w}^{3}}\frac{{\partial p}}{{\partial \theta }}} \right)$

1.2. Начальные условия

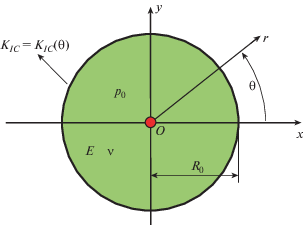
В начальный момент трещина имеет дискообразную форму с радиусом R0 (рис. 1), и предполагается, что гидравлическая жидкость в трещине неподвижна и находится под однородным давлением p0. Неоднородная трещиностойкость пласта распределяется так

(1.5)
${{K}_{{IC}}} = {{K}_{{IC}}}(\theta )$

Это значит, что трещиностойкость пласта KIC зависит только от кольцевой координаты θ. Эта функция может выражать различные величины KIC на различных областях пласта, особенно для слоистой структуры породы. Другие свойства материала, такие как модуль Юнга E и коэффициент Пуассона ν, постоянны, как на рис. 2, в котором скважина рассматривается как точечный источник (красная точка в рис. 2), поскольку в дискообразных моделях [22–24] радиусом скважины можно пренебречь. Это не влияет на конечные результаты. Подобное упрощение требует только специальной обработки при расчете давления в области скважины, чтобы избежать бесконечного давления на скважине.

Рис. 2.

Начальные условия: проекция трещины на плоскость xoy и параметры материала.

1.3. Граничные условия

В этой модели используется условие постоянного расхода на скважине. Согласно уравнению (1.2) скорость течения на сечении, перпендикулярном к плоскости трещины

(1.6)
${\mathbf{q}} = w{\mathbf{u}} = - \frac{{{{w}^{3}}}}{{\mu {\kern 1pt} '}}\nabla p$

Из-за отсутствия кольцевой скорости, скорость течения на скважине имеет вид

(1.7)
${{q}_{0}} = - \frac{{w_{0}^{3}}}{{\mu {\kern 1pt} '}}\frac{{\partial p}}{{\partial r}} = \frac{{{{Q}_{0}}}}{{2\pi {{r}_{0}}}},\quad r = {{r}_{0}}$
где Q0 – объемная скорость закачки на скважине, w0 – раскрытие трещины на скважине.

На конце трещины мы предполагаем, что поток жидкости равен нулю, ввиду отсутствия утечки жидкости в пласт,

(1.8)
$q = - \frac{{{{w}^{3}}}}{{\mu {\kern 1pt} '}}\frac{{\partial p}}{{\partial r}} = 0,\quad r = R(\theta )$
где R(θ) – радиус фронта трещины, который зависит от кольцевой координаты θ, потому что трещина может расти с различными скоростями по разным направлениям из-за неоднородной трещиностойкости пласта (KIC). Кроме того, на конце трещины имеет место еще одно граничное условие, более сильное, чем (1.8)
(1.9)
$w(r,\theta ,t) = {\mathbf{0}},\quad r = R$
поскольку при подстановке условия (1.9) в условие (1.8), условие (1.8) автоматически выполняется и градиент давления, а значит и скорость жидкости, в кончике трещины не влияет на его выполнение. Как будет показано ниже, в силу выбранной модели разрушения распространение трещины идет скачкообразно. При этом рост трещины происходит на несколько порядков быстрее, чем наполнение ее жидкостью (отношение скорости волн Рэлея в породе к скорости фильтрационных течений). Следовательно, большую часть времени при решении задачи гидродинамики в трещине ее носик покоится, что позволяет использовать граничное условие (1.9).

1.4. Условие роста трещины

Согласно линейной упругой механике разрушения трещина распространяется, когда коэффициент интенсивности напряжений превышает или равен прочности породы (KIC), т.е.

(1.10)
${{K}_{I}}(\theta ) \geqslant {{K}_{{IC}}}(\theta )$
если на какой-либо точке фронта трещины выполняется условие (1.10), то профиль на этой точке распространяется радиально. Следует отметить, что в данной модели не предполагается, что фронт трещины находится в динамическом равновесии KI ≈ KIC, поскольку это ведет к необходимости вводить дополнительные связанные между собой переменные для отслеживания точного положения фронта трещины в каждой радиальной области. Такой подход мог бы позволить более точно определять положение фронта трещины, но подходящей теории, которая позволила бы разрешить эти дополнительные n переменных, пока не разработано. Вместо этого рост трещины приближен небольшими приращениями, происходящими в момент, когда выполняется условие (1.10). Для представленной модели характерен не непрерывный, а кусочно-постоянный рост трещины (различные радиальные области растут в различные моменты времени на величину, кратную Δr при выполнении условия роста трещины), так что фронт трещины не имеет какой-то заданной непрерывной скорости.

2. ПОСТРОЕНИЕ РЕШЕНИЯ

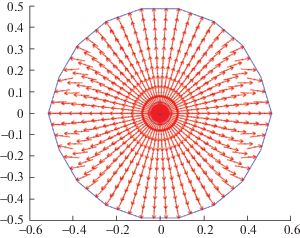
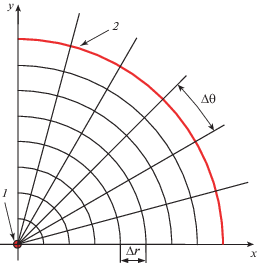
Система уравнений (1.1) и (1.4) с граничными условиями (1.7)–(1.9) замкнута. Неравномерный рост трещины определяется условием (1.10) из-за неоднородной трещиностойкости пласта. Решение модели сосредоточено на решении связанной системы (1.1) и (1.4) и расчете коэффициента интенсивности напряжений. В соответствии с используемой цилиндрической системой координат, трещина дискретизируется по радиальному и кольцевому направлениям, как на рис. 3 (где показана дискретизация первого квадранта трещины).

Рис. 3.

Дискретизация трещины. Δr, Δθ – размеры ячеек трещины по радиальному и кольцевому направлениям: 1 – скважина, 2 – фронт трещины.

2.1. Численные методы

Уравнение (1.1) для модели пласта дискретизируется следующим образом:

(2.1)
$p(x,y) = \frac{{E{\kern 1pt} '}}{{8\pi }}\sum\limits_{i = 1}^{i = m} {\sum\limits_{j = 1}^{j = n} {I(x,y,{{x}_{i}},{{y}_{j}}) \cdot w({{x}_{i}},{{y}_{j}})} } $
где w(xi, yj) – раскрытие ячейки (xi, yi) трещины. m и n – количество ячеек по радиальному и кольцевому направлениям. I(x, y, xi, yi) представляет собой коэффициент жесткости, выражающийся следующим образом:

(2.2)
$I(x,y,{{x}_{i}},{{y}_{j}}) = - \frac{{A({{x}_{i}},{{y}_{i}})}}{{{{{[{{{({{x}_{i}} - x)}}^{2}} + {{{({{y}_{i}} - y)}}^{2}}]}}^{{3/2}}}}}$

Координаты x, y, xi, yi в декартовой системе координат легко преобразуются в цилиндрической системе координат

(2.3)
$x = r \cdot \cos \theta r = r \cdot {\text{sin}}\theta ,\quad {{x}_{i}} = {{r}_{i}} \cdot \cos {{\theta }_{j}},\quad {{y}_{j}} = {{r}_{i}} \cdot \sin {{\theta }_{j}}$
где (r, θj) представляют собой координаты центра тяжести ячейки в цилиндрической системе координат. Уравнение (1.1) также переводим в цилиндрическую систему координат, используя (2.3).

Согласно методу конечных объемов, уравнение движение жидкости (1.4) преобразуется следующим образом [25]:

(2.4)
$\begin{gathered} \Delta w = \frac{{\Delta t}}{{\mu {\kern 1pt} '}}\frac{1}{{{{r}_{i}}}}\frac{1}{{\Delta {{r}_{i}}}}\left[ {{{{\left( {r{{w}^{3}}\frac{{\partial p}}{{\partial r}}} \right)}}_{{i + 1/2,j}}} - {{{\left( {r{{w}^{3}}\frac{{\partial p}}{{\partial r}}} \right)}}_{{i - 1/2,j}}}} \right] + \\ + \frac{{\Delta t}}{{\mu {\kern 1pt} '}}\frac{1}{{{{r}_{i}}}}\frac{1}{{\Delta {{\theta }_{j}}}}\left[ {{{{\left( {\frac{{{{w}^{3}}}}{r}\frac{{\partial p}}{{\partial \theta }}} \right)}}_{{i,j + 1/2}}} - {{{\left( {\frac{{{{w}^{3}}}}{r}\frac{{\partial p}}{{\partial \theta }}} \right)}}_{{i,j - 1/2}}}} \right] \\ \end{gathered} $
где Δw = wi,j,k+ 1 – wi, j, k представляет собой приращение раскрытия ячейки (ri, θj) трещины. Индекс k – номер шага по времени.

Граничные условия (1.7), (1.8) выражаются в дискретном виде

(2.5)
${{\left( {r{{w}^{3}}\frac{{\partial p}}{{\partial r}}} \right)}_{{1 - 1/2,j}}} = - \frac{{{{Q}_{0}}\mu {\kern 1pt} '}}{{2\pi }}$
(2.6)
${{\left( {r{{w}^{3}}\frac{{\partial p}}{{\partial r}}} \right)}_{{m + 1/2,j}}} = 0$

При анализе уравнений (2.4)–(2.6) можно заметить, что от самого давления прочие переменные не зависят, лишь от градиента давления. Уравнения (2.5) и (2.6) называются условиями Неймана [26], что значит, что давление в какой-либо точке надо зафиксировать, и поскольку граничное условие на скважине уже задано, остается делать это на конце трещины (r = R), поэтому давление pr =R на границе трещины вводится в качестве параметра в управляющее уравнение (2.4), после чего используется итерационный метод для поиска значения pr =R.

Согласно определению коэффициента интенсивности напряжений, выражение для расчета KI(θ)принимает вид [27]

(2.7)
${{K}_{I}}(\theta ) = \frac{{E{\kern 1pt} '}}{4}\sqrt {\frac{\pi }{2}} \frac{{{{w}_{{m,j}}}}}{{\sqrt {{{R}_{{j'}}} - {{r}_{m}}} }},\quad \theta = {{\theta }_{j}}$
где wm,j – раскрытие ячейки, самой близкой к границе трещины в радиальном направлении θ = θj. rm – радиальная координата этой ячейки. Rj – радиус трещины в радиальном направлении θ = θj.

2.2. Численный алгоритм

В начале, подставляя дискретное уравнение (2.1) в (2.4)–(2.6), получаем нелинейную систему уравнений для раскрытия трещины wi,j,k+ 1, которая решается итерационным методом Ньютона. Но поскольку давление pr =R на границе трещины водится в систему (2.4)–(2.6) в качестве известного параметра, для поиска его численного решения требуется дополнительный итерационный цикл.

Кроме того, для моделирования распространения трещины, на каждом шаге необходимо вычислять коэффициенты интенсивности напряжений на граничных сетках трещины KI(θj), чтобы определить направления, в которых будет распространяться трещина. Если есть граничные ячейки θj, для которых выполняется

(2.6)
${{K}_{I}}({{\theta }_{{j*}}}) \geqslant {{K}_{{IC}}}({{\theta }_{{j*}}})$
то трещина растет в этих направлениях, и зону расчета системы (2.4)–(2.6) нужно изменить. После этого снова циклически решить эту нелинейную систему, получить распространяющиеся границы трещины θj* и изменить зону расчета, пока все (KI(θj), (j = 1, 2, 3, …, n) не будут удовлетворять условию KI(θj) < KIC(θj). Тогда в качестве решений wi,j,k+ 1, pi,j,k+ 1, и pr =R, берутся значения последних численных решений на текущем шаге по времени, после чего решение повторяется для следующего шага t = tk + 1.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ИХ АНАЛИЗ

Вычислительные программы для расчета данной задачи написаны в математическом пакете “MATLABR2018a”. Основные параметры показаны в табл. 1. Неоднородность трещиностойкости пласта предполагается такой: трещиностойкость большей части пласта принимает фиксированное значение KIC = 2.0 МПа ⋅ м0.5, а трещиностойкость в паре симметричных радиальных зон задается в зависимости от задачи и обеспечивает неоднородность трещиностойкости. Эти области (выделенные области на рис. 4) далее именуются неоднородными областями, хотя в случае однородных трещиностойкостей это название и не вполне справедливо. Далее представлены результаты для трех различных случаев: однородный случай, когда KIC в этих зонах равен, случай более прочных областей, когда KIC = 2.5 МПа ⋅ м0.5 и, наконец, случай ослабленных областей, с KIC = 1.5 МПа ⋅ м0.5, см. рис. 4. Кольцевой шаг сетки Δθ = 20°, радиальный шаг сетки Δr = 0.02 м, размерность сеток для начальной трещины m × n = 25 × 18.

Таблица 1
начальный радиус R0 (м) 0.5 начальное давление p0 (МПа) 1
модуль Юнга E (ГПа) 30 скорость закачки Q0 (м3/с) 10–4
коэффициент Пуассона ν 0.2 вязкость жидкости µ (Па ⋅ с) 10–3
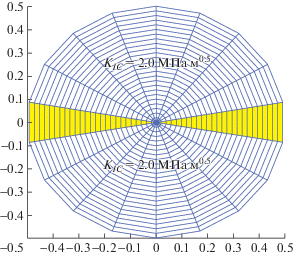
Рис. 4.

Распределение трещиностойкости пласта: белые зоны – это обычные зоны с KIC = 2.0 МПа ⋅ м0.5, выделенные зоны – это неоднородные зоны с меньшей, равной или большей трещиностойкостью KIC = 1.5, 2.0, 2.5 МПа ⋅ м0.5.

Для более точного определения порядка распространения различных границ трещины берется малый шаг по времени: Δt = 0.01 с. Суммарное число шагов для каждого случая: Т = 3000, т.е. итоговое время расчета T = 30 с.

Влияние неоднородных трещиностойкостей на форму трещины показано на рис. 5. Если обратить внимание на кривую 2 на рис. 5, видно, что наличие в пласте ослабленных зон не только повышает скорость роста трещины в них и в соседних к ним областях, но и понижает ее в отдаленных от них областях. Кроме того, легко заметить, что наличие ослабленной зоны ведет к образованию небольшой области, где рост трещины происходит существенно быстрее, чем в соседних областях (кривая 2 на рис. 5), а наличие более прочных областей, наоборот, приводит к замедлению роста трещины и вогнутой форме фронта (кривая 4 на рис. 5). Сравнение результатов показывает, что отношение сторон трещины в неоднородной среде чуть меньше, чем обратное соотношение трещиностойкостей, но держится на постоянном уровне по мере роста трещины. Так, для случая ослабленного участка отношение трещиностойкостей равно 2.0/1.5 = 1.33, что чуть больше соотношения сторон трещины (график 1 на рис. 6 (г)). Для случая усиленного участка отношение трещиностойкостей равно 2.0/2.5 = 0.8, что также близко к полученному отношению сторон (график 3 на рис. 6 (г)). Для однородного случая соотношение сторон и соотношение трещиностойкостей тривиальным образом совпадают. Таким образом, отношение длин трещины в направлении максимальной трещиностойкости и минимальной трещиностойкости до некоторого предела обратно пропорционально отношению этих трещиностойкостей.

Рис. 5.

Профили трещины: 1 – в момент t = 0, остальные в момент t = 30 c, для различных трещиностойкостей неоднородных зон: 2 – KIC = 1.5 МПа ⋅ м0.5, 3 – KIC = 2.0 МПа ⋅ м0.5, 4 – KIC = 2.5 МПа ⋅ м0.5.

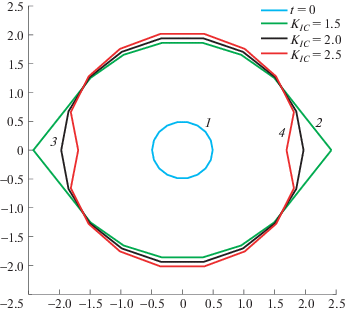
Рис. 6.

Сравнения зависимости радиусов различных радиальных областей от времени: а–в – радиальных областей θ = 0°, θ = 40°, θ = 80°; г – соотношение между длиной и высотой трещины от времени; длина и высота трещины – горизонтальный и вертикальный радиусы трещины θ = 0° и θ = 80°. Графики для различных трещиностойкостей неоднородных зон пласта: 1 – KIC = 1.5 МПа ⋅ м0.5, 2 – KIC = 2.0 МПа ⋅ м0.5, 3 – KIC = 2.5 МПа ⋅ м0.5.

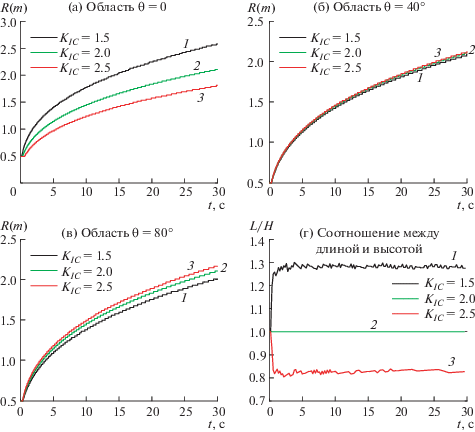
Из-за симметрии трещины и распределения трещиностойкости пласта выбраны только три типичных радиальных области θ = 0°, θ = 40° и θ = 80° для демонстрации радиуса трещины от времени при различных трещиностойкостях на неоднородных зонах, см. рис. 6а, б и в, из которых видно, что радиус области θ = 0°, соответствующей зоне неоднородных напряжений, сильнее всего реагирует на изменение трещиностойкости этой зоны, в то время как рост трещины в области θ = 40° практически от него не зависит. Из рис. 6в видно, что трещиностойкость неоднородных зон может влиять на рост перпендикулярной им зоны, причем это влияние не мало. Сравнение результатов на рис. 6в с результатами на рис. 6а показывает, что наличие ослабленных зон способствует своему росту и препятствует росту перпендикулярных им зон, а наличие зон повышенной прочности препятствует своему росту и способствует росту перпендикулярных им зон.

Назовем длиной трещины радиус неоднородной зоны (θ = 0°) и обозначим его как L, а радиус зоны θ = 90°, равный среднему между областями θ = 80° и θ = 100°, примем за высоту трещины и обозначим как H. Из рис. 6г видно, что для случаев, когда KIC = 1.5, 2.5 МПа м0.5 на неоднородных зонах, соотношение L/H сильно меняется только на ранней стадии роста трещины, после чего стабилизируется на значении 1.3 для случая наличия ослабленной зоны (KIC = 1.5 МПа м0.5), и на значении около 0.8 для случая наличия зоны повышенной прочности (KIC = 2.5 МПа м0.5). Эти значения близки к отношениям трещиностойкостей (2.0/1.5 = 1.33 для ослабленной зоны и 2.0/2.5 = 0.8 для зоны повышенной прочности). Это показывает, что на ранней стадии роста трещины неоднородность трещиностойкостей существенно влияет на скорость роста отдельных областей трещины, после чего это влияние уменьшается и скорость устанавливается на значениях, пропорциональных отношениям трещиностойкостей. Следует отметить, что такое точное совпадение этих отношений не говорит об их прямой пропорциональности, поскольку это отношение длины и высоты также зависит, например, от доли областей с той или иной трещиностойкостью, их расположения и величины перепада трещиностойкостей, на чем мы сейчас останавливаться не будем. Колебания соотношения L/H на рис. 6г не связаны со сходимостью метода интегрирования и являются характерной особенностью рассматриваемой задачи: колебания обусловлены тем, что для каждой радиальной области рост трещины происходит в различные моменты времени, и значение L/H увеличивается в момент роста вдоль направления θ = 0°, и уменьшается в момент роста вдоль направления θ = 0°.

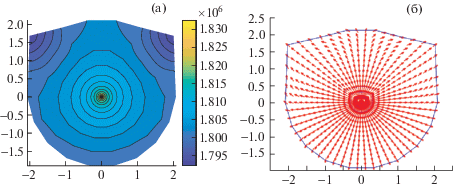
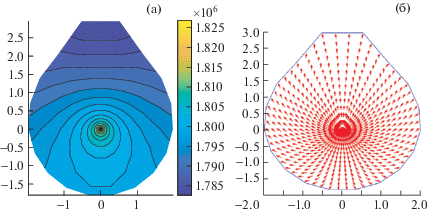
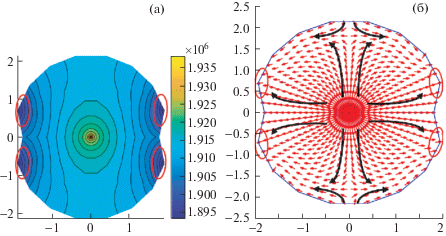
Неоднородная трещиностойкость также заметно влияет на течение жидкости в трещине (рис. 7–9). В случае наличия ослабленных зон появляются 4 зоны пониженного давления: концы радиальных областей θ = 40°, θ = 140°, θ = 220° и θ = 320°, см. рис. 7а, а в случае наличия зон повышенной прочности также имеются 4 зоны пониженного давления: θ = 20°, θ = 160°, θ = 200° и θ = 340°, отличные от тех, что возникают в ослабленном случае, см. рис. 9а. В случае однородных трещиностойкостей подобные зоны не возникают и течение остается радиальным. Причина возникновения зон пониженного давления кроется в том, что эти четыре радиальные области были последними распространившимися зонами на данный момент, в то время как другие области на предыдущем шаге не распространялись. Из соответствующих полей скорости жидкости (рис.7б и 9б) видно, что вся гидравлическая жидкость втекает в эти 4 зоны (красные эллипсы), более того, на находящихся далеко от зон слабого давления радиальных областях образуются два различных потока, особенно ясно различимых на областях θ = 80° и θ = 100° и на областях, симметричных им θ = 260° и θ = 280° (см. черные стрелки на рис. 7(б) и рис. 9(б)). Это показывает, что из-за неоднородной трещиностойкости пласта появляются локальные сильные кольцевые течения гидравлической жидкости в трещине, сильно отличающиеся от полностью радиальных течений в случае однородного пласта. Кроме того, можно заметить, что течение в области максимальной длины (области θ = 0° и θ = 180° для случая ослабленной области и θ = 80°, θ = 100°, θ = 260° и θ = 280° для случая наличия более прочных областей) не обязательно направлено от скважины и сильно зависит от распространения соседних областей. Этот эффект можно отметить, сравнив рис. 7б и рис. 10, где показан момент начала роста трещины для случая ослабленной области, где распространились пока только ослабленные области. В обоих случаях жидкость движется в направлении новых образовавшихся поверхностей трещины, однако в начале движения влияние скважины еще велико и движение в основном радиально, в то время как в более поздний момент новые поверхности трещины находятся далеко от скважины, что выражается в преобладании кольцевых токов у фронта трещины.

Рис. 7.

Распределение давления жидкости (а) и поле скоростей жидкости (б) в трещине при KIC = 1.5 МПа ⋅ м0.5 для неоднородных зон в момент t = 30 с: случай пласта с ослабленными зонами.

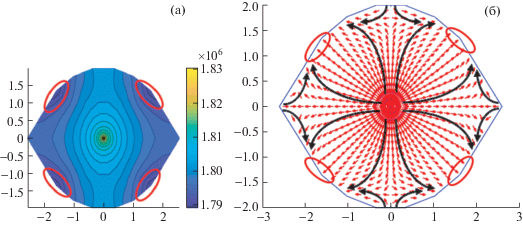
Рис. 8.

Распределение давления жидкости (а) и поле скоростей жидкости (б) в трещине при KIC = 2.0 МПа ⋅ м0.5 в момент t = 30 c: случай однородного пласта.

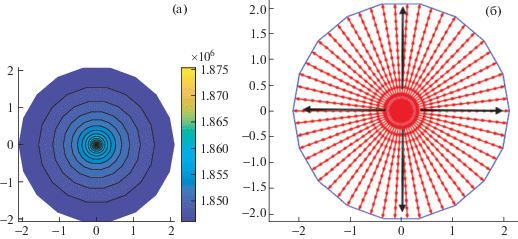
Рис. 9.

Распределение давления жидкости (а) и поле скоростей жидкости (б) в трещине при KIC = 2.5 МПа ⋅ м0.5 для неоднородных зон в момент t = 30 с: случай пласта с зонами повышенной прочности.

Рис. 10.

Распределение скоростей для случая ослабленной области в момент начала роста трещины.

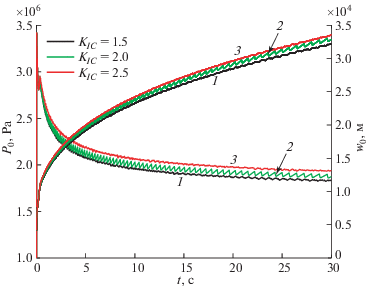
Из рис. 11 видно, что давление и раскрытие на скважине максимальны при KIC = 2.5 МПа ⋅ м0.5 на неоднородных зонах, и минимальны при KIC = 1.5 МПа ⋅ м0.5. Это значит, что уменьшение трещиностойкости на неоднородных зонах влечет за собой меньшее общее давление жидкости и меньшее общее раскрытие трещины. Так, наличие ослабленных зон (или зон повышенной прочности) пласта увеличивает (или уменьшает) радиусы некоторых радиальных областей и создает больше (или меньше) свободной поверхности трещины, оно мешает (или, соответственно, способствует) росту общего раскрытия трещины, так как при одинаковом расходе из скважины площадь поверхности трещины и среднее раскрытие трещины обратно пропорциональны.

Рис. 11.

Зависимость давления p0 и раскрытия w0 на скважине от времени t при различных значениях трещиностойкости неоднородных зон пласта: 1 – KIC = 1.5 МПа ⋅ м0.5, 2 – KIC = 2.0 МПа ⋅ м0.5, 3 – KIC = 2.5 МПа ⋅ м0.5.

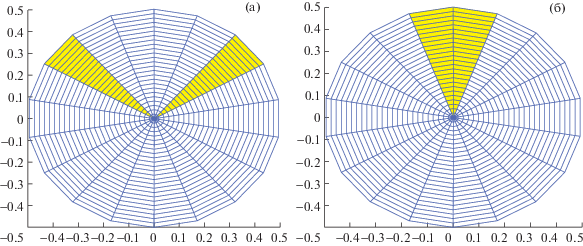
Для более детального изучения течения жидкости в трещине, развивающейся в условиях неоднородных трещиностойкостей, был проведен еще один численный эксперимент: рост трещины при наличии двух ослабленных зон, находящихся под некоторым углом друг к другу, в первом случае ослабленные области находятся под углом Δθ = 100° (рис. 12а), во втором – под углом Δθ = 20° (рис. 12б).

Рис. 12.

Распределения трещиностойкости пласта: белые зоны – это обычные зоны с KIC = 2.0 МПа ⋅ м0.5, выделенные зоны – это неоднородные зоны с меньшей трещиностойкостью KIC = 1.5 МПа⋅м0.5: (а), слева, ослабленные зоны находятся под углом 100° друг к другу, (б), справа, ослабленные зоны находятся под углом 20° друг к другу.

На рис. 13 видно, что для более выраженных зон роста трещины обратного течения жидкости уже не происходит, возникающее кольцевое течение сосредоточено в области между ослабленными областями и почти не затрагивает область, удаленную от ослабленных. Рисунок 14 же, напротив, показывает, что наличие единственной ослабленной зоны существенно влияет на течение во всей трещине, вызывая кольцевые течения в удаленной области трещины и изгибая линии тока в направлении ослабленной области, в которой происходит самый быстрый рост трещины. Таким образом, можно отметить, что влияние ослабленных областей меняется в зависимости от их взаимного положения: противостоящие узкие области могут приводить к тому, что течение жидкости в них замедляется и меняет направление при открытии соседних поверхностей трещины; расположенные ближе друг к другу ослабленные области сильно влияют на течение жидкости в зоне между ними; находящиеся же вплотную ослабленные области растут настолько быстрее остальной трещины, что образовавшиеся области низкого давления создают направленные к ним кольцевые течения, охватывающие всю трещину.

Рис. 13.

Распределение давления жидкости (а) и поле скоростей жидкости (б) в трещине при Δθ = 100° для неоднородных зон в момент t = 30 с: случай ослабленных зон, находящихся с одной стороны трещины.

Рис. 14.

Распределение давления жидкости (а) и поле скоростей жидкости (б) в трещине при Δθ = 20° для неоднородных зон в момент t = 30 с: случай примыкающих друг к другу ослабленных зон.

ЗАКЛЮЧЕНИЕ

Сравнительный анализ профилей трещины, скоростей радиальных областей θ = 0°, θ = 40° и θ = 0° для 3 различных случаев трещиностойкостей в неоднородных зонах позволяет сделать вывод о том, что при одинаковом изменении (уменьшение или увеличение) трещиностойкости на неоднородном слое профиль трещины более чувствителен к уменьшению трещиностойкости, но в целом отношение длин трещины в различных направлениях обратно пропорционально отношению трещиностойкостей. Кроме того, неоднородный слой существенно влияет не только на свой рост (θ = 0° и θ = 180°), но также и на рост перпендикулярного ему направления (θ = 90° и θ = 270°), в то время как промежуточные направления (θ = 40°, θ = 140°, θ = 220° и θ = 320°) куда менее подвержены этому влиянию. Воздействие этого неоднородного слоя на форму трещины в основном сосредоточено на ранней стадии, после чего соотношение между длиной и высотой трещины остается примерно постоянным.

Более того, из-за неравномерного роста трещины появляются переменные зоны пониженного давления на границе трещины, которые существенно влияют на поле скоростей жидкости в окрестности фронта трещины (в трещине возникают локальные кольцевые течения), так как в различные моменты трещина растет в различных направлениях. В случае, когда ослабленные области находятся ближе друг к другу, образующиеся зоны пониженного давления сосредоточены ближе к ослабленным областям и либо сильнее влияют на течение в областях, находящихся между ослабленными, либо, если ослабленные области примыкают друг к другу, существенно влияют на течение жидкости во всей трещине.

Авторы благодарны поддержке Китайского стипендиального Совета (ChinaScholarshipCouncil) и программе фундаментальных исследований Российской академии наук АААА-А18-118041190145-1 (0065-2019-0021 и 0580-2021-0021).

Список литературы

  1. Perkins T.K., Kern L.R. Widths of hydraulic fractures // Journal of Petroleum Technology. 1961. V. 13 (9). P. 937–949.

  2. Nordgren R.P. Propagation of a vertical hydraulic fracture // Society of Petroleum Engineers Journal. 1972. V. 12 (4). P. 306–314.

  3. Warpinski N.R., Schimidt R.A., Northrop D.A. In-situ stresses: the predominant influence on hydraulic fracture containment // Journal of Petroleum Technology. 1982. V. 34 (3). P. 653–664.

  4. Nolte K.G. Application of fracture design based on pressure analysis // SPE Production Engineering. 1988. V. 3 (1). P. 31–42.

  5. Advani S.H., Lee J.K. Finite element model simulations associated with hydraulic fracturing// Society of Petroleum Engineers Journal. 1982. V. 22 (2). P. 209–218.

  6. Settari A., Cleary M.P. Development and testing of a pseudo-three-dimensional model of hydraulic fracture geometry // SPE Production Engineering. 1986. V. 1 (6). P. 449–466.

  7. Adachi J., Siebrits E., Peirce A., Desroches J. Computer simulation of hydraulic fractures // International Journal of Rock Mechanics & Mining Science. 2007. V. 44. P. 739–759.

  8. Гордеев Ю.Н. Автомодельное решение задачи о распространении псевдотрехмерной вертикальной трещины гидроразрыва в непроницаемом пласте // ИЗВ. РАН. МЖГ. 1995. № 6. С. 79–86.

  9. Li D., Zhang S., Zhang S. Experimental and numerical simulation study on fracturing through interlayer to coal seam // Journal of Natural Gas Science and Engineering. 2014. V. 21. P. 386–396.

  10. Xiao H.T., Yue Z.Q. A three- dimensional displacement discontinuity method for crack problems in layered rocks // International Journal of Rock Mechanics & Mining Sciences. 2011. V. 48. P. 412–420.

  11. Wardie L.J. Displacement discontinuity method for three-dimensional stress analysis of tabular excavations in non-homogeneous rock // The 25th U. S. Symposium on Rock Mechanics (USRMS), 1984, 25–27 June, Evanston, Illinois. P. 702–709.

  12. Settari A., Cleary M.P. Three-dimensional simulation of hydraulic fracturing // Journal of Petroleum Technology. 1984. V. 36 (7). P. 1177–1190.

  13. Акулич А.В., Звягин А.В. Взаимодействие трещины гидроразрыва с естественной трещиной // Изв. РАН. МЖГ. 2008. № 3. С. 104–112.

  14. Смирнов Н.Н., Тагирова В.Р. Автомодельные решения задачи о формировании трещины гидроразрыва в пористой среде // Изв. РАН. МЖГ. 2007. № 1. С. 70–82.

  15. Josh M., Esteban L., Piane C.D., Sarout J., Dewhurst D.N., Clennell M.B. Laboratory characterisation of shale properties // Journal of Petroleum Science and Engineering. 2012. V. 88–89. P. 107–124.

  16. Siebrits E., Peirce A.P. An efficient multi-layer planar 3D fracture growth algorithm using a fixed mesh approach// International Journal for Numerical Methods in Engineering. 2002. V. 53. P. 691–717.

  17. Zia H., Lecampion B. PyFrac: A planar 3D hydraulic fracture simulator // Computer Physics Communications. 2020. V. 255. 107368.

  18. Zia H., Lecampion B., Zhang W. Impact of the anisotropy of fracture toughness on the propagation of planar 3D hydraulic fracture// International Journal of Fracture. 2018. V. 211. P. 103–123.

  19. Moukhtari F.-E., Lecampion B., Zia H. Planar hydraulic fracture growth perpendicular to the isotropy plane in a transversely isotropic material // Journal of the Mechanics and Physics of Solids. 2020. V. 137, 103878. https://doi.org/10.1016/j.jmps.2020.103878

  20. Peirce A., Detournay E. An implicit level set method for modelling hydraulically driven fractures // Computer methods in applied mechanics and engineering. 2008. V. 19. P. 2858–2885.

  21. Spence D.A., Sharp P. Self-similar solutions for elastohydrodynamic cavity flow // Proceedings Mathematical Physical & Engineering Sciences. 1985. V. 400 (18). P. 289–313.

  22. Zhang X., Detournay E., Jeffrey R. Propagation of a penny-shaped hydraulic fracture parallel to the free-surface of an elastic half-space// International Journal of Fracture. 2002. V. 115. P. 125–158.

  23. Savitski A.A., Detournay E. Propagation of a penny-shaped fluid-driven fracture in an impermeable rock: asymptotic solutions. International Journal of Solid and Structures. 2002. V. 39. P. 6311–6337.

  24. Savitski A., Detournay E. Similarity solution of a penny-shaped fluid-driven fracture in a zero-toughness linear elastic solid // ComptesRendus de l’Académie des Sciences – Series IIB – Mechanics. 2001. V. 329. P. 255–262.

  25. Chen X., Li Y., Zhao J., Xu W., Fu D. Numerical investigation for simultaneous growth of hydraulic fractures in multiple horizontal wells. Journal of Natural Gas Science and Engineering. 2018. V. 51. P. 44–52.

  26. Sesetty V., Ghassemi A. A numerical study of sequential and simultaneous hydraulic fracturing in single and multi-lateral horizontal wells // Journal of Petroleum Science and Engineering. 2015. V. 132. P. 65–76.

  27. Xiao H.T., Yue Z.Q. A three- dimensional displacement discontinuity method for crack problems in layered rocks // International Journal of Rock Mechanics & Mining Sciences. 2011. V. 48. P. 412–420.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал