1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 1, 2021

Известия РАН. Механика жидкости и газа, 2021, № 1, стр. 134-141

ОБРАЗОВАНИЕ И ОТРЫВ ВИХРЕЙ ОТ ПОВЕРХНОСТИ ЗАРЯЖЕННОЙ ДИЭЛЕКТРИЧЕСКОЙ МИКРОЧАСТИЦЫ В СИЛЬНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Е. А. Франц a, Д. А. Артюхов a, Т. С. Киреева a, Г. С. Ганченко a, Е. А. Демехин a, *

a Краснодарский филиал финансового университета, лаборатория электро- и гидродинамики микро- и наномасштабов
Краснодар, Россия

* E-mail: eafrants@fa.ru

Поступила в редакцию 06.04.2020
После доработки 21.06.2020
Принята к публикации 21.06.2020

Полный текст (PDF)

Аннотация

Впервые на основе численного решения системы Нернста–Планка–Пуассона–Стокса в широком диапазоне параметров исследовано движение заряженной диэлектрической микрочастицы в электрическом поле. Наиболее важным результатом является обнаружение формирования на задней стороне частицы микровихрей, которые при увеличении электрического поля теряют стационарность, периодически отрываясь от поверхности; при дальнейшем увеличении поля отрыв приобретает хаотический характер. Явление сильно напоминает образование цепочки Кармана, но в силу практически нулевых чисел Рейнольдса для микро-нанотечений имеет другой физический механизм. В работе даются асимптотический анализ и теоретическое обоснование механизма образования и отрыва микровихрей для малых чисел Дебая.

Ключевые слова: электрофорез, диэлектрическая частица, система Нернста–Планка–Пуассона–Стокса, сильное электрическое поле, неравновесные процессы

Электрофорез представляет собой фундаментальную проблему теоретической физики, теоретическое изучение которой берет начало более ста лет назад, с классической работы Смолуховского [1] для диэлектрических частиц. Практический интерес к задаче резко возрос в последние двадцать лет в связи с задачами управления заряженными частицами в микрофлюидных устройствах, задачами медицинской диагностики, изучением движения и разделения различных ДНК и белков по их свойствам [2, 3]. Помимо названных приложений, в микрофлюидике важную роль играет возможность перемешивания жидкости путем создания микровихрей, в частности, для снятия тепловых напряжений. Поведение частицы, ее поля скоростей, потенциала и плотности ионов критически зависят от типа поверхности: ионоселективный, металлический, диэлектрический или более сложный тип (частицы Янусы с неоднородностью их поверхностных или объемных свойств [4], белки, ДНК и т.д.). Настоящая работа полностью сконцентрирована на частицах с диэлектрическими поверхностями.

Линейная теория Смолуховского перестает работать для сильных электрических полей, когда становятся важны нелинейные эффекты. Теоретическое описание некоторых таких эффектов появились недавно [5–7], причем по большей части были предложены только асимптотические методы для некоторых частных случаев. Численный же анализ ограничен малыми и умеренными напряженностями электрического поля. Среди экспериментальных работ упомянем только наиболее свежую [8], которая содержит ссылки на другие более ранние экспериментальные работы. Основное внимание, как в экспериментальных, так и в теоретических работах, уделено зависимости скорости микрочастицы от напряженности внешнего электрического поля, числа Дебая и плотности заряда на поверхности частицы. Сравнение теории и эксперимента для скорости электрофореза дано только в [8], причем сравнение ограничено наноразмерами частицы.

Для приложений микрофлюидики, кроме скорости электрофореза, важно знать распределения скорости жидкости, электрического потенциала и концентрации ионов вблизи поверхности частицы, однако, экспериментальные методы плохо приспособлены для измерения деталей полей неизвестных. Для этих целей идеально подходит прямое численное моделирование, проведенное в данной работе в широком диапазоне параметров, от нано- до микроразмеров.

Наиболее важным полученным результатом является обнаружение формирования на задней стороне частицы микровихрей, которые при увеличении электрического поля теряют стационарность, периодически отрываясь от поверхности; при дальнейшем увеличении напряженности поля отрыв приобретает хаотический характер. Явление сильно напоминает образование цепочки Кармана, но в силу приближения ползущего течения имеет другой физический механизм. Экспериментально известно [9] и подтверждено расчетами [10, 11], что стационарные микровихри образуются вблизи ионоселективной частицы (частицы, поверхность которой пропускает ионы только одного знака) около точки поверхности, где поток ионов меняет знак. В случае диэлектрической частицы поток ионов через ее поверхность отсутствует, но тем не менее микровихри образуются. Для объяснения физического механизма образования и отрыва микровихрей проводится асимптотический анализ для малых чисел Дебая.

1. ФОРМУЛИРОВКА ЗАДАЧИ

Рассматривается движение сферической микрочастицы диэлектрика с радиусом $\tilde {a}$, находящейся в растворе электролита, под действием внешнего электрического поля напряженности ${{\tilde {E}}_{\infty }}$.

В задачах электрокинетики наиболее распространены два подхода к описанию поведения заряда в жидкостях. Первый из них предполагает, что жидкость является диэлектрической, а заряд в ней образуется в результате инжекции из электродов [12]. В этом случае заряд может распространяться в объем жидкости и приводить к электрогидродинамическим эффектам. Второй подход, основанный на принципах электрокинетики, предполагает, что жидкость является электролитом, и заряд образуется за счет разности концентрации ионов растворенных в жидкости солей. В данной работе будет использован второй подход, так как он в большей степени соответствует задачам микрогидродинамики.

В качестве буферного электролита рассматривается бинарный одновалентный раствор электролита. Коэффициенты диффузии катионов и анионов предполагаются равными, т.е. ${{\tilde {D}}^{ + }} = {{\tilde {D}}^{ - }}$ = = $\tilde {D}$. Поведение электролита описывается системой уравнений Нернста–Планка, относительно концентраций ионов ${{\tilde {c}}^{ \pm }}$. Система дополняется уравнениями Пуассона относительно электрического потенциала $\tilde {\Phi }$ и Навье–Стокса относительно поля скоростей ${\mathbf{\tilde {U}}} = (\tilde {U},\tilde {V})$. В силу малости масштаба и, как следствие, малости числа Рейнольдса, для описания движения жидкости используется приближение Стокса для ползущего течения. Электрическое поле внутри микрочастицы описывается уравнением Лапласа для потенциала $\tilde {\varphi }$; на поверхности частицы предполагается существование поверхностного заряда, плотность которого $\tilde {\sigma }$ однородна по всей поверхности.

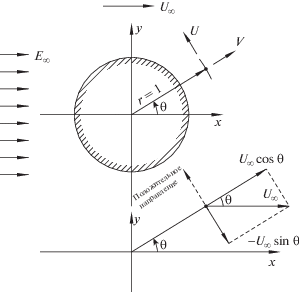
Постановка задачи проводится в сферической системе координат, движущейся со скоростью частицы, в центре которой находится точка отсчета (см. рис. 1).

Рис. 1.

Схема течения в системе координат микрочастицы.

Для перехода к безразмерной постановке были использованы следующие характерные величины: радиус микрочастицы $\tilde {a}$, термический потенциал ${{\tilde {\Phi }}_{0}} = \tilde {R}\tilde {T}{\text{/}}\tilde {F}$, равновесная концентрация электролита ${{\tilde {c}}_{\infty }}$, динамическая вязкость жидкости $\tilde {\mu }$ и коэффициент диффузии ионов $\tilde {D}$. Здесь $\tilde {R}$ – универсальная газовая постоянная, $\tilde {T}$ – абсолютная температура, $\tilde {F}$ – постоянная Фарадея.

Система описывается следующими безразмерными параметрами: напряженность электрического поля ${{E}_{\infty }} = \tilde {a}{{\tilde {E}}_{\infty }}{\text{/}}{{\tilde {\Phi }}_{0}}$; число Дебая $\nu = {{\tilde {\lambda }}_{D}}{\text{/}}\tilde {a}$, где $\tilde {\lambda }_{D}^{2} = \tilde {\varepsilon }R\tilde {T}{\text{/}}{{\tilde {F}}^{2}}{{\tilde {c}}_{\infty }}$ – толщина двойного электрического слоя; коэффициент сцепления между гидродинамической и электростатической частями задачи $\varkappa = \tilde {\varepsilon }{{\tilde {\Phi }}_{0}}{\text{/}}\tilde {\mu }\tilde {D}$, и отношение диэлектрических проницаемостей $\delta = {{\tilde {\varepsilon }}_{d}}{\text{/}}\tilde {\varepsilon }$, где ${{\tilde {\varepsilon }}_{d}}$ и $\tilde {\varepsilon }$ – соответственно, диэлектрические проницаемости материала микрочастицы и жидкой среды.

Безразмерная система уравнений в электролите имеет вид:

(1.1)
$\frac{{\partial {{c}^{ \pm }}}}{{\partial t}} + {\mathbf{U}} \times \nabla {{c}^{ \pm }} = \pm \nabla \times ({{c}^{ \pm }}\nabla \Phi ) + {{\nabla }^{2}}{{c}^{ \pm }},\quad {{\nu }^{2}}{{\nabla }^{2}}\Phi = {{c}^{ - }} - {{c}^{ + }}$
(1.2)
$ - \nabla P + {{\nabla }^{2}}{\mathbf{U}} = \frac{\varkappa }{{{{\nu }^{2}}}}({{c}^{ + }} - {{c}^{ - }})\nabla \Phi ,\quad \nabla \times {\mathbf{U}} = 0$

Электрический потенциал $\varphi $ в микрочастице описывается уравнением Лапласа

(1.3)
${{\nabla }^{2}}\varphi = 0$

При пересечении поверхности частицы электрический потенциал предполагается непрерывным, в то время как его нормальная к поверхности производная испытывает скачок, обусловленный поверхностным зарядом σ; на поверхности частицы поток положительных и отрицательных ионов равен нулю, а компоненты скорости удовлетворяют условиям непроницаемости и непроскальзывания:

(1.4)
$r = 1{\text{:}}\quad \Phi = \varphi ,\quad \nu \frac{{\partial \Phi }}{{\partial r}} = \delta \nu \frac{{\partial \varphi }}{{\partial r}} - \sigma ,\quad \pm {{c}^{ \pm }}\frac{{\partial \Phi }}{{\partial r}} + \frac{{\partial {{c}^{ \pm }}}}{{\partial r}} = 0,\quad U = V = 0$

Вдали от микрочастицы, при $r \to \infty $, концентрация ионов стремится к равновесной, напряженность электрического поля – к внешнему наложенному полю, а скорость жидкости – к скорости частицы:

(1.5)
$r \to \infty {\text{:}}\quad {{c}^{ \pm }} \to 1;\quad \Phi \to - {{E}_{\infty }}rcos\theta ;\quad U \to - {{U}_{\infty }}sin\theta ;\quad V \to - {{U}_{\infty }}cos\theta $

На потенциал внутри микрочастицы $\varphi $ должно быть наложено условие отсутствия особенности при r = 0.

Для замыкания задача дополняется начальными условиями для концентраций ${{c}^{ \pm }}$; в начальный момент времени концентрации однородно распределены по пространству:

(1.6)
$t = 0{\text{:}}\quad {{c}^{ \pm }} = 1$

2. ЧИСЛЕННОЕ РЕШЕНИЕ

В проведенном численном моделировании задачи значение параметров $\varkappa $ и δ фиксировалось для водного раствора NaCl и стеклянной диэлектрической микрочастицы, для которых $\varkappa = 0.26$ и δ = 0.1. Расчеты проводились для нескольких значений параметра ν, однако в силу того, что результаты не имеют принципиального отличия, в данной работе приводятся результаты только для $\nu = 0.0086$, что соответствует размерному радиусу частицы 5 мкм. Отдельно были проведены расчеты при δ = 0, показавшие малое отличие от расчетов при δ = 0.1, порядка 3–5%. Это соответствует результатам Ярива [6, 7], полученным аналитически для умеренных значений напряженности внешнего поля ${{E}_{\infty }}$.

Для решения нестационарной задачи (1.1)–(1.6) использовался метод прямого численного моделирования, основанный на конечно-разностном подходе, адаптированный из работы [13]. Интегрирование по времени производится полунеявным методом Рунге–Кутты третьего порядка точности. Установившиеся решения были найдены при $t \to \infty $. Для проведения массовых расчетов и обнаружения новых феноменов задача распараллеливалась на суперкомпьютере “Ломоносов”.

Для наночастиц, $\nu = O(1)$, решения быстро выходили на стационарный режим, $\partial {\text{/}}\partial t = 0$, и хорошо совпадали с полученными в [5–7]. Наиболее интересные результаты были получены для микрочастиц, при малых числах Дебая $\nu \ll 1$ и больших напряженностях поля ${{E}_{\infty }}$. При некотором критическом значении $E_{\infty }^{ * }$ на задней стороне частицы возникала система стационарных тороидальных микровихрей. Удобно характеризовать каждый вихрь углом $a = {{\theta }_{T}}$, при котором $\partial \Psi {\text{/}}\partial \theta = 0$ (см. рис. 2). Типичное распространение микровихрей в системе координат неподвижного наблюдателя изображено на рис. 3.

Рис. 2.

Максимум функции тока $\Psi $ вдоль радиуса от угла $\theta $ для ${{E}_{\infty }} = 400$, $\nu = 0.0086$ и σ = 20. Значение r согласно с рис. 3.

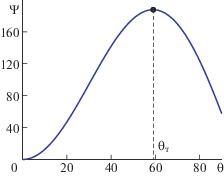
Рис. 3.

Распространение нестационарного отрывающегося вихря: ${{E}_{\infty }} = 320$, $\nu = 0.0086$, $\sigma = 5$; моменты времени $t = {{t}_{1}}$ (а), ${{t}_{2}}$ (б), ${{t}_{3}}$ (в), ${{t}_{4}}$ (г); ${{t}_{1}} < {{t}_{2}} < {{t}_{3}} < {{t}_{4}}$.

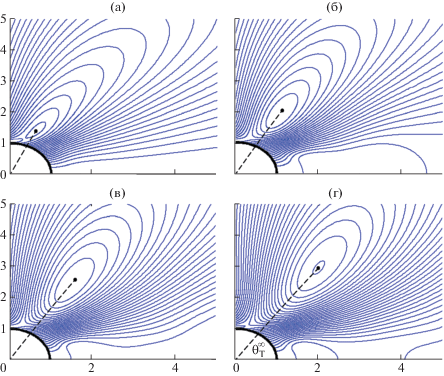
Из рис. 3, где приведены последовательные кадры распространения вихря, видно, что вихрь зарождается на экваторе при ${{\theta }_{T}} = 90^\circ $. При отходе от поверхности частицы вихри вытягиваются вдоль течения и заканчиваются при предельном значении угла $\theta _{T}^{\infty } \approx 60^\circ $, когда вихрь схлопывается в точку. Для всех наших расчетов угол $\theta _{T}^{\infty }$ менялся слабо и находился в диапазоне $\theta _{T}^{\infty } \approx 50{\kern 1pt} - {\kern 1pt} 60^\circ $.

При дальнейшем увеличении ${{E}_{\infty }}$ микровихрь теряет стационарность и происходит его периодический отрыв от поверхности и унос вместе с потоком (см. рис. 3). При достаточно большом ${{E}_{\infty }}$ отрыв приобретает хаотический характер. Явление сильно напоминает образование цепочки Кармана, но в силу приближения ползущего течения имеет другой физический механизм.

Около ионоселективной частицы стационарный микровихрь был обнаружен ранее, причем сначала экспериментально [9], а затем численно [10, 11]. Существование этого вихря, называемого вихрем Духина-Мищук, обычно связывают с неравновесностью процессов около ионоселективной поверхности. Вихрь возникает вблизи точки поверхности, где поток ионов меняет знак. Диэлектрическая же поверхность является непроницаемой для обоих типов ионов и процессы около диэлектрической частицы носят равновесный характер. Следовательно, должен быть какой-то другой физический механизм, ответственный за возникновение микровихря около диэлектрической частицы.

Чтобы понять результаты численного моделирования, рассмотрим аналитическое решение полной задачи при $\nu \to 0$. Оно распадается на решение для внутреннего разложения по ν при $r - 1 = O(\nu )$ и для внешнего разложения при $r - 1 = O(1)$. При $(r - 1){\text{/}}\nu \to \infty $ и $r - 1 \to 0$ производится сращивание двух разложений [14].

В задачах электростатики обычно предполагается, что плотность заряда $\rho = {{c}^{ + }} - {{c}^{ - }}$ является ненулевой только вблизи поверхности, на расстоянии порядка числа Дебая, $O(\nu )$, т.е. для внутреннего решения, а для внешнего решения раствор является электронейтральным (см., например, [15]), в результате:

(2.1)
$\rho \ne 0{\text{:}}\quad \frac{{r - 1}}{\nu } = O(1);\quad \rho = 0{\text{:}}\quad r - 1 = O(1)$

Из внутреннего разложения для $(r - 1){\text{/}}\nu \to \infty $ находится скорость скольжения ${{U}_{m}}(\theta )$; нормальная компонента скорости ${{V}_{m}}$ равна нулю.

Для внешнего разложения, вдали от поверхности, правая часть уравнений Стокса, обусловленная силами Кулона, обращается в ноль. Жидкость приводится в движение не массовыми силами, а поверхностными, за счет скорости скольжения, которая дает эффективное гидродинамическое краевое условие при r = 1. Именно это предположение делается в работах группы Ярива [5–7].

Исключив давление из системы (1.2) перекрестным дифференцированием и введением функции тока, $\Psi $ в осесимметричной постановке в координатах $r$ и $\theta $ определяется из соотношения:

(2.2)
$U = - \frac{1}{{sin\theta }}\frac{1}{r}\frac{{\partial \Psi }}{{\partial r}},\quad V = \frac{1}{{sin\theta }}\frac{1}{{{{r}^{2}}}}\frac{{\partial \Psi }}{{\partial \theta }}$

Уравнения системы (1.2) для электронейтрального внешнего решения перейдут в однородное бигармоническое уравнение относительно функции тока $\Psi $ с эффективными краевыми условиями для внешнего решения:

$r = 1{\text{:}}\quad \Psi = 0,\quad \frac{{\partial \Psi }}{{\partial r}} = - sin\theta \times {{U}_{m}}(\theta )$
$r \to \infty {\text{:}}\quad \Psi \to \frac{{{{r}^{2}}}}{{2si{{n}^{2}}\theta }}{{U}_{\infty }},\quad \frac{{\partial \Psi }}{{\partial r}} \to r{{U}_{\infty }}si{{n}^{2}}\theta $

Из однородного уравнения Стокса в сферической системе координат со скоростью скольжения ${{U}_{m}}(\theta )$ и скоростью ${{U}_{\infty }}$ на бесконечности функцию тока Ψ можно представить как линейную комбинацию решения с нулевой скоростью скольжения и решения с нулевой скоростью на бесконечности:

(2.3)
$\Psi = {{\Psi }_{0}} + {{\Psi }_{1}}$

В системе координат частицы решение имеет вид:

(2.4)
${{\Psi }_{0}} = {{U}_{\infty }}\left( {\frac{3}{2}r - \frac{1}{{2r}}} \right){{Q}_{1}}(cos\theta )$
(2.5)
${{\Psi }_{1}} = \sum\limits_{i = 1}^\infty {{{C}_{i}}} {{Q}_{i}}(cos\theta )({{r}^{{2 - i}}} - {{r}^{{ - i}}})$
где Qi – полином Гегенбауэра [16], а ${{C}_{i}}$ – коэффициенты разложения скорости скольжения Um по полиномам Гегенбауэра:

(2.6)
${{C}_{i}} = - \frac{{i(i + 1)(2i + 1)}}{4}\int\limits_0^\pi {{{U}_{m}}} (\theta ){{Q}_{i}}(cos\theta )d\theta $

Согласно теореме Г. Лила (см. [17], соотношение 4-180): для того, чтобы выполнялся баланс сил, действующих на сферическую частицу в бесконечном объеме жидкости в отсутствие объемных сил, необходимо, чтобы функция тока была ортогональна первому полиному Гегенбауэра ${{Q}_{1}} = {\text{cos}}\theta $. В нашем случае это условие означает, что

(2.7)
${{C}_{1}} = - \frac{3}{2}{{U}_{\infty }}$

Используя это выражение, можно переписать формулу для функции тока в виде:

(2.8)
$\Psi = \frac{{{{U}_{\infty }}}}{r}{{Q}_{1}}(cos\theta ) + {{C}_{2}}\left( {1 - \frac{1}{{{{r}^{2}}}}} \right){{Q}_{2}}(cos\theta ) + \sum\limits_{i = 3}^\infty {{{C}_{i}}} {{Q}_{i}}(cos\theta )({{r}^{{2 - i}}} - {{r}^{{ - i}}})$

Кривая ${{\theta }_{T}} = {{\theta }_{T}}(r)$ – это кривая, на которой расположены центры вихря в сечении по углу θ, которую можно посчитать как экстремум функции тока по углу:

(2.9)
$\frac{{\partial \Psi }}{{\partial \theta }}({{\theta }_{T}}) = 0$

На самой частице r = 1, из (2.8) этот угол равен π/2, как корень первого полинома Лежандра:

(2.10)
$\frac{{\partial {{Q}_{1}}}}{{\partial \theta }} = - sin\theta {{P}_{1}}(cos\theta ) = - sin\theta cos\theta $
(2.11)
$\frac{{\partial {{Q}_{2}}}}{{\partial \theta }} = - sin\theta {{P}_{2}}(cos\theta ) = - \frac{{sin\theta }}{2}(3co{{s}^{2}}\theta - 1)$

В результате $\theta _{T}^{\infty } \approx 54.7^\circ $. Причем значение этого угла не зависит ни от скорости скольжения ${{U}_{m}}$, ни от ${{U}_{\infty }}$. Эти величины влияют только на скорость перехода ${{\theta }_{T}}$ от 90° на частице до 54.7° на бесконечности. Причем численная картина показывает, что выход на угол 54.7° происходит достаточно быстро. В этом случае при численном моделировании в полной постановке как раз в области 54.7° наблюдается отрыв зоны пространственного заряда, вызванный, по всей видимости, именно конвективным влиянием вихря Духина. В пользу этой гипотезы также говорит тот факт, что угол отрыва практически не зависит от параметров.

Оба угла ${{\left. {{{\theta }_{T}}} \right|}_{{r = 1}}}$ и ${{\left. {{{\theta }_{T}}} \right|}_{{r = \infty }}}$ хорошо коррелируют с полученными в численном эксперименте.

Таким образом, существование стационарного вихря физически объясняется неравномерностью распределения заряда, а следовательно, и силы Кулона вблизи поверхности частицы. Возникает вопрос, почему при достаточно большой напряженности поля микровихри начинают отрываться от поверхности частицы?

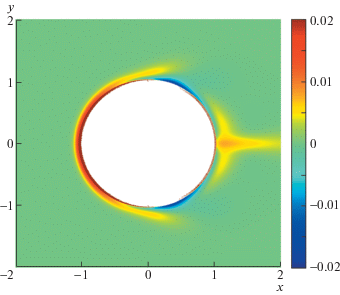
Одним из оснований для вышеприведенного асимптотического анализа является допущение о балансе сил во внешнем решении, что обусловливает применение теоремы Г. Лила [17]. Фактически предполагается, что для внешнего течения правая часть уравнений Стокса, обусловленная силами Кулона, обращается в ноль. Однако, как показывают численные расчеты, такое предположение верно только для достаточно малых напряженностей поля ${{E}_{\infty }}$. При достаточно больших ${{E}_{\infty }}$ происходит интересное явление: заряд начинает увлекаться потоком жидкости и выходит во внешнее решение. Одно из следствий: невыполнение баланса сил, приводящая к отрыву вихря. Типичное распределение заряда для этого случая приведено на рис. 4: отделение заряда происходит как на экваторе $\theta = 90^\circ $, так и на полюсе $\theta = 0^\circ $ частицы.

Рис. 4.

Распределение плотности заряда $\rho = {{c}^{ + }} - {{c}^{ - }}$ около микрочастицы, ${{E}_{\infty }} = 400$, $\nu = 0.0086$, σ = 20.

ЗАКЛЮЧЕНИЕ

С помощью прямого численного моделирования системы было обнаружено формирование вихря Духина для диэлектрической частицы. Было показано наличие как стационарных, так и неустойчивых и нестационарных вихрей. При малых закритичностях вихри отрываются строго периодично. При увеличении напряженности электрического поля отрыв вихрей становится хаотичным, что напоминает известную картину дорожки фон Кармана. В отличие от дорожки фон Кармана, где механизмом образования вихрей служит инерция, в нашей задаче инерционные силы пренебрежимо малы, и механизмом возникновения вихрей Духина служит сила Кулона.

Авторы приносят глубокую благодарность проф. МГУ имени М.В. Ломоносова В.А. Полянскому за замечания к постановке задачи, обсуждение и анализ результатов расчетов и указание на некоторые важные работы, выпавшие из поля внимания авторов, что в конечном итоге способствовало существенному улучшению качества статьи. Работа выполнена с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова.

Исследование выполнено при финансовой поддержке РФФИ и администрации Краснодарского края в рамках научного проекта № 19-48-235001.

Список литературы

  1. Smoluchowski M. Contribution to the theory of electro-osmosis and related phenomena // Bull. Int. Acad. Sci. Cracovie 1903. V. 184. P. 199.

  2. Napoli M., Eijkel J.C.T., Pennathur S. Nanofluidic technology for biomolecule applications // Lab. Chip. 2010. V. 10. P. 957.

  3. Chang H.-C., Yossifon G., Demekhin E.A. Nanoscale electrokinetics and microvortices // Annu. Rev. Fluid Mech. 2012. V. 44. P. 401.

  4. Granick S., Jiang S. Janus particle synthesis, self-assembly and applications. The Royal Society of Chemistry, 2012. 292 p.

  5. Schnitzer O., Yariv E. Macroscale description of electrokinetic flows at large zeta potentials: Nonlinear surface conduction // Phys. Rev. E. 2012. V. 86. № 2. P. 021503.

  6. Schnitzer O., Zeyde R., Yavneh I., Yariv E. Weakly nonlinear electrophoresis of a highly charged colloidal particle // Physics of Fluids. 2013. V. 25. № 5. P. 052004.

  7. Schnitzer O., Yariv E. Nonlinear electrophoresis at arbitrary field strengths: small-Dukhin-number analysis // Physics of Fluids. 2014. V. 26. № 12. P. 122002.

  8. Tottori S., Misiunas K., Keyser U.F. Nonlinear Electrophoresis of Highly Charged Nonpolarizable Particles // Physical Review Letters. 2019. V. 123. № 1. P. 014502.

  9. Mishchuk N.A., Takhistov P.V. Electroosmosis of the second kind // Colloids and Surfaces A. 1995. V. 95. P. 119.

  10. Ben Y., Demekhin E.A., Chang H.-C. Nonlinear electrokinetics and “superfast” electrophoresis // J. Colloid Interface Sci. 2004. V. 276. P. 483.

  11. Ganchenko G., Frants E., Shelistov V., Nikitin N., Amiroudine S., Demekhin E., Extreme nonequilibrium electrophoresis of an ion-selective microgranule // Physical Review Fluids. 2019. V. 4. № 4. P. 043703.

  12. Vázquez P.A., Pérez A.T., Castellanos A., Atten P. Dynamics of electrohydrodynamic laminar plumes: Scaling analysis and integral model // Phys Fluids. 2000. V. 12. № 11. P. 2809.

  13. Nikitin N.V. Third-order-accurate semi-implicit Runge-Kutta scheme for incompressible Navier–Stokes equations // Int. J. Numer. Meth. Fluids. 2006. V. 51. P. 221–233.

  14. Van Dyke M. Perturbation Methods in Fluid Mechanics. New York: Academic press, 1964.

  15. Probstein R.F. Physicochemical Hydrodynamics. An Introduction. New York: Wiley-Interscience, 2005.

  16. Суетин П.К. Классические ортогональные многочлены. Физматлит, 2007.

  17. Gary Leal L. Laminar Flow and Convective Transport Processes: Scaling Principles and Asymptotic Analysis. Butterworth-Heinemann, 1992.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал