1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 1, 2021

Известия РАН. Механика жидкости и газа, 2021, № 1, стр. 120-133

НОВЫЙ ПОДХОД К ЧИСЛЕННОМУ МОДЕЛИРОВАНИЮ СВЕРХЗВУКОВОГО НЕВЯЗКОГО ОСЕСИММЕТРИЧНОГО СЖИМАЕМОГО ТЕЧЕНИЯ СЕТОЧНЫМ МЕТОДОМ БОЛЬЦМАНА С ИСПОЛЬЗОВАНИЕМ МЕТОДА КОНЕЧНОГО ОБЪЕМА

Р. Камали Могхадам a, *, **, Н. Сахранавард Фард a, ***, Х. Джалали a, ****, Е.А. Пушкаря

a Аэрокосмический исследовательский институт
Тегеран, Иран

* E-mail: rkamali@ari.ac.ir
** E-mail: ramin.kamali82@gmail.com
*** E-mail: nasrinfard95@gmail.com
**** E-mail: hamed8722@gmail.com

Поступила в редакцию 12.02.2020
После доработки 21.06.2020
Принята к публикации 21.06.2020

Полный текст (PDF)

Аннотация

Развивается новый подход к численному моделированию сверхзвукового невязкого течения с использованием осесимметричного сжимаемого сеточного метода Больцмана конечного объема. Реализована идея использования круговых функций для учета эффекта сжимаемости в сверхзвуковом поле течения. В настоящем исследовании осесимметричные уравнения для сеточного метода Больцмана, использующие круговые функции, впервые выведены и подробно представлены вместе с соответствующими граничными условиями применительно к двумерным сеткам с тринадцатью компонентами скорости и двумя энергетическими уровнями. Для проверки развитого численного метода расчета моделируются два сверхзвуковых осесимметричных обтекания полусферической лобовой части и затупленного под 60° тела. Сравнение полученных результатов с некоторыми надежными эмпирическими данными демонстрирует точность развитого численного алгоритма. Кроме того, результаты двумерного и осесимметричного моделирований изучены для оценки влияния новой рассмотренной постановки задачи на макроскопические параметры течения.

Ключевые слова: осесимметричное течение, сжимаемое течение, сверхзвуковое течение, сеточный метод Больцмана, конечный объем

Физические явления в потоке жидкости могут классифицироваться как происходящие на трех масштабах, а именно, на макроскопическом, мезоскопическом и микроскопическом масштабе. Использование непрерывных (континуальных) уравнений Навье–Стокса и Эйлера при численном моделировании явлений на мезоскопических и микроскопических масштабах приводит к результатам с некоторыми погрешностями, тогда как на мезоскопическом масштабе уравнения Больцмана могут быть применены без каких-либо ограничений как для непрерывных, так и разрывных полей течения [1]. В последние два десятилетия численный метод, основывающийся на уравнениях Больцмана, был повсеместно развит и использован для решения практических задач в широком диапазоне. Сеточный метод Больцмана является некоторой коррекцией метода сеток в газовой динамике. В этой модели течение жидкости моделируется движениями виртуальных частиц на квадратной сетке [2]. Для моделирования течения сеточным методом Больцмана в [3] вместо квадратной сетки была предложена гексагональная сетка. В [4] была рассмотрена кинетическая теория и описана связь между непрерывным уравнением Больцмана и уравнением Навье–Стокса в случае несжимаемой среды. Базовая модель уравнения Больцмана была представлена в [5]. За счет развития сеточного метода Больцмана его применение было существенным образом расширено для моделирования разнообразных физических явлений, таких как поле многофазного течения, течение в пористой среде, гидродинамика ньютоновской и неньютоновской жидкости, моделирование акустических явлений, подавление шума и турбулентные течения [3, 6]. Например, используя метод Больцмана, в [7] было моделировано такое явление, как пламя, и были исследованы его эффективные внешние элементы или, например, в [8] течение крови было изучено за счет развития двухвязкостной модели в рамках сеточного метода Больцмана. В [9] были изучены особенности моделирования методом Больцмана псевдоожиженного слоя в случае несжимаемого течения.

Стандартный сеточный метод Больцмана ограничивается анализом несжимаемых течений, поскольку он определен на основе равновесной функции Максвелла при малых числах Маха. Моделирование полей сжимаемых течений с использованием функции распределения Максвелла является одним из недостатков стандартной сеточной модели Больцмана, поскольку не рассматриваются вращательные степени свободы для двухатомных или многоатомных молекул. Однако сжимаемое течение может наблюдаться во многих физических явлениях, происходящих в таких объектах, как высокоскоростные самолеты, реактивные и ракетные двигатели, возвращаемые космические аппараты и газопроводы. Из-за важности моделирования эффектов сжимаемости и разнообразных потенциальных возможностей метода Больцмана при моделировании широкого диапазона полей течения с различными числами Кнудсена, многочисленные исследователи развили сеточный метод Больцмана с целью моделирования на его основе сжимаемых течений [3–8, 10]. В [11] метод Больцмана и уравнение Бюргерса были использованы для численного моделирования сжимаемых течений. В [12] за счет использования неравновесного члена в функциях распределения частиц была обобщена упрощенная модель Бхатнагара–Гросса–Крука (BGK) для вязкого течения. Было показано, что результаты могут быть более точными, чем результаты, полученные с помощью уравнений Навье–Стокса, а также развиваемая модель может быть использована для моделирования пограничного слоя и ударных волн. В [13] была продемонстрирована возможность использования дуальной функции распределения для моделирования сжимаемых течений. В [14] этот метод был модифицирован посредством добавления скорости макроскопического течения к скорости частиц с целью моделирования сжимаемого течения в широком диапазоне чисел Маха. Таким образом, появилась возможность моделировать распространение волн и их отражение при больших числах Маха. В [15] был развит трехмерный конечно-разностный метод для сеточного метода Больцмана с использованием дуальной функции распределения для моделирования сжимаемого течения. В [16] был предложен двумерный сеточный метод Больцмана с девятью компонентами скорости и тремя энергетическими уровнями для моделирования сжимаемых течений. Кроме того, в [17] была использована двумерная модель сеточного метода Больцмана с девятью компонентами скорости и тремя энергетическими уровнями, которая имела возможность охватить результаты BGK модели конечно-разностным методом и TVD методом минимизации полной вариации. В [18] простая круговая функция была использована для вычисления равновесных функций распределения без ограничения по числу Маха. Максвелловская равновесная функция была представлена в сеточном методе Больцмана с круговой функцией для учета эффекта сжимаемости поля течения с более простыми математическими расчетами.

Возможности использования уравнений Больцмана при моделировании сложных полей течения в широком диапазоне числа Кнудсена и их эффективность при параллельной обработке делают их привлекательными для исследователей с целью удаления ограничений в различных полях течения. Одним из недостатков методов частиц, подобных сеточному методу Больцмана, являются их высокие затраты на вычисления при моделировании полей течения по сравнению с общепринятыми моделями сплошной среды. Этот недостаток становится наиболее очевидным, когда необходимо провести трехмерное моделирование с использованием сеточного метода Больцмана. В качестве возможного выхода из этой ситуации, во многих приложениях может быть использована осесимметричная версия сеточного метода Больцмана с существенно меньшими вычислительными издержками по сравнению с трехмерным моделированием. Многие физические явления имеют цилиндрическую симметрию и поэтому могут моделироваться с использованием осесимметричных уравнений с гораздо меньшими вычислительными затратами по сравнению с трехмерным моделированием [19]. Большое количество обзоров литературы указывают на наличие теоретического пробела при моделировании осесимметричных сверхзвуковых течений с помощью сеточного метода Больцмана. В [20] была представлена первая осесимметричная модель Больцмана, и в уравнении Больцмана были введены источниковые члены, которые согласуются с осесимметричными уравнениями Навье–Стокса на основе разложения Чепмена–Энскога. Этот метод был применен к многофазным течениям с учетом внутримолекулярных столкновений в жидкости [21, 22]. В этом методе не были рассмотрены некоторые слагаемые, связанные с осевой скоростью. В [23] этот недостаток был устранен за счет развития более точной модели на основе осесимметричных уравнений Больцмана. В [24] была предложена другая упрощенная версия, в которой вынуждающие слагаемые подобны таким же слагаемым в уравнения[ гидродинамики. Недавно в [25] были исследованы симметричные граничные условия для осесимметричных уравнений Больцмана, основывающиеся не неравновесной дискретизации.

В этих литературных ссылках все развитые осесимметричные сеточные методы Больцмана применялись для численного моделирования несжимаемых низкоскоростных течений. Например, в [26] был представлен потоковый солвер для сеточного метода Больцмана, предназначенный для моделирования несжимаемых вязких и невязких течений и основывающийся на анализе разложений Чепмена–Энскога. Кроме того, в [27] был проведен анализ вынуждающих схем для осесимметричных сеточных методов Больцмана при условии несжимаемости течения. Все ситуации в осесимметричной геометрии ранее не были исследованы в сжимаемом сверхзвуковом режиме, а такой режим является главной целью настоящей работы. В упомянутых исследованиях сжимаемый сеточный метод Больцмана был также развит только для двумерной геометрии [28–30].

В настоящем исследовании представлен новый подробный вывод невязкого осесимметричного сжимаемого уравнения Больцмана. Метод конечного объема на двумерных сетках с 13 компонентами скорости используется для точного учета наличия ударных разрывов в поле течения. Кроме того, MUSCL алгоритм третьего порядка точности используется для дискретизации выражения линейного смещения в BGK модели. Результаты, полученные с помощью нового разработанного метода, проверяются путем моделирования осесимметричного сверхзвукового обтекания двух тел со сферической геометрией и затупленной носовой частью. Сравнение полученных результатов с достоверными экспериментальными данными демонстрирует точность предлагаемого алгоритма. В настоящей работе результаты как двумерного, так и осесимметричного моделирования сравниваются между собой, чтобы выявить важность предположений об осесимметричности течения. Отметим, что предлагаемое исследование является первым шагом в разработке обобщенной численной схемы, которая позволит моделировать широкий диапазон режимов от течения сплошной среды до разреженного потока.

1. ОСНОВНЫЕ УРАВНЕНИЯ

Поскольку рассмотрение новой предлагаемой постановки задачи концентрируется на использовании осесимметричного сжимаемого сеточного уравнения Больцмана, основанного на круговой функции, основные уравнения определяются в два этапа. Во-первых, даются общие объяснения сжимаемому сеточному уравнению Больцмана, основанному на круговой функции, и далее дается детальный вывод осесимметричного сжимаемого сеточного уравнения Больцмана.

1.1. Сжимаемый сеточный метод Больцмана

Рассмотрим сеточный метод Больцмана, основанный на мезоскопических кинетических уравнениях. Поскольку макроскопическая динамика жидкости является результатом мезоскопического поведения частиц, уравнение Больцмана определяет статистическую концепцию системы выражением для функции распределения плотности $f\left( {x,~c,t} \right)$. Эта функция задает число частиц в момент времени $t~$в положении между x и $x + dx$ в диапазоне скоростей от c до $c + dc$. В общем виде стандартное уравнение Больцмана может быть записано в следующем виде:

(1.1)
$\frac{{\partial {{f}_{{{\alpha \nu }}}}}}{{\partial t}} + {{{\xi }}_{{\alpha }}}.\nabla {{f}_{{{\alpha \nu }}}} = - \frac{1}{{\tau }}({{f}_{{{\alpha \nu }}}} - f_{{\alpha \nu }}^{{(eq)}}),\quad {\alpha } = 1..N,~\quad {\nu } = 1,2~$

Здесь fα обозначает вероятность существования частицы в момент времени $t$ в положении x с дискретной скоростью ${{{\xi }}_{{\alpha }}} = ({{{\xi }}_{{{\alpha }x}}},{{{\xi }}_{{{\alpha }r}}}$), а ${\tau }$ есть безразмерное время релаксации, которое для невязкого течения очень мало (около ${{10}^{{ - 4}}}\sim {{10}^{{ - 3}}}$). В настоящем исследовании дискретные скорости определены в 13 направлениях (N = 13) на каждой сетке, а $f_{{\alpha \nu }}^{{(eq)}}$ есть равновесная функция распределения, которая рассчитывается по функции Максвелла в стандартном сеточном уравнении Больцмана. Эта функция справедлива только для несжимаемых течений при малых скоростях [31]. Функция распределения Максвелла не может быть использована при моделировании сжимаемых течений, так как она не учитывает вращательную степень свободы двух- и многоатомных молекул. В настоящей работе используется идея применения круговых функций для вычисления равновесных функций распределения и исключения каких-либо ограничений при моделировании сжимаемых течений [18]. В двумерном случае круговая функция gc может быть определена следующим образом:

(1.2)
${{g}_{c}} = \left\{ \begin{gathered} \frac{{\rho }}{{2{\pi }c}}\quad {\text{если}}\quad \left\| {{\psi } - u} \right\| = c \equiv \sqrt {D\left( {{\gamma } - 1} \right)e} \hfill \\ {\text{\;и}}~\quad {{{\lambda }}_{{\text{v}}}} = {{e}_{p}} = \left[ {1 - \frac{D}{2}\left( {{\gamma } - 1} \right)} \right]e \hfill \\ 0,~\quad {\text{в противном случае}} \hfill \\ \end{gathered} \right.$
где ep – удельная энергия, u – средняя скорость течения, c – эффективная специфическая (пекулярная) скорость, и D = 2 – размерность пространства. Физический смысл уравнения (2.1) состоит в том, что вся масса, количество движения и энергия сосредоточены на некотором круге, расположенном в трехмерном пространстве. Эта функция очень простая, она удовлетворяет всем необходимым статистическим соотношениям, чтобы исходя из BGK модели воссоздать уравнения Навье–Стокса для течения сжимаемой жидкости [18].

Интерполяция Лагранжа применяется для определения круговой функции на множестве дискретных точек без предположения о малости числа Маха. В настоящем исследовании используются ${\alpha } = 13$ дискретных точек для дискретизации круговой функции на все дискретные скорости ${{{\xi }}_{{\alpha }}}$. Для каждой дискретной точки плотность ${\alpha }$ и скорость ${{{\xi }}_{{\alpha }}}$ определяются, используя весовую функцию ${{{\varphi }}_{{\alpha }}}\left( {{\xi },{{{\lambda }}_{{\text{v}}}}} \right)$, следующим образом:

(1.3)
${{{\rho }}_{{\alpha }}} = \frac{{\rho }}{{2{\pi }c}}\oint {{{{\varphi }}_{{\alpha }}}({\xi },{{{\lambda }}_{{\text{v}}}})ds} $
где энергия покоя на двух уровнях задается как [18]:

(1.4)
${{{\lambda }}_{1}} = 0,\quad {{{\lambda }}_{2}} = 1$

Окончательный вид равновесных круговых функций $f_{{\alpha v}}^{{eq}}$ может быть получен с использованием весовой функции [31]:

(1.5)
$f_{{{\alpha }{{{\lambda }}_{{\text{v}}}}}}^{{(eq)}} = \frac{{\rho }}{{2{\pi }c}}\oint {{{{\varphi }}_{{{\alpha }{{{\lambda }}_{{\text{v}}}}}}}({\xi },{{{\lambda }}_{{\text{v}}}})ds} $

Равновесная круговая функция включает 26 уравнений для всех дискретных скоростей (α = 1, …, 13) на двух уровнях энергии. Все эти равновесные функции подробно определены в [18]. В качестве примера приведем две равновесные функции распределения для первой дискретной скорости на двух уровнях энергии:

(1.6)
$\left\{ \begin{gathered} f_{{{\alpha }0}}^{{(eq)}} = {{{\varphi }}_{{{\alpha }0}}}\left( {{\xi },{{{\lambda }}_{{\text{v}}}}} \right)(1 - {{e}_{p}})\quad {\text{при}}\quad {{{\lambda }}_{1}} = 0 \hfill \\ f_{{{\alpha }1}}^{{(eq)}} = {{{\varphi }}_{{{\alpha }1}}}\left( {{\xi },{{{\lambda }}_{{\text{v}}}}} \right)({{e}_{p}})\quad {\text{при}}\quad {{{\lambda }}_{2}} = 1 \hfill \\ \end{gathered} \right.$
где весовая функция вычисляется следующим образом [31]:

(1.7)
$\left\{ \begin{gathered} {{{\varphi }}_{{{\alpha }1}}}\left( {{\xi },{{{\lambda }}_{{\text{v}}}}} \right) = {{{\varphi }}_{{\alpha }}}\left( {\xi } \right)\left( {1 - {{{\lambda }}_{{\text{v}}}}} \right)\quad {\text{при}}\quad ~{{{\lambda }}_{1}} = 0 \hfill \\ {{{\varphi }}_{{{\alpha }2}}}\left( {{\xi },{{{\lambda }}_{{\text{v}}}}} \right) = {{{\varphi }}_{{\alpha }}}\left( {\xi } \right)\left( {{{{\lambda }}_{{\text{v}}}}} \right)\quad {\text{при}}\quad {{{\lambda }}_{2}} = 1 \hfill \\ \end{gathered} \right.$

Как упомянуто выше, сеточное уравнение Больцмана для сжимаемых течений было подробно описано в [18]. Подводя итоги, можно сказать, что в данном разделе были представлены только уравнения, необходимые для выкладок в осесимметричном случае.

1.2. Сеточный метод Больцмана для осесимметричного сжимаемого течения

В осесимметричном случае уравнение Больцмана описывает радиальную, осевую и азимутальную компоненты поля течения. Теория сеточного метода Больцмана для осесимметричного несжимаемого течения с малыми скоростями приведена в [19]; однако, вплоть до настоящего времени отсутствует уравнение для сеточного метода Больцмана для осесимметричного сжимаемого невязкого течения. Уравнения, выведенные в данном разделе, представлены впервые. Поскольку осесимметричные течения могут моделироваться в виде двумерной задачи с учетом эффектов осевых течений в используемых уравнениях, вычислительные затраты будут значительно уменьшены по сравнению с трехмерным моделированием.

В настоящей работе подход к выводу осесимметричной формы сеточного уравнения Больцмана для сжимаемого течения начинается с предложения уравнения Больцмана с некоторыми источниковыми членами. Источниковые члены будут выписаны, чтобы воссоздать все уравнения Эйлера для массы, количества движения и энергии в цилиндрических координатах.

Общий вид уравнения Больцмана для осесимметричного сжимаемого течения предлагается записать следующим образом:

(1.8)
$\frac{{\partial {{f}_{{{\alpha \nu }}}}}}{{\partial t}} + \frac{{\partial \left( {{{f}_{{{\alpha \nu }}}}{{{\xi }}_{{{\alpha }x}}}} \right)}}{{\partial x}} + \frac{{\partial \left( {{{f}_{{{\alpha \nu }}}}{{\xi }_{{{\alpha }r}}}} \right)}}{{\partial r}} + S = {{{\Omega }}_{{{\alpha \nu }}}}$
где ${{{\xi }}_{{\alpha }}} = \left( {{{{\xi }}_{{{\alpha }x}}},{{{\xi }}_{{{\alpha }r}}}} \right)$ – вектор дискретной скорости и

(1.9)
${{{\Omega }}_{{{\alpha \nu }}}} = - \frac{{{{f}_{{{\alpha \nu }}}} - f_{{{\alpha \nu }}}^{{eq}}}}{{\tau }}$

Отметим, что для включения в рассмотрение и учет при моделировании эффектов сжимаемости следует использовать равновесную круговую функцию $f_{{{\alpha \nu }}}^{{eq}}$ в соответствии с уравнением (1.6). Источниковый член S может быть записан как сумма четырех различных членов ${{S}_{1}},{{S}_{2}},~{{S}_{3}}$ и S4, которые позволяют получить заново в цилиндрических координатах уравнение неразрывности, радиальную и осевую проекции уравнения движения и уравнение энергии соответственно:

(1.10)
$S = {{S}_{1}} + {{S}_{2}} + {{S}_{3}} + {{S}_{4}}$

При выводе каждого слагаемого уравнения Эйлера для осесимметричного сжимаемого течения должны быть получены заново из уравнения (1.8):

(1.11)
$\frac{{\partial {\rho }}}{{\partial t}} + \frac{{\partial \left( {{\rho }{{u}_{r}}} \right)}}{{\partial r}} + \frac{{\partial \left( {{\rho }{{u}_{x}}} \right)}}{{\partial x}} + \frac{{{\rho }{{u}_{r}}}}{{~r}} = 0$
(1.12)
$\frac{{\partial \left( {{\rho }{{u}_{x}}} \right)}}{{\partial t}} + \frac{{\partial ({\rho }u_{x}^{2})}}{{\partial x}} + \frac{{\partial \left( {{\rho }{{u}_{r}}{{u}_{x}}} \right)}}{{\partial r}} + \frac{{{\rho }u_{r}^{{}}u_{x}^{{}}}}{r} + \frac{{\partial P}}{{\partial x}}~~ = 0$
(1.13)
$\frac{{\partial \left( {{\rho }{{u}_{r}}} \right)}}{{\partial t}} + \frac{{\partial ({\rho }u_{r}^{2})}}{{\partial r}} + \frac{{\partial \left( {{\rho }{{u}_{r}}{{u}_{x}}} \right)}}{{\partial x}} + \frac{{{\rho }u_{r}^{2}}}{r} + \frac{{\partial P}}{{\partial r}} = 0$
(1.14)
$\frac{{\partial \left( {{\rho E}} \right)}}{{\partial t}} + \frac{\partial }{{\partial r}}\left( {\left( {{\rho E} + p} \right)~{{u}_{r}}~} \right)~ + \frac{\partial }{{\partial x}}\left( {\left( {{\rho E} + p} \right){{u}_{x}}} \right) + \frac{{{{u}_{r}}}}{r}\left( {{\rho E} + p} \right) = 0$
где ux и ur – средние скорости течения в осевом x и радиальном r направлениях соответственно.

Макроскопические свойства течения с N дискретными скоростями и двумя уровнями энергии могут быть получены с помощью вычисленной сеточным методом Больцмана функции распределения ${{f}_{{{\alpha v}}}}$:

(1.15)
$\mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{f}_{{{\alpha v}}}} = {\rho }$
(1.16)
$\mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{f}_{{{\alpha v}}}}{{{\xi }}_{{{\alpha }x}}} = {\rho }{{u}_{x}}$
(1.17)
$\mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{f}_{{{\alpha v}}}}{{{\xi }}_{{{\alpha }x}}}{{{\xi }}_{{{\alpha }r}}} = {\rho }\left( {{{u}_{x}}{{u}_{r}} + R{\text{T}}{{{\delta }}_{{xr}}}} \right)$
(1.18)
$\mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{f}_{{{\alpha v}}}}\left( {\frac{1}{2}{\xi }_{{{\alpha }\aleph \left( {x,r} \right)}}^{2} + {{{\lambda }}_{{\text{v}}}}} \right) = {\rho }\left( {\frac{1}{2}u_{{\aleph \left( {x,r} \right)}}^{2} + \frac{b}{2}R{\text{T}}} \right)$
(1.19)
$\mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{f}_{{{\alpha v}}}}\left( {\frac{1}{2}{\xi }_{{{\alpha }\aleph \left( {x,r} \right)}}^{2} + {{{\lambda }}_{{\text{v}}}}} \right){{u}_{x}} = {\rho }\left( {\frac{1}{2}u_{{\aleph \left( {x,r} \right)}}^{2} + \frac{{b + 2}}{2}R{\text{T}}} \right){{u}_{x}}$
где $\aleph $ обозначает x или r направление, δxr есть символ Кронекера и b равно общему числу степеней свободы, которое для двухатомных газов равно 5 [32]. Чтобы показать, что из уравнения Больцмана (1.8) можно воссоздать уравнение Эйлера для сплошной среды, можно использовать разложение Чепмена–Энскога первого порядка:
(1.20)
$f_{{{\alpha \nu }}}^{{}} = f_{{{\alpha \nu }}}^{{\left( 0 \right)}} + o\left( {\varepsilon } \right)$
где $f_{{{\alpha \nu }}}^{{\left( 0 \right)}} = f_{{{\alpha \nu }}}^{{eq}}$ и ${{{\Omega }}_{{{\alpha \nu }}}}$ равно нулю, согласно уравнению (1.9) для невязкого случая.

Чтобы найти первый источниковый член в уравнении (1.8) и воссоздать уравнение неразрывности (1.11), можно записать осесимметричное уравнение Больцмана в следующем виде:

(1.21)
$\frac{{\partial f_{{{\alpha \nu }}}^{{\left( 0 \right)}}}}{{\partial t}} + \frac{{\partial (f_{{{\alpha \nu }}}^{{\left( 0 \right)}}{{{\xi }}_{{{\alpha }x}}})}}{{\partial x}} + \frac{{\partial (f_{{{\alpha \nu }}}^{{\left( 0 \right)}}{{{\xi }}_{{{\alpha }r}}})}}{{\partial r}} + {{S}_{1}} = 0$

Суммирование этого уравнения по N дискретным скоростям и двум уровням энергии дает

(1.22)
$\mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 \frac{{\partial f_{{{\alpha \nu }}}^{{\left( 0 \right)}}}}{{\partial t}} + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 \frac{{\partial (f_{{{\alpha \nu }}}^{{\left( 0 \right)}}{{{\xi }}_{{{\alpha }x}}})}}{{\partial x}} + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 \frac{{\partial (f_{{{\alpha \nu }}}^{{\left( 0 \right)}}{{{\xi }}_{{{\alpha }r}}})}}{{\partial r}} + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{S}_{1}} = 0$

Подставляя уравнения (1.15) и (1.16) в уравнение (1.22), можно найти следующее соотношение

(1.23)
$\frac{{\partial {\rho }}}{{\partial t}} + \frac{{\partial \left( {{\rho }{{u}_{r}}} \right)}}{{\partial r}} + \frac{{\partial \left( {{\rho }{{u}_{x}}} \right)}}{{\partial x}} + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{S}_{1}} = 0{\text{\;\;\;\;\;}}$

Для N = 13 дискретных скоростей, использованных в настоящем алгоритме, и двух уровнях энергии последнее слагаемое может быть записано в следующем виде:

(1.24)
$\mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{S}_{1}} = 26{\text{\;}}{{S}_{1}}$

Таким образом, для получения уравнения неразрывности (1.11) первый источниковый член выражается следующим образом:

(1.25)
${{S}_{1}} = \frac{{{\rho }{{u}_{r}}}}{{26r}}$

Следующий шаг состоит в вычислении второго и третьего источниковых членов уравнения (1.8), связанных с r- и x-проекциями уравнения количества движения (1.12) и (1.13). Рассмотрим теперь другой источниковый член в уравнении Больцмана

(1.26)
$\frac{{\partial f_{{{\alpha \nu }}}^{{\left( 0 \right)}}}}{{\partial t}} + \frac{{\partial (f_{{{\alpha \nu }}}^{{\left( 0 \right)}}{{{\xi }}_{{{\alpha }x}}})}}{{\partial x}} + \frac{{\partial (f_{{{\alpha \nu }}}^{{\left( 0 \right)}}{{{\xi }}_{{{\alpha }r}}})}}{{\partial r}} + {{S}_{2}} = 0$

Умножение уравнения (1.26) на ${{{\xi }}_{{{\alpha }r}}}$ и суммирование по N дискретным скоростям и двум уровням энергии дает:

(1.27)
$\mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 \frac{{\partial (f_{{{\alpha \nu }}}^{{}}{{{\xi }}_{{{\alpha }r}}})}}{{\partial t}} + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 \frac{{\partial (f_{{{\alpha \nu }}}^{{}}{{{\xi }}_{{{\alpha }x}}}{{{\xi }}_{{{\alpha }r}}})}}{{\partial r}} + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 \frac{{\partial (f_{{{\alpha \nu }}}^{{}}{\xi }_{{{\alpha }r}}^{2})}}{{\partial x}} + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{S}_{2}}{{{\xi }}_{{{\alpha }r}}} = 0{\text{\;\;\;}}$

Подставляя уравнения (1.15)–(1.17) в уравнение (1.27), можно получить следующее уравнение:

(1.28)
$\frac{{\partial \left( {{\rho }{{u}_{r}}} \right)}}{{\partial t}} + \frac{{\partial \left( {{\rho }{{u}_{r}}{{u}_{x}}} \right)}}{{\partial x}} + \frac{{\partial ({\rho }u_{r}^{2})}}{{\partial r}} + \frac{{\partial P}}{{\partial r}} + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{S}_{2}}{{{\xi }}_{{{\alpha }r}}} = 0{\text{\;}}$

Для получения радиальной проекции уравнения количества движения (1.12) можно выразить второй источниковый член в следующем виде:

(1.29)
${{S}_{2}} = \frac{{{\rho }u_{r}^{2}}}{r}{\text{*}}\frac{{{{{\xi }}_{{{\alpha }r}}}}}{{\sum\limits_{\alpha = 1}^N {\sum\limits_{{\text{v}} = 1}^2 {{\xi }_{{{\alpha }r}}^{2}} } }}$

Третий источниковый член в уравнении (1.8) вычисляется таким же образом для получения осевой проекции уравнения движения Эйлера

(1.30)
${{S}_{3}} = \frac{{{\rho }{{u}_{r}}{{u}_{x}}}}{r}{\text{*}}\frac{{{{{\xi }}_{{{\alpha }x}}}}}{{\sum\limits_{\alpha = 1}^N {\sum\limits_{{\text{v}} = 1}^2 {{\xi }_{{{\alpha }r}}^{2}} } }}$

Для выделения последнего источникового члена уравнения (1.8) нужно преобразовать уравнение Больцмана по форме к уравнению энергии (1.14):

(1.31)
$\frac{{\partial f_{{{\alpha \nu }}}^{{\left( 0 \right)}}}}{{\partial t}} + \frac{{\partial (f_{{{\alpha \nu }}}^{{\left( 0 \right)}}{{{\xi }}_{{{\alpha }x}}})}}{{\partial x}} + \frac{{\partial (f_{{{\alpha \nu }}}^{{\left( 0 \right)}}{{{\xi }}_{{{\alpha }r}}})}}{{\partial r}} + {{S}_{4}} = 0$

Умножая уравнение (1.31) на $\left( {\frac{1}{2}{\xi }_{{{\alpha }\aleph }}^{2} + {{{\lambda }}_{{\text{v}}}}} \right)$ и суммируя это уравнение по N дискретным скоростям и двум уровням энергии, можно получить следующее соотношение:

(1.32)
$\begin{gathered} \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 \frac{{\partial f_{{{\alpha \nu }}}^{{}} \cdot \left( {\frac{1}{2}{\xi }_{{{\alpha }\aleph }}^{2} + {{{\lambda }}_{{\text{v}}}}} \right)}}{{\partial t}} + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 \frac{{\partial (f_{{{\alpha \nu }}}^{{}}{{{\xi }}_{{{\alpha }x}}}) \cdot \left( {\frac{1}{2}{\xi }_{{{\alpha }\aleph }}^{2} + {{{\lambda }}_{{\text{v}}}}} \right)}}{{\partial x}} + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 \frac{{\partial (f_{{{\alpha \nu }}}^{{}}{{{\xi }}_{{{\alpha }r}}}) \cdot \left( {\frac{1}{2}{\xi }_{{{\alpha }\aleph }}^{2} + {{{\lambda }}_{{\text{v}}}}} \right)}}{{\partial r}} + \\ + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{S}_{3}}\left( {\frac{1}{2}{\xi }_{{{\alpha }\aleph }}^{2} + {{{\lambda }}_{{\text{v}}}}} \right) = 0 \\ \end{gathered} $

Подставляя уравнения (1.18) и (1.19) в уравнение (1.32), получаем следующее уравнение:

(1.33)
$\frac{{\partial \left( {{\rho E}} \right)}}{{\partial T}} + \frac{\partial }{{\partial r}}\left( {\left( {{\rho E} + p} \right){{u}_{r}}} \right) + \frac{\partial }{{\partial x}}\left( {\left( {{\rho E} + p} \right){{u}_{x}}} \right) + \mathop \sum \limits_{{\alpha } = 1}^N \mathop \sum \limits_{{\text{v}} = 1}^2 {{S}_{4}}\left( {\frac{1}{2}{\xi }_{{{\alpha }\aleph }}^{2} + {{{\lambda }}_{{\text{v}}}}} \right) = 0{\text{\;\;}}$
где

(1.34)
${\text{E}} = \frac{1}{2}(u_{x}^{2} + u_{r}^{2}) + \frac{b}{2}R{\text{T}}$
(1.35)
$p = {\rho }R{\text{T}}$

Чтобы воссоздать уравнение энергии (1.14), последний источниковый член ${{S}_{4}}$ выражается в виде

(1.36)
${{S}_{4}} = \frac{{{{u}_{r}}}}{r}\left( {{\rho E} + p} \right)\frac{1}{{\sum\limits_{\alpha = 1}^N {\sum\limits_{{\text{v}} = 1}^2 {\left( {\frac{1}{2}{\xi }_{{{\alpha }\aleph }}^{2} + {{{\lambda }}_{{\text{v}}}}} \right)} } }}$

2. АЛГОРИТМ РЕШЕНИЯ

Чтобы дискретизировать новое выведенное осесимметричное уравнение Больцмана с использованием метода конечного объема с центрированными ячейками, следует использовать консервативную форму уравнения (1.8):

(2.1)
$\frac{{\partial {{f}_{{{\alpha \nu }}}}}}{{\partial t}} + \frac{{\partial {{F}_{{{\alpha \nu }}}}}}{{\partial x}} + \frac{{\partial {{G}_{{{\alpha \nu }}}}}}{{\partial r}} = {{{\Omega }}_{{{\alpha \nu }}}} - S$
где Ωαν есть функция столкновений, а $F$ и $G$ представляют собой конвективные потоки в направлениях осей x и y соответственно. Уравнение (2.1) в дискретном виде для конечного объема можно записать следующим образом:

(2.2)
$f_{{{\alpha \nu },i,j}}^{{n + 1}}\, = \,f_{{{\alpha \nu },i,j}}^{n}\, - \,\frac{{\Delta t}}{{Vo{{l}_{{i,j}}}}}{\kern 1pt} \left( {F_{{{\alpha \nu },i + \frac{1}{2},j}}^{n}\Delta {{s}_{{i + \frac{1}{2},j}}}\, + \,F_{{{\alpha \nu },i - \frac{1}{2},j}}^{n}\Delta {{s}_{{i - \frac{1}{2},j}}}} \right){\kern 1pt} \left( {G_{{{\alpha },i,j + \frac{1}{2}}}^{n}\Delta {{s}_{{i,j + \frac{1}{2}}}}\, + \,G_{{{\alpha \nu },i,j - \frac{1}{2}}}^{n}\Delta {{s}_{{i,j - \frac{1}{2}}}}} \right)\Delta t{{{\Omega }}_{{{\alpha \nu },i,j}}}\, - \,\Delta t{{S}_{{{\alpha \nu },i,j}}}$

В уравнении (2.2) нижние индексы i и j соответствуют центрам ячеек, $Vo{{l}_{{i,j}}}$ обозначает объем ячейки, ${{F}_{{{\alpha \nu },i \pm \frac{1}{2},j}}}$ и ${{G}_{{{\alpha \nu },i,j \pm \frac{1}{2}}}}$ – конвективные численные потоки в направлении осей x и y соответственно, и Δs есть поверхность ячейки.

Численные потоки могут быть вычислены Римановым солвером и интерполяционными методами. Чтобы учесть наличие ударных волн при моделировании сжимаемого течения, в солвере применялась численная диссипация или искусственная вязкость. Для пространственной дискретизации численных потоков использовался алгоритм MUSCL третьего порядка точности с гладким ограничителем для интерполяции потоков по обе стороны поверхности ячейки. Например, поток $F$ можно дискретизировать следующим образом:

(2.3)
$F_{{{\alpha \nu },i + \frac{1}{2},j}}^{n} = ~~\left\{ {\begin{array}{*{20}{c}} {{{{\left( {{{f}_{L}}} \right)}}_{{{\alpha \nu },i + \frac{1}{2},j}}}\left( {{{\xi }_{{x{\alpha }}}} \cdot {{N}_{{i + 1/2,j}}}} \right)\quad {\text{если}}\quad \left( {{{{\xi }}_{{x{\alpha }}}} \cdot {{N}_{{i + 1/2,j}}}} \right) \geqslant 0~} \\ {{{{\left( {{{f}_{R}}} \right)}}_{{{\alpha \nu },i + \frac{1}{2},j}}}\left( {{{\xi }_{{x{\alpha }}}} \cdot {{N}_{{i + 1/2,j}}}} \right)\quad {\text{если}}\quad \left( {{{{\xi }}_{{x{\alpha }}}} \cdot {{N}_{{i + 1/2,j}}}} \right) \leqslant 0} \end{array}} \right.$
где ${{N}_{{i + 1/2,j}}}$ есть вектор нормали к поверхности, а ${{f}_{L}}$ и ${{f}_{{R~}}}$ представляют собой функции распределения слева и справа от поверхности соответственно. Они определены следующим образом:
(2.4)
$\left\{ {\begin{array}{*{20}{c}} {{{{\left( {{{f}_{L}}} \right)}}_{{k,i + \frac{1}{2},j}}} = {{f}_{{{\alpha \nu },i,j}}} + {{{\left\{ {\frac{s}{4}\left[ {\left( {1 - {\text{k}}s} \right){{\Delta }_{ - }} + \left( {1 + {\text{k}}s} \right){{\Delta }_{ + }}} \right]} \right\}}}_{i}}} \\ {{{{\left( {{{f}_{R}}} \right)}}_{{k,i + \frac{1}{2},j}}} = {{f}_{{{\alpha \nu },i + 1,j}}} - {{{\left\{ {\frac{s}{4}\left[ {\left( {1 - {\text{k}}s} \right){{\Delta }_{ + }} + \left( {1 + {\text{k}}s} \right){{\Delta }_{ - }}} \right]} \right\}}}_{{i + 1}}}} \end{array}} \right.$
где k определяет точность интерполяции. Например, k = 1/3, 0 и 1 дают интерполяцию третьего порядка, интерполяцию второго порядка вверх по потоку и центральную интерполяция второго порядка соответственно. Ограничитель Ван Альбада (s) определяется следующим образом [14]:
(2.5)
$s = \frac{{2{{\Delta }_{ + }}{{\Delta }_{ + }} + {{{\varepsilon }}^{2}}}}{{\Delta _{ + }^{2} + \Delta _{ - }^{2} + {\varepsilon }}}$
где ε имеет очень маленькое значение порядка 10–6 и оператор Δ определен следующим образом:

(2.6)
${{\left( {{{\Delta }_{ + }}} \right)}_{i}} = {{f}_{{k,i + 1,j}}} - {{f}_{{k,i,j}}},~\quad {{\left( {{{\Delta }_{ - }}} \right)}_{i}} = {{f}_{{k,i,j}}} - {{f}_{{k,i - 1,j}}}$

Остальные численные потоки вычисляются аналогично.

3. ГРАНИЧНЫЕ УСЛОВИЯ

Чтобы задать равновесную функцию распределения $f_{{\alpha }}^{{eq}}$ на границах, нужно определить макроскопические свойства течения на этих границах. Условие скольжения применяется в случае невязкого течения на стенке. Чтобы использовать такую границу в криволинейных сетках, сетка рассматривается как неподвижная без вращения. Для того чтобы точно определить функцию распределения на искривленной виртуальной ячейке ${{f}_{{j{\nu }}}}(1{\kern 1pt} ')$, используется проекционный метод, чтобы отобразить все 13 дискретных скоростей ${\xi }_{{\alpha }}^{{\text{'}}}$ [6]:

(3.1)
${{f}_{{j{\nu }}}}\left( {1{\text{'}}} \right) = \mathop \sum \limits_{{\alpha } = 1}^{13} {{f}_{{{\alpha \nu }}}}\left( 1 \right){{{\varphi }}_{j}}({\xi }_{{x{\alpha }}}^{{\text{'}}},{\xi }_{{r{\alpha }}}^{{\text{'}}})$

Здесь скорости отражения ${\xi }_{{\alpha }}^{{\text{'}}}$ вычисляются посредством умножения двумерной матрицы коэффициентов отражения на матрицу дискретных скоростей:

(3.2)
$\left[ {\begin{array}{*{20}{c}} {{\xi }_{{x{\alpha }}}^{{\text{'}}}} \\ {{\xi }_{{r{\alpha }}}^{{\text{'}}}} \end{array}} \right] = {{R}_{{2D}}}\left[ {\begin{array}{*{20}{c}} {{{{\xi }}_{{x{\alpha }}}}} \\ {{{{\xi }}_{{r{\alpha }}}}} \end{array}} \right]$

Матрица коэффициентов отражения R2D определяется следующим образом:

(3.3)
${{R}_{{2D}}} = \left[ {\begin{array}{*{20}{c}} {\cos \left( {2{{{\theta }}_{s}}} \right)}&{{\text{sin}}\left( {2{{{\theta }}_{s}}} \right)} \\ {{\text{sin}}\left( {2{{{\theta }}_{s}}} \right)}&{ - {\text{cos}}\left( {2{{{\theta }}_{s}}} \right)} \end{array}} \right]$

Аналогично функция распределения ${{f}_{{j{\nu }}}}\left( {2{\kern 1pt} '} \right)~{\text{\;}}$ может быть вычислена в виртуальной ячейке 2’. После определении функций распределения в двух виртуальных ячейках поток через стенку вычисляется с использованием алгоритма MUSCL. Доказано, что метод отражения удовлетворяет условию скольжения и имеет второй порядок точности. Этот же метод также используется для граничного условия симметрии.

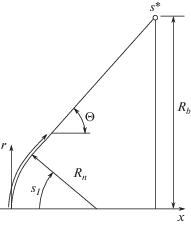
Другие граничные условия, такие как дозвуковое и сверхзвуковое течения на входе и выходе и условия на бесконечности, используются совершенно аналогично методам вычислительной гидродинамики. После расчета макроскопических свойств равновесная функция распределения вычисляется в граничных виртуальных ячейках. Например, свойства течения на дозвуковой границе могут быть получены при использовании метода характеристик Римана, после чего равновесная функция распределения вычисляется с использованием макроскопических величин [6]. Область решения и определение границ в настоящем исследовании приведены на рис. 1.

Рис. 1.

Граничные условия в области решения.

4. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Чтобы проверить достоверность выведенного сеточного метода Больцмана для осесимметричных сжимаемых течений и разработанного пакета программ, было рассмотрено сверхзвуковое обтекание двух тел с разными геометриями, а именно сферы и затупленной носовой части.

4.1. Сверхзвуковое обтекание сферы

Число Маха в набегающем потоке равнялось двум, а другие условия течения были выбраны в соответствии с экспериментальным тестом из [29]. Численные расчеты были выполнены как для двумерного, так и осесимметричного течения, так что эффект бокового потока на осесимметричной границе был также исследован.

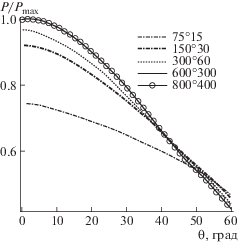
Для распределения решетки использовалась структурированная сетка, на которой моделировалось обтекание сферы. Сеточные расчеты были выполнены с использованием пяти разных размеров сетки, а именно, сетки с 75 × 15, 150 × 30, 300 × 60, 600 × 300 и 800 × 400 ячейками вдоль тангенциального и нормального направлений поверхности соответственно. Сравнение давления на поверхности сферы, проведенное на рис. 2 для сеток с разным количеством ячеек, показывает, что сетка размером 600 × 300 ячеек подходит для численного моделирования.

Рис. 2.

Сеточное исследование давления на поверхности сферы.

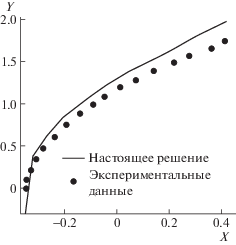
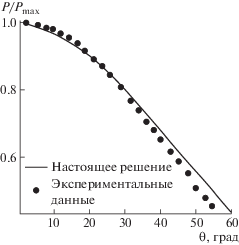
Для оценки точности численного решения на рис. 3 сравниваются положения ударной волны, полученные в настоящем исследовании, и результаты из [33]. Проведенное сравнение показывает, что результаты, полученные с помощью разработанного пакета программ для сеточного метода Больцмана для осесимметричного сжимаемого течения, сопоставимы с данными эксперимента. Положение ударной волны рассчитывалось на основе градиента плотности в течении. Причина небольших отклонений может быть связана с неопределенностью экспериментальных данных и ошибками при расчете положения ударной волны. Сравнение распределения поверхностного давления, проведенное на рис. 4, показывает, что результаты расчетов точно согласуются с данными экспериментов [33]. Чтобы обеспечить сходимость решения, численный остаток не должен был превышать 10–8.

Рис. 3.

Сравнение положения ударной волны при обтекании сферы.

Рис. 4.

Сравнение давления на поверхности сферы при обтекании сферы.

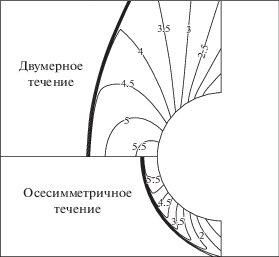
Для исследования влияния бокового течения на осесимметричные тела на рис. 5 сравниваются линии равного давления (изобары) в двумерном и осесимметричном случаях. Показано, что ударная волна правильно изображается как при двумерном, так и при осесимметричном моделировании. Положение ударной волны ближе к обтекаемому телу в осесимметричной геометрии, чем в двумерном случае из-за рассмотрения эффектов бокового течения, таких как скорость и энергия. Наблюдается, что осесимметричный случай требует большей вычислительной области, поскольку в осесимметричном поле течения жидкость может обтекать тело во всех направлениях, а не только сверху и снизу, как в двумерном случае. По мере того, как жидкость удаляется от тела, радиус потока также возрастает и через соответствующее радиальное сечение может протечь бóльшая масса по сравнению с двумерным случаем. Другими словами, осесимметричный поток ограничен или заключен в какие-то пределы в меньшей степени, чем соответствующее плоское двумерное течение. Математически осесимметричное течение имеет только две независимые переменные, но проявляет некоторые из таких физических характеристик, которые присущи общим трехмерным течениям [34].

Рис. 5.

Сравнение линий постоянного давления (изобар).

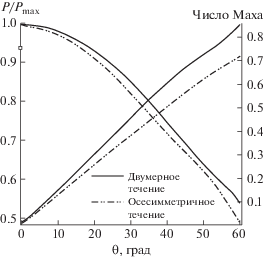
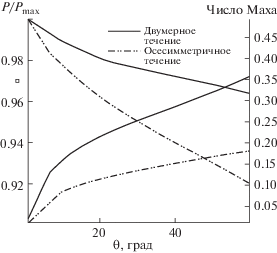
Для более точного сравнения были исследованы распределения числа Маха и безразмерного давления на поверхности тела для двумерного (цилиндр) и осесимметричного (сфера) моделирования при одинаковых условиях (рис. 6). Обтекание сферы несколько ослаблено (разгружено) по сравнению с обтеканием цилиндра. При обтекании сферы есть дополнительная размерность (направление), в котором поток может удаляться от твердого тела, он может двигаться не только сверху и снизу от тела, но и в сторону от него. По сравнению с обтеканием сферы, обтекание цилиндра имеет больше ограничений, поток может двигаться только сверху и снизу от цилиндра. Было установлено, что результаты как двумерного, так и осесимметричного моделирования имеют одинаковую тенденцию. Максимальное значение числа Маха при обтекании сферы больше аналогичного значения при обтекании цилиндра (разница около 16.32% при сравнении максимумов), поскольку в осесимметричном течении скорость любой точки зависит не только от радиального и осевого расстояния, но также от азимутального расстояния, так что это является примером трехмерного разгружающего эффекта [34]. Отметим, что абсолютное значение магнитуды разности давлений на сфере меньше, чем эта же величина для цилиндра из-за трехмерного разгружающего эффекта [34]. Сравнение давления на поверхности тела в настоящих решениях демонстрирует такой же эффект, и максимальная разность давлений достигает 1.5%. Изменение плотности на поверхности тела можно объяснить с помощью изоэнтропического уравнения для сжимаемых течений за ударной волной. Используя изоэнтропические соотношения, можно доказать, что при уменьшении числа Маха давление и плотность в двумерном потоке возрастают по сравнению с осесимметричным обтеканием сферы. Кроме того, плотность более чувствительна к изменению числа Маха по сравнению с давлением.

Рис. 6.

Сравнение давления на поверхности сферы и цилиндра.

4.2. Сверхзвуковое обтекание затупленной носовой части

Результаты, полученные в предыдущем тестовом случае, показывают, что давление и плотность на поверхности тела слабо различаются для сферы и цилиндра из-за небольшого эффекта бокового течения в этом случае. Для того, чтобы продемонстрировать потенциальные возможности предлагаемого численного метода для учета эффекта бокового течения в осесимметричной геометрии, было выполнено моделирование двумерного и осесимметричного течений с числом Маха, равным 2 вокруг затупленной носовой части с $\theta = 60^\circ ,{{R}_{b}} = 1~$ и Rn = 0.25 (детали геометрии см. на рис. 7). Распределения числа Маха и давления на поверхности тела имеют такой же характер, как в предыдущем случае. Причины более низкого уровня давления и плотности в осесимметричном случае по сравнению с двумерным моделированием, а также разница между распределениями числа Маха были полностью объяснены в предыдущем разделе (см. рис. 8). Однако результаты, полученные в настоящем случае, показывают, что параметры течения при двумерном и осесимметричном моделировании имеют бóльшие различия из-за бóльшего угла наклона тела (θ = 60°). Для двумерного и осесимметричного течений эти отличия составляют около 48 и 5% для числа Маха и давления соответственно.

Рис. 7.

Геометрия затупленной носовой части.

Рис. 8.

Сравнение давления на поверхности тела для двумерного и осесимметричного затупленного носика.

ЗАКЛЮЧЕНИЕ

Выведена новая форма сеточного уравнения Больцмана для численного моделирования сжимаемого невязкого течения около осесимметричных объектов. Из-за этих ограничений стандартный сеточный метод Больцмана с функцией распределения Максвелла справедлив только для несжимаемого течения. В настоящем исследовании подробно изложен новый вывод сеточного метода Больцмана для невязкого осесимметричного сжимаемого течения. Метод основывается на круговой функции, используемой для удаления ограничения стандартного сеточного метода Больцмана при моделировании сжимаемого сверхзвукового поля течения. Метод конечного объема и MUSCL алгоритм третьего порядка точности использованы в двумерных сетках с 13 компонентами скоростей для дискретизации новых полученных уравнений, чтобы точно учесть возможность присутствия ударных разрывов. Для проверки правильности предложенного метода, во-первых, было предпринято сеточное моделирование и, во-вторых, выполнен расчет сжимаемого осесимметричного сверхзвукового обтекания полусферической носовой части и затупленного под 60° тела. Сравнение полученных результатов с экспериментальными данными показало точность развитого численного алгоритма. Кроме того, чтобы продемонстрировать потенциальные возможности развитого численного метода для учета эффекта бокового течения около тел с осесимметричной геометрией, были сравнены результаты моделирования двумерного и осесимметричного сверхзвукового течений и дано убедительное объяснение относительно разной физической сущности этих течений.

Авторы заявляют об отсутствии конфликта интересов.

Список литературы

  1. Mohamad A.A. Lattice Boltzmann method. London: Springer, 2011. V. 70

  2. Hardy J., Pomeau Y., De Pazzis O. Time evolution of a two-dimensional model system. I. Invariant states and time correlation functions // Journal of Mathematical Physics. 1973. V. 14. № 12. P. 1746–1759.

  3. Frisch U., Hasslacher B., Pomeau Y. Lattice-gas automata for the Navier–Stokes equation // Physical review letters. 1986. V. 56. № 14. P. 1505.

  4. Liboff R.L. Kinetic theory: classical, quantum, and relativistic descriptions. Springer Science & Business Media, 2003.

  5. Chen H., Chen S., Matthaeus W.H. Recovery of the Navier-Stokes equations using a Lattice-gas Boltzmann method // Physical Review A. 1992. V. 45. № 8. P. R5339.

  6. Jalali H. Finite volume-lattice Boltzmann method in fluid flow simulation using curvilinear grid system with conformal mapping. Master’s thesis. Tehran: Faculty of Aerospace Engineering, Khaje Nasir-Al-Din Tusi University. 2014.

  7. Wei X., Li W., Mueller K., Kaufman A. Simulating fire with texture splats. In IEEE Visualization, 2002. VIS 2002. IEEE. P. 227–234.

  8. Liu Y. A lattice Boltzmann model for blood flows // Applied Mathematical Modelling. 2012. V. 36. № 7. P. 2890–2899.

  9. Third J.R., Chen Y., Müller C.R. Comparison between finite volume and lattice-Boltzmann method simulations of gas-fluidized beds: bed expansion and particle–fluid interaction force // Computational Particle Mechanics. 2016. V. 3. № 3. P. 373–381.

  10. Qu K., Shu C., Chew Y.T. Alternative method to construct equilibrium distribution functions in lattice-Boltzmann method simulation of inviscid compressible flows at high Mach number // Physical Review E. 2007. V. 75. № 3. P. 036706.

  11. Alexander F.J., Chen H., Chen S., Doolen G.D. Lattice Boltzmann model for compressible fluids // Physical Review A. 1992. V. 46. №. 4. P. 1967.

  12. Xu K. A gas-kinetic BGK scheme for the Navier–Stokes equations and its connection with artificial dissipation and Godunov method // Journal of Computational Physics. 2001. V. 171. № 1. P. 289–335.

  13. Li Q., He Y.L., Wang Y., Tao W.Q. Coupled double-distribution-function lattice Boltzmann method for the compressible Navier–Stokes equations // Physical Review E. 2007. V. 76. № 5. P. 056705.

  14. Sun C. Lattice-Boltzmann models for high speed flows // Physical review E. 1998. V. 58. № 6. P. 7283.

  15. He Y.L., Liu Q., Li Q. Three-dimensional finite-difference lattice Boltzmann model and its application to inviscid compressible flows with shock waves // Physica A: Statistical Mechanics and its Applications. 2013. V. 392. № 20. P. 4884–4896.

  16. Guangwu Y., Yaosong C., Shouxin H. Simple lattice Boltzmann model for simulating flows with shock wave // Physical review E. 1999. V. 59. № 1. P. 454.

  17. Shi W., Shyy W., Mei R. Finite-difference-based lattice Boltzmann method for inviscid compressible flows // Numerical Heat Transfer: Part B: Fundamentals. 2001. V. 40. № 1. P. 1–21.

  18. Qu K., Shu C., Chew Y.T. Lattice Boltzmann and finite volume simulation of inviscid compressible flows with curved boundary // Adv. Appl. Math. Mech. 2010. V. 2. № 5. P. 573–586.

  19. Guo Z., Han H., Shi B., Zheng C. Theory of the lattice Boltzmann equation: lattice Boltzmann model for axisymmetric flows // Physical Review E. 2009. V. 79. № 4. P. 046708.

  20. Halliday I., Hammond L.A., Care C.M., Good K., Stevens A. Lattice Boltzmann equation hydrodynamics // Physical review E. 2001. V. 64. № 1. P. 011208.

  21. Premnath K.N., Abraham J. Lattice Boltzmann model for axisymmetric multiphase flows // Physical Review E. 2005. V. 71. № 5. P. 056706.

  22. Mukherjee S., Abraham J. Lattice Boltzmann simulations of two-phase flow with high density ratio in axially symmetric geometry // Physical Review E. 2007. V. 75. № 2. P. 026701.

  23. Lee T.S., Huang H., Shu C. An axisymmetric incompressible lattice Boltzmann model for pipe flow // International Journal of Modern Physics C. 2006. V. 17. № 05. P. 645–661.

  24. Zhou J.G. Axisymmetric lattice Boltzmann method // Physical Review E. 2008. V. 78. № 3. P. 036701.

  25. Zhao-Li G., Chu-Guang Z., Bao-Chang S. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method // Chinese Physics. 2002. V. 11. № 4. P. 366.

  26. Zhang L., Yang S., Zeng Z., Yin L., Zhao Y., Chew J.W. Consistent lattice Boltzmann methods for incompressible axisymmetric flows // Physical Review E. 2016. V. 94. № 2. P. 023302.

  27. Zhang L., Yang S., Zeng Z., Chen J., Yin L., Chew J.W. Forcing scheme analysis for the axisymmetric lattice Boltzmann method under incompressible limit // Physical Review E. 2017. V. 95. № 4. P. 043311.

  28. Frapolli N., Chikatamarla S.S., Karlin I.V. Entropic lattice Boltzmann model for compressible flows // Physical Review E. 2015. V. 92. № 6. P. 061301.

  29. Chen Z., Shu C., Zhang L.Q. A simplified axisymmetric lattice Boltzmann method for incompressible swirling and rotating flows // Physics of Fluids. 2019. V. 31. № 2. P. 023605.

  30. Wu Q.F., Shu C., Wang Y., Yang L.M. An effective lattice Boltzmann flux solver on arbitrarily unstructured meshes // Modern Physics Letters B. 2018. V. 32. № 12n13. P. 1840012.

  31. Sun C., Hsu A.T. Three-dimensional lattice Boltzmann model for compressible flows // Physical Review E. 2003. V. 68. № 1. P. 016303.

  32. Kun Q. Development of lattice Boltzmann method for compressible flows (Doctoral dissertation), 2009.

  33. Van Dyke M., Gordon H.D. Supersonic flow past a family of blunt axisymmetric bodies, Vol. 1. US Government Printing Office, 1959.

  34. Anderson J.D. Fundamentals of Aerodynamics. Tata McGraw-Hill Education, 2010.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал