1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2019

Известия РАН. Механика жидкости и газа, 2019, № 6, стр. 99-113

ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ПОДВОДНОГО ОБТЕКАНИЯ ТОНКИХ ТЕЛ ПРИ НАЛИЧИИ ЕСТЕСТВЕННОЙ КАВИТАЦИИ

Нгуен Тат Тханг a, *, **, Дуонг Нгок Хай b, c, d

a Posts and Telecommunications Institute of Technology
Hanoi, 122-Hoang Quoc Viet, Vietnam

b Institute of Mechanics, Vietnam Academy of Science and Technology – VAST
Hanoi, 264-Doi Can, Vietnam

c Graduate University of Science and Technology – GUST, VAST
Hanoi, 18-Hoang Quoc Viet, Vietnam

d University of Engineering and Technology – UET, Vietnam National University – VNU
Hanoi, 144-Xuan Thuy, Vietnam

* E-mail: ntthang@imech.vast.vn
** E-mail: ntthang_imech@yahoo.com

Поступила в редакцию 09.11.2018
После доработки 20.03.2019
Принята к публикации 20.03.2019

Полный текст (PDF)

Аннотация

Важность кавитационных течений в высокоскоростной подводной гидродинамике обусловлена созданием благоприятного эффекта снижения сопротивления. Придание подходящей формы телу, погруженному в жидкость, может не только обеспечить устойчивость обтекания такого тела, но и максимально увеличить проходимое им расстояние. Для исследования динамики кавитационного течения и взаимодействия между телом и окружающей средой могут быть использованы как физический эксперимент, так и численное моделирование. На эту тему проведен ряд исследований, но влияние формы обтекаемого тела изучено недостаточно. В настоящей работе численно исследовано обтекание погруженных тел при наличии естественной кавитации. Тела отличаются формой и длиной кавитатора; рассматривается их стационарное обтекание. Исследование проводится в рамках модели двухфазной смеси, k–ε-модели турбулентности и модели кавитации Зварта–Гебера–Беламри (ЗГБ). Выполнено сравнение с опубликованными данными. Изучено обтекание различных тел при наличии естественной кавитации. Предложено модифицированное значение коэффициента сопротивления.

Ключевые слова: вычислительная гидромеханика, кавитация, двухфазные течения, подводное движение, высокоскоростное движение

Исследование явлений естественной кавитации и их возможных эффектов в технических и промышленных приложениях имеет долгую историю. Одно из главных негативных последствий этого явления состоит в эрозии твердых поверхностей в окрестности облака кавитационных пузырьков. Критическую роль в создании этого эффекта играет схлопывание пузырьков (см., например, [1, 2]). С другой стороны, эффект снижения сопротивления, связанный с наличием пузырька (пузырьков) вблизи погруженного тела, может быть технически полезен и привлекателен [3–6]. Очевидно, что кавитационные явления включают в себя весьма широкий круг самых сложных течений, включая двухфазные течения с тепломассопереносом [7]. Поэтому существуют важные побудительные причины для лучшего понимания, управления и применения таких течений.

Значительные успехи достигнуты в развитии численных методов решения задач о двухфазных течениях, как в целом, так и применительно к кавитационным явлениям. Численные методы моделирования этих сложных течений имеют такие важные общие характеристики, как аккуратное представление разрывов параметров течения при переходе через поверхности раздела фаз, что играет важную роль в получении надежных результатов [8–11]. В последнее время численное моделирование стало эффективным инструментом для детального изучения снижения сопротивления, обусловленного высокоскоростным кавитационным обтеканием погруженных тел.

При рассмотрении явлений естественной кавитации, когда твердое тело движется под водой с достаточно большой скоростью, давление в областях, примыкающих к телу, может упасть ниже давления насыщенного пара. В этих условиях пониженного давления может произойти естественное кипение. Вокруг тела образуется газовый карман, наполненный образовавшимся водяным паром. Такое течение известно как естественно-кавитационное течение. Если карман пара полностью покрывает тело, то эта область называется суперкаверной (см., например, [12, 13]). Наличие кавитации приводит к критическим эффектам в динамике тел, движущихся под водой с большой скоростью, и управлении ими.

В практике высокоскоростного движения погруженных тел важную роль могут играть режимы как частичной, так и суперкавитации. В первом из них поверхностное трение значительно ослабевает, поскольку тело находится в меньшем контакте с жидкой фазой, чьи плотность и вязкость значительно больше, чем у пара. Это может значительно повлиять на динамику течения при изменении скорости движения и совершении маневров. В суперкавитационном течении области пониженного давления еще более расширяются и паровой карман становится достаточно длинным, чтобы покрыть собой все тело. Соответственно суперкавитация минимизирует поверхностное трение. Именно в суперкавитационном режиме может быть реализовано высокоскоростное (или даже сверхзвуковое) подводное течение [12–15]. Оптимальный режим высокоскоростного движения тела под водой может быть реализован, лишь когда динамика и эффекты кавитации приняты во внимание и верно использованы.

Надлежащий выбор формы тела, движущегося под водой с большой скоростью, то есть высокоскоростного тонкого кавитатора, должен обеспечить не только устойчивое движение по прямолинейной траектории, но также довести до максимума расстояние, пройденное под водой при заданном расходе энергии. С этой целью для исследования кавитационного обтекания тел могут быть использованы физические эксперименты [12], аналитические аппроксимации [3, 16–18] и численное моделирование [10, 19, 20]. Выполнено некоторое количество исследований (см., например, [10, 12, 14–20]). Однако в доступной литературе мало данных о выборе формы тела и его влиянии. Экспериментальное исследование этого вопроса технически довольно затруднительно и затратно, особенно для случая высокоскоростных двухфазных кавитационных течений. Аналитические аппроксимации эффективны, но с их помощью трудно определить детали течений. Мощным инструментом детального исследования кавитационных течений является на сегодня численное моделирование.

Численный подход к моделированию кавитационных течений может быть основан на различных теоретических предпосылках, таких как одножидкостная модель, метод объемов жидкости (VOF, Volume оf Fluid), двух- или многожидкостная модели, комбинация одножидкостной модели и VOF и т.д. [21]. При моделировании частично или суперкавитационных течений достаточно точной и эффективной с вычислительной точки зрения представляется модель двухфазной смеси, основанная на одножидкостном приближении и уравнениях Навье–Стокса. Рассмотрение других недавно разработанных моделей, основанных на теории термодинамически совместимых систем гиперболических законов сохранения (см., например, [9, 22, 23]) окончательно и еще более детально обосновывает математическую корректность модели смеси, основанной на уравнениях Навье–Стокса. Модели, основанные на этих уравнениях, успешно применялись в предшествующих исследованиях кавитационных течений [24–26]. В связи с этим в настоящей работе для исследования динамики кавитационных течений и влияния различных конфигураций тел применен подход, основанный на уравнениях Навье–Стокса для двухфазных течений.

При исследовании кавитационных течений с помощью численного моделирования или аналитических аппроксимаций динамика течения и поведение каверны были рассчитаны для нескольких конкретных конфигураций тел [16, 19, 20]. Естественное кавитационное течение и принудительное кавитационное течение (то есть течение, искусственно созданное вдувом воздуха или иного газа в поток) были изучены, например, в [19, 20]. Для кавитаторов затупленной формы было выполнено сравнение частично и суперкавитационных режимов. В [16] частично кавитационное течение исследовано в зависимости от диаметра тела. Выяснение вопроса о влиянии формы кавитатора (полусферической, конической и т.д.) и/или длины тела, а также размера каверны на динамику течения требует дальнейших исследований. Предварительные результаты данного исследования были доложены на конференции, посвященной прогрессу в вычислительной механике. Обсуждение на конференции весьма способствовало улучшению настоящей работы [27].

До настоящего времени влияние формы погруженного тела на кавитацию рассматривалось как один из важнейших вопросов при управлении кавитационными течениями и уменьшении сопротивления тел. Надежная оценка поведения тела конкретной формы в различных реальных ситуациях (то есть при частично и суперкавитационном режимах течения) может быть получена на основе точных расчетов формы и размеров кавитационной каверны. Однако детальные исследования влияния формы тела в частично и суперкавитационном режимах течения до сих пор отсутствуют в литературе.

В настоящей работе, посвященной естественно-кавитационному высокоскоростному обтеканию погруженных тел, численное моделирование выполнено для тел нескольких форм. Они отличаются формой кавитатора и длиной тела. Проведено моделирование стационарного одно- и двухфазного кавитационного обтекания тел. Исследование частично- и суперкавитационных режимов обтекания выполнено в рамках модели двухфазной смеси с использованием модели турбулентности k–ε [28] и модели кавитации Зварта–Гебера–Беламри (ЗГБ) [29]. С целью валидации модели выполнены сравнения с опубликованными экспериментальными данными [30] и численными результатами [19, 20]. Исследован эффект измельчения вычислительной сетки. Оттестированная таким образом модель была применена для изучения динамики кавитационного обтекания тел.

1. ПОСТАНОВКА ЗАДАЧИ И ЧИСЛЕННЫЙ МЕТОД

При численном моделировании кавитационного течения используется одножидкостная модель смеси [24–26, 31, 32]. В этой модели две фазы (жидкость и пар) математически рассматриваются как взаимопроникающие континуумы. Такая модель смеси может быть развита для двух или более фаз; детали можно найти в работах [27, 33].

1.1. Основные уравнения для естественно-кавитационного течения

Уравнение неразрывности для смеси

Уравнение неразрывности для смеси (1.1) используется для расчета объемных долей фаз

(1.1)
$\frac{\partial }{{\partial t}}\left( {{{\rho }_{m}}} \right) + \nabla \left( {{{\rho }_{m}}{{{{\vec {v}}}}_{m}}} \right) = 0$

Здесь ${{{\vec {v}}}_{m}}$ и ${{\rho }_{m}}$ – среднемассовая скорость и плотность смеси соответственно.

Уравнение количества движения для смеси. Для расчета распределения скорости смеси используется уравнение количества движения смеси (1.2)

(1.2)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{\rho }_{m}}{{{{\vec {v}}}}_{m}}} \right) + \nabla \times \left( {{{\rho }_{m}}{{{{\vec {v}}}}_{m}}{{{{\vec {v}}}}_{m}}} \right) = - \nabla p + \nabla \times [{{{\mu }}_{m}}(\nabla {{{{\vec {v}}}}_{m}} + \nabla {\vec {v}}_{m}^{{ - T}})] + {{\rho }_{m}}{\vec {g}} + {\vec {F}} - \\ - \;\nabla \times \left( {\sum\limits_{{\text{k}} = 1}^{\text{n}} {{{\alpha }_{k}}{{\rho }_{k}}} {{{{\vec {v}}}}_{{{\text{dr,}}k}}}{{{{\vec {v}}}}_{{{\text{dr,}}k}}}} \right) \\ \end{gathered} $
где p – давление смеси, ${{{\mu }}_{m}}$ – вязкость смеси (${{{\mu }}_{m}} = \sum\nolimits_{k = 1}^n {{{\alpha }_{k}}{{{\mu }}_{k}}} $, где ${{{\mu }}_{k}}$ – молекулярная динамическая вязкость фазы k), ${\vec {g}}$ – ускорение свободного падения, ${\vec {F}}$ – массовая сила, ${{{\vec {v}}}_{{{\text{dr,}}k}}}$ – скорость дрейфа конкретной фазы (фазы k) и ${{\alpha }_{k}}$ – объемная доля фазы k.

Уравнение коррекции давления смеси. Распределение давления смеси рассчитывается итерациями на основе известного уравнения для коррекции давления. В этом подходе значения скорости и давления корректируются так, чтобы было удовлетворено уравнение неразрывности; детали можно найти в работах [27, 33].

1.2. Модель кавитации

В настоящей работе используется ЗГБ модель кавитации; она менее чувствительна к возмущениям и легче в управлении, чем другие известные модели (см., например, [38, 39]).

Уравнение для объемной доли пара – уравнение переноса пара. Массоперенос жидкости и пара, т.е. процессы испарения и конденсации, описывается уравнением переноса пара (1.3)

(1.3)
$\frac{\partial }{{\partial t}}\left( {{{\alpha }_{k}}{{{\rho }}_{k}}} \right) + \nabla \times \left( {{{\alpha }_{k}}{{{\rho }}_{k}}{{{{\vec {v}}}}_{m}}} \right) = - \nabla \times \left( {{{\alpha }_{k}}{{{\rho }}_{k}}{{{{\vec {v}}}}_{{{\text{dr,}}k}}}} \right) + {{\dot {m}}_{{kl}}} - {{\dot {m}}_{{lk}}}$
где индексы k и l относятся к фазам пара и жидкости двухфазной жидкости соответственно, а ρk – плотность фазы k. Описывающие массоперенос члены ${{{\dot {m}}}_{{kl}}}$ (конденсация) и ${{\dot {m}}_{{lk}}}$ (испарение) моделируются на основе уравнения Рэлея–Плессета динамики пузырьков; детали можно найти в работах [27, 33].

ЗГБ-модель кавитации. Модель кавитации ЗГБ описывается уравнениями (1.4), (1.5) для членов, определяющих массоперенос в уравнении переноса пара. Уравнение (1.4) записано для испарения (т.е., p ≤ ${{p}_{{v}}}$, где ${{p}_{{v}}}$ – давление пара), а уравнение (1.5) записано для конденсации (p ≥ ${{p}_{{v}}}$).

(1.4)
${{\dot {m}}_{{lk}}} = {{F}_{{vap}}}3{{\alpha }_{{nuc}}}\left( {1 - {{\alpha }_{{v}}}} \right){{\rho }_{{v}}}{\text{/}}{{R}_{b}}\sqrt {\frac{2}{3}\frac{{({{p}_{{v}}} - p)}}{{{{\rho }_{l}}}}} $
(1.5)
${{\dot {m}}_{{kl}}} = {{F}_{{cond}}}3{{\alpha }_{{v}}}{{\rho }_{{v}}}{\text{/}}{{R}_{b}}\sqrt {\frac{2}{3}\frac{{(p - {{p}_{{v}}})}}{{{{\rho }_{l}}}}} $

Здесь Rb – радиус кавитационного пузырька. Более подробные данные о параметрах модели Rb, Fvap, αnuc и Fcond можно найти в работах [27, 33].

1.3. Формы тел, расчетная область и граничные условия.

Формы и длины тел

Рассматривались четыре тела в виде круговых цилиндров с различными формами кавитатора (рис. 1). Диаметры всех тел одинаковы: dbody = 6.6 мм. Рассматривались три длины тел Lbody = 50, 100 и 150 мм.

Рис. 1.

Тела с кавитаторами различных форм

Расчетная область. Пример расчетной области для тел с длиной 100 мм приведен на рис. 2. При исследовании естественно-кавитационных течений можно принять, что поле течения около тела симметрично и проводить расчет лишь в половине области.

Рис. 2.

Двумерная расчетная область для тела длиной 100 мм с полусферическим кавитатором (для тел иной длины расстояние от кормы тела до выходной границы меняется в соответствии с длиной тела; AB (и DC), BC и расстояния от кавитатора до входной границы остаются неизменными, т.е. 100, 700 и 100 мм соответственно)

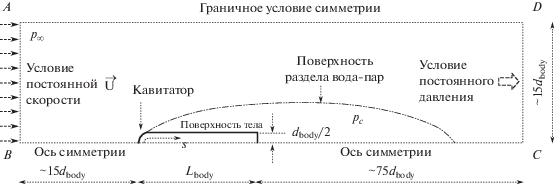
Основываясь на опубликованных данных (см., например, [32, 40]), выбор размера расчетной области, окружающей обтекаемое тело (рис. 2), можно считать обоснованным. Помимо того, исследования по зависимости результатов моделирования обтекания погруженных тел от размера расчетной области [41, 42] показали, что минимальное расстояние от поверхности погруженного тела до внешней границы в поперечном направлении должно быть не менее 15–20 диаметров тела. Выбранные в этой работе размеры расчетной области удовлетворяют этому требованию.

Граничные условия и параметры задачи

На границе AB, вдоль которой втекает поток жидкости, используется условие постоянной скорости. На выходной границе DC используется условие постоянного статического (гидростатического) давления. На оси симметрии ставится граничное условие симметрии. На границе AD, где течение можно считать невозмущенным, также ставится условие симметрии. Остальные условия задачи таковы. Двухфазная смесь состоит только из жидкости (воды) и ее пара. Рабочее давление полагается равным давлению окружающей среды (атмосферному давлению) плюс гидростатическое давление на глубине погруженного тела (в настоящей работе 1 м). В модели кавитации значение давления насыщенного пара принимается равным 2338 Па. Опорное давление, которое требуется лишь на этапе постобработки данных для вычисления коэффициента давления Cp, полагается равным нулю. Детали постановки граничных условий можно найти в [27, 33].

1.4. Расчетная сетка и численная дискретизация основных уравнений

Расчетная сетка

Расчетная область дискретизируется разбиением на структурированные четырехсторонние ячейки (элементы), как показано на рис. 3 для случая тела длиной 100 мм с оживальным кавитатором, длина которого равна диаметру тела. Детали процесса построения сетки можно найти в [27].

Рис. 3.

Часть двумерной расчетной сетки вокруг тела длиной 100 мм с оживальным кавитатором, длина которого равна диаметру тела

Численная дискретизация основных уравнений. Основные уравнения решались численно методом конечных объемов. Использован алгоритм корректировки давления. Давление на гранях ячеек рассчитывалось по значениям массовой силы. Уравнения переноса количества движения и турбулентности дискретизировались по противопоточной схеме второго порядка. Для численного решения уравнения объемной доли (т.е. уравнения переноса пара) использована схема QUICK (Quadratic Upstream Interpolation for Convective Kinematics). Для расчета ячеек, примыкающих к поверхности тела, использовалась модель турбулентности Realizable k–ε с улучшенной аппроксимацией в окрестности стенки. Более подробное описание включения в модель различных физических эффектов, таких как сила тяжести, поверхностное натяжение и др., можно найти, например, в [43].

1.5. Валидация модели для тел с тупым, коническим, сферическим и оживальным кавитаторами

Экспериментальные и численные данные для валидации модели

Модель стационарного естественно-кавитационного обтекания четырех рассмотренных тел была реализована численно. Для валидации модели использованы данные работ [19, 20], в которых содержатся данные для тех же четырех форм тел. В них приводятся экспериментальные и численные зависимости безразмерного параметра, а именно, коэффициента давления Cp = = $({{p}_{{local}}} - {{p}_{\infty }}){\text{/}}(0.5{{\rho }_{l}}{{U}^{2}})$ от безразмерной длины дуги вдоль поверхности тела s/dc (рис. 2). Здесь plocal – местное статическое давление на поверхности тела, p∞ – статическое давление в дальнем поле, ρl – плотность жидкой фазы, U – скорость набегающего потока, s – длина дуги, dc – диаметр кавитатора (для кавитаторов четырех рассмотренных типов dc = dbody, как показано на рис. 2). Данные по Cp были получены при различных значениях числа кавитации $\sigma = ({{p}_{\infty }} - {{p}_{c}}){\text{/}}(0.5{{\rho }_{l}}{{U}^{2}})$, как показано в табл. 1 для случая частично кавитационного течения, когда каверна замыкается на теле. В этом случае величина σ сравнительно велика (σ > 0.1). Помимо того, выполнено сравнение со случаем однофазного течения. Здесь pc – давление в каверне. В естественно-кавитационном течении это также давление насыщенного пара (рис. 2).

Таблица 1.

Число кавитации и скорость набегающего потока при моделировании частично-кавитационного и однофазного течений [19, 20]

σ 0.20 0.24 0.30 0.32 0.40 0.46 0.50 Однофазное
U [м/с] 32.81 29.95 26.79 25.94 23.20 21.64 20.75 5.00

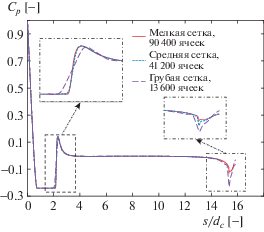
Измельчение сетки. Для оценки эффекта измельчения расчетной сетки для всех тел были выполнены расчеты на сетках с тремя различными разрешениями (грубой, средней и мелкой). Грубые сетки насчитывали примерно 14 000 вычислительных ячеек для всех форм кавитатора и длин тел. Средние сетки имели примерно 42 000 ячеек, а мелкие сетки около 91 000 ячеек. Безразмерное расстояние первой сеточной точки от стенки, т.е. значение координаты стенки (или единица стенки [33]) y+ для всех вариантов сетки равно приблизительно 1. Для краткости рассчитанные распределения коэффициента давления Cp вдоль оси тела, которая продлена далее в область следа, приведены на рис. 4 для оживального тела длиной 100 мм и длиной оживала, равной диаметру тела. В остальных случаях полученные результаты почти идентичны представленным на рис. 4. Расчеты проведены при одном и том же значении числа кавитации σ = 0.24 (U = 30 м/с), что соответствует частично-естественно-кавитационному обтеканию тела длиной 100 мм. Как показано на рис. 4, различие между результатами, полученными на трех различных сетках, пренебрежимо мало, за исключением областей следа (т.е. области замыкания каверны и области следа за кормой тела). Различия между результатами, полученными на средней и мелкой сетках, также пренебрежимо мало, что показывает увеличенный фрагмент на рис. 4. В связи с этим в дальнейших исследованиях использовалась средняя сетка.

Рис. 4.

Влияние измельчения сетки (s/dc – безразмерная длина дуги s на рис. 2)

Сравнение результатов. Пример результатов расчетов приведен на рис. 5 для тела с тупым кавитатором. Для всех четырех тел результаты исследований, представленные в безразмерном виде, сравниваются с экспериментальными данными, взятыми из [30], и численными результатами из [19]. Опубликованные данные были получены как для однофазного, так и двухфазного кавитационных течений. Результаты сравнения для всех форм кавитатора [27] показывают, что численные результаты, полученные в настоящей работе, близки к опубликованным данным.

Рис. 5.

Сравнение распределений коэффициента давления Cp для четырех тел (s/dc – безразмерная длина дуги s)

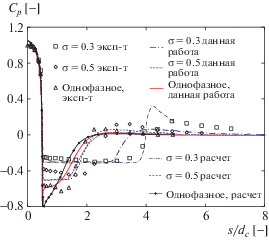
Результаты сравнения для трех остальных форм кавитатора содержатся в работе [27]. Очевидно, что результаты валидации модели указывают на то, что вычислительная модель, принятая в данной работе, пригодна для дальнейших исследований кавитационного обтекания четырех рассмотренных тел. Использование принятых схем дискретизации, модели кавитации ЗГБ, сеточных параметров, граничных условий оправдано.

2. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

2.1. Условия моделирования

Формы и длины тел

Для изучения влияния формы кавитатора на режимы частично- и суперкавитационного течения рассмотрены четыре типичных формы кавитатора, представленные на рис. 1.

Установление режима частичной или суперкавитации зависит от длины тела. При заданной длине тела суперкавитационный режим течения сменится частично кавитационным режимом, если длина тела превзойдет текущую длину суперкаверны. Для изучения эффекта длины тела моделирование было выполнено для трех длин, 50, 100 и 150 мм для каждой формы кавитатора. Для каждой длины расчеты проведены в некотором диапазоне чисел кавитации. Этот диапазон симметричен относительно числа кавитации перехода, т.е. значения σ, соответствующего переходу от режима частичной кавитации к режиму суперкавитации.

Условия обтекания. Для тел всех длин и форм рабочие условия были одинаковы. Менялась лишь скорость набегающего потока U, что соответствовало изменению числа кавитации. В табл. 2 представлены рассмотренные диапазоны U и чисел кавитации для тупого кавитатора при всех длинах тела. Затененные клетки в таблице соответствуют условиям частично-кавитационного течения (по соотношению между длиной каверны и длиной тела), а остальные клетки соответствуют условиям суперкавитации. Что касается условий обтекания трех других форм кавитатора, они могут быть найдены в работе [27].

Таблица 2.

Число кавитации и скорость набегающего потока при обтекании тупого кавитатора для тел с тремя различными длинами

σ, 50 мм 0.086 0.094 0.102 0.111 0.117 0.122 0.128 0.135 0.142 0.149 0.158 0.166 0.187 0.211 0.240
U [м/с], 50 мм 50 48 46 44 43 42 41 40 39 38 37 36 34 32 30
σ, 100 мм 0.060 0.064 0.069 0.074 0.077 0.080 0.083 0.086 0.090 0.094 0.098 0.102 0.111 0.122 0.135
U [м/с], 100 мм 60 58 56 54 53 52 51 50 49 48 47 46 44 42 40
σ, 150 мм 0.050 0.053 0.056 0.060 0.062 0.064 0.066 0.069 0.071 0.074 0.077 0.080 0.086 0.094 0.102
U [м/с], 150 мм 66 64 62 60 59 58 57 56 55 54 53 52 50 48 46

2.2. Обсуждение результатов

Форма и размер каверны

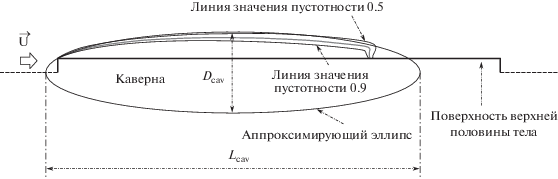
Вычисления были проведены при вышеописанных условиях. Сходимость вычислений удовлетворялась. После каждого расчета определялась область каверны, ограниченная линией, соответствующей значению пустотности 0.5. Данное значение критерия выбрано таким же, как и в численном исследовании кавитационного течения в работе [19]. Длина Lcav и диаметр Dcav каверны, показанные на рис. 6, определялись затем, следуя опять-таки подходу, представленному в [19]. В настоящей работе Lcav и Dcav представляют собой большую и малую оси эллипса, имеющего те же оси симметрии, что и тело. Эллипс проходит через точку отрыва потока и точку на линии, соответствующей значению пустотности 0.5, наиболее удаленной от твердой стенки (т.е. боковой поверхности тела) (рис. 6).

Рис. 6.

Форма, длина и диаметр каверны для тела длиной 100 мм с тупым кавитатором; σ = 0.111; U = 44 м/с

На рис. 7 результаты численных расчетов величин Lcav и Dcav (обезразмеренных по dc) в случае тупого кавитатора построены в зависимости от числа кавитации. Результаты моделирования для кавитаторов других форм содержатся в работе [27]. На рисунке численные данные (обозначенные CFD) приведены для режимов частичной и суперкавитации. Кроме того, на рисунке представлены результаты расчета длины и диаметра каверны по теоретическим зависимостям из [44]. Эти зависимости имеют следующий вид

(2.1)
${{L}_{{{\text{cav}}}}} = ({{d}_{c}}{\text{/}}\sigma )\sqrt {{{C}_{D}}\ln (1{\text{/}}\sigma )} $
(2.2)
${{D}_{{{\text{cav}}}}} = {{d}_{c}}\sqrt {{{C}_{D}}{\text{/}}\sigma } $
где CD = CD0 × (1 + σ) – коэффициент сопротивления. Эта зависимость CD от CD0 и σ очень точно следует экспериментальным данным, полученным для дискового кавитатора. CD0 есть коэффициент сопротивления, соответствующий σ = 0 для всех четырех форм кавитатора [12]. В табл. 3 приведены значения CD0, использованные при анализе в данной работе.

Рис. 7.

Безразмерные длина Lcav/dc (а) и диаметр Dcav/dc (б) каверны как функции числа кавитации (для тупого кавитатора)

Таблица 3.

Коэффициент CD0 для каждого типа кавитатора

  Тупой Полусферический Конический Оживальный
CD0 (предыдущие работы) 0.815 [12], 0.827 [44–48], 0.820 [49] 0.255–0.266 [12] 0.225 [12] 0.114, 0.195 и 0.22 [12]
CD0 (данная работа) 0.815 0.329 0.293 0.245

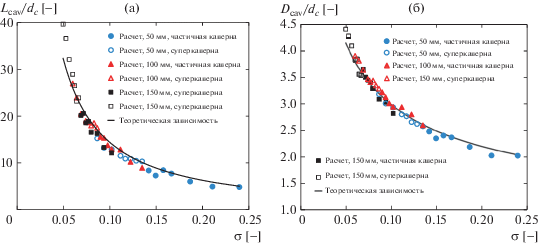
Как можно видеть на рис. 7а и 7б, в большей части диапазона числа кавитации σ длина и диаметр каверны находятся в хорошем соответствии с теоретическими формулами. Однако в случае суперкавитационного обтекания тела длиной 150 мм с тупым кавитатором их значения начинают отклоняться от теоретических. Причина этого заключается в первую очередь в неблагоприятном влиянии пространственной (сеточной) дискретизации на рассчитанную линию равной пустотности. Чем длиннее каверна, тем более очевиден этот неблагоприятный эффект. Контур становится более плоским по отношению к максимальной ширине каверны. Соответственно возрастает неопределенность в определении размеров каверны, что и показывает рис. 6.

В целом численные зависимости безразмерных длины и диаметра полости от числа кавитации находятся в хорошем соответствии с теоретическими зависимостями [44]. Размеры каверны, рассчитанные в рамках модели, прошедшей, в соответствии с описанным выше, валидацию, вполне надежны, по крайней мере, для рассмотренных условий обтекания и конфигураций тел. Это подтверждает тот факт, что рассчитанные результаты правильно отображают поведение естественно-кавитационного обтекания тел.

Для каждой формы кавитатора расчеты были проведены в режимах частично и суперкавитационного обтекания тел трех разных длин. Как отмечается выше, суперкавитационное обтекание тела заданной длины становится частично кавитационным при увеличении длины тела. Примером этому служат условия обтекания, указанные в табл. 2. В диапазоне скоростей от 40 до 48 м/с обтекание тела длиной 50 мм при тупом кавитаторе является суперкавитационным, но в том же диапазоне скоростей обтекание такого же тела длиной 100 мм оказывается частично кавитационным.

Физически существует различие между полями течения в области замыкания каверны в частично и суперкавитационном режимах течения. Полученные численно результаты показывают, что частичная каверна меньше, чем суперкаверна. Такое поведение менее заметно, чем в случае кавитационного течения при входе в воду [47, 48]. В целом же результаты расчеты для обоих режимов (частично и суперкавитационного течения) находятся в хорошем соответствии с общей тенденцией, предсказываемой теоретическими зависимостями [44].

Соотношение между частичной и суперкавитацией при одних и тех же значениях числа кавитации, но для тел разной длины. Как показано на рис. 8, для более детального анализа поведения кавитационного течения при одних и тех же значениях числа кавитации, но для тел разной длины области перехода от одного режима к другому даны в увеличенном масштабе. В этих областях обтекание более короткого тела происходит в суперкавитационном режиме, а обтекание более длинного тела происходит в частично кавитационном режиме. Помимо того, на рисунках для каждого набора данных приводятся аппроксимации степенными функциями (графики построены в логарифмических (по основанию 10) переменных).

Рис. 8.

Величины Lcav/dc (а) и Dcav/dc (б) в зависимости от числа кавитации: соотношение между частичной кавитацией и суперкавитациейа)

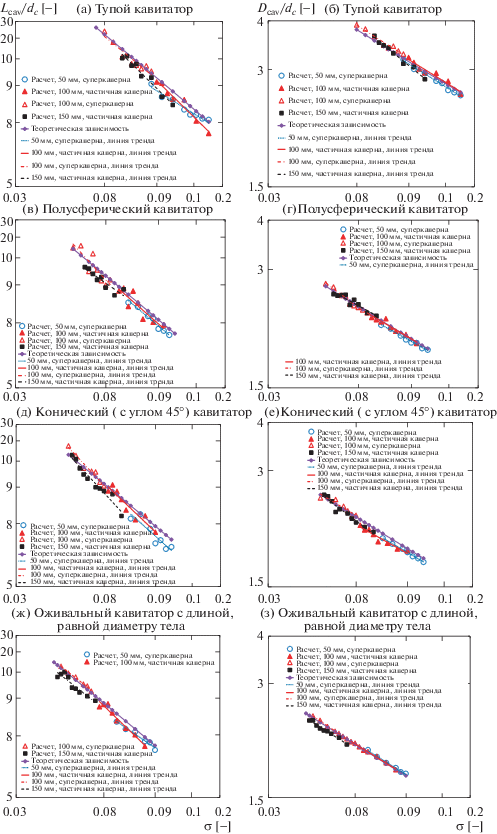
На рис. 8а и 8б приведены данные для случая тупого кавитатора. При рассмотренных условиях обтекания и спецификациях модели результаты расчетов, представленные на этих двух рисунках, позволяют сделать вывод, что различие между длинами частичной каверны и суперкаверны становится заметным лишь при малых числах кавитации. При этом ширина каверны приблизительно одинакова в обоих режимах обтекания.

Аналогичным образом, результаты расчетов, приведенные на рис. 8в, г и 8д, 8е для тел с полусферическим и коническими кавитаторами, соответственно, демонстрируют то же поведение, что и в случае тел с тупым кавитатором (рис. 8а, 8б). Так, различие в длине каверны в двух режимах обтекания для всех указанных трех конфигураций зависит лишь от числа кавитации. Ширина каверны остается почти одинаковой.

Однако результаты расчетов для тела с оживальным кавитатором, приведенные на рис. 8ж, 8з, показывают, что в этом случае различие между длиной и шириной каверны в двух режимах обтекания имеет место лишь при малых числах кавитации. Как длина, так и ширина каверны зависят от числа кавитации.

В целом, как можно видеть на рис. 8, в исследованных диапазонах чисел кавитации для рассмотренных тонких тел результаты расчетов размеров суперкаверны хорошо совпадают с теоретическими зависимостями [44]. Заметим, что теоретические зависимости выведены для суперкавитационного течения. Согласование результатов лучше для нижней половины диапазона чисел кавитации (приблизительно от 0.08 до 0.09 для тел с тупым кавитатором и от 0.05 до 0.08 для других тел).

С увеличением длины тела суперкавитация переходит в частичную кавитацию, если число кавитации (то есть, скорость потока) фиксировано. В нижней части диапазонов размеры частичной каверны меньше, чем у суперкаверны. Это соответствует аналитическим результатам, полученным в [16] для естественно-кавитационного течения, и экспериментальным результатам, полученным в [48] для кавитационного течения при входе в воду.

Однако в верхних половинах исследованных диапазонов изменения величины σ ситуация не вполне ясная. В некоторых случаях размеры частичной каверны оказываются даже несколько больше. Заметим, что при больших значениях σ из исследованных диапазонов результаты численного моделирования также указывают на то, что размеры суперкаверны несколько меньше, чем теоретическое значение. Это справедливо для большинства случаев, представленных на рис. 8. Следовательно, основываясь на результатах моделирования настоящей работы и литературных данных (см., например, [16, 48]), касающихся аналогичных тонких тел, можно заключить, что увеличение размера суперкаверны может быть достигнуто путем уменьшения длины тела. Более конкретно такое поведение наблюдается в нижней половине исследованных диапазонов величины σ, как показано на рис. 8.

Зависимость частично и суперкавитационного режимов течения от длины тела. Согласно результатам численного моделирования, критическое значение числа кавитации σc, определяющее существование суперкавитационного режима обтекания тела, непосредственно зависит от длины тела. Физически σc убывает с увеличением длины тела. Результаты моделирования, выполненного в данной работе, дают более четкое количественное представление об этой зависимости, чем обычно содержится в опубликованных работах, где утверждается, что суперкавитационный режим обтекания обычно наступает, когда σ менее, чем 0.1 (см., например, [13]).

На рис. 9a для четырех исследованных конфигураций тонких тел видно, что кривые зависимости σc от длины тела хорошо аппроксимируются степенными функциями. Анализ этих приближенных степенных зависимостей показывает, что суперкавитационный режим обтекания имеет место в широком диапазоне длин тел, если

Рис. 9.

Изменение критического числа кавитации σc с длиной тела (а) и коэффициент сопротивления CD0 (б)

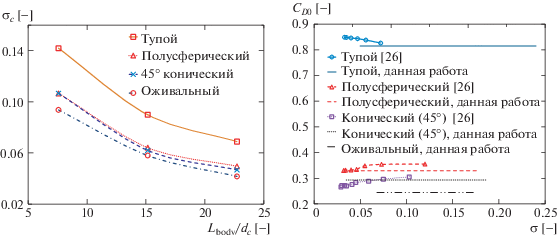
– σ менее, чем 0.015 (для тел с тупым кавитатором);

– σ менее, чем 0.01 (для других кавитаторов, рассмотренных в работе).

В этих случаях безразмерная длина тела, при которой осуществляется суперкавитационный режим течения, может достигнуть примерно 250. Заметим, что в практических приложениях проектируемые погруженные тела не слишком длинны. Поэтому большинство конфигураций могут попасть в указанный диапазон длин.

Коэффициент сопротивления. Результаты моделирования данной работы, так же как и результаты, содержащиеся в опубликованной литературе, подтверждают тот известный факт, что тела с тупым кавитатором образуют наиболее обширные каверны. Как следует из теоретических зависимостей (уравнения (2.1) и (2.2) и [44]), различие в размерах каверны при одном и том же числе кавитации (при разных формах кавитатора и одной и той же длине тела) зависит только от коэффициента сопротивления CD, который, в свою очередь, зависит от CD0. Значения CD0, принятые в настоящей работе для каждой формы кавитатора, приведены в табл. 3. Эти значения получены сопоставлением рассчитанных размеров каверн со значениями, полученными на основе уравнений (2.1) и (2.2). Заметим, что теоретические значения зависят от CD0. Меняя CD0 и используя процесс оптимальной подгонки, можно получить наиболее адекватные значения этого коэффициента, которые и приведены в табл. 3.

Как следует из табл. 3, тупой форме кавитатора соответствует наибольшее значение коэффициента сопротивления CD0. Для трех остальных форм кавитатора значения CD0 значительно меньше. Полученное в данной работе значение CD0 для тупого кавитатора, равное 0.815, практически совпадает со значениями, полученными ранее в работах [12, 44–46, 49]. Для трех остальных форм кавитатора при использовании значений CD0 из табл. 3 численные расчеты хорошо коррелируют с теоретическими зависимостями. Однако эти три значения не очень хорошо согласуются со значениями, приводимыми в литературе. Так, в [12] значения CD0 приблизительно равны 0.259, 0.243 и 0.2 для полусферического, конического (45°) и оживального кавитаторов соответственно.

Отмеченные расхождения следует приписать экспериментальным условиям, которые могут отличаться в различных работах. Более того, экспериментальные данные были получены в гидродинамических трубах. Ограниченность потока в трубах также может быть причиной такого расхождения [50]. Напротив, такой эффект отсутствует при численном моделировании неограниченных течений, которые имеют место в практических ситуациях.

Для дальнейшего подтверждения результатов по коэффициенту сопротивления и сделанных выше замечаний заметим, что значение коэффициента сопротивления CD0, приведенное в недавно опубликованной работе [26] и показанное на рис 9б, очень близко к значениям, полученным в данной работе. В [26] CD0 также получено численным моделированием естественно-кавитационного неограниченного течения. Моделирование в [26] также выполнено для трех форм кавитатора (тупой, полусферической и конической с углом 45°).

Таким образом, значения CD0, предложенные в табл. 3, наилучшим образом подходят для рассмотренных конфигураций и условий кавитационного течения.

ЗАКЛЮЧЕНИЕ

Численно исследовано высокоскоростное кавитационное обтекание тел различных форм, погруженных в воду. Тела представляют собой круговой цилиндр диаметром 6.6 мм и имеют кавитаторы различных форм. Именно, это тупой, полусферический, конический (с углом 45°) и оживальный (с длиной равной диаметру) кавитаторы. Для каждой формы кавитатора исследования проведены для трех длин тел (50, 100 и 150 мм). Рассмотрены частично и суперкавитационные режимы течений.

Выполнено моделирование стационарного однофазного и двухфазного кавитационного обтекания тел. Использованы хорошо известная модель двухфазной среды и модель турбулентности Realizable k–ε. Процесс кавитации рассчитывался на основе модели Зварта–Гебера–Беламри. Исследован эффект измельчения расчетной сетки. На основе исследования выбрано подходящее сеточное разрешение. С целью валидации вычислительной модели рассчитанное значение коэффициента сопротивления сравнивалось с экспериментальными и численными данными, имеющимися в опубликованной литературе. При этом имело место хорошее согласование результатов, что подтверждает точность результатов, полученных в данной работе.

Расчеты были выполнены для режимов частично и суперкавитационного обтекания тел. Проведенный анализ полученных результатов позволил сделать следующие выводы, в том числе касающиеся новых обнаруженных данных.

– Для кавитаторов всех типов рассчитанные размеры каверны хорошо согласуются с имеющимися теоретическими зависимостями в режимах как частично, так и суперкавитационного обтекания.

– Для кавитаторов всех типов исследовано влияние длины тела на поведение течения, т.е. на размеры каверны. При фиксированном числе кавитации частичная каверна, созданная более длинным телом, оказывается меньше, чем суперкаверна, созданная более коротким телом. Для тупого кавитатора этот эффект проявляется в примерном диапазоне от 0.08 до 0.09. Для других тел этот диапазон простирается от 0.05 до 0.08. Это поведение менее заметно, чем в случае кавитационного течения при горизонтальном входе в воду. В диапазонах высоких чисел кавитации указанное поведение не имеет места.

– При увеличении длины тела критическое значение числа кавитации, соответствующее зарождению суперкавитации, убывает, что соответствует увеличению скорости потока. Для исследованных тел с тупым кавитатором минимальное значение числа кавитации, равное 0.015, обеспечивает наличие суперкавитации в широком диапазоне безразмерной длины тела (примерно до 250). В случаях полусферического, конического и оживального кавитаторов соответствующее минимальное число кавитации равно 0.01.

– Для исследованных условий течения и для кавитатора каждого типа предложено модифицированное значение коэффициента сопротивления. Этот результат может быть при расчете сопротивления тонких тел, движущихся под водой с большой скоростью.

Работа выполнена при частичной финансовой поддержке научно-исследовательского проекта NCVCC42.02/19-19.

Список литературы

  1. Быковцев Г.И., Разаренов Г.С. О пульсации сферического пузырька в несжимаемой жидкости // Изв. РАН. МЖГ. 1975. № 2. С. 153–155.

  2. Георгиевский Д.В. Схлопывание кавитационного пузырька в нелинейно-вязких и вязкопластических средах // Изв. РАН. МЖГ. 1994. № 2. С. 181–184.

  3. Гонор А.Л., Забутная В.И., Ясько Н.Н. О существовании оптимального кавитатора // Изв. РАН. МЖГ. 1991. № 2. С. 63–68.

  4. Murai Y., Fukuda H., Oishi Y., Kodama Y., Yamamoto F. Skin friction reduction by large air bubbles in a horizontal channel flow // Int. J. Multiphase Flow. 2007. V. 33. № 2. P. 147–163.

  5. Ceccio S.L. Friction drag reduction of external flows with bubble and gas injection // Annu. Rev. Fluid Mech. 2010. V. 42. P. 183–203.

  6. Karn A., Arndt R.E., Hong J. An experimental investigation into the physics of supercavity closure // J. Fluid Mech. 2015. V. 789. P. 259–284.

  7. Нигматулин Р.И. Динамика многофазных сред. Часть 1. М.: Наука, 1987. 464 с. Часть 2. М.: Наука, 1987. 360 с.

  8. Shyue K.M. A fluid-mixture type algorithm for compressible multicomponent flow with van der Waals equation of state // J. Comput. Phys. 1999. V. 156. № 1. P. 43–88.

  9. Zeidan D. Numerical resolution for a compressible two-phase flow model based on the theory of thermodynamically compatible systems // Appl. Math. Comput. 2011. V. 217. № 11. P. 5023–5040.

  10. Saurel R., Boivin P., Le Métayer O. A general formulation for cavitating, boiling and evaporating flows // Computers Fluids. 2016. V. 128. P. 53–64.

  11. Fechter S., Munz C.D., Rohde C., Zeiler C. A sharp interface method for compressible liquid–vapor flow with phase transition and surface tension // J. Comput. Phys. 2017. V. 336. P. 347–374.

  12. May A. Water entry and the cavity-running behavior of missiles // SEAHAC Technical Report № 75-2 (Naval Surface Weapons Center, White Oak Laboratory, Silver Spring, MD, 1975).

  13. Franc J.P., Michel J.M. Fundamentals of cavitation. Springer, 2006.

  14. Vanek B. Control methods for high-speed supercavitating vehicles // Ph.D. Thesis (University of Minnesota, 2008).

  15. Truscott T.T., Brenden P.E., Jesse Belden. Water entry of projectiles // Annu. Rev. Fluid Mech. 2014. V. 46. P. 355–378.

  16. Varghese A.N., Uhlman J.S., Kirschner I.N. Numerical analysis of high-speed bodies in partially cavitating axisymmetric flow // J. Fluids Eng. 2005. V. 127. № 1. P. 41–54.

  17. Rashidi I., Passandideh-Fard M. The optimum design of a cavitator for high-speed axisymmetric bodies in partially cavitating flows // J. Fluids Eng. 2013. V. 135. № 1. P. 011301-1–011301-12.

  18. Nouroozi M., Pasandidehfard M., Djavareshkian M.H. Simulation of partial and supercavitating flows around axisymmetric and quasi-3D bodies by boundary element method using simple and reentrant jet models at the closure zone of cavity // Math. Probl. Eng. Paper № 1593849 (2016).

  19. Kunz R.F., Boger D.A., Stinebring D.R., Chyczewski T.S., Lindau J.W., Gibeling H.J., Sankaran V., Govindan T.R. A preconditioned Navier–Stokes method for two-phase flows with application to cavitation prediction // Computers Fluids. 2000. V. 29. № 8. P. 849–875.

  20. Kunz R.F., Lindau J.W., Billet M.L., Stinebring D.R. Multiphase CFD modeling of developed and supercavitating flows. Pennsylvania State University, University Park Applied Research Lab., 2001.

  21. Hsiao C.T., Ma J., Chahine G.L. Multiscale two-phase flow modeling of sheet and cloud cavitation // Int. J. Multiphase Flow. 2017. V. 90. P. 102–117.

  22. Romenski E., Resnyansky A., Toro E.F. Conservative hyperbolic formulation for compressible two-phase flow with different phase pressures and temperatures // Quart. Appl. Math. 2007. V. 65. № 2. P. 259–279.

  23. Peshkov I., Romenski E. A hyperbolic model for viscous Newtonian flows // Continuum Mech. Therm. 2016. V. 28. № 1–2. P. 85–104.

  24. Kim D.H., Park W.G., Jung C.M. Numerical simulation of cavitating flow past axisymmetric body // Int. J. Nav. Arch. Ocean Eng. 2012. V. 4. № 3. P. 256–266.

  25. Paik K.J., Park H.G., Seo J. RANS simulation of cavitation and hull pressure fluctuation for marine propeller operating behind-hull condition // Int. J. Nav. Arch. Ocean Eng. 2013. V. 5. № 4. P. 502–512.

  26. Yang D., Xiong Y.L., Guo X.F. Drag reduction of a rapid vehicle in supercavitating flow // Int. J. Nav. Arch. Ocean Eng. 2017. V. 9. № 1. P. 35–44.

  27. Nguyen T.T., Duong H.N., Nguyen T.Q., Kikura H. CFD simulations of the natural cavitating flow around high-speed submerged bodies // Int. Conf. Advances Comput. Mech. 2017, ACOME 2017, Lecture Notes in Mech. Eng., Ed. by H. Nguyen-Xuan, P. Phung-Van, and T. Rabczuk (Springer, Singapore, 2018). P. 851–873.

  28. Shih T.H., Liou W.W., Shabbir A., Yang Z., Zhu J. A new eddy-viscosity model for high Reynolds number turbulent flows – model development and validation // Computers Fluids. 1995. V. 24. № 3. P. 227–238.

  29. Zwart P.J., Gerber A.G., Belamri T. A two-phase flow model for predicting cavitation dynamics // Fifth Int. Conf. Multiphase Flow, Yokohama, Japan. Ed. by Y. Matsumoto, K. Hishida, A. Tomiyama, et al. (Tsukuba, Japan, 2004).

  30. Rouse H., McNown J.S. Cavitation and pressure distribution, head forms at zero angle of yaw. Studies in Engineering Bulletin, State University of Iowa. 1948. V. 32.

  31. Sarkar T., Sayer P.G., Fraser S.M. Flow simulation past axisymmetric bodies using four different turbulence models // Appl. Math. Model. 1997. V. 21. № 12. P. 783–792.

  32. Asnaghi A., Jahanbakhsh E., Seif M.S. Unsteady multiphase modeling of cavitation around NACA 0015 // J. Mar. Sci. Tech. Taiwan. 2010. V. 18. № 5. P. 689–696.

  33. Yeoh G.H., Tu J. Computational Techniques for Multiphase Flows // Butterworth-Heinemann, Elsevier Science and Technology, 2009.

  34. Senocak I., Shyy W. A pressure-based method for turbulent cavitating flow computations // J. Comput. Phys. 2002. V. 176. № 2. P. 363–383.

  35. Bernad S.I., Susan-Resiga R. Numerical model for cavitational flow in hydraulic poppet valves // Modelling and Simulation in Engineering. 2012. V. 10.

  36. Ducoin A., Huang B., Young Y.L. Numerical modeling of unsteady cavitating flows around a stationary hydrofoil // Int. J. Rotating Machinery. 2012.

  37. Coussirat M., Moll F., Cappa F., Fontanals A. Study of available turbulence and cavitation models to reproduce flow patterns in confined flows // J. Fluids Eng. 2016. V. 138. № 9. Paper № 091304.

  38. Saha K., Li X. Assessment of different cavitation models in mixture and Eulerian framework for two-phase flow in Diesel injectors // American Society of Mechanical Engineers, 2013, p. V002T02A011.

  39. Liu H.L., Wang J., Wang Y., Zhang H., Huang H. Influence of the empirical coefficients of cavitation model on predicting cavitating flow in the centrifugal pump // Int. J. Nav. Arch. Ocean Eng. 2014. V. 6. № 1. P. 119–131.

  40. Shereena S.G., Vengadesan S., Idichandy V.G., Bhattacharyya S.K. CFD study of drag reduction in axisymmetric underwater vehicles using air jets // Eng. Appl. Comp. Fluid. 2013. V. 7. № 2. P. 193–209.

  41. Prosperetti A., Tryggvason G. Computational Methods for Multiphase Flow // Cambridge University Press, 2009.

  42. Jain M., Puranik B., Agrawal A. A numerical investigation of effects of cavity and orifice parameters on the characteristics of a synthetic jet flow // Sens. Actuator A – Phys. 2011. V. 165. № 2. P. 351–366.

  43. Manninen M., Taivassalo V., Kallio S. On the Mixture Model for Multiphase Flow // Technical Research Centre of Finland-VTT, 1996.

  44. Garabedian P.R. Calculation of axially symmetric cavities and jets // Pac. J. Math. 1956. V. 6. № 4. P. 611–684.

  45. Semenenko V.N. Artificial supercavittaion. Physics and calculation // Ukrainian Academy of Sciences, Kiev Institute of Hydromechanics, Technical Report, 2001.

  46. Choi J.K., Ahn B.K., Kim H.T. A numerical and experimental study on the drag of a cavitating underwater vehicle in cavitation tunnel // Int. J. Nav. Arch. Ocean Eng. 2015. V. 7. № 5. P. 888–905.

  47. Duong H.N., Nguyen T.T., Truong T.P., Nguyen Q.T. Some results of the experimental measurements of the cavitating flow after horizontal water entry // 8th Asia Pacific Workshop on Marine Hydrodynamics-APHydro 2016. Ed. by H. N. Duong (Publishing House for Science and Technology, Hanoi, 2016), P. 341–353.

  48. Nguyen T.T., Duong H.N., Nguyen Q.T., Truong T.P. Experimental measurements of the cavitating flow after horizontal water entry // Fluid Dyn. Res. 2017. V. 49. № 5. Paper № 055508.

  49. Stinebring D.R., Billet M.L., Lindau J.W., Kunz R.F. Developed Cavitation-Cavity Dynamics // Pennsylvania State University, University Park Applied Research Lab., 2001.

  50. Карликов В.П., Шоломович Г.И. Метод приближенного учета влияния стенок при кавитационном обтекании тел в гидродинамических трубах // Изв. РАН. МЖГ. 1966. № 4. С. 60–65.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал