1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2019

Известия РАН. Механика жидкости и газа, 2019, № 6, стр. 84-98

Анализ глобальной устойчивости пограничного слоя, развивающегося в пространстве. Влияние продольного градиента давления

Р. Бхоранья a, *, Н. Винод b

a Department of Mechanical Engineering, Marwadi Education Foundation Group of Institutions
Rajkot, India

b Department of Mechanical Engineering, Indian Institute of Technology Pala
Gandhinagar, India

* E-mail: rameshbhoraniya@gmail.com

Поступила в редакцию 15.01.2019
После доработки 15.02.2019
Принята к публикации 20.03.2019

Полный текст (PDF)

Аннотация

Выполнен анализ глобальной устойчивости двумерного несжимаемого пограничного слоя при наличии продольного градиента давления. Рассмотрено обтекание симметричного клина при различных значениях безразмерного параметра βH, характеризующего градиент давления. Градиент давления $dp{\text{/}}dx$ в направлении течения равен нулю при ${{\beta }_{H}} = 0$, сопутствующий (отрицательный) при ${{\beta }_{H}} > 0$ и встречный (положительный) при ${{\beta }_{H}} < 0$. Базовое течение определяется численным решением уравнения Фолкнера—Скэна. Число Рейнольдса определяется по толщине вытеснения $\delta {\text{*}}$ на входной границе течения. Уравнения, описывающие возмущения течения, выведены в системе координат, связанной с телом. Эти уравнения дискретизированы при помощи метода спектральной коллокации Чебышева. Дискретизированные уравнения, совместно с граничными условиями, образуют задачу о собственных значениях, которая решается посредством алгоритма Арнольди. Глобальные временные моды возмущений рассчитаны при ${{\beta }_{H}} = 0.022$, 0.044 и 0.066 для сопутствующих и встречных градиентов давления. Для всех глобальных мод инкремент возмущений во времени ωi оказывается отрицательным. При одном и том же числе Рейнольдса ${\text{Re}} = 340$ значения ωi меньше в случае сопутствующего градиента давления (СГД), чем в случае встречного градиента давления (ВГД). Таким образом, СГД оказывает стабилизирующее влияние на пограничный слой. Сравнение пространственных собственных мод и характеристик усиления возмущений в пространстве для случаев СГД и ВГД показывает, что СГД оказывает стабилизирующее, а ВГД дестабилизирующее влияние на возмущения пограничного слоя.

Ключевые слова: пограничный слой, несжимаемая жидкость, продольный градиент давления, глобальная устойчивость, численные решения

Пограничные слои, развивающиеся на твердых поверхностях, обычно являются ламинарными вблизи передней кромки тела. С увеличением расстояния от передней кромки растет и число Рейнольдса. Число Рейнольдса, при котором происходит переход к турбулентности, принято называть критическим числом Рейнольдса. Область, в которой имеет место переход, называют зоной перехода или длиной перехода. При весьма малом уровне турбулентности в набегающем потоке переход определяется механизмом волн Толлмиена–Шлихтинга (ТШ). Процесс перехода начинается со случайного усиления малых возмущений. Стандартная процедура определения начала перехода состоит в расчете инкремента малых возмущений в ламинарной области. Неустойчивость, или рост малых возмущений, представляет собой самый первый шаг в процессе перехода. На этот процесс могут влиять многие факторы, как например, турбулентность набегающего потока, продольный градиент давления (ГД), кривизна тела, шероховатость поверхности, и т.д. Информация о переходном процессе полезна как в тех случаях, когда турбулентности желательно избежать, так и в случаях, когда ее следует развивать, например, для улучшения смешения. Существует сильная взаимосвязь между явлениями перехода и отрыва потока; последнее явление нежелательно в большинстве технических приложений. Таким образом, понимание механизма перехода может обеспечить лучшее управление отрывом потока. Исследование влияния ГД на устойчивость течения представляет особый интерес как одно из возможных средств пассивного управления потоком. Предыдущие исследования показали, что СГД увеличивает критическое число Рейнольдса в несжимаемом пограничном слое, тогда как ВГД оказывает противоположное влияние. Продольный градиент давления существует в таких технических приложениях, как течения в турбомашинах и обтекание крыльев самолетов. Линейный анализ устойчивости параллельных течений показывает, что возмущения растут быстрее в пограничных слоях с встречным градиентом давления (ВГД). Иногда переход случается и в зонах течения с сопутствующим градиентом давления (СГД), например, при обтекании лопаток турбин и компрессоров при низком давлении и высоком уровне турбулентности в набегающем потоке.

В работе [1] показано, что СГД стабилизирует несжимаемый пограничный слой, а ВГД оказывает противоположное влияние. Данные летных испытаний, представленные в [2], показывают, что увеличение СГД приводит к росту критического числа Рейнольдса. Течение с очень сильным ВГД имеет точку перегиба в своем профиле и является неустойчивым даже в невязком случае. Неустойчивость невязкого течения с точкой перегиба в профиле скорости следует из критерия Рэлея. Продольный ГД коренным образом влияет на рост малых возмущений. СГД приводит к образованию более наполненного профиля скорости с относительно малым коэффициентом формы, что оказывает стабилизирующее влияние, тогда как ВГД способствует значительному усилению степени роста волн возмущения. В работе [3] показано, что СГД стабилизирует, а ВГД дестабилизирует течение.

Интенсивный ВГД способствует отрыву пограничного слоя и ускоряет переход к турбулентности. Такие пограничные слои значительно более неустойчивы, чем пограничные слои на пластине. В работе [4] экспериментально исследован резонансный рост тройки волн неустойчивости, состоящей из плоской ТШ волны и двух наклонных волн с равными по величине и противоположно направленными углами. Показано, что имеет место субгармонический переход пограничного слоя Фолкнера–Скэна при изменении параметра ВГД в диапазоне $0 > = {{\beta }_{H}} > $ = –0.09. Хотя в этих экспериментах не наблюдалось особенно большой неустойчивости, процесс перехода существенно и во многих отношениях отличался от случая Блазиуса. Например, участок амплитуды насыщения в продольном направлении был значительно короче, чем в слое Блазиуса, а максимальные амплитуды, достигаемые субгармоническими модами, вдвое превосходили соответствующие амплитуды в слое Блазиуса при одинаковых начальных условиях. Моделирование, проведенное в [5], показало, что субгармонические трехмерные волны особенно опасны при наличии ВГД. В этом случае опять-таки степень усиления возмущений значительно больше, чем в течении Блазиуса. Соответственно, переход в пограничном слое с замедлением потока осуществляется при гораздо меньших числах Рейнольдса, зона перехода существенно короче, а сам переход начинается выше по течению. В работах [6, 7] экспериментально обнаружены более интенсивное образование турбулентных пятен и расширение потока в замедляющихся течениях. В [8, 9] показано, что в пограничных слоях со значительным ВГД существует прямая связь между характером распада турбулентных пятен и характеристиками ламинарной устойчивости. В экспериментах [10, 11] обнаружено, что рост турбулентных пятен в направлении по потоку является автомодельным и не зависит от типа ГД. При виде сверху картина имеет форму наконечника стрелы. В работе [12] изучено поведение собственных решений непрерывного спектра в пограничном слое под действием градиента давления в направлении потока. При наличии ВГД обнаружен более быстрый рост амплитуд возмущений по сравнению с течением Блазиуса. Возможное образование вторичных неустойчивостей более вероятно у границы пограничного слоя из-за наличия интенсивной скорости сдвига. Степень роста возмущений в пространстве ${{\alpha }_{i}}$ также меньше, чем в течении Блазиуса. Величины собственных функций не могут превосходить соответствующие значения в течении Блазиуса, даже если градиент давления сопутствующий. Однако число Рейнольдса перехода оказывается выше и, следовательно, ${{\alpha }_{i}}$ тоже велико. В работе [13] исследован случай сжимаемого пограничного слоя и показано, что СГД оказывает стабилизирующее, а ВГД дестабилизирующее влияние на двумерные волны. Эффективность СГД ослабевает при гиперзвуковых числах Маха. Очевидно, что сопутствующие градиенты давления стабилизируют, а встречные дестабилизируют пограничные слои. Таким образом, пограничные слои, находящиеся под действием СГД и ВГД, устойчивы и неустойчивы соответственно. Спектр частот, приводящих к усилению возмущений в несжимаемом пограничном слое, расширяется при наличии ВГД. В работе [14] обнаружены совершенно отличные формы перехода в высокоскоростных пограничных слоях при наличии ВГД. В этой работе ВГД имеет место в набегающем потоке и оказывается не в состоянии существенно изменить характер перехода. Однако он ускоряет переход и обеспечивает максимальную степень роста первой и второй мод неустойчивости. Сам переход в случае небольших ВГД аналогичен случаю перехода при нулевом градиенте давления (НГД). В работе [15] проведены расчеты глобальной устойчивости двумерного обтекания наклонного треугольного цилиндра. Показано, что пространственные структуры возмущений почти одинаковы при $\alpha < = 30^\circ $, а временнóй инкремент чувствителен к течению в ближнем следе, тогда как при $\alpha < = 40^\circ $ имеет место чрезвычайно сильное нарастание возмущений в поперечном направлении и удлинение возмущенной области в продольном направлении, а инкремент чувствителен к течению в дальнем следе.

В экспериментах [16] обнаружено, что в гиперзвуковых пограничных слоях зона перехода в случае СГД в 1.7–2 раза короче, чем в случае НГД. Наличие ВГД приводит к более раннему переходу, а число Рейнольдса в конце этой зоны больше, чем в случае НГД. В случае дозвуковых течений закономерности, касающиеся длины перехода, противоположны. В [17] исследовано влияние градиентов давления в двух направлениях, а также угла стреловидности крыла на устойчивость трехмерных пограничных слоев. Обнаружено, что в области продольного СГД подходящий выбор ГД в поперечном течении может удержать поперечное течение на весьма слабом уровне, обеспечив, таким образом, устойчивый пограничный слой с высоким критическим числом Рейнольдса. В работе [18] численно исследовано влияние НГД, СГД и ВГД на чувствительность трехмерных пограничных слоев. Обнаружено, что такой пограничный слой чувствителен лишь к узкой полосе длин волн возмущений, в диапазоне от одной до четырех локальных толщин пограничного слоя. Слой с ВГД более чем в два раза чувствителен, чем слой с СГД. Эффект волн ТШ оказался существенным лишь в случае ВГД; однако, он обнаружен и в случае НГД. В работе [19] исследовано влияние ГД на первую моду неустойчивости в сжимаемых до- и сверхзвуковых пограничных слоях при числах Маха от 0 до 7. Рассчитаны максимальные инкременты возмущений при различных уровнях СГД и ВГД и различных числах Маха на границе пограничного слоя. СГД оказывает стабилизирующее влияние на первую моду. Однако этот эффект ослабляется с увеличением числа Маха на границе пограничного слоя. Частота и поперечные и продольные волновые числа, соответствующие максимальным инкрементам, убывают с увеличением СГД. В работе [20] обнаружено, что СГД уменьшает немодальный рост возмущений, а ВГД усиливает его. В [21] разработано устройство измерения перемежаемости, позволяющее проводить наблюдение в режиме реального времени в течение примерно 100 с. Результаты, полученные для четырех различных уровней турбулентности в режиме НГД, находятся в соответствии с результатами предыдущих исследований. Переходная область при отсутствии градиента давления была длинной, а наличие ВГД приводило к ее резкому сокращению. Увеличивалась также степень образования турбулентных пятен. В экспериментах [22] обнаружено, что при угле полураствора 3.6° процесс перехода отличался от случая с НГД. Рост возмущений при θ = 3.6° был почти на порядок сильнее, чем при $\theta = 0$. Это показывает, что переход пограничного слоя в турбулентное состояние является следствием неустойчивости ламинарного пограничного слоя. Обнаружено, что частотный спектр перехода был белым при θ = 0 и небелым при больших ВГД. В [23] представлена новая постановка задачи об устойчивости пограничного слоя при наличии ГД. Предполагалось, что длина волны и собственная функция возмущений меняются не быстрее, чем толщина пограничного слоя. Сильный ВГД оказывает существенное дестабилизирующее влияние на пограничный слой. На высоких частотах эффект непараллельности течения может быть значителен при малых числах Рейнольдса. В работе [24] дан обзор всех существующих моделей перехода и недостатков в предсказании длины перехода при наличии ВГД. Предложена новая, экспериментально обоснованная модель перехода с учетом влияния числа Рейнольдса и ВГД. Показано, что при увеличении ВГД от нуля до значений, соответствующих отрыву, поведение волн ТШ эволюционирует от случайного до периодического, что приводит к постоянному уменьшению длины перехода. В работе [25] выполнено прямое численное моделирование пространственной неустойчивости нормальной моды для профиля скорости Фолкнера–Скэна (при наличии ВГД). Обнаружено, что максимальные амплитуды возмущений продольной скорости в конце области на 10–20% выше, чем в экспериментальных измерениях работы [4]. При малых ВГД (${{\beta }_{H}}$ = –0.06) возмущения не обнаруживали взрывной неустойчивости, однако, при ${{\beta }_{H}}$ = –0.15 они резко нарастали. Причина этого состояла в том, что с увеличением ВГД критический слой находится дальше от стенки. В работе [26] прямым сопряженным методом исследован механизм алгебраического роста в пограничном слое Фолкнера–Скэна. Наличие ВГД увеличивает рост возмущений, а эффект СГД противоположен. Обнаружено, что возмущения, имеющие тенденцию к максимальному усилению в кратчайший период времени, как правило, являются наклонными и могут испытывать существенный рост во времени. Основная цель настоящей работы состоит в изучении влияния продольного градиента давления на глобальную неустойчивость пограничных слоев. В прошлом оно исследовалось на основе подхода локальной устойчивости, пренебрегающим продольными изменениями в базовом течении и предполагающим, что амплитуды возмущений зависят лишь от расстояния по нормали от стенки. Глобальные моды рассчитывались для пограничных слоев с НГД в нескольких работах [27–29]. В работах [30–32] авторы показали для случая осесимметричного пограничного слоя, что поперечная кривизна и СГД оказывают стабилизирующее влияние. Таким образом, данная работа представляет собой первую попытку рассчитать глобальные моды двумерных пограничных слоев при наличии продольных градиентов давления.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается обтекание потоком несжимаемой жидкости симметричного клина с различными параметрами βH, соответствующими СГД и ВГД. Таким образом, набегающий поток составляет некоторый угол с линией симметрии клина. Базовое течение двумерное и непараллельное. Уравнения Навье–Стокса для возмущений выводятся с использованием стандартной процедуры. Уравнения приводятся к безразмерному виду при масштабах скорости и длины ${{U}_{\infty }}$ и $\delta {\text{*}}$. Число Рейнольдса определяется по величине $\delta {\text{*}}$ на входе в область ${{x}_{{in}}}$, как показано на рис. 1. Для анализа устойчивости двумерного пограничного слоя решается двумерная задача на собственные значения. Рассматриваются двумерные возмущения.

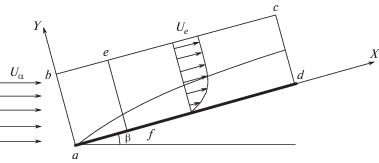
Рис. 1.

Растущий в пространстве несжимаемый пограничный слой на наклонной плоской пластине. Наличие угла наклона ${{\beta }_{H}}$ порождает градиент давления в продольном направлении. Положительное значение угла ${{\beta }_{H}}$, отсчитываемого в направлении против часовой стрелки, приводит к образованию СГД, а отрицательное значение к образованию ВГД

Число Рейнольдса

(1.1)
$\operatorname{Re} = \frac{{{{U}_{\infty }}\delta {\text{*}}}}{\nu }$

Параметры течения разлагаются на параметры основного потока и возмущения

(1.2)
$\bar {U} = {{U}_{b}} + {{u}_{p}},\quad \bar {V} = {{V}_{b}} + {{v}_{p}},\quad \bar {P} = {{P}_{b}} + {{p}_{p}},$
где $\bar {U}$, $\bar {V}$ и $\bar {P}$ – мгновенные значения параметров, Ub, ${{V}_{b}}$ и ${{P}_{b}}$ – параметры базового течения и ${{u}_{p}}$, ${{{v}}_{p}}$ и ${{p}_{p}}$ – возмущения.

Нормальные моды возмущений с амплитудами, меняющимися по нормали к стенке $y$ и в продольном направлении, имеют вид:

(1.3)
${{u}_{p}}(x,y,t) = {{\hat {u}}_{p}}(x,y){{e}^{{ - i\omega t}}},\quad {{{v}}_{p}}(x,y,t) = {{{\hat {v}}}_{p}}(x,y){{e}^{{ - i\omega t}}},\quad {{p}_{p}}(x,y,t) = {{\hat {p}}_{p}}(x,y){{e}^{{ - i\omega t}}}$

Линеаризованные уравнения Навье–Стокса, используемые при анализе устойчивости, имеют вид

(1.4)
$\frac{{\partial {{u}_{p}}}}{{\partial t}} + {{U}_{b}}\frac{{\partial {{u}_{p}}}}{{\partial x}} + {{u}_{p}}\frac{{\partial {{U}_{b}}}}{{\partial x}} + {{V}_{b}}\frac{{\partial {{u}_{p}}}}{{\partial y}} + {{{v}}_{p}}\frac{{\partial {{U}_{b}}}}{{\partial y}} + \frac{{\partial {{p}_{p}}}}{{\partial x}} - \frac{1}{{{\text{Re}}}}[{{\nabla }^{2}}{{u}_{p}}] = 0$
(1.5)
$\frac{{\partial {{v}_{p}}}}{{\partial t}} + {{U}_{b}}\frac{{\partial {{{v}}_{p}}}}{{\partial x}} + {{u}_{p}}\frac{{\partial {{V}_{b}}}}{{\partial x}} + {{V}_{b}}\frac{{\partial {{{v}}_{p}}}}{{\partial y}} + {{{v}}_{p}}\frac{{\partial {{V}_{b}}}}{{\partial y}} + \frac{{\partial {{p}_{p}}}}{{\partial y}} - \frac{1}{{{\text{Re}}}}[{{\nabla }^{2}}{{{v}}_{p}}] = 0$
(1.6)
$\frac{{\partial {{u}_{p}}}}{{\partial x}} + \frac{{\partial {{{v}}_{p}}}}{{\partial y}} = 0$
где

(1.7)
${{\nabla }^{2}} = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}$

1.1. Граничные условия

На твердой поверхности вследствие вязкости возмущения ${{u}_{p}}$ и ${{{v}}_{p}}$ равны нулю (прилипание и непроницаемость)

(1.8)
${{u}_{p}}(x,0) = 0,\quad {{{v}}_{p}}(x,0) = 0$

Амплитуды возмущений экспоненциально убывают с удалением от стенки и обращаются в нуль в дальнем поле. Итак, все возмущения компонент скорости и давления полагаются в дальнем поле равными нулю

(1.9)
${{u}_{p}}(x,\infty ) = 0,\quad {{{v}}_{p}}(x,\infty ) = 0,\quad {{p}_{p}}(x,\infty ) = 0$

Исследуем рост или затухание малых возмущений в рассматриваемой области течения под действием градиента давления. Все возмущения компонент скорости равны нулю на входной границе области. Это соответствует предположению, сделанному в работе [33].

(1.10)
${{u}_{p}}({{x}_{{in}}},y) = 0,\quad {{{v}}_{p}}({{x}_{{in}}},y) = 0.$

На выходной границе можно поставить условия, основанные на информации, передаваемой волнами [34]. Эти условия весьма ограничительны, поскольку они постулируют волновой характер возмущений. Физически эти условия не слишком хороши для анализа устойчивости. В глобальном анализе устойчивости продольное волновое число α заранее не известно. Альтернативный способ задания граничных условий состоит в экстраполяции данных из внутренних точек вычислительной области. В ряде работ условия на выходной границе задаются посредством линейной экстраполяции. Обзор литературы по анализу глобальной устойчивости показывает, что именно такие условия наиболее подходят для постановки на выходной границе [27, 33, 35]. Таким образом, на выходной границе ставятся условия, полученные путем линейной экстраполяции

(1.11)
${{u}_{{{{p}_{{n - 2}}}}}}[{{x}_{n}} - {{x}_{{n - 1}}}] - {{u}_{{{{p}_{{n - 1}}}}}}[{{x}_{n}} - {{x}_{{n - 2}}}] + {{u}_{{{{p}_{n}}}}}[{{x}_{{n - 1}}} - {{x}_{{n - 2}}}] = 0$

где xn, ${{x}_{{n - 1}}}$, ${{x}_{{n - 2}}}$ – самые внешние узлы вычислительной сетки, а up – возмущение продольной компоненты скорости. Аналогично могут быть записаны экстраполированные граничные условия для нормальной компоненты скорости ${{{v}}_{p}}$. Для давления на твердой стенке ставятся условия совместимости, выведенные из самих уравнений устойчивого течения [33]

(1.12)
$\frac{{\partial {{p}_{p}}}}{{\partial x}} = \frac{1}{{{\text{Re}}}}\frac{{{{\partial }^{2}}{{u}_{p}}}}{{\partial {{y}^{2}}}}$
(1.13)
$\frac{{\partial {{p}_{p}}}}{{\partial y}} = \frac{1}{{{\text{Re}}}}\frac{{{{\partial }^{2}}{{{v}}_{p}}}}{{\partial {{y}^{2}}}}$

При выводе уравнений устойчивости применен метод, основанный на использовании примитивных переменных. Преимущество этого подхода над численным подходом высокого порядка состоит в том, что он использует лишь первые производные параметров базового течения и вторые производные возмущенных величин. Производные невысокого порядка приводят к меньшим ошибкам дискретизации. Уравнения (1.4) и (1.5) дискретизируются с использованием полиномов Чебышева в обоих пространственных направлениях. Полиномы Чебышева порождают неравномерную сетку со сгущением точек коллокации к обеим концам области

(1.14)
${{x}_{{cheb}}} = cos\left( {\frac{{\pi i}}{n}} \right)\quad {\text{для}}\quad i = 0,1,2,3\;....\;n$
(1.15)
${{y}_{{cheb}}} = cos\left( {\frac{{\pi j}}{m}} \right)\quad {\text{для}}\quad j = 0,1,2,3\;....\;m$

В пристеночной области тонкого пограничного слоя градиенты амплитудных функций возмущений весьма велики. Это требует введения большого количества узлов сетки для улучшения пространственного разрешения. Сгущение сетки проводится на основе следующего алгебраического уравнения [36]

(1.16)
${{y}_{{real}}} = \frac{{{{y}_{i}}{{L}_{y}}(1 - {{y}_{{cheb}}})}}{{{{L}_{y}} + {{y}_{{cheb}}}({{L}_{y}} - 2{{y}_{i}})}}$

В вышеописанном методе растяжения сетки половина узлов коллокации сосредоточена внутри области, находящейся на расстоянии yi от нижней границы. Неравномерность распределения узлов коллокации в продольном направлении нежелательна. Максимальные и минимальные расстояния между узлами сетки приходятся на центральную и граничную части области соответственно. Недостаточное разрешение в центре области и малость расстояний между узлами у границы приводят к возникновению феномена Гиббса. Для улучшения разрешения и минимизации осцилляций Гиббса совершается преобразование сетки в продольном направлении по следующей алгебраической формуле [37].

(1.17)
${{x}_{{map}}} = \frac{{{\text{arcsin}}({{\alpha }_{m}}{{x}_{{cheb}}})}}{{{\text{arcsin}}({{\alpha }_{m}})}}$

Значение ${{\alpha }_{m}}$ выбирается тщательным образом, чтобы улучшить пространственное разрешение в продольном направлении. При очень малом значении ${{\alpha }_{m}}$ распределение узлов сетки близко к чебышевскому, а при ${{\alpha }_{m}}$, близких к единице, сетка получается почти равномерной. Детальное описание преобразования сетки содержится в работе [37]. Влияние физических размеров области [Lx, Ly], совместно с растяжением и преобразованием сетки, определяется умножением матриц дифференцирования Чебышева на соответствующую матрицу Якоби. Линейный оператор дискретизированной системы линеаризованных уравнений Навье–Стокса образует матрицы K и M. Эти квадратные, действительные, разреженные матрицы формулируют общую задачу на собственные значения

(1.18)
$\left[ {\begin{array}{*{20}{c}} {{{K}_{{11}}}}&{{{K}_{{12}}}}&{{{K}_{{13}}}} \\ {{{K}_{{21}}}}&{{{K}_{{22}}}}&{{{K}_{{23}}}} \\ {{{K}_{{31}}}}&{{{K}_{{32}}}}&{{{K}_{{33}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{u}_{p}}} \\ {{{{v}}_{p}}} \\ {{{p}_{p}}} \end{array}} \right] = i\omega \left[ {\begin{array}{*{20}{c}} {{{M}_{{11}}}}&{{{M}_{{12}}}}&{{{M}_{{13}}}} \\ {{{M}_{{21}}}}&{{{M}_{{22}}}}&{{{M}_{{23}}}} \\ {{{M}_{{31}}}}&{{{M}_{{32}}}}&{{{M}_{{33}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{u}_{p}}} \\ {{{{v}}_{p}}} \\ {{{p}_{p}}} \end{array}} \right]$
$[K][\psi ] = i\omega [M][\psi ]$
где K и M – квадратные матрицы размера 3 nm $ \times $ 3 нм, $i\omega $ – собственное значение и $\psi $ – вектор неизвестных амплитуд возмущений параметров течения ${{u}_{p}}$, ${{{v}}_{p}}$ и ${{p}_{p}}$. Все вышеупомянутые граничные условия должным образом содержатся в этих матрицах. Численное решение уравнения (1.18) осуществляется при помощи итерационного алгоритма Арнольди. Подробное описание решения задач на собственные значения можно найти в работах [31, 32].

2. РЕШЕНИЕ ДЛЯ БАЗОВОГО ТЕЧЕНИЯ

В качестве базового профиля скорости выбран профиль скорости Фолкнера–Скэна. Значение параметра βH определяет, является ли течение ускоренным (${{\beta }_{H}} > 0$) или замедленным (${{\beta }_{H}} < 0$).

(2.1)
$f{\kern 1pt} {\text{''}} + ff{\kern 1pt} {\text{''}} + {{\beta }_{H}}(1 - {{f}^{{'2}}}) = 0$

Базовая скорость определяется решением уравнения (2.1) при граничных условиях

(2.2)
$\eta = 0{\text{:}}\quad f = f{\kern 1pt} {\text{'}} = 0;\quad \eta \to \infty {\text{:}}\quad f{\kern 1pt} {\text{'}} = 1$

Продольная и нормальная скорости вычисляются следующим образом:

(2.3)
${{U}_{b}} = {{U}_{\infty }}f{\kern 1pt} {\text{'}};\quad {{V}_{b}} = \frac{{ - 1}}{2}\sqrt {\frac{{\nu {{U}_{\infty }}}}{x}[\eta f{\kern 1pt} {\text{'}}(\eta ) - f(\eta )]} $

Численное решение уравнения (2.1) находится методом Рунге–Кутта четвертого порядка точности.

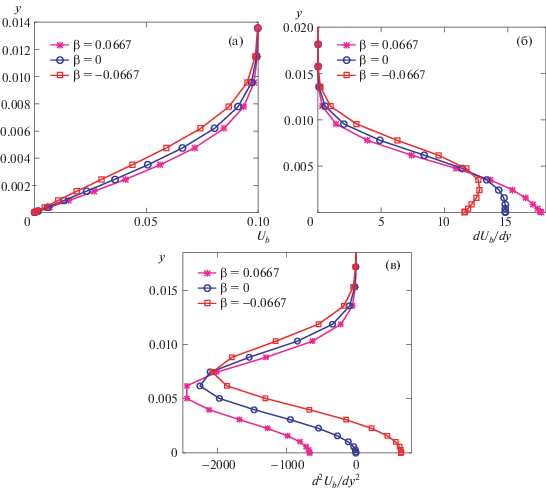
При значении угла ${{\beta }_{H}} = 0$ имеет место пограничный слой на плоской пластине с нулевым градиентом давления; при ${{\beta }_{H}} > 0$ и ${{\beta }_{H}} < 0$ развиваются, соответственно, течения с ВГД и СГД в продольном направлении. На рис. 2а, 2б и 2в сравниваются величины Ub, $d{{U}_{b}}{\text{/}}dy$ и ${{d}^{2}}{{U}_{b}}{\text{/}}d{{y}^{2}}$ для СГД, НГД и ВГД при одном и том же значении продольной координаты x = 0.5 м. Величина первой производной $d{{U}_{b}}{\text{/}}dy$ больше в случае СГД, ускоряющего поток. Величина второй производной ${{d}^{2}}{{U}_{b}}{\text{/}}d{{y}^{2}}$ отрицательна для СГД и положительна для ВГД. Можно отметить, что отрицательное значение ${{d}^{2}}{{U}_{b}}{\text{/}}d{{y}^{2}}$ имеет стабилизирующее, а положительное значение ${{d}^{2}}{{U}_{b}}{\text{/}}d{{y}^{2}}$ дестабилизирующее влияние.

Рис. 2.

Изменение ${{U}_{b}}$ (а), $\tfrac{{\partial {{U}_{b}}}}{{\partial y}}$ (б) и $\tfrac{{{{\partial }^{2}}{{U}_{b}}}}{{\partial {{y}^{2}}}}$ (в) в нормальном направлении в случае СГД, ВГД и НГД при $x = 0.5$ м. Положительные значения угла ${{\beta }_{H}}$ приводят к образованию СГД, а отрицательные значение к образованию ВГД

3. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Данный анализ устойчивости включает рассмотрение пограничного слоя на плоской пластине при наличии продольного градиента давления. Рассмотрены углы полураствора клина βH, равные 0.022, 0.0444 и 0.0667, создающие градиент давления в направлении потока. Рассмотрены как положительные (СГД), так и отрицательные (ВГД) значения угла βH. Рассмотрены три значения числа Рейнольдса (340, 416 и 480), вычисленные по величине $\delta {\text{*}}$ на входной границе. Линейные размеры в обоих направлениях отнесены к $\delta {\text{*}}$. Высота области в направлении, нормальном к стенке, взята равной $20\delta {\text{*}}$. Это достаточно большое значение, не оказывающее влияния на результаты расчетов [27]. Количество узлов коллокации в продольном и нормальном направлениях равно 251 и 61 соответственно. Исследованы временные и пространственные характеристики наименее устойчивых собственных мод. Сходимость решения дополнительно проверялась при меньшем пространственном разрешении.

3.1. Валидация программы

Для валидации программы численного анализа глобальной устойчивости двумерная задача устойчивости решалась в области размером в одну длину волны ($Lx = 2\pi {\text{/}}\alpha $) при одном и том же профиле скорости в каждой точке в продольном направлении. Это означает, что $\tfrac{{\partial U}}{{\partial x}} = 0$ и V = 0. Валидация подхода, развитого в [38], осуществлялась сравнением с пограничным слоем в случае НГД (${{\beta }_{H}} = 0$) при критическом числе Рейнольдса, вычисленном по толщине вытеснения, ${\text{R}}{{{\text{e}}}_{{\delta *}}}$ = 580 и продольном волновом числе ${{\alpha }_{r}} = 0.179$. Для того чтобы реализовать волнообразное поведение возмущений, ставились граничные условия Робина (3.1) и периодические граничные условия (3.2). Одни и те же граничные условия в направлении, нормальном к стенке, ставились при исследовании локальной и глобальной устойчивости [30].

(3.1)
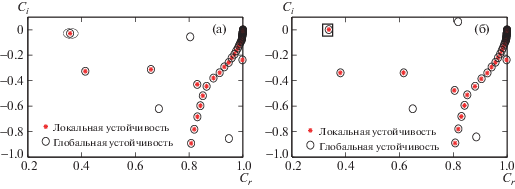
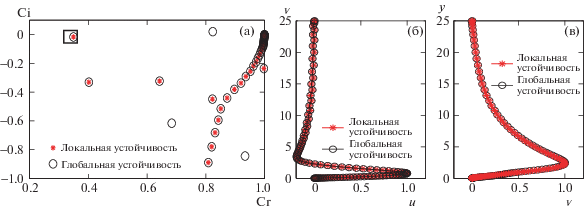
$\frac{{{{\partial }^{2}}{{u}_{p}}}}{{\partial {{x}^{2}}}} = - {{\alpha }^{2}}{{u}_{p}},\quad \frac{{{{\partial }^{2}}{{{v}}_{p}}}}{{\partial {{x}^{2}}}} = - {{\alpha }^{2}}{{{v}}_{p}},$
(3.2)
${{u}_{p}}(x,y) = {{u}_{p}}(x + Lx,y),\quad {{{v}}_{p}}(x,y) = {{{v}}_{p}}(x + Lx,y)$

На рис. 3а, 3б и 3в проведено сравнение собственных спектров и собственных функций, полученных при анализе локальной и глобальной устойчивости для Re = 580 и ${{\alpha }_{r}} = 0.179$. Собственные спектры и функции, рассчитанные методом глобального анализа, отлично совпадают с результатами локального анализа устойчивости [38]. Дополнительные сравнения были выполнены для случая СГД с ${{\beta }_{H}} = 0.066$ и ВГД с ${{\beta }_{H}} = - 0.066$. Сравнение собственных спектров на рис. 4а, 4б показывает хорошее согласование между результатами глобального и локального анализа. Собственные функции для обоих случаев также хорошо совпадают (не приведены в данной работе). Таким образом, результаты глобального анализа устойчивости при использовании граничных условий Робина и периодических условий находятся в хорошем соответствии с результатами локального анализа устойчивости.

Рис. 3.

Сравнение собственного спектра (а), продольной собственной функции u (б) и нормальной к стенке собственной функции v (в) при глобальном и локальном анализе устойчивости двумерного пограничного слоя на пластине при Re = 580 и ${{\alpha }_{r}} = 0.179$ в случае НГД. Значение Re = 580 соответствует критическому числу Рейнольдса при локальном анализе устойчивости

Рис. 4.

Сравнение собственных спектров двумерного пограничного слоя на пластине при Re = 580 и ${{\alpha }_{r}} = 0.178$ при глобальном и локальном анализе устойчивости в случае СГД (${{\beta }_{H}} = 0.0667$ (а) и ВГД ($\beta = - 0.0667$ (б)

3.2. Сходимость по сетке

Для проверки независимости решения от размеров сетки и его точности был выполнен следующий тест. В табл. 1 представлены численные значения двух наименее устойчивых собственных мод, вычисленных при Re = 340, и осесимметричной моды, полученные при трех существенно различных размерах сетки. Вычислены относительные ошибки для действительной и мнимой частей собственных значений. Приводится наибольшая из всех вычисленных ошибок. При увеличении пространственного разрешения имеет место монотонная сходимость вычисленных собственных значений. Относительная ошибка для сетки 1 находится в разумных пределах и дальнейшие результаты излагаются для этой сетки. Высота области Ly = 25 в направлении, нормальном к стенке, достаточна для того, чтобы можно было поставить граничные условия, соответствующие набегающему потоку [27].

Таблица 1.

Наименее устойчивые собственные значения ${{\omega }_{1}}$ и ${{\omega }_{2}}$, рассчитанные при различном количестве узлов сетки при ${{R}_{e}} = 340$ и ${{\beta }_{H}} = 0.044$. Продольный и нормальный к стенке размеры расчетной области ${{L}_{x}} = 420$ и ${{L}_{y}} = 20$. В последовательных сериях расчетов количество узлов сетки изменялось с коэффициентом 1.1412

Сетка n $ \times $ m ${{\omega }_{1}}$ ${{\omega }_{2}}$ Ошибка, %
1 251 × 61 0.07049 – 0.01998i 0.07707 – 0.02009i 3.450
2 193 × 53 0.07045 – 0.01937i 0.07706 – 0.01942i 6.353
3 171 × 47 0.07043 – 0.01822i 0.07703 – 0.01826i –

3.3. Влияние конечной длины области

Анализ устойчивости открытого сдвигового течения, подобного пограничному слою на пластине, в области конечной длины (укороченной численной области) требует постановки соответствующих граничных условий на выходной границе области. Искусственные граничные условия не должны влиять на динамику и устойчивость течения в такой области. Глобальные спектры в укороченной области, данные по которым можно найти в литературе, такие как пограничные слои [28, 29], следы за цилиндром [39, 40] и струи [41, 42], весьма сильно зависят от типа граничных условий и места, где они поставлены. Для понимания влияния длины расчетной области в продольном направлении были проведены расчеты для областей с тремя различными длинами.

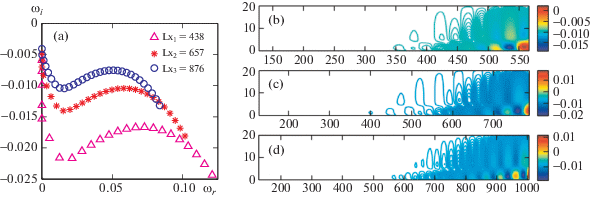
На рис. 5 проведено сравнение участка собственного спектра, рассчитанного при трех длинах расчетной области: 438, 657 и 876. Длина обезразмерена по величине $\delta {\text{*}}$ на входной границе области. Очевидно, что длина области оказывает влияние на рассчитанный спектр. При фиксированном числе Рейнольдса инкремент возмущений во времени растет с увеличением длины области. Иными словами, увеличение длины области приводит к росту числа Рейнольдса на выходе из нее, что влияет на степень роста возмущений во времени ${{\omega }_{i}}$. Распределение частоты ${{\omega }_{r}}$ также зависит от длины области Lx. Расстояние между двумя последовательными частотами ${{\omega }_{r}}$ уменьшается при увеличении длины области. В идеальном случае это расстояние уменьшается до нуля, когда длина расчетной области неограниченно растет. Таким образом, представленные в работе собственные спектры зависят от длины расчетной области. На рис. 5а, 5б и 5в представлены двумерные пространственные структуры амплитуд возмущений ${{u}_{p}}$ при ${{\omega }_{r}} = 0.07028$, Re = 340 и нулевом градиенте давления для областей с длинами ${{L}_{x}} = 438$, 657 и 876. При движении вниз по течению возмущения периодически осциллируют, причем их пространственные размеры и амплитуды растут.

Рис. 5.

Сравнение собственных спектров для трех длин расчетной области в случае СГД при Re = 340 и ${{\beta }_{H}} = 0.0222$ (а). Сравнение двумерной пространственной структуры действительной части ${{u}_{p}}$ при ${{L}_{x}} = 438$ (б), ${{L}_{x}} = 657$ (в) и ${{L}_{x}} = 876$ (г)

3.4. Влияние сопутствующего градиента давления

Спектры, полученные при решении двумерной задачи на собственные значения при Re = 340 и наличии СГД, представлены на рис. 6а. Отдельные участки спектров показаны для различных значений угла наклона βH. Наименее устойчивые моды для каждого из этих углов отмечены прямоугольниками. Глобальные моды являются устойчивыми, так как мнимые части наименее устойчивых мод отрицательны. На рис. 6а сравниваются отдельные участки собственных спектров, соответствующие волнам Толлмиена–Шлихтинга (ТШ) при наличии НГД и СГД. Увеличение СГД приводит к росту степени затухания или уменьшению роста во времени ${{\omega }_{i}}$ собственной моды, имеющей наибольшее значение ${{\omega }_{i}}$, что делает глобальную моду более устойчивой во времени. Это поведение сходственно с результатами анализа для параллельного течения. Однако градиент давления не оказывает влияния на распределение частот ТШ волн. Отсюда следует, что СГД в продольном направлении имеет глобальный стабилизирующий эффект. Для изучения пространственной структуры двумерных собственных мод выбраны наименее устойчивые во времени собственные моды ${{\omega }_{i}}$.

Рис. 6.

Сравнение собственных спектров (а), зависимостей ${{u}_{p}}$ (б) и ${{{v}}_{p}}$ (в) в направлении y и зависимостей ${{u}_{p}}$ (г) и ${{{v}}_{p}}$ (д) в направлении течения для различных ${{\beta }_{H}}$ при ${\text{Re}} = 340$ и $y = 0.114$ в случае СГД. Здесь ${{\beta }_{H}} = 0$ для НГД и ${{\beta }_{H}} = 0.0222$, ${{\beta }_{H}} = 0.0444$ и ${{\beta }_{H}} = 0.0667$ для СГД. Символы: ${\text{V}} = 0.0702 - 0.0209i$, $ * = 0.0704 - 0.0217i$, $ \circ = 0.0706 - 0.0225i$, $ = 0.0708 - 0233i$

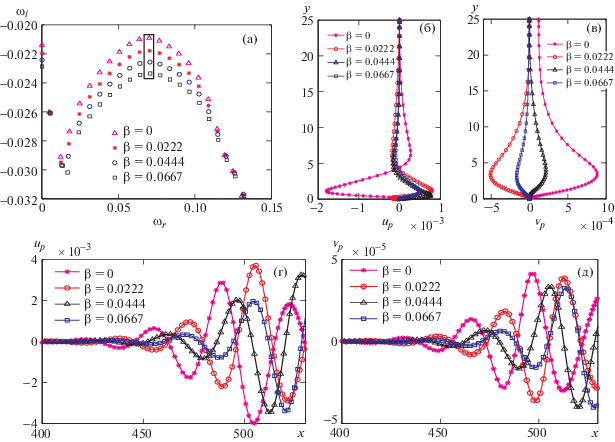
На рис. 6г и 6д представлена зависимость амплитуд возмущений от продольной координаты при $y = 0.114$, Re = 340 и различных значениях параметра βH (в случае СГД) для наименее устойчивых мод, отмеченных прямоугольниками на рис. 6а. Поведение собственных мод, осциллирующее в силу того, что ${{\omega }_{r}} > 0$. Как показывают рис. 6г и 6д, изменения амплитуд возмущений ${{u}_{p}}$ и ${{{v}}_{p}}$ в направлении потока имеют одинаковый характер; при этом величины амплитуд уменьшаются с увеличением СГД (положительные значения βH). Структура амплитуд возмущений ${{u}_{p}}$ и ${{{v}}_{p}}$ волновая. При движении вниз по потоку возмущения растут. Это означает, что течение конвективно неустойчиво. Пространственная структура возмущений одинакова для пограничных слоев с НГД и СГД. При перемещении вниз по течению растут размеры возмущенных структур и величины возмущений. Последние уменьшаются с ростом βH от 0.0222 до 0.0666. Таким образом, увеличение СГД оказывает стабилизирующее влияние на пространственный рост возмущений.

На рис. 6б и 6в построена зависимость амплитуд возмущений скорости ${{u}_{p}}$ и ${{{v}}_{p}}$ в направлении y при значении продольной координаты $x = 461$. Характер изменений в случаях НГД и СГД почти одинаков. На самой стенке, благодаря вязкости, амплитуды возмущений равны нулю; затем они постепенно возрастают в направлении y и убывают до нуля в дальнем поле. Можно видеть, что с увеличением градиента давления величины возмущений скорости ${{u}_{p}}$ и ${{{v}}_{p}}$ убывают в продольном направлении. Таким образом, СГД помогает стабилизации течения.

Рост или затухание пространственных собственных мод имеет место в продольном направлении. Для определения общего роста/затухания всех возмущений в направлении потока рассчитывается пространственный инкремент ${{A}_{x}}$ по формуле

(3.3)
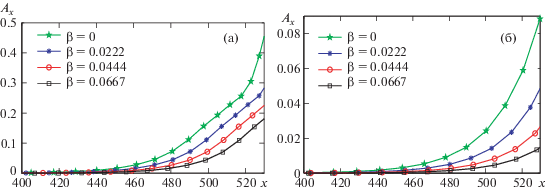
${{A}_{x}} = \sqrt {\int\limits_0^{{{y}_{{{\text{max}}}}}} {(u_{p}^{*}(x,y)} {{u}_{p}}(x,y) + {v}_{p}^{*}(x,y){{{v}}_{p}}(x,y))dy} $
где звездочкой обозначено комплексно-сопряженное значение.

На рис. 7a и 7б представлена зависимость пространственного инкремента Ax возмущений скорости от продольной координаты при различных значениях βH и числах Рейнольдса. Как видно из рис. 7, инкремент Ax растет в направлении течения; при этом увеличение параметра βH от 0.0222 (НГД) до 0.0666 (СГД) приводит к уменьшению Ax. Это указывает на тот факт, что увеличение СГД в продольном направлении уменьшает пространственный рост возмущений и, следовательно, оказывает стабилизирующее влияние на их рост, приводя к их затуханию. Обнаружено также, что увеличение числа Рейнольдса от 340 до 480 при одном и том же значении ГД приводит к уменьшению пространственного инкремента.

Рис. 7.

Изменение пространственного инкремента Ax в направлении течения в случае СГД при различных значениях ${{\beta }_{H}}$ для Re = 340 (а) и Re = 480 (б). Значение Ax рассчитано для наименее устойчивой глобальной моды

3.5. Влияние встречного градиента давления

Анализ глобальной устойчивости выполнен для пограничных слоев при различных значениях встречного градиента давления. Собственный спектр для различных значений βH при Re = 340 представлен на рис. 8. На рис. 8а приведен участок спектра при различных βH. Наименее устойчивые моды отмечены прямоугольниками для каждого значения βH; все они отрицательны. Это означает, что все глобальные собственные моды устойчивы во времени. Этот результат находится в соответствии с результатами, полученными в [27], где мнимые части глобальных мод также отрицательны. На рис. 8 сравниваются участки собственного спектра, соответствующие волнам Толлмиена–Шлихтинга при наличии ВГД (${{\beta }_{H}} > 0$). Рост возмущений во времени наиболее неустойчивой моды усиливается с увеличением βH. Это значит, что ВГД в направлении потока оказывает общее дестабилизирующее влияние на пограничный слой. Однако градиент давления не оказывает влияния на распределение частот. Для изучения пространственной эволюции амплитуд двумерных возмущений выбраны наименее устойчивые собственные моды.

Рис. 8.

Сравнение собственных спектров (а), амплитуд продольных возмущений ${{u}_{p}}$ (б) и амплитуд возмущений, нормальных к стенке ${{{v}}_{p}}$ (в) для различных ${{\beta }_{H}}$ при Re = 340 и $y = 0.114$. Здесь ${{\beta }_{H}} = 0$ для НГД и ${{\beta }_{H}} = - 0.022$, ${{\beta }_{H}} = - 0.044$ и ${{\beta }_{H}} = - 0.0667$ для ВГД. Символы: ${\text{V}} = 0.0696 - 0.0177i$, $ * = 0.0698 - 0.0188i$, $ \circ = 0.0700 - 0.0199i$, $ = 0.0702 - 0209i$

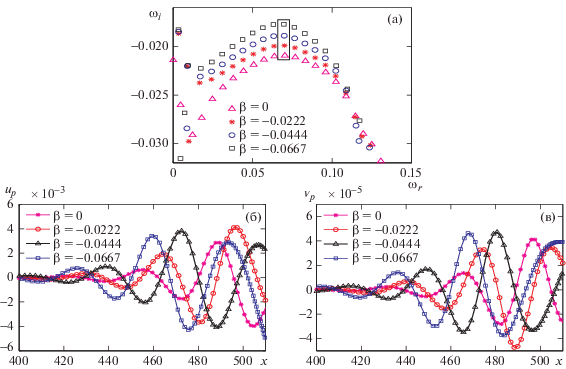
На рис. 8б и 8в представлена зависимость действительных частей амплитуд возмущений ${{u}_{p}}$ и ${{{v}}_{p}}$ от продольной координаты при Re = 340, $y = 0.114$ и различных значениях βH (ВГД). Для исследования пространственного роста амплитуд возмущений выбраны наименее устойчивые моды с ${{\omega }_{r}} = 0.07$. Обнаружено, что наименее устойчивые глобальные моды глобально устойчивы, поскольку ${{\omega }_{i}} < 0$, тогда как безразмерная частота имеет почти одно и то же значение для всех наименее устойчивых глобальных мод при различных βH. Амплитуды возмущений растут, осциллируя, при перемещении вниз по течению. Амплитуды возмущений увеличиваются при изменении угла наклона пластины βH от 0 до –0.06676. Таким образом, увеличение ВГД усиливает пространственный рост возмущений и оказывает дестабилизирующее влияние на пограничный слой.

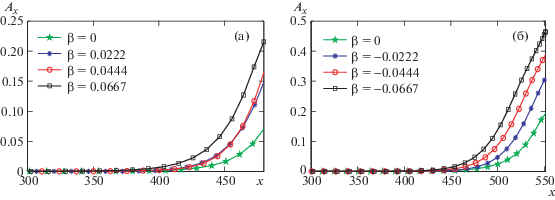
На рис. 9 представлена зависимость пространственного инкремента возмущений скорости Ax от продольной координаты для различных значений угла наклона пластины βH и чисел Рейнольдса. Можно видеть, что инкремент Ax растет в направлении потока и увеличивается с ростом ВГД. Таким образом, ВГД оказывает общее дестабилизирующее влияние на пограничный слой.

Рис. 9.

Изменение пространственного инкремента Ax в направлении течения в случае ВГД при различных значениях ${{\beta }_{H}}$ для ${\text{Re}} = 340$ (а) и ${\text{Re}} = 480$ (б). Значение Ax рассчитано для наименее устойчивой глобальной моды

ЗАКЛЮЧЕНИЕ

Проведен анализ глобальной устойчивости несжимаемого пограничного слоя на наклонной плоской пластине при наличии продольного градиента давления. Рассмотрены углы наклона ${{\beta }_{H}}$, равные 0.0222, 0.0444 и 0.0667. Двумерная задача на собственные значения решена численно при помощи алгоритма Арнольди. Рассчитанные глобальные моды оказались устойчивыми, так как наибольшие мнимые части собственных значений ${{\omega }_{i}}$ отрицательны. Пространственная структура возмущений показывает, что при перемещении вниз по течению они растут в размерах с увеличением их амплитуд. Распределение частот остается практически одинаковым при отрицательных и положительных градиентах давления. При увеличении положительного угла наклона βH от 0 до 0.0667 инкременты возмущений во времени ${{\omega }_{i}}$ и пространстве уменьшаются, что делает глобальные моды более устойчивыми. Таким образом, СГД приводит к временнóй и пространственной стабилизации течения. При увеличении отрицательного угла наклона βH от 0 до –0.0667 инкремент возмущений во времени ${{\omega }_{i}}$ растет и глобальные моды становятся менее устойчивыми. Инкремент возмущений в пространстве Ax также растет в направлении потока. Таким образом, увеличение ВГД делает глобальные моды менее устойчивыми. В целом СГД приводит к затуханию, а ВГД к усилению возмущений. Изучено также влияние длины расчетной области и показано, что глобальная устойчивость существенно зависит от выбранного размера области в продольном направлении.

Список литературы

  1. Obremski H.J., Morkovin M.V., Landahl M. A portfolio of stability characteristics of incompressible boundary layer // AGARDograph 134 (1969).

  2. Van Driest E.R., Blumer C.B. Boundary layer transition: freestream turbulence and pressure gradient effect, AIAA J. 1963. V. 1. P. 1303–1306.

  3. Saxena S.K., Bose T.K. Numerical study of effect of pressure gradient on stability of an incompressible boundary layer // Phys. Fluids. 1974. V. 17. P. 1910–1912.

  4. Corke T.C., Gruber S. Resonant growth of three-dimensional modes in falkner-skan boundary layers with adverse pressure gradient // J. Fluid Mech. 1996. V. 320. P. 211–233.

  5. Liu C., Maslowe S.A. A numerical investigation of resonant interactions in adverse pressure gradient boundary layers // J. Fluid Mech. 1999. V. 378. P. 269–289.

  6. Abu-Ghannam B.J., Shaw R. Natural transition of boundary layers – the effects of turbulence,pressure gradient, and flow history // J. Mech. Engng. Sci. 1980. V. 22. P. 213–228.

  7. Gostelow J.P., Blunden A.R., Walker G.J. Effect of free-stream turbulence and adverse pressure gradients on boundary layer transition // J. Turbomach. 1994. V. 116. P. 392–404.

  8. Vinod N., Govindarajan R. Pattern of breakdown of laminar flow into turbulent spots // Phys. Rev. Lett. 2004. V. 93. P. 114501.

  9. Vinod N., Govindarajan R. The signature of laminar instabilities in the zone of transition to turbulence // J. Turbulence. 2007. V. 8. № 2.

  10. Narasimha R. The laminar-turbulent transition zone in the boundary layer // Prog. Aero. Sci. 1985. V. 22. P. 29–80.

  11. Seifert A., Hodson H.P. Periodic turbulent strips and calmed regions in a transitional boundary layer // AIAA J. 1999. V. 37. P. 1127–1129.

  12. Maslowe S.A., Spiteri R.J. The continuous spectrum for a boundary layer in a streamwise pressure gradient // Phys. Fluids. 2001. V. 13. P. 1294.

  13. Zurigat Y.H., Nayfeh A.H., Masad J.A. Effect of pressure gradient on the stability of compressible boundary layers // AIAA J. 1992. V. 30. P. 2204–2211.

  14. Franko K.J., Lele S. Effect of adverse pressure gradient on high speed boundary layer transition // Phys. Fluids. 2014. V. 26. P. 24106.

  15. Zhang W., Yang H., Hua-Shu D., Zuchao Z. Flow unsteadiness and stability characteristics of low-Re flow past an inclined triangular cylinder // J. Fluids Eng. 2017. V. 139. P. 121203.

  16. Kimmel R.L. The effect of pressure gradients on transition zone length in hypersonic boundary layer // Flight Dynamics Directorate. 1993.

  17. Itoh N. Effect of pressure gradients on the stability of three-dimensional boundary layers // Fluid Dyn. Res. 1991. V. 7. P. 37–50.

  18. Johnson M.W., Pinarbasi A. The effect of pressure gradients on boundary layer receptivity // Flow, Turbulence and Combustion. 2014. V. 93. P. 1–24.

  19. Masad J.A., Zurigat Y.H. Effect of pressure gradients on first mode of instability in compressible boundary layers // Phys. Fluids. 1994. V. 6. P. 3945.

  20. Tumin A., Ashpis D.E. Optimal disturbances in boundary layers subject to streamwise pressure gradient // 33rd AIAA Fluid Dynamics Conference (2003).

  21. Gostelow J.P., Blunden A.R. Investigation of boundary layer transition in an adverse pressure gradient // ASME J. Turbomachinery. 1989. V. 111. P. 366–374.

  22. Igarashi S., Sasaki H., Honda M. Influence of pressure gradient upon boundary layer stability and transition // Acta Mechanica. 1988. V. 73. P. 187–198.

  23. Govindarajan R., Narasimha R. Stability of spatially developing boundary layers in pressure gradients // J. Fluid Mech. 1995. V. 300. P. 117–147.

  24. Walker G.J., Gostelow J.P. Effect of adverse pressure gradients on the nature and length of boundary layer transition // Gas Turbines and Aeroengine Congress and Exposition (1989).

  25. Chonghui L. Numerical investigation of instability and transition in adverse pressure gradient boundary layers // Ph. D. Thesis, McGill University, Montreal (1997).

  26. Corbett P., Bottaro A. Optimal perturbations for boundary layers subject to streamwise pressure gradient // Phys. Fluids. 2000. V. 12. P. 120–131.

  27. Alizard V., Robinet J.C. Spatially convective global modes in a boundary layer // Phys. Fluids. 2007. V. 19. P. 114105.

  28. Ehrenstein U., Gallaire F. On two-dimensional temporal modes in spatially evolving open flow: the flat-plate boundary layer // J. Fluid Mech. 2005. V. 536. P. 209–218.

  29. Akervik E., Ehrenstein U., Gallaire F., Henningson D.S. Global two-dimensional stability measures of the flat-plate boundary-layer flow // Eur. J. Mech. B/Fluids. 2008. V. 27. P. 501–513.

  30. Bhoraniya R., Vinod N. Global stability analysis of axisymmetric boundary layer over a circular cylinder // Theor. Comput. Fluid Dyn. 2018. V. 32. P. 425–449.

  31. Bhoraniya R., Vinod N. Global stability analysis of axisymmetric boundary layer over a circular cone // J. Phys.: Conf. Ser. 2017. V. 822. P. 012018.

  32. Bhoraniya R., Vinod N. Global stability analysis of axisymmetric boundary layer over a circular cone // Phys. Rev. Fluids. 2017. V. 02. P. 063901.

  33. Theofilis V. Advances in global linear instability analysis of nonparallel and three-dimensional flows // Prog. Aerosp. Sci. 2003. V. 39. P. 249–315.

  34. Fasel H., Rist U., Konzelmann U. Numerical investigation of the three-dimensional development in boundary layer transition // AIAA J. 1990. V. 28. P. 29–37.

  35. Swaminathan G., Sahu K.C., Sameen A., Govindarajan R. Global instabilities in diverging channel flows // Theor. Comput. Fluid Dyn. 2011. V. 25. P. 53–64.

  36. Malik M.R. Numerical methods for hypersonic boundary layer stability // J. Comput. Phys. 1990. V. 86. № 2. P. 376–412.

  37. Costa B., Don W.S., Simas A. Spatial resolution properties of mapped spectral Chebyshev methods // Proc. SCPDE. 2007. P. 179–188.

  38. Mach L.M. A numerical study of temporal eigenvalue spectrum of the Blasius boundary layer // J. Fluid Mech. 1976. V. 73. P. 497–520.

  39. Sipp D., Lebedev D. Global stability of base and mean flows: a general approach to its applications to cylinder and open cavity flow // J. Fluid Mech. 2007. V. 593. P. 333–358.

  40. Marquet O., Sipp D., Lebedev D. Sensitivity analysis and passive control of cylinder flow // J. Fluid Mech. 2008. V. 615. P. 221–252.

  41. Nichols J.W., Lele S.K. Global modes and transient response of a cold supersonic jet // J. Fluid Mech. 2011. V. 669. P. 225–241.

  42. Garnaud X., Lesshafft L., Schimd P. J., Huerre P. Modal and transient dynamics of jet flows // Phys. Fluids. 2013. V. 25. P. 044103.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал