Известия РАН. Механика жидкости и газа, 2019, № 6, стр. 75-83
РАЗВИТИЕ НАЧАЛЬНЫХ ВОЗМУЩЕНИЙ В ЗАДАЧЕ О ДВИЖЕНИИ ЦИЛИНДРА, ОБТЕКАЕМОГО ЦИРКУЛЯЦИОННЫМ ПОТОКОМ
В. Ф. Копьев a, С. А. Чернышев a, М. А. Юдин a, b, *
a ЦАГИ им. проф. Н.Е. Жуковского, Московский комплекс
Москва, Россия
b Московский физико-технический институт ГУ
Московская обл., Долгопрудный, Россия
* E-mail: mikleudin@yandex.ru
Поступила в редакцию 11.04.2019
После доработки 21.05.2019
Принята к публикации 25.06.2019
Аннотация
Настоящая работа посвящена исследованию устойчивости цилиндра в циркуляционном потоке невязкой несжимаемой жидкости. Исследование устойчивости в простой двумерной системе представляет значительный интерес, так как в этой задаче можно получить аналитическое решение, как для спектральной, так и для начальной задачи. Особый интерес представляет исследование области критического слоя, в которой фазовая скорость возмущений совпадает со скоростью среднего течения, поскольку именно в этой области происходит концентрация возмущений и их безграничный рост.
В статье рассмотрена начальная задача о развития возмущений в двумерной системе, которая представляет собой незакрепленный круговой цилиндр, помещенный внутрь неподвижного цилиндрического кожуха, и циркуляционный поток несжимаемой идеальной жидкости между ними. Данная работа является продолжением работ [1–4], в которых было показано, что эта система обладает двумя различными типами неустойчивости. Одна неустойчивость является следствием ограниченности течения (эта неустойчивость отсутствует в безграничном случае) и может возникать уже в потенциальном потоке или в потоке с постоянной завихренностью. Другая неустойчивость – сдвиговая (или Майлсовская) возникает как в ограниченном, так и в безграничном случае в течении с монотонно меняющейся завихренностью вследствие взаимодействия возмущений со средним течением в окрестности критического слоя (слоем, на котором фазовая скорость возмущений совпадает со скоростью основного циркуляционного потока).
В настоящей работе рассматривается случай потенциального течения и более общий случай течения с постоянной завихренностью. Случай произвольной завихренности в течении между цилиндром и кожухом будет рассмотрен в следующей работе. В работах [1–4] рассматривались собственные колебания такой системы, т.е. была рассмотрена только дискретная часть спектра. В частности, были получены инкременты неустойчивых колебаний. Однако рассматриваемая система обладает не только дискретным, но и непрерывным спектром, который в задаче с нулевой или постоянной завихренностью возникает при описании возмущений на языке поля смещения, а в общем случае произвольной завихренности имеет место также для возмущений скорости. Для систем с непрерывным спектром получение дискретных собственных частот дает лишь частичное описание эволюции поля течения, и некоторые важные особенности остаются неясными. В частности, представляет интерес вопрос о том, как происходит нарастание возмущений и возникновение особенности при $t \to \infty $ в окрестности критического слоя из начального состояния с гладкими начальными условиями. Ответ на этот вопрос может дать решение начальной задачи, которое учитывает вклад возмущений как дискретного, так и непрерывного спектра. Важно, что в случае колебаний цилиндра в циркуляционном потоке задача может быть решена точно. Возможность аналитического описания возмущений связана с использованием поля смещения в качестве основной переменной [1, 3]. Хотя в рассматриваемом случае нулевой или постоянной завихренности возмущения скорости не обладают непрерывным спектром, система обладает непрерывным спектром для поля смещения жидких частиц, и соответственно, задача содержит в себе все особенности, связанные с наличием критического слоя. В частности, в окрестности критического слоя происходит нарастание смещений жидких частиц. Физически это может проявиться при добавлении пассивной примеси или малой неоднородной завихренности в поток. В этом смысле ситуация во многом аналогична нарастанию возмущений в критическом слое с постоянной завихренностью в плоскопараллельном случае [5, 6].
Как отмечалось выше, в общем случае циркуляционного потока с неоднородной завихренностью непрерывным спектром обладает не только поле смещения, но также возмущения скорости и завихренности. Предложенный в этой работе подход к решению задачи Коши может быть полностью перенесен на общий случай.
1. ПОСТАНОВКА ЗАДАЧИ
Рассматривается двумерная система, состоящая из двух коаксиальных цилиндров с циркуляционным потоком невязкой несжимаемой жидкости между ними (рис. 1). Завихренность в потоке предполагается постоянной или равной нулю (потенциальное обтекание). Внутренний цилиндр с радиусом R1 может совершать свободные колебания, а внешний цилиндр с радиусом R2 жестко закреплен.
В предыдущей работе [3] рассматривалась спектральная задача об устойчивости данной системы. Были найдены собственные частоты колебаний, включая неустойчивые колебания с мнимой добавкой к частоте $\omega $.
В настоящей работе рассматривается начальная задача. Предполагается, что при t < 0 система находится в равновесии, а в начальный момент времени t = 0 внутреннему цилиндру сообщается заданная скорость V0. Исследуются динамика внутреннего цилиндра и развитие возмущений в потоке, в частности, особенности в окрестности критического слоя, связанные с ростом смещения жидких частиц.
Решение задачи Коши определяется не только возмущениями дискретного спектра задачи, но и возмущениями непрерывного спектра, играющими существенную роль в эволюции системы. Для получения решения используется поле смещения ${\mathbf{\varepsilon }}$ [7], которое ранее применялось для описания возмущений цилиндра в циркуляционном потоке безграничной [1] и ограниченной внешним цилиндром [3, 4] жидкости, возмущений вихревого кольца в [2, 8], а также для описания возмущений вихревых течений на языке лагранжевой и гамильтоновой механики [9]. Поле смещения можно ввести по-разному – через деформации поля стационарной завихренности при выполнении условия изозавихренности [2], или через разность между положениями жидких частиц на траекториях в возмущенном и невозмущенном течениях [9]. Второй подход, использованный в [7], подходит для рассмотрения не только завихренных, но и потенциальных течений.
В несжимаемом течении поле смещения является бездивергентым, т.е. $\nabla \times {\mathbf{\varepsilon }} = 0$, а эволюция поля смещения описывается уравнением [1, 7]
(1.1)
$\frac{{\partial {\mathbf{\varepsilon }}}}{{\partial t}} + \nabla \times \left( {{\mathbf{\varepsilon }} \times {{{\mathbf{V}}}_{{\mathbf{0}}}}} \right) = {\mathbf{v}}$В случае стационарного вихревого потока с неоднородной завихренностью для замыкания уравнения (1.1) требуется дополнительное условие изозавихренности возмущений, введенное Арнольдом [10, 11]. Для таких возмущений поле смещения ${\mathbf{\varepsilon }}$ связывает возмущение поля завихренности $\delta {\mathbf{\Omega }}$ со значением завихренности в стационарном течении ${{{\mathbf{\Omega }}}_{0}}$ с помощью соотношения [2]
(1.2)
$\delta {\mathbf{\Omega }} = \nabla \times \left( {{\mathbf{\varepsilon }} \times {{{\mathbf{\Omega }}}_{0}}} \right)$Возмущение скорости v, входящее в правую часть уравнения (1.1), связано с возмущением завихренности $\delta {\mathbf{\Omega }}$ (1.2)
Уравнения (1.1)–(1.3) полностью описывают динамику изозавихренных возмущений в течении с произвольной стационарной завихренностью. Отметим, что класс изозавихренных возмущений, который может быть получен произвольным бездивергентным смещением жидких частиц, включает класс потенциальных возмущений, рассмотренных выше.
2. МЕТОД РЕШЕНИЯ ДЛЯ ПРОИЗВОЛЬНОГО ПРОФИЛЯ ЗАВИХРЕННОСТИ
Стационарное течение в данной задаче (рис. 1) описывается заданием угловой скорости ${{U}_{0}}\left( r \right)$ и может быть представлено в цилиндрической системе координат $r$, $\varphi $ в виде ${{{\mathbf{V}}}_{0}} = (0,{{U}_{0}}(r) \times r)$. Смещение границы цилиндра в линейном приближении по смещению центра цилиндра является первой азимутальной гармоникой $\exp \left( {i\varphi } \right)$, поэтому решение задачи ищется в следующем виде [3]:
С учетом этого условие бездивергентности поля смещения можно переписать так:
После взятия операции ротора от уравнения (1.1) получим
(2.2)
$\nabla \times \left( {\frac{{\partial {\mathbf{\varepsilon }}}}{{\partial t}} + \nabla \times \left( {{\mathbf{\varepsilon }} \times {{{\mathbf{V}}}_{0}}} \right)} \right) = \delta {\mathbf{\Omega }}$Используя (2.1), (2.2) и (1.2), можно записать уравнение на радиальную компоненту поля смещения
(2.3)
$ir\frac{{{{\partial }^{3}}{{\varepsilon }^{r}}}}{{\partial t\partial {{r}^{2}}}} - r{{U}_{0}}\frac{{{{\partial }^{2}}{{\varepsilon }^{r}}}}{{\partial {{r}^{2}}}} + 3i\frac{{{{\partial }^{2}}{{\varepsilon }^{r}}}}{{\partial t\partial r}} - (3{{U}_{0}} + 2rU_{0}^{'})\frac{{\partial {{\varepsilon }^{r}}}}{{\partial r}} = 0$Граничное условие непротекания на внешнем неподвижном цилиндре соответствует равенству нулю на нем радиальной компоненты поля смещения
На внутреннем цилиндре радиальная компонента поля смещения, с учетом зависимости всех компонент решения от φ вида $\exp \left( {i\varphi } \right)$ определяется смещением центра цилиндра $\xi = {{x}_{0}} - i{{y}_{0}}$
Динамика рассматриваемой системы определяется не только динамикой жидкости (2.3), но также динамикой внутреннего незакрепленного цилиндра. Для того, чтобы рассмотреть динамику цилиндра, требуется вычислить силу $F = {{F}_{x}} - i{{F}_{y}}$, действующую на цилиндр со стороны жидкости, и решить динамическое уравнение $F = M\ddot {\xi }$, определяющее движение цилиндра и граничное условие для движения жидкости (2.5).
Из (1.1) и (2.1) выразим компоненты возмущения скорости через радиальную компоненту поля смещения
(2.6)
${{{v}}^{r}} = \frac{{\partial {{\varepsilon }^{r}}}}{{\partial t}} + i{{U}_{0}}\left( r \right){{\varepsilon }^{r}}$(2.7)
${{{v}}^{\varphi }} = \frac{{\partial r{{\varepsilon }^{r}}}}{{\partial t\partial r}} + i{{U}_{0}}\left( r \right)\frac{{\partial r{{\varepsilon }^{r}}}}{{\partial r}} - rU_{0}^{'}\left( r \right){{\varepsilon }^{r}}$Из уравнений Эйлера можно выразить возмущение поля давления через возмущения скорости. Без ограничения общности положим ρ = 1 и запишем уравнение Эйлера для φ компоненты в цилиндрической системе координат
Используя то, что решение пропорционально $\exp \left( {i\varphi } \right)$, получим для возмущения давления
Тогда, используя (2.6) и (2.7), получим
(2.8)
$p{\text{'}} = - r\left( {U_{0}^{2}{{\varepsilon }^{r}} + \frac{{{{\partial }^{2}}{{\varepsilon }^{r}}}}{{\partial {{t}^{2}}}}} \right) + {{r}^{2}}U_{0}^{2}\frac{{\partial {{\varepsilon }^{r}}}}{{\partial r}} - 2i{{r}^{2}}\frac{{{{\partial }^{2}}{{\varepsilon }^{r}}}}{{\partial r\partial t}} - {{r}^{2}}\frac{{{{\partial }^{3}}{{\varepsilon }^{r}}}}{{\partial r\partial {{t}^{2}}}}$Давление на поверхности смещенного цилиндра в линейном приближении будет складываться из возмущения давления (2.8) при r = R1 и среднего давления P0 на смещенной поверхности $\delta P = {{\left. {p{\text{'}}} \right|}_{{r = {{R}_{1}}}}} + \left. {{{\xi \times d{{P}_{0}}} \mathord{\left/ {\vphantom {{\xi \times d{{P}_{0}}} {dr}}} \right. \kern-0em} {dr}}} \right|$, где в силу стационарных уравнений Эйлера ${{d{{P}_{0}}} \mathord{\left/ {\vphantom {{d{{P}_{0}}} {dr}}} \right. \kern-0em} {dr}} = rU_{0}^{2}$. Используя (2.5), на поверхности цилиндра запишем давление
(2.9)
$\delta P = - r\frac{{{{\partial }^{2}}{{\varepsilon }^{r}}}}{{\partial {{t}^{2}}}} + {{r}^{2}}U_{0}^{2}\frac{{\partial {{\varepsilon }^{r}}}}{{\partial r}} - 2i{{r}^{2}}\frac{{{{\partial }^{2}}{{\varepsilon }^{r}}}}{{\partial r\partial t}} - {{r}^{2}}\frac{{{{\partial }^{3}}{{\varepsilon }^{r}}}}{{\partial r\partial {{t}^{2}}}}$С учетом зависимости всех величин от азимутального угла вида $\exp \left( {i\varphi } \right)$ проинтегрируем давление (2.9) по поверхности смещенного цилиндра и вычислим силу
Тогда уравнение, определяющее динамику цилиндра, перепишется в виде
(2.10)
${{\left. {M\ddot {\xi } = - \pi {{R}_{1}} \times \left( { - r\frac{{{{\partial }^{2}}{{\varepsilon }^{r}}}}{{\partial {{t}^{2}}}} + {{r}^{2}}U_{0}^{2}\frac{{\partial {{\varepsilon }^{r}}}}{{\partial r}} - 2i{{r}^{2}}\frac{{{{\partial }^{2}}{{\varepsilon }^{r}}}}{{\partial r\partial t}} - {{r}^{2}}\frac{{{{\partial }^{3}}{{\varepsilon }^{r}}}}{{\partial r\partial {{t}^{2}}}}} \right)} \right|}_{{r = {{R}_{1}}}}}$Динамика системы определяется следующими уравнениями: уравнение (2.3), описывающее динамику жидкости, и уравнение (2.10) для динамики движения цилиндра. Совместное решение этой системы уравнений будет определять подведение системы.
Спектральная задача с решением вида $\exp \left( { - i\omega t} \right)$ была рассмотрена в работе [3], где были найдены собственные дискретные частоты. Подставляя гармоническое решение в (2.3), получим, что член со старшей (второй) производной $r(\omega - {{U}_{0}}(r)){{{{\partial }^{2}}{{\varepsilon }^{r}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{\varepsilon }^{r}}} {\partial {{r}^{2}}}}} \right. \kern-0em} {\partial {{r}^{2}}}}$ может обращаться в ноль на линии критического слоя, где фазовая скорость возмущений совпадает со скоростью потока $\omega = {{U}_{0}}\left( r \right)$. Это может приводить к бесконечно большим (в линейном приближении) решениям вблизи критического слоя.
Представляет интерес рассмотреть процесс развития особенности из первоначально гладкого состояния. Для этого рассмотрим задачу Коши. Уравнение (2.3), определяющее эволюцию поля смещения, а следовательно, и динамику жидкости, имеет первый порядок по времени t и для него необходимо задать одно начальное условие. Пусть в начальный момент времени течение невозмущенное, тогда
Уравнение (2.10) на динамику цилиндра имеет второй порядок по времени $t$ и для него необходимо задать два начальных условия, совместных с (2.11) и (2.5). Не нарушая общности, рассмотрим одно из возможных начальных условий, когда в начальный момент времени цилиндры располагаются коаксиально, поле смещения (2.11) всюду равно нулю, и при этом внутреннему цилиндру сообщается начальная скорость ${{V}_{0}}$ в направлении оси $Ox$
(2.12)
${{\left. \xi \right|}_{{t = 0}}} = 0,\quad {{\left. {\frac{{\partial \xi }}{{\partial t}}} \right|}_{{t = 0}}} = {{V}_{0}}$Таким образом, задачу Коши можно сформулировать следующим образом: необходимо совместно решить уравнения динамики жидкости (2.3) и твердого тела (2.10) с граничными условиями (2.4) и (2.5) и начальными условиями (2.11) и (2.12).
3. ЗАДАЧА КОШИ ДЛЯ ПРОИЗВОЛЬНОГО ПРОФИЛЯ ЗАВИХРЕННОСТИ
Для решения задачи Коши, сформулированной выше, удобно использовать одностороннее преобразование Фурье. Далее во всех гидродинамических величинах будет опущен множитель $\exp \left( {i\varphi } \right)$, если не будет оговорено отдельно.
Поскольку при t < 0 возмущения отсутствуют, Фурье компоненту поля можно записать в виде
(3.1)
${{E}^{r}}\left( {r,\omega } \right) = \int\limits_0^\infty {{{\varepsilon }^{r}}\left( {r,t} \right)\exp \left( {i\omega t} \right)dt} $Отметим, что для нарастающих возмущений (с нарастанием не сильнее экспоненциального $\exp ({{\sigma }_{0}}t)$) можно считать ω комплексной величиной с мнимой частью $\operatorname{Im} \left( \omega \right) = \sigma > {{\sigma }_{0}}$. Тогда интеграл (3.1) является сходящимся. Контур обратного преобразования Фурье необходимо провести выше всех особенностей [12]
Замыкание контура в верхней полуплоскости автоматически приводит к решению, равному нулю для t < 0. Функцию ${{E}^{r}}\left( {r,\omega } \right)$, определенную при $\operatorname{Im} \left( \omega \right) = \sigma > {{\sigma }_{0}}$, можно аналитически продолжить на всю комплексную плоскость.
С учетом вышесказанного выполним преобразование Фурье (3.1) для уравнения (2.3). С учетом начального условия ${{\varepsilon }^{r}}{{{\text{|}}}_{{t = 0}}} = 0$ получим
(3.2)
$r\left( {\omega - {{U}_{0}}\left( r \right)} \right)\frac{{{{\partial }^{2}}{{E}^{r}}}}{{\partial {{r}^{2}}}} + 3\left( {\omega - {{U}_{0}}\left( r \right)} \right)\frac{{\partial {{E}^{r}}}}{{\partial r}} - 2rU_{0}^{'}\frac{{\partial {{E}^{r}}}}{{\partial r}} = 0$Решение уравнения (3.2) может быть выписано в квадратурах
(3.3)
${{E}^{r}}\left( {r,\omega } \right) = {{C}_{1}}\left( \omega \right) + {{C}_{2}}\left( \omega \right)I\left( {r,\omega } \right)$(3.4)
$I\left( {r,\omega } \right) = \int\limits_r^{{{R}_{2}}} {\frac{{dr{\text{'}}}}{{{{{\left( {\omega - {{U}_{0}}\left( {r{\text{'}}} \right)} \right)}}^{2}}{{r}^{{'3}}}}}} $Определение коэффициентов C1(ω) и C2(ω) осуществляется с помощью удовлетворения граничным условиям (2.4) и (2.5). Выполняя преобразование Фурье в (2.4), получим, что ${{C}_{1}}\left( \omega \right) = 0$.
Теперь рассмотрим преобразование Фурье от уравнения (2.10) с учетом (2.5)
(3.5)
${{\left[ {(\pi R_{1}^{2} - M){{\omega }^{2}}{{E}^{r}} + R_{1}^{3}\pi {{{\left( {\omega - {{U}_{0}}} \right)}}^{2}}\frac{{\partial {{E}^{r}}}}{{\partial r}}} \right]}_{{r = {{R}_{1}}}}} = (M - \pi R_{1}^{2})\frac{{\partial {{\varepsilon }^{r}}}}{{\partial t}} - \pi R_{1}^{3}{{\left. {\frac{{{{\partial }^{2}}{{\varepsilon }^{r}}}}{{\partial t\partial r}}} \right|}_{{t = 0,r = {{R}_{1}}}}}$Правая часть уравнения (3.5) содержит производную по времени от радиальной компоненты поля смещения в начальный момент времени ${{\left. {{{\partial {{\varepsilon }^{r}}} \mathord{\left/ {\vphantom {{\partial {{\varepsilon }^{r}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right|}_{{t = 0}}}$. Для нахождения правой части рассмотрим уравнение (1.1) при t = 0. Второй член в уравнении равен нулю согласно начальному условию ${{\varepsilon }^{r}}{{{\text{|}}}_{{t = 0}}} = 0$. Вследствие этого уравнение (1.1) перепишется в виде ${{\left. {{{\partial {{\varepsilon }^{r}}} \mathord{\left/ {\vphantom {{\partial {{\varepsilon }^{r}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right|}_{{t = 0}}} = {{\left. {{{{v}}^{r}}} \right|}_{{t = 0}}}$. Тогда уравнение (3.5) может быть переписано в виде
(3.6)
${{\left[ {(\pi R_{1}^{2} - M){{\omega }^{2}}{{E}^{r}} + R_{1}^{3}\pi {{{\left( {\omega - {{U}_{0}}} \right)}}^{2}}\frac{{\partial {{E}^{r}}}}{{\partial r}}} \right]}_{{r = {{R}_{1}}}}} = (M - \pi R_{1}^{2}){{{v}}^{r}} - \pi R_{1}^{3}{{\left. {\frac{{\partial {{{v}}^{r}}}}{{\partial r}}} \right|}_{{t = 0,r = {{R}_{1}}}}}$Согласно (1.2) и начальному условию (2.11) возмущения завихренности в начальный момент времени отсутствуют и поле скорости является потенциальным. Поле скорости в начальный момент времени должно удовлетворять граничным условиям на границах цилиндров ${{{v}}^{r}}{{{\text{|}}}_{{t = 0,r = {{R}_{2}}}}} = 0$ и ${{{v}}^{r}}{{{\text{|}}}_{{t = 0,r = {{R}_{1}}}}}$ = V0. Учитывая, что рассматривается первая гармоника, для потенциального поля скорости, получим ${{{v}}^{r}}{{{\text{|}}}_{{t = 0}}} = {{A}_{1}} + {{{{A}_{2}}} \mathord{\left/ {\vphantom {{{{A}_{2}}} {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}}$, где константы ${{A}_{1}}$ и ${{A}_{2}}$ могут быть найдены из граничных условий. Окончательно поле скорости в начальный момент времени имеет следующий вид
Тогда с использованием (3.3) в (3.6) получим
(3.7)
${{C}_{2}}\left( \omega \right) = \frac{{(R_{1}^{4}\pi + MR_{2}^{2} + R_{1}^{2}(\pi R_{2}^{2} - M)){{V}_{0}}}}{{(R_{2}^{2} - R_{1}^{2})\left( {(\pi R_{1}^{2} - M){{\omega }^{2}}I\left( {{{R}_{1}},\omega } \right) + R_{1}^{3}\pi {{{\left( {\omega - {{U}_{0}}\left( {{{R}_{1}}} \right)} \right)}}^{2}}{{{\left. {\frac{{\partial I\left( {r,\omega } \right)}}{{\partial r}}} \right|}}_{{r = {{R}_{1}}}}}} \right)}}$Подставляя (3.7) и условие ${{C}_{1}}\left( \omega \right) = 0$ в (3.3), получим искомое решение в пространстве ω, от которого затем следует взять обратное преобразование Фурье для того, чтобы получить решение поставленной начальной задачи во временной области.
4. ПОТЕНЦИАЛЬНОЕ ТЕЧЕНИЕ И ТЕЧЕНИЕ С ПОСТОЯННОЙ ЗАВИХРЕННОСТЬЮ
Далее рассматривается наиболее простой случай среднего течения с постоянной завихренностью ${{U}_{0}}\left( r \right) = {{{{U}_{m}}} \mathord{\left/ {\vphantom {{{{U}_{m}}} {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}} + {{\Omega }_{0}}$ (для потенциального течения Ω0 = 0). В этом случае интеграл в (3.4) может быть вычислен аналитически
Тогда решение (3.3) в частотном пространстве примет следующий вид:
(4.1)
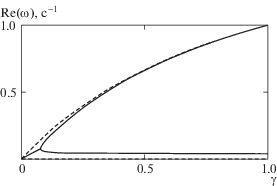
${{E}^{r}}\left( {r,\omega } \right) = \frac{{(R_{2}^{2} - {{r}^{2}})(R_{1}^{4}\pi + MR_{2}^{2} + R_{1}^{2}(\pi R_{2}^{2} - M)){{V}_{0}}( - {{U}_{m}} + R_{1}^{2}\left( {\omega - {{\Omega }_{0}}} \right))}}{{(R_{2}^{2} - R_{1}^{2})({{U}_{m}} + {{r}^{2}}\left( {{{\Omega }_{0}} - \omega } \right))D\left( \omega \right)}}$Найденное решение (4.1) в комплексной плоскости ω имеет только полюса, которые соответствуют условиям $D\left( \omega \right) = 0$ и ${{U}_{m}} + {{r}^{2}}\left( {{{\Omega }_{0}} - \omega } \right) = 0$. Рассмотрим каждый полюс отдельно. Уравнение $D\left( \omega \right) = 0$ имеет два корня ω1, 2, которые соответствуют дискретному спектру задачи, найденному ранее в [3]. Оба полюса являются полюсами первого порядка. Зависимость действительной части корней ω1, 2 от параметра $\gamma $, представляющего собой отношение плотности жидкости к плотности цилиндра (γ = 0 соответствует бесконечно тяжелому цилиндру) изображена на рис. 2. Сплошная линия соответствуют случаю конечного ${{R}_{2}}$ (${{R}_{2}} = 5$ м, R1 = 1 м, ${{U}_{m}} = 1$ м2/c, ${{\Omega }_{0}} = 0$), а пунктирная неограниченному случаю ${{R}_{2}} \to \infty $.
Там, где действительная часть корней совпадает, они имеют одинаковые по модулю и разные по знаку мнимые части. Таким образом, из рис. 2 видно, что при наличии ограничивающего внешнего цилиндра существует область параметров, при которых потенциальное течение или течение с постоянной завихренностью оказываются неустойчивыми:
Эта неустойчивость связана именно с ограниченностью области течения [3]. Полюс ω3 = ${{{{U}_{m}}} \mathord{\left/ {\vphantom {{{{U}_{m}}} {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}} + {{\Omega }_{0}} = {{U}_{0}}(r)$ включает в себя все частоты в интервале $\left( {{{U}_{0}}\left( {{{R}_{2}}} \right),{{U}_{0}}\left( {{{R}_{1}}} \right)} \right)$.
Выполним обратное преобразование Фурье так, чтобы контур интегрирования оказался выше всех особенностей (полюсов в данном случае). Замыкая контур в верхней полуплоскости, получим, что для отрицательных t решение тождественно равно нулю (задача Коши). При положительных t, замыкая контур интегрирования в нижней полуплоскости, получим, что искомое решение состоит из суммы вычетов функции ${{E}^{r}}(r,\omega )\exp ( - i\omega t)$ в полюсах ${{\omega }_{{1,2}}}$ и в полюсе ${{\omega }_{3}} = {{U}_{0}}(r)$
(4.2)
${{\varepsilon }^{r}}\left( {r,t} \right) = {{A}_{1}}\left( r \right)\exp \left( { - i{{\omega }_{1}}t} \right) + {{A}_{2}}\left( r \right)\exp \left( { - i{{\omega }_{2}}t} \right) + {{A}_{3}}\left( r \right)\exp \left( { - i{{U}_{0}}\left( r \right)t} \right)$При значениях r в окрестности ${{r}_{{cr}}}$, таких что ${{U}_{0}}\left( {{{r}_{{cr}}}} \right) = {{\omega }_{{1,2}}}$, корень ${{\omega }_{3}} = {{U}_{0}}\left( r \right)$ приближается к одному из корней ${{\omega }_{{1,2}}}$. Рассмотрим случай, когда полюса ${{\omega }_{3}}$ и ${{\omega }_{1}}$ оказываются близкими. Тогда введем обозначения ${{\omega }_{3}} = {{\omega }_{1}} + \delta \omega $ и преобразуем (4.2)
(4.3)
${{\varepsilon }^{r}}\left( t \right) = \left( {{{B}_{1}} + O\left( {\delta \omega } \right)} \right)\left( {\frac{{\exp \left( {it\delta \omega } \right) - 1}}{{\delta \omega }}} \right) + {{A}_{2}}\left( {{{r}_{{cr}}}} \right)\exp \left( { - i{{\omega }_{2}}t} \right)$Решение (4.3) при разложении в ряд по малому $\delta \omega $ нарастает пропорционально времени t. Такое разложение справедливо для всех $t \ll \delta \omega $, а в силу того, что в течении есть критический слой ${{U}_{0}}({{r}_{{cr}}}) = {{\omega }_{1}}$, то в окрестности него решение будет нарастать неограниченно долгое время.
Рассмотрим решение (4.2) в области между цилиндрами в устойчивом случае $\gamma > {{\gamma }_{*}}$. На рис. 3 представлена эволюция во времени радиальной компоненты поля смещения во всем пространстве течения при параметрах, ${{R}_{1}} = 1$ м, ${{R}_{2}} = 5$ м, ${{U}_{m}} = 1$ м2/c, ${{\Omega }_{0}} = 0$, $\gamma = 0.15$ и ${{V}_{0}} = 0.1$ м/c. На рис. 4 представлен график нарастания поля смещения вблизи критического слоя вдоль линии φ = 0.
Рис. 3.
Эволюция радиальной компоненты поля смещения в устойчивом случае: t = 3 (а), 15 (б), 40 с (в)
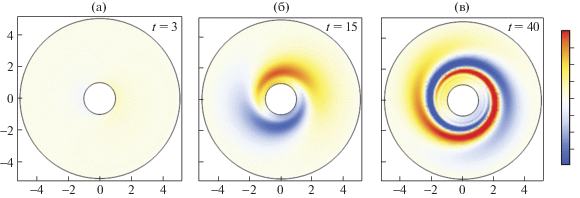
Рис. 4.
Эволюция радиальной компоненты поля смещения вдоль линии φ = 0 в устойчивом случае в одном масштабе: t = 10 (а), 40 (б), 150 с (в)

На рис. 3 и рис. 4 видно, что в отличие от решения спектральной задачи, имеющего логарифмическую особенность в критическом слое, в начальной задаче с гладкими начальными условиями особенность на конечных временах не возникает, но происходит интенсификация радиальной компоненты поля смещения в районе критического слоя и ее спиралевидное закручивание. Это связано с тем, что в решение начальной задачи вносят вклад все возмущения непрерывного спектра так, что особенность в критическом слое возникает лишь асимптотически при больших временах.
Поскольку в потенциальном потоке и потоке с постоянной завихренностью, в соответствии с (1.2), возмущение завихренности не возникает, то возмущения поля скорости в этом случае являются потенциальными. Это означает, что интенсификация смещения жидких частиц в окрестности критического слоя в переменных скорости и завихренности никак не проявляется. Тем не менее, при изменении параметров задачи, а именно, при добавлении скалярной или векторной примеси, например, малой неоднородности температуры или завихренности, возникает линейная связь между полем смещения и этими переменными. Предложенный в этой работе подход, основанный на применении поля смещения, позволяет провести анализ развития возмущений в системе с произвольным неоднородным вихревым течением.
ЗАКЛЮЧЕНИЕ
В работе получено решение начальной задачи для подвижного цилиндра, обтекаемого циркуляционным потоком несжимаемой идеальной жидкости в неподвижном кожухе. Показано, что в случае устойчивой системы, в начальной задаче с гладкими начальными условиями особенность в критическом слое возникает лишь асимптотически при больших временах, а на конечных временах происходит интенсификация радиальной компоненты поля смещения в районе критического слоя и ее спиралевидное закручивание. В случае неустойчивой системы экспоненциально нарастающее решение доминирует на больших временах, и интенсификация возмущений происходит во всем течении, а не только в области критического слоя.
Помимо самостоятельного интереса, связанного с решением задачи Коши для смещений жидких частиц, вызванных возмущениями цилиндра, предложенные здесь подходы могут служить основой для обобщения решения на случай неоднородной завихренности, которая будет рассмотрена в следующей работе.
Работа выполнена при поддержке гранта РНФ № 17-11-01271.
Список литературы
Копьев В.Ф., Чернышев С.А. Неустойчивость колеблющегося цилиндра в циркуляционном потоке идеальной жидкости // Изв. РАН. МЖГ. 2000. № 6. С. 78–92.
Копьев В.Ф., Чернышев С.А. Колебания вихревого кольца, возникновение в нем турбулентности и генерации звука // УФН. 2000. Т. 170. № 7. С. 713–742.
Копьев В.Ф., Чернышев С.А., Юдин М.А. Неустойчивость цилиндра в циркуляционном потоке несжимаемой идеальной жидкости // ПММ. 2017. Т. 81. № 2. С. 216–229.
Petrov A.G., Yudin M.A. Cylinder instability in bounded flow with constant vorticity // Conf. Ser.: J. Phys. 894. 2017.
Miles J.W. On the generation of surface waves by shear flow. Part 2 // J. Fluid Mech. 1959. V. 6. № 4. P. 568–582.
Belcher S.E., Hunt J.C.R. Turbulent flows over hills and waves. // Annu. Rev. Fluid Mech. 1998. № 30. P. 507–528.
Drazin P.G., Reid W.H. Hydrodynamic Stability. Cambridge: Univ. Press, 2004. P. 605.
Kopiev V.F., Chernyshev S.A. Vortex ring eigen-oscillations as a source of sound // J. Fluid Mech. 1997. V. 341. P. 19–47.
Копьев В.Ф., Чернышев С.А. Развитие методов лагранжевой и гамильтоновой механики применительно к задачам аэроакустики // Акуст. журн. 2018. Т. 64. № 6. С. 677–688.
Арнольд В.И. Об условии нелинейной устойчивости плоских стационарных криволинейных течений идеальной жидкости //Докл. АН СССР. 1965. Т. 162. № 5. С. 975–978.
Арнольд В.И. Вариационный принцип для трехмерных стационарных течений идеальной жидкости // ПММ. 1965. Т. 29. № 5. С. 846–851.
Копьев В.Ф., Чернышев С.А. О возможности интенсификации излучения звука крупномасштабным вихрем в слабом пространственно неоднородном внешнем поле // Акуст. журн. 1998. Т. 44. № 3. С. 373–379.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа