Известия РАН. Механика твердого тела, 2020, № 6, стр. 65-72

КРУЧЕНИЕ НЕОДНОРОДНЫХ ЦИЛИНДРИЧЕСКИХ И ПРИЗМАТИЧЕСКИХ СТЕРЖНЕЙ ИЗ ИДЕАЛЬНО ПЛАСТИЧЕСКОГО МАТЕРИАЛА ПРИ ЛИНЕАРИЗОВАННОМ УСЛОВИИ ПЛАСТИЧНОСТИ

Б. Г. Миронов^a, *, Ю. Б. Миронов^b, **

^a Российский университет транспорта
Москва, Россия

^b Московский технический университет связи и информатики
Москва, Россия

^* E-mail: mbg.chspu@yandex.ru
^** E-mail: i.b.mironov@mtuci.ru

Поступила в редакцию 01.06.2020
После доработки 18.06.2020
Принята к публикации 30.06.2020

DOI: 10.31857/S0572329920060100

Полный текст (PDF)

Аннотация

Рассмотрены общие соотношения теории кручения неоднородных стержней из идеального жесткопластического материала. В случае линеаризованного условия пластичности получены интегралы, определяющие напряженное и деформированное состояния идеального жесткопластического неоднородного стержня при кручении. Построено поле характеристик основных соотношений, найдены линии разрыва напряжений.

Ключевые слова: пластичность, неоднородность, кручение, деформация, напряжение

Кручение представляет собой один из видов деформации тел, характеризующийся взаимным поворотом его поперечных сечений под влиянием моментов, действующих в этих сечениях. Кручение стержней довольно часто встречается в инженерной практике, особенно в машиностроении. Теория кручения изотропных и анизотропных стержней из идеального жесткопластического материала изложена в работах [1–4]. Переход к случаю стержня из неоднородного материала приводит к определенным трудностям: задачу в общем случае невозможно проинтегрировать. Кручение составных призматических и цилиндрических стержней рассмотрены в [5, 7]. В работе [6] исследованы общие соотношения теории кручения стержней из идеального жесткопластического материала.

Соотношения теории кручения неоднородных цилиндрических и призматических стержней из идеально пластического материала [6] могут быть записаны в виде:

(1)

$\begin{array}{*{20}{c}} {{{{\sigma }}_{x}} = {{{\sigma }}_{y}} = {{{\sigma }}_{z}} = {{{\tau }}_{{xy}}} = 0} \\ {{{{\tau }}_{{xz}}} = {{{\tau }}_{{xz}}}(x,~y),\quad {{{\tau }}_{{yz}}} = {{{\tau }}_{{yz}}}(x,~y)} \end{array}$

– уравнение равновесия

(2)

$\frac{{\partial {{{\tau }}_{{xz}}}}}{{\partial x}} + \frac{{\partial {{{\tau }}_{{yz}}}}}{{\partial y}} = 0$

– условие пластичности

(3)

$f\left( {{{{\tau }}_{{xz}}},{{{\tau }}_{{yz}}},x,y} \right) = 0$

– соотношения ассоциированного закона пластического течения

(4)

$\frac{{{{{\varepsilon }}_{{xz}}}}}{A} = \frac{{{{{\varepsilon }}_{{yz}}}}}{B},\quad {{{\varepsilon }}_{x}} = {{{\varepsilon }}_{y}} = {{{\varepsilon }}_{z}} = {{{\varepsilon }}_{{xy}}} = 0$

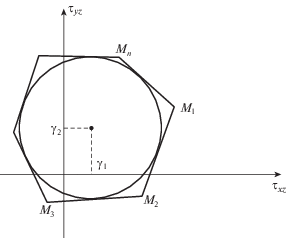
где σ_ij – компоненты напряжения, ε_ij – компоненты скорости деформации,

(5)

$A = \frac{{\partial f}}{{\partial {{{\tau }}_{{xz}}}}}({{{\tau }}_{{xz}}},{{{\tau }}_{{yz}}},x,y),\quad ~B = \frac{{\partial f}}{{\partial {{{\tau }}_{{yz}}}}}({{{\tau }}_{{xz}}},{{{\tau }}_{{yz}}},x,y)$

Условие пластичности (3) в плоскости τ_xz, τ_yz при фиксированных x, y представляет замкнутую выпуклую кривую (рис. 1), начало координат находится в области, ограниченной данной кривой$.$

Рис. 1

Предположим, что кривая текучести (3) заменена замкнутой ломанной ${{M}_{1}}{{M}_{2}}{{M}_{3}} \ldots {{M}_{n}}{{M}_{1}}$ (рис. 1)

(6)

${{A}_{i}}{{{\tau }}_{{xz}}} + {{B}_{i}}{{{\tau }}_{{yz}}} = {{K}_{i}}$

где $~{{A}_{i}} = \frac{{\partial f}}{{\partial {{{\tau }}_{{xz}}}}}({\tau }_{{xz}}^{{i0}},{\tau }_{{yz}}^{{i0}},{{x}_{0}},{{y}_{0}}),{{B}_{i}} = \frac{{\partial f}}{{\partial {{{\tau }}_{{yz}}}}}({\tau }_{{xz}}^{{i0}},{\tau }_{{yz}}^{{i0}},{{x}_{0}},{{y}_{0}}),f({\tau }_{{xz}}^{{i0}},{\tau }_{{yz}}^{{i0}},{{x}_{0}},{{y}_{0}}) = 0$

${{K}_{i}} = {{A}_{i}}{\tau }_{{xz}}^{i} + {{B}_{i}}{\tau }_{{yz}}^{i},\quad {{A}_{i}} = {\mu }\frac{{\partial f}}{{\partial {{{\tau }}_{{xz}}}}}({\tau }_{{xz}}^{i},{\tau }_{{yz}}^{i},x,y),\quad {{B}_{i}} = {\mu }\frac{{\partial f}}{{\partial {{{\tau }}_{{yz}}}}}({\tau }_{{xz}}^{i},{\tau }_{{yz}}^{i},x,y)$

$f({\tau }_{{xz}}^{i},{\tau }_{{yz}}^{i},x,y) = 0,\quad {\mu } - {\text{const}},\quad i = 1,2, \ldots ,{\text{n}}$

Условие (6) представляет на некотором отрезке линеаризованное условие пластичности (3). Дифференцируя уравнение (6) по переменной y, получим

(7)

${{A}_{i}}\frac{{\partial {{{\tau }}_{{xz}}}}}{{\partial y}} + {{B}_{i}}\frac{{\partial {{{\tau }}_{{yz}}}}}{{\partial y}} = \frac{{\partial {{K}_{i}}}}{{\partial y}}$

С учетом (2) из уравнения (7) имеем

(8)

${{A}_{i}}\frac{{\partial {{{\tau }}_{{xz}}}}}{{\partial y}} - {{B}_{i}}\frac{{\partial {{{\tau }}_{{xz}}}}}{{\partial x}} = \frac{{\partial {{K}_{i}}}}{{\partial y}}$

Система уравнений для определения характеристик соотношения (8) и соотношений вдоль характеристик имеет вид

(9)

$\frac{{dx}}{{ - {{B}_{i}}}} = \frac{{dy}}{{{{A}_{i}}}} = \frac{{d{{{\tau }}_{{xz}}}}}{{\frac{{\partial {{K}_{i}}}}{{\partial y}}}}$

Из (9) следует, что прямые

(10)

${{A}_{i}}x + {{B}_{i}}y = {{C}_{{i1}}}\quad ({{C}_{{i1}}} = {\text{const}})$

являются характеристиками соотношения (8). Вдоль характеристик (10) справедливы следующие соотношения

(11)

${{A}_{i}}{{{\tau }}_{{xz}}} = \int {\frac{{\partial {{K}_{i}}}}{{\partial y}}\left( {{\alpha },y} \right)dy,\quad - {\kern 1pt} {{B}_{i}}{{{\tau }}_{{xz}}} = \int {\frac{{\partial {{K}_{i}}}}{{\partial y}}\left( {x,{\beta }} \right)dx} } $

где ${\alpha } = \frac{1}{{{{A}_{i}}}}\left( {{{C}_{{i1}}} - {{B}_{i}}y} \right),~~{\beta } = \frac{1}{{{{B}_{i}}}}\left( {{{C}_{{i1}}} - {{A}_{i}}x} \right)$

Аналогично дифференцируя уравнение (6) по переменной x, с учетом (2) получим, что вдоль характеристик (10) справедливы следующие соотношения для компонент напряжения

(12)

$ - {{A}_{i}}{{{\tau }}_{{yz}}} = \int {\frac{{\partial {{K}_{i}}}}{{\partial x}}\left( {{\alpha },y} \right)dy,\quad {{B}_{i}}{{{\tau }}_{{yz}}} = \int {\frac{{\partial {{K}_{i}}}}{{\partial x}}\left( {x,{\beta }} \right)dx} } $

Рассматривая условие (6) в качестве пластического потенциала, получим вместо (4) соотношение

(13)

$\frac{{{{{\varepsilon }}_{{xz}}}}}{{{{A}_{i}}}} = \frac{{{{{\varepsilon }}_{{yz}}}}}{{{{B}_{i}}}}$

Интегрируя соотношение (6) и часть соотношений (4) и учитывая, что в начальный момент закручивания компоненты деформации e_ij равны 0, получим

(14)

$\frac{{{{e}_{{xz}}}}}{{{{A}_{i}}}} = \frac{{{{e}_{{yz}}}}}{{{{B}_{i}}}},\quad {{e}_{x}} = {{e}_{y}} = {{e}_{z}} = {{e}_{{xy}}} = 0$

Из (14) следует

(15)

${{B}_{i}}{{e}_{{xz}}} - {{A}_{i}}{{e}_{{yz}}} = 0$

Предположим, что компоненты перемещения u, $v$, w имеют вид

(16)

$u = {\theta }yz,\quad {v} = - {\theta }xz,\quad w = w\left( {x,y} \right)$

где θ – крутка, w – депланация.

Выражая компоненты деформации через компоненты перемещения

(17)

${{e}_{{xz}}} = \frac{1}{2}\left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right),~\quad {{e}_{{yz}}} = \frac{1}{2}\left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial z}}} \right)$

из (15), (16) получим

(18)

$ - {{B}_{i}}\frac{{\partial w}}{{\partial x}} + {{A}_{i}}\frac{{\partial w}}{{\partial y}} = {\theta }\left( {{{A}_{i}}x + {{B}_{i}}y} \right)$

Из (18) следует, что прямые (10) являются характеристиками. Вдоль характеристик (10) имеют место соотношения

(19)

${{B}_{i}}w + {\theta }{{C}_{{i1}}}x = {{C}_{{i2}}}\quad {\text{или}}\quad {{A}_{i}}w - {\theta }{{C}_{{i1}}}y = {{C}_{{i3}}}$

где ${{C}_{{i2}}},{{C}_{{i3}}} = {\text{const}}~$ вдоль характеристики.

Дифференцируя соотношение (18) по переменной x, получим уравнение

(20)

$ - {{B}_{i}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial w}}{{\partial x}}} \right) + {{A}_{i}}\frac{\partial }{{\partial y}}\left( {\frac{{\partial w}}{{\partial x}}} \right) = {\theta }{{A}_{i}}$

Из уравнения (20) следует, что вдоль характеристик (10) справедливы соотношения

(21)

${{B}_{i}}\frac{{\partial w}}{{\partial x}} + {\theta }{{A}_{i}}x = {{C}_{{i4}}}\quad {\text{или}}\quad \frac{{\partial w}}{{\partial x}} - {\theta }y = {{C}_{{i5}}}$

где ${{C}_{{i4}}},{{C}_{{i5}}} = {\text{const}}$ вдоль характеристики.

Аналогично дифференцируя соотношение (18) по переменной y, получим уравнение

(22)

$ - {{B}_{i}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial w}}{{\partial y}}} \right) + {{A}_{i}}\frac{\partial }{{\partial y}}\left( {\frac{{\partial w}}{{\partial y}}} \right) = {\theta }{{B}_{i}}$

Из уравнения (22) следует, что вдоль характеристик (10) справедливы соотношения

(23)

$\frac{{\partial w}}{{\partial x}} + {\theta }x = {{C}_{{i6}}}\quad {\text{или}}\quad {{A}_{i}}\frac{{\partial w}}{{\partial y}} - {\theta }{{B}_{i}}y = {{C}_{{i7}}}$

где ${{C}_{{i6}}},{{C}_{{i7}}} = {\text{const}}$ вдоль характеристики.

Используя второе соотношение (21) и первое соотношение (23) получим, что вдоль характеристик (10) справедливы соотношения

(24)

${{e}_{{xz}}} - {\theta }y = \frac{1}{2}{{C}_{{i5}}},\quad {{e}_{{yz}}} + {\theta }x = \frac{1}{2}{{C}_{{i6}}}$

Следует отметить, что из соотношений (24), (10), (15) вытекает

(25)

${{A}_{i}}{{C}_{{i6}}} - {{B}_{i}}{{C}_{{i5}}} = 2{\theta }{{C}_{{i1}}}$

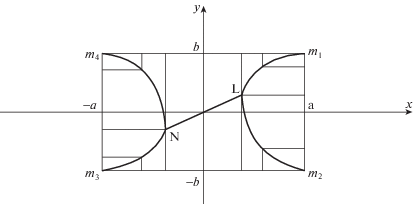
Рассмотрим кручение стержня прямоугольного сечения m₁m₂m₃m₄ со сторонами 2a и 2b (рис. 2). На контуре сечения вектор касательного напряжения ${\mathbf{\tau }} = \left( {{{{\tau }}_{{xz}}},{{{\tau }}_{{yz}}}} \right)$ параллелен контуру.

Рис. 2

В случае изотропного идеально пластического материала характеристики направлены перпендикулярно к контуру. В рассматриваемом случае направление характеристик (10) фиксировано, поэтому для данного контура сечения стержня всегда можно выбрать линеаризованное условие пластичности (6) таким образом, чтобы характеристики оставались перпендикулярными к контуру. Для этого A_i, B_i в условии (6) необходимо выбрать так, чтобы вектор ${{{\mathbf{n}}}_{{\mathbf{i}}}} = \left( {{{A}_{i}},{{B}_{i}}} \right)$ был параллелен отрезку m_im_i _{+ 1} контура (рис. 2).

Здесь мы имеем четыре семейства характеристик

(26)

${{A}_{1}}x + {{B}_{1}}y = {{C}_{{11}}}$

(27)

${{A}_{2}}x + {{B}_{2}}y = {{C}_{{21}}}$

(28)

${{A}_{3}}x + {{B}_{3}}y = {{C}_{{31}}}$

(29)

${{A}_{4}}x + {{B}_{4}}y = {{C}_{{41}}}$

Для того, чтобы характеристики (26) были ортогональны отрезку m₁m₂ контура сечения стержня, следует положить A₁ = 0, B₁ = –1. Условие пластичности (6) принимает вид

(30)

${{{\tau }}_{{yz}}} = - {{K}_{1}}$

Характеристики (26) запишутся в виде

(31)

$y = - {{C}_{{11}}}$

Из (25) следует

(32)

${{C}_{{15}}} = 2{\theta }{{C}_{{11}}}$

Тогда из (11), (30) и (2) вдоль характеристик (31) имеем

(33)

${{{\tau }}_{{yz}}} = - {{K}_{1}},\quad {{{\tau }}_{{xz}}} = \int {\frac{{\partial {{K}_{1}}}}{{\partial y}}\left( {x, - {{C}_{{11}}}} \right)dx = {{k}_{1}}} $

Для того, чтобы характеристики (27) были ортогональны отрезку m₂m₃ контура сечения стержня, следует положить A₂ = –1, B₂ = 0. Условие пластичности (6) принимает вид

(34)

${{{\tau }}_{{xz}}} = - {{K}_{2}}$

Характеристики (27) запишутся в виде

(35)

$x = - {{C}_{{21}}}$

Из (25) следует

(36)

${{C}_{{26}}} = - 2{\theta }{{C}_{{21}}}$

Тогда из (12), (34) и (2) вдоль характеристик (35) имеем

(37)

${{{\tau }}_{{xz}}} = - {{K}_{2}},\quad {{{\tau }}_{{yz}}} = \int {\frac{{\partial {{K}_{2}}}}{{\partial x}}\left( { - {{C}_{{21}}},y} \right)dy = {{k}_{2}}} $

Для того, чтобы характеристики (28) были ортогональны отрезку m₃m₄ контура сечения стержня, следует положить A₃ = 0, B₃ = 1. Условие пластичности (6) принимает вид

(38)

${{{\tau }}_{{yz}}} = {{K}_{3}}$

Характеристики (28) запишутся в виде

(39)

$y = {{C}_{{31}}}$

Из (25) следует

(40)

${{C}_{{35}}} = - 2{\theta }{{C}_{{31}}}$

Тогда из (11), (38) и (2) вдоль характеристик (39) имеем

(41)

${{{\tau }}_{{yz}}} = {{K}_{3}},\quad {{{\tau }}_{{xz}}} = - \int {\frac{{\partial {{K}_{3}}}}{{\partial y}}\left( {x,{{C}_{{31}}}} \right)dx = - {{k}_{3}}} $

Для того, чтобы характеристики (29) были ортогональны отрезку m₄m₁ контура сечения стержня, следует положить A₄ = 1, B₄ = 0. Условие пластичности (6) принимает вид

(42)

${{{\tau }}_{{xz}}} = {{K}_{4}}$

Характеристики (29) запишутся в виде

(43)

$x = {{C}_{{41}}}$

Из (25) следует

(44)

${{C}_{{46}}} = 2{\theta }{{C}_{{41}}}$

Тогда из (12), (42) и (2) вдоль характеристик (41) имеем

(45)

${{{\tau }}_{{xz}}} = {{K}_{4}},\quad {{{\tau }}_{{yz}}} = - \int {\frac{{\partial {{K}_{4}}}}{{\partial x}}\left( {{{C}_{{41}}},y} \right)dy = - {{k}_{4}}} $

Особо следует остановиться на линиях разрыва напряжений (линии ${{m}_{1}}L,~~{{m}_{2}}L,~{{m}_{3}}N$, ${{m}_{4}}N$, LN на рис. 2), которые возникают в случае, когда через данную точку сечения проходят две и более характеристики.

Линии разрыва напряжений являются следом исчезающих жестких областей. На них всегда выполняются соотношения

(46)

${{e}_{{xz}}} = {{e}_{{yz}}} = 0$

Кривая m₁L есть линия разрыва напряжений, выходящая из вершины m₁ контура сечения стержня и образованная за счет пересечения семейства характеристик (31) и (43).

Из (33) и (45) имеем уравнение линии разрыва напряжений m₁L

(47)

$\frac{{dx}}{{{{K}_{4}} - {{k}_{1}}}} = \frac{{dy}}{{{{K}_{1}} - {{k}_{4}}}}$

Кривая m₂L есть линия разрыва напряжений, выходящая из вершины m₂ контура сечения стержня и образованная за счет пересечения семейства характеристик (31) и (35).

Из (33) и (37) имеем уравнение линии разрыва напряжений m₂L

(48)

$\frac{{dx}}{{ - {{K}_{2}} - {{k}_{1}}}} = \frac{{dy}}{{{{K}_{1}} + {{k}_{2}}}}$

Кривая m₃N есть линия разрыва напряжений, выходящая из вершины m₃ контура сечения стержня и образованная за счет пересечения семейства характеристик (35) и (39).

Из (37) и (41) имеем уравнение линии разрыва напряжений m₃N

(49)

$\frac{{dx}}{{{{K}_{2}} - {{k}_{3}}}} = \frac{{dy}}{{{{K}_{3}} - {{k}_{2}}}}$

Кривая m₄N есть линия разрыва напряжений, выходящая из вершины m₄ контура сечения стержня и образованная за счет пересечения семейства характеристик (39) и (43).

Из (41) и (45) имеем уравнение линии разрыва напряжений m₄N

(50)

$\frac{{dx}}{{ - {{K}_{4}} - {{k}_{3}}}} = \frac{{dy}}{{{{K}_{3}} + {{k}_{4}}}}$

Кривая NL есть линия разрыва напряжений, образованная за счет пересечения семейства характеристик (35) и (43).

Из (37) и (45) имеем уравнение линии разрыва напряжений NL

(51)

$\frac{{dx}}{{{{K}_{4}} + {{K}_{2}}}} = \frac{{dy}}{{ - {{k}_{4}} - {{k}_{2}}}}$

Рассмотрим случай, кода условие пластичности (3) имеет вид

(52)

${{\left( {{{{\tau }}_{{xz}}} - {{{\gamma }}_{1}}} \right)}^{2}} + {{\left( {{{{\tau }}_{{yz}}} - {{{\gamma }}_{2}}} \right)}^{2}} = {{k}_{0}}$

где ${{{\gamma }}_{1}} = {{a}_{1}}x + {{b}_{1}}y,{{{\gamma }}_{2}} = {{a}_{2}}x + {{b}_{2}}y,{{k}_{0}} = {\text{const}}$

Согласно (6), (33), (37), (41), (45) компоненты напряжения определяются следующим образом:

– в области ${{m}_{1}}L{{m}_{2}}$

(53)

${{{\tau }}_{{xz}}} = - {{b}_{2}}\left( {x - a} \right),\quad {{{\tau }}_{{yz}}} = - {{k}_{0}} + {{a}_{2}}x + {{b}_{2}}y$

– в области ${{m}_{2}}LN{{m}_{3}}$

(54)

${{\tau }_{{xz}}} = - {{k}_{0}} + {{a}_{1}}x + {{b}_{1}}y,\quad {{{\tau }}_{{yz}}} = ~ - {{a}_{1}}\left( {y + b} \right)$

– в области ${{m}_{3}}N{{m}_{4}}$

(55)

${{{\tau }}_{{xz}}} = - {{b}_{2}}\left( {x + a} \right),\quad {{{\tau }}_{{yz}}} = {{k}_{0}} + {{a}_{2}}x + {{b}_{2}}y$

– в области ${{m}_{4}}NL{{m}_{1}}$

(56)

${{{\tau }}_{{xz}}} = {{k}_{0}} + {{a}_{1}}x + {{b}_{1}}y,\quad {{{\tau }}_{{yz}}} = ~ - {{a}_{1}}\left( {y - b} \right)$

Из (53), (54), (55), (56) получим уравнения линий разрыва напряжений

(57)

${{m}_{1}}L~{\text{:\;}}\,~{{a}_{2}}{{x}^{2}} + 2\left( {{{a}_{1}} + {{b}_{2}}} \right)xy + {{b}_{1}}{{y}^{2}} - 2\left( {{{k}_{0}} + {{a}_{1}}b} \right)x + 2\left( {{{k}_{0}} - {{b}_{2}}a} \right)y = r$

(58)

${{m}_{2}}L~{\text{:\;}}\,~{{a}_{2}}{{x}^{2}} + 2\left( {{{a}_{1}} + {{b}_{2}}} \right)xy + {{b}_{1}}{{y}^{2}} - 2\left( {{{k}_{0}} - {{a}_{1}}b} \right)x - 2\left( {{{k}_{0}} + {{b}_{2}}a} \right)y = r$

(59)

${{m}_{3}}N{\text{:\;}}\,~{{a}_{2}}{{x}^{2}} + 2\left( {{{a}_{1}} + {{b}_{2}}} \right)xy + {{b}_{1}}{{y}^{2}} + 2\left( {{{k}_{0}} + {{a}_{1}}b} \right)x - 2\left( {{{k}_{0}} - {{b}_{2}}a} \right)y = r$

(60)

${{m}_{4}}N~{\text{:}}~~{{a}_{2}}{{x}^{2}} + 2\left( {{{a}_{1}} + {{b}_{2}}} \right)xy + {{b}_{1}}{{y}^{2}} + 2\left( {{{k}_{0}} - {{a}_{1}}b} \right)x + 2\left( {{{k}_{0}} + {{b}_{2}}a} \right)y = r$

(61)

$LN{\text{:}}\,~~ - {{a}_{1}}bx + {{k}_{0}}y = 0$

где $~r = {{a}_{2}}{{a}^{2}} - 2{{k}_{0}}\left( {a - b} \right) + {{b}_{1}}{{b}^{2}}$

Таким образом, в работе:

получены интегралы, определяющие напряженное и деформированное состояния неоднородного идеального жесткопластического стержня при кручении для линеаризованного условия пластичности, найдены характеристики основных соотношений и соотношения для компонент напряжений и деформаций;

исследовано предельное состояние неоднородного идеального жесткопластического стержня с прямоугольным сечением: определено поле характеристик основных соотношений, найдены соотношения вдоль характеристик и линии разрыва напряжений.

Список литературы

Соколовский В.В. Теория пластичности. Москва: Высшая школа, 1969. 608 с.
Ивлев Д.Д. Механика пластических сред. В 2 т. Т 2. Общие вопросы. Жесткопластическое и упругопластическое состояние тел. Упрочнение. Деформационные теории. Сложные среды. Москва: Физматлит, 2002. 448 с.
Прагер В. Теория идеально пластических тел. Москва: ИЛ, 1956. 398 с.
Быковцев Г.И. Теория пластичности. Владивосток: Дальнаука, 1998. 528 с.
Ольшак В. Теория пластичности неоднородных тел. Москва: Мир, 1964. 156 с.
Миронов Б.Г. К теории кручения неоднородных стержней // Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. Серия: Механика предельного состояния. 2014. № 4 (22). С. 236–240.
Mironov B.G. Torsion anisotropic and composite cylindrical rod //Journal of Physics: Conference Series. 1203. 2019. 012009.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал

Известия РАН. Механика твердого тела, 2020, № 6, стр. 65-72

КРУЧЕНИЕ НЕОДНОРОДНЫХ ЦИЛИНДРИЧЕСКИХ И ПРИЗМАТИЧЕСКИХ СТЕРЖНЕЙ ИЗ ИДЕАЛЬНО ПЛАСТИЧЕСКОГО МАТЕРИАЛА ПРИ ЛИНЕАРИЗОВАННОМ УСЛОВИИ ПЛАСТИЧНОСТИ

(1)

(2)

(3)

(4)

(5)

Рис. 1

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

Рис. 2

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

(47)

(48)

(49)

(50)

(51)

(52)

(53)

(54)

(55)

(56)

(57)

(58)

(59)

(60)

(61)

Свяжитесь с нами

Время работы