Известия РАН. Механика твердого тела, 2019, № 4, стр. 129-140
О ВЕЛИЧИНАХ, ХАРАКТЕРИЗУЮЩИХ СТЕПЕНЬ УПРУГОЙ АНИЗОТРОПИИ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНЫХ ГОРНЫХ ПОРОД; РОЛЬ СДВИГОВОГО МОДУЛЯ
А. Б. Журавлев a, *, К. Б. Устинов a
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: ustinov@ipmnet.ru
Поступила в редакцию 16.10.18
После доработки 16.10.18
Принята к публикации 22.10.18
Аннотация
Исследовано влияние упругих констант трансверсально изотропных пород на величины концентраций напряжений на контуре скважины. Показано, что при равнокомпонентном исходном напряженном состоянии основным параметром, характеризующим отклонение концентрации напряжения на контуре скважины от концентрации, характерной для изотропного тела, является отношение независимого сдвигового модуля в плоскости, нормальной к плоскости изотропии, к величине сдвигового модуля, характерного для одного из подклассов трансверсально изотропной среды, выделенных Сен-Венаном, являющегося комбинацией других упругих констант. При данном отношении, равном единице, концентрации напряжений для изотропной и анизотропной среды совпадают. Известный факт близости данного отношения к единице для большинства трансверсально изотропных горных пород позволяет использовать для них в первом приближении упругое решение для изотропного тела. Показано, что близость к единице отношения независимого сдвигового модуля к комбинациям остальных упругих констант, характерными для других подклассов, выделенных Сен-Венаном, также наблюдается для большинства пород, хотя и с несколько меньшей точностью.
1. Введение. При решении практических задач важным вопросом является выявление характера и степени анизотропии. При слабо выраженной анизотропии различие между результатами, полученными с ее учетом, и результатами для изотропной среды, несущественно. Количественно степень анизотропии определяется, очевидно, через некоторые безразмерные параметры, характеризующие свойства среды вдоль различных направлений. В случае проницаемости, теплопроводности, электропроводности и других свойств, характеризуемых тензорами второго ранга, компоненты которых выражаются через три независимые величины – главные значения, в качестве величины, характеризующей степень анизотропии естественно принять отношение максимального и минимального из главных значений (или произвольную функцию от этого отношения). В случае трансверсальной изотропии, характерной для слоистых сред число независимых величин, определяющих тензорные свойства второго ранга, сокращается до двух. Для тензора проницаемости это величины проницаемости в плоскости изотропии и по нормали к ней. Отклонение отношения проницаемостей вдоль этих направлений от единицы и будет характеризовать степень анизотропии.
Для упругости, характеризуемой тензором четвертого ранга, вопрос определения степени анизотропии становится не столь очевидным. Даже в рассматриваемом случае трансверсальной изотропии число независимых величин, определяющих упругие свойства равно пяти, и из них можно составить четыре независимые безразмерные комбинации. Для двумерной задачи (плоская деформация и плоское напряженное состояние), как показано Лехницким [1, 2], степень анизотропии описывается двумя независимыми параметрами. Обычно, для трансверсально изотропных сред в качестве наиболее существенного параметра принимают отношение модулей в продольном и поперечном направлении [3]. Данный выбор, несмотря на кажущуюся естественность, как будет показано ниже, не является столь однозначным и оптимальным.
С практической точки зрения наибольший интерес представляют величины, характеризующие отклонения в распределении полей напряжений по сравнению с распределениями напряжений в изотропной среде, а не формальные комбинации упругих констант. Поскольку едва ли можно ожидать нахождение универсального параметра, пригодного для произвольных геометрий и граничных условий, логично рассмотреть наиболее характерные, часто встречающиеся, и по возможности простые задачи. К таким задачам, в первую очередь следует отнести задачи о концентрации напряжений на контуре цилиндрических выработок (скважин), расположенных горизонтально, либо наклонно по отношению к осям упругой анизотропии. Далее будут рассмотрены случаи скважины в трансверсально изотропном массиве, расположенной вдоль плоскости изотропии и под наклоном к ней.
2. Общие соотношения. Закон Гука для трансверсальной анизотропии, характерной для большинства осадочных пород обычно записывается в виде [1, 2]
(2.1)
$\begin{gathered} \varepsilon _{{11}}^{{}} = {{s}_{{11}}}{{\sigma }_{{11}}} + {{s}_{{12}}}{{\sigma }_{{22}}} + {{s}_{{13}}}{{\sigma }_{{33}}} \\ \varepsilon _{{22}}^{{}} = {{s}_{{12}}}{{\sigma }_{{11}}} + {{s}_{{12}}}{{\sigma }_{{22}}} + {{s}_{{13}}}{{\sigma }_{{33}}} \\ \varepsilon _{{33}}^{{}} = {{s}_{{13}}}{{\sigma }_{{11}}} + {{s}_{{13}}}{{\sigma }_{{22}}} + {{s}_{{33}}}{{\sigma }_{{33}}} \\ 2\varepsilon _{{12}}^{{}} = {{s}_{{66}}}{{\sigma }_{{12}}} \\ 2\varepsilon _{{13}}^{{}} = {{s}_{{44}}}{{\sigma }_{{13}}} \\ 2\varepsilon _{{23}}^{{}} = {{s}_{{44}}}{{\sigma }_{{23}}} \\ \end{gathered} $Здесь $\varepsilon _{{ij}}^{{}},{{\sigma }_{{ij}}}$ – компоненты тензоров деформации и напряжения в системе координат с осью ${{x}_{3}}$ направленной по нормали к плоскости изотропии; ${{s}_{{ij}}}$ – компоненты матрицы податливости, составленной из компонент тензора податливости, причем
Компоненты матрицы податливости выражаются через технические константы – модули Юнга в плоскости изотропии и по нормали к ней ${{E}_{1}},\,\,{{E}_{3}}$; коэффициенты Пуассона ${{\nu }_{{12}}},\,\,{{\nu }_{{13}}},\,\,{{\nu }_{{31}}}$ (два последних связаны между собой); модули сдвига в плоскости изотропии и в любой плоскости, нормальной к ней, ${{G}_{{12}}},\,\,{{G}_{{13}}}$ (первый из них не является независимой величиной)
(2.2)
$\begin{gathered} {{G}_{{13}}} = s_{{44}}^{{ - 1}},\quad {{G}_{{12}}} = s_{{12}}^{{ - 1}},\quad {{E}_{1}} = s_{{11}}^{{ - 1}},\quad {{E}_{3}} = s_{{33}}^{{ - 1}}, \\ - \frac{{{{\nu }_{{12}}}}}{{{{E}_{1}}}} = {{s}_{{12}}},\quad - \frac{{{{\nu }_{{13}}}}}{{{{E}_{1}}}} = - \frac{{{{\nu }_{{31}}}}}{{{{E}_{3}}}} = {{s}_{{13}}} \\ \end{gathered} $Отметим, что при использовании технических констант наличие двух коэффициентов Пуассона в плоскости, нормальной к плоскости изотропии, ${{\nu }_{{31}}},\,\,{{\nu }_{{13}}}$, вызывает неудобства и является потенциальным источником ошибок.
3. Скважина с осью, лежащей в плоскости изотропии. Равнокомпонентное исходное напряженное состояние. Задача о цилиндрическом отверстии, ось которого совпадает с одной из главных осей тензора упругости, в плоской постановке была решена Лехницким и Солдатовым [4] (см. также [1, 2]). Используя указанное решение, концентрацию напряжений на контуре цилиндрического отверстия (скважины) (отношение окружных напряжений на контуре к напряжениям, приложенным на бесконечности) в трансверсально изотропной среде, ось которого лежит в плоскости изотропии, а среда сжата на бесконечности гидростатическими напряжениями, $\sigma _{{xx}}^{\infty } = \sigma _{{zz}}^{\infty }$, можно записать следующим образом
(3.1)
${{f}_{0}}\left( \theta \right) = \frac{{\sigma _{{\theta \theta }}^{{}}}}{{\sigma _{{zz}}^{\infty }}} = 1 + \frac{{{{E}_{\theta }}}}{{{{E}_{1}}}}\{ n - k + n\left( {k - 1} \right){{\cos }^{2}}\theta + [{{(k + 1)}^{2}} - {{n}^{2}}]{{\sin }^{2}}\theta {{\cos }^{2}}\theta \} $Здесь ${{E}_{\theta }}$ – модуль упругости в направлении касательной к контуру.
(3.2)
$\frac{{{{E}_{\theta }}}}{{{{E}_{1}}}} = {{({{\sin }^{4}}\theta + m{{\sin }^{2}}\theta {{\cos }^{2}}\theta + {{k}^{2}}{{\cos }^{4}}\theta {\text{)}}}^{{ - 1}}}$Угол $\theta $ отсчитывается от оси ${{x}_{1}}$ по направлению оси ${{x}_{3}}$. Константы $k,m,\,n$ определены следующим образом
(3.3)
${{k}^{2}} = \frac{{{{s}_{{33}}}}}{{{{s}_{{11}}}}} = \frac{{{{E}_{1}}}}{{{{E}_{3}}}},\quad m = \frac{{2{{s}_{{13}}} + {{s}_{{44}}}}}{{{{s}_{{11}}}}} = \frac{{{{E}_{1}}}}{{{{G}_{{13}}}}} - 2{{\nu }_{{13}}},\quad {{n}^{2}} = 2k + m$(3.4)
${{k}^{2}} = \frac{{{{\beta }_{{33}}}}}{{{{\beta }_{{11}}}}},\quad m = \frac{{2{{\beta }_{{13}}} + {{\beta }_{{44}}}}}{{{{\beta }_{{11}}}}} = \frac{{2{{s}_{{13}}} + {{s}_{{44}}}}}{{{{s}_{{11}}}}} - {{\left( {\frac{{{{s}_{{12}}} - {{s}_{{13}}}}}{{{{s}_{{11}}}}}} \right)}^{2}},\quad {{n}^{2}} = 2k + m$Здесь постоянные $\beta $ имеют смысл модифицированных для условий плоской деформации постоянных:
(3.5)
${{\beta }_{{11}}} = {{s}_{{11}}} - \frac{{s_{{12}}^{2}}}{{{{s}_{{11}}}}},\quad {{\beta }_{{33}}} = {{s}_{{33}}} - \frac{{s_{{13}}^{2}}}{{{{s}_{{11}}}}},\quad {{\beta }_{{13}}} = {{s}_{{13}}} - \frac{{{{s}_{{13}}}{{s}_{{12}}}}}{{{{s}_{{11}}}}},\quad {{\beta }_{{44}}} = {{s}_{{44}}}$Отметим, что во второй формуле (3.4) отношения $ - {{s}_{{12}}}{\text{/}}{{s}_{{11}}}$ и $ - {{s}_{{13}}}{\text{/}}{{s}_{{11}}}$ суть коэффициенты Пуассона для плоскостей ${{x}_{1}}{{x}_{2}}$ и ${{x}_{1}}{{x}_{3}}$, соответственно. Для горных пород значения коэффициентов Пуассона редко превосходят значение 0.3, и разность их значений в разных плоскостях обычно не превосходит значение 0.1. Значение же $\left( {2{{s}_{{12}}} + {{s}_{{44}}}} \right){\text{/}}{{s}_{{11}}}$ имеет порядок единицы (равно двум для изотропного тела). Поэтому вклад второго члена во второй формуле (3.4) обычно составляет менее одного процента от вклада первого члена, и в большинстве случаев им можно пренебречь.
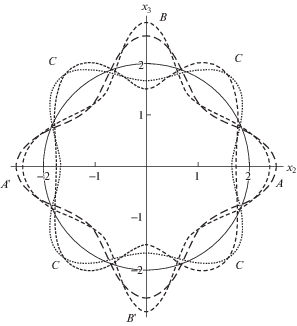
Согласно решению (3.1) экстремальные концентрации напряжений на контуре достигаются на контуре в точках $A,\,A'$ соответствующих полярным углам $\theta = 0,\,\,\pi $ и в точках $B,\,B'$ соответствующих полярным углам $\theta = \pm \;\pi {\text{/}}2$, то есть на главных осях тензора упругости (податливости) (рис. 1 )
(3.6)
${{f}_{A}} = 1 + \frac{{n - 1}}{k} = 1 + \frac{{\sqrt {2k + m} - 1}}{k},\quad {{f}_{B}} = 1 + n - k = 1 + \sqrt {2k + m} - k$,Из решения (3.1) следует, что при условии
концентрация напряжений на контуре всюду равно двойке, что совпадает с решением для изотропной среды.Условие (3.7) может быть записано через упругие постоянные следующим образом
для плоского напряженного состояния и(3.9)
${{s}_{{55}}} = \frac{1}{{G_{{13}}^{{''}}}} = {{\beta }_{{11}}} + {{\beta }_{{33}}} - 2{{\beta }_{{13}}} = {{s}_{{11}}} + {{s}_{{33}}} - 2{{s}_{{13}}} - \frac{{{{{\left( {{{s}_{{12}}} - {{s}_{{13}}}} \right)}}^{2}}}}{{{{s}_{{11}}}}}$Из сказанного следует, что весьма существенным параметром, характеризующим анизотропию, для описания механического поведение горных пород является отклонение ${{s}_{{44}}} = G_{{13}}^{{ - 1}}$ от величины, определяемой (3.9) или (3.8). Наиболее естественным видится использование отношения независимого сдвигового модуля ${{G}_{{13}}} = s_{{44}}^{{ - 1}}$ (роль независимого модуля сдвига ${{G}_{{13}}}$ в величину концентрации напряжений на контуре отверстия отмечалась Лехницким [2]) к сдвиговому модулю, посчитанному по формуле (3.8)
(3.10)
${{k}_{A}} = \frac{{{{G}_{{13}}}}}{{G_{{13}}^{'}}},\quad G_{{13}}^{'} = {{\left( {{{s}_{{11}}} + {{s}_{{33}}} - 2{{s}_{{13}}}} \right)}^{{ - 1}}} = \frac{{{{E}_{1}}{{E}_{3}}}}{{{{E}_{1}}\left( {1 + {{\nu }_{{31}}}} \right) + {{E}_{3}}}}$Более точным, хотя менее удобным является параметр
где $G_{{13}}^{{''}}$ определяется (3.9). Как будет показано ниже, различие между введенными параметрами обычно пренебрежимо мало.При ${{k}_{A}} < 1$, что соответствует $n - k - 1 > 0$, концентрации напряжений имеют максимумы в точках, пересечения контура с главными осями тензора упругости ($A,\,A'$, $B,\,B'$), и минимумы в точках $\frac{\pi }{4} < \theta < \frac{\pi }{2}$ (точные значения даются весьма громоздкими выражениями, получаемыми приравниванием нулю производных $f\left( \theta \right)$, определяемых формулой (3.1), по углу $\theta $) и симметричных относительно главных осей тензора упругости (точки $C$ на рис. 1 ). При ${{k}_{A}} > 1$, что соответствует $n - k - 1 < 0$, максимумы и минимумы меняются местами. Приближенной формулу для максимума концентрации напряжения для ${{k}_{A}} > 1$ можно получить, раскладывая точное решение в ряд по параметру ${{k}_{A}} - 1$. Для $k > 1$ данное разложение имеет вид
(3.12)
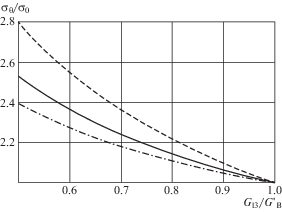
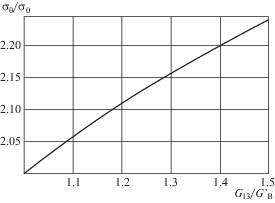
${{f}_{C}} = 2 + \frac{{(3 + 2\sqrt k + 3k)\left( {1 + {{k}^{2}} - 2\frac{{{{\beta }_{{13}}}}}{{{{\beta }_{{11}}}}}} \right)}}{{2{{{(1 + \sqrt k )}}^{2}}{{{\left( {1 + k} \right)}}^{2}}}}({{k}_{A}} - 1)$Влияние параметра kA на концентрацию напряжений на контуре иллюстрируют рис. 2 и 3 . На рис. 2 представлены зависимости концентраций напряжений fA и ${{f}_{B}}$ для ${{k}_{A}} \leqslant 1$ от отношения kA, соответствующие значению параметров ${{s}_{{12}}}{\text{/}}{{s}_{{11}}} = - 0.2,{{s}_{{13}}}{\text{/}}{{s}_{{11}}}$ = = –0.2, ${{s}_{{44}}} = {{s}_{{55}}} = {{k}_{A}}\left( {{{s}_{{11}}} + {{s}_{{33}}} - 2{{s}_{{13}}}} \right)$: сплошная линия – ${{f}_{A}} = {{f}_{B}}$ для k = 1; пунктирная линия – ${{f}_{B}}$ для $k = 2$; штрих-пунктирная линия – fA для k = 2. На рис. 3 представлена зависимость концентраций напряжений в точках максимума для ${{k}_{A}} \geqslant 1$ для тех же значений параметров ${{s}_{{ij}}}$ (кривые для k = 1 и k = 2 используемых параметров не различимы, отличие в численных значениях наблюдалось в четвертом знаке для ${{k}_{A}} = 1.5$).
Важным фактом, хорошо подтверждаемым приведенными иллюстрациями, является сохранение отклонения концентрации напряжений от изотропного случая даже при равенстве главных значений модулей (k = 1). Из рис. 1–3 видно, что для ${{k}_{A}} < 1$ отклонение отношения модулей k от единицы приводит к увеличению концентрации напряжений fB и уменьшению концентрации напряжений fA, (но только при условии ${{k}_{A}} \ne 1$). Однако, для ${{k}_{A}} > 1$ отношения модулей практически перестает (по крайней мере для рассмотренных значений параметров) влиять на величину концентрации напряжений, а лишь приводит к смещению положения максимума концентрации ближе к направлению, соответствующему минимальному модулю (рис. 1 ).
Безусловно, использование непосредственно любой пары из величин $m,\,\,n,\,\,k$ в качестве параметров характеризующих анизотропию является математически более строгим, однако кроме параметра $k$ остальные параметры выражаются через упругие постоянные посредством достаточно громоздких формул и лишены прозрачного смысла.
Интересно отметить, что сочетание упругих характеристик, соответствующее выполнению условия (3.8) (или, что то же самое, (3.10)) соответствует одному из частных случаев, рассмотренных еще де Сен-Венаном [5] (см. также [1, 6]), для которых зависимость упругих модулей от ориентации в пространстве имеет наиболее простой вид.
Выражение (3.10) было отмечено в работе Батугина и Ниренбург [3], как условие постоянства директрисы сдвигового модуля в плоскости, нормальной к плоскости изотропии трансверсально изотропного материала, и показано, что данная формула с точностью до 10% дает верные значения для 45 из 47 горных пород, которые в первом приближении можно рассматривать, как трансверсально-изотропные (алевролиты, филлиты, сланцы, песчаники, известняки, граниты, гранодиориты и др.). Значения упругих констант были взяты из экспериментальных исследований разных авторов [7–14]. В ссылках на данную работу, формулу (3.10) обычно характеризуют как эмпирическую, полученную в результате обобщения опытных данных. С учетом значения величины отношения сдвигового модуля к модулю, посчитанному по формуле (3.10) для определения напряжений, а также исследований де Сен-Венана, данную формулу едва ли можно считать эмпирической.
Отметим, что условие (3.9) используется также при исследовании распространения фронтов волн (условие Гассманна [15, 16]) и соответствует эллипсоидальности поверхности рефракции.
Для 39 из 47 пород, исследованных в [3] (для остальных пород набор исходных данных по упругим константам был неполным, что не позволило провести для них требуемый анализ), значения отношения независимого сдвигового модуля к модулю, посчитанному по формулам (3.10), (3.9) представлены в Таблице – их относительная разница не превосходит 2% (выполнение условия для того же набора данных, что и в настоящей работе было исследовано Анниным [16], где было показано, что оно выполняется точностью, определяемой из условия (3.10)). В табл. 1 также приведены параметры $k,\,m,\,n$ для условий плоской деформации и значения добавок к коэффициентам концентрации напряжения, посчитанные по формулам (3.6), (3.12). Результаты показывают, что для большинства пород, при выполнении условия (3.10) либо (3.9), изменения в коэффициентах концентрации имеют тот же порядок, что и отклонения от значений, даваемых (3.10), т.е. для практических целей пренебрежимо малы. Однако для одной из пород отклонения в обоих случаях весьма существенны. Представлены также значения отклонения коэффициентов концентрации напряжений для случая одноосного сжатия вдоль максимального модуля (обсуждение дано ниже, раздел 2).
Также были проверены гипотезы приближенного выполнения соотношений, даваемых оставшимися тремя из четырех частных случаев анизотропии, рассмотренных де Сен-Венаном [5] (см. также [17]). Данные подклассы (${{G}_{4}},\,\,{{F}_{4}},\,\,{{F}_{2}}$) соответствуют эллипсоидальным индикаторным поверхностям в пространствах $\sqrt[{ - 4}]{{{{s}_{{nn}}}\left( {\mathbf{n}} \right)}},\,\,\sqrt[{ - 4}]{{{{C}_{{nn}}}\left( {\mathbf{n}} \right)}},\,\,\sqrt[{ - 2}]{{{{C}_{{nn}}}\left( {\mathbf{n}} \right)}}$ (рассмотренный выше случай, ${{G}_{2}}$, соответствует эллипсоидальной индикаторной поверхности в пространстве $\sqrt[{ - 2}]{{{{s}_{{nn}}}\left( {\mathbf{n}} \right)}}$) [5, 17]) и возникают в моделях механики повреждений, теории эффективных сред; кроме того для данных подклассов получен ряд аналитических решений [17]. Здесь n – вектор нормали в пространстве; ${{s}_{{nn}}}\left( {\mathbf{n}} \right)$ – податливость в направлении n; ${{C}_{{nn}}}\left( {\mathbf{n}} \right)$ – жесткость в направлении n; матрица жесткости ${\mathbf{C}} = {{{\text{s}}}^{{ - 1}}}$ есть обратная матрица от матрицы податливости. Для данных подклассов также введем коэффициенты ${{k}_{A}}$, для которых величины ${{s}_{{55}}}$ определяются следующим образом [17]
(3.13)
${{k}_{A}}\left( {{{G}_{4}}} \right) = \frac{{{{s}_{{55}}}\left( {{{G}_{4}}} \right)}}{{{{s}_{{55}}}}};\quad {{s}_{{55}}}\left( {{{G}_{4}}} \right) = 2\left( {\sqrt {{{s}_{{11}}}{{s}_{{33}}}} - {{s}_{{13}}}} \right)$(3.14)
${{k}_{A}}\left( {{{F}_{4}}} \right) = \frac{{{{s}_{{55}}}\left( {{{F}_{4}}} \right)}}{{{{s}_{{55}}}}};\quad {{s}_{{55}}}\left( {{{F}_{4}}} \right) = \frac{2}{{\sqrt {{{C}_{{11}}}{{C}_{{33}}}} - {{C}_{{13}}}}}$(3.15)
${{k}_{A}}\left( {{{F}_{2}}} \right) = \frac{{{{s}_{{55}}}\left( {{{F}_{2}}} \right)}}{{{{s}_{{55}}}}};\quad {{s}_{{55}}}\left( {{{F}_{2}}} \right) = \frac{{{{C}_{{11}}} + {{C}_{{33}}} - 2{{C}_{{13}}}}}{4}$Результаты расчетов для указанных величин для 39 пород представлены в Таблице. Из анализа данных следует, что хотя используемая формула (3.10) дает лучшее соответствие, различие в точности не столь велико: средние отклонения $\frac{1}{N}\sum\limits_{n = 1}^N {\left( {k - 1} \right)} $ и среднеквадратичные отклонения $\sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{{{\left( {k - 1} \right)}}^{2}}} } $, где $N = 39$, $k = {{k}_{A}},{{k}_{B}},{{k}_{A}}\left( {{{G}_{4}}} \right),{{k}_{A}}\left( {{{F}_{4}}} \right),{{k}_{A}}\left( {{{F}_{2}}} \right)$ равны –0.031, –0.034, –0.036, –0.069, –0.078, и 0.121, 0.121, 0.125, 0.135, 0.146, соответственно. Во всех случаях присутствует систематическое занижение значения.
Небольшое различие в точности формул свидетельствует скорее о не слишком выраженной анизотропии рассматриваемых пород, чем о наличии глубинной связи между упругими константами, даваемой различными соотношениями.
Из результатов исследования [3] и анализа упругого решения [1, 2, 4] для концентрации напряжений вблизи кругового отверстия (скважины), а также результатов расчетов для скважины, наклоненной к плоскости изотропии, можно сделать вывод, что для анализа напряженного состояния вокруг скважин в анизотропных породах в большинстве случаев можно использовать решение Ламе для изотропного тела. Однако, для тех редко встречающихся пород, для которых указанное соотношение не выполняется с необходимой точностью, использование решения для изотропной среды будет приводить к заниженным значениям величины концентрации напряжений. Особенно опасен случай ${{k}_{A}} = {{G}_{{13}}}{\text{/}}G' > 1$, поскольку для него максимумы напряжений приходятся на зоны, где максимальные касательные напряжения действуют в плоскостях изотропии, и именно эти плоскости в горных породах обычно менее прочны [18–22].
Таким образом, с одной стороны, для большинства пород параметр ${{k}_{A}} = {{G}_{{13}}}{\text{/}}G'$ примерно равен единице, что позволяет использовать решение для изотропной среды, с другой стороны, для пород у которых отклонение данного параметра от единицы наблюдается, именно этот параметр становится определяющим при расчете напряженного состояния.
4. Неравнокомпонентное исходное напряженное состояние. Напряженное состояние пород, слагающих углеводородные месторождения, а также вмещающих пород, обычно близки к равнокомпонентным (гидростатическим), поскольку девиаторная составляющая напряженного состояния обычно за геологические времена успевает релаксировать [23]. Релаксации способствует и то, что пласты, слагающие углеводородные месторождения, как правило, перекрыты “ловушками”, слагаемыми непроницаемыми породами, обладающими высокой пластичностью. Релаксации, конечно, могут препятствовать тектонические процессы, однако, слишком большая их интенсивность приводила бы к дизъюнктивным нарушениям в “ловушках” и, как следствие, утечки углеводорода. Поскольку процессы релаксации и тектонические процессы разнонаправлены (первые приводят к выравниванию напряженного состояния, а вторые к появлению неравнокомпонентности), в общем случае, напряженное состояние может оказаться неравнокомпонентным, причем главные оси тензора действующих напряжений не обязательно должны быть соосны ни глобальным координатным осям, связанным с дневной поверхностью, ни осям, связанным с упругими свойствами породы. Однако в силу вышесказанного, для условий большинства углеводородных месторождений едва ли можно ожидать ярко выраженной неравнокомпонентности.
Обычно, одно из главных напряжений (σzz) предполагается вертикальным и определяемым весом вышележащих пород. Два другие, предполагаются независимыми
(4.1)
${{\sigma }_{{xx}}} = {{\lambda }_{x}}{{\sigma }_{{zz}}},\quad {{\sigma }_{{yy}}} = {{\lambda }_{y}}{{\sigma }_{{zz}}}$Для описания напряженного состояния вблизи скважины, пробуренной горизонтально, с осью, совпадающей с направлением одного из главных напряжений и лежащей в плоскости изотропии трансверсально изотропной породы, можно использовать общее решение [1, 2, 4] плоской задачи об отверстии в ортотропной среде, ось которого совпадает с одной из осей ортотропии. Концентрация напряжений на контуре может быть записана следующим образом (по-прежнему используются соотношения плоской деформации)
(4.2)
$f\left( \theta \right) = \frac{{\sigma _{{\theta \theta }}^{{}}}}{{\sigma _{{zz}}^{\infty }}} = {{f}_{0}}\left( \theta \right) - \left( {1 - \lambda } \right){{f}_{1}}\left( \theta \right)$(4.3)
${{f}_{1}}\left( \theta \right) = \frac{{{{E}_{\theta }}}}{{{{E}_{1}}}}\{ - k{\text{co}}{{{\text{s}}}^{2}}\theta + (1 + n){\text{si}}{{{\text{n}}}^{2}}\theta \} $Экстремальные значения данного выражения всегда приходятся на точки A, A' $(\theta = 0,\pi )$ и $B,B'\left( {\theta = \pm \;\pi {\text{/}}2} \right)$ для всех допустимых значений упругих параметров
Для данного случая относительная величина независимого сдвигового модуля (3.10) перестает быть решающей для определения концентраций напряжений и их отличие от изотропного случая.
Концентрация напряжений в точках $A,\,A'\,\,\left( {\theta = 0,\,\,\pi } \right)$ и $B,B'\left( {\theta = \pm \,\pi {\text{/}}2} \right)$ получается подстановкой (3.6), (4.4) в (4.2)
(4.5)
${{f}_{A}} = 1 + \frac{{n - 1}}{k} + \left( {1 - \lambda } \right)\frac{1}{k} = 1 + \frac{{n - \lambda }}{k},\quad {{f}_{B}} = 1 + \frac{{n - 1}}{k} - \left( {1 - \lambda } \right)\left( {1 + n} \right)$Из формул (4.5) видно, что, подобно изотропному случаю, снижение напряжения вдоль оси $A,\,A'\,\,$ по сравнению с гидростатическим приводит к увеличению концентрации напряжений в точках $A,A{\text{'}}$ и снижению концентрации в точках $B,\,B'\,.$
Значения концентраций напряжений для 39 пород представлены в Таблице. Из анализа данных видно, что при не слишком выраженной неравнокомпонентности исходного напряженного состояния влияние анизотропии на концентрацию напряжений для большинства пород невелико.
5. Наклонная скважина. Для выяснения роли параметра ${{k}_{A}} = {{G}_{{13}}}{\text{/}}G_{{13}}^{'}$ на распределение напряжений на контуре скважины, наклоненной к главным осям тензора упругости горной породы, (наклонной скважины в трансверсально изотропной породе с горизонтально расположенной плоскостью изотропии) были проведены конечно-элементные расчеты, показавшие, что при выполнении условия (3.10) отличие концентрации напряжений от двойки (величины, характерной для изотропной среды) составляет менее 1%. Полученное различие вполне могло быть вызвано погрешностью метода конечных элементов.
6. Заключение. Исследовано влияние упругих констант трансверсально изотропного тела на величины концентраций на контуре скважины. Для большинства пород параметр ${{k}_{A}} = {{G}_{{13}}}{\text{/}}G'$ примерно равен единице, что позволяет использовать решение для изотропной среды; для пород, у которых наблюдается отклонение kA от единицы, именно этот параметр становится определяющим при расчете напряженного состояния.
Показано, что при неравнокомпонентном исходном напряженном состоянии снижение напряжения вдоль оси $A,\,A'\,\,\left( {\theta = 0,\,\,\pi } \right)$ по сравнению с гидростатическим приводит к увеличению концентрации напряжений в точках $A,A{\text{'}}$ и снижению концентрации в точках $B,B'\left( {\theta = \pm \,\pi {\text{/}}2} \right)$.
Расчеты напряжений на контуре скважины, наклоненной к главным осям тензора упругости горной породы, показали, что при выполнении условия (3.10) концентрация напряжений отличается от двойки (величины, характерной для изотропной среды) менее чем на 1%.
Работа выполнена при финансовой поддержке РНФ, проект 16-11-10325 (для К.Б.У.).
Таблица 1.
| Порода | a11 | a33 | a12 | a13 | a44 | kA | kB | k | m | n | fA | fB | fC | fA1 | fB1 | kA (G4) | kA (F4) | kA (F2) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| песчаный сланец [10] | 0.93 | 1.92 | –0.38 | –0.19 | 8.33 | 0.39 | 0.38 | 1.56 | 10.04 | 3.63 | 0.69 | 1.07 | –0.88 | –0.36 | 1.63 | 0.37 | 0.35 | 0.31 |
| перидотит [8] | 0.10 | 0.19 | –0.03 | –0.03 | 0.48 | 0.75 | 0.75 | 1.35 | 4.09 | 2.61 | 0.19 | 0.25 | –0.37 | –0.26 | 0.61 | 0.72 | 0.69 | 0.64 |
| хлористый сланец [8] | 0.08 | 0.12 | –0.01 | –0.02 | 0.28 | 0.87 | 0.86 | 1.24 | 3.04 | 2.35 | 0.09 | 0.11 | –0.19 | –0.19 | 0.35 | 0.85 | 0.82 | 0.79 |
| известняк [12] | 0.24 | 0.29 | –0.07 | –0.04 | 0.69 | 0.90 | 0.89 | 1.14 | 2.64 | 2.22 | 0.07 | 0.08 | –0.14 | –0.12 | 0.22 | 0.89 | 0.87 | 0.86 |
| известняк [13] | 0.25 | 0.28 | –0.06 | –0.05 | 0.69 | 0.90 | 0.90 | 1.07 | 2.45 | 2.14 | 0.07 | 0.07 | –0.13 | –0.07 | 0.14 | 0.90 | 0.88 | 0.87 |
| амфиболит [14] | 0.08 | 0.10 | –0.02 | –0.03 | 0.25 | 0.91 | 0.91 | 1.06 | 2.43 | 2.13 | 0.07 | 0.07 | –0.13 | –0.06 | 0.13 | 0.91 | 0.84 | 0.83 |
| сильвинит бедный с зубером [9] | 0.35 | 0.41 | –0.09 | –0.10 | 1.05 | 0.92 | 0.92 | 1.08 | 2.41 | 2.14 | 0.06 | 0.06 | –0.11 | –0.07 | 0.14 | 0.92 | 0.86 | 0.86 |
| базальт 1 [8] | 0.21 | 0.29 | –0.02 | –0.04 | 0.63 | 0.93 | 0.93 | 1.15 | 2.52 | 2.20 | 0.04 | 0.05 | –0.09 | –0.13 | 0.20 | 0.93 | 0.91 | 0.89 |
| зубер чистый [9] | 0.35 | 0.35 | –0.08 | –0.08 | 0.93 | 0.94 | 0.94 | 1.00 | 2.18 | 2.04 | 0.04 | 0.04 | –0.08 | 0.00 | 0.04 | 0.94 | 0.90 | 0.90 |
| гранит свежий [14] | 0.15 | 0.16 | –0.03 | –0.03 | 0.39 | 0.94 | 0.94 | 1.05 | 2.26 | 2.09 | 0.04 | 0.04 | –0.07 | –0.05 | 0.09 | 0.94 | 0.92 | 0.92 |
| известняк [12] | 0.26 | 0.29 | –0.06 | –0.05 | 0.69 | 0.95 | 0.94 | 1.06 | 2.29 | 2.10 | 0.03 | 0.04 | –0.07 | –0.06 | 0.10 | 0.94 | 0.93 | 0.92 |
| мрамор [13] | 0.15 | 0.20 | –0.03 | –0.01 | 0.38 | 0.96 | 0.95 | 1.19 | 2.57 | 2.23 | 0.03 | 0.03 | –0.06 | –0.16 | 0.23 | 0.95 | 0.93 | 0.92 |
| песчаник [14] | 0.19 | 0.21 | –0.02 | –0.02 | 0.48 | 0.95 | 0.95 | 1.05 | 2.22 | 2.08 | 0.03 | 0.03 | –0.06 | –0.05 | 0.08 | 0.95 | 0.94 | 0.94 |
| гранит [14] | 0.15 | 0.17 | –0.03 | –0.03 | 0.39 | 0.95 | 0.95 | 1.04 | 2.21 | 2.07 | 0.03 | 0.03 | –0.06 | –0.04 | 0.07 | 0.95 | 0.94 | 0.94 |
| песчаник [14] | 0.18 | 0.20 | –0.03 | –0.03 | 0.45 | 0.96 | 0.96 | 1.04 | 2.18 | 2.06 | 0.02 | 0.02 | –0.05 | –0.04 | 0.06 | 0.96 | 0.95 | 0.95 |
| гранит красно-серый [14] | 0.17 | 0.18 | –0.04 | –0.02 | 0.40 | 0.98 | 0.97 | 1.04 | 2.16 | 2.06 | 0.02 | 0.02 | –0.03 | –0.04 | 0.06 | 0.98 | 0.96 | 0.96 |
| алевролит [7] | 0.16 | 0.18 | –0.05 | –0.04 | 0.44 | 0.97 | 0.97 | 1.07 | 2.23 | 2.09 | 0.02 | 0.02 | –0.04 | –0.07 | 0.09 | 0.97 | 0.93 | 0.92 |
| сильвинит богатый [9] | 0.42 | 0.47 | –0.11 | –0.12 | 1.15 | 0.98 | 0.98 | 1.06 | 2.20 | 2.08 | 0.02 | 0.02 | –0.03 | –0.06 | 0.08 | 0.97 | 0.92 | 0.92 |
| песчаник [14] | 0.22 | 0.23 | –0.03 | –0.03 | 0.52 | 0.98 | 0.98 | 1.02 | 2.10 | 2.03 | 0.01 | 0.01 | –0.03 | –0.02 | 0.03 | 0.98 | 0.97 | 0.97 |
| базальт 3 [8] | 0.19 | 0.20 | –0.03 | –0.04 | 0.48 | 0.98 | 0.98 | 1.03 | 2.12 | 2.05 | 0.01 | 0.01 | –0.03 | –0.03 | 0.05 | 0.98 | 0.95 | 0.95 |
| гнейсо-гранит красный [14] | 0.18 | 0.19 | –0.03 | –0.03 | 0.44 | 0.98 | 0.98 | 1.03 | 2.12 | 2.05 | 0.01 | 0.01 | –0.02 | –0.03 | 0.05 | 0.98 | 0.96 | 0.96 |
| базальт 2 [8] | 0.23 | 0.24 | –0.02 | –0.03 | 0.56 | 0.98 | 0.98 | 1.02 | 2.08 | 2.03 | 0.01 | 0.01 | –0.02 | –0.02 | 0.03 | 0.98 | 0.97 | 0.97 |
| гранит крупнозернистый [14] | 0.20 | 0.20 | –0.04 | –0.04 | 0.49 | 0.99 | 0.99 | 1.01 | 2.05 | 2.02 | 0.01 | 0.01 | –0.01 | –0.01 | 0.02 | 0.99 | 0.96 | 0.96 |
| гранит мелкозернистый [14] | 0.12 | 0.12 | –0.03 | –0.03 | 0.30 | 1.00 | 1.00 | 0.99 | 2.00 | 1.99 | 0.00 | 0.00 | –0.01 | 0.01 | –0.01 | 1.00 | 0.93 | 0.93 |
| плагиогранит [14] | 0.15 | 0.16 | –0.04 | –0.04 | 0.38 | 1.01 | 1.01 | 1.01 | 1.99 | 2.00 | –0.01 | –0.01 | 0.02 | –0.01 | 0.00 | 1.01 | 0.96 | 0.96 |
| гранодиорит темно-серый [14] | 0.13 | 0.13 | –0.03 | –0.03 | 0.31 | 1.01 | 1.01 | 1.00 | 1.97 | 2.00 | –0.01 | –0.01 | 0.02 | 0.00 | 0.00 | 1.01 | 0.97 | 0.97 |
| гранодиорит розовый [14] | 0.17 | 0.17 | –0.03 | –0.04 | 0.41 | 1.01 | 1.01 | 1.02 | 2.00 | 2.01 | –0.01 | –0.01 | 0.02 | –0.02 | 0.01 | 1.01 | 0.98 | 0.98 |
| гранит серый [14] | 0.15 | 0.20 | –0.03 | –0.03 | 0.40 | 1.02 | 1.02 | 1.18 | 2.33 | 2.16 | –0.01 | –0.01 | 0.02 | –0.15 | 0.16 | 1.01 | 0.99 | 0.98 |
| песчаник [13] | 1.05 | 1.49 | –0.09 | –0.11 | 2.70 | 1.02 | 1.02 | 1.19 | 2.37 | 2.18 | –0.01 | –0.01 | 0.02 | –0.16 | 0.18 | 1.01 | 1.00 | 0.98 |
| гранит [13] | 0.26 | 0.32 | –0.05 | –0.01 | 0.58 | 1.04 | 1.03 | 1.13 | 2.21 | 2.12 | –0.01 | –0.01 | 0.03 | –0.11 | 0.12 | 1.03 | 1.02 | 1.01 |
| алевролит [8] | 0.23 | 0.25 | –0.04 | –0.07 | 0.59 | 1.04 | 1.04 | 1.01 | 1.93 | 1.99 | –0.02 | –0.02 | 0.05 | –0.01 | -0.01 | 1.04 | 0.98 | 0.98 |
| магматит [14] | 0.18 | 0.19 | –0.03 | –0.04 | 0.42 | 1.04 | 1.04 | 1.03 | 1.95 | 2.00 | –0.03 | –0.03 | 0.06 | –0.03 | 0.00 | 1.04 | 1.01 | 1.01 |
| филит 1 [7] | 0.14 | 0.17 | –0.04 | –0.04 | 0.38 | 1.05 | 1.05 | 1.13 | 2.13 | 2.09 | –0.03 | –0.03 | 0.07 | –0.11 | 0.09 | 1.04 | 0.97 | 0.95 |
| плагиогранит [14] | 0.13 | 0.15 | –0.02 | –0.03 | 0.32 | 1.05 | 1.05 | 1.05 | 1.98 | 2.02 | –0.03 | –0.03 | 0.06 | –0.05 | 0.02 | 1.05 | 1.02 | 1.01 |
| песчаник [11] | 0.64 | 1.04 | –0.13 | –0.18 | 1.92 | 1.06 | 1.06 | 1.28 | 2.45 | 2.24 | –0.03 | –0.04 | 0.08 | –0.22 | 0.24 | 1.03 | 1.00 | 0.95 |
| хибинит [14] | 0.18 | 0.20 | –0.04 | –0.05 | 0.44 | 1.07 | 1.07 | 1.05 | 1.91 | 2.00 | –0.04 | –0.05 | 0.10 | –0.04 | 0.00 | 1.07 | 1.02 | 1.02 |
| гранит бурый [14] | 0.16 | 0.19 | –0.03 | –0.04 | 0.39 | 1.07 | 1.07 | 1.07 | 1.97 | 2.03 | –0.04 | –0.04 | 0.09 | –0.07 | 0.03 | 1.07 | 1.03 | 1.03 |
| туфопесчаник [8] | 0.14 | 0.17 | 0.00 | –0.04 | 0.34 | 1.10 | 1.08 | 1.09 | 1.99 | 2.04 | –0.05 | –0.05 | 0.10 | –0.08 | 0.04 | 1.10 | 1.04 | 1.03 |
| филит 2 [7] | 0.13 | 0.18 | –0.03 | –0.04 | 0.34 | 1.12 | 1.12 | 1.16 | 2.01 | 2.08 | –0.07 | –0.08 | 0.17 | –0.14 | 0.08 | 1.11 | 1.06 | 1.04 |
Список литературы
Лехницкий С.Г. Теория упругости анизотропного тела М.-Л.: Госиздат. технико-теор. л-ры, 1950. 299 с.
Лехницкий С.Г. Теория упругости анизотропного тела. М.: Наука, 1977. 415 с.
Батугин С.А., Ниренбург Р.К. Приближенная зависимость между упругими константами горных пород и параметры анизотропии // Физико-технические проблемы разработки полезных ископаемых. 1972. № 1. С. 7–11.
Лехницкий С.Г., Солдатов В.В. Влияние положения эллиптического отверстия на концентрацию напряжений в растягиваемой ортотропной пластинке // Изв. АН СССР, ОТН, Механика и машиностроение. 1961. № 1. С. 3–8.
De Saint-Venant Mémoire sur la distribution des élasticités autour de chaque point d’un solide ou d’un milieu de contexture quelconque, particulièrement lorsqu’il est amorphe sans être isotrope (Deuxième article) // Journal de mathématiques pures et appliquées 2e série, tome 8. 1863. P. 257–430.
Рабинович А.И. Об упругих постоянных и прочности авиационных материалов // Труды ЦАГИ № 582. Изд. АН СССР, Москва. 1946. С. 1–12.
Лехницкий С.Г. Теоретическое исследование напряжений в упругом анизотропном массиве вблизи подземной выработки эллиптического сечения // Труды ВНИМИ. Сб. 45. Л., 1962. С. 5–14.
Скорикова М.Ф. Об анизотропии упругих свойств горных пород о. Сахалина // Изв. АН СССР, сер. геологическая. 1965. № 3. С. 61–75.
Мячкин В.И., Соловьева Р.П. Распространение упругих волн ультразвуковой частоты // Изв. АН СССР, серия геофизическая. I. 1960. С. 15–21.
Розовский М.И., Зорин А.Н. Приложение интегральных операторов к определению напряжений и перемещений контура подземного сооружения с учетом влияния фактора времени и анизотропии / Проблемы механики горных пород. Алма-Ата: Наука. 1966. С. 367–372.
Серсембаев А.А. и др. Исследования по механике горных пород // Наука, Алма-Ата. 1965. 145 с.
Clark S.P. (editor) Handbook of Physical Constants, Geological Soc. 1942. 325 p.
Isaacson E. Rock Pressure in Mines, London, Mining Publications Ltd. 1958. 212 p.
Беликов Б.П. Упругие и прочностные свойства горных пород // Труды ИГЕМ. 1961. Вып. 43. С. 47–110.
Gassmann F. Introduction to seismic travel time methods in anisotropic media // Pure and Appl. Geoph. 1964. V. 58. P. 63–112.
Аннин Б.Д. Трансверсально-изотропная модель геоматериалов // Сиб. журн. индустр. матем. 2009. Т. 12. № 3. С. 5–14.
Pouya A. Ellipsoidal anisotropies in linear elasticity Extension of Saint Venant’s work to phenomenological modelling of materials // International Journal of DAMAGE MECHANICS. V. 16. January 2007. P. 95–126.
Goodman R.E. Introduction to rocks mechanics // New York: John Wiley and Sons. 1980. 478 p.
Jaeger J.C., Cook N.G.W., Zimmerman R.W. Fundamentals of rock mechanics // Malden, Mass.; Oxford: Blackwell, MyiLibrary, 2007, 475 p.
Zobak M.D. Reservoir Geomechanics // Cambridge University Press 2007, 443 p.
Карев В.И., Климов Д.М., Коваленко Ю.Ф., Устинов К.Б. О разрушении осадочных горных пород в условиях сложного трехосного напряженного состояния // Изв. РАН. МТТ. 2016. № 5. С. 15–21.
Карев В.И., Климов Д.М., Коваленко Ю.Ф., Устинов К.Б. Модель разрушения анизотропных горных пород при сложном нагружении // Физическая мезомеханика. 2016. Т. 19. № 6. С. 34–40.
Христианович С.А., Желтов Ю.П. О гидравлическом разрыве нефтеносного пласта // Известия АН СССР. 1955. № 5. С. 3–41.
Mimouna A., Prioul R. Closed-form approximations to borehole stresses for weak transverse isotropic elastic media // International Journal of Rock Mechanics & Mining Sciences, June. 2018. P. 203–216.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела