Известия РАН. Механика твердого тела, 2019, № 4, стр. 141-148

О колебаниях поршневого пальца с эксцентрично расположенным центром тяжести

М. М. Сорочкин^*

Конструкторское бюро беспилотных геликоптеров
Хайфа, Израиль

Поступила в редакцию 28.12.2016
После доработки 27.04.2017
Принята к публикации 28.02.2019

DOI: 10.1134/S0572329919040093

Аннотация

Повышение давления сгорания в цилиндре современных дизельных двигателей увеличивает нагрузки, действующие на подшипники поршневого пальца и смазка подшипников поршневого пальца становится серьезной проблемой. Поршневой палец с эксцентрично расположенным центром тяжести позволяет решить эту проблему. Эта статья посвящена феномену параметрических резонансных колебаний поршневого пальца во время возвратно-поступательного движения поршня. Цель состоит в использовании явления, которое увеличивает амплитуду колебаний и, следовательно, скорость скольжения в относительном вращательном движении поршневого пальца.

1. Введение. Для создания масляной пленки между поршневым пальцем и его подшипником поршневой палец должен вращаться или колебаться. Для обеспечения его вращения центр тяжести поршневого пальца должен быть расположен эксцентрично относительно его продольной оси. По мере того, как поршень совершает возвратно-поступательное движение на поршневой палец действует периодическая сила инерции, которая вызывает колебания поршневого пальца вокруг его продольной оси. Движение центра тяжести поршневого пальца описывается обыкновенным дифференциальным уравнением второго порядка с коэффициентами, зависящими от времени – уравнением Хилла.

Известно, что в системе, описываемой дифференциальным уравнением с периодическими коэффициентами существуют резонансные зоны. Ширина резонансной зоны зависит от параметров системы, и, в частности, от величины эксцентриситета центра тяжести поршневого пальца, частоты вращения двигателя, трения в подшипниках поршневого пальца. Чтобы увеличить амплитуду колебаний (вибрации) и, следовательно, относительную скорость скольжения вращательного движения поршневого пальца, изменением экс-центриситета центра тяжести поршневого пальца резонанс может быть сдвинут в область рабочей частоты вращения двигателя.

Когда поршневой палец осциллирует он всплывает (под действием масляной пленки, образованной между поршневым пальцем и подшипником) по направлению к противоположной стороне опорной поверхности, что приводит к снижению контактной нагрузки, трения, износа и нагрева деталей.

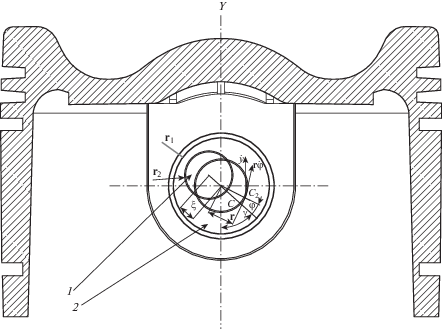
2. Уравнение движения поршневого пальца и резонансная область. Рассмотрим возвратно-поступательное движение поршня, движущегося вдоль оси Y (рис. 1).

Рис. 1

Центр тяжести С поршневого пальца смещен эксцентрично, т.е. находится на некотором расстоянии r от его продольной оси.

Введем следующие обозначения: r – расстояние между центром тяжести поршневого пальца и его продольной осью, γ – угловое положение центра тяжести, $\dot {y}$ – скорость поршня, m – масса поршневого пальца, J – момент инерции поршневого пальца вокруг его продольной оси, ρ – радиус инерции поршневого пальца, φ – угол поворота при колебаниях. Цифрой 1 на рис. 1 обозначено отверстие, а цифрой 2 – поршневой палец. Кинетическая энергия поршневого пальца будет

(2.1)

$~T = \frac{1}{2}(m\dot {y}_{c}^{2} + J{{\dot {\varphi }}^{2}})~$

где $\dot {y}_{c}^{2}$ – квадрат величины скорости центра тяжести поршневого пальца

$\dot {y}_{c}^{2} = {{\dot {y}}^{2}} + 2r\dot {y}\dot {\varphi }\,{\text{sin}}\,(\gamma + \varphi ) + {{r}^{2}}{{\dot {\varphi }}^{2}}$

Точки здесь обозначают дифференцирование по времени t. Подставляя это выражение в (2.1), найдем

$T = \frac{1}{2}m[{{\dot {y}}^{2}} + 2r\dot {y}\dot {\varphi }\sin (\gamma + \varphi ) + ({{r}^{2}} + {{\rho }^{2}}){{\dot {\varphi }}^{2}}]$

Потенциальная энергия поршневого пальца

$\Pi = mgr[1 - \cos (\gamma + \varphi )]$

Диссипативная функция сил трения (диссипативная функция Рэлея)

$\Phi = b{{\dot {\varphi }}^{2}}{\text{/}}2$

где b – коэффициент трения в подшипниках. Движение поршневого пальца описывается одним уравнением Лагранжа

(2.2)

$\frac{d}{{dt}}\frac{{\partial T}}{{\partial{ \dot {\varphi }}}} - \frac{{\partial T}}{{\partial \varphi }} = - \frac{{\partial \Phi }}{{\partial{ \dot {\varphi }}}} - \frac{{\partial \Pi }}{{\partial \varphi }}$

Подставляя значения $\partial T{\text{/}}\partial{ \dot {\varphi }},\partial T{\text{/}}\partial \varphi ,\partial \Phi {\text{/}}\partial{ \dot {\varphi }}$ и $\partial \Pi {\text{/}}\partial \varphi ~$ в уравнение Лагранжа (2.2), получаем дифференциальное уравнение движения поршневого пальца

$m({{r}^{2}} + {{\rho }^{2}})\ddot {\varphi } + b\dot {\varphi } + mr\ddot {y}\sin (\gamma + \varphi ) = - mgr\sin (\gamma + \varphi )$

Полагаем, что угол φ будет малой величиной. Чтобы записать дифференциальное уравнение малых колебаний поршневого пальца полагаем cosφ ≅ 1 и sinφ ≅ φ.

В результате получим

(2.3)

$m({{r}^{2}} + {{\rho }^{2}})\ddot {\varphi } + b\dot {\varphi } + mr(g\cos \gamma + \ddot {y}\cos \gamma )\varphi = - mgr\sin \gamma - mr\ddot {y}\cos \gamma $

Разделив обе части уравнения (3) на m(r² + ρ²) и вводя обозначения

$\frac{b}{{m({{r}^{2}} + {{\rho }^{2}})}}~ = \mu ,\quad \frac{{r(g{\text{cos}}\gamma + \ddot {y}{\text{cos}}\gamma )}}{{~{{r}^{2}} + {{\rho }^{2}}}}~ = f(t),\quad \frac{{r(~g{\text{sin}}\gamma + \ddot {y}{\text{cos}}\gamma )}}{{~{{r}^{2}} + {{\rho }^{2}}}} = - M(t)$

приведем уравнение (2.3) к виду

(2.4)

$\ddot {\varphi } + \mu \dot {\varphi } + f(t)\varphi = M(t)$

Рассмотрим линейное однородное дифференциальное уравнение второго порядка, соответствующеe неоднородному уравнению (2.4)

(2.5)

$\ddot {\varphi } + \mu \dot {\varphi } + f(t)\varphi = 0$

Представляя ускорение поршня двигателя $\ddot {y}$ в виде ряда Фурье получим

$f(t) = \frac{{rg{\text{cos}}\gamma + rR{{\omega }^{2}}{\text{cos}}\gamma [{\text{cos}}\omega t + \lambda (1 + 0.5{{\lambda }^{3}}){\text{cos}}2\omega t - 0.25{{\lambda }^{3}}{\text{cos}}4\omega t + ...]}}{{~{{r}^{2}} + {{\rho }^{2}}}}~$

где ω – угловая скорость вращения коленчатого вала, λ = R/L, R – радиус кривошипа, L – длина шатуна. На практике конечное число слагаемых (первые 3 члена) ряда Фурье будет использоваться для хорошего приближения ускорения поршня. Введем замену

$\omega t = 2\tau .$

Однородное дифференциальное уравнение (2.5) принимает вид

(2.6)

$\varphi {\text{''}} + \frac{{2\mu }}{\omega }\varphi {\text{'}} + \frac{{4r\{ g{\text{cos}}\gamma + R{{\omega }^{2}}{\text{cos}}\gamma [{\text{cos}}2\tau + \lambda (1 + 0.5{{\lambda }^{2}}){\text{cos}}4\tau - 0.25{{\lambda }^{3}}{\text{cos}}8\tau + ...]\} }}{{{{\omega }^{2}}(~{{r}^{2}} + {{\rho }^{2}})}}\varphi = 0$

Штрихи здесь означают дифференцирование по τ.

Подставляя

$\varphi = {{e}^{{\frac{{ - \mu \tau }}{\omega }}}}\alpha $

в (2.6), получим

$\alpha {\text{''}} + \varepsilon \left( {1 + 2\sum\limits_{n = 1}^\infty {{{\delta }_{n}}\cos 2n\tau } } \right)\alpha = 0$

или

(2.7)

$\alpha {\text{''}} + \varepsilon \sum\limits_{n = - \infty }^\infty {{{\delta }_{n}}{{e}^{{i2n\tau }}}} \alpha = 0$

где

$\varepsilon = \frac{{4{{m}^{2}}rg({{\rho }^{2}} + {{r}^{2}})\cos \gamma - {{b}^{2}}}}{{{{m}^{2}}{{\omega }^{2}}{{{({{\rho }^{2}} + {{r}^{2}})}}^{2}}}}\quad {{\delta }_{n}} = - \frac{{2{{m}^{2}}{{\omega }^{2}}({{\rho }^{2}} + {{r}^{2}})rR\cos \gamma }}{{4{{m}^{2}}rg({{\rho }^{2}} + {{r}^{2}})\cos \gamma - {{b}^{2}}}}{{a}_{n}}$

${{a}_{1}} = 1,\quad {{a}_{2}} = \lambda (1 + 0.25{{\lambda }^{2}}),\quad {{a}_{3}} = - 0.25{{\lambda }^{3}},\quad ...\,{{a}_{{ - n}}} = {{a}_{n}}$

Отметим, что ε и δ_n – безразмерные величины.

Это позволяет повысить точность вычислений, чтобы получить приемлемое решение.

Отметим, что ряд $\sum\nolimits_{n = 1}^\infty {{{\delta }_{n}}} $ абсолютно сходится и δ₀ = 1.

Уравнение (2.7) является классическим примером дифференциального уравнения Хилла. Будем искать решение линейного однородного дифференциального уравнения второго порядка (2.7) в виде ряда

$\alpha = {{e}^{{i\nu \tau }}}\sum\limits_{k = - \infty }^\infty {{{b}_{k}}{{e}^{{i2k\tau }}}} $

с неизвестными коэффициентами b_k, не зависящими от τ. Здесь параметр ν является характеристическим показателем.

Подставляя ряд в уравнение и приравнивая коэффициенты при одинаковых степенях e^i2kτ нулю, получим бесконечную систему уравнений с неизвестными коэффициентами b_k

${{(2k + \nu )}^{2}}{{b}_{k}} + \varepsilon \sum\limits_{n = - \infty }^\infty {{{\delta }_{n}}{{b}_{{k - n}}} = 0\quad k = - \infty ,...,\infty } $

или

(2.8)

$\begin{gathered} - \frac{\varepsilon }{{{{{(2k + \nu )}}^{2}}}}\sum\limits_{n = - \infty }^{ - 1} {{{\delta }_{n}}{{b}_{{k - n}}} + \left[ {1 - \frac{\varepsilon }{{{{{(2k + \nu )}}^{2}}}}} \right]{{b}_{k}} - \frac{\varepsilon }{{{{{(2k + \nu )}}^{2}}}}\sum\limits_{n = 1}^\infty {{{\delta }_{n}}{{b}_{{k - n}}}} } = 0 \\ k = - \infty ,...,\infty \\ \end{gathered} $

или в матричной форме

${\mathbf{A}}{\text{*}}{\mathbf{b}} = 0$

где А – бесконечная матрица системы уравнений (2.8).

Следует отметить, что элементы матрицы A безразмерные величины. Здесь

$A = \mathop {\left\| {\begin{array}{*{20}{c}} {...}&{1 - \frac{\varepsilon }{{{{{(\nu - 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{{(\nu - 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{{(\nu - 2)}}^{2}}}}}&{...} \\ {...}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{\nu }^{2}}}}}&{1 - \frac{\varepsilon }{{{{\nu }^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{\nu }^{2}}}}}&{...} \\ {...}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{{(\nu + 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{{(\nu + 2)}}^{2}}}}}&{1 - \frac{\varepsilon }{{{{{(\nu + 2)}}^{2}}}}}&{...} \end{array}} \right\|}\limits_{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\,\,\,\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.}^{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\,\,\,\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.} $

${\mathbf{b}} = \mathop {\left\| \begin{gathered} {{b}_{{ - 1}}} \\ {{b}_{0}} \\ {{b}_{1}} \\ \end{gathered} \right\|}\limits_.^. .$

Определитель Δ($\nu $) бесконечной матрицы А равен

$\begin{gathered} \Delta (\nu ) = \mathop {\left\| {\begin{array}{*{20}{c}} {...}&{1 - \frac{\varepsilon }{{{{{(\nu - 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{{(\nu - 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{{(\nu - 2)}}^{2}}}}}&{...} \\ {...}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{\nu }^{2}}}}}&{1 - \frac{\varepsilon }{{{{\nu }^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{\nu }^{2}}}}}&{...} \\ {...}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{{(\nu + 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{{(\nu + 2)}}^{2}}}}}&{1 - \frac{\varepsilon }{{{{{(\nu + 2)}}^{2}}}}}&{...} \end{array}} \right\|}\limits_{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\,\,\,\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.}^{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\,\,\,\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.} = \\ = {{\Delta }_{1}}(\nu )\prod\limits_{n = - \infty }^\infty {\frac{{{{{(2n + \nu )}}^{2}} - \varepsilon }}{{{{{(2n + \nu )}}^{2}}}} = } \\ \end{gathered} $

${{\Delta }_{1}}(\nu )\frac{{{{\nu }^{2}} - \varepsilon }}{{{{\nu }^{2}}}}\prod\limits_{n = 1}^\infty {\frac{{\left[ {1 - \frac{{{{{(\nu + \sqrt \varepsilon )}}^{2}}}}{{4{{n}^{2}}}}} \right]\left[ {1 - \frac{{{{{(\nu - \sqrt \varepsilon )}}^{2}}}}{{4{{n}^{2}}}}} \right]}}{{{{{\left( {1 - \frac{{{{\nu }^{2}}}}{{4{{n}^{2}}}}} \right)}}^{2}}}}} $

где

${{\Delta }_{1}}(\nu ) = \mathop {\left\| {\begin{array}{*{20}{c}} {...}&1&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{{(\nu - 2)}}^{2}} - \varepsilon }}}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{{(\nu - 2)}}^{2}} - \varepsilon }}}&{...} \\ {...}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{\nu }^{2}} - \varepsilon }}}&1&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{\nu }^{2}} - \varepsilon }}}&{...} \\ {...}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{{(\nu + 2)}}^{2}} - \varepsilon }}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{{(\nu + 2)}}^{2}} - \varepsilon }}}&1&{...} \end{array}} \right\|}\limits_{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\,\,\,\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.}^{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\,\,\,\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.} $

Согласно известной формуле Эйлера [1]

$\frac{{{{\nu }^{2}} - \varepsilon }}{{{{\nu }^{2}}}}\prod\limits_{n = 1}^\infty {\frac{{\left[ {1 - \frac{{{{{(\nu + \sqrt \varepsilon )}}^{2}}}}{{4{{n}^{2}}}}} \right]\left[ {1 - \frac{{{{{(\nu - \sqrt \varepsilon )}}^{2}}}}{{4{{n}^{2}}}}} \right]}}{{{{{\left( {1 - \frac{{{{\nu }^{2}}}}{{4{{n}^{2}}}}} \right)}}^{2}}}}} = \frac{{\sin \frac{\pi }{2}(\nu + \sqrt \varepsilon )\sin \frac{\pi }{2}(\nu - \sqrt \varepsilon )}}{{{{{\sin }}^{2}}\left( {\frac{\pi }{2}\nu } \right)}}$

тогда

$\Delta (\nu ) = {{\Delta }_{1}}(\nu )\frac{{\sin \frac{\pi }{2}(\nu + \sqrt \varepsilon )\sin \frac{\pi }{2}(\nu - \sqrt \varepsilon )}}{{{{{\sin }}^{2}}\left( {\frac{\pi }{2}\nu } \right)}}$

Так как бесконечный определитель Δ₁(ν) удовлетворяет условиям теоремы Коха [2, т. 1] имеет нормальную форму: произведение его диагональных элементов и сумма недиагональных сходятся абсолютно, определитель Δ₁(ν) сходится. Откуда следует, что система уравнений (2.8) имеет такие же свойства, как и система с конечным числом неизвестных.

Следовательно, условием, при котором система уравнений (2.8) имеет нетривиальное решение, будет

$\Delta (\nu ) = 0$

Заметим, что определитель Δ₁(ν) является четной периодической функцией с периодом t = 2.

Кроме того, Δ₁(ν) имеет бесконечное число простых полюсов в точках ν = 2n ± $\sqrt \varepsilon $, где n – действительное число. Введем функцию D(ν), определяемую уравнением

$D(\nu ) = {{\Delta }_{1}}(\nu ) + K\left[ {{\text{ctg}}\frac{\pi }{2}(\nu + \sqrt \varepsilon ) - {\text{ctg}}\frac{\pi }{2}(\nu - \sqrt \varepsilon )} \right]$

Здесь коэффициент K выбран таким образом, что D(ν) не имеет полюсов в точках ν = 2n ± $\sqrt \varepsilon $.

Функция D(ν) ограничена при Reν → ∞. Очевидно, что

$\mathop {\lim }\limits_{\operatorname{Re} \nu \to \infty } D(\nu ) \to 1$

Из теоремы Лиувилля [1, T1] следует, что D(ν) = const, D(ν) ≡ 1. Следовательно

${{\Delta }_{1}}(\nu ) = 1 - K\left[ {{\text{ctg}}\frac{\pi }{2}(\nu + \sqrt \varepsilon ) - {\text{ctg}}\frac{\pi }{2}(\nu - \sqrt \varepsilon )} \right]$

Подставляя Δ₁(ν), получим

$\Delta (\nu ) = \frac{{\sin \frac{\pi }{2}(\nu + \sqrt \varepsilon )\sin \frac{\pi }{2}(\nu - \sqrt \varepsilon )}}{{{{{\sin }}^{2}}\left( {\frac{\pi }{2}\nu } \right)}} + K\frac{{\sin \pi \sqrt \varepsilon }}{{{{{\sin }}^{2}}\left( {\frac{\pi }{2}\nu } \right)}}$

Представим определитель А(ν) в виде

$\Delta (\nu ) = \mathop {\left\| {\begin{array}{*{20}{c}} {...}&{1 - \frac{\varepsilon }{{{{{(\nu - 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{{(\nu - 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{{(\nu - 2)}}^{2}}}}}&{...} \\ {...}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{\nu }^{2}}}}}&{1 - \frac{\varepsilon }{{{{\nu }^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{\nu }^{2}}}}}&{...} \\ {...}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{{(\nu + 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{{(\nu + 2)}}^{2}}}}}&{1 - \frac{\varepsilon }{{{{{(\nu + 2)}}^{2}}}}}&{...} \end{array}} \right\|}\limits_{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\,\,\,\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.}^{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\,\,\,\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.} = $

$ = - \frac{\varepsilon }{{{{\nu }^{2}}}}\mathop {\left\| {\begin{array}{*{20}{c}} {...}&{1 - \frac{\varepsilon }{{{{{(\nu - 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{{(\nu - 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{{(\nu - 2)}}^{2}}}}}&{...} \\ {...}&{{{\delta }_{1}}}&{\frac{{\varepsilon - {{\nu }^{2}}}}{\varepsilon }}&{{{\delta }_{1}}}&{...} \\ {...}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{{(\nu + 2)}}^{2}}}}}&{ - \frac{{\varepsilon {{\delta }_{1}}}}{{{{{(\nu + 2)}}^{2}}}}}&{1 - \frac{\varepsilon }{{{{{(\nu + 2)}}^{2}}}}}&{...} \end{array}} \right\|}\limits_{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\,\,\,\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.}^{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\,\,\,\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.} = - \frac{\varepsilon }{{{{\nu }^{2}}}}{{\Delta }_{2}}(\nu )$

Tогда

$ - \frac{\varepsilon }{{{{\nu }^{2}}}}{{\Delta }_{2}}(\nu ){{\sin }^{2}}\left( {\frac{\pi }{2}\nu } \right) = \sin \frac{\pi }{2}(\nu + \sqrt \varepsilon )\sin \frac{\pi }{2}(\nu - \sqrt \varepsilon ) + K\sin \pi \sqrt \varepsilon $

Так как уравнение должно быть верно при любом значении ν, положим ν = 0.

Откуда следует выражение для коэффициента K

$K = \frac{{{{{\sin }}^{2}}\frac{{\pi \sqrt \varepsilon }}{2} - \frac{\varepsilon }{4}{{\pi }^{2}}{{\Delta }_{2}}(0)}}{{\sin \pi \sqrt \varepsilon }}$

где

$\mathop {{{\Delta }_{2}}(0) = \left\| {\begin{array}{*{20}{c}} {...}&{1 - \frac{\varepsilon }{{{{2}^{2}}}}}&{\,\, - \frac{{\varepsilon {{\delta }_{1}}}}{{{{2}^{2}}}}}&{\,\, - \frac{{\varepsilon {{\delta }_{2}}}}{{{{2}^{2}}}}}&{...} \\ {...}&{{{\delta }_{1}}}&1&{{{\delta }_{1}}}&{...} \\ {...}&{ - \frac{{\varepsilon {{\delta }_{2}}}}{{{{2}^{2}}}}}&{\,\, - \frac{{\varepsilon {{\delta }_{1}}}}{{{{2}^{2}}}}}&{\,\,1 - \frac{\varepsilon }{{{{2}^{2}}}}}&{...} \end{array}} \right\|}\limits_{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,.\,\,\,\,.\,\,\,\,.}^{\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,\,..\,\,\,\,\,\,\,\,.\,\,\,\,.\,\,\,\,.} $

Тогда определитель Δ(ν) будет

$\Delta (\nu ) = 1 - \frac{{{{\pi }^{2}}\varepsilon {{\Delta }_{2}}(0)}}{{4{{{\sin }}^{2}}\left( {\frac{\pi }{2}\nu } \right)}}$

откуда получаем уравнение для вычисления характеристического показателя ν

${{\sin }^{2}}\frac{\pi }{2}\nu = \frac{{{{\pi }^{2}}}}{4}\varepsilon {{\Delta }_{2}}(0)$

В случае, когда ε и δ_n таковы, что правая часть этого уравнения >1 характеристический показатель ν будет чисто мнимым. Это означает, что решение дифференциального уравнения будет расти неограниченно.

Неравенство

${{\Delta }_{2}}(0) < \frac{4}{{\varepsilon {{\pi }^{2}}}}$

определяет границы параметрического резонанса.

3. Определение необходимых значений для выполнения расчета. Смещение центра тяжести С поршневого пальца (рис. 1), может быть достигнуто путем сверления эксцентрично расположенного отверстия. Величина смещения центра тяжести поршневого пальца может быть выражена как

$r = \frac{\xi }{{{{{\left( {\frac{{{{r}_{1}}}}{{{{r}_{2}}}}} \right)}}^{2}} - 1}}$

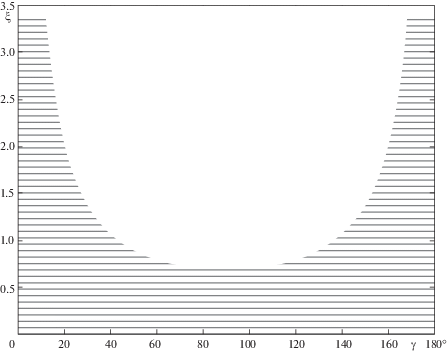
где ξ – расстояние между продольной осью поршневого пальца и осью отверстия, r₁ – радиус поршневого пальца, r₂ – радиус отверстия. Заметим, что ξ < r₁ – r₂. Величина радиуса инерции ρ поршневого пальца будет

$\rho = \sqrt {\frac{{{{{\left( {\frac{{{{r}_{1}}}}{{{{r}_{2}}}}} \right)}}^{2}}r_{1}^{2} - r_{2}^{2} - 2{{\xi }^{2}}}}{{2\left[ {{{{\left( {\frac{{{{r}_{1}}}}{{{{r}_{2}}}}} \right)}}^{2}} - 1} \right]}}} $

Область неустойчивости, в соответствии с неравенством представлена на pис. 2.

Расчеты охватывают здесь область значений γ = 0–180°, r₁ = 15 см, r₂ = 11.25 см, ξ < r₁ – r₂, b = 0, λ = 0.25, n = 100 оборотов в минуту.

Заштрихована область устойчивых колебаний.

4. Вывод. С помощью выбора параметра ξ – смещения центра отверстия (рис. 1) параметрический резонанс вращательных колебаний поршневого пальца может быть расположен на режиме максимальной мощности двигателя. Это поможет сохранить масляную пленку для смазки подшипников поршневого пальца, таким образом, уменьшая контактные нагрузки и износ подшипников.

Рис. 2.

Список литературы

Сансоне Дж. Обыкновенные дифференциальные уравнения. 1963. Т. 1. 346 с.
Уиттекер Э.Т., Ватсон Дж.Н. Курс современного анализа. 1963. Т. 1. Т. 2.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал