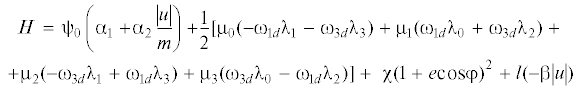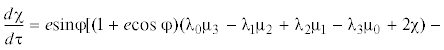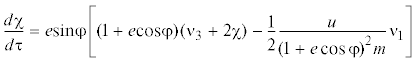Известия РАН. Механика твердого тела, 2019, № 4, стр. 109-128
КВАТЕРНИОННОЕ РЕШЕНИЕ ЗАДАЧИ ОПТИМАЛЬНОГО ПОВОРОТА ПЛОСКОСТИ ОРБИТЫ КОСМИЧЕСКОГО АППАРАТА ПЕРЕМЕННОЙ МАССЫ С ПОМОЩЬЮ ТЯГИ, ОРТОГОНАЛЬНОЙ ПЛОСКОСТИ ОРБИТЫ
Я. Г. Сапунков a, Ю. Н. Челноков a, *
a Институт проблем точной механики и управления РАН
Саратов, Россия
* E-mail: ChelnokovYuN@gmail.com
Поступила в редакцию 28.09.2017
После доработки 28.09.2017
Принята к публикации 08.10.2017
Аннотация
Решена в нелинейной постановке с использованием кватернионного дифференциального уравнения ориентации орбитальной системы координат и принципа максимума Понтрягина задача оптимального поворота плоскости орбиты космического аппарата (КА) переменной массы в инерциальной системе координат. Рассмотрены задачи быстродействия, минимизации импульса тяги, характеристической скорости КА, а также задачи минимизации комбинированных функционалов качества: времени и суммарного импульса величины тяги, затраченных на процесс управления, времени и характеристической скорости КА. Управление поворотом плоскости орбиты КА на любые по величине углы производится с помощью ограниченной по модулю реактивной тяги, ортогональной плоскости оскулирующей орбиты КА. Учитывается изменение массы аппарата за счет расхода рабочего тела на процесс управления. Частным случаем изучаемой задачи является задача оптимальной коррекции угловых элементов орбиты КА. Приведены результаты расчетов оптимального управления плоскостью орбиты КА посредством малой ограниченной реактивной тяги с большим количеством пассивных и активных участков траектории.
1. Введение. В работе рассматривается в нелинейной постановке задача оптимальной переориентации плоскости орбиты космического аппарата в инерциальной системе координат с помощью реактивной тяги, ортогональной плоскости оскулирующей орбиты КА, в непрерывных постановках с использованием ограниченной (малой) реактивной тяги и с использованием кватернионного дифференциального уравнения ориентации орбитальной системы координат. Плоскость оскулирующей орбиты проходит через радиус-вектор и вектор скорости центра масс КА для текущего момента времени. При таком управлении орбита КА поворачивается в инерциальном пространстве как неизменяемая (недеформируемая) фигура (эллипс или окружность), вращаясь в инерциальной системе координат с мгновенной угловой скоростью, направленной вдоль радиуса-вектора центра масс КА. Частным случаем этой задачи является хорошо известная и имеющая большое практическое значение в механике космического полета задача коррекции угловых элементов орбиты КА, когда изменения угловых элементов орбиты в процессе управления имеют малые значения. Использование управления, ортогонального плоскости оскулирующей орбиты КА, позволяет корректировать элементы орбиты КА, сохраняя форму и размеры орбиты КА неизменными. Это ценное свойство изучаемого процесса переориентации орбиты КА является полезным как при решении задачи коррекции угловых элементов орбиты КА, так и других задач механики космического полета, например, при управлении конфигурацией группировки спутников.
Задача оптимальной переориентации плоскости орбиты КА решается в общем случае, когда изменения угловых элементов орбиты в процессе управления могут принимать любые конечные значения. Исследуются задачи быстродействия, минимизации импульса тяги реактивного двигателя, характеристической скорости КА, а также задачи, когда функционал, определяющий качество процесса управления, представляет собой линейную свертку с весовыми множителями двух критериев: 1) времени и суммарного импульса величины тяги, затраченных на процесс управления, 2) времени и характеристической скорости КА.
В ранее опубликованных и цитируемых ниже наших работах исследовалась задача оптимальной переориентации орбиты КА посредством реактивного ускорения центра масс КА, ортогонального плоскости оскулирующей орбиты, в различных постановках с использованием различных кватернионных моделей орбитального движения (кватернионного дифференциального уравнения ориентации орбитальной системы координат или кватернионного дифференциального уравнения ориентации орбиты КА) и различных критериев качества. Рассматривалось решение задачи с использованием двигателя малой тяги (в непрерывной постановке), или с использованием двигателя большой тяги (в импульсной постановке). В качестве управления использовался вектор ускорения центра масс КА от тяги реактивного двигателя, ортогональный плоскости оскулирующей орбиты КА.
В настоящей работе в качестве управления используется ограниченный по модулю вектор реактивной тяги, ортогональной плоскости оскулирующей орбиты КА. Учитывается изменение массы аппарата за счет расхода рабочего тела на процесс управления. В состав используемой для решения задачи математической модели, описывающей процесс переориентации плоскости орбиты КА, входят, как уже отмечалось, кватернионное дифференциальное уравнение ориентации орбитальной системы координат, дифференциальное уравнение для истинной аномалии, характеризующей положение центра масс КА на орбите и разворот орбитальной системы координат относительно системы координат, связанной с орбитой КА, а также дифференциальное уравнение, описывающее изменение массы КА в процессе переориентации плоскости его орбиты.
2. Дифференциальные уравнения ориентации орбиты космического аппарата и орбитальной системы координат и задачи оптимальной переориентации орбиты и плоскости орбиты КА. Будем считать, что вектор a реактивного ускорения центра масс КА от тяги реактивного двигателя КА, а, следовательно, и вектор тяги u* реактивного двигателя во все время управляемого движения КА направлены ортогонально плоскости оскулирующей орбиты КА, т.е. ортогонально радиусу-вектору r и вектору v скорости центра масс КА (коллинеарно вектору с = r × v момента скорости центра масс КА). Тогда дифференциальные уравнения движения центра масс КА в ньютоновском гравитационном поле, описывающие изменение размеров и формы мгновенной орбиты КА, интегрируются, давая уравнение конического сечения. Поэтому управляемое движение центра масс КА в этом случае описывается дифференциальными уравнениями, описывающими изменение мгновенной ориентации орбиты КА или используемой (например, орбитальной) вращающейся системы координат, в которой записываются исходные уравнения движения центра масс КА, и дифференциальным уравнением для истинной аномалии, характеризующей положение центра масс КА на орбите.
Орбита КА в процессе такого управления движением центра масс КА не меняет своей формы и своих размеров, а поворачивается в пространстве под действием управления a или u* как неизменяемая (недеформируемая) фигура.
Движение центра масс КА будем рассматривать в инерциальной системе координат X – геоцентрической экваториальной системе координат OX1X2X3 (X) c началом в центре O притяжения Земли. Ось OX3 этой системы координат направлена вдоль оси суточного вращения Земли, оси OX1 и OX2 лежат в плоскости экватора Земли, ось OX1 направлена в точку весеннего равноденствия для Земли, ось OX2 дополняет систему до правой тройки векторов.
Введем также в рассмотрение систему координат ξ, связанную с плоскостью и перицентром орбиты КА. Начало этой системы координат находится в центре O (или в перицентре орбиты), ось ξ1 направлена вдоль радиуса-вектора перицентра орбиты, ось ξ3 перпендикулярна плоскости орбиты и имеет направление постоянного по модулю вектора c момента скорости центра масс КА относительно центра O, а ось ξ2 образует правую тройку с осями ξ1 и ξ3. Ориентация системы координат ξ в инерциальной системе координат X характеризует собой ориентацию орбиты КА в инерциальном пространстве и традиционно задается тремя угловыми оскулирующими элементами орбиты [1, 2]: долготой восходящего узла Ωu, наклоном орбиты I и угловым расстоянием перицентра от узла ωπ.
Дифференциальные уравнения, описывающие мгновенную ориентацию орбиты КА в инерциальной системе координат в угловых элементах орбиты в рассматриваемом случае ортогональности вектора реактивной тяги плоскости оскулирующей орбиты КА, имеют вид [1, 2]
(2.1)
$\begin{gathered} d{{\Omega }_{u}}{\text{/}}dt = \left( {r{\text{/}}c} \right)a{\text{sin}}({{\omega }_{\pi }} + \varphi ){\text{cosec}}I \\ dI{\text{/}}dt = \left( {r{\text{/}}c} \right)a{\text{cos}}({{\omega }_{\pi }} + \varphi ), \\ d{{\omega }_{\pi }}{\text{/}}dt = - \left( {r{\text{/}}c} \right)a{\text{sin}}({{\omega }_{\pi }} + \varphi ){\text{ctg}}I{\text{ }} \\ d\varphi {\text{/}}dt = c{\text{/}}{{r}^{{\text{2}}}},\quad r = p{\text{/}}({\text{1}} + e{\text{cos}}\varphi ),\quad c = {\text{const}}~ \\ \end{gathered} $Задача переориентации орбиты КА в угловых переменных формулируется следующим образом: требуется построить управление a, переводящее орбиту, изменение ориентации которой описывается уравнениями (2.1) из заданного начального положения
При этом должен минимизироваться выбранный функционал качества процесса переориентации орбиты КА.
Частный случай этой задачи рассматривался в работах [3–7]. В работе [4] изучался поворот плоскости околоземной круговой орбиты при помощи тяги, нормальной к мгновенной плоскости орбиты, с использованием усредненных уравнений в угловых элементах орбиты. В работе [6] исследовался поворот плоскости круговой орбиты спутника поперечной тягой (тягой, направленной перпендикулярно к мгновенной плоскости орбиты, называемой также в [6] “бинормальной тягой”). Для описания движения использованы уравнения (2.1), записанные в безразмерных переменных. Задача рассматривалась в предположении, что начальная орбита спутника лежит в плоскости экватора и что требуемый наклон орбиты является малым (поэтому в дальнейшем полагалось sin I ≈ I, cos I ≈ 1).
В работе [7] рассматривалась задача поворота плоскости оскулирующей орбиты КА с помощью “бинормальной силы”, создающей “бинормальное ускорение”, с использованием уравнений для угловых оскулирующих элементов (2.1). Рассмотрение ограничивается случаем круговой орбиты, который, по словам авторов этой работы, был исследован в работах [3, 5]. Анализируется оптимальный в смысле минимизации характеристической скорости поворот плоскости круговой орбиты на угол наклонения орбиты ΔI за неограниченное время. Поворот орбиты на угол ΔI рассматривается в работе [7] в приближенной постановке с использованием лишь второго уравнения системы (2.1) для наклонения орбиты.
В статье [8] рассматривается вековое изменение угловых элементов орбиты Ωu, I, ωπ под действием реактивного ускорения, ортогонального плоскости оскулирующей орбиты КА. Эта задача называется в статье задачей коррекции элементов орбиты Ωu, I, ωπ “бинормальным реактивным ускорением”. Используемые в статье [8] исходные уравнения движения КА имеют вид уравнений в угловых элементах (2.1). Для решения задачи авторы статьи переходят в этих уравнениях к новой независимой переменной (истинной аномалии φ) по формуле dt = (r2/c)dφ и дополняют их дифференциальным уравнением для характеристической скорости ${{v}_{{ch}}}$. Граничные условия маневра коррекции записываются в виде
Задача решается с помощью принципа максимума и усреднения уравнений. Из усредненных уравнений получен ряд аналитических соотношений для определения затрат характеристической скорости в частных случаях коррекции одного или двух элементов орбиты (наклона орбиты, долготы восходящего узла) при условии малости изменения наклона орбиты и долготы восходящего узла.
Решение задачи оптимальной переориентации орбиты КА посредством реактивного ускорения, ортогонального плоскости оскулирующей орбиты, с помощью уравнений (2.1) в угловых элементах орбиты в строгой нелинейной постановке достаточно сложно в силу нелинейности этих уравнений, наличия в них особых точек I = 0, π, а также в силу громоздкости уравнений для сопряженных множителей. Поэтому для решения этой задачи вместо угловых элементов орбиты целесообразно использовать параметры Эйлера (Родрига–Гамильтона).
Дифференциальные уравнения ориентации орбиты КА в параметрах Эйлера имеют вид [9–13]
(2.2)
$\begin{gathered} {\text{2}}d{{\Lambda }_{0}}{\text{/}}dt = - {{\Omega }_{{\text{1}}}}{{\Lambda }_{{\text{1}}}} - {{\Omega }_{{\text{2}}}}{{\Lambda }_{{\text{2}}}},\quad {\text{2}}d{{\Lambda }_{{\text{1}}}}{\text{/}}dt = {{\Omega }_{{\text{1}}}}{{\Lambda }_{0}} - {{\Omega }_{{\text{2}}}}{{\Lambda }_{{\text{3}}}} \\ {\text{2}}d{{\Lambda }_{{\text{2}}}}{\text{/}}dt = {{\Omega }_{{\text{2}}}}{{\Lambda }_{0}} + {{\Omega }_{{\text{1}}}}{{\Lambda }_{{\text{3}}}},\quad {\text{2}}d{{\Lambda }_{{\text{3}}}}{\text{/}}dt = {{\Omega }_{{\text{2}}}}{{\Lambda }_{{\text{1}}}} - {{\Omega }_{{\text{1}}}}{{\Lambda }_{{\text{2}}}} \\ \end{gathered} $(2.3)
$\begin{gathered} d\varphi {\text{/}}dt = c{\text{/}}{{r}^{{\text{2}}}},\,\,\,\,r = p{\text{/}}({\text{1}} + e{\text{cos}}\varphi ),\,\,\,\,c = {\text{const}} \\ {{\Omega }_{{\text{1}}}} = \left( {r{\text{/}}c} \right)a{\text{cos}}\varphi ,\quad {{\Omega }_{{\text{2}}}} = \left( {r{\text{/}}c} \right)a{\text{sin}}\varphi \\ \end{gathered} $Параметры Эйлера Λj связаны с угловыми элементами орбиты соотношениями
(2.4)
$\begin{gathered} {{\Lambda }_{0}} = {\text{cos}}\left( {I{\text{/2}}} \right){\text{cos}}(({{\Omega }_{u}} + {{\omega }_{\pi }}){\text{/2}}),\quad {{\Lambda }_{{\text{1}}}} = {\text{sin}}\left( {I{\text{/2}}} \right){\text{cos}}(({{\Omega }_{u}} - {{\omega }_{\pi }}){\text{/2}}) \\ {{\Lambda }_{{\text{2}}}} = {\text{sin}}\left( {I{\text{/2}}} \right){\text{sin}}(({{\Omega }_{u}} - {{\omega }_{\pi }}){\text{/2}}),\quad {{\Lambda }_{{\text{3}}}} = {\text{cos}}\left( {I{\text{/2}}} \right){\text{sin}}(({{\Omega }_{u}} + {{\omega }_{\pi }}){\text{/2}}) \\ \end{gathered} $Уравнения (2.2) в кватернионной записи принимают вид [9–13]
(2.5)
${\text{2}}d\Lambda {\text{/}}dt = \Lambda \,\bigcirc \,{{\Omega }_{\xi }},\,\,\,{{\Omega }_{\xi }} = {{\Omega }_{{\text{1}}}}{\mathbf{i}} + {{\Omega }_{{\text{2}}}}{\mathbf{j}} = \left( {r{\text{/}}c} \right)a({\text{cos}}\varphi {\mathbf{i}} + {\text{sin}}\varphi {\mathbf{j}})$Уравнения (2.2), (2.3) или (2.5), (2.3) – система пяти нелинейных стационарных дифференциальных уравнений первого порядка относительно параметров Эйлера Λj и истинной аномалии φ. Эти уравнения, в отличие от четырех нелинейных дифференциальных уравнений (2.1) ориентации орбиты в угловых элементах орбиты Ωu, I, ωπ, не имеют особых точек I = 0, π, к тому же при переходе в них от времени t к новой независимой переменной φ в соответствии с дифференциальным соотношением dφ = = (c/r2)dt получается (при a = a(φ)) система четырех линейных нестационарных дифференциальных уравнений относительно параметров Эйлера Λj (в то время как дифференциальные уравнения в угловых элементах орбиты остаются существенно нелинейными).
Указанные обстоятельства делают использование уравнений (2.2), (2.3) или (2.5), (2.3) для решения задач переориентации орбиты, плоскости орбиты и коррекции угловых элементов орбиты более удобным и эффективным в сравнении с использованием уравнений в угловых оскулирующих элементах (2.1). Такое решение задачи переориентации орбиты КА в непрерывной постановке (с использованием ограниченной (малой) тяги) рассмотрено в работах [14–17]. В них в качестве функционала качества процесса переориентации орбиты КА рассмотрены комбинированный функционал, равный взвешенной сумме времени переориентации и интеграла от квадрата модуля управления, а также комбинированный функционал, равный взвешенной сумме времени переориентации и импульса управления (характеристической скорости) за время переориентации орбиты КА. В работах [18, 19] с использованием уравнений (2.5), (2.3) построена теория решения задачи оптимальной переориентации орбиты КА в импульсной постановке (с использованием импульсной (большой) реактивной тяги). Приведены алгоритмы решения краевых задач оптимальной двухимпульсной и многоимпульсной переориентации орбиты КА (для нефиксированного числа импульсов реактивной тяги) и примеры численного решения краевых задач оптимальной переориентации орбиты КА с использованием ограниченной (малой) или импульсной (большой) тяги, в которых для описания ориентации орбиты КА используется кватернионный оскулирующий элемент ориентации орбиты.
Отметим, что в работах [14–19] для решения задач переориентации орбиты КА использован принцип максимума, а в качестве управления использовано реактивное ускорение a центра масс КА.
Наряду с дифференциальными уравнениями (2.2), (2.3) или (2.5), (2.3) ориентации орбиты КА в параметрах Эйлера Λj для решения задач переориентации орбиты, плоскости орбиты КА и коррекции угловых элементов КА могут быть использованы дифференциальные уравнения ориентации орбитальной системы координат η в параметрах Эйлера λj, имеющие вид [11, 12, 20, 21]
(2.6)
$\begin{gathered} {\text{2}}d{{\lambda }_{0}}{\text{/}}dt = - {{\omega }_{{\text{1}}}}{{\lambda }_{{\text{1}}}} - {{\omega }_{{\text{3}}}}{{\lambda }_{{\text{3}}}},\quad {\text{2}}d{{\lambda }_{{\text{1}}}}{\text{/}}dt = {{\omega }_{{\text{1}}}}{{\lambda }_{0}} + {{\omega }_{{\text{3}}}}{{\lambda }_{{\text{2}}}} \\ {\text{2}}d{{\lambda }_{{\text{2}}}}{\text{/}}dt = - {{\omega }_{{\text{3}}}}{{\lambda }_{{\text{1}}}} + {{\omega }_{{\text{1}}}}{{\lambda }_{{\text{3}}}},\quad {\text{2}}d{{\lambda }_{{\text{3}}}}{\text{/}}dt = {{\omega }_{{\text{3}}}}{{\lambda }_{0}} - {{\omega }_{{\text{1}}}}{{\lambda }_{{\text{2}}}} \\ \end{gathered} $(2.7)
$\begin{gathered} d\varphi {\text{/}}dt = c{\text{/}}{{r}^{{\text{2}}}},\quad r = p{\text{/}}({\text{1}} + e{\text{cos}}\varphi ),\quad c = {\text{const}} \\ {{\omega }_{{\text{1}}}} = (r{\text{/}}c)a,\,\,\,\,{{\omega }_{{\text{2}}}} = 0,\quad {{\omega }_{{\text{3}}}} = c{\text{/}}{{r}^{{\text{2}}}} \\ \end{gathered} $Отметим, что управление a входит в уравнения (2.6) мультипликативно в одну из двух компонент вектора абсолютной угловой скорости вращения орбитальной системы координат, направленную вдоль радиуса-вектора центра масс КА, а в уравнениях (2.2) это управление входит мультипликативно в две компоненты вектора абсолютной угловой скорости вращения орбиты КА.
Параметры λj связаны с угловыми переменными Ωu, I, ωπ, φ соотношениями, аналогичными соотношениям (2.4):
(2.8)
$\begin{gathered} {{\lambda }_{0}} = {\text{cos}}\left( {I{\text{/2}}} \right){\text{cos}}(({{\Omega }_{u}} + {{\omega }_{\pi }} + \varphi ){\text{/2}}),\quad {{\lambda }_{{\text{1}}}} = {\text{sin}}\left( {I{\text{/2}}} \right){\text{cos}}(({{\Omega }_{u}} - {{\omega }_{\pi }} - \varphi ){\text{/2}}) \\ {{\lambda }_{{\text{2}}}} = {\text{sin}}\left( {I{\text{/2}}} \right){\text{sin}}(({{\Omega }_{u}} - {{\omega }_{\pi }} - \varphi ){\text{/2}}),\quad {{\lambda }_{{\text{3}}}} = {\text{cos}}\left( {I{\text{/2}}} \right){\text{sin}}(({{\Omega }_{u}} + {{\omega }_{\pi }} + \varphi ){\text{/2}}) \\ \end{gathered} $Уравнения (2.6) в кватернионной записи принимают вид [11, 12, 20, 21]
(2.9)
${\text{2}}d\lambda {\text{/}}dt = \lambda \,^\circ \,{{\omega }_{\eta }},\quad {{\omega }_{\eta }} = {{\omega }_{{\text{1}}}}{\mathbf{i}} + {{\omega }_{{\text{3}}}}{\mathbf{k}} = (r{\text{/}}c)a{\mathbf{i}} + (c{\text{/}}{{r}^{{\text{2}}}}){\mathbf{k}}$(2.10)
$\lambda = \Lambda \,^\circ \,({\text{cos}}(\varphi {\text{/2}}) + {\mathbf{k}}{\text{sin}}(\varphi {\text{/2}}))$Отметим также, что кватернионное дифференциальное уравнение ориентации орбитальной системы координат, аналогичное (2.9), также использовалось для описания орбитального движения в работах [22, 23].
Уравнения (2.6), (2.7) или (2.7), (2.9) использовались в работах [12, 24–26] для решения c использованием принципа максимума Понтрягина задачи оптимальной переориентации орбиты КА посредством реактивной тяги, ортогональной плоскости орбиты, в непрерывной постановке (с использованием ограниченной (малой) тяги и с использованием в качестве управления реактивного ускорения a). В качестве критерия оптимальности был использован комбинированный функционал, равный взвешенной сумме времени переориентации и интегрального квадратичного (в отношении управления) функционала качества, или функционал, равный взвешенной сумме времени переориентации и импульса управления (характеристической скорости) за время переориентации орбиты КА. Управление полагалось ограниченным по модулю.
В работах [27, 28] уравнения (2.7), (2.9) использованы для решения задачи оптимальной переориентации орбиты КА посредством импульсной (большой) реактивной тяги, ортогональной плоскости оскулирующей орбиты. В качестве управления использовано ускорение a центра масс КА от тяги реактивного двигателя. Минимизируется комбинированный функционал, равный взвешенной сумме времени переориентации и импульса реактивного ускорения центра масс КА (характеристической скорости) за время переориентации орбиты КА. Решение задачи построено с помощью предельных переходов в уравнениях и соотношениях, полученных в результате решения задачи оптимальной переориентации орбиты КА в непрерывной постановке (с использованием ограниченной (малой) реактивной тяги и принципа максимума Понтрягина). Алгоритмы импульсного решения задачи, построенные в [28], позволяют определять оптимальные моменты включения реактивного двигателя, оптимальные величины импульсов реактивного ускорения КА и их оптимальное число. Приведены примеры численного решения задачи оптимальной импульсной переориентации орбиты КА, демонстрирующие возможности предлагаемого метода. В [28] также показано, что задача оптимальной импульсной переориентации орбиты КА в случае, когда оптимальное управление состоит из двух импульсов реактивного ускорения, сообщаемых КА в начальный и конечный моменты времени движения, решается аналитически.
Использование как уравнений (2.2), (2.3) (или (2.5), (2.3)), описывающих собой ориентацию орбиты КА и положение КА на орбите, так и уравнений (2.6), (2.7) (или (2.9), (2.7)), описывающих собой ориентацию орбитальной системы координат и положение КА на орбите, для решения задач оптимальной переориентации орбиты КА имеет свои достоинства. Так, уравнения (2.6), (2.7) являются при r = const (в случае круговой орбиты) и a = const линейными дифференциальными уравнениями с постоянными коэффициентами, в то время как уравнения (2.2), (2.3) в этом случае являются линейными дифференциальными уравнениями с переменными коэффициентами. Поэтому уравнения (2.6), (2.7) (или (2.9), (2.7)) более удобны и эффективны в сравнении с уравнениями (2.2), (2.3) (или (2.5), (2.3)) с аналитической точки зрения. Однако в состав уравнений (2.2), (2.3) входят уравнения (2.2) в скалярных оскулирующих элементах Λj, а в состав уравнений (2.5), (2.3) – уравнение (2.5) для кватернионного оскулирующего элемента орбиты Λ. Переменные Λj, а также составленный из них кватернион Λ, как уже отмечалось, непосредственно характеризуют собой ориентацию орбиты КА в инерциальном пространстве. При равенстве нулю управления a (реактивного ускорения) эти переменные становятся постоянными величинами, поэтому переменные Λj являются скалярными оскулирующими (медленно изменяющимися) элементами орбиты КА, а переменная Λ – кватернионным оскулирующим (медленно изменяющимся) элементом орбиты КА. Такими свойствами скалярные переменные λj и эквивалентная им кватернионная переменная λ, фигурирующие в уравнениях (2.6), (2.7) и (2.9), (2.7), не обладают (они являются быстро меняющимися функциями времени). Поэтому изучение задач оптимальной переориентации орбиты, плоскости орбиты и коррекции угловых элементов орбиты КА представляется актуальным как с использованием кватернионного дифференциального уравнения ориентации орбитальной системы координат (2.9), так и с использованием кватернионного дифференциального уравнения ориентации орбиты КА (2.5).
В настоящей статье задача оптимальной переориентации плоскости орбиты КА изучается с использованием уравнений (2.6), (2.7) (или (2.9), (2.7)), более удобных с аналитической точки зрения. При этом в качестве управления принимается не алгебраическая величина a реактивного ускорения центра масс КА, как это делалось во всех цитированных выше работах, а алгебраическая величина u* вектора реактивной тяги u* = m*(t)a двигателя КА, ортогонального плоскости оскулирующей орбиты КА. Масса аппарата m* полагается кусочно дифференцируемой функцией времени t: m* = m*(t). В состав математической модели, описывающей процесс переориентации плоскости орбиты КА, дополнительно включается дифференциальное уравнение, описывающее изменение массы КА в процессе управляемого движения.
3. Постановка задачи оптимального поворота плоскости орбиты КА переменной массы посредством ограниченной (малой) реактивной тяги. Дифференциальные уравнения задачи переориентации орбиты КА переменной массы (и задачи переориентации плоскости орбиты КА) в инерциальной системе координат с помощью реактивной тяги, ортогональной плоскости оскулирующей орбиты КА, в случае использования для решения задачи кватернионного дифференциального уравнения ориентации орбитальной системы координат имеют следующий вид:
(3.1)
$2\frac{{d{\mathbf{\lambda }}}}{{dt}} = $ λ ∘ $\left( {\frac{r}{{cm{\text{*}}}}\,u{\text{*}}\,{\mathbf{i}} + \frac{с}{{{{r}^{2}}}}\,{\mathbf{k}}} \right)$, $\frac{{d\varphi }}{{dt}} = \frac{с}{{{{r}^{2}}}}$, $r = $ $\frac{p}{{{\text{1}} + e{\text{cos}}\varphi }}$Ориентация плоскости орбиты КА в инерциальной системе координат характеризуется направляющими косинусами nk единичного вектора n нормали к плоскости орбиты в этой системе координат, которые запишем через параметры Эйлера λj и угловые элементы орбиты КА в следующем виде:
(3.3)
${{n}_{2}} = 2({{\lambda }_{2}}{{\lambda }_{3}} - {{\lambda }_{0}}{{\lambda }_{1}})\; = $ $ - {\text{sin}}\,I\,{\text{cos}}\,{{\Omega }_{u}}$Перейдем к безразмерным переменным ρ, τ, m, u, um, β по формулам
(3.4)
$r = R\rho ,\quad t = \frac{{{{R}^{2}}}}{c}\tau ,\quad m* = m_{0}^{*}m,\quad u* = \frac{{{{c}^{2}}m_{0}^{*}}}{{{{R}^{3}}}}u,\quad u_{m}^{*} = \frac{{{{c}^{2}}m_{0}^{*}}}{{{{R}^{3}}}}{{u}_{m}},\quad R = p,\quad \beta * = \frac{R}{c}\beta $Уравнения движения КА (3.1), (3.2) в безразмерных переменных примут вид
(3.5)
$2\frac{{d{\mathbf{\lambda }}}}{{d\tau }} = $ λ ∘ $\left( {\frac{u}{{{\text{(1}} + e{\text{cos}}\varphi {\text{)}}m}}{\mathbf{i}} + {{{\left( {{\text{1}} + e{\text{cos}}\varphi } \right)}}^{2}}{\mathbf{k}}} \right)$(3.6)
$\frac{{d\varphi }}{{d\tau }} = {{({\text{1}} + e{\text{cos}}\varphi )}^{2}},$ $\frac{{dm}}{{d\tau }} = - \beta \left| u \right|$Постановка задачи: требуется определить ограниченное по модулю управление u:
ортогональное плоскости оскулирующей орбиты космического аппарата, переводящее КА, движение центра масс которого описывается уравнениями (3.5), (3.6), из заданного начального состояния(3.8)
$\tau = {{\tau }_{0}} = 0,\quad \varphi (0) = {{\varphi }_{0}},\quad \lambda (0) = \Lambda (0)\,^\circ \,({\text{cos}}({{\varphi }_{0}}{\text{/2}}) + {\mathbf{k}}{\kern 1pt} {\text{sin}}({{\varphi }_{0}}{\text{/2}})),\,\,\,\,m = {\text{1}}$(3.9)
$\begin{gathered} \tau = {{\tau }_{1}},\quad 2({{\lambda }_{1}}({{\tau }_{1}}){{\lambda }_{3}}({{\tau }_{1}}) + {{\lambda }_{0}}({{\tau }_{1}}){{\lambda }_{2}}({{\tau }_{1}})) - \sin I({{\tau }_{1}})\sin {{\Omega }_{u}}({{\tau }_{1}}) = 0 \\ 2({{\lambda }_{2}}({{\tau }_{1}}){{\lambda }_{3}}({{\tau }_{1}}) - {{\lambda }_{0}}({{\tau }_{1}}){{\lambda }_{1}}({{\tau }_{1}})) + \sin I({{\tau }_{1}})\cos {{\Omega }_{u}}({{\tau }_{1}}) = 0 \\ \end{gathered} $(3.10)
$J = \int\limits_0^{{{\tau }_{1}}} {({{\alpha }_{1}} + {{\alpha }_{2}}{\text{|}}u{\text{|}})d\tau ,\quad {{\alpha }_{1}} = {\text{const}} \geqslant 0} ,\quad {{\alpha }_{2}} = {\text{const}} \geqslant 0$(3.11)
$J = \int\limits_0^{{{\tau }_{1}}} {\left( {{{\alpha }_{1}} + {{\alpha }_{2}}\frac{{{\text{|}}u{\text{|}}}}{m}} \right)d\tau ,\quad {{\alpha }_{1}} = {\text{const}} \geqslant 0} ,\quad {{\alpha }_{2}} = {\text{const}} \geqslant 0$Функционалы (3.10) и (3.11) представляют собой линейные свертки с постоянными весовыми множителями α1 и α2 двух критериев: (3.10) – времени и импульса величины тяги реактивного двигателя, затраченных на процесс управления, (3.11) – времени и характеристической скорости КА.
Безразмерное время τ1 процесса управления заранее не задается. В частном случае, когда ${{\alpha }_{1}} \ne 0,\,\,{{\alpha }_{2}} = 0$, критерием оптимальности является длительность процесса управления и задача оптимального управления становится задачей быстродействия. В других частных случаях, когда ${{\alpha }_{1}} = 0,\,{\kern 1pt} {\kern 1pt} {{\alpha }_{2}} = 1$, критерием оптимальности является импульс величины тяги реактивного двигателя (функционал (3.10)) или характеристическая скорость КА (функционал (3.11)).
Фигурирующие в начальных условиях кватернион Λ(0) и скалярная величина φ0 характеризуют начальную ориентацию орбиты КА и начальное положение КА на орбите. Величины c, p, e, φ0, Λ(0) заданы (начальное Λ(0) значение кватерниона Λ ориентации орбиты КА может быть найдено через заданные начальные значения угловых элементов орбиты Ωu, I, ωπ по формулам (2.4)). Также заданы конечные значения Ωu(τ1), I(τ1) угловых элементов орбиты Ωu, I, характеризующие требуемую (конечную) ориентацию плоскости орбиты КА и входящие в уравнения (3.9) многообразия, которому принадлежит конечное состояние управляемой системы. Подлежат определению оптимальный закон управления u = u(τ), под действием которого плоскость орбиты КА займет требуемое положение, и величины τ1, φ1, характеризующие время процесса управления и конечное положение КА на орбите.
Поставленная задача – задача оптимального управления с подвижным правым концом траектории. Условия (3.9) на правом конце траектории записаны в соответствии с соотношениями (3.3) для направляющих косинусов nk единичного вектора n нормали к плоскости орбиты КА. Отметим, что направляющие косинусы nk связаны условием $n_{1}^{2}$ + $n_{2}^{2}$ + $n_{3}^{2}$ = 1. Поэтому для решения задачи взяты только первые два из трех условий (3.3) на правом конце траектории. Вместо них могут быть взяты первое и третье из условий (3.3) или второе и третье из этих условий.
4. Законы (структура) оптимального управления и условия трансверсальности. Поставленную задачу будем решать с помощью принципа максимума. Для этого введем дополнительные переменные μ, χ и l, сопряженные по отношению к фазовым переменным λ, φ и m. Функция Гамильтона–Понтрягина в случае минимизации функционала (3.10) имеет вид
(4.1)
$\begin{gathered} H = {{{\psi }}_{0}}({{{\alpha }}_{1}} + ~{{{\alpha }}_{2}}{\text{|}}u{\text{|}}) + ~\frac{1}{2}[{{{\mu }}_{0}}( - {{{\omega }}_{{1d}}}{{{\lambda }}_{1}} - {{{\omega }}_{{3d}}}{{{\lambda }}_{3}}) + {{{\mu }}_{1}}({{{\omega }}_{{1d}}}{{{\lambda }}_{0}} + {{{\omega }}_{{3d}}}{{{\lambda }}_{2}}) + \\ + ~{{{\mu }}_{2}}( - {{{\omega }}_{{3d}}}{{{\lambda }}_{1}} + {{{\omega }}_{{1d}}}{{{\lambda }}_{3}}) + {{{\mu }}_{3}}({{{\omega }}_{{3d}}}{{{\lambda }}_{0}} - {{{\omega }}_{{1d}}}{{{\lambda }}_{2}})] + {\chi \;}{{(1 + e{\text{\;cos}}\varphi {\text{\;}})}^{2}} + l( - ~{\beta }~{\text{|}}u{\text{|}}) \\ \end{gathered} $Здесь μj – компоненты сопряженной кватернионной переменной μ,
(4.3)
${{\omega }_{{1d}}} = $ $\frac{u}{{{\text{(1}} + e{\text{cos}}\varphi {\text{)}}m}}$, ${{\omega }_{{3d}}} = $ ${{\left( {{\text{1}} + e{\text{cos}}\varphi } \right)}^{2}}$В соответствии с принципом максимума постоянная ψ0 ≤ 0. В дальнейшем рассматривается случай, когда постоянная ψ0 < 0. В этом случае в силу однородности функции Гамильтона–Понтрягина относительно сопряженных переменных константу ψ0 можно выбрать произвольным образом, поэтому в дальнейшем нами полагается ψ0 = – 1.
Система уравнений для сопряженных переменных в случае минимизации функционала (3.10) имеет вид уравнений (4.4)–(4.6):
(4.4)
$2\frac{{d{\mathbf{\mu }}}}{{d\tau }} = $ ${\mathbf{\mu }}$ ∘ $\left( {\frac{u}{{{\text{(1}} + e\,{\text{cos}}\,\varphi {\text{)}}m}}\,{\mathbf{i}} + {{{\left( {{\text{1}} + e\,{\text{cos}}\,\varphi } \right)}}^{2}}\,{\mathbf{k}}} \right)$(4.5)
$ - \frac{1}{2}$$\frac{u}{{{{{{\text{(1}} + e\,{\text{cos}}\varphi {\text{)}}}}^{{\text{2}}}}m}}$(${{{\lambda }}_{0}}{{{\mu }}_{{1{\text{\;}}}}} - {{{\lambda }}_{1}}{{{\mu }}_{0}} - {{{\lambda }}_{2}}{{{\mu }}_{3}} + {{{\lambda }}_{3}}{{{\mu }}_{2}}$)](4.6)
$\frac{{dl}}{{d\tau }} = \frac{1}{2}\frac{u}{{{\text{(1}} + e\,{\text{cos}}\varphi {\text{)}}{{m}^{2}}}}$(${{{\lambda }}_{0}}{{{\mu }}_{{1{\text{\;}}}}} - {{{\lambda }}_{1}}{{{\mu }}_{0}} - {{{\lambda }}_{2}}{{{\mu }}_{3}} + {{{\lambda }}_{3}}{{{\mu }}_{2}}$)В случае минимизации функционала (3.11) система уравнений для сопряженных переменных имеет вид уравнений (4.4), (4.5) и уравнения (4.7):
(4.7)
$\frac{{dl}}{{d\tau }} = \frac{1}{{{{m}^{2}}}}{\text{[}}{{{\alpha }}_{2}}{\text{|}}u{\text{| + }}\frac{1}{2}\frac{u}{{{\text{(1}} + e\,{\text{cos}}\varphi {\text{)}}}}({{{\lambda }}_{0}}{{{\mu }}_{{1{\text{\;}}}}} - {{{\lambda }}_{1}}{{{\mu }}_{0}} - {{{\lambda }}_{2}}{{{\mu }}_{3}} + {{{\lambda }}_{3}}{{{\mu }}_{2}})]$Введем новую кватернионную переменную
(4.8)
${\mathbf{\nu }}$ = ${{{\nu }}_{{0~}}} + ~{{{\nu }}_{{1~}}}{\mathbf{i}} + ~{{{\nu }}_{{2~}}}{\mathbf{j}} + ~{{{\nu }}_{{3~}}}{\mathbf{k}}$ = ${\mathbf{\bar {\lambda }}} \circ {\mathbf{\mu }}$Компоненты ${{{\nu }}_{j}}$ кватерниона μ в соответствии с (4.8) определяются формулами
(4.9)
${{{\nu }}_{{2~}}} = {{{\lambda }}_{0}}{{{\mu }}_{{2{\text{\;}}}}} + {{{\lambda }}_{1}}{{{\mu }}_{3}} - {{{\lambda }}_{2}}{{{\mu }}_{0}} - {{{\lambda }}_{3}}{{{\mu }}_{1}},\quad {{{\nu }}_{{3~}}} = {{{\lambda }}_{0}}{{{\mu }}_{{3{\text{\;}}}}} - {{{\lambda }}_{1}}{{{\mu }}_{2}} + {{{\lambda }}_{2}}{{{\mu }}_{1}} - {{{\lambda }}_{3}}{{{\mu }}_{0}}$,С использованием новых переменных νj выражения (4.1), (4.2), (4.3) для функции Гамильтона–Понтрягина и сопряженные уравнения (4.5), (4.6) и (4.7) принимают более простой вид:
(4.10)
$H = - ({{{\alpha }}_{1}} + ({{{\alpha }}_{2}} + {\beta }l)\left| u \right|) + \frac{1}{2}\left[ {\frac{u}{{{\text{(1}} + e\,{\text{cos}}\,\varphi {\text{)}}m}}{{\nu }_{1}} + {{{{\text{(1}} + e\,{\text{cos}}\,\varphi {\text{)}}}}^{{\text{2}}}}\left( {{{\nu }_{3}} + 2\chi } \right)} \right]$(4.11)
$H = - \left( {{{\alpha }_{1}} + \frac{{{{\alpha }_{2}}}}{m} + \beta l} \right){\text{|}}u{\text{|}} + \frac{1}{2}\left[ {\frac{u}{{{\text{(1}} + e\,{\text{cos}}\varphi {\text{)}}m}}{{\nu }_{1}} + {{{{\text{(1}} + e\,{\text{cos}}\varphi {\text{)}}}}^{{\text{2}}}}\left( {{{\nu }_{3}} + 2\chi } \right)} \right]$(4.14)
$\frac{{dl}}{{d\tau }} = \frac{1}{{{{m}^{2}}}}\left[ {{{\alpha }_{2}}{\text{|}}u{\text{|}} + \frac{1}{2}\frac{u}{{(1 + e\cos \varphi )}}{{\nu }_{1}}} \right]$Отметим, что кватернионное сопряженное уравнение (4.4) совпадает по своей форме с кватернионным фазовым уравнением (3.5), поскольку кватернионное уравнение (3.5) обладает свойством самосопряженности. Отметим также, что свойство самосопряженности кватернионного кинематического уравнения было впервые установлено В.Н. Бранцем и И.П. Шмыглевским при решении задач оптимальных пространственных разворотов твердого тела [30].
Из (4.5) или (4.12) видно, что в случае круговой орбиты, когда эксцентриситет орбиты e = 0, сопряженная переменная
Закон оптимального управления (т.е. закон управления, удовлетворяющий необходимым условиям оптимальности) находится из условия максимума функции H по переменной u с учетом наложенного ограничения (3.7) и в случае минимизации функционала (3.10) имеет вид (4.16):
(4.16)
$u = {\text{\;}}0,$ если $\frac{{\left| {{{\nu }_{1}}} \right|}}{{{\text{2(1}} + e{\text{cos}}\varphi {\text{)}}m}}$ $ < ~{{{\alpha }}_{2}} + {\beta }l$(4.17)
$u = {\text{\;}}0,$ если $\frac{1}{m}\left( {\frac{{\left| {{{\nu }_{1}}} \right|}}{{{\text{2(1}} + e{\text{cos}}\varphi {\text{)}}}} - {{\alpha }_{2}}} \right) < {\beta }l$Отметим, что особый режим управления в статье не рассматривается.
Условия трансверсальности, соответствующие многообразию конечного состояния (3.9), после исключения из них двух неопределенных множителей Лагранжа принимают следующий вид:
при τ = τ1
(4.18)
${{{\lambda }}_{0}}{{{\mu }}_{{3{\text{\;}}}}} - {{{\lambda }}_{1}}{{{\mu }}_{2}} + {{{\lambda }}_{2}}{{{\mu }}_{1}} - {{{\lambda }}_{3}}{{{\mu }}_{0}} = {\text{\;}}{{{\nu }}_{{3~}}} = 0$, ${\chi } = 0,~\quad l = 0$(4.19)
${{{\lambda }}_{0}}{{{\mu }}_{{0{\text{\;}}}}} - {{{\lambda }}_{1}}{{{\mu }}_{1}} - {{{\lambda }}_{2}}{{{\mu }}_{2}} + {{{\lambda }}_{3}}{{{\mu }}_{3}} = {\text{\;}}{{{\nu }}_{{0~}}} - ~2({{{\lambda }}_{1}}{{{\mu }}_{1}} + {{{\lambda }}_{2}}{{{\mu }}_{2}}) = 0$5. Анализ задачи оптимальной переориентации плоскости орбиты КА. В случае минимизации функционала (3.10) задача сведена к краевой задаче с подвижным правым концом траектории, описываемой системой нелинейных дифференциальных уравнений (3.5), (3.6), (4.4), (4.12), (4.13), (4.16) двенадцатого порядка и восемью краевыми условиями (3.8), (3.9), которые необходимо дополнить четырьмя условиями трансверсальности (4.18), (4.19) и равенством
(5.1)
$H = - ({{{\alpha }}_{1}} + ({{{\alpha }}_{2}} + {\beta }l){\text{|}}u{\text{|}}) + \frac{1}{2}\left[ {\frac{u}{{{\text{(1}} + e{\text{cos}}\varphi {\text{)}}m}}{{\nu }_{1}} + {{{{\text{(1}} + e{\text{cos}}\varphi {\text{)}}}}^{{\text{2}}}}\left( {{{\nu }_{3}} + 2\chi } \right)} \right] = 0$В случае минимизации функционала (3.11) задача сведена к краевой задаче с подвижным правым концом траектории, описываемой системой нелинейных дифференциальных уравнений (3.5), (3.6), (4.4), (4.12), (4.14), (4.17) двенадцатого порядка и восемью краевыми условиями (3.8), (3.9), которые необходимо дополнить четырьмя условиями трансверсальности (4.18), (4.19) и равенством
(5.2)
$\begin{gathered} H = - \left( {{{\alpha }_{1}} + \frac{{{{\alpha }_{2}}}}{m} + \beta l} \right){\text{|}}u{\text{|}} + \\ + \frac{1}{2}\left[ {\frac{u}{{{\text{(1}} + e{\text{cos}}\varphi {\text{)}}m}}{{\nu }_{1}} + {{{{\text{(1}} + e{\text{cos}}\varphi {\text{)}}}}^{{\text{2}}}}({{\nu }_{3}} + 2\chi )} \right] = 0 \\ \end{gathered} $Дифференциальные уравнения задачи имеют первые интегралы
(5.3)
${\text{||}}{\mathbf{\lambda }}{\text{|}}{{{\text{|}}}^{2}}{\text{\;}} = {\lambda }_{0}^{{2~}} + {\lambda }_{1}^{{2~}} + {\lambda }_{2}^{{2~}} + {\lambda }_{3}^{{2~}} = {\text{||}}{\mathbf{\lambda }}(0){\text{|}}{{{\text{|}}}^{{2~}}} = 1$(5.4)
${\text{||}}{\mathbf{\mu }}{\text{|}}{{{\text{|}}}^{2}}{\text{\;}} = {\mu }_{0}^{{2~}} + {\mu }_{1}^{2} + {\mu }_{2}^{2} + {\mu }_{3}^{2} = {\text{||}}{\mathbf{\mu }}(0){\text{|}}{{{\text{|}}}^{{2~}}} = {\text{const}}$(5.5)
${\mathbf{\mu }}~ \circ ~{\mathbf{\bar {\lambda }}}$ = ${\mathbf{\nu }}{\text{*}}$ = ${\nu }{{_{0}^{*}}_{~}} + ~{\nu }_{1}^{*}{\mathbf{i}} + ~{\nu }_{2}^{*}{\mathbf{j}} + ~{\nu }_{3}^{*}{\mathbf{k}} = {\text{const}}$(5.6)
${{{\lambda }}_{0}}{{{\mu }}_{{0{\text{\;}}}}} + {{{\lambda }}_{1}}{{{\mu }}_{1}} + {{{\lambda }}_{2}}{{{\mu }}_{2}} + {{{\lambda }}_{3}}{{{\mu }}_{3}} = {{{\nu }}_{{0~}}} = ~{{{\nu }}_{0}}(0) = {\text{const}}$Интегралы (5.3)–(5.6) имеют место для любого управления u. Интегралы (5.3), (5.4) отражают неизменность норм кватернионных переменных λ и μ. Интеграл (5.5) имеет место в силу самосопряженности кватернионного фазового уравнения (3.5).
В силу автономности системы уравнений для фазовых и сопряженных переменных равенства (5.1) и (5.2) будут выполняться в любой момент времени оптимального управляемого движения, т.е. будут являться первыми интегралами этих уравнений для оптимального управления u. В случае круговой орбиты уравнения задачи имеют также первый интеграл (4.15): χ = χ0 = const.
На активном участке траектории оптимальное управление u является постоянной величиной, поэтому дифференциальное уравнение для массы m (второе уравнение подсистемы (3.6)) интегрируется и дает соотношение
описывающее изменение массы КА на этом участке и показывающее, что на активном участке безразмерная масса m аппарата является линейной функцией безразмерного времени τ (уменьшается линейно с течением времени τ).Размерная q* и безразмерная q характеристические скорости КА связаны соотношением q* = (c/R)q. Изменение безразмерной характеристической скорости описывается дифференциальным уравнением
Из сопоставления этого уравнения с комбинированным функционалом (3.11) видно, что характеристическая скорость q является частным случаем функционала (3.11), когда коэффициенты этого функционала ${{\alpha }_{1}} = 0,\,{\kern 1pt} {\kern 1pt} {{\alpha }_{2}} = 1$.
Интегрирование уравнения (5.8) с учетом (5.7) на активном участке траектории дает следующий закон изменения характеристической скорости в процессе управляемого движения КА на этом участке траектории:
Оба функционала (3.10) и (3.11) можно выразить через конечное безразмерное время движения τ1 и конечное значение безразмерной массы аппарата m1. Имеем:
Таким образом, поставленная выше задача Лагранжа оптимального управления сводится к задаче Майера. Из последних приведенных формул следует, что при α1 = 0 задачи минимизации импульса тяги и характеристической скорости сводятся к задаче минимизации топлива. Это также видно из ниже приводимых таблиц 4, 5 и 7 численных расчетов.
Из функций Гамильтона–Понтрягина (4.10), (4.11) и законов оптимального управления (4.16), (4.17) видно, что они фактически являются функциями не сопряженных переменных μj (j = 0, 1, 2, 3) (компонент кватернионной сопряженной переменной μ), а функциями скалярных переменных ${{{\nu }}_{1}}$ и ${{{\nu }}_{{3~}}}$ (компонент кватерниона ν), которые в свою очередь являются мультипликативными композициями фазовых λj и сопряженных μj переменных, имеющими вид (4.9). При этом величина ν0 = const (она равна компоненте $\nu _{0}^{*}$ кватернионной константы ν* управляемого движения, определяемой соотношением (5.5)) и входит она лишь в условие трансверсальности (4.19). Поэтому вместо выше перечисленных двенадцати дифференциальных уравнений краевой задачи оптимального управления относительно фазовых и сопряженных переменных λj (j = 0, 1, 2, 3), φ, m, μj, χ, l можно использовать для решения задачи оптимальной переориентации плоскости орбиты КА систему одиннадцати дифференциальных уравнений относительно переменных λj, φ, m, νk (k = 1, 2, 3), χ, l, опуская дифференциальное уравнение для переменной ν0, переходящее в соотношение ν0 = const, и условие трансверсальности (4.19), содержащее величину ν0.
Дифференцируя кватернионное соотношение (4.8) по переменной τ и учитывая уравнения (3.5), (4.4), получаем следующие дифференциальные уравнения для скалярной ${{{\nu }}_{0}}$ и векторной ${{{\mathbf{\nu }}}_{{v}}}$ = ν1i + ν2 j + ν3k частей кватернионной переменной ν:
(5.10)
$\frac{{d{{{\mathbf{\nu }}}_{v}}}}{{d\tau }} = {{{\mathbf{\nu }}}_{v}} \times \left( {\frac{u}{{{\text{(1}} + e{\text{cos}}\varphi {\text{)}}m}}{\mathbf{i}} + {{{\left( {{\text{1}} + e{\text{cos}}\varphi } \right)}}^{2}}{\mathbf{k}}} \right)$Из уравнения (5.9) имеем: ${{{\nu }}_{{0~}}} = ~{{{\nu }}_{0}}(0) = {\text{const}}.$ Из векторного уравнения (5.10) получаем следующую систему трех скалярных дифференциальных уравнений для компонент νk векторной переменной ${{{\mathbf{\nu }}}_{{v}}}$:
(5.11)
$\frac{{d{{\nu }_{2}}}}{{d\tau }} = \frac{u}{{{\text{(1}} + e{\text{cos}}\varphi {\text{)}}m}}{{\nu }_{3}} - {{\left( {{\text{1}} + e{\text{cos}}\varphi } \right)}^{2}}{{\nu }_{1}}$Уравнения (5.11) ((5.10)) имеют (для любого управления) первый интеграл
Уравнения (5.11) являются дифференциальными уравнениями функции переключения ${{{\nu }}_{1}}$ = ${{{\nu }}_{1}}({\tau })$, поскольку управление, как это видно из соотношений (4.16) и (4.17), переключается с одной ветви на другую в зависимости от значения координаты ν1. Переменные νk, входящие в уравнения (5.11), связаны с кватернионным первым интегралом (5.5) уравнений краевой задачи преобразованием вращения: ${{{\mathbf{\nu }}}_{{v}}} = ~{\mathbf{\bar {\lambda }}}~ \circ ~{\mathbf{\nu }}_{{v}}^{*}~ \circ ~{\mathbf{\lambda }}.$
Таким образом, задача оптимальной переориентации плоскости орбиты КА в непрерывной постановке (с использованием ограниченной (малой) реактивной тяги) сводится к решению краевой задачи с подвижным правым концом траектории, описываемой в случае минимизации функционала (3.10) системой одиннадцати нелинейных стационарных дифференциальных уравнений (3.5), (3.6), (5.11), (4.12), (4.13), (4.16), а в случае минимизации функционала (3.11) – системой одиннадцати нелинейных стационарных дифференциальных уравнений (3.5), (3.6), (5.11), (4.12), (4.14), (4.17) относительно переменных λj, φ, m, νk, χ, l и восемью краевыми условиями (3.8), (3.9), которые необходимо дополнить тремя условиями трансверсальности (4.18) и равенством (5.1) в первом случае или равенством (5.2) во втором случае.
Оптимальное управление, как это видно из (4.16) и (4.17), состоит из двух возможных режимов: активного участка движения с постоянной максимально возможной по модулю реактивной тягой u = ±um, направление (знак) которой определяется знаком переменной ν1, и пассивного участка движения с нулевой тягой (напомним, что особый режим управления в статье не рассматривается).
Как видно из условий трансверсальности (4.18), переменные ν3 и χ на правом конце траектории равны нулю, поэтому условие (5.1) (в случае минимизации функционала (3.10)) и условие (5.2) (в случае минимизации функционала (3.11)), имеющие место для оптимального управления u и оптимальной траектории на этом конце траектории принимают соответственно вид (5.12) и (5.13):
(5.12)
$ - ({{{\alpha }}_{1}} + ({{{\alpha }}_{2}} + {\beta }l)\left| u \right|) + \frac{u}{{{\text{2(1}} + e\,{\text{cos}}\varphi {\text{)}}m}}\,{{\nu }_{1}} = 0$(5.13)
$ - \left( {{{{\alpha }}_{1}} + \frac{{{{{\alpha }}_{2}}}}{m} + {\beta }l} \right)\left| u \right| + \frac{u}{{{\text{2(1}} + e\,{\text{cos}}\varphi {\text{)}}m}}\,{{\nu }_{1}} = 0$Сопряженная переменная χ и второе условие трансверсальности (4.18) исключаются из рассмотрения, а краевая задача будет описываться системой нелинейных стационарных дифференциальных уравнений (3.5), (3.6), (5.11), (4.13), (4.16) или (3.5), (3.6), (5.11), (4.14), (4.17) десятого порядка относительно переменных λj, φ, m, νk, l и восемью краевыми условиями (3.8), (3.9), которые необходимо дополнить двумя условиями трансверсальности ν3 = 0, l = 0 и равенством (5.12) или (5.13) на правом конце траектории.
Отметим, что возможно понижение размерности исходной краевой задачи, описываемой дифференциальными уравнениями для переменных λj, φ, m, νk, χ, l одиннадцатого порядка, на две единицы за счет перехода к новой независимой переменной – истинной аномалии φ (при таком переходе исключаются из рассмотрения дифференциальные уравнения для истинной аномалии φ и сопряженной к ней переменной χ, а дифференциальные уравнения краевой задачи становятся нестационарными).
Отметим также, что дифференциальные уравнения (5.11), описывающие функцию ν1 = ν1(φ) переключения управления, и второе дифференциальное уравнение подсистемы (3.6) для массы m при переходе в них к новой независимой переменной φ (истинной аномалии) выделяются для оптимального управления u = ±um в замкнутую подсистему четырех нелинейных нестационарных дифференциальных уравнений первого порядка относительно переменных νk, m, имеющую вид
6. Результаты численного решения задачи оптимальной переориентации плоскости орбиты КА и их анализ. Приводимые ниже решения задачи для одних и тех же исходных данных, но для разных функционалов качества процесса управления, представлены в безразмерных переменных, угловые величины выражены в градусах. Эксцентриситет орбиты е = 0.1, коэффициент, характеризующий расход топлива на создание единицы тяги β = 4.0, начальная масса аппарата m0 = 1.0. Начальная ориентация орбиты КА определяется угловыми элементами орбиты In = 65.8°, Ωun = 217.0°, ${{\omega }_{{\pi n}}} = 0.0^\circ ;$ положение КА на орбите в начальный момент τ = 0 определяется истинной аномалией ${{\varphi }_{n}}$ = = 30.0° . Ориентация плоскости, на которую необходимо перевести орбиту КА, определяется угловыми элементами Ik = 64.8°, Ωuk = 215.25°.
6.1.1. Решение задачи быстродействия для максимальной тяги ${{u}_{m}}$ = 0.004. Оптимальное управление состоит из 4-х этапов с постоянными управлениями ${{u}_{m}}$ или $ - {{u}_{m}}$. За время процесса управления КА совершает один полный виток. В табл. 1 описаны этапы управления: приводятся моменты ${{\tau }_{i}}$ окончания этапов, истинная аномалия φi, угловые элементы орбиты, масса mi КА в конце i-го этапа, значение ui управления на этом этапе. Из табл. 1 видно, что длительность оптимального процесса составляет 10.998431 единиц безразмерного времени и за это время израсходовано 0.175975 топлива (от начальной массы аппарата).
Таблица 1
| Номер этапа | τi | φi | Ii | Ωui | ${{\omega }_{{\pi i}}}$ | mi | ui |
|---|---|---|---|---|---|---|---|
| 1 | 2.096597 | 149.2167 | 65.8433 | 216.5530 | 0.1837 | 0.966454 | –0.004 |
| 2 | 5.494421 | 329.2171 | 65.4720 | 216.0780 | 0.3815 | 0.912089 | 0.004 |
| 3 | 8.475241 | 149.2176 | 65.3290 | 215.5773 | 0.5915 | 0.864396 | –0.004 |
| 4 | 10.998431 | 274.0070 | 64.8000 | 215.2500 | 0.7309 | 0.824025 | 0.004 |
6.1.2. Решение задачи быстродействия для максимальной тяги um = 0.002. Оптимальное управление состоит из 8 этапов с постоянными управлениями um или –um. За время процесса управления КА совершает 3 полных витка. В табл. 2 описаны этапы управления. Видно, что длительность оптимального процесса составляет 22.948044 единиц безразмерного времени и за это время израсходовано 0.183584 топлива (от начальной массы аппарата). На каждом внутреннем этапе (т.е. за исключением первого и последнего этапов) с управлением u = 0.002 истинная аномалия изменяется на 180.0004°, а на этапе с управлением u = –0.002 на 180.0002°. Длительности внутренних этапов с управлением u = 0.002 постепенно уменьшались на 0.000004, а длительности этапов управлением u = – 0.002 увеличивалась на 0.000002 единиц безразмерного времени.
Таблица 2
| Номер этапа | τi | φi | Ii | Ωui | ${{\omega }_{{\pi i}}}$ | mi | ui |
|---|---|---|---|---|---|---|---|
| 1 | 2.105966 | 149.6650 | 65.8217 | 216.7777 | 0.0912 | 0.983152 | –0.002 |
| 2 | 5.501053 | 329.6654 | 65.6409 | 216.5487 | 0.1858 | 0.955992 | 0.002 |
| 3 | 8.484604 | 149.6656 | 65.5726 | 216.3139 | 0.2832 | 0.932123 | –0.002 |
| 4 | 11.879687 | 329.6659 | 65.3827 | 216.0709 | 0.3846 | 0.904963 | 0.002 |
| 5 | 14.863240 | 149.6662 | 65.3113 | 215.8218 | 0.4888 | 0.881094 | –0.002 |
| 6 | 18.258319 | 329.6664 | 65.1112 | 215.5630 | 0.5979 | 0.853933 | 0.002 |
| 7 | 21.241875 | 149.6667 | 65.0366 | 215.2979 | 0.7101 | 0.830065 | –0.002 |
| 8 | 22.948044 | 230.5039 | 64.8000 | 215.2500 | 0.7306 | 0.816416 | 0.002 |
В табл. 3 приводятся результаты решения задачи быстродействия для различных значений максимальной тяги. Нижний индекс k у величин τ, φ, ${{{\omega }}_{{\pi }}}$ означает, что приводятся их значения для конечного момента времени τk. Видно, что с уменьшением максимальной величины управления um увеличивается время τk процесса управления, число этапов управления и полных витков траектории КА. Так, для ${{u}_{m}} = ~$ 0.0005 число этапов управления и полных витков траектории КА становится равным 30 и 14 соответственно.
Таблица 3
| um | τk | Число этапов | Число полных витков | Расход топлива | $\varphi _{k}^{^\circ }$ | $\omega _{{\pi k}}^{^\circ }$ |
|---|---|---|---|---|---|---|
| 0.004 | 10.998431 | 4 | 1 | 0.175975 | 274.0070 | 0.7309 |
| 0.002 | 22.948043 | 8 | 3 | 0.183584 | 230.5039 | 0.7306 |
| 0.001 | 45.697142 | 15 | 7 | 0.182789 | 95.1737 | 0.7314 |
| 0.0005 | 92.432460 | 30 | 14 | 0.184865 | 197.6370 | 0.7314 |
6.2. Решение задачи в случае минимизации импульса величины тяги реактивного двигателя КА. В этом случае коэффициенты функционалов оптимизации ${{\alpha }_{1}} = 0,\,{\kern 1pt} {\kern 1pt} {{\alpha }_{2}} = 1$. Установлено, что краевая задача оптимизации допускает в этом случае при одних и тех же граничных условиях бесчисленное множество решений. В полученных решениях для максимальной тяги um = 0.001 с увеличением длительности процесса управления уменьшается значение импульса величины тяги и по мере увеличения длительности оно стремится к некоторому пределу. В табл. 4 приведены решения задачи оптимального управления, в которых в одном полном витке траектории укладываются четыре этапа с управлениями u = 0.001, u = 0.0, u = –0.001, u = 0.0.
Таблица 4
| Длительность процесса ${{\tau }_{k}}$ | 52.523586 | 74.803842 | 115.606753 | 151.105858 |
| Число этапов | 33 | 47 | 74 | 94 |
| Число полных витков φk | 8 | 11 | 18 | 23 |
| Истинная аномалия ϕk | 119.3230 | 275.1223 | 80.4386 | 261.3726 |
| Угловое расстояние до перицентра ${{\omega }_{{\pi k}}}$ | 0.7319 | 0.7315 | 0.7315 | 0.7314 |
| Расход топлива $\Delta {{m}_{k}}$ | 0.147081 | 0.130290 | 0.124351 | 0.122125 |
| Значение функционала J | 0.036773 | 0.032572 | 0.031088 | 0.030531 |
С увеличением длительности процесса управления изменяется структура оптимального управления. В один полный виток укладываются только два этапа с управлениями u = 0.0, u = 0.001. При длительности τk = 214.875157 значение функционала J = = 0.029935, а при τk = 297.674094, J = 0.029557. Результаты для этих длительностей процесса управления представлены в табл. 5.
Таблица 5
| Длительность процесса ${{\tau }_{k}}$ | 214.875157 | 297.675157 | 552.675945 |
| Число этапов управления | 68 | 94 | 174 |
| Число полных витков φk | 33 | 46 | 86 |
| Истинная аномалия ${{\phi }_{k}}$ | 260.4280 | 253.6861 | 246.0391 |
| Угловое расстояние до перицентра ${{\omega }_{{\pi k}}}$ | 0.7315 | 0.7314 | 0.7314 |
| Расход топлива $\Delta {{m}_{k}}$ | 0.119739 | 0.118224 | 0.117122 |
| Значение функционала J | 0.029935 | 0.029557 | 0.029280 |
6.3. Решение задачи в случае минимизации комбинированного функционала, включающего в себя время и импульс величины тяги реактивного двигателя КА. Установлено, что краевая задача оптимизации допускает в этом случае при одних и тех же исходных данных задачи несколько решений, из которых необходимо выбрать оптимальное (с меньшим значением функционала). В табл. 6 (в ней $\Delta {{m}_{k}}$ – безразмерный расход топлива, ${{\varphi }_{k}}$ – конечная истинная аномалия) приводятся два решения такой задачи для максимальной тяги um = 0.001 в случае минимизации функционала
Таблица 6
| ${{\tau }_{k}}$ | $\Delta {{m}_{k}}$ | φk | J |
|---|---|---|---|
| 49.320972 | 0.153777 | 276.9730° | 0.087765 |
| 51.746055 | 0.148850 | 75.9973° | 0.088959 |
Из таблицы видно, что оптимальным является решение, представленное в первой строке. Решения для оптимальных управлений на каждом полном витке траектории содержат четыре этапа: u = 0.001, u = 0.0, u = –0.001, u = 0.0.
6.4. Решение задачи в случае минимизации характеристической скорости КА. Установлено, что краевая задача оптимизации допускает в этом случае много решений при одних и тех же исходных данных задачи. В табл. 7 приводится несколько таких решений для случая ${{u}_{m}} = 0.001$. Решения для оптимальных управлений, представленные в двух верхних строках, в каждом полном витке содержат четыре этапа: u = 0.001, u = 0.0, u = –0.001, u = 0.0. В решениях, представленных в третьей, четвертой и пятой строках, при указанном в таблице времени τ* происходит переход от режима с четырьмя этапами в одном полном витке траектории к режиму с двумя этапами в одном полном витке: u = 0.0, u = –0.001.
Таблица 7
| ${{\tau }_{k}}$ | $\varphi _{k}^{^\circ }$ | $\Delta {{m}_{k}}$ | Число этапов | Число полных витков | ${{\omega }_{{\pi k}}}$ | J |
|---|---|---|---|---|---|---|
| 52.418780 | 113.8536 | 0.147491 | 33 | 8 | 0.7318 | 0.039893 |
| 74.635590 | 265.4729 | 0131242 | 47 | 11 | 0.7314 | 0.035173 |
| 112.690580 | 253.5030 | 0.126391 | τ* = 80.901470 | 0.7310 | 0.033781 | |
| 150.808957 | 245.3223 | 0.124428 | τ* = 68.162150 | 0.7310 | 0.033219 | |
| 201.653104 | 235.7468 | 0.123696 | τ* = 68.151568 | 0.7309 | 0.033012 | |
6.5. Решение задачи в случае минимизации комбинированного функционала
Решение для оптимального управления, приведенное в табл. 8, в каждом полном витке содержит четыре этапа: u = 0.001, u = 0.0, u = –0.001, u = 0.0.
Таблица 8
| ${{\alpha }_{1}}$ | ${{\tau }_{k}}$ | J | $\varphi _{k}^{^\circ }$ | Число этапов | Число оборотов | $\omega _{{\pi k}}^{^\circ }$ | Расход топлива |
|---|---|---|---|---|---|---|---|
| 0.001 | 49.230108 | 0.091174 | 271.6881 | 31 | 7 | 0.7313 | 0.154458 |
7. Заключение. Решена с использованием кватернионного дифференциального уравнения ориентации орбитальной системы координат и принципа максимума Понтрягина задача оптимального поворота плоскости орбиты КА переменной массы в инерциальной системе координат. Управление поворотом плоскости орбиты КА на любые по величине углы производится с помощью ограниченной по модулю реактивной тяги, ортогональной плоскости оскулирующей орбиты КА. Под действием такой тяги форма и размеры орбиты КА остаются неизменными во все время процесса управления, а сама орбита поворачивается в инерциальном пространстве как неизменяемая (недеформируемая) фигура (окружность, эллипс). Учитывается изменение массы аппарата за счет расхода рабочего тела на процесс управления. Частным случаем изучаемой задачи является задача оптимальной коррекции угловых элементов орбиты КА, имеющая важное значение в механике космического полета.
Рассмотрены задачи быстродействия, минимизации импульса тяги, характеристической скорости КА, а также задачи, когда функционал, определяющий качество процесса управления, представляет собой линейную свертку с весовыми множителями двух критериев: 1) времени и суммарного импульса величины тяги, затраченных на процесс управления, 2) времени и характеристической скорости КА. Структура оптимального управления имеет в зависимости от выбранного функционала качества процесса управления различный характер и включает в себя пассивные участки траектории, на которых тяга отсутствует и плоскость орбиты остается неизменной, и активные участки траектории, на которых реактивная тяга принимает максимальное значение и происходит поворот плоскости орбиты КА.
Получены численные решения задачи оптимального управления плоскостью орбиты КА посредством малой ограниченной реактивной тяги с большим количеством пассивных и активных участков траектории (этапов управления). Проведенные расчеты показывают, что в случаях, когда критерием качества процесса управления является импульс величины тяги или характеристическая скорость КА, принципу максимума Понтрягина удовлетворяет множество решений, в которых с увеличением промежутка времени процесса управления значение функционала качества процесса управления убывает и стремится к некоторому пределу. При этом с увеличением промежутка времени процесса управления увеличивается число этапов управления, уменьшаются длительности активных этапов, увеличиваются длительности пассивных этапов, изменяется структура оптимального управления. В случаях минимизации комбинированного функционала качества, включающего в себя время и импульс величины тяги, затраченных на процесс управления, или время и характеристическую скорость КА, краевые задачи оптимального управления допускают несколько решений, из которых необходимо выбрать решение с минимальным значением функционала.
Список литературы
Дубошин Г.Н. Небесная механика. Основные задачи и методы. M.: Наука, 1968. 799 с.
Абалакин В.К., Аксенов Е.П., Гребенников Е.А., Демин В.Г., Рябов Ю.А. Справочное руководство по небесной механике и астродинамике. М.: Наука, 1976. 864 с.
Копнин Ю.М. К задаче поворота плоскости орбиты спутника // Космические исследования. 1965. Т. 3. Вып. 4. С. 22–30.
Лебедев В.Н. Расчет движения космического аппарата с малой тягой. М.: ВЦ АН СССР, 1968. 108 с.
Борщевский М.З., Иослович М.В. К задаче о повороте плоскости орбиты спутника при помощи реактивной тяги // Космические исследования. 1969. Т. 7. Вып. 6. С. 8–15.
Гродзовский Г.Л., Иванов Ю.Н., Токарев В.В. Механика космического полета. Проблемы оптимизации. М.: Наука, 1975. 702 с.
Охоцимский Д.Е., Сихарулидзе Ю.Г. Основы механики космического полета: Учеб. пособие. М.: Наука, 1990. 448 с.
Ишков С.А., Романенко В.А. Формирование и коррекция высокоэллиптической орбиты спутника земли с двигателем малой тяги // Космические исследования. 1997. Т. 35. № 3. С. 287–296.
Челноков Ю.Н. Применение кватернионов в теории орбитального движения искусственного спутника. Ч. 2 // Космические исследования. 1993. Т. 31. Вып. 3. С. 3–15. Chelnokov Yu.N. Application of quaternions in the theory of orbital motion of an artificial satellite. II // Cosmic Research. 1993. V. 31. No. 3. P. 409–418.
Челноков Ю.Н. Кватернионные и бикватернионные модели и методы механики твердого тела и их приложения. Геометрия и кинематика движения. М.: Физматлит, 2006. 512 с.
Челноков Ю.Н. Кватернионные модели и методы динамики, навигации и управления движением. М.: Физматлит, 2011. 560 с.
Челноков Ю.Н. Оптимальная переориентация орбиты космического аппарата посредством реактивной тяги, ортогональной плоскости орбиты // Прикладная математика и механика. 2012. Т. 76. № 6. С. 897–914. Chelnokov Yu.N. Optimal reorientation of a spacecraft’s orbit using a jet thrust orthogonal to the orbital plane // J. Appl. Math. Mech. 2012. V. 76. No. 6. P. 646–657.
Челноков Ю.Н. Кватернионная регуляризация в небесной механике и астродинамике и управление траекторным движением. II // Космические исследования. 2014. Т. 52. № 4. С. 322–336. Chelnokov Yu.N. Quaternion Regularization in Celestial Mechanics and Astrodynamics and Trajectory Motion Control. II // Cosmic Research. 2014. V. 52. No. 4. P. 350–361.
Ненахов С.В., Челноков Ю.Н. Кватернионное решение задачи оптимального управления ориентацией орбиты космического аппарата // Бортовые интегрированные комплексы и современные проблемы управления: Сб. тр. междунар. конф. М.: МАИ, 1998. С. 59–60.
Сергеев Д.А., Челноков Ю.Н. Оптимальное управление ориентацией орбиты космического аппарата // Математика. Механика: Сб. науч. тр. Саратов: Изд-во Сарат. ун-та, 2001. Вып. 3. С. 185–188.
Сергеев Д.А., Челноков Ю.Н. Оптимальное управление ориентацией орбиты космического аппарата // Проблемы точной механики и управления: Сб. науч. тр. ИПТМУ РАН. Саратов: Изд-во СГТУ, 2002. С. 64–75.
Панкратов И.А., Сапунков Я.Г., Челноков Ю.Н. Об одной задаче оптимальной переориентации орбиты космического аппарата // Изв. Сарат. ун-та. Нов. сер. Сер.: Математика. Механика. Информатика. 2012. Т. 12. № 3. С. 87–95.
Сапунков Я.Г., Челноков Ю.Н. Исследование задачи оптимальной переориентации орбиты космического аппарата посредством ограниченной или импульсной реактивной тяги, ортогональной плоскости орбиты. Часть 1. Мехатроника, автоматизация, управление. 2016. Т. 17. № 8. С. 567–575.
Сапунков Я.Г., Челноков Ю.Н. Исследование задачи оптимальной переориентации орбиты космического аппарата посредством ограниченной или импульсной реактивной тяги, ортогональной плоскости орбиты. Часть 2. Мехатроника, автоматизация, управление. 2016. Т. 17. № 9. С. 633–643.
Челноков Ю.Н. Применение кватернионов в теории орбитального движения искусственного спутника. Ч. 1 // Космические исследования. 1992. Т. 30. № 6. С. 759–770. Chelnokov Yu.N. Application of quaternions in the theory of orbital motion of an artificial satellite. I // Cosmic Research. 1992. V. 30. No. 6. P. 612–621.
Челноков Ю.Н. Построение оптимальных управлений и траекторий движения космического аппарата, использующее кватернионное описание пространственной ориентации орбиты // Космические исследования. 1997. Т. 35. № 5. С. 534–542. Chelnokov Yu. N. Construction of optimum control and trajectories of spacecraft flight by employing quaternion description of orbit spatial orientation // Cosmic Research. 1997. V. 35. No. 5. P. 499–507.
Брагазин В.Н., Бранец В.Н., Шмыглевский И.П. Описание орбитального движения с использованием кватернионов и скоростных параметров // Анн. докладов шестого Всесоюзного съезда по теорет. и прикладной механике. Ташкент: ФАН, 1986. С. 133.
Бранец В.Н., Шмыглевский И.П. Введение в теорию бесплатформенных инерциальных навигационных систем. М.: Наука, 1992. 280 с.
Челноков Ю.Н. Оптимальная переориентация орбиты космического аппарата посредством реактивной тяги, ортогональной плоскости орбиты // Математика. Механика: Сб. науч. тр. Саратов: Изд-во Сарат. ун-та, 2006. Вып. 8. С. 231–234.
Челноков Ю.Н. Оптимальная переориентация орбиты космического аппарата: Кватернионный подход к решению задачи // Проблемы и перспективы прецезионной механики и управления в машиностроении: Материалы междунар. конф. / ИПТМУ РАН. Саратов: Изд-во СГТУ, 2006. С. 54–60.
Панкратов И.А., Сапунков Я.Г., Челноков Ю.Н. Решение задачи оптимальной переориентации орбиты космического аппарата с использованием кватернионных уравнений ориентации орбитальной системы координат // Изв. Сарат. ун-та. Нов. сер. Сер.: Математика. Механика. Информатика. 2013. Т. 13. № 1–1. С. 84–92.
Сапунков Я.Г., Челноков Ю.Н. Импульсная оптимальная переориентация орбиты космического аппарата посредством реактивной тяги, ортогональной плоскости оскулирующей орбиты. I // Изв. РАН. Механика твердого тела. 2018. № 5. С. 70–89.
Сапунков Я.Г., Челноков Ю.Н. Импульсная оптимальная переориентация орбиты космического аппарата посредством реактивной тяги, ортогональной плоскости оскулирующей орбиты. II // Изв. РАН. Механика твердого тела. 2019. № 1. С. 3–22.
Ильин В.А., Кузмак Г.Е. Оптимальные перелеты космических аппаратов с двигателями большой тяги. M.: Наука, 1976. 741 с.
Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации твердого тела М.: Наука, 1973. 320 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела