Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 494, № 1, стр. 56-59

1. ВВЕДЕНИЕ

Коса из n нитей называется квазиположительной, если она является произведением кос, сопряженных стандартным образующим ${{\sigma }_{1}}, \ldots ,{{\sigma }_{{n - 1}}}$ группы кос ${{B}_{n}}$. Коса называется сильно квазиположительной, если она является произведением кос вида ${{\tau }_{{k,j}}}{{\sigma }_{j}}\tau _{{k,j}}^{{ - 1}}$, $j \leqslant k$, где ${{\tau }_{{k,j}}} = {{\sigma }_{k}}{{\sigma }_{{k - 1}}} \ldots {{\sigma }_{j}}$. Все зацепления в данном сообщении предполагаются ориентированными зацеплениями в трехмерной сфере ${{S}^{3}}$. Зацепление называется (сильно) квазиположительным, если оно представимо (сильно) квазиположительной косой. Этот класс зацеплений очень важен для изучения плоских алгебраических кривых. Как показано в [3], зацепление квазиположительно тогда и только тогда, когда оно высекается комплексной алгебраической кривой на стандартно вложенной трехмерной сфере в ${{\mathbb{C}}^{2}}$. В [3] также доказано, что зацепление, высекаемое комплексной алгебраической кривой на любой гладко вложенной трехмерной сфере, являющейся границей строго псевдовыпуклой области в ${{\mathbb{C}}^{2}}$, квази-положительно. Критерии квазиположительности играют существенную роль в изучении плоских вещественных алгебраических кривых (1-я часть 16-й проблемы Гильберта), см., например, [11].

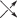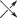Диаграмма зацепления называется положительной, если все ее пересечения положительны. При устранении пересечений с учетом ориентаций (т.е. при замене или на 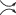) диаграмма распадается на непересекающиеся простые замкнутые кривые, которые называются окружностями Зейферта, см., например, [9, 14, 15].

С. Баадер [1, с. 268, вопрос (4)] поставил вопрос: Верно ли, что альтернированные квазиположительные зацепления имеют положительные диаграммы? Заметим, что все положительные диаграммы представляют сильно квазиположительные зацепления (см. [10, 13]) и что все альтернированные сильно квазиположительные зацепления представимы положительными альтернированными диаграммами в силу [2, Cor. 7.3]. Отметим также, что положительные альтернированные диаграммы специальны (диаграмма называется специальной [9], если ее окружности Зейферта ограничивают непересекающиеся диски).

В настоящем сообщении мы на этот вопрос даем утвердительный ответ для широкого класса альтернированных зацеплений – для зацеплений, обладающих альтернированной диаграммой, у которой число окружностей Зейферта равно брэйд-индексу (т. е. минимально возможному числу нитей представляющей косы). Такие диаграммы мы будем называть диаграммами Дяо–Хетьея–Лю, или DHL-диаграммами (а соответствующие зацепления – DHL-зацеплениями), так как эти авторы в работе [5] дали им следующую очень простую и изящную характеризацию.

Теорема 1 [5, Thm. 1.1]. Альтернированная диаграмма является DHL-диаграммой тогда и только тогда, когда она не имеет пары окружностей Зейферта, соединенных через одно-единственное пересечение.

Сформулируем основной результат сообщения.

Теорема 2. Пусть D – DHL-диаграмма квазиположительного зацепления. Тогда $D$ положительна.

Доказательство этой теоремы получается сочетанием результатов из [6, 7, 9, 14, 15] (см. раздел 2). Теоремы 1 и 2 позволяют без каких-либо вычислений строить многочисленные примеры неквазиположительных зацеплений (см. рис. 1).

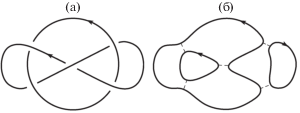
Поскольку все положительные диаграммы представляют сильно квазиположительные зацепления (см. [10, 13]), мы получаем

Следствие 1. Пусть L – DHL-зацепление.Тогда следующие условия эквивалентны:

(i) $L$ квазиположительно;

(ii) $L$ сильно квазиположительно;

(iii) $L$ имеет положительную альтернированную диаграмму.

В разделе 3 мы обобщаем теорему 2 на все альтернированные зацепления, брэйд-индекс которых вычислен в [4]; см. теорему 4 и замечание 2.

2. ДОКАЗАТЕЛЬСТВО ОСНОВНОЙ ТЕОРЕМЫ

Пусть $D$ – связная диаграмма некоторого зацепления. Графом Зейферта диаграммы $D$ назовем граф ${{G}_{D}}$, вершины которого отвечают окружностям Зейферта, а ребра – пересечениям. Определим знаки ребер как знаки соответствующих пересечений. Диаграмма $D$ называется редуцированной, если ${{G}_{D}}$ не имеет ребер, удаление которых делает граф ${{G}_{D}}$ несвязным. Обозначим через $d(D)$ сумму знаков всех ребер некоторого остовного дерева графа ${{G}_{D}}$, и пусть $w(D)$ – сумма знаков пересечений (writhe) диаграммы $D$.

Для зацепления $L$ обозначим через $\sigma (L)$ и ${\mathbf{n}}(L)$ его сигнатуру и дефект (nullity) – последний определен как дефект симметризованной формы Зейферта, отвечающей связной поверхности Зейферта.

Теорема 3 (Traczyk [14]). Пусть D – связная редуцированная альтернированная диаграмма зацепления $L$. Тогда $\sigma (L) = d(D) - w(D)$ и ${\mathbf{n}}(L) = 0$.

Данная формула для $\sigma (L)$ приведена в [14, Thm. 2(1)] (множитель 1/2 там ошибочен). То, что ${\mathbf{n}}(L) = 0$ (эквивалентно, $det(L) \ne 0$), доказано в [9, Lem. 5.1] и в приложении к статье [14]. Это также легко вывести из [14, Thm. 1].

Доказательство теоремы 2. Пусть D – DHL-диаграмма квазиположительного зацепления L. Очевидно, что каждая компонента связности диаграммы D – тоже DHL-диаграмма, причем она задает квазиположительное зацепление в силу [12]. Поэтому мы будем рассматривать только тот случай, когда D связна.

Обозначим брэйд-индекс зацепления $L$ через $n$. По определению DHL-диаграмм, D имеет $n$ окружностей Зейферта. Следовательно, по [15, Thm. 1] (см. обсуждение этой теоремы во введении статьи [15]), $L$ представима косой из $n$ нитей ${{\beta }_{1}}$, причем

Согласно [7, Thm. 1.2] L представима квазиположительной косой из n нитей ${{\beta }_{2}}$. Неравенство Мурасуги–Тристрама [9] для квазиположительной косы можно записать следующим образом (см. [11, Cor. 3.2]):

По теореме Дынникова–Прасолова [6] (обобщенная гипотеза Джонса)

Заметим, что все DHL-диаграммы редуцированны. Поэтому из (1)–(3) и теоремы 3 вытекает, что ${\text{|}}d(D) - w(D){\text{|}} \leqslant 1 - n + w(D)$, откуда w(D) – d(D) ≤ ≤ $1 - n$ + w(D), т.е. $d(D) \geqslant n - 1$. Напомним, что $d(D)$ есть сумма знаков всех ребер остовного дерева графа G_D. Любое остовное дерево имеет n – 1 ребро, следовательно, все его ребра положительны. Поскольку каждое ребро графа G_D лежит в некотором остовном дереве, мы заключаем, что все пересечения в D положительны. Теорема 2 доказана.

3. ОБОБЩЕНИЕ ОСНОВНОЙ ТЕОРЕМЫ

Пусть D – альтернированная диаграмма некоторого зацепления L. Обозначим через $b = b(L)$ брэйд-индекс зацепления $L$, а через $s = s(D)$ – число окружностей Зейферта диаграммы D. Пусть d^± = = ${{d}^{ \pm }}(D)$ – число ребер соответствующего знака в остовном дереве графа G_D, тем самым d = d(D) = = ${{d}^{ + }} - {{d}^{ - }}$.

Пусть $\beta $ – коса из b нитей, задающая L. По теореме Дынникова–Прасолова [6] $w(\beta )$ не зависит от выбора косы $\beta $, что позволяет нам определить числа ${{{\mathbf{r}}}^{ \pm }} = {{{\mathbf{r}}}^{ \pm }}(D)$ как решения системы уравнений

Замечание 1. Определение чисел ${{r}^{ \pm }}$, данное в [4], не вполне ясно, однако во всех случаях, когда эти числа найдены в [4], они совпадают с нашими r^±; ср. [4, Rem. 3.1–3.3].

Если D есть DHL-диаграмма, то ${{{\mathbf{r}}}^{ + }} = {{{\mathbf{r}}}^{ - }} = 0$ (напомним, что в этом случае $w(D) = w(\beta )$ по [15, Thm. 1]), таким образом, следующее утверждение обобщает теорему 2.

Теорема 4. Пусть D – редуцированная альтернированная диаграмма квазиположительного зацепления $L$, причем

Тогда $D$ положительна (а значит, $L$ сильно квазиположительно в силу [10, 13]).

Доказательство. Поскольку все рассуждения почти те же, что и для теоремы 2, мы только приведем заключительные вычисления. Итак, мы имеем $w(D) - d \leqslant {\text{|}}\sigma {\text{|}} \leqslant 1 - b + w(\beta )$, следовательно,

откуда ${{d}^{ + }} \geqslant s - 1$, и из этого вытекает требуемый результат.

Замечание 2. Во всех случаях, когда брэйд-индекс редуцированной альтернированной диаграммы вычислен в [4], имеет место неравенство (4), в частности, оно выполнено для минимальных диаграмм зацеплений с двумя мостами и для альтернированных зацеплений Монтесиноса.

Вопрос 1. Выполнено ли (4) для всех редуцированных альтернированных диаграмм?

Замечание 3. Тецуя Ито [8] обобщил теорему 2 на однородные диаграммы, у которых число окружностей Зейферта равно брэйд-индексу (отметим, однако, что неизвестен алгоритм проверки этого условия). Некоторые другие близкие вопросы также обсуждаются в [8].