Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 494, № 1, стр. 9-13
КОМБИНИРОВАННАЯ МНОГОМЕРНАЯ БИКОМПАКТНАЯ СХЕМА, ИМЕЮЩАЯ ПОВЫШЕННУЮ ТОЧНОСТЬ В ОБЛАСТЯХ ВЛИЯНИЯ НЕСТАЦИОНАРНЫХ УДАРНЫХ ВОЛН
М. Д. Брагин 1, 2, *, Б. В. Рогов 1, **
1 Федеральный исследовательский центр
Институт прикладной математики им. М.В. Келдыша Российской академии наук
Москва, Россия
2 Институт гидродинамики им. М.А. Лаврентьева Сибирского отделения Российской академии наук
Новосибирск, Россия
* E-mail: michael@bragin.cc
** E-mail: rogov.boris@gmail.com
Поступила в редакцию 06.07.2020
После доработки 06.07.2020
Принята к публикации 24.08.2020
Аннотация
Впервые предложен метод построения многомерной комбинированной схемы сквозного счета, которая монотонно локализует фронты ударных волн и одновременно имеет повышенную точность в областях гладкости рассчитываемых обобщенных решений. Решение комбинированной схемы в этом методе строится на основе монотонных решений бикомпактной схемы первого порядка аппроксимации по времени и четвертого порядка аппроксимации по пространству, полученных для разных временных шагов во всей расчетной области. Такой метод построения является существенно более простым по сравнению с другими методами построения комбинированных схем с подобными свойствами. Приведены результаты тестовых расчетов, демонстрирующие высокую точность предложенной комбинированной схемы при счете многомерного течения с ударными волнами.
1. В работах [1, 2] было показано, что NFC (Nonlinear Flux Correction) схемы сквозного счета, к которым относятся MUSCL-схемы, TVD-схемы, WENO-схемы, DG-схемы, САВARET-схемы (ссылки на эти схемы см., например, в [2]), имеют не более чем первый порядок локальной сходимости в областях влияния ударных волн. В [1–4] установлена причина падения порядка сходимости NFC-схем до первого. Она связана с тем, что в NFC-схемах коррекция численных потоков приводит к снижению их гладкости и, как следствие, снижению порядка аппроксимации ε-условий Гюгонио на фронтах ударных волн [1].
В работе [3] было предложено решение проблемы, связанной с понижением порядка точности схем сквозного счета в областях влияния ударных волн. Оно заключается в построении комбинированных схем сквозного счета, которые монотонно локализуют фронты ударных волн и одновременно имеют повышенную точность в областях гладкости рассчитываемых обобщенных решений. Решение в комбинированной схеме строится путем коррекции решения базисной немонотонной схемы, которое находится во всей расчетной области и имеет повышенный порядок сходимости в областях влияния ударных волн, где решение является гладким. В областях больших градиентов, где решение базисной схемы имеет нефизические осцилляции, оно корректируется путем численного решения внутренних начально-краевых задач по одной из NFC-схем. Комбинированная схема [3] состояла из разнородных схем: в качестве базисной использовалась неявная симметричная компактная схема третьего порядка слабой аппроксимации, а в качестве внутренней NFC-схемы – монотонизированный вариант явной схемы CABARET второго порядка точности на гладких решениях. Недостаток, связанный с указанной разнородностью схем, был устранен в работах [4, 5], где базисная и внутренняя схемы были немонотонным и монотонизированным вариантами разрывного метода Галёркина и бикомпактной схемы [6] соответственно. В работах [3–5] свойства комбинированных схем демонстрировались на примере модельной одномерной задачи Коши для системы уравнений первого приближения теории мелкой воды. Среди предложенных способов построения комбинированных схем [3–5] способ [5] является наименее трудоемким, поскольку для его реализации не требуется решать внутренние начально-краевые задачи в отличие от способов [3, 4], где эти задачи необходимо численно решать с помощью одной из NFC-схем. В настоящей работе способ построения комбинированной схемы [5] для численного решения одномерных задач для систем уравнений гиперболического типа впервые обобщается на многомерные задачи. Повышенный (второй) порядок сходимости комбинированной схемы, построенной по предложенному способу, показывается на примере модельной периодической задачи Коши для системы двумерных уравнений первого приближения теории мелкой воды с разрывным решением.
2. Для квазилинейной гиперболической системы законов сохранения
(1)
${{\partial }_{t}}{\mathbf{u}} + {{\partial }_{x}}{\mathbf{f}}({\mathbf{u}}) + {{\partial }_{y}}{\mathbf{g}}({\mathbf{u}}) = 0$(2)
$\begin{gathered} {\mathbf{u}}(x,y,0) = {\mathbf{v}}(x,y), \\ {\mathbf{v}}(x,y) = {\mathbf{v}}(x + X,y), \\ {\mathbf{v}}(x,y) = {\mathbf{v}}(x,y + Y), \\ \end{gathered} $Полудискретная бикомпактная схема четвертого порядка аппроксимации по x, y для системы (1) имеет вид (см. [6])
(3)
$\begin{array}{*{20}{c}} {\frac{d}{{dt}}(A_{0}^{y}A_{0}^{x}{{{\mathbf{u}}}_{C}}) + A_{0}^{y}\Lambda _{1}^{x}{{{\mathbf{f}}}_{C}} + \Lambda _{1}^{y}A_{0}^{x}{{{\mathbf{g}}}_{C}} = {\mathbf{0}},} \\ {\frac{d}{{dt}}(A_{0}^{y}\Lambda _{1}^{x}{{{\mathbf{u}}}_{C}}) + A_{0}^{y}\Lambda _{2}^{x}{{{\mathbf{f}}}_{C}} + \Lambda _{1}^{y}\Lambda _{1}^{x}{{{\mathbf{g}}}_{C}} = {\mathbf{0}},} \\ {\frac{d}{{dt}}(\Lambda _{1}^{y}A_{0}^{x}{{{\mathbf{u}}}_{C}}) + \Lambda _{1}^{y}\Lambda _{1}^{x}{{{\mathbf{f}}}_{C}} + \Lambda _{2}^{y}A_{0}^{x}{{{\mathbf{g}}}_{C}} = {\mathbf{0}},} \\ {\frac{d}{{dt}}(\Lambda _{1}^{y}\Lambda _{1}^{x}{{{\mathbf{u}}}_{C}}) + \Lambda _{1}^{y}\Lambda _{2}^{x}{{{\mathbf{f}}}_{C}} + \Lambda _{2}^{y}\Lambda _{1}^{x}{{{\mathbf{g}}}_{C}} = {\mathbf{0}},} \end{array}$(4)
$\begin{gathered} A_{0}^{x}{{U}_{{j + 1/2}}} = \frac{{{{U}_{j}} + 4{{U}_{{j + 1/2}}} + {{U}_{{j + 1}}}}}{6}, \\ \Lambda _{1}^{x}{{U}_{{j + 1/2}}} = \frac{{{{U}_{{j + 1}}} - {{U}_{j}}}}{{{{h}_{{x,j + 1/2}}}}}, \\ \Lambda _{2}^{x}{{U}_{{j + 1/2}}} = \frac{{4({{U}_{j}} - 2{{U}_{{j + 1/2}}} + {{U}_{{j + 1}}})}}{{h_{{x,j + 1/2}}^{2}}}, \\ \end{gathered} $Система четырех обыкновенных дифференциальных уравнений (ОДУ) (3) решается относительно четырех сеточных функций ${{{\mathbf{u}}}_{{j,k}}}(t)$, ${{{\mathbf{u}}}_{{j + 1/2,k}}}(t)$, ${{{\mathbf{u}}}_{{j,k + 1/2}}}(t)$, ${{{\mathbf{u}}}_{{j + 1/2,k + 1/2}}}(t)$, определенных при целых xj, yk и полуцелых ${{x}_{{j + 1/2}}} = {{({{x}_{j}} + {{x}_{{j + 1}}})} \mathord{\left/ {\vphantom {{({{x}_{j}} + {{x}_{{j + 1}}})} 2}} \right. \kern-0em} 2}$, yk + 1/2 = (yk + + ${{y}_{{k + 1}}}){\text{/}}2$ значениях независимых переменных x и y.
Начальные условия (2) для функций ${{{\mathbf{u}}}_{{j,k}}}(t)$, ${{{\mathbf{u}}}_{{j + 1/2,k}}}(t)$, ${{{\mathbf{u}}}_{{j,k + 1/2}}}(t)$, ${{{\mathbf{u}}}_{C}}(t)$ будут следующими:
Граничные условия периодичности для сеточных функций ${{{\mathbf{u}}}_{{j,k}}}(t)$, ${{{\mathbf{u}}}_{{j + 1/2,k}}}(t)$, ${{{\mathbf{u}}}_{{j,k + 1/2}}}(t)$ имеют вид
Дисперсионные свойства бездиссипативной полудискретной схемы (3) в линейном приближении исследованы в работе [7], где показано, что эта схема имеет улучшенные дисперсионные свойства по сравнению с известными компактными схемами того же порядка аппроксимации, а также имеет незначительную анизотропию во всем диапазоне длин волн, разрешимых на пространственной сетке.
3. Полностью дискретные бикомпактные схемы получаются путем применения какого-либо устойчивого численного метода интегрирования по времени к системе ОДУ (3). В данной работе рассмотрены две такие схемы.
Первая из схем, далее обозначаемая как DIRK1B4, получается путем интегрирования уравнений (3) по неявному методу Эйлера. Она имеет погрешность аппроксимации $O(\tau ,{{h}^{4}})$, является абсолютно устойчивой и консервативной [6, 8, 9]. В работах [8, 9] исследованы дисперсионные и диссипативные свойства, а также свойства монотонности схемы DIRK1B4. Аналитически доказано, что эта схема для линейного скалярного одномерного уравнения переноса является монотонной по Годунову при числе Куранта $\kappa \geqslant 0.25$. Численный эксперимент [8] показал, что схема DIRK1B4 для квазилинейного одномерного уравнения Хопфа монотонна, если локальное число Куранта $\kappa \geqslant 0.15$.
Численные решения второй схемы, обозначаемой как Rich2B4, получаются уточнением разностных решений схемы DIRK1B4 со вторым порядком точности по времени методом экстраполяции Ричардсона. Для этого проводятся два вычисления во всей расчетной области по схеме DIRK1B4 на сетках с временными шагами $\tau $ и $\tau {\text{/}}2$. При сгущении пространственно-временной сетки поддерживается постоянство величины отношения шагов $r = \tau {\text{/}}h$. Решение экстраполяционной бикомпактной схемы Rich2B4 в момент времени ${{t}_{n}} = n{\kern 1pt} \tau $ рассчитывается по формуле:
4. Из рассмотренных выше бикомпактных схем построим комбинированную схему, монотонно локализующую фронты ударных волн и имеющую повышенную точность в областях гладкости рассчитываемых обобщенных решений. При этом будем следовать концепции [3], в которой решение базисной схемы повышенного порядка сходимости корректируется в окрестности ударных волн с помощью монотонной внутренней схемы.
Решение двумерной комбинированной схемы CombinB4 зададим по формулам, которые были использованы для построения одномерной комбинированной схемы [5]:
(5)
$\begin{gathered} {{u}_{s}}({\text{CombinB4;}}\tau ) = u_{s}^{B} + {{\alpha }_{s}}{{D}_{s}},\quad {{D}_{s}} = u_{s}^{A} - u_{s}^{B}, \\ u_{s}^{A} = {{u}_{s}}({\text{DIRK1B4;0}}{\text{.5}}\tau ),\quad u_{s}^{B} = {{u}_{s}}({\text{Rich2B4;}}\tau ), \\ \end{gathered} $(6)
$\begin{gathered} {{\alpha }_{s}} = \left\{ {\begin{array}{*{20}{c}} {0\quad {\text{при}}\quad \left| {{{D}_{s}}} \right| \leqslant C{{N}_{s}},} \\ {1 - {{C{{N}_{s}}} \mathord{\left/ {\vphantom {{C{{N}_{s}}} {\left| {{{D}_{s}}} \right|\quad {\text{иначе,}}}}} \right. \kern-0em} {\left| {{{D}_{s}}} \right|\quad {\text{иначе,}}}}} \end{array}} \right. \\ {{N}_{s}} = \mathop {\max }\limits_{x \in \Omega } u_{s}^{A} - \mathop {\min }\limits_{x \in \Omega } u_{s}^{A}, \\ \end{gathered} $5. В качестве конкретной гиперболической системы (1) возьмем систему двумерных уравнений первого приближения теории мелкой воды [10] без учета донного трения, для которой
(7)
$\begin{gathered} {\mathbf{u}} = \left( {\begin{array}{*{20}{c}} H \\ {HU} \\ {HV} \end{array}} \right),\quad {\mathbf{f}}({\mathbf{u}}) = \left( {\begin{array}{*{20}{c}} {HU} \\ {H{{U}^{2}} + {{g{{H}^{2}}} \mathord{\left/ {\vphantom {{g{{H}^{2}}} 2}} \right. \kern-0em} 2}} \\ {HUV} \end{array}} \right), \\ {\mathbf{g}}({\mathbf{u}}) = \left( {\begin{array}{*{20}{c}} {HV} \\ {HUV} \\ {H{{V}^{2}} + {{g{{H}^{2}}} \mathord{\left/ {\vphantom {{g{{H}^{2}}} 2}} \right. \kern-0em} 2}} \end{array}} \right), \\ \end{gathered} $(8)
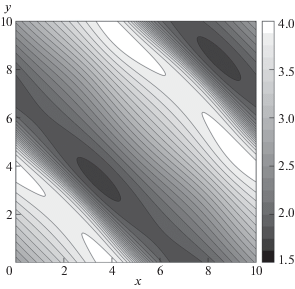
$\begin{gathered} U(x,y,0) = V(x,y,0) = \frac{a}{{\sqrt 2 }}\sin \left( {\frac{{2\pi x}}{X} + \frac{{2\pi y}}{Y} + \frac{\pi }{4}} \right), \\ H(x,y,0) = \frac{1}{{4g}}{{\left[ {a\sin \left( {\frac{{2\pi x}}{X} + \frac{{2\pi y}}{Y} + \frac{\pi }{4}} \right) + b} \right]}^{2}} \times \\ \times \;\left[ {1 + 0.1\left( {{{{\sin }}^{2}}\left( {\frac{{2\pi x}}{X} + \frac{\pi }{4}} \right) + {{{\sin }}^{2}}\left( {\frac{{2\pi y}}{Y} + \frac{\pi }{4}} \right)} \right)} \right], \\ \end{gathered} $Результаты расчета задачи Коши (1), (7), (8) для момента времени T = 0.5 представлены на рис. 1, а для момента времени T = 1.0 – на рис. 2–4.
Рис. 3.
Картина локальных порядков сходимости решения комбинированной бикомпактной схемы для глубины H в момент времени T = 1.0.
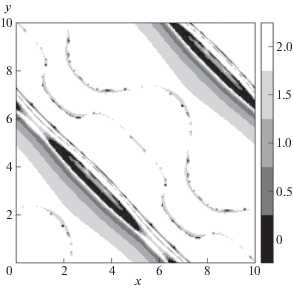
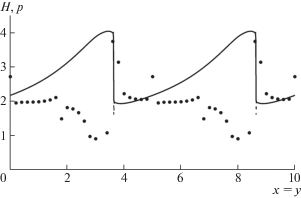
Рис. 4.
Профили глубины H вдоль прямой x – y = 0 в момент времени T = 1.0: сплошная кривая – решение комбинированной схемы, штриховая кривая – решение схемы Rich2B4. Точки показывают локальные порядки сходимости комбинированной схемы.
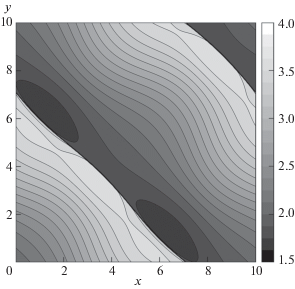
На рис. 1 и 2 показаны изолинии глубины H, рассчитанной по комбинированной схеме с параметром C = 0.01 (см. (6)) на сетке в области (x, y) ∈ (0, 10) × (0, 10) с N = Nx = Ny = 400. Шаг между изолиниями величины H равен 0.125 на рис. 1 и 0.15 на рис. 2. Видно, что решение для H при T = 0.5 является гладким, в этом случае решение комбинированной схемы совпадает с решением схемы Rich2B4. Из рис. 2 видно, что на момент времени T = 1.0 сформировались два фронта разрыва глубины H. Компоненты скоростей этих фронтов положительны. Оценки показывают, что область влияния этих фронтов разрыва в момент времени T = 1.0 охватывает все показанные на рисунке области за фронтами.
На рис. 3 приведена картина локальных порядков сходимости p решения комбинированной схемы для величины H. Эти порядки определялись по методу Рунге, подробно описанному в [11], на основании расчетов на трех вложенных сетках с N = = 100, 200 и 400. Из рис. 3 видно, что практически во всей области влияния фронтов разрыва, где решение является гладким, порядок сходимости комбинированной бикомпактной схемы близок ко второму.
Профили глубины H, рассчитанной по немонотонной схеме Rich2B4 и комбинированной схеме CombinB4 на сетке с N = 400, показаны на рис. 4 вдоль прямой x – y = 0 в момент времени T = 1.0. Видно, что комбинированная схема дает монотонный профиль H, а схема Rich2B4 второго порядка аппроксимации по времени дает профиль с немонотонностями, локализованными вблизи фронтов разрыва величины H. На рис. 4 также показаны локальные порядки сходимости монотонной комбинированной схемы для каждого 8-го узла. Видно, что в бóльшей части области влияния фронтов разрыва глубины H комбинированная схема имеет повышенный (выше первого) порядок сходимости. Из рисунка также видно, что локальная по пространству монотонизация, используемая при построении комбинированной схемы, приводит к понижению порядка сходимости комбинированной схемы до первого вблизи фронтов разрыва.
Список литературы
Остапенко В.В. // ЖВМиМФ. 2000. Т. 40. № 12. С. 1857–1874.
Ладонкина М.Е., Неклюдова О.А., Остапенко В.В., Тишкин В.Ф. // ЖВМиМФ. 2018. Т. 58. № 8. С. 148–156.
Ковыркина О.А., Остапенко В.В. // ДАН. 2018. Т. 478. № 5. С. 517–522.
Ладонкина М.Е., Неклюдова О.А., Остапенко В.В., Тишкин В.Ф. // ДАН. 2019. Т. 489. № 2. С. 119–124.
Брагин М.Д., Рогов Б.В. // Доклады РАН. Математика, информатика, процессы управления. 2020. Т. 492. С. 79–84.
Рогов Б.В. // ДАН. 2012. Т. 445. № 6. С. 631–635.
Chikitkin A.V., Rogov B.V. // Appl. Numer. Math. 2019. V. 142. P. 151–170.
Михайловская М.Н., Рогов Б.В. // ЖВМиМФ. 2012. Т. 52. № 4. С. 672–695.
Рогов Б.В. // ЖВМиМФ. 2013. Т. 53. № 2. С. 264–274.
Остапенко В.В. // ПММ. 2018. Т. 82. Вып. 4. С.441–458.
Остапенко В.В. // ЖВМиМФ. 1997. Т. 37. № 10. С. 1201–1212.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления