Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 494, № 1, стр. 5-8

Рассматриваются первая и вторая начально-краевые задачи для одномерных по пространственной переменной x параболических по Петровскому [1] систем второго порядка в ограниченной области Ω с негладкими, вообще говоря, боковыми границами. В работах [2–4] получены теоремы о существовании и свойствах классических решений u этих задач. В настоящей работе устанавливается единственность классических решений таких задач в классе ${{C}^{{1,0}}}({\bar {\Omega }})$ функций, непрерывных в ${\bar {\Omega }}$ вместе с пространственной производной первого порядка. В случае области с гладкими боковыми границами однозначная разрешимость указанных задач в классе Гёльдера 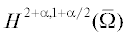следует из [5] (см. также [6, с. 706–707]). Если боковые границы области негладкие, то в случае одного уравнения единственность решения первой начально-краевой задачи следует из принципа максимума (см., например, [7]), а единственность решения второй начально-краевой задачи получена в [8, 9] с помощью теоремы о знаке косой производной. В [10, 11] установлена единственность решения первой начально-краевой задачи для одномерной параболической системы второго порядка с постоянными коэффициентами в полуограниченной области Ω с негладкой боковой границей в классе ${{C}^{{1,0}}}({\bar {\Omega }})~$ при дополнительном условии на старшую производную $\partial _{x}^{2}u$ решения, а также в классе Гёльдера ${{H}^{{1 + \alpha ,\left( {1 + \alpha } \right)/2}}}(\bar {\Omega }).$ Заметим, что для систем не имеет места, вообще говоря, принцип максимума (см. [12]).

В полосе $D = \{ (x,t) \in \mathbb{R} \times (0,T)\} $, $0 < T < + \infty ,$ рассмотрим линейный параболический по И.Г. Петровскому матричный оператор

где ${{A}_{k}} = {\text{||}}a_{{ij}}^{k}{\text{||}}_{{i,j = 1}}^{m}~~$ – матрицы размерности m × m, элементы которых есть вещественные функции, определенные в $\bar {D}$ и удовлетворяющие условиям:

а) собственные числа μ_r матрицы A₂ подчиняются неравенству ${\text{Re}}{{\mu }_{r}}(x,t) \geqslant \delta $ для некоторого δ > 0 и всех $(x,t) \in \overline {D,} \,\,r = 1,2,...,m;$

б) $a_{{ij}}^{k} \in {{H}^{{\alpha ,\alpha /2}}}(\bar {D}),\alpha \in (0,1),~~i,j = 1,2,...,m,~$ k = 0, 1, 2, где ${{H}^{{\beta ,\beta /2}}}(\bar {D})$ (β – нецелое число) – пространство Гёльдера ([6, с. 16]).

В D выделяется область Ω = $\{ (x,t) \in D$ : g₁(t) < x < < g₂(t)} c негладкими боковыми границами Σ_k = = $\{ (x,t) \in \bar {D}:~x = ~{{g}_{k}}(t)\} ~$, k = 1, 2, где функции g_k удовлетворяют условиям:

В Ω ставится задача отыскания классического решения системы

удовлетворяющего начальному условию и одному из граничных условий или

Определим следующие функциональные пространства. Через $\mathop C\limits_0 \left[ {0,T} \right]$ обозначим пространство вектор-функций ${\psi :}\,\,[0,T] \to {{R}^{m}}$, непрерывных на [0, T], для которых ${\psi }$ при этом ||${\psi }$; [0, T]||⁰ = = $\mathop {{\text{max}}}\limits_{\left[ {0,T} \right]} \left| {\psi } \right|.$ Пусть

есть оператор дробного дифференцирования порядка 1/2. Через ${{\mathop C\limits_0 }^{{1/2}}}\left[ {0,T} \right]$ обозначим [2, 3] пространство вектор-функций ${\psi } \in \mathop C\limits_0 \left[ {0,T} \right],$ для которых существует ${{\partial }^{{1/2}}}{\psi } \in \mathop C\limits_0 \left[ {0,T} \right]$; при этом ||${\psi }$; [0, T]||^1/2 = = $\mathop {{\text{max}}}\limits_{[0,T]} \left| {\psi } \right| + \mathop {{\text{max}}}\limits_{[0,T]} {\text{|}}{{\partial }^{{1/2}}}{\psi |}.$ Здесь и далее для любого вектора b под |b| понимаем максимум из модулей компонент b.

Через ${{H}^{{\alpha /2}}}\left[ {0,T} \right]~$ обозначим пространство непрерывных вектор-функций ${\psi }:\left[ {0,T} \right] \to {{R}^{m}},$ для которых конечна величина

Через $~\mathop C\limits_0 ({\bar {\Omega }})$ обозначим пространство непрерывных вектор-функций $u:\overline {{\Omega \;}} \to {{R}^{m}},$ для которых $u(x,0)$ = 0, при этом ${{\left\| {u;{\Omega }} \right\|}^{0}} = \mathop {{\text{max}}}\limits_{\Omega } \left| u \right|.$ Через ${{\mathop C\limits_0 }^{{1,0}}}\left( {{\bar {\Omega }}} \right)$ обозначим пространство вектор-функций $u \in \mathop C\limits_0 ({\bar {\Omega }}),$ для которых ${{\partial }_{x}}u \in \mathop C\limits_0 \left( {{\bar {\Omega }}} \right),$ при этом ||u; Ω||^1,0 = = $\mathop {{\text{max}}}\limits_{\Omega } \left| u \right| + \mathop {{\text{max}}}\limits_{\Omega } \left| {{{\partial }_{x}}u} \right|.$ Под значениями вектор-функций и их производных на границе области Ω понимаем их предельные значения “изнутри” Ω$.$

Существование классических решений задач (3)–(5) и (3), (4), (6) при сформулированных условиях на коэффициенты системы и боковые границы области установлено в [2, 3] и [4], соответственно, если граничные функции ${{{\psi }}_{k}} \in {{\mathop C\limits_0 }^{{1/2}}}[0,T]$, k = 1, 2 и ${{{\theta }}_{k}} \in \mathop C\limits_0 \left[ {0,T} \right],~~k = 1,~2$. В этих работах получено также интегральное представление решений в виде суммы векторных параболических потенциалов простого слоя. Основной результат настоящей работы – следующие теоремы единственности.

Теорема 1. Пусть выполнены условия а), б), (1), (2). Пусть u – классическое решение задачи

такое, что $u \in {{\mathop C\limits_0 }^{{1,0}}}\left( {{\bar {\Omega }}} \right).$ Тогда $u \equiv 0$ в $\bar {\Omega }$.

Теорема 2. Пусть выполнены условия а), б), (1), (2). Пусть u – классическое решение задачи

такое, что $u \in {{\mathop C\limits_0 }^{{1,0}}}\left( {{\bar {\Omega }}} \right).$ Тогда $u \equiv 0$ в $\bar {\Omega }$.

Замечание. Если усилить требование на боковые границы области, а именно, если g_k ∈ ∈ ${{H}^{{1 + \alpha /2}}}[0,T]$, k = 1, 2, т.е. функции g_k дифференцируемы на [0, T] и их производные принадлежат пространству ${{H}^{{\alpha /2}}}\left[ {0,T} \right]$, то из [5] вытекает единственность решения рассматриваемых задач в классе Гёльдера ${{\mathop H\limits_0 }^{{2 + \alpha ,1 + \alpha /2}}}(\bar {\Omega }).$ В случае параболического оператора с постоянными коэффициентами и полуограниченной области теорема 1 получена в [10, 11] при дополнительном условии на старшую производную $\partial _{x}^{2}u$ решения.

Для доказательства теорем 1, 2 сначала с помощью метода работ [10, 11] получаем теоремы единственности решений первой и второй начально-краевых задач для оператора с дифференцируемыми по x коэффициентами. Затем рассматриваем оператор со “сглаженными” коэффициентами, зависящими от параметра r,

где $A_{k}^{{\left( r \right)}} = {\text{||}}a_{{ij}}^{{k\left( r \right)}}{\text{||}}_{{i,j = 1}}^{m}$. Коэффициенты оператора L^(r) получаются стандартным образом с помощью свертки с гладкой функций (“шапочкой”). Для достаточно малых r коэффициенты оператора L^(r)$~$удовлетворяют условию а) с постоянной параболичности $\frac{\delta }{2}$ равномерно по r и удовлетворяют условию б). Кроме того, $a_{{ij}}^{{k\left( r \right)}} \to a_{{ij}}^{k}$ при r → 0 равномерно на любом компакте из D.

Далее доказываем теорему 2. Фиксируем произвольное число ε > 0, произвольную точку (x₀, ${{t}_{0}}) \in {\Omega }$ и рассматриваем область Ω_d = $\{ (x,t) \in {\Omega }~$: g₁(t) + d < x < g₂(t) – d, d < t < T} такую, что $({{x}_{0}},{{t}_{0}}) \in {{{\Omega }}_{d}}$ для достаточно малого $d \in \left( {0,T} \right).$ Обозначим через $\bar {u}$ – продолжение вектор-функции u с ${\bar {\Omega }}$ на $\bar {D}$ с сохранением нормы ||⋅||^{1, 0} (см. [6, с. 342]), причем такое, что $\bar {u}(x,0) = {{\partial }_{x}}\bar {u}(x,0) = 0$, $x \in \mathbb{R}.$ Рассматриваем “сглаженные” вектор-функции ${{u}_{s}}(x,t)$ такие, что ${{u}_{s}}(x,t) \to \bar {u}(x,t)$, s → 0, равномерно на любом компакте из D. Для любых 0 < s < $\frac{d}{2}$ и r > 0 вектор-функция u_s является решением задачи

где ${{f}_{s}}(x,t)\, = \,{{L}^{{(r)}}}{{u}_{s}}(x,t)$, ${{h}_{s}}(x)\, = \,{{u}_{s}}(x,d)$, ${\theta }_{s}^{1}(t)$ = = ${{\partial }_{x}}{{u}_{s}}$(g₁(t) + d, t), ${\theta }_{s}^{2}(t) = {{\partial }_{x}}{{u}_{s}}(~{{g}_{2}}(t) - d,t)$. Из работы [4] и в силу теоремы единственности для оператора с гладкими коэффициентами и свойств параболических потенциалов [3, 4, 13] следует, что для каждого $0 < s < \frac{d}{2}$ вектор-функцию u_s можно представить в виде суммы векторных параболических потенциалов простого слоя, оценивая которые, получаем, что найдутся достаточно малые числа d > 0, ${{s}_{0}} = {{s}_{0}}(d) < \frac{d}{2}$ и $r = r(d) > 0~$ такие, что ${\text{|}}{{u}_{s}}({{x}_{0}},{{t}_{0}}){\text{|}} < \frac{\varepsilon }{2}$ для любого $s \leqslant {{s}_{0}}.~$ Отсюда, учитывая, что |u_s(x, t) – – $\bar {u}(x,t){\text{|}} < Cs,$ $(x,t) \in \bar {D},$ для любого s > 0 и в силу произвольности ε, следует утверждение теоремы 2. Затем, используя [3] и теорему 2, получаем утверждение теоремы 1.