Теплофизика высоких температур, 2023, T. 61, № 2, стр. 265-278
Интенсификация теплообмена и характеристики потока наножидкости при обтекании усеченного конуса в неограниченной полости
B. Ghozlani 1, S. Hadj-Salah 2, 3, S. Bezi 3, 4, B. Souayeh 4, 5, *
1 University of Tunis El Manar, National Engineers School of Tunis Modeling in Hydraulic and Environment Laboratory
Tunisia
2 Research Unit of Ionized Backgrounds and Reagents Studies, University of Monastir
Tunisia
3 University of Hafer al Batin, College of Science, Department of Physics
Hafer Al Batin, Saudi Arabia
4 Laboratory of Fluid Mechanics, Physics Department, University of Tunis El Manar, Faculty of Sciences of Tunis
Tunisia
5 King Faisal University, College of Science, Department of Physics
Saudi Arabia
* E-mail: basma.souayeh@gmail.com
Поступила в редакцию 30.11.2020
После доработки 31.10.2021
Принята к публикации 15.02.2022
Аннотация
Проведено численное исследование вынужденного обтекания нагретого усеченного конуса наножидкостью на водной основе, содержащей различные типы наночастиц (Al2O3, Cu и CuO) с объемной долей φ твердого вещества от 0 до 8%. Расчеты на основе метода конечных объемов с алгоритмом SIMPLE проводились для установившегося ламинарного режима течения в диапазоне чисел Пекле 25 ≤ Pe ≤ 150. Обнаружено, что характеристики течения и теплообмена наножидкостей сильно зависят от объемной доли твердого вещества, числа Пекле и формы наночастиц. В наножидкостях наблюдаются увеличенная длина следа и поверхностная завихренность, уменьшенное сопротивление и более высокая скорость теплообмена. Кроме того, результаты показывают, что один тип наночастиц позволяет существенно улучшить некоторые технические параметры. При использовании наночастиц Cu получены высокие значения среднего числа Нуссельта Nuav, максимальные поверхностная завихренность ωs,max и безразмерная длина следа Lr. Однако значения коэффициента сопротивления CD выше для наночастиц из Al2O3. Разработаны надежные корреляции для ωs, max, CD и Nuav в виде функций от φ и Pe.
ВВЕДЕНИЕ
Существует множество практических приложений в промышленных процессах физического явления, которое происходит за обтекаемым телом. Среди наиболее распространенных примеров такого течения можно перечислить течения в трубчатых и штифтовых теплообменниках, при охлаждении электроники, обтекании зданий, датчиков и вихревых расходомеров. Среди изучаемых проблем, наряду с исследованием условий обтекания, важное место занимает оценка конвективного обтекания пучков труб, затупленных тел или оребренных каналов [1–4]. Из опубликованной литературы можно сделать вывод о том, что обтекание цилиндров с круглым и квадратным основаниями исследовалось многими авторами с использованием как чистых жидкостей, так и наножидкостей. Однако теплообмену при вынужденной конвекции [5–8] около трапециевидного тела с использованием различных наножидкостей внимание практически не уделялось.
Работы [9–14] посвящены обтеканию цилиндра квадратного сечения чистой жидкостью, где такие параметры, как лобовое сопротивление, коэффициенты подъемной силы и частота образования вихрей, влияют на скорость потока и теплообмена. Усеченные конусы исследовались ранее в [15–19].
В [20] рассмотрено обтекание воздухом изолированного тела с острыми кромками с переменным отношением высот при поперечном течении в стационарном и периодическом режимах при числах Рейнольдса Re от 1 до 150. Сделан вывод о том, что эффект вихреобразования проявляется при теплообмене вокруг объектов.
В [21] выполнено численное исследование для изучения влияния теплообмена при смешанной конвекции от нагретых трапециевидных тел двух различных конфигураций, а именно, сходящихся и расходящихся конусов в вертикальной области. Обнаружено, что коэффициент лобового сопротивления у расширяющегося конусa меньше, чем у сходящегося. Локальное число Нуссельта значительно увеличивается с ростом чисел Рейнольдса Re и Ричардсона Ri, что приводит к интенсификации теплообмена.
Двумерный свободный поток и теплообмен поперек длинного сужающегося трапециевидного обтекаемого тела исследованы в [15] для диапазона Re = 1–150 при числе Прандтля Pr = 0.7 (воздух). Исследован ряд технических параметров, таких как коэффициенты лобового сопротивления и подъемной силы, число Струхаля, локальное и среднее числа Нуссельта. Установлено, что отрыва потока от поверхности усеченного конуса при Re ≤ 5 не происходит, однако уже при Re = 6 поток начинает отрываться.
В [22] изучались гидродинамические и тепловые характеристики двумерных, несжимаемых, разжижающихся и загущающихся при нагрузке неньютоновских жидкостей со степенными законами при вынужденной конвекции в усеченном конусе. Авторы обнаружили, что коэффициент лобового сопротивления уменьшается, а размер следа и среднее число Нуссельта растут с увеличением Re.
Экспериментальные исследования в [23] проведены на вихревом расходомере методом измерения перепада пристеночного давления с использованием трапециевидного тела. Рабочим телом была вода. Трапециевидное тело обтекания выполнено из трубы диаметром 101 мм с тремя различными коэффициентами запирания: 0.14, 0.24 и 0.30. Сделан вывод о том, что блокировка при 0.30 является лучшей среди трех исследованных, поскольку она дает сигналы высокой амплитуды и наименьшее отклонение числа Стентона St в условиях полностью развитого потока.
Несмотря на значительные усилия по исследованию течения и теплообмена в чистых жидкостях с низкой теплопроводностью при обтекании тела в соответствующих условиях, в этой области проведено очень мало исследований с использованием наножидкостей [24, 25]. Наножидкости – это жидкости, содержащие взвешенные частицы нанометрового размера, которые имеют более высокие порядки теплопроводности по сравнению с базовой жидкостью. Они считаются “умными” жидкостями, потому что теплообмен может быть снижен или усилен за счет изменения концентрации наночастиц.
Обмен импульсом и теплом при вынужденной конвекции ламинарного и устойчивого свободного потока наножидкостей (Al2O3 и CuO) мимо изолированного цилиндра с квадратным сечением исследован численно в [26]. Авторы отмечают, что характеристики теплообмена при обтекании цилиндра с квадратным сечением наножидкостью заметно улучшаются по сравнению с обтеканием базовыми жидкостями. Это улучшение более очевидно в потоках с более высокими числами Пекле и объемной концентрацией частиц.
В [27] изучено обтекание тела (в том числе цилиндра с квадратным сечением) наножидкостью CuO–вода. После тщательного выбора контрольных параметров авторы выявили, что при определенной объемной концентрации уменьшение размера наночастиц приводит к увеличению интенсивности теплообмена от цилиндра квадратного сечения и уменьшению амплитуды коэффициента подъемной силы.
Исследование теплообмена при вынужденной конвекции наножидкостью около неограниченного нагретого цилиндра квадратного сечения проведено в [28]. Отношение общей плотности потока тепла в наножидкости по сравнению с базовой жидкостью увеличивается с ростом объемной доли твердого вещества. При увеличении объемной доли твердого вещества наблюдается уменьшение различий в характере течения между базовой жидкостью и наножидкостью.
Существующие экспериментальные и теоретические исследования теплообмена с использованием наножидкостей при обтекании тел подробно рассмотрены в [29–34].
Однако, как видно из приведенного выше обзора, исследование в данной работе является первым испытанием вынужденного конвективного обтекания усеченного конуса однородным потоком наножидкости (Al2O3, CuO и Cu), несмотря на то что трапециевидное тело считается наиболее подходящей формой тела обтекания для конструкции вихревого расходомера. Таким образом, данная работа призвана восполнить этот пробел в литературе и исследовать теплообмен при вынужденной конвекции от трапециевидного обтекаемого тела с использованием разных типов наножидкостей с различными техническими параметрами. Записаны корреляционные выражения для средних чисел Нуссельта в зависимости от управляющих параметров для каждого типа наножидкости.
МОДЕЛИРОВАНИЕ
Геометрия задачи. Система, исследуемая в настоящей работе, представляет собой неограниченный поток наножидкости, обтекающий двумерный усеченный конус (с шириной передней грани b, шириной задней грани a = 0.5b и длиной конуса по оси b), расположенный симметрично между верхней и нижней искусственными границами, с постоянной температурой Tw. Центр конуса считается находящимся в начале системы координат (r, z). Конус подвергается воздействию свободного потока наножидкости с постоянной скоростью u∞ и температурой T∞ < Tw (рис. 1). На границах приняты условия свободного скольжения. После исследований независимости расчетной области безразмерное расстояние вверх по потоку от входа в канал до передней поверхности конуса Zu/b принято равным 15, а безразмерное расстояние между задней поверхностью конуса и выходом из канала Zd/b = 30. Поэтому общая безразмерная длина расчетной области L/b равна 46, безразмерная высота расчетной области H/b = 30. Подробности процедуры выбора данных значений приведены ниже.
Основные уравнения. Наножидкости, рассматриваемые в данном исследовании, представляют собой сильно разбавленные суспензии наночастиц очень малого размера. Поскольку взвешенные наночастицы имеют небольшой размер и концентрацию, они становятся однородными и ведут себя как базовая жидкость. Наночастицы и основная жидкость находятся в тепловом равновесии, и между твердой и жидкой фазами не происходит прилипания [35]. При всех перечисленных предположениях наножидкости можно рассматривать как однородные чистые жидкости с эффективными свойствами и применять к ним те же основные уравнения, что и для чистых жидкостей [36]. В рассматриваемом диапазоне объемных долей наночастиц наножидкости проявляют ньютоновское поведение [37]. Вязкой диссипацией также можно пренебречь. Таким образом, основные уравнения для двумерного осесимметричного течения и теплообмена вокруг трапеции в режиме вынужденной конвекции и в стационарном режиме могут быть выражены в цилиндрических безразмерных координатах следующим образом:
– уравнение неразрывности
(1)
$\frac{{\partial U}}{{\partial Z}} + \frac{1}{R}\frac{{\partial \left( {RV} \right)}}{{\partial R}} = 0;$– уравнения движения
(2)
$\begin{gathered} \frac{{\partial \left( {{{U}^{2}}} \right)}}{{\partial Z}} + \frac{1}{R}\frac{{\partial \left( {RUV} \right)}}{{\partial R}} = \\ = - \frac{{\partial P}}{{\partial Z}} + \frac{1}{{{\text{Re}}\left[ {\frac{{{{\partial }^{2}}U}}{{\partial {{Z}^{2}}}} + \frac{1}{R}\frac{\partial }{{\partial R}}\left( {R\frac{{\partial U}}{{\partial R}}} \right)} \right]}}, \\ \end{gathered} $(3)
$\begin{gathered} \frac{{\partial \left( {UV} \right)}}{{\partial Z}} + \frac{1}{R}\frac{{\partial \left( {R{{V}^{2}}} \right)}}{{\partial R}} = \\ = - \frac{{\partial P}}{{\partial R}} + \frac{1}{{{\text{Re}}\left[ {\frac{{{{\partial }^{2}}V}}{{\partial {{Z}^{2}}}} + \frac{1}{R}\frac{\partial }{{\partial R}}\left( {R\frac{{\partial V}}{{\partial R}}} \right)} \right]}}; \\ \end{gathered} $– уравнение сохранения энергии
(4)
$\frac{{\partial \left( {U\theta } \right)}}{{\partial Z}} + \frac{1}{R}\frac{{\partial \left( {RV\theta } \right)}}{{\partial R}} = \frac{1}{{{\text{Pe}}}}\left[ {\frac{{{{\partial }^{2}}\theta }}{{\partial {{Z}^{2}}}} + \frac{1}{R}\frac{\partial }{{\partial R}}\left( {R\frac{{\partial \theta }}{{\partial R}}} \right)} \right],$Для решения задачи обтекания на границах применяются следующие безразмерные условия:
• на входной границе предполагаются равномерный поток в направлении x и однородная температура жидкости
• на выходе диффузионный поток в направлении, нормальном к поверхности выхода, равен нулю для всех переменных
• на верхней и нижней границах заданы нулевая нормальная скорость и нулевой нормальный градиент всех переменных
• на поверхности усеченного конуса применяются условия прилипания и постоянной температуры стенки:
Параметры потока, вычисляемые по полям скоростей, давления и температур, определяются следующим образом.
Коэффициент аэродинамического сопротивления конуса рассчитывается как
где FD – сила сопротивления, действующая на поверхность конуса. Комбинация силы сопротивления и силы вязкого сопротивления составляет полное сопротивление FD. После сходимости численного моделирования можно получить вязкость, давление и силу сопротивления. Затем коэффициент сопротивления CD (5) рассчитывается после задания соответствующих данных (ширины передней части трапеции b, скорости набегающего потока на входе u∞ и плотности наножидкости ρnf). Для настоящего двумерного осесимметричного потока безразмерный вектор завихренности имеет только одну компоненту:В данной работе теплообмен вокруг усеченного конуса характеризуется средним по поверхности числом Нуссельта
(6)
$\begin{gathered} E\left( {{\varphi }} \right) = \frac{{{\text{N}}{{{\text{u}}}_{{{\text{av}},nf}}}\left( {{\varphi }} \right) - {\text{N}}{{{\text{u}}}_{{{\text{av}},bf}}}}}{{{\text{N}}{{{\text{u}}}_{{{\text{av}},bf}}}}}, \\ {\text{Nu}} = \frac{{{{h}_{{{\text{loc}}}}}b}}{{{{k}_{{bf}}}}} = - \left( {\frac{{{{k}_{{nf}}}}}{{{{k}_{{bf}}}}}} \right)\frac{{\partial \theta }}{{\partial n}}, \\ \end{gathered} $Моделирование наножидкостей. Предполагается, что наножидкость представляет собой однородную жидкость с эффективными свойствами и рассматривается как одна фаза. Наличие наночастиц в жидкости учитывается с помощью изменения физических свойств смешанной жидкости. Также предполагается, что наночастицы и базовая жидкость находятся в тепловом равновесии друг с другом и относительная скорость пренебрежимо мала или равна нулю. Из этого предположения следует, что эффективные теплофизические свойства зависят от объемной концентрации наночастиц и свойств как базовой жидкости, так и взвешенных частиц. Теплофизические свойства наночастиц и базовой жидкости, измеренные при эталонной температуре (300 К), приведены в табл. 1. Эффективные плотность, теплоемкость, динамическая вязкость и эффективная теплопроводность рассчитываются следующим образом.
Таблица 1.
Теплофизические свойства наночастиц и воды
| Вещество | ρ, кг/м3 | cp, Дж/(кг К) | k, Вт/(м К) |
|---|---|---|---|
| Al2O3 | 3970 | 765 | 40 |
| Cu | 8933 | 385 | 401 |
| CuO | 6350 | 531.8 | 76.5 |
| Вода | 997.1 | 4179 | 0.63 |
Эффективная плотность наножидкости определяется выражением [38]
Эффективная теплоемкость находится с помощью уравнения, предложенного в [39]:
Эффективная вязкость наножидкости определяется по модели Бринкмана [40]:
В настоящем исследовании учитывается влияние формы наночастиц на теплообмен. Поэтому рассматривается эффективная теплопроводность, заданная моделью Гамильтона и Кроссера [41]:
(7)
$\frac{{{{k}_{{nf}}}}}{{{{k}_{{bf}}}}} = \frac{{{{k}_{{np}}} + \left( {m - 1} \right){{k}_{{bf}}} - \left( {m - 1} \right)\left( {{{k}_{{bf}}} - {{k}_{{np}}}} \right){{\varphi }}}}{{{{k}_{{np}}} + \left( {m - 1} \right){{k}_{{bf}}} + \left( {{{k}_{{bf}}} - {{k}_{{np}}}} \right){{\varphi }}}},$ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ
Система уравнений. Уравнения (1)–(4) течения и теплообмена с соответствующими граничными условиями решаются с использованием метода конечных объемов в пакете Fluent [43]. Конвективные и диффузионные члены дискретизируются по схеме против потока первого порядка и центрально-разностной схеме соответственно. Поскольку поток практически совпадает с сеткой, то численная диффузия низкая и схема первого порядка против ветра может быть использована для дискретизации конвективных членов без существенной потери точности и с меньшими затратами по времени. Алгоритм SIMPLE применялся для связи давления и скорости. Поточечная итерационная схема Гаусса–Зейделя использовалась в сочетании с алгебраическим многосеточным методом для решения результирующей системы уравнений для всех зависимых переменных в каждой ячейке. Сходимость итерационного решения проверяется путем вычисления суммы абсолютных разностей переменных решения между двумя последовательными итерациями. Для всех расчетов, выполненных в этом исследовании, итерации продолжаются до тех пор, пока для всех уравнений не достигается критерий сходимости 10–9.
Размер расчетной области. Согласно литературным данным, численное моделирование течения и теплообмена вокруг обтекаемых тел показало, что числовые параметры, такие как высота расчетной области H, расчетное расстояние вверх по течению Zu и расчетное расстояние вниз по течению Zd, имеют большое значение и должны выбираться внимательно [44, 45]. Для изучения влияния безразмерного расстояния вверх по потоку на такие физические параметры, как коэффициент сопротивления CD и среднее число Нуссельта Nuav, рассмотрены три значения Zu/b = 10, 15, 20 для наножидкости Cu–вода с объемной долей твердого вещества φ = 0.08 при наименьшем числе Пекле (Pe = 25) и постоянном Zd/b = 30. В соответствии с данными табл. 3 значения CD и Nuav меняются на 0.038 и 0.015% для Zu/b = 15 и 20 соответственно. Так, Zu/b = 15 выбрана для дальнейшего анализа.
Таблица 3.
Оценка независимости размера расчетной области для наножидкости медь–вода (φ = 0.08) при течении по потоку и ${\text{Pe}} = 150$, против потока и на высоте при ${\text{Pe}} = 25$
| Расстояние | CD | Отклонение, % | Nuav | Отклонение, % |
|---|---|---|---|---|
| ${{{{Z}_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{u}}} b}} \right. \kern-0em} b}$ = 10 | 3.530 | 1.41 | 3.768 | 1.08 |
| 15 | 3.481 | – | 3.728 | – |
| 20 | 3.479 | 0.038 | 3.727 | 0.015 |
| ${{{{Z}_{d}}} \mathord{\left/ {\vphantom {{{{Z}_{d}}} b}} \right. \kern-0em} b}$ = 25 | 1.629 | 1.36 | 6.874 | 1.29 |
| 30 | 1.608 | – | 6.787 | – |
| 35 | 1.607 | 0.02 | 6.785 | 0.016 |
| ${H \mathord{\left/ {\vphantom {H b}} \right. \kern-0em} b}$ = 25 | 3.533 | 1.52 | 3.843 | 1.63 |
| 30 | 3.481 | – | 3.782 | – |
| 35 | 3.480 | 0.025 | 3.778 | 0.085 |
Аналогично в табл. 3 показано влияние изменения Zd/b (от 25 до 35) на CD и Nuav для наножидкости Cu–вода с объемной долей φ = 0.08 при максимальном числе Пекле (Pe = 150) и Zu/b = 15. Отклонения CD и Nuav оказываются равными 0.02 и 0.016% соответственно за счет значительного увеличения процессорного времени при росте Zd/b от 30 до 35. В результате Zd/b = 30 оказывается подходящим для всех расчетов в этом исследовании.
Для изучения верхней и нижней границ три безразмерных домена высотой H/b = 25, 30 и 35 испытаны для наножидкости Cu–вода с φ = 0.08 при Pe = 25. Данные о влиянии изменения H/b на CD и Nuav также представлены в табл. 3. В результате анализа относительных отклонений выходных параметров для исследований выбрана высота H/b = 30.
Исследование независимости решетки. Расчетная сетка создана с помощью Gambit [46] и показана на рис. 2. Получена неравномерная сетка для всей расчетной области с безразмерной длиной L/b = 46 и безразмерной высотой H/b = 30. Вблизи усеченного конуса реализована мелкая равномерная сетка с постоянным размером ячеек для адекватного расчета взаимодействия следа и стенки. Гораздо более грубая неравномерная сетка распределена вне области вокруг цилиндра с помощью алгебраических выражений. Исследование чувствительности сетки проводилось с использованием трех различных неравномерных сеток, перечисленных в табл. 4. Общее количество использованных ячеек составило 122 050, 134 220 и 150 580 с контрольными объемами CV = 120, 145 и 170 на каждой стороне конуса соответственно. Исследование проводилось при Pe = 150, в качестве наножидкости выбрана Cu–вода с φ = 0.08. Для первых двух размеров сетки относительное изменение значений CD и Nuav составило 2 и 1.2% соответственно. Однако для двух последних сеток изменения этих величин ‒ 0.6% и 0.2% соответственно. Чрезмерное время вычислений, необходимое для решения на сетке с 150 580 ячейками, “перевешивает” небольшие ошибки, возникающие при использовании сетки с 134 220 ячейками. Поэтому в данном исследовании используется сетка, состоящая из 134 220 ячеек, с каждой стороной цилиндра по 145 точек.
Таблица 4.
Оценки независимости сетки для наножидкости медь–вода (φ = 0.08) при ${\text{Pe}} = 150$
| Полное количество ячеек | CV с каждой стороны конуса | Минимальный размер сетки | ${{C}_{D}}$ | Отклонение, % | Nuav | Отклонение, % |
|---|---|---|---|---|---|---|
| 122 050 | 120 | 0.008 | 1.640 | 2 | 6.868 | 1.2 |
| 134 220 | 145 | 0.006 | 1.608 | – | 6.787 | – |
| 150 580 | 170 | 0.005 | 1.618 | 0.65 | 6.773 | 0.2 |
Валидация результатов. Для установления точности кода использованы данные, доступные в литературе и полученные в основном для воздушного потока (Pr = 0.7), которые приведены в табл. 5. Поэтому для определения результатов необходимы отдельные расчеты при конкретных числах Рейнольдса 5, 20 и 40. Между настоящими результатами и данными [15, 20] обнаружено превосходное соответствие. Максимальные отклонения в значениях CD оказываются менее 2.5%, а для соответствующих вариаций Nuav менее 2%.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
В результате настоящего исследования получены характеристики течения наножидкости и тепловые характеристики вокруг усеченного конуса в полностью ламинарном стационарном режиме. Числа Пекле выбраны равными 25, 50, 100 и 150 с ограничением, чтобы соответствующие числа Рейнольдса не превышали 45 (поскольку при Re > 50 течение становится нестационарным). Всего проведено 52 расчета для трех наножидкостей Al2O3–вода, Cu–вода и CuO–вода при различных объемных долях (0 ≤ φ ≤ 0.08) твердого вещества. Эмпирические корреляции разработаны для получения связи между сопротивлением, энергией и другими исследуемыми параметрами, охватывающими широкий диапазон Pe и φ. Также выполнено 20 дополнительных расчетов для анализа влияния формы наночастиц на теплообмен и поток жидкости.
Характеристики потока. На рис. 3 представлены линии тока течения наножидкости Cu–вода в непосредственной близости от усеченного конуса. Для краткости представлены графики только для φ = 0.08. Линии тока зависят от числа Пекле. По мере увеличения значений Pe происходит отрыв потока от меньшего основания конуса и за ним образуются два вихря (рис. 3в). Размер этих вихрей увеличивается с ростом числа Пекле и становится максимальным при Pe = 150 (рис. 3г). При 100 ≤ Pe ≤ 150 (рис. 3в) поток отрывается не только с задней стороны, но и с верхней и нижней сторон усеченного конуса.
Рис. 3.
Линии тока при вынужденной конвекции наножидкости Cu–вода (φ = 0.08) около конуса при различных числах Пекле: (а) – Pe = 25, (б) – 50, (в) – 100, (г) – 150.

Судя по линиям тока при 50 ≤ Pe ≤ 150, можно говорить, что поток полностью отрывается от задней поверхности конуса и образует рециркуляционный след за ним. Длина этой зоны от задней части конуса до точки присоединения по центральной линии (т.е. в точке Z = 0) известна как длина рециркуляции (или длина следа). Влияние типа наночастиц, их объемной доли и числа Пекле на безразмерную длину следа ${{L}_{r}} = L_{r}^{*}{\text{/}}b~$ представлено на рис. 4. Во всех рассмотренных наножидкостях длина следа растет при увеличении как объемной доли наночастиц, так и числа Пекле. Это означает, что сепарации потока способствуют добавление наночастиц и увеличение числа Пекле, что приводит к ускоренному обтеканию конуса. Также наблюдается, что значение длины следа при определенных φ и Pe выше в наножидкости Cu–вода, в CuO–вода длина меньше и, наконец, в Al2O3–вода еще меньше. Когда объемная доля наночастиц увеличивается, различия между наножидкостями четко видны при Pe = 100, 150. В то время как при Pe = 25 влияние типа наночастиц слабое, а длина следа изменяется мало.
Рис. 4.
Изменение длины следа ${{L}_{r}}$ в зависимости от доли наночастиц при трех значениях Pe для разных наножидкостей: 1 – Cu–вода, 2 – Al2O3–вода, 3 – CuO–вода.

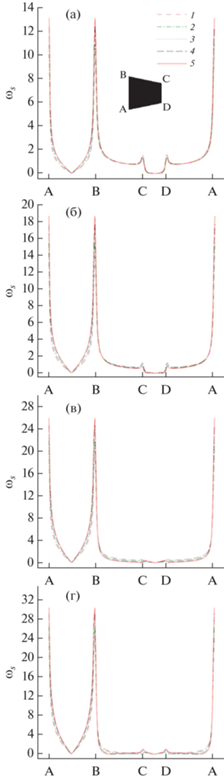
Распределение безразмерной завихренности вдоль поверхности конуса приведено на рис. 5 при 25 ≤ Pe ≤ 150, 0 ≤ φ ≤ 0.08. Для краткости представлены только результаты для наножидкости Cu–вода. С увеличением Pe значения поверхностной завихренности возрастают при фиксированных значениях φ. Это связано с тем, что инерционные силы становятся доминирующими с увеличением Pe и способствуют вращательному движению жидкости, тем самым приводя к увеличению распределения завихренности. Во всех диапазонах Pe и φ поверхностная завихренность равна нулю в передней критической точке (между А и В), резко возрастает на передних кромках (А и В) и резко снижается в середине задней поверхности (между C и D). При увеличении Pe подъем, наблюдаемый у задней поверхности, становится намного меньше. Кроме того, изменение распределения завихренности при добавлении наночастиц относительно слабое: вблизи передних краев конуса наблюдается незначительное увеличение завихренности при росте объемной доли частиц.
Рис. 5.
Распределение пристеночной завихренности ${{\omega }_{s}}$ вдоль конуса для Cu–вода при различных долях наночастиц и Pe: (а) ‒ Pe = 25, (б) ‒ 50, (в) ‒ 100, (г) ‒ 150; 1 – φ = 0, 2 – 0.02, 3 – 0.04, 4 – 0.06, 5 – 0.08.
На рис. 6 показано изменение максимальной поверхностной завихренности ωs, max, полученной вблизи передних краев конуса, в зависимости от φ и Pe для различных наножидкостей. Снова в Cu–вода наблюдаются максимальные значения ωs, max, затем в CuO–вода и, наконец, в Al2O3–вода. Также замечено, что влияние типа наночастиц становится более заметным при увеличении числа Пекле и объемной доли твердого вещества. Интересно отметить, что вариация ωs, max линейно возрастает с увеличением φ и Pe. Кроме того, получена корреляция ωs, max для наножидкостей с 0 ≤ φ ≤ 0.08 при 25 ≤ Pe ≤ 150:
(8)
${{\omega }_{s}}_{{{\text{, max}}}} = \left( {A + B\varphi } \right){\text{P}}{{{\text{e}}}^{C}}.$Рис. 6.
Распределение максимальной поверхностной завихренности ωs, max у передних кромок в зависимости от φ при различных Pe для разных наножидкостей: 1 – Cu–вода, 2 – Al2O3–вода, 3 – CuO–вода.

Константы A, B и C уравнения (8) приведены в табл. 6 для рассмотренных наножидкостей. Максимальное отклонение настоящих результатов по отношению к значениям, полученным по уравнению (8), составляет 1.19, 3.6 и 2.2% для Al2O3–вода, Cu–вода и CuO–вода соответственно, и почти 92% точек ωs, max имеют отклонение менее 2%. Коэффициенты достоверности R2 лежат в пределах от 0.998 до 0.999.
Таблица 6.
Коэффициенты уравнений (8)–(10)
| Наножидкость | A | B | C | R2 |
|---|---|---|---|---|
| (8) | ||||
| Al2O3–вода | 2.119 | 3.271 | 0.489 | 0.999 |
| Cu–вода | 2.225 | 7.474 | 0.477 | 0.998 |
| CuO–вода | 2.175 | 5.304 | 0.484 | 0.999 |
| (9) | ||||
| Al2O3–вода | 22.311 | –33.898 | –0.491 | 0.997 |
| Cu–вода | 20.95 | –61.303 | –0.477 | 0.994 |
| CuO–вода | 21.625 | –48.97 | –0.484 | 0.996 |
| (10) | ||||
| Al2O3–вода | 0.935 | 3.077 | 0.347 | 0.999 |
| Cu–вода | 0.967 | 3.474 | 0.34 | 0.999 |
| CuO–вода | 0.952 | 3.279 | 0.3447 | 0.998 |
Аналогичным образом на рис. 7 представлены зависимости коэффициента сопротивления CD вокруг конуса от объемной доли твердого вещества и числа Пекле для трех типов наножидкостей. Коэффициент лобового сопротивления уменьшается с увеличением φ, как и с увеличением Pe. При определенных значениях φ и Pe наножидкость Al2O3–вода имеет самое высокое значение CD, меньше у CuO–вода, и наименьшее у Cu–вода. Заметим, что влияние типа наночастиц становится более заметным по мере увеличения φ. Однако это влияние ослабевает при увеличении числа Пекле.
Рис. 7.
Зависимости ${{C}_{D}}$ от доли наночастиц при различных Pe для разных наножидкостей: 1 – Cu–вода, 2 – Al2O3–вода, 3 – CuO–вода.

Набор численных результатов, представленных на рис. 6, аппроксимирован кривой для построения зависимости, которая связывает коэффициент сопротивления CD с объемной долей наночастиц (0 ≤ φ ≤ 0.08) и числом Пекле (25 ≤ Pe ≤ 150) для трех типов наножидкости. Полученная корреляция имеет вид
с константами A, B и C, приведенными в табл. 6. Уравнение (9) позволяет воспроизвести численные результаты с разницей менее 4, 5.5 и 6.3% для Al2O3–вода, Cu–вода и CuO–вода соответственно. Кроме того, коэффициенты детерминации R2 попадают в диапазон от 0.994 до 0.997, и почти 65% данных CD имеют отклонение менее 2%. Насколько известно авторам, предложенная корреляционная зависимость публикуется впервые.Характеристики теплообмена. Характеристики теплообмена при обтекании наножидкостью нагретого усеченного конуса зависят от объемной доли наночастиц φ, числа Пекле и типа наночастиц. Исследовано также влияние формы наночастиц.
На рис. 8 показаны изотермы вокруг конуса при различных числах Пекле. Верхние и нижние половины графиков изображают изотермы чистой воды (φ = 0) и наножидкости Cu–вода (φ = 0.08) соответственно. Поскольку течение, рассматриваемое в данном исследовании, является ламинарным и установившимся при 25 ≤ Pe ≤ 150, изотермы симметричны относительно оси. Наибольшее скопление изотерм наблюдается на передней кромке усеченного конуса. Это свидетельствует о более высоком градиенте температуры и, как следствие, о более интенсивном теплообмене. Кроме того, на поле температуры влияет число Пекле. При Pe = 25 (рис. 8а) изотермы более выражены, так как здесь преобладает проводимость. Однако с увеличением числа Пекле температурное поле затухает (рис. 8в, 8г), и изотермы располагаются плотнее по сравнению со случаем меньшего Pe. Добавление наночастиц вызывает сравнительно большее скопление изотерм, чем в чистой воде, и способствует повороту изотерм в сторону задней поверхности конуса, особенно при более высоких числах Пекле (рис. 8г).
Рис. 8.
Изотермы для вынужденного обтекания конуса наножидкостью Cu–вода при φ = 0.08 и различных Pe: (а) ‒ Pe = 25, (б) ‒ 50, (в) ‒ 100, (г) ‒ 150.

На рис. 9 изображено изменение локального числа Нуссельта на гранях конуса при различных значениях Pe и φ при обтекании наножидкостью Cu–вода. Хорошо видно, что локальное число Нуссельта зависит от Pe. При увеличении от 25 до 150 значения Nu заметно увеличиваются. Изменение симметрично для верхней и нижней половин конуса. Также замечено, что из-за максимального скопления изотерм у передней грани конуса на этой грани наблюдаются максимальные значения Nu, меньше ‒ на верхней и нижней поверхностях конуса и минимальные ‒ на задней поверхности. Значения Nu резко возрастают на всех углах конуса, причем на передних углах больше, чем на задних. Локальные минимальные значения существуют в серединах передней и задней поверхностей. Увеличение объемной доли наночастиц приводит к увеличению значений Nu. Это происходит из-за роста теплопроводности наножидкости с увеличением φ.
Рис. 9.
Распределение локальных Nu вдоль поверхности конуса для наножидкости Cu–вода при различных долях наночастиц и Pe: (а) ‒ Pe = 25, (б) ‒ 50, (в) ‒ 100, (г) ‒ 150; 1 – φ = 0, 2 – 0.02, 3 – 0.04, 4 – 0.06, 5 – 0.08.

Изменение среднего числа Нуссельта Nuav в зависимости от объемной доли твердого вещества при различных числах Пекле представлено на рис. 10. Для всех исследованных наножидкостей среднее число Нуссельта увеличивается с одновременным увеличением как объемной доли наночастиц, так и числа Пекле. Более того, наибольшая интенсивность теплообмена достигнута в случае наножидкости Cu–вода, а наножидкость CuO–вода имеет наименьшую. Фактически у Cu более высокое значение теплопроводности по сравнению с Al2O3 и CuO, что приводит к более высоким температурным градиентам и, следовательно, способствует улучшению теплообмена. Также из-за роста φ увеличивается разница в интенсивности теплообмена для различных наножидкостей. С использованием численных результатов на рис. 10 разработано соотношение для среднего числа Нуссельта
константы A, B и C приведены в табл. 6. При анализе данных и сравнении с предложенной корреляцией (10) видно, что почти 76% точек данных показывают отклонение до 1%. Кроме того, коэффициенты детерминации R2 попадают в диапазон от 0.998 до 0.999, а воспроизводят численные результаты с разницей менее 1.15, 2.07 и 1.79% для наножидкостей Al2O3–вода, Cu–вода и CuO–вода соответственно.Рис. 10.
Изменение Nuav в зависимости от φ при различных Pe для разных наножидкостей: 1 – Cu–вода, 2 – Al2O3–вода, 3 – CuO–вода.

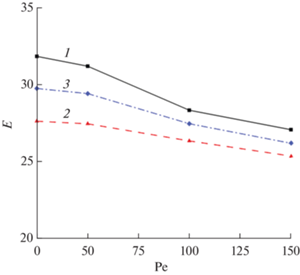
Изменение интенсивности теплообмена за счет добавления в чистую воду различных наночастиц с объемной долей φ = 0.08 при различных значениях числа Пекле показано на рис. 11. Процент изменения теплообмена рассчитан по уравнению (6). Максимальное увеличение скорости теплопередачи наблюдается при Pe = 25 для Cu–вода с коэффициентом усиления 31.74%, а минимальная – при Pe = 150, для Al2O3–вода с коэффициентом усиления 26.14%. Влияние наличия наночастиц более выражено при низких Pe.
Рис. 11.
Влияние типа наночастиц и числа Пекле на интенсификацию теплообмена: 1 – Cu–вода, 2 – Al2O3–вода, 3 – CuO–вода.
Для оценки влияния формы наночастиц на скорость теплообмена вокруг конуса рассмотрена только наножидкость Cu–вода, поскольку она гарантирует максимальную интенсификацию теплообмена и представляет большой интерес для инженерных приложений. Исследован случай при Pe = 150, дающий наибольшее число Нуссельта. В данных условиях изотермы вокруг конуса для различных форм наночастиц (пластинчатых m = 5.7, цилиндрических m = 4.8, “кирпич” m = 3.7 и сферических m = 3) при φ = 0.08 показаны на рис. 12. Симметрия относительно оси отчетливо видна для всех перечисленных форм наночастиц. Самая высокая плотность изотерм, а следовательно, и самый интенсивный теплообмен, наблюдается для наночастиц пластинчатой формы (m = 5.7). Наибольший поворот изотерм в сторону задней поверхности конуса также отмечается для наночастиц пластинчатой формы. Этот результат подтверждается и формулой (7). Наночастицы пластинчатой формы имеют более высокую теплопроводность.
Рис. 12.
Изотермы вынужденной конвекции для наножидкости Cu–вода вокруг конуса при φ = 0.08 и Pe = 150 и разных форм наночастиц: (а) ‒ сферическая, (б) ‒ “кирпич”, (в) ‒ цилиндрическая, (г) ‒ пластинчатая; вертикальные линии – длины изотерм.

На рис. 13 показано изменение среднего числа Нуссельта в зависимости от объемной доли твердого вещества вдоль цилиндра при выбранных условиях. С увеличением φ от 0 до 0.08 влияние формы наночастиц становится более заметным. Кроме того, добавление наночастиц в виде пластинок (m = 5.7) приводит к самой высокой интенсивности теплообмена. Наименьшая интенсивность теплообмена получена для сферической формы наночастиц. Таким образом, можно сделать вывод, что форма наночастиц оказывает существенное влияние на интенсивность теплообмена при обтекании тел.
ЗАКЛЮЧЕНИЕ
Влияние числа Пекле (25 ≤ Pe ≤ 150) и объемной доли частиц (0 ≤ φ ≤ 0.08) на характеристики течения и теплообмена при обтекании наножидкостью усеченного конуса исследовано в двумерном стационарном режиме с использованием различных наночастиц. Представлены картины линий тока, изотерм, графики изменений поверхностной завихренности, длин рециркуляции, коэффициента сопротивления, локального и среднего чисел Нуссельта. Разработаны корреляции для таких параметров, как Nuav, CD и ωs, max, в виде функций от Pe и φ. По результатам исследования можно сделать следующие выводы.
• Течение и теплообмен сильно зависят от числа Пекле и объемной доли твердого вещества.
• Значения длины следа, максимальной поверхностной завихренности и среднего числа Нуссельта при определенных Pe и φ выше для Cu–вода, чем для CuO–вода и Al2O3–вода.
• При фиксированном φ увеличение Pe создает более высокие градиенты скорости и температуры вокруг тела.
• Самый высокий коэффициент сопротивления получен для наножидкости Al2O3–вода.
• Тип наночастиц является ключевым фактором в интенсификации теплообмена. А именно, добавление наночастиц Cu в жидкость обеспечивает увеличение интенсивности теплообмена на 31.74% при Pe = 25 и φ = 0.08.
• Наночастицы пластинчатой формы позволяют получить наиболее высокую интенсивность теплообмена по сравнению с другими исследованными формами.
Таким образом, выбор типа и формы наночастиц играет важную роль при оценке характеристик потока и теплообмена наножидкостей при свободной и комбинированной конвекции вокруг обтекаемых тел.
Список литературы
Pope S.B. Turbulent Flows. Cambridge, UK: Cambridge University Press, 2000. 771 p.
Wilcox D.C. Turbulence Modeling for CFD. 3rd ed. California: DCW Industries, 2006. 515 p.
Versteeg H.K., Malalasekera W. An Introduction to Computational Fluid Dynamics. The Finite Volume Method. 1st ed. England: Longman, 2007. 257 p.
Sagaut P. Large Eddy Simulation for Incompressible Flows: An Introduction. Springer, 2006. 556 p.
Igarashi T. Heat Transfer from a Square Prism to an Air Stream // Int. J. Heat Mass Transfer. 1985. V. 28. P. 175.
Lyn D.A., Einav S., Rodi W., Park J.H. A Laser-Doppler Velocimetry Study of Ensemble-averaged Characteristics of the Turbulent near Wake of a Square Cylinder // J. Fluid Mech. 1995. V. 304. P. 285.
Bouris D., Bergeles G. 2D LES of Vortex Shedding from a Square Cylinder // J. Wind Eng. Ind. Aerodyn. 1999. V. 80. P. 31.
Parnaudeau P., Carlier J., Heitz D., Lamballais E. Experimental and Numerical Studies of the Flow over a Circular Cylinder at Reynolds Number 3900 // Phys. Fluids. 2008. V. 20. 085101.
Breuer M., Bernsdorf J., Zeiser T., Durst F. Accurate Computations of the Laminar Flow Past Square Cylinder-based on Two Different Methods: Lattice-Boltzman and Finite-volume // Int. J. Heat Fluid Flow. 2000. V. 21. P. 186.
Darekar R.M., Sherwin S.J. Flow Past a Square-section Cylinder with a Wavy Stagnation Face // J. Fluid Mech. 2001. V. 426. P. 263.
Turki S., Abbassi H., Ben Nasrallah S. Effect of the Blockage Ratio on the Flow in a Channel with a Built-in Squarecylinder // Comput. Mech. 2003. V. 33. P. 22.
Turki S., Abbassi H., Ben Nasrallah S. Two-dimensional Laminar Fluid Flow and Heat Transfer in a Channel with Abuilt-in Heated Square Cylinder // Int. J. Therm. Sci. 2003. V. 42. P. 1105.
Bouaziz M., Kessentini S., Turki S. Numerical Prediction of Flow and Heat Transfer of Power-law Fluids in a Planechannel with a Built-in Heated Square Cylinder // Int. J. Heat Mass Transfer. 2010. V. 53. P. 5420.
Liu M.S., Lin M.C.C., Huang I.T., Wang C.C. Enhancement of Thermal Conductivity with CuO for Nanofluids // Chem. Eng. Technol. 2006. V. 29. P. 72.
Dhiman A., Hasan M. Flow and Heat Transfer over a Trapezoidal Cylinder: Steady and Unsteady Regimes // Asia-Pac. J. Chem. Eng. 2013. V. 8. P. 433.
Dhiman A., Verma S., Ghosh R. Laminar Momentum and Heat Transfer in a Channel with a Built-in Tapered Trapezoidal Bluff Body // Heat Transfer-Asian Res. 2015. V. 44. P. 324.
Parveez M., Dhiman A., Rasool T. Transition to Periodic Unsteady and Effects of Prandtl and Richardson Numbers on the Flow Across a Confined Heated Trapezoidal Cylinder // J Braz. Soc. Mech. Sci. 2015. V. 37. P. 1291.
Verma V.K., Dhiman A. A Comparative Study on Cross-buoyancy Mixed Convection around Expanded and Tapered Trapezoidal Bluff Bodies // Proc. P. I. Mech. Eng. E.-J. Pro. 2017. V. 231. P. 513.
Dhiman A., Ghosh R. Computer Simulation of Momentum and Heat Transfer Across an Expanded Trapezoidal Bluff Body // Int. J. Heat Mass. Transfer. 2013. V. 59. P. 338.
Parveez M., Dhiman A.K., Harmain G.A. Influence of Height Ratio on Flow and Heat Transfer around Trapezoidal Geometry (a Generic Sharp-edged Body) Covering Transition to Periodic Flow // Int. J. Heat Mass Transfer. 2018. V. 124. P. 1285.
Parveez M., Dhiman A., Harmain G.A. Aiding Buoyancy Driven Flow and Heat Transfer Features of Converging and Diverging Trapezoidal Cylinders // Sådhanå. 2018. V. 43. P. 118.
Dhiman A., Ghosh R., Baranyi L. Hydrodynamic and Thermal Study of a Trapezoidal Cylinder Placed in Shear-thinning and Shear-thickening Non-Newtonian Liquid Flows // Int. J. Mech. Sci. 2019. V. 157–158. P. 304.
Venugopal A., Agrawal A., Prabhu S.V. Influence of Blockage and Upstream Disturbances on the Performance of a Vortex Flowmeter with a Trapezoidal Bluff Body // Measurement. 2010. V. 43. P. 603.
Bouakkaz R., Salhi F., Khelli Y., Quazzazi M., Talbi K. Unconfined Laminar Nanofluid Flow and Heat Transfer around a Rotating Circular Cylinder in the Steady Regime // Arch. Thermodyn. 2017. V. 38. № 2. P. 3.
Brinkman H.C. The Viscosity of Concentrated Suspensions and Solutions // J. Chem. Phys. 1952. V. 20. P. 571.
Etminan-Farooji V., Ebrahimnia-Bajestan E., Niazmand H., Wongwises S. Unconfined Laminar Nanofluid Flow and Heat Transfer around a Square Cylinder // Int. J. Heat Mass Transfer. 2012. V. 55. P. 1475.
Bouazizi L., Turki S. Numerical Investigation of CuO–Water Nanofluid Flow and Heat Transfer Across a Heated Square Cylinder // Int. J. Fluid Mach. Systems. 2016. V. 9. № 4. P. 382.
Rajendra S., Dhinakaran R.S. Study of Heat Transfer from a Square Cylinder Utilizing Nanofluids with Multiphase Modeling Approach // Materials Today: Proc. 4. 2017. P. 10069.
Sarkar S., Ganguly S., Biswas G. Mixed Convective Heat Transfer of Nanofluids Past a Circular Cylinder in Cross Flow in Unsteady Regime // Int. J. Heat Mass Transfer. 2012. V. 55. № 17–18. P. 4783.
Sarkar S., Suvankar G., Dalal A. Buoyancy Driven Flow and Heat Transfer of Nanofluids Past a Square Cylinder in a Vertically Upward Flow // Int. J. Heat Mass Transfer. 2013. V. 59. P. 433.
Sivakumar P., Bharti R.P., Chhabra R.P. Steady Flow of Power-law Fluids Across an Unconfined Elliptical Cylinder // Chem. Eng. Sci. 2007. V. 62(6). P. 1682.
Dennis S.C.R., Young P.J.S. Steady Flow Past an Elliptic Cylinder Inclined to the Stream // J. Eng. Math. 2003. V. 47(2). P. 101.
Selvakumar R.D., Dhinakaran S. Forced Convective Heat Transfer of Nanofluids around a Circular Bluff Body with the Effects of Slip Velocity Using a Multi-phase Mixture Model // Int. J. Heat Mass Transfer. 2017. V. 106. P. 816.
Selvakumar R.D., Dhinakaran S. Heat Transfer and Particle Migration in Nanofluid Flow around a Circular Bluff Body Using a Two-way Coupled Eulerian-Lagrangian Approach // Int. J. Heat Mass Transfer. 2017. V. 115. P. 282.
Valipour M.S., Ghadi A.Z. Numerical Investigation of Fluid and Heat Transfer around a Solid Circular Cylinder Utilizing Nanofluid // Int. Commun. Heat Mass Transfer. 2011. V. 38(9). P. 1296.
Xuan Y., Roetzel W. Conceptions for Heat Transfer Correlation of Nanofluids // Int. J. Heat Mass Transfer. 2000. V. 43(19). P. 3701.
Duangthongsuk W., Wongwises S. Measurement of Temperature-dependent Thermal Conductivity and Viscosity of TiO2−water Nanofluids // Exp. Thermal Fluid Sci. 2009. V. 33(4). P. 706.
Pak B.C., Cho Y.I. Hydrodynamic and Heat Transfer Study of Dispersed Fluids with Submicron Metallic Oxide Particles // Exp. Heat Transfer. 1998. V. 11(2). P. 151.
Xuan Y., Li Q. Investigation on Convective Heat Transfer and Flow Features of Nanofluids // J. Heat Transfer. 2003. V. 125(1). P. 151.
Brinkman H.C. The Viscosity of Concentrated Suspensions and Solutions // J. Chem. Phys. 1952. V. 20(4). P. 571.
Sheikholeslami M., Sadoughi M.K. Mesocopic Method for MHD Nanofluid Flow Inside a Porous Cavity Considering Various Shapes of Nanoparticles // Int. J. Heat Mass Transfer. 2017. V. 113. P. 106.
Timofeeva E.V., Routbort J.L., Singh D. Particle Shape Effects on Thermophysical Properties of Alumina Nanofluids // J. Appl. Phys. 2009. V. 106(1). 014304.
Fluent 6.3 User’s Guide. Lebanon, New Hampshire: Fluent Inc., 2006.
Sohankar A., Norberg C., Davidson L. Low-Reynolds-number Flow around a Square Cylinder at Incidence: Study of Blockage, Onset of Vortex Shedding and Outlet Boundary Condition // Int. J. Numer. Methods Fluids. 1998. V. 26(1). P. 39.
Paliwal B., Sharma A., Chhabra R.P., Eswaran V. Power Law Fluid Flow Past a Square Cylinder: Momentum and Heat Transfer Characteristics // Chem. Eng. Sci. 2003. V. 58. № 23–24. P. 5315.
Gambit User’s Guide. Lebanon, New Hampshire: Fluent Inc., 2006.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур





