Теплофизика высоких температур, 2021, T. 59, № 6, стр. 925-947

ВВЕДЕНИЕ

В гидродинамике хорошо известно [1–8], что наряду с непрерывными решениями, основных уравнений сплошной среды, большую роль играют разрывные решения. В таких решениях давление, плотность и скорость движения или их производные, определяющие состояния среды, испытывают скачок на некоторой стационарной или движущейся поверхности. Существуют слабые и сильные разрывы. Часто первоначальный разрыв распадется на серию движущихся разрывов [1, 3, 5]. Ограничимся газовыми средами, обладающими конечной электропроводимостью и рассмотрим влияние внешнего, постоянного магнитного поля на изменение параметров сред в слабых и сильных разрывах, включая устойчивость плоского фронта ударной волны. Анализ устойчивости ударных волн во многом опирается на уравнение состояния плотных сред и поведение адиабаты Гюгонио, в изучение которых В.Е. Фортов внес значительный вклад [4].

Напомним основные методы анализа соотношений между параметрами среды на разрывах и определения скорости перемещения разрывов. Интенсивность скачков величин в точке некоторой поверхности для функции $f$ можно характеризовать величинами (ось направлена по внешней нормали к поверхности):

Здесь х_ф – координата поверхности разрыва; первые члены в обоих выражениях берутся за фронтом разрыва, но бесконечно близко к нему.

Напомним способ определения типа скачка:

Согласно (2) в слабых разрывах претерпевают только скачки производных параметров состояния. На рис. 1 показано изменение давления среды на поверхности слабого разрыва. Аналогичные разрывы может претерпевать плотность и скорость течения.

СЛАБЫЕ РАЗРЫВЫ В МАГНИТНОМ ПОЛЕ

Далее рассмотрим влияние внешнего, постоянного магнитного поля, на распространение разрывов, считая, что в декартовой системе координат движение происходит в направлении оси x, магнитное полое направлено по оси y или z. Влияние внешнего магнитного на характеристики разрывов связано с тем, что магнитное поле может приводить к генерации электрического тока. Наличие электрического тока может приводить к возникновению силы Ампера, и к джоулеву нагреву. Однако появление самого тока зависят от ориентации магнитного поля, вектор скорости потока и проводимости среды.

Действительно при движении проводящей среды в поперечном магнитном поле возникает электрический ток $j$

Здесь $E$ – напряженность электрического поля, $B$ – индукция магнитного поля, $\sigma $ – электропроводность среды. Значение напряженности электрического поля зависит от способа замыкания электрического тока. Часто при движении разрыва в канале электрическое поле выражают через про-изведение $U \times B$и электрический ток $j$ записывают в виде Здесь $k$($0 \leqslant k \leqslant 1$) – носит название коэффициента нагрузки. Режим $k = 1,$ $j = 0$ называется режима холостого хода, $k = 0$ – режим короткого замыкания, в котором ток максимален.

В любом режиме согласно уравнениям Максвелла электрический ток удовлетворяет уравнению ${\text{div}}j = 0.$

Следовательно, на слабом скачке имеет место соотношение

Рассмотрим слабый разрыв в магнитном поле, $B = (B,0,0),$ когда оно коллинеарно скорости движения среды $U = (U(x),0,0).$ В таком разрыве электрический ток отсутствует (сила Ампера и джоулев нагрев отсутствуют) и движение является изоэнтропийным. Скорость распространения такого слабого разрыва можно определить, рассмотрев сплошную среду, описание которой проводится в рамках уравнений Эйлера. Задача о распространение слабого разрыва решается известным образом [1], используя который выразим производную от давления через производную от плотности

где ${{a}_{{s0}}} = \sqrt {\mathop {\left( {\frac{{\partial P}}{{\partial \rho }}} \right)}\nolimits_S } $ – скорость звука.

Из системы уравнений неразрывности и движения для слабых разрывов плотности и скорости среды в проекции на ось х получаем следующие уравнения

Здесь $U = (U(x),0,0)$ – скорость движения среды и учтено равенство (7).

Если сама функция f непрерывна, то ее приращение на границе разрыва имеет вид

Используя (10) и выражая разрывы производных по времени через скачки производных по координатам, получаем

Здесь ${{d{{x}_{{\text{ф}}}}} \mathord{\left/ {\vphantom {{d{{x}_{{\text{ф}}}}} {dt}}} \right. \kern-0em} {dt}}$ – скорость распространения фронта в лабораторной системе координат.

Введем скорость, с которой фронт скачка движется относительно потока (скорость движения слабого разрыва относительно жидкости)

Тогда справедливо следующее равенство

Таким образом, систему уравнений (8), (9) для производных скачков плотности ρ и скорости U можно представить в виде

Однородная система уравнений (11), (12) имеет нетривиальное решение, если выполняется условие

Таким образом, когда магнитное поле, $B = (B,0,0)$ коллинеарно скорости движения среды $U = (U(x),0,0)$ и электрический ток отсутствует, слабый разрыв плотности (давления) и скорости движется относительно газа со скоростью звука а₀.

При отсутствии электрического тока могут существовать течения, в которых распространяется слабый скачек энтропии:

Как следует из (14), энтропийный разрыв распространяется со скоростью движения среды, что характерно и для волн малых возмущений [1].

Теперь рассмотрим слабый разрыв, который находится в постоянном магнитном поле $B = (0,0,B),$ перпендикулярном скорости движения среды $U = (U(x),0,0).$ Следовательно, при $k \ne 1$ в таком разрыве существует электрический ток, приводящий к возникновению силы Ампера ${{j}_{y}}{{B}_{0}}$ и джоулева нагрева ${{j_{y}^{2}} \mathord{\left/ {\vphantom {{j_{y}^{2}} \sigma }} \right. \kern-0em} \sigma }$ (движение уже не является изоэнтропийным). Однако для слабых разрывов выполняются условия

поэтому уравнения (6) принимают прежний вид

В поперечном магнитном поле снова можно воспользоваться соотношением (7) и свести задачу о скорости распространения слабого разрыва к предыдущей и заключить, что слабый разрыв плотности (давления) и скорости движется относительно газа со скорость звука а₀, а энтропийный разрыв распространяется со скоростью движения среды.

Известно [9‒12], что для анализа ряда явлений удобно использовать инварианты Римана:

удовлетворяющие следующей системe уравнений

Используя уравнения (17), можно показать появление разрывов – образование ударных волн. Существуют частные случаи решения системы уравнений (17), когда один из инвариантов Римана постоянен во всей области решения задач:

Для идеального газа, тогда уравнение адиабаты и адиабатическая скорость звука принимают вид

где γ ‒ показатель адиабаты. Тогда инварианты Римана принимают значения

Зависимость инвариантов Римана, а, следовательно, скорости $U = F\left[ {x + \left( {U + {{a}_{{s0}}}} \right)t} \right]$ и давления, от координаты и времени определяется из начальных и граничных условий.

Для частного случая случая неоднородной среды, когда выполняются условия

На рис. 2 представлена качественная схема образования крутого фронта или ударной волны. На рис. 2a показан профиль скорости среды в начальный момент времени, на рис. 2б стрелками показаны направления скоростей движения различных точек волны в этот же момент времени (размеры стрелок демонстрируют различие в скоростях движения различных точек волны). На рис. 2в показан случай, когда две волны с разными скоростями выходят из разных точек и догоняют одна другу. Действительно, пусть скорость движения волн зависит от координаты x (рис. 2б) так, что в точке 1 максимума амплитуды возмущения (рис. 2в) и максимальная скорость движения волны, а в точке 2 минимума амплитуды возмущения и минимальная скорость движения волны. Тогда с течением времени точка 1, волны с высокой амплитудой, и точка 2 волны, низкой амплитуды, будут смещаться к точке к A. Следовательно, с течением времени может наступить момент, когда область с максимальной амплитудой “догонит” область с маленькой амплитудой (рис. 2в) ‒ получится практически вертикальный фронт волны. На рис. 2в показаны траектории движения характеристик, выходящих в момент времени t = 0 из точек 1 и 2 и последующее пересечение их в точке x_r в момент времени t_r, а на рис. 2г показано превращение в момент времени t_r непрерывного профиля, изображенного на рис. 2a, в разрывный.

Представленная на рис. 2г разрывная зависимость давления от координат является идеализацией реальной картины. Вязкость и теплопроводность, роль которых особенно велика именно при больших градиентах скорости и температуры, приводят к “сглаживанию” решений. Тем не менее, рассмотренный пример демонстрирует образование разрыва и показывает, что для рассмотрения непрерывного перехода от состояния перед фронтом к состоянию за ним необходимо учитывать вязкость и теплопроводность среды.

В постоянном магнитном поле $B = (0,0,B),$ перпендикулярном скорости движения среды $U = (U(x),0,0)$ при $k \ne 1$ системы уравнений для функций Римана учитывает силу Ампера и принимает вид

Из (20) следует, что в магнитном поле функции ${{J}_{ + }},{{J}_{ - }}$ не являются инвариантами вдоль характеристик $U + {{a}_{{s0}}}$ и $U - {{a}_{{s0}}}.$ Использую разобранную выше аналогию с нелинейности скорости звука, заключаем (20), что сила Ампера может приводить к образованию разрыва.

Соответственно, протекание электрического тока и вызванное им джоулево тепловыделение приводит к изменению энтропии

Влияние магнитного поля на инварианты Римана плазме бесконечной проводимостью обсуждается в работах [5, 10, 11].

СИЛЬНЫЕ РАЗРЫВЫ. УДАРНЫЕ ВОЛНЫ

Типы сильных разрывов. Как было показано ранее сильными разрывами являются плоскости в координатном пространстве, на которых претерпевают разрывы свойства среды или их функции. Рассмотрим влияние внешнего постоянного магнитного поля на сильные разрывы в газовых средах, обладающие конечной электропроводимостью при высоких температурах, Примерами сильных разрывов являются: граница раздела плотностей двух жидкостей или газов, тангенциальный разрыв скоростей, ударные волны, детонационные и ионизирующие волны.

Рассмотрим сильный разрыв, находится в постоянном внешнем магнитном поле $B = (0,0,B),$ перпендикулярном скорости движения среды $U = (U(x),0,0)$ и, следовательно, при $k \ne 1$ существует электрический ток $j(0, - {{j}_{y}},0).$ В этом случае следует учесть силу Ампера и джоулев нагрев (движение является не изоэнтропийным). В проводящих электрический ток средах с постоянным внешним магнитным полем анализ сильных разрывов проводится в рамках полной системы уравнений неразрывности, движения и энергии, записанных в дивергентном виде. Иногда уравнение энергии удобно представить через полную удельную энтальпию $h* \equiv h + {{{{U}^{2}}} \mathord{\left/ {\vphantom {{{{U}^{2}}} 2}} \right. \kern-0em} 2}$ системы [13‒15]:

где $i(1,0,0)$ ‒ единичный базисный вектор в декартовой системе координат, $\tilde {\Pi }$ ‒ тензор

Система уравнений должна быть дополнена уравнением состояния

Пусть фронт, изображенный на рис. 3, движется с постоянной скоростью, тогда в системе координат, движущейся с фронтом волн в положительном направлении оси x. Течение в этой системе стационарно и все производные по времени t выпадают. Тогда стационарной системы уравнений (20) с учетом бесконечно тонкого фронта скака, получаем

В таких случаях для сильных разрывов на поверхности волны получим известные следующие соотношения [1, 2].

Из уравнения неразрывности следует сохранение потока массы

Из уравнений изменения импульса следуют сохранения потоков импульса

Поверхность, на которой претерпевает разрыв только плотность среды называется, контактным разрывом.

Из уравнения энергии следует сохранение потока энергии

Из (23) следует сохранение для потоков массы

На основе представленных соотношений можно дать классификацию сильных разрывов.

Если скорость вдоль оси х отсутствует $\left( {{{U}_{{x,1}}} = } \right.$ $\left. { = {{U}_{{x,2}}} = 0} \right)$ то из уравнения (26) получаем, что давления за фронтом и перед ним должны равняться $\left( {{{P}_{1}} = {{P}_{2}}} \right).$ При этом возможны два случая:

а) контактный разрыв, когда тангенциальные скорости равны нулю ${{U}_{y}} = {{U}_{z}} = 0,$ а плотности не равны ${{\rho }_{1}} \ne {{\rho }_{2}}.$ Такой разрыв разделяет две покоящиеся, не перемешивающиеся среды с разными плотностями;

б) Тангенциальный разрыв возникает, когда одна из тангенциальных составляющих скорости претерпевает разрыв ${{U}_{{y,1}}} \ne {{U}_{{y,2}}},$ т.е. существуют две, движущиеся с разными скоростями в одном направлении среды.

Если скорости сред в направлении оси х не равны нулю $\left( {{{U}_{{x,1}}} \ne 0,\,\,{{U}_{{x,2}}} \ne 0} \right),$ то существует сильный разрыв, называемый ударной волной. Он сопровождается потоками массы, импульса и энергии в направлении нормали к фронту волны,

Соотношения на фронте ударной волны. Используя систему уравнений (25)‒(29), рассмотрим поверхность сильного разрыва, на которой тангенциальные составляющие скоростей равны нулю ${{U}_{y}} = {{U}_{z}} = 0.$

Из уравнения неразрывности следует условие сохранения потока массы

где ${{v}_{1}} \equiv {1 \mathord{\left/ {\vphantom {1 {{{\rho }_{1}}}}} \right. \kern-0em} {{{\rho }_{1}}}}$ и ${{v}_{2}} \equiv {1 \mathord{\left/ {\vphantom {1 {{{\rho }_{2}}}}} \right. \kern-0em} {{{\rho }_{2}}}}$ ‒ удельные объемы среды за фронтом и перед ним, $G = {\text{const}}$ – расход газа.

Из уравнений движения остается только одно ‒ уравнение

Или в другой эквивалентной форме

где ${{{\text{M}}}_{1}}$ – число Маха ударной волны, определенное по скорости звука в среде перед фронтом волны, $\gamma $ ‒ показатель адиабаты для этой среды.

Так как ${{j}^{2}}$ не зависит от P и v, то на плоскости P–v уравнение (28) представляет собой прямую линию а, идущую из точки 1.

Из уравнения энергии следует

Кривой б на рис. 4 в координатах P–v изображена зависимость $h = h\left( {P;v} \right),$ выходящая из точки, соответствующей состоянию перед волной (точка 1). Проведем в координатах P,v из точки 1 прямую линию, соответствующую уравнению (33). Пересечение линии а и кривой б дают состояние системы после ударной воны. Таким образом, построив P–v-диаграмму для ударной волны и зная параметры системы перед фронтом, т.е. скорость движения фронта, можно определить параметры системы за ним. Наоборот, задавая давление за фронтом давление и плотность газа перед фронтом можно определить скорость движения фронта.

Кривая, описываемая уравнением (34), называется адиабатой Гюгонио (или ударной адиабатой). Ударная адиабата отличается от реальной адиабаты, в которой энтропия не меняется $\left( {s = const} \right).$ Однако, как это будет показано далее, изменение энтропии в процессе б незначительно и в первом приближении ее можно назвать адиабатой.

На рис. 4. в координатах P–v изображены характерные зависимости, вытекающие их уравнений (36), (37): а ‒ прямая, описываемая уравнением (36); б ‒ адиабата Гюгонио, вытекающая из уравнения сохранения потока энергии. Вспомогательные линии: в ‒ реальная адиабата, выходящая из точки 1; r ‒ асимптота адиабаты Гюгонио, построенная; 1 и 2 ‒ состояния системы до фронта и после него.

Можно показать, что касательные к ударной адиабате соответствуют локальной скорости звука. Обратим внимание на расположение касательных к ударной адиабате (наклон линий) в ее начальной и конечной точках. Из рис. 4 видно, что имеют место неравенства

которые означают, что ударная волна движется со сверхзвуковой скоростью, а скорость среды за фронтом меньше локальной скорости звука.

Для идеального газа можно получить простые соотношения между различными величинами на фронте ударной волны.

Для энтальпии идеального газа

из (35)‒(37) находим

Изменение энтропии во фронте ударной волны. Ранее были установлены изменения скорости, плотности и давления в ударной волне, а теперь рассмотрим изменения энтальпии и энтропии во фронте ударной волны:

Здесь учтены известныe термодинамическиe тождествa:

Удельный объем за фронтом волны можно определить разложить в ряд Тейлора по изменению давления. Если ограничиться третьим членом ряда, получим

Используя вышеприведенные результаты, находим изменение энтропии в ударной волне пропорционально кубу изменения давления

Уравнение (43) свидетельствует о том, что ударная волна с уменьшением ее интенсивности (${{P}_{2}} \to {{P}_{1}}$) стремится к волне, в которой энтропия не изменяется, а ее скорость равна скорости звука в газе

т.е. превращается в акустическую волну.

Обратим внимание

1. Если повышать давление за фронтом, скорость волны ${{U}_{{x,1}}}$ увеличивается.

2. Сжать вещество нельзя плотнее, чем в ${{\left( {\gamma + 1} \right)} \mathord{\left/ {\vphantom {{\left( {\gamma + 1} \right)} {\left( {\gamma - 1} \right)}}} \right. \kern-0em} {\left( {\gamma - 1} \right)}}$ раз, так как

Для γ = 5/3

Температура за фронтом может увеличиваться неограниченно пропорционально давлению Р. При этом рост температуры приводит образованию за фронтом ударной волны плазмы, способной проводить электрический ток и обеспечивать воздействие магнитного поля на течение за фронтом ударной волны. Следовательно, ударные волны ‒ мощный источник получения вещества при высоких температурах. Следует учитывать, что в интенсивных ударных волнах и, соответственно, при высоких плотностях ударносжатого газа следует учитывать эффекты неидеальности в уравнении состояния $h = h(P,\rho ,T).$

На рис. 5 показаны экспериментальные данные и численные расчеты ударной адиабаты для дейтерия, которые наглядно демонстрируют роль неидеальности плазмы за фронтом ударной волны. В экспериментах [17] были получены значения $\frac{{{{\rho }_{2}}}}{{{{\rho }_{1}}}},$ превышающие предельное значение для идеального газа 4. При больших интенсивностях ударной волны и, следовательно, более высоких температурах плазмы роль эффектов неидеальности плазмы ослабевает и в расчетах $\mathop {\lim }\limits_{{{P}_{2}} \to \infty } \frac{{{{\rho }_{2}}}}{{{{\rho }_{1}}}} \to 4.$

Более детально о расчете ударных адиабат воздуха можно найти в работе [21].

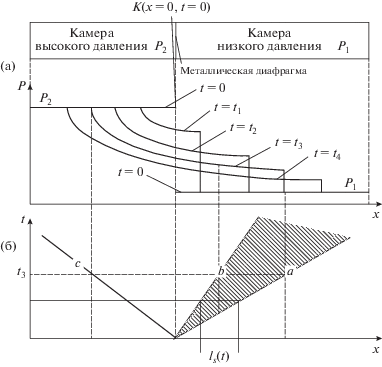
Генерация ударных волн и слабые разрывы. Кратко остановимся на способе получения ударных волн. Среди всех способов остановимся на методе генерации ударных волн в ударных трубах, состоящих из двух камеры высокого и низкого давлений, разделенных металлической диафрагмой. Такие системы эффективно используются для исследования термодинамических свойств плотных газов при высоких температурах среды. Камеры могут заполняться различными газами под разным давлением $\left( {{{P}_{2}} > {{P}_{1}}} \right).$ После разрыва диафрагмы образуется ударная волна, которая распространяется по камере низкого давления, оставляя за собой область ударного сжатого газа и волну разряжения.

Заштрихованная на рис. 6 область ab в момент времени t₃ находящаяся между фронтом ударной волны, движущейся со скоростью U_a в положительном направлении оси x, и контактным разрывом, движущимся со скоростью U в положительном направлении оси x, содержит ударно сжатый газ, находящийся в камере низкого давления; область bc в момент времени t₃, находится между фронтом контактным разрывом и фронтом волны разряжения, движущимся со скоростью звука a_s в отрицательном направлении оси x, и содержит толкающий ударную волну газ.

Кроме ударных труб для генерации ударных волн используются взрывы конденсированного взрывчатого вещества и электрические разряды в газе, жидкости или твердом теле.

Поскольку степень сжатия вещества в отдельной ударной волне ограничена (45), то для получения высоких плотностей используется серия ударных волн, в которой осуществляется последовательное сжатие вещества. Напомним, что без магнитного поля и протекания электрического тока при ${{P}_{2}} \to {{P}_{1}}$ ударная волна вырождается в акустическую. Поэтому все соотношения для ударных волн в пределе стремятся к соотношению для акустических волн. Поскольку для ионизующих ударных волн холодный газ перед фронтом волны является не проводящим, магнитное поле не оказывает влияние на среду перед фронтом.

ГРАНИЦЫ УСТОЙЧИВОСТИ УДАРНЫХ ВОЛН С МАГНИТНЫМ ПОЛЕМ И БЕЗ НЕГО

За фронтом волны при высоких температурах среда (плазма) обладает конечной проводимостью, и в постоянном поперечном магнитном поле возникает электрический ток, величина которого зависит от магнитного поля и способов замыкания тока. При коэффициенте нагрузки k < 1, согласно уравнению (5), ударная волна превращается в МГД генератор и затухает за счет отбора энергии во внешнюю нагрузку [22]. Торможение потока за фронтом ударной волны может приводить к образованию вторичной ударной волны [22, 23], при коэффициенте нагрузки 1 < k возникает ускорительный режим, в котором ударная волна и газ за ее фронтом ускоряются. Изменение магнитного поля за фронтом ударной волны, вызванное протеканием электрического тока зависит от магнитного числа Рейнольдса [6‒8]

Здесь $0 \leqslant {{l}_{s}}(t)$ ‒ размеры области ударно нагретого газа за фронтом волны, обладающей конечной электропроводностью (рис. 5). Размер области ${{l}_{s}}(t)$ возрастет по мере движения ударной волны. В большинстве рассматриваемых в данном обзоре случаев ${{\operatorname{Re} }_{m}} \ll 1$ и играет роль только внешнее магнитное поле.

Для целого ряда технических приложений важным является сохранение плоского фронта ударной волны и однородной среды за ним, поэтому далее остановимся на проблеме устойчивости плоского фронта ударной волны.

Как показывают эксперименты [24, 25], фронт волны может искривляться, испытывать колебания и даже распадаться на два сильных разрыва. Природу этих явлений можно понять, исследуя устойчивость фронта ударной волны. В анализе можно пренебречь вязкостью и теплопроводностью, которые не могут приводить к неустойчивости, а лишь обеспечить затухание возмущений. Поэтому без магнитного поля неустойчивость может быть обусловлена лишь процессами на границе среды – на фронте ударной волны. В магнитном поле и протекании электрического тока следует учитывать наличие объемных источников тепловыделения, когда акустические волны усиливаются за счет рэлеевского механизма, либо за счет флуктации силы Ампера [7]. Сначала рассмотрим процессы, оказывающие влияние на устойчивость ударной волны без учета магнитного поля, т.к. они нам понадобятся при анализе роли поперечного магнитного поля и, следовательно, протекания электрического тока.

Границы устойчивости плоской ударной волны без магнитного поля. Для случая без магнитного поля, поведение ударной волны зависит от ее интенсивности и вида адиабаты Гюгонио – производной ${{\left( {\frac{{\partial P}}{{\partial v}}} \right)}_{H}}.$ Известно, что в зависимости от этих параметров могут существовать области областей устойчивости, неустойчивости и генерации колебаний. В области устойчивости возмущения затухают по закону $\xi \sim {{t}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}$ [26], в области неустойчивости возникает так называемая, структурная неустойчивость [25, 26].

Задача об устойчивость фронта ударной волны (рис. 6) была решена С.П. Дьяковым [26], дальнейшие обсуждения и уточнения этой задачи можно найти в работах [25, 27‒38]. Эксперимент, демонстрирующий влияние неустойчивости ударной волны на обтекания твердого тела можно увидеть в [39].

Поскольку фундаментальные результаты С.П. Дьякова нам понадобятся при анализе роли магнитного поля кратко воспроизведем их ниже. Когда ударная волна движется с постоянной скоростью, то исследования ее устойчивости можно провести, переходя в систему координат, связанную с фронтом волны, рассматривая эволюцию малых возмущений [36, 37]. При линеаризации системы уравнений сохранения потока массы, импульса и энергии, следует учитывать и возмущение скорости фронта волны, решая системы линеаризованных уравнений в областях перед и за фронтом и сшивая их на движущейся поверхности разрыва.

Фронт движется со скоростью большей скорости звука ${{U}_{{x,1}}} > {{a}_{{s0}}},$ а возмущения могут перемещаться только со скоростью звука, поэтому возмущения, наблюдаемые в области за фронтом, не могут оказывать на него никакого влияния, но могут оказывать влияние возмущения, находящиеся на поверхности фронта и перед ним. Качественный анализ показывает, что устойчивость ударных волн в первую очередь может быть связана с процессами во фронте ударной волны.

Представим малые возмущения за фронтом волны в виде

Аналогичные разложения можно написать и для среды перед фронтом. Тогда система решаемых уравнений должна состоять из системы линеаризованных уравнений сохранения массы, импульса и энергии за и перед фронтом волны.

Граничные условия для возмущений сводятся к ограниченности возмущений на бесконечности в любой момент времени. К линеаризованным уравнениям (31)‒(34) на фронте ударной волны добавляется кинематического условия, имеющего вид

где $\xi \left( t \right)$ ‒ поверхность фронта.

Решение задачи для вектора возмущений будем искать в виде плоской волны

Систему координат всегда можно направить так, чтобы волновой вектор имел только две проекции $k = \left( {{{k}_{x}};{{k}_{y}};0} \right).$ Здесь ${{k}_{x}}$ – проекция волнового вектора в направлении нормали к фронту волны; ${{k}_{y}}$ – проекция волнового вектора в поперечном направлении (${{l}_{y}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{k}_{y}}}}} \right. \kern-0em} {{{k}_{y}}}}$ – длина волны в поперечном направлении).

Из системы уравнений для малых возмущений после ряда преобразований [21] можно получить дисперсионное уравнение, содержащее проекции волнового вектора ${{k}_{x}},$ ${{k}_{y}}$ и частоту ω

Находя корни дисперсионного уравнения ${{k}_{{xj}}}$ и подставляя общее решение для возмущений

в граничные условия, находим характеристическое уравнение

На основе полученных корней характеристического уравнения $\omega = \omega \left( {{{k}_{y}},m} \right)$ можно судить об устойчивости ударной волны.

В отсутствии магнитного поля, параметрами задачи являются

где индекс H показывает, что производная берется по адиабате Гюгонио; $G$ ‒ поток массы через фронт.

В общем случае частота, найденная из уравнения (50), может содержать действительную и мнимую части: ${{\omega }_{n}}(m,{{k}_{v}}) = {{\omega }_{{nr}}}(m,{{k}_{v}}) + i{{\omega }_{{ni}}}(m,{{k}_{v}}),$ зависящие от волнового числа ${{k}_{y}}$ и параметра m (51), который обычно и определяет границы устойчивости ударной волны. При ${{\omega }_{{ni}}}(m,{{k}_{v}}) < 0$ возникают неустойчивости плоской ударной волны, связанные с особенностями адиабаты Гюгонио – параметра m, и называемые структурными [25]. На рис. 7 представлена диаграмма устойчивости ударных волн в зависимости от параметра m.

Таким образом анализ корней характеристического уравнения показывает:

1. Если параметр $m$ удовлетворяет условию

то плоская ударная волна устойчива, $\delta = {{{{\rho }_{2}}} \mathord{\left/ {\vphantom {{{{\rho }_{2}}} {{{\rho }_{1}}}}} \right. \kern-0em} {{{\rho }_{1}}}} > 1,$ ${{\operatorname{M} }_{2}} \equiv {{{{U}_{{x,2}}}} \mathord{\left/ {\vphantom {{{{U}_{{x,2}}}} {a_{{s0}}^{{\left( 2 \right)}}}}} \right. \kern-0em} {a_{{s0}}^{{\left( 2 \right)}}}}$ ‒ число Маха за фронтом. Асимптотический закон затухания возмущений имеет вид t^–3/2. Видно, что положение верхней границы области устойчивости зависит от интенсивности ударений волны – числа Маха. При малых интенсивностях ударных волн ${{{\text{M}}}_{2}} < {{{\text{M}}}_{{2{\text{cr}}}}} = \sqrt {{1 \mathord{\left/ {\vphantom {1 {\left( {1 + \delta } \right)}}} \right. \kern-0em} {\left( {1 + \delta } \right)}}} $ ${{\Gamma }_{{st + }}} > 0,$ при ${{{\text{M}}}_{2}} < {{{\text{M}}}_{{2cr}}}$ верхняя граница области устойчивости перемещается в отрицательную область ${{\Gamma }_{{st + }}} < 0,$ а нижняя остается неименной при всех значениях интенсивности ударной волны.

Для значения параметра $m = \frac{{1 - {\text{M}}_{2}^{2}\left( {1 + \delta } \right)}}{{1 + {\text{M}}_{2}^{2}\left( {\delta - 1} \right)}}$ затухание происходит по закону $\xi \sim {{t}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}.$

При $m < - 1$ или $m > 1 + 2{{{\text{M}}}_{2}}$ ударная волна неустойчива. В этих областях амплитуда возмущений возрастает по экспоненциальному закону.

2. Если имеет место соотношение

то возможно излучение звука колеблющимся разрывом, т.е. затухание отсутствует.

Суммируя вышесказанное и рис. 7, в зависимости от параметра m можно выделить несколько характерных областей поведения малых возмущений фронта ударной волны.

Поскольку квадрат потока массы всегда положителен ${{G}^{2}},$ то из (51) следует, что знак параметра $m$ определяется производной ${{\left( {{{\partial v} \mathord{\left/ {\vphantom {{\partial v} {\partial P}}} \right. \kern-0em} {\partial P}}} \right)}_{H}}{\kern 1pt} .$ Для идеального газа она всегда отрицательна, однако, как показывают эксперименты, существуют реальные вещества, у которых ${{\left( {{{\partial v} \mathord{\left/ {\vphantom {{\partial v} {\partial P}}} \right. \kern-0em} {\partial P}}} \right)}_{H}}$ может быть положительной (рис. 8). Если адиабата Гюгонио имеет вид, представленный на рис. 6б, то неустойчивая ударная волна расщепляется на две устойчивые ударные волны, идущие одна за д ругой. Более детальное обсуждения поведения неустойчивой ударной волны можно найти в [25‒30].

Если еще газ посмотреть на рис. 6, где представленные экспериментальные значения и численные расчеты ударных адиабат с учетом не идеальности сред при высоких плотностях за фронтом с ударной волны, то легко видеть возможности возникновения неустойчивости.

Как уже отмечалось неустойчивость ударных волн, связанная с поведением производной ${{\left( {\frac{{\partial P}}{{\partial \rho }}} \right)}_{H}}$ называется структурной неустойчивостью, поскольку в результате неустойчивости ударная волна может распадаться на несколько ударных волн [25] (рис. 9). Некоторые вопросы, связанные с нелинейными эффектами при развитии структурной неустойчивости ударных волн содержатся в обзоре [25].

Устойчивость плоской ионизующей ударной волны в магнитном поле. В предыдущем пункте была исследована устойчивость ударной волны в газах без магнитного поля, где структурная неустойчивость зависела от особенностей ударной адиабаты – производной ${{\left( {{{\partial v} \mathord{\left/ {\vphantom {{\partial v} {\partial P}}} \right. \kern-0em} {\partial P}}} \right)}_{H}}{\kern 1pt} .$ Теперь в дополнении к этому механизму рассмотрим влияние электрических и магнитных полей на устойчивость ударной волны, следуя работам [39‒44], и используя методы, изложенные в [44, 45]. В поперечном магнитном поле на поведение возмущений могут оказывать влияние как особенности адиабаты Гюгонио, приводящие к структурной неустойчивости и без магнитного поля [25, 26]; так и возмущения силы Ампера $\delta {{j}_{2}}{{B}_{0}}.$ Возмущения силы Ампера могут возникать за счет двух механизмов. Первый $\delta {{j}_{2}}{{B}_{0}} = {{\delta {{U}_{2}}{{\sigma }_{2}}B_{2}^{2}} \mathord{\left/ {\vphantom {{\delta {{U}_{2}}{{\sigma }_{2}}B_{2}^{2}} {{{\rho }_{2}}}}} \right. \kern-0em} {{{\rho }_{2}}}}$ связан с возмущением скорости плазмы $\delta {{U}_{2}}$ и приводит к затуханию возмущений за счет так называемой, магнитной вязкости $\frac{{{{\sigma }_{2}}B_{2}^{2}}}{{{{\rho }_{2}}}}.$ С учетом этого механизма магнитное поле влияет на вид асимптотического разложения при анализе структурной неустойчивости ударной волны. В области устойчивости, амплитуда возмущения может затухать гораздо быстрее, чем в отсутствии магнитного поля. Второй механизм $\delta {{j}_{2}}{{B}_{0}} = {{\delta {{\sigma }_{2}}{{U}_{2}}B_{2}^{2}} \mathord{\left/ {\vphantom {{\delta {{\sigma }_{2}}{{U}_{2}}B_{2}^{2}} {{{\rho }_{2}}}}} \right. \kern-0em} {{{\rho }_{2}}}}$ = ${{\sigma }_{2}}{{U}_{2}}B_{2}^{2}{{\left( {\frac{{\partial \ln {{\sigma }_{2}}}}{{\partial {{T}_{2}}}}} \right)}_{P}}\delta {{T}_{2}}{\text{/}}{{\rho }_{2}}$ соответствует известной в плазме перегревной неустойчивости [8], вызванной зависимостью электропроводности от температуры ${{\sigma }_{2}}({{T}_{2}}).$ Эта неустойчивость возникает в ударно нагретой плазме за фронтом волны и не связанна с особенностями адиабаты Гюгонио. Кроме того, при больших значениях параметра взаимодействия торможение потока плазмы может приводить к снижению скорости распространения фронта и к генерации вторичной ударной волны в нагретом газе [39‒44].

Поведение электрических и магнитных полей на поверхности разрыва. Пусть ударная волна, плоскость которой совпадает с плоскостью y0z, движется в электрическом и магнитном полях в положительном направлении оси x (рис. 3). Электропроводность холодного газа перед фронтом волны равна нулю, а за фронтом нагретый газ термически ионизован и способен проводить электрический ток. Следовательно, коэффициент электропроводности изменяется скачком при переходе через поверхность разрыва от значения ${{\sigma }_{1}} = 0$ перед фронтом до значения $\infty > {{\sigma }_{2}} > 0$ за ним.

Рассмотрим случай движения ударной волны во внешнем постоянном магнитном поле, которое лежит в плоскости ударной волны и направленно по оси z $\left( {{{В}_{x}} = {{В}_{y}} = 0} \right).$ За фронтом ударной волны движение проводящей среды приводит к генерации электрического поля и электрического тока. Ударные волны, в которых электропроводность за фротом волны достигает больших величин, называются ионизующими ударными волнами [5, 46‒48].

Электрическое поле $E$ и электрический ток $j$ связанны с индукцией магнитного поля $B$ соотношением (4) $j = \sigma {\text{(}}E + U \times B{\text{)}}{\text{.}}$ Если происходит замыкание электрического тока через внешнюю сеть, то приходим к закону Ома (5):

Если стенки канала непроводящие, приходим к режиму холостого хода. В этом случае связь между напряженностью электрического поля E, индукцией магнитного поля и скоростью движения газа сводится к соотношению,

В таком случае согласно уравнению Максвелла $\nabla \times B = {{\mu }_{0}}j$ на поверхности разрыва газодинамической ударной волны должны выполняться условия, связывающие возмущения магнитного и электрических полей и

Напомним, что символ $\left\{ А \right\}$ здесь, как и ранее, обозначает скачок величины А на поверхности разрыва.

Исследуем устойчивость плоского фронта ударной волны относительно малых смещений параметров зрелы от положения равновесия. Пренебрегая эффектом Холла (это связано с большим значением частоты столкновений частиц в среде за фронтом ударной волны), вязкостью и теплопроводностью. Последнее связано с преимущественным учетом длинноволновых возмущений. В рассматриваемой задаче ${{\operatorname{Re} }_{m}} \ll 1$ и играет роль только внешнее постоянное магнитное поле.

В системе координат, движущейся вместе с невозмущенным фронтом ударной волны, смещение фронта ударной волны от положения равновесия в направлении к нормали к плоскому фронту волны (${{n}_{0}}\left\{ {1,0,0} \right\}$) в начальный момент времени выражается в виде

Обозначим через n вектор, направленный по нормали к возмущенной поверхности разрыва, и τ ‒ вектор, лежащий в касательной плоскости. Их вид дается уравнениями

Ионизующая ударная волна движется со сверхзвуковой скоростью по отношению к среде, находящейся перед фронтом волны, поэтому возмущения газодинамических параметров, вызванные смещением плоского фронта от положения равновесия, в область перед фронтом волны не проникают. Возмущения электромагнитного поля туда проникают, но так как среда перед фронтом не проводящая, то электрические токи и в этой области не возникают, и не происходит возмущения газодинамических параметров. Ввиду отсутствия электрических токов в невозмущенном состоянии считается, что невозмущенные параметры среды не зависят от координат и времени. Кроме того, будем считать магнитное число Рейнольдса малым (пренебрегать влиянием индуцированного магнитного поля по сравнению с невозмущенным). Параметр МГД взаимодействия произволен.

Система уравнений (21), линеаризованная относительно малых возмущений в проводящей области, имеет вид:

Нижний индекс 1 относится к параметрам перед фронтом ударной волны, индекс 2 ‒ за фронтом. Возмущения электромагнитного поля в области перед фронтом ударной волны описываются системой уравнений Максвелла без учета тока смещения. Для линейных возмущений электрического тока джоулев нагрев не учитывается

Линеаризуя уравнения (36), (37) и (34) на поверхности разрыва, приходим к следующим соотношениям при координате х = 0

Здесь ${{\rho }_{1}}{{U}_{1}} = {{\rho }_{2}}{{U}_{2}} = G = {\text{const}}$ ‒ поток массы. Производная ${{\left( {\frac{{\partial P}}{{\partial v}}} \right)}_{H}}$ в последнем уравнении системы (58) берется вдоль ударной адиабаты. Из условия не протекания электрического тока в область, находящуюся перед фронтом ударной волны получим

Доказательство этого условия приводится в разделе “Ввывод граничного условия для электрического тока в задаче об устойчивости ударной волны в поперечном магнитном поле”. Откуда следует, что для бесконечно тонкого разрыва, электрический ток на возмущенном фронте ударной волны принимает следующее значение:

Системы уравнений для малых возмущений. Дисперсионное и характеристическое уравнения. Здесь проведем исследование устойчивость ударной волны в рамках задачи с начальными данными, считая, что все свойства исходного состояния за фронтом ударной волны не зависят от координаты x. В этом случае малые возмущения всех свойств представим решение исходной системы уравнений в виде

Применяя к уравнениям (58) преобразование Лапласа

и вводя вектор преобразованных по Лапласу возмущений запишем исходную систему уравнений следующим образом:

Матрица $\tilde {\Omega }$ имеет вид

Матрицы $\tilde {T}$ и $\tilde {\Lambda }$ имеют виды

Граничные условия (58)‒(60) могут быть записаны в виде вектора

Компоненты векторов ${{\chi }_{1}},$ ${{\chi }_{2}}$ имеют вид

где

Как уже говорилось, производная ${{\left( {\frac{{\partial v}}{{\partial P}}} \right)}_{H}}$ берется вдоль адиабаты Гюгонио.

Решение уравнения (63) представим в виде

Можно показать, что решение (67) ограничено тогда и только тогда, когда

Здесь ${{q}^{1}}\left( {0;\omega } \right)$ ‒ собственный вектор матрицы ${{\tilde {\Pi }}^{1}}$ (${{\tilde {\Pi }}^{1}}$ ‒ транспонированная матрица $\tilde {\Pi }$ $\left( {{{\Pi }_{{i,j}}} \equiv \Pi _{{j,i}}^{1}} \right)$). Смещение фронта ударной волны от положения равновесия запишется из уравнений (66), (68) в виде

После возвращения к функциям – оригиналам, получаем для амплитуды смещения соотношение

Здесь Здесь

Анализ корней характеристического уравнения. Зависимость амплитуды смещения от времени определяется особенностями функции $D\left( {\omega ,k} \right)$ из-за члена $l(\omega *),$ в общем случае, является двузначной. Если выбрать два листа римановой поверхности, склеенной вдоль разреза, проходящего между точками ветвления функции $D\left( \omega \right),$ то контур интегрирования выбирается на верхнем листе римановой поверхности (перед корнем l в (70) выбираем знак плюс).

В том случае, когда все особенности подынтегрального выражения, входящего в первое выражение l, лежат на нижнем листе римановой поверхности и вклад в асимптотику дают лишь точки ветвления, для анализа удобно использовать дробно – линейное преобразование

С использованием этого преобразования интеграл (70) принимает вид

В качестве контура интегрирования С выбирается окружность единичного радиуса $\left( {{\text{C}}:\left| z \right| = 1} \right).$ Проводя интегрирование, находим поведение амплитуды смещения. При больших временах $\left( {t \to \infty } \right)$ из (72) методом перевала получаем

где ${{C}_{{2n}}}$ – коэффициенты асимптотического разложения, $\varphi \left( t \right)$ – гармоническая функция $\left( {\left| \varphi \right| < 1} \right).$

Положение нулей функции $D\left( {\omega ,k} \right)$ зависит от газодинамических параметров М₂, m⁺ и величины магнитного поля ${{R}_{\sigma }} = {1 \mathord{\left/ {\vphantom {1 {\tau _{\sigma }^{*}}}} \right. \kern-0em} {\tau _{\sigma }^{*}}}$ (параметра взаимодействия). Рассмотрим расположение границ устойчивости. Когда магнитное поле стремится к нулю $\left( {\tau _{\sigma }^{{ - 1}} \to 0} \right),$ из уравнения (63) приходим к хорошо известному в газовой динамике результату [26], где при решении задачи с начальными данными возмущения затухают не экспоненциально, а степенным образом

Проследим влияние магнитного поля на границы областей устойчивости.

Прежде всего, рассмотрим частный случай, когда

и, следовательно, зависят только от интенсивности ударной волны. При выполнении этого условия функция $D\left( {\omega ,k} \right)$ является многочленом второй степени, и его корни с учетом $\left( {1 - m + 2{{{\text{M}}}_{2}} \ne 0} \right)$ определяются как где

Диапазон изменений параметра $m$

где $\Gamma = \max \left( { - 1;{{\Gamma }_{1}}} \right),$ ${{\Gamma }_{1}} = \,\,\,\,\frac{{1 + 2{{{\text{M}}}_{2}}\left( {\delta - 1} \right)\left( {1 - \beta {{{\text{M}}}_{2}}} \right){\gamma \mathord{\left/ {\vphantom {\gamma \beta }} \right. \kern-0em} \beta }}}{{2\delta - 1}},$

соответствует области устойчивости ионизующей ударной волны.

Диапазоны

соответствуют областям неустойчива плоской ударной волны.

Если ${{\Gamma }_{1}} < 1,$ то существует единственное значение параметра m (при этом k = 0)

при котором смещение поверхность разрыва изменяется по гармоническому закону – происходит генерация колебаний. Т.е. магнитное поле приводит к тому, что область нейтральных колебаний полностью исчезает или вырождается в точку.

При произвольном значении параметра взаимодействия ${{R}_{\sigma }} = {{\left( {\tau _{\sigma }^{*}} \right)}^{{ - 1}}}$ для оценки числа корней функции $D\left( {\omega ,k} \right)$ (71), лежащих в правой полуплоскости, удобно использовать принцип аргумента. Точки ветвления функции $D\left( {\omega ,k} \right)$ всегда лежат в левой полуплоскости, причем, и при условии $\tau _{\sigma }^{*} < 0.5{{{\text{M}}}_{2}},$ они находятся на отрицательной части действительной оси. При условии $\tau _{\sigma }^{*} \to \infty $ одна точка стремится к ‒∞, а другая ‒ к нулю слева. Можно показать, что как при условии $\tau _{\sigma }^{*} \gg 0.5{{{\text{М}}}_{2}},$ так и при условии $\tau _{\sigma }^{*} < 0.5{{{\text{M}}}_{2}}$ функция $D\left( {\omega ,k} \right)$ имеет в правой полуплоскости хотя бы один корень, если выполнено условие (79).

Для малых значений параметра взаимодействия $\left( {\tau _{\sigma }^{*} \ll 0.5{{{\text{M}}}_{2}}} \right)$ область устойчивости определяется неравенствами

При превышении критического значения параметра взаимодействия

область устойчивости сужается.

Положение левой границы области устойчивости (правая граница $m > 1 + 2{{{\text{M}}}_{2}}$ от величины $\tau _{\sigma }^{*}$ не зависит и равняется $1 + 2{{{\text{M}}}_{2}}$). При условии $\tau _{\sigma }^{*} \ll 0.5{{{\text{M}}}_{2}}$ и выполнении неравенства

где функция $D\left( {\omega ,k} \right)$ не имеет корней, лежащих в правой полуплоскости.

Из выше сказанного следует, что положение границ области устойчивости при больших параметрах взаимодействия определяется только интенсивностью ударной волны и не зависит от величины самого параметра взаимодействия, т.е. неустойчивости зависит от вида адиабаты Гюгонио.

Длина волны возмущения $k$влияет на положение границы области устойчивости только через величину параметра взаимодействия ${{R}_{\sigma }} = {{\left( {\tau _{\sigma }^{*}} \right)}^{{ - 1}}}.$ Если в начальный момент времени заданы возмущение давления, скорости, плотности среды и плотности электрического тока, поведение амплитуды смещения по-прежнему определяется особенностями функции $D\left( {\omega ,k} \right).$

Суммируем результаты воздействия магнитного поля на устойчивость ионизующей ударной волны, когда основным механизмом структурной неустойчивости являются особенности ударной адиабаты.

1. Для малых значений параметра взаимодействия $\left( {\tau _{\sigma }^{*} \ll 0.5{{{\text{M}}}_{2}}} \right)$ область устойчивости определяется неравенствами

т.е. вся область нейтральных колебаний, существующая без магнитного поля, переходит в область устойчивости. Это связано с затуханием возмущения скорости $\delta {{U}_{2}}$ за счет магнитной вязкости $\frac{{{{\sigma }_{2}}B_{2}^{2}}}{{{{\rho }_{2}}}}.$

2. Для сильной ударной волны $\left( {{{{\text{M}}}_{1}} \gg 1} \right)$ магнитное поле приводит к сужению области устойчивости

Следует отметить, для идеального газа

Следовательно, сильная ионизующая ударная волна может оказаться структурно не устойчивой.

Полученные в этом разделе результаты показывают, что поперечное магнитное поле влияет на структурную неустойчивость ударной волны, Теперь границы области устойчивости определяются как величиной ${{\left( {{{\partial v} \mathord{\left/ {\vphantom {{\partial v} {\partial P}}} \right. \kern-0em} {\partial P}}} \right)}_{H}},$ так и величиной магнитной вязкости ${{{{\sigma }_{2}}B_{2}^{2}} \mathord{\left/ {\vphantom {{{{\sigma }_{2}}B_{2}^{2}} {{{\rho }_{2}}}}} \right. \kern-0em} {{{\rho }_{2}}}}$ (параметра взаимодействия). Совместное воздействие этих механизмов приводит к тому, что область устойчивости смещается, вбирая в себя область, нейтральных колебаний, существующей при отсутствии магнитного поля. Область устойчивости для малых значений параметра взаимодействия шире, чем область устойчивости для больших параметров. Протекание электрического тока, вызванного магнитным полем, приводит к тому, что амплитуда возмущения может затухать гораздо быстрее, чем в отсутствии магнитного поля. Как уже отмечалось, этот эффект объясняется влиянием так называемой, магнитной вязкости ${{{{\sigma }_{2}}B_{2}^{2}} \mathord{\left/ {\vphantom {{{{\sigma }_{2}}B_{2}^{2}} {{{\rho }_{2}}}}} \right. \kern-0em} {{{\rho }_{2}}}},$ связанной с флуктуацией скорости среды.

О роли других неустойчивостей, связанных с протеканием электрического тока и развивающихся в плазме за фронтом ударной волны. Если в области за фронтом ударной волны протекает электрический ток, то даже при структурной устойчивости ударной волны необходимо учитывать различные плазменные эффекты. Во-первых, следует учитывать, что коэффициент электропроводности является функцией термодинамических параметров среды. Во-вторых, протекание электрического тока приводит к джоулеву тепловыделению и, соответственно, неоднородности температуры плазмы [22, 23].

Для газовой плазмы электропроводность возрастает с ростом температуры ${{\left( {\frac{{\partial \ln {{\sigma }_{2}}}}{{\partial \ln {{T}_{2}}}}} \right)}_{P}} \ne 0.$ Если ${{\left( {\frac{{\partial \ln {{\sigma }_{2}}}}{{\partial \ln {{T}_{2}}}}} \right)}_{P}} > 0$ и параметр взаимодействия ${{R}_{\sigma }} = {{\left( {\tau _{\sigma }^{*}} \right)}^{{ - 1}}} = \frac{{{{\sigma }_{2}}B_{2}^{2}}}{{{{\rho }_{2}}{{U}_{2}}}}k > 1,$ то протекание электрического тока в области за фронтом волны может приводить к неустойчивостям перегревного типа, вызванными флуктуациями силы Ампера и джоулева тепловыделения. Эти неустойчивость могут возникать даже в совершенном газе. Подробный анализ этой ситуации, характерной для МГД-генераторов на ударных волнах, разобран в [39].

Качественно воспроизведем результаты [39] и рассмотрим влияние магнитного поля на устойчивость плазмы за фронтом ударной волны не связанную с повелением адиабаты Гюгонио. Здесь следует учесть, что протекание электрического тока все свойства за фронтом ударной волны зависят от координаты x из-за воздействия силы Ампера и джоулева тепловыделения. В этом случае флуктуации силы Ампера $\delta {{j}_{2}}{{B}_{0}} = \delta {{\sigma }_{2}}{{U}_{2}}B_{2}^{2}{\text{/}}{{\rho }_{2}}$ = = ${{\sigma }_{2}}{{U}_{2}}B_{2}^{2}{{\left( {\frac{{\partial \ln {{\sigma }_{2}}}}{{\partial {{T}_{2}}}}} \right)}_{P}}\delta {{T}_{2}}{\text{/}}{{\rho }_{2}}$ могут генерироваться возмущением температуры, связанной с зависимостью коэффициента электропроводности от температуры ${{\sigma }_{2}}({{T}_{2}})$ и магнитным полем.

Если джоулев нагрев приводит к неоднородности температуры

то при условии развивается неустойчивость, в которой возмущения изменяются во времени по закону: где ${{\lambda }_{2}}$ – коэффициент теплопроводности плазмы, ${{a}_{2}}$ – скорость звука. Здесь учтено изменение области нагретого газа за фронтом волны.

Из выражения (84) следует, что при условии (83) ситуация меняется. Если ранее в устойчивой ударной волне без магнитного возмущения затухают по закону $\xi \sim {{t}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}},$ то при наличии магнитного поля возмущения могут нарастать экспоненциально $\xi \sim {\text{exp(}}{{t}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}).$ На рис. 10 представлена зависимость параметра ${{\left( {\frac{{\partial \ln {{\sigma }_{2}}}}{{\partial \ln {{T}_{2}}}}} \right)}_{{P{\text{cr}}}}}$ от скорости ударной волны в аргоне [39]. Заштрихована область устойчивости.

Когда область магнитного поля ограничена, следует иметь в виду, что неустойчивость носит конвективных характер [1] и может не успеть развиться. В тех случаях, когда ударная волна формируется разлетающимися плотными продуктами взрыва конденсированного взрывчатого вещества, в среде за фронтом может развиваться неустойчивость Рэлея–Тейлора, которая здесь не рассматривается.

ЗАДАЧИ О СТРУКТУРЕ УДАРНЫХ ВОЛН

Структура ударной волны без магнитного поля. В ряде задач связь между характеристиками сред перед фронтом ударной волны и за ним можно установить, рассматривая структуру переходного слоя L (рис. 11). Такой непрерывный переход происходит в диапазоне нескольких длин свободного пробега и, строго говоря, его следует рассматривать в рамках кинетической теории. Структуру ударной волны можно рассчитать, используя решения уравнения Больцмана 13-моментным методом Грэда. Однако существуют подходы, в рамках которых используются уравнения сплошной среды. Исследования, относящиеся к различным вопросам о структуре ударных волн без магнитного поля, содержатся в работах [27, 28, 50‒54].

Сначала рассмотрим более подробно задачу, о непрерывном стационарном переходе во фронте ударной волны без магнитного поля. Задача о непрерывном переходе от однородного состояния перед волной к однородному состоянию за ней носит название задачи о структуре ударной волны. Решение этой задачи позволяет выявить поведение свойств среды в структуры ударной волны. Рассмотрим подход к решению задачи о структуре ударной волны с использованием системы уравнений Навье‒Стокса, учитывая влияния вязкости и теплопроводности. Несмотря на то, что фронт ударной волны тонок и составляет несколько длин свободного пробега молекулы ${{l}_{{{\text{с}}{\text{.п}}{\text{.}}}}},$ скорость, давление и температура претерпевают значительные изменения (рис. 11). В простейшем случае стационарная система уравнений Навье‒Стокса, используемых для описания структуры фронта ударной волны, записанная в системе координат движущегося с постоянной скоростью фронта имеет вид

Здесь η ‒ коэффициент динамической вязкости, λ ‒ коэффициент теплопроводности. Следует пояснить отсутствие диссипативного члена в уравнении энергии. Он отсутствует, т.к. уравнение записано относительно полной энтальпии h. Изменение полной энтальпии автоматически учитывает вклад от изменения состава и температуры при нагреве за счет диссипации скорости и протекания химических реакций. Например, при протекании химической реакции или ионизации газа происходит изменение состава среды и ее суммарной энтальпии.

Систему уравнений (85) можно упростить, проинтегрировав одни раз. Интегрирование первого уравнения системы (85) приводит, как и раньше в (30), к получению одного из инвариантов в структуре фронта ударной волны ‒ постоянству потока массы:

Из второго уравнения системы (85) получаем

Здесь $I = const$ ‒ поток импульса, который должен быть определен из граничных условий.

Из третьего уравнения системы (85), используя связь между энтальпией и температурой $h(P(T,\rho ),$ получаем еще одно уравнение, описывающее изменение температуры в структуре волны:

Здесь $\Pi = {\text{const}}$ ‒ поток энергии, который должен быть определен из граничных условий.

С использованием уравнения состояния, энтальпию можно представить в виде функция температуры и плотности $h(P(T,\rho )$ или температуры и скорости $\rho = {G \mathord{\left/ {\vphantom {G {{{U}_{x}}}}} \right. \kern-0em} {{{U}_{x}}}}.$

Вводим вектор

Сведем задачу о структуре ударной волны к решение следующей системы обыкновенных уравнений:

Здесь

Эту систему необходимо дополнить граничными условиями перед и за фронтом ударной волны. Можно считать, что состояния среды перед фронтом и за ним однородны и, соответственно, находятся в точках x = $ \pm \infty {\text{:}}$

Математические аспекты решения такой задачи для системы дифференциальных уравнений (89) можно найти [55, 56]. Они состоят из определения тип особых точек и условий непрерывного перехода между ними. Для определения тип особых точек чего линеаризуем систему уравнений (92) относительно малых возмущений. Из анализа особых точек следует, если выполняются условия

то особые точки при $x = + \infty $ и $x = - \infty $ являются седлами. Проекция фазового портрет дифференциального уравнения (89) на плоскость ${{U}_{{x,}}},x$ представлена на рис. 12. Структура ударной волны соответствует сепаратрисе, выходящей их токи 1 перед волной и входящей в точку 2 – за волной (рис. 13).

Характерный размер фронта ударной волны можно оценить следующим образом:

где ${{l}_{f}}$ ‒ длина свободного пробега частиц.

Из этой оценки следует, что структура ударной волны превышает несколько длин свободного пробега и переход из состояния перед волной в состояние за ней можно заменить разрывом. Решение задачи о структуре ударной волны в газе ничего не добавляет к полученным ранее соотношениям между состоянием перед и за фронтом, полученным из законов сохранения потоков массы, импульса и энергии. Однако существует большой класс задач (детонационные волны, магнитогазодинамические ионизующие ударные волны и др.), в которых соотношений, вытекающих из законов сохранения потоков массы, импульса и энергии не хватает, чтобы определить скорость волны и связи между параметра перед и за разрывом. В этом случае решение задачи о структуре такой волны позволяет найти дополнительные соотношения и связать параметры перед волной с параметрами за ней.

СТРУКТУРА ИОНИЗУЮЩЕЙ УДАРНОЙ ВОЛНЫ В МАГНИТНОМ ПОЛЕ

При анализе структуры ионизирующей ударной волны с учетом изменяющегося магнитного поля кроме уравнений для потоков массы, импульса и энергии (82)‒(84) следует учитывать дополнительные соотношения для электрического и магнитного полей, вытекающие из уравнений Максвелла. В этом случаем, считая, что ударная волна движется в направлении оси x $U({{U}_{x}},0,0),$ и учитывая лишь одну компоненту поперечного магнитного поля $B(0,0,\mathop B\nolimits_z (x)),$ вместо системы уравнений (82)‒(84) получаем следующую:

к которой должны быть добавлены соотношения, вытекающие из уравнений Максвелла Здесь ${{\mu }_{0}}$ ‒ магнитная проницаемость вакуум, $\sigma $ ‒ коэффициент электропроводности плазмы.

Отсутствие диссипативного члена в уравнении сохранения патока энергии связано с тем, что при конечных значением электрического тока ${{i}_{y}}$ и больших значениях коэффициент электропроводности плазмы $\sigma ,$ слагаемом ${{j_{y}^{2}} \mathord{\left/ {\vphantom {{j_{y}^{2}} \sigma }} \right. \kern-0em} \sigma }$ можно пренебречь по сравнению с $\frac{\partial }{{\partial x}}{{E}_{y}}{{B}_{z}}.$ Изменение состава среды, связанное с протеканием реакции термической ионизации нужно учесть в энтальпии.

Вводя трехкомпонентный вектор

Можно свести задачу о структуре ударной волны к решению следующей системы обыкновенных уравнений:

Здесь трехкомпонентный вектор F имеет вид

Здесь $G = {\text{const}}$ – расход плазмы, $I = {\text{const}}$ ‒ поток импульса, $\Pi = {\text{const}}$ ‒ поток энергии, ${{E}_{y}} = {\text{const}},$ которые должны быть определены при решении задаче о нахождения структуры ионизующей волны из граничных условий.

Граничные условиями перед фронтом ударной волны и за ним находятся в точках x = $ \pm \infty ,$ соответствующих однородным состояниям среды перед фронтом ионизующей ударной волны и за ним:

Следовательно, состояния среды перед фронтом и за ним являются точками равновесия (особыми точками [55, 56]) системы (89) $F = 0$ и связаны между собой уравнениями:

Как и ранее, используя уравнение состояния, энтальпию можно представить в виде функция температуры и плотности $h(P(T,\rho )$ или температуры и скорости $\rho = {G \mathord{\left/ {\vphantom {G {{{U}_{x}}}}} \right. \kern-0em} {{{U}_{x}}}}.$

В точке $x = \infty $ известны следующие параметры системы ${{P}_{1}},{{\rho }_{1}},{{B}_{{z1}}},$ по которой движется ударная волна со скоростью ${{U}_{{x,1}}} = D,$ которая определяется в процессе решения задачи. Если считать, что в особой точке $x = - \infty $ параметры системы ${{T}_{2}}({{P}_{2}},{{\rho }_{2}}),{{U}_{{x,2}}},{{B}_{{z2}}}$ (соответственно ${{T}_{2}}({{P}_{2}}{{\rho }_{2}})$), то трех уравнений (98) не хватает, чтобы зная лишь ${{T}_{1}}({{P}_{1}},{{\rho }_{1}}),$ определить две величины за фронтом ${{T}_{2}}({{P}_{2}},{{\rho }_{2}}),{{U}_{{x,2}}},{{B}_{{z,2}}}$ и скорость самой ударной волны ${{U}_{{x,1}}} = D$. Учитывая, что структура ударной волны соответствует переходу в фазовом пространстве ${{U}_{x}},T,{{B}_{z}},x$ из одной особой точки системы в другую ее особую точку. Вновь задача сводится к известной задаче на собственные значения ${{U}_{{x,1}}} = D$ для системы дифференциальных уравнений (89) [56, 57], однако в пространстве большей размерности.

Решение задач о структуре ионизующей ударной волны можно найти в работах [5, 46, 47, 57, 58] и в литературе, указанной в них.

Более сложные структуры типа ударных волн могут возникать в двухтемпературной газовой плазме с магнитным полем и в полупроводниках. Описание такой среды состоит из уравнений сплошной среды отдельно для электронов и тяжелых частиц (атому и ионы). В таких системах наряду одинарными ударными волнами ионизации и рекомбинации плазмы, могут образовываться, своеобразные слоевые волны ионизации и рекомбинации (кинки). В такой волне передний фронт соответствует волне ионизации, а в задний – рекомбинации (рис. 14) [59, 60]. Слоевая волна распространяется с постоянной скоростью D, на переднем фронте волны происходит ионизация, где концентрация электронов изменяется от n₁ до n₂ > n₁. На заднем фронте происходит рекомбинация, где концентрация электронов изменяется от n₂ до n₁ < n₂. Эти волны аналогично волгам, возникающим в плазме полупроводников [61].

Использование вышеизложенного подхода оказывается продуктивным и при исследовании влияние магнитного поля на детонационные волны. Например, в экспериментальных и теоретических исследованиях [62] было показано, что наличие поперечного магнитного поя влияет на критический диаметр канала, в котором происходит движение детонационной волны. Более детальные исследования различных эффектов, связанных с детонационными волнами можно найти в работе [63]. При достаточно высоких плотностях среды за фронтом ионизующей ударной волны следует учитывать эффекты не идеальности плазмы в уравнение состояние и их влияние на переносные и оптические процессы. Обсуждение вкладов не идеальности плазмы в различные свойства плотной плазмы можно найти в работах В.Е. Фортова [4, 64]. Оптические процессы в ударных волнах детально обсуждаются в [2].

Вывод граничного условия для электрического тока в задаче об устойчивости ударной волны в поперечном магнитном поле. Представим вывод граничного условия (60). Из уравнений $div\left( {\delta j} \right) = 0$ приходим к следующему соотношению:

Считаем, что область перед фронтом обладает малой, но конечной проводимостью σ₁ и возмущение поверхности разрыва имеет вид $\xi \left( {t;y} \right).$ Перейдем к новой системе координат путем замены переменных (рис. 15)

В результате замены уравнение (99) примет вид

Умножая это уравнение на $d\chi ,$ интегрируя от ‒ε до +ε и затем, устремляя ε к нулю, получим

Здесь скобки $\left\langle {} \right\rangle $ означают среднее на отрезке интегрирования. При равной нулю проводимости в области перед поверхностью разрыва последнее соотношение может быть записано в виде

Остальные интегралы при $\varepsilon \to 0$ стремятся к нулю:

Проведя линеаризацию полученных соотношений и учитывая, что в области перед поверхностью разрыва электрические токи отсутствуют, из уравнения (100) приходим к (60).

Когда необходимо учитывать влияние индуцированного магнитного поля (магнитное число Рейнольдса произвольно), вид граничного условия (60) изменяется.

ЗАКЛЮЧЕНИЕ

Обсуждаются эффекты, связанные c влиянием внешнего постоянного магнитного поля на слабые и сильные разрывы в газовых средах, обладающие конечной электропроводимостью. Показано, что в газовых средах с конечной электропроводностью магнитное поле не оказывает влияние на скорость их перемещения слабых разрывов.

Для случая без магнитного поля воспроизведен вывод характер положения границ между областями устойчивости, неустойчивости и генерации колебаний в зависимости от ее интенсивности ударной волны и вида адиабаты Гюгонио – производной ${{\left( {\frac{{\partial P}}{{\partial v}}} \right)}_{H}}.$

Проведен детальный анализ влияния внешнего магнитного поля на устойчивость плоской ионизующей ударной волны. Показано, что могут существовать два независимых механизма, приводящих к неустойчивости: a) первый механизм связан с особенностями адиабаты Гюгонио, приводит к структурной неустойчивости; б) второй тип неустойчивости вызывается возмущением силы Ампера и зависимостью электропроводности от температуры ${{\sigma }_{2}}({{T}_{2}}\mathop )\nolimits_{} $ (она не связанна с особенностями адиабаты Гюгонио). Второй случай соответствует известной плазменной неустойчивость, он может реализоваться при больших значениях параметра взаимодействия в сильных ударных волнах и приводить к генерации вторичной ударной волны в нагретом газе.

Проведен детальный анализ роли влияния внешнего, постоянного магнитного поля на структурную неустойчивость, связанную с особенностями адиабаты Гюгонио. Показано, что положение границ областей устойчивости зависит теперь от газодинамических параметров ${{{\text{М}}}_{{\text{2}}}},$ $m \sim \approx {1 \mathord{\left/ {\vphantom {1 {{{{\left( {\frac{{\partial P}}{{\partial v}}} \right)}}_{H}}}}} \right. \kern-0em} {{{{\left( {\frac{{\partial P}}{{\partial v}}} \right)}}_{H}}}}$ М₂, m⁺ и величины магнитного поля – параметра взаимодействия ${{R}_{\sigma }} = {1 \mathord{\left/ {\vphantom {1 {\tau _{\sigma }^{*}}}} \right. \kern-0em} {\tau _{\sigma }^{*}}}.$

Для малых значений параметра взаимодействия область устойчивости расширяется за счет того, что к области устойчивости ударной волне без магнитного поля присоединяется область нейтральных колебаний, т.е. бывшая область генерации звука при наличии магнитного поля исчезает. Если параметр взаимодействия превышает критическое, то область устойчивости сужается. В области устойчивости возмущения затухают по закону $\exp \left[ { - {t \mathord{\left/ {\vphantom {t {\left( {2{{\tau }_{\sigma }}} \right)}}} \right. \kern-0em} {\left( {2{{\tau }_{\sigma }}} \right)}}} \right]{{t}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}.$

Для сильной ударной волны $\left( {{{{\text{М}}}_{1}} \gg 1} \right)$ магнитное поле приводит к тому, что область нейтральных колебаний вырождается в точку или полностью исчезает.

Обсуждается перегревная неустойчивость, вызванная возмущением силы Ампера, неоднородностью температуры и зависимостью электропроводности от температуры (${{\sigma }_{2}}({{T}_{2}}).$ Она возникает, если электропроводность возрастает с ростом температуры ${{\left( {\frac{{\partial \ln {{\sigma }_{2}}}}{{\partial \ln {{T}_{2}}}}} \right)}_{P}} > {{\left( {\frac{{\partial \ln {{\sigma }_{2}}}}{{\partial \ln {{T}_{2}}}}} \right)}_{{P{\text{cr}}}}} > 0$) и параметр взаимодействия превышает некоторое критическое значение. В сильных ударных волнах с учетом изменения области ударно нагретой проводящей плазмы возмущения нарастают по закону

Эта неустойчивость не связана с видом ударной адиабаты и может развиваться в интенсивных ударных волнах в идеальном газе, когда плазма образуется за счет термической ионизации.

Обсуждается влияние поперечного магнитного поля на структуру плоской ионизирующей ударной волны. Показано, как изменяются границы области устойчивости, Обсуждаются условия, когда необходим учет собственного магнитного поля.

Дан вывод граничного условия для электрического тока в задаче об устойчивости ударной волны в поперечном магнитном поле.

Автор благодарит В.С. Филинова за представления ряда материалов и комментарии.