Прикладная математика и механика, 2023, T. 87, № 3, стр. 423-431
Моделирование динамики всплывающего пузырька
А. Н. Зотова 1, *, А. А. Кандауров 1, Ю. И. Троицкая 1, Д. А. Сергеев 1
1 Институт прикладной физики РАН
Нижний Новгород, Россия
* E-mail: aniazotova@yandex.ru
Поступила в редакцию 28.02.2023
После доработки 19.04.2023
Принята к публикации 24.04.2023
- EDN: ZUPAJW
- DOI: 10.31857/S003282352303013X
Аннотация
Проведено прямое численное моделирование всплывания изначально покоившегося пузырька воздуха в воде без течения. Для сравнения с экспериментом взята усложненная начальная форма пузырька, соответствующая экспериментальной. Изменения формы пузырька в процессе всплывания, полученные в результате численного моделирования, близки к экспериментальным изменениям формы пузырька. Для сравнения с результатами численного моделирования, имеющимися в литературе, проведено моделирование всплывающего пузырька, имеющего изначально сферическую форму. Получено, что в процессе всплывания форма пузырька сначала близка к эллиптической и испытывает колебания, но далее усложняется – в нижней части пузырька появляется “хвост”. Данный режим динамики всплывающего пузырька подтверждается опубликованными в литературе результатами численного моделирования.
1. Введение. Пузырьки воздуха играют важную роль при взаимодействии океана и атмосферы. Они усиливают газообмен между атмосферой и океаном, вносят существенный вклад в потоки аэрозольных частиц, создают окружающий шум и поглощают биологические поверхностно-активные вещества. Одним из параметров, характеризующих эти процессы, является время жизни пузырька до его достижения поверхности воды и разрыва. Можно предположить, что наличие в жидкости сдвигового течения, может повлиять на этот параметр, и поэтому конечной целью наших исследований будет именно моделирование всплывания пузырька газа в жидкости со сдвиговым течением. Но в данной работе речь пойдет о начальном этапе исследования – моделировании динамики пузырька в жидкости без течения для сравнения с экспериментом и результатами моделирования, приведенными в литературе.
Экспериментально динамика всплывающего пузырька была исследована во множестве работ, например в [1, 2], кроме того эксперимент по всплыванию пузырька воздуха в воде в отсутствие и в присутствии сдвигового течения проводился авторами данной работы. На рис. 1,а можно увидеть последовательность кадров съемки всплывающего пузырька в воде без сдвигового течения для различных моментов времени, моменты времени выбраны из соображений наглядности демонстрации изменения формы пузырька. Численные трехмерные исследования всплывающего в жидкости пузырька проводились, например, в [3–9], в части исследований моделировалась динамика ансамбля пузырьков в жидкости [3, 4, 10, 11]. Траектории всплывающих пузырьков исследовались в работах [12–14]. Результаты данного численного моделирования в конце работы будут сопоставлены с результатами проведенного авторами эксперимента и результатами [9].
Рис. 1.
а: Кадры высокоскоростной съемки всплывающего пузырька, полученные в предварительном эксперименте, с использованием оборудования УНУ ККГС; б: результат численного эксперимента (MAXLEVEL = = 10, uerr > 10–2, ferr > 10–3, ωerr > 10–1): форма пузырька в различные моменты в процессе всплывания.

2. Моделирование. Для прямого численного моделирования всплывания воздушного пузырька в воде был использован программный пакет Basilisk [15]. В Basilisk реализован численный алгоритм, решающий уравнения Навье–Стокса для несжимаемых сред с переменной плотностью и поверхностным натяжением [16]:
В расчетах используется метод адаптивной сетки – размер ячейки дискретизации может варьироваться в разных областях домена с использованием метода вейвлет-адаптации. Минимальный размер ячейки задается максимальным уровнем дискретизации – MAXLEVEL. Линейный размер ячейки, соответствующий максимальному уровню дискретизации может быть получен делением размера домена L0 на 2 в степени, равной значению MAXLEVEL. Алгоритм дробления сетки вызывается каждый временной шаг, сетка дробится, когда оцененная по вейвлету ошибка превышает uerr, ferr или ωerr (в некоторых расчетах) для полей скорости, объемной доли первой жидкости или завихренности поля скорости соответственно.
Была рассмотрена задача следующей конфигурации (рис. 2): в верхней части области моделирования (использовались ее линейные размеры L0 = 50, 60 мм) воздух, нижняя ее часть заполнена водой, толщина слоя воды – 40 или 50 мм. В начальный момент времени пузырек газа находится в жидкости на глубине h (30 или 41 мм), радиус пузырька r = 2.8 или 3 мм. Параметры сред соответствуют воде и воздуху. Начальная форма пузырька сферическая или более сложная, соответствующая начальной форме пузырька в проведенном авторами предварительном эксперименте (см. рис. 1,а).
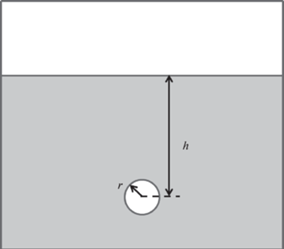
Рис. 2.
Схема численного эксперимента: в начальный момент времени пузырек находится в жидкости на глубине h, радиус пузырька r.
В работе [9] отмечается, что динамика всплывающего пузырька может быть описана с помощью четырех безразмерных чисел: Галилея ${\text{Ga}} = {{\rho }_{w}}\sqrt g {{r}^{{3/2}}}{\text{/}}{{\mu }_{w}}$, характеризующего соотношение гравитационных и вязких сил, Этвёша ${\text{Eo}} = {{\rho }_{w}}g{{r}^{2}}{\text{/}}\sigma $, характеризующего соотношение гравитационных сил и сил поверхностного натяжения, соотношения плотностей ρr= ρa/ρw и вязкостей μr = μa/μw сред. Здесь $g$, r и σ – ускорение свободного падения, начальный радиус пузырька и коэффициент поверхностного натяжения для рассматриваемых сред, соответственно, ρa и μa – плотность и вязкость воздуха, ρw и μw – плотность и вязкость воды. Параметры нашей задачи при моделировании сферического пузырька соответствуют следующим значениям этих чисел: Ga = = 514, Eo = 1.2, ρr = 10–3, μr = 10–2, что соответствует IV режиму всплывания пузырька из работы [9].
3. Результаты. Расчеты проводились с использованием различных значений параметров MAXLEVEL, uerr, ferr и ωerr. В начальный момент времени для интерфейса пузырька задавался максимальный уровень дискретизации MAXLEVEL, в то время как остальная часть домена оставалась на начальном уровне дискретизации равном семи.
Для сравнения с нашим экспериментом было проведено моделирование всплывающего пузырька, начальная форма которого совпадала с начальной формой пузырька в эксперименте в момент отрыва его от сопла. Радиус сферической части пузырька был равен r = 2.8 мм, нижняя часть пузырька была вытянута в конус (см. рис. 1). Значения максимального уровня дискретизации сетки и параметров дробления сетки определялись следующими соотношениями: MAXLEVEL = 10, uerr > 10–2, ferr > 10–3, ωerr > 10–1. Получены некоторые различия в характерных временах деформации пузырька между экспериментом и численным моделированием, это может объясняться как неточностями в задании начальной формы пузырька, так и недостаточным разрешением сетки. Но изменения формы пузырька в процессе всплывания, полученные в результате численного моделирования, в основных деталях повторяют изменения формы пузырька, полученные в эксперименте (см. рис. 1).
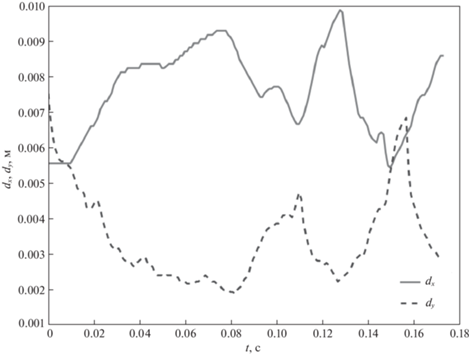
В момент отрыва от сопла возникают возмущения формы поверхности, которые приводят к возбуждению объемных колебаний пузырька. На рис. 3 представлены зависимости вертикального (сплошная кривая) и горизонтального (пунктирная кривая) размеров пузырька от времени. Можно заметить, что за время, которое требуется пузырьку, чтобы достигнуть поверхности жидкости, происходит приблизительно 2.5 цикла изменения его формы; вертикальный и горизонтальный размеры пузырька ожидаемо колеблются в противофазе.
Рис. 3.
Зависимость вертикального – сплошная кривая – (dy) и горизонтального – пунктирная кривая – (dx) размеров пузырька от времени.
Также было проведено несколько численных экспериментов по всплыванию пузырька со сферической начальной формой. Это позволило провести сравнение полученных результатов с результатами работы [9]. В первом численном эксперименте было использовано значение параметра MAXLEVEL = 12. Для взятого в данном исследовании размера домена L0 = 0.05 м получим минимальный линейный размер ячейки ∆l = 0.05/212 = 1.2 × 10–5 м (иными словами ∆l = 0.004r). Сетка дробилась при условиях uerr > 10–3, ferr > 10–2, ωerr как критерий дискретизации в данном случае мы не использовали. Изменение формы пузырька в процессе всплывания, полученное в результате численного моделирования, показано на рис. 4,а, также на рисунке отображена сетка для вертикальной плоскости, проходящей в начальный момент времени через центр пузырька. Для второго расчета было взято значение параметра MAXLEVEL = 11 (минимальный линейный размер ячейки ∆l = 2.4 × 10–5 м), условия дробления сетки: uerr > 10–2, ferr > 10–2, кроме того было добавлено еще условие дробления сетки по ошибке поля завихренности ωerr > 10–1. Результаты моделирования приведены на рис. 4,б. На рисунке видно, что изменение параметров счета существенным образом повлияло на вид сетки. Для второго случая дробление сетки происходит в значительно большем объеме вокруг пузырька, что, по-видимому, связано с добавленным критерием дробления по ωerr. Результаты для двух расчетов очень близки, есть небольшое различие в характерных временах деформации пузырька. В обоих случаях сначала изменения формы пузырька больше похожи на отклонения от эллиптической формы, но с некоторого момента времени пузырек уже далек от эллиптической формы, и в итоге у него образуется резко выдающийся “хвост” (на рис. 4. а: t = 0.126 с; б: t = 0.128 с). Примечательно, что такое причудливое изменение формы пузырька находится в хорошем соответствии с результатами, полученными в [9] (см. [9], рис. 8). Отметим, что в [9] минимальный линейный размер ячейки относительно радиуса пузырька ∆l = 0.029r больше, чем в данной работе, значит, в нашем случае пузырек моделируется с лучшим разрешением.
Рис. 4.
Результат численного эксперимента – форма пузырька в различные моменты в процессе всплывания: (а) MAXLEVEL = 12, uerr > 10–3, ferr > 10–2; (б) MAXLEVEL = 11, uerr > 10–2, ferr > 10–2, ωerr > 10–1.

Также был проведен численный эксперимент для пузырька радиусом r = 1 мм, но таких же как в предыдущих экспериментах безразмерных чисел Ga = 514, Eo = 1.2 (значения чисел Ga и Eo сохранились неизменными за счет изменения вязкости воды и поверхностного натяжения). На рис. 5 видно, что изменения формы пузырька повторяют изменения его формы в двух предыдущих численных экспериментах, но процессы деформации происходят существенно быстрее, таким образом, полученный в численном счете режим деформации действительно определяется именно безразмерными числами Ga и Eo.
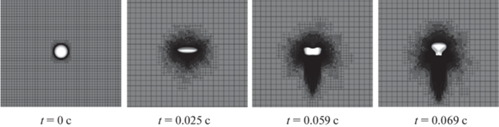
Рис. 5.
Результат численного эксперимента (r = 0.001 м, Ga = 514, Eo = 1.2, MAXLEVEL = 11, uerr > 10–2, ferr > 10–2, ωerr > 10–1): форма пузырька в различные моменты в процессе всплывания.
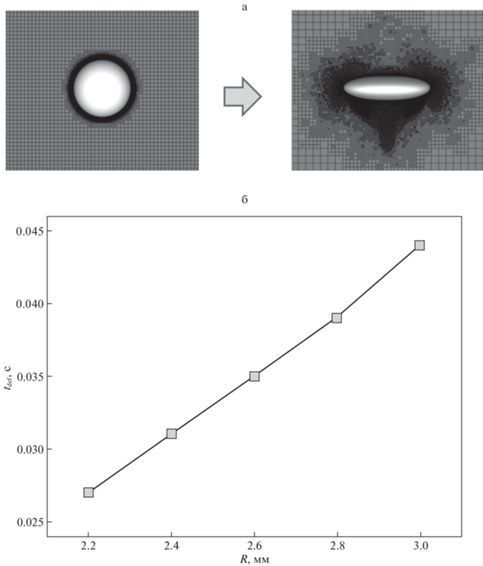
Далее были проведены расчеты для пузырьков различных радиусов меньших r = 3 мм – r = 2.8, 2.6, 2.4, 2.2 мм, но остальные параметры задачи при этом оставались неизменными (соответствующими воде и воздуху), т.е. безразмерные числа Ga и Eo изменялись от эксперимента к эксперименту. Было также замечено, что при изменении радиуса пузырька меняются характерные времена его деформации. На рис. 6,а приведен пример начальной деформации пузырька из сферической формы в эллипсоидальную, рис. 6,б демонстрирует зависимость времени такой деформации от радиуса пузырька. Видно, что при увеличении радиуса время деформации также увеличивается.
Рис. 6.
а: Пример деформации сферического пузырька до эллипсоидальной формы для r = 0.003 м; б: зависимость времени деформации сферического пузырька до эллипсоидальной формы в зависимости от радиуса пузырька, параметры соответствуют воде и воздуху.
Заключение. С использованием программного пакета Basilisk проведено численное моделирование всплывания газообразного пузырька в жидкости. Для сравнения с проведенным лабораторным экспериментом при моделировании учитывалась сложная начальная форма пузырька. Полученные в результате численного расчета деформации пузырька в основных деталях совпадают с деформациями пузырька в эксперименте.
Проведено моделирование всплывания пузырька со сферической начальной формой. Получен режим деформации, для соответствующих безразмерных чисел Ga и Eo совпадающий с режимом деформации, обнаруженным в работе [9]. Проведено моделирование всплывания пузырьков различных радиусов, получено, что при увеличении радиуса пузырька характерное время его деформации увеличивается.
Работа по прямому численному моделированию поддержана проектом РНФ № 19-17-00209, экспериментальная часть исследования поддержана проектом РФФИ № 21-55-52005, работа Зотовой А.Н. поддержана в рамках проекта по гос. заданию № 0030-2022-0005, результаты получены с использованием оборудования Уникальной научной установки “Комплекс крупномасштабных геофизических стендов” ИПФ РАН.
Список литературы
Haberman W.L., Morton R.K. An Experimental Investigation of the Drag and Shape of Air Bubbles Rising in Various Liquids. Washington (DC): David Taylor Model Basin, 1953.
Tagawa Y., Takagi S., Matsumoto Y. Surfactant effect on path instability of a rising bubble // J. Fluid Mech. 2014. V. 738. P. 124–142.
Bunner B., Tryggvason G. Direct numerical simulations of three-dimensional bubbly flows // Phys. Fluids. 1999. V. 11. P. 1967–1969.
Lu J., Tryggvason G. Effect of bubble deformability in turbulent bubbly upflow in a vertical channel // Phys. Fluids. 2008. V. 20. P. 040701.
Sussman M., Puckett E.G. A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows // J. Comput. Phys. 2000. V. 162. P. 301–337.
Shin S., Juric D. Modeling three-dimensional multiphase flow using a level contour reconstruction method for front tracking without connectivity // J. Comput. Phys. 2002. V. 180. P. 427–470.
Hua J., Stene J.F., Lin P. Numerical simulation of 3D bubbles rising in viscous liquids using a front tracking method // J. Comput. Phys. 2008. V. 227. P. 3358–3382.
Pivello M., Villar M. Serfaty R. et al. A fully adaptive front tracking method for the simulation of two phase flows // Int. J. Multiphase Flow. 2014. V. 58. P. 72–82.
Tripathi M.K., Sahu K.C., Govindarajan R. Dynamics of an initially spherical bubble rising in quiescent liquid // Nature Commun. 2015. V. 6. № 1. P. 1–9.
Bonometti T., Magnaudet J., Gardin P. On the dispersion of solid particles in a liquid agitated by a bubble swarm // Metall Mater Trans. B. 2007. V. 38. P. 739–750.
Roghair I., Van Sint Annaland M., Kuipers H.J.A.M. Drag force and clustering in bubble swarms // AIChE J. 2013. V. 59. Iss. 5. P. 1791–1800.
Roghair I., Sint Annaland M., Kuipers H.J. Drag force and clustering in bubble swarms // AIChE J. 2013. V. 59. P. 1791–1800.
Magnaudet J., Mougin G. Wake instability of a fixed spheroidal bubble // J. Fluid Mech. 2007. V. 572. P. 311–337.
Shew W.L., Pinton J. Dynamical model of bubble path instability // Phys. Rev. Lett. 2006. V. 97. P. 144508.
Wichterle K., Vecer M., Ruzicka M.C. Asymmetric deformation of bubble shape: cause or effect of vortex-shedding? // Chem. Papers. 2014. V. 68. P. 74–79.
Popinet S. The Basilisk code: http://basilisk.fr
Popinet S. An accurate adaptive solver for surface-tension-driven interfacial flows // J. Comput. Phys. 2009. V. 228 (16). P. 5838–5866.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика


