Прикладная математика и механика, 2023, T. 87, № 3, стр. 432-441

1. Введение. Геофизическая гидродинамика предлагает большой ряд задач распространения волн в среде, анизотропия которой связана с эффектами вращения и стратификации [1–4]. В этих задачах корректное применение асимптотических методов дает возможность исследовать ряд физически интересных эффектов, определяемых свойствами гидрофизических сред. Импульсные источники возмущений являются одним из механизмов генерации достаточно интенсивных внутренних гравитационных волн (ВГВ) в природных (океан, атмосфера Земли) и искусственных стратифицированных средах [5–9]. Такие источники ВГВ могут иметь как природный (схлопывание области турбулентного перемешивания, быстрая подвижка океанического дна), так и антропогенный (подводные и надземные взрывы) характеры [10–13].

В природных стратифицированных средах вращение среды как целого влияет на основные характеристики полей ВГВ. В линейном приближении волновая картина может быть описана многомерными интегралами Фурье или с помощью геометрического подхода в рамках кинематической теории диспергирующих волн, на основе которой возможно получить аналитическое представление только для фазовых поверхностей (линий), огибающих и волновых фронтов [4, 14, 15]. Более сложной в математическом плане является задача построения равномерных асимптотик интегральных представлений, позволяющих рассчитать амплитудно-фазовую структуру волновых полей. В общем случае интегральные представления аналитически не вычисляемы, и для их анализа эффективно могут быть использованы только различные асимптотические методы. В современной литературе математический аппарат асимптотических методов изложен достаточно полно: многомерный метод стационарной фазы, метод эталонных интегралов, метод канонического оператора Маслова [16–20]. Асимптотики интегральных представлений позволяют качественно анализировать волновые поля, в том числе, и от нелокальных источников возмущений различной физической природы, что актуально, в частности, для решения задач оперативной океанологии.

В результате проведения модельных многовариантных расчетов по асимптотическим формулам смоделированная волновая система может быть приближена к наблюдаемым в натурных условиях волновым картинам, что позволяет оценить физические параметры реальных импульсных источников возбуждения ВГВ в природных стратифицированных средах [5, 6, 8, 9]. Поэтому полученные асимптотические результаты дают возможность определить основные характеристики начальных возмущений, варьируя модельные значения исходных параметров. Таким образом, математические модели волновой генерации от импульсного источника возмущений в стратифицированной вращающейся среде могут быть верифицированы, а также использованы для проведения прогнозных оценок.

Была рассмотрена [21] задача о дальних полях ВГВ при стационарном движении источника возмущений в стратифицированной вращающейся среде. Исследовались [22] дальние поля ВГВ от начального радиально симметричного возмущения без учета вращения среды. Целью настоящей работы является решение ранее не рассматриваемой задачи построения равномерных асимптотик дальних полей внутренних гравитационных волн, возбуждаемых локализованным импульсным источником возмущений во вращающейся стратифицированной среде конечной глубины.

2. Постановка задач, интегральные формы решений. Рассматривается слой $ - H < z < 0$ вращающейся как целое c частотой ${{\Omega }}$ стратифицированной жидкости с постоянной частотой Брента–Вяйсяля $N\left( z \right) = N = {\text{const}}$. В момент времени $t = 0$ точечный источник, находящийся в точке $\left( {0,0,{{z}_{0}}} \right)$, ${{z}_{0}} < 0$ мгновенно выбрасывает объем жидкости $q$. Тогда возвышение изопикн (линий равной плотности) ${{\xi }} = {{\xi }}\left( {x,y,z,{{z}_{0}},t} \right)$ в приближении Буссинеска определяется из уравнения [1, 4, 21]

В качестве граничных условий используется приближение “твердой крышки”: ${{\xi }} = 0$, $z = 0, - H$. Начальное условие берется в виде: $\xi \equiv 0$, $t < 0$. В безразмерных переменных $x* = \pi x{\text{/}}H$, $y* = \pi y{\text{/}}H$, $z* = \pi z{\text{/}}H$, $z_{0}^{*} = \pi {{z}_{0}}{\text{/}}H$, $f* = f{\text{/}}N$, $t* = Nt$, $q* = {{\pi }^{3}}q{\text{/}}{{H}^{3}}$, задача формулируется следующим образом (индекс “*” далее опускается)

Фурье образ возвышения изопикн

удовлетворяет уравнению

Решение (2.1)–(2.2) ищется в виде ряда по собственным функциям ${{{{\varphi }}}_{n}} = {{{{\varphi }}}_{n}}\left( {z,k} \right)$ соответствующей однородной спектральной задачи

Задача (2.3)–(2.4) имеет на отрезке [$ - \pi $, 0] полную ортонормированную с весом $\left( {1 - {{f}^{2}}} \right)$ систему собственных функций ${{{{\varphi }}}_{n}}\left( z \right) = \sqrt {\frac{2}{\pi }} \frac{{\sin nz}}{{\sqrt {1 - {{f}^{2}}} }}$ и собственных значений ${{{{\omega }}}_{n}}\left( k \right) = \sqrt {\frac{{{{k}^{2}} + {{f}^{2}}{{n}^{2}}}}{{{{f}^{2}} + {{n}^{2}}}}} $. Тогда, используя соотношение

можно получить выражение для возвышения изопикн в виде

Внутренний интеграл по переменной $\omega $ вычисляется с помощью теоремы о вычетах, при этом контур интегрирования необходимо сместить в область $\operatorname{Im} \omega > 0$. Тогда, замыкая его в нижнюю полуплоскость, и учитывая полюса ${{\omega }} = \pm {{{{\omega }}}_{n}}\left( k \right)$, получаем при $t > 0$ следующее выражение в виде суммы мод

3. Асимптотики решений. Далее будет рассматриваться отдельная волновая мода, индекс n опускается. Перейдем к полярным координатам: $\nu = k\sin \psi $, $\mu = x\cos \psi $, $x = r\cos \alpha $, $y = r\sin \alpha $, и проинтегрируем (2.5) по переменной ${{\psi }}$

Заменим в выражении (3.1) функцию Бесселя ${{J}_{0}}\left( {kr} \right)$ на ее асимптотику при $kr \gg 1$: ${{J}_{0}}\left( {kr} \right) \approx \sqrt {\frac{2}{{\pi kr}}} \cos \left( {kr - \frac{\pi }{4}} \right)$. В результате можно получить

Далее будем рассматривать асимптотику слагаемых ${{I}^{ \pm }}$ при больших значениях $t$ и $V = {\text{const}}$, то есть в точке, движущейся в радиальном направлении со скоростью V. Поскольку ${{\omega }}\left( k \right)$ – монотонно возрастающая функция, то фазовая функция $kV + {{\omega }}\left( k \right)$ не имеет стационарных точек на действительной оси, следовательно интеграл ${{I}^{ + }}$ экспоненциально мал при $t \to \infty $. Обозначим далее: ${{\gamma }}\left( k \right) = kV - {{\omega }}\left( k \right)$, $K = f\sqrt {\frac{{ - 1 + \sqrt {1 + 3{{f}^{{ - 2}}}} }}{3}} $ – значение волнового числа, при котором достигается максимум групповой скорости отдельной волновой моды, и через ${{V}_{*}} = \omega {\kern 1pt} '\left( k \right)$ – величину этого максимума. Тогда фазовая функция ${{\gamma }}\left( k \right)$ интеграла ${{I}^{ - }}$ при $0 < V < {{V}_{*}}$ имеет две стационарные точки на действительной оси: $~{{k}_{2}} < K < {{k}_{1}}$. Главный член асимптотики ${{I}^{ - }}$ определяется вкладом этих точек, и может быть вычислен с помощью метода стационарной фазы. В результате можно получить

Асимптотики (3.3) становятся непригодными при $V \to {{V}_{*}}$, то есть вблизи фронта каждой волновой моды, где стационарные точки сливаются друг с другом, и, соответственно, $\gamma {\kern 1pt} ''\left( k \right) \to 0$. Для нахождения асимптотики интеграла ${{I}^{ - }}$ в окрестности волнового фронта (локальной асимптотики) отдельной волновой моды необходимо разложить амплитудную и фазовую функции в ряды вблизи при $k \approx K$, ограничиваясь для амплитуды одним членом, и для фазы – тремя

В результате, заменяя в (3.2) нижний предел интегрирования на $ - \infty $, можно получить

Интеграл (3.5) выражается через функцию Эйри [18, 19]

В результате выражение для локальной асимптотики отдельной моды возвышения изопикн имеет вид

Таким образом, при больших временах поле отдельной моды вблизи волнового фронта (переходной зоны), имеет порядок малости $O\left( {{{t}^{{ - 1/3}}}} \right)$, то есть в ${{t}^{{1/6}}}$ раз больше, чем за фронтом. Ширина (временной интервал) волнового фронта (переходной зоны) каждой моды $T$ определяется условием, чтобы аргумент функции Эйри в (3.6) имел порядок единицы: T ≈ $\sqrt {\gamma {\kern 1pt} '''\left( K \right)} {{\left( {\gamma {\kern 1pt} '\left( K \right)} \right)}^{{ - 3/2}}}$. Асимптотика (3.6) непригодна вдали от волнового фронта отдельной моды.

Построим асимптотику, которая в окрестности фронта совпадает с (3.6), а вдали от волнового фронта с выражением (3.3). Для этого необходимо выполнить регулярную замену переменных $k = k\left( s \right)$, переводящую фазовую функцию ${{\gamma }}\left( k \right) = kV - {{\omega }}\left( k \right)$ интеграла ${{I}^{ - }}$ в новую функцию $\tau \left( s \right) = C - \sigma s$ + ${{s}^{3}}{\text{/3}}$, имеющую, как и ${{\gamma }}\left( k \right)$, две стационарные точки. Таким образом

При этом стационарной точке ${{k}_{1}}$ будет отвечать точка ${{s}_{1}} = \sqrt \sigma ,$ а стационарной точке ${{k}_{2}}$ – точка ${{s}_{2}} = - \sqrt {{\sigma }} $. Тогда из (3.7) находим

В результате подстановки (3.7) интеграл ${{I}^{ - }}$ преобразуется к виду

где $P$ – образ точки $k = 0$ при отображении, обратном к $k = k\left( s \right)$. Далее, следуя общим принципам построения равномерных асимптотик, функцию $G\left( s \right)$ разложим по степеням $({{s}^{2}} - \sigma )$ [17, 20]

Ограничиваясь главными членами разложения, можно получить

Тогда при $s = \pm \sqrt {{\sigma }} $ имеем

Подставляя главные члены разложения в (3.7) и заменяя нижний предел интегрирования P на $ - \infty $ можно получить

Интеграл (3.9) выражается через функцию Эйри и ее производную [18, 19]

Асимптотика (3.10) является равномерной по параметру V при $t \to \infty $. Чтобы показать, что равномерная асимптотика (3.10) переходит в окрестности волнового фронта в локальную (3.6) необходимо решить уравнение $\gamma {\kern 1pt} '\left( k \right) = 0~$ в приближении (3.4). В результате можно получить

При малых значениях ${{k}_{{1,2}}} - K$ имеем: $C = {{\gamma }}\left( K \right)$, $\sigma = - \gamma {\kern 1pt} '\left( K \right){{\left( {\frac{2}{{\gamma {\kern 1pt} '''\left( K \right)}}} \right)}^{{1/3}}}$, $G\left( {\sqrt \sigma } \right)$ – ‒ $G\left( { - \sqrt \sigma } \right)$ = $2G\left( 0 \right)$ = $F\left( K \right){{\left( {\frac{2}{{\gamma {\kern 1pt} '''\left( K \right)}}} \right)}^{{1/3}}}$. Подставляя эти выражения в (3.10) и пренебрегая слагаемыми, содержащими производную функции Эйри (поскольку вблизи фронта эти слагаемые имеют более высокий порядок малости) получим в итоге локальную асимптотику (3.6). Равномерная асимптотика (3.10) при больших значениях $t$ и ${{\sigma }}$, то есть при ${{\sigma }}{{t}^{{2/3}}} \to \infty $ переходит в неравномерную асимптотику стационарной фазы (3.3). Действительно, воспользовавшись соответствующими асимптотическими разложениями функции Эйри и ее производной при больших отрицательных значениях аргумента в виде: ${\text{Ai}}\left( { - x} \right)$ ≈ $\frac{{{{x}^{{ - 1/4}}}}}{{\sqrt \pi }}\sin \left( {\frac{3}{2}{{x}^{{2/3}}} + \frac{\pi }{4}} \right)$, ${\text{Ai}}{\kern 1pt} '\left( { - x} \right)$ ≈ $ - \frac{{{{x}^{{1/4}}}}}{{\sqrt \pi }}\cos \left( {\frac{3}{2}{{x}^{{2/3}}} + \frac{\pi }{4}} \right)$, можно показать, что оба слагаемых в (2.10) имеют один порядок малости $O\left( {{{t}^{{1/2}}}} \right)$. Таким образом локальная асимптотика (3.6) и неравномерная асимптотика (3.3) являются частными случаями равномерной асимптотики (3.10), что является основным результатом работы.

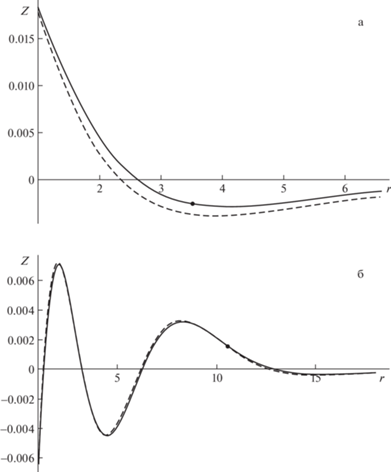
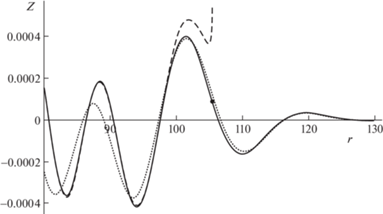
На рис. 1, 2 представлены результаты расчетов первой моды возвышения ${{\xi }}$ для следующих значений безразмерных параметров: $q = 1$, $f = 0.2$, $z = - 2$, ${{z}_{0}} = - 1$. Сплошная линия на всех рисунках – точное решение, точка – положение волнового фронта. Штриховая линия на рис. 1 – равномерная асимптотика (3.10). На рис. 2 штриховая линия – приближение стационарной фазы (3.3), пунктирная линия – локальная асимптотика (3.6). Численные расчеты показывают, что на расстояниях порядка толщины слоя жидкости и на временах порядка нескольких периодов Брента–Вяйсяля равномерная асимптотика с достаточной степенью точности описывает точное решение. Локальная асимптотика совпадает с точным решением на масштабах не более первой полуволны Эйри. Вдали от волнового фронта приближение стационарной фазы хорошо описывает точное решение.

Заключение. Построенные в работе равномерные асимптотические решения позволяют описать амплитудно-фазовые характеристики дальних полей внутренних гравитационных волн от импульсного локализованного источника возмущений во вращающейся как целое стратифицированной среде конечной толщины как вблизи, так и вдали от волновых фронтов отдельной волновой моды. Полученные результаты описывают характер асимптотического поведения волновых пакетов при больших временах и на большом удалении от источника волн. В частности, асимптотический анализ показывает затухание амплитуды волны как корня квадратного от времени за исключением особых случаев вырождения дисперсионного соотношения – обращения в нуль второй производной дисперсионной зависимости. Естественное решение проблемы вырождения, включение в анализ высших дифференциалов дисперсионной зависимости приводит к решению в терминах функции Эйри и ее производной, а также к более медленному дисперсионному затуханию амплитуды волны как корня третьей степени от времени.

Наибольший выигрыш при использовании данного подхода можно получить при исследовании эволюции волновых пакетов, возбуждаемых распределенными в пространстве возмущениями, так как, используя операцию свертки, построенные в работе асимптотики позволяют аналитически рассчитывать дальние волновые поля от нелокальных источников возмущений различной физической природы в стратифицированных вращающихся средах. Полученные асимптотики дальних полей дают возможность не только эффективно рассчитывать основные характеристики волновых полей, но и проводить качественный анализ получаемых решений. Асимптотические результаты с различными значениями входящих в них физических параметров позволяют провести оценку характеристик пакетов внутренних гравитационных волн, наблюдаемых в реальных океанических условиях. Такие волновые картины полей могут наблюдаться при дистанционном зондировании, наблюдении и измерениях внутренних гравитационных волн, возбуждаемых различными источниками возмущений в природных (океан, атмосфера Земли) и искусственных вращающихся стратифицированных средах.

Работа выполнена за счет гранта РНФ № 23-21-00194.